Abstract
Due to the lack of signal from solid bone in normal MR sequences for the purpose of MR-based attenuation correction, investigators have proposed using the ultrashort echo time (UTE) pulse sequence, which yields signal from bone. However, UTE-based segmentation approach might not fully capture the intra- and inter-subject bone density variation, which will inevitably lead to bias in reconstructed PET images. In this work, we investigated using the Water- And fat-Suppressed proton Projection Imaging (WASPI) sequence to obtain accurate and continuous attenuation for the bones. This approach is capable to account for intra- and inter-subject bone attenuation variations. Using data acquired from a phantom, we have found that that attenuation correction based on WASPI sequence is more accurate and precise when compared to either conventional MR attenuation correction or UTE based segmentation approaches.
Keywords: PET-MR, attenuation correction, bone imaging
1. Introduction
PET-MR is a hybrid imaging modality that has generated substantial interest in recent years. This marriage of two modalities with very different physics allows the development of many novel synergistic techniques and applications including MR-assisted PET motion correction (Fürst et al., 2015; Polycarpou et al., 2014; Huang et al., 2014; Fayad et al., 2014; Petibon et al., 2014; Bickell et al., 2014), MR-assisted partial volume correction (Yan et al., 2015; Bickell et al., 2014; Wang and Fei, 2012), PET guided MR spectroscopy (Zhang et al., 2014), and PET-MR joint reconstruction (Knoll et al., 2014).
One of the biggest hurdles of quantitative PET-MR is accurate PET attenuation correction (AC), (especially for bone (Wagenknecht et al., 2013; Keereman et al., 2011; Samarin et al., 2012).j In stand-alone PET, the attenuation maps (μ-maps) are obtained by a separate transmission scan using an external source. In PET-CT, the attenuation coefficients are measured with X-rays (energy often in the neighbourhood of 100 keV) and remapped to estimate the attenuation coefficients for 511 keV photons. For PET-MR, the PET μ-map typically needs to be derived from the MR images. The problem is that the attenuation coefficient of the photons depends on the electron density, but clinical 1H MR contrast arises from proton spin density and spin-spin/spin-lattice relaxation. The standard approach is to segment an MR image volume into different tissue classes and then assign the corresponding attenuation coefficients to them (Le Goff-Rougetet et al., 1994; Zaidi et al., 2003; Zaidi et al., 2007; Beyer et al., 2008; Catana et al., 2010; Berker et al., 2012; Ouyang et al., 2013). (Some earlier works also investigated mapping MR to CT data using histogram matching (Beyer et al., 2008). Current commercial PET-MR scanners use 3-class (air, lungs, soft tissues) (Schulz et al., 2011), 4-class (air, lungs, fat and other soft tissues) (Martinez-Möller et al., 2009), or 4-class with continuous fat/water (Wollenweber et al., 2013b) segmentation method. (Previous patient studies reported that the standardised uptake value (SUV) bias using 4-class MR-based segmentation is generally less than 10% for most of the lesions, however these lesions are located within soft tissue. (Martinez-Möller et al., 2009; Steinberg et al., 2010; Hofmann et al., 2011; Eiber et al., 2011; Keereman et al., 2011; Drzezga et al., 2012). [For regions inside or near bones, the SUV values can be considerably underestimated using the segmentation approaches not taking bone into consideration (Ouyang et al., 2013; Keereman et al., 2011; Samarin et al., 2012).
In the context of MR derived attenuation maps, investigators have previously proposed atlas-based techniques (Poynton et al., 2014; Wollenweber et al., 2013a) and ultrashort/zero echo time (UTE or ZTE) pulse sequence based segmentation techniques (Keereman et al., 2010; Berker et al., 2012; Navalpakkam et al., 2013; Delso et al., 2015). Although atlas-based μ-maps can provide continuous bone attenuation, such approaches are generally not feasible in practice because anatomy-based registration other than brain is extremely challenging. Moreover, such approaches do not capture the inter-subject bone density variation. The UTE approach can identify bones in the body, but it cannot be used to measure the bone density variation. Bone density in Hounsfield units (HU) can vary from 700 for cancellous bone to 3000 for dense bone (De Vos et al., 2009). Without capturing the intra- and inter-subject bone density variation, a UTE-based μ-map will inevitably lead to bias in reconstructed PET images. Besides UTE/ZTE types of sequences, SWIFT (Sweeping Imaging using Fourier Transforms) (Wang et al., 2014; Idiyatullin et al., 2006) is also capable of visualizing structures with very short T2 or T2* such as bones.
Attenuation maps can also be derived from PET emission data (Keereman et al., 2013). This type of technique includes techniques that simultaneously reconstruct the activity and attenuation distributions such as MLAA (Maximum Likelihood reconstruction of Attenuation and Activity) (Censor et al., 1979; Nuyts et al., 1999; Ahn et al., 2013), and techniques that reconstruct the attenuation map with some a priori conditions (Welch et al., 1998; Bromiley et al., 2001). The former techniques suffer from crosstalk between attenuation and activity estimates, which can be alleviated by using Time-Of-Flight (TOF) reconstruction (Defrise et al., 2012), and no visualization of non-emitting objects. The latter class of techniques are not yet stable without attenuation measurements (Bromiley et al., 2001).
In this work, we investigated the possibility of using the Water- And fat-Suppressed proton Projection Imaging (WASPI) sequence to obtain an accurate and continuous bone μ-map which should account for intra- and inter-subject bone attenuation variation. Similar techniques capable of short T2* imaging have previously been used in studying tendon microstructure (Han et al., 2014), bone water content (Li et al., 2015), and detection of iron oxide nanoparticles (Wang et al., 2014), etc.
2. Methods
2.1 WASPI sequence
WASPI (Wu et al., 2003) is a 3D radial zero-TE (a conventional terminology describing sequences with 0 effective TE) pulse sequence with fat and water suppression leaving signal only from very short T2 protons, primarily the immobile proteins and tightly bound water in the bone matrix. Previous work (Cao et al., 2008) has shown that the signal intensity is proportional to bone matrix density, which for normally mineralized bone is in turn proportional to bone mineral density. As shown in Figure 1a, the WASPI sequence first saturates the fluid (molecularly mobile) tissue constituents with chemical shift selective radiofrequency (RF) pulses at the water and fat frequencies; each saturation pulse is followed by a crusher gradient pulse to dephase the fluid signals. Then a fixed-amplitude gradient is turned on, and a very brief (10 μs in this work) rectangular hard RF pulse covering the full bandwidth of the field of view is applied, eliciting a free induction decay (FID) which is sampled to yield a single radial line in k-space. The direction of the fixed amplitude gradient is advanced to successive orientations to cover a spherical volume of k-space. The acquired data can be reconstructed using a regridding algorithm (O'Sullivan, 1985; Jackson et al., 1991). Figure 1c shows the chemical selective water and fat saturation pulse module. The pulse module is comprised of 4 π/2 RF pulses and the corresponding dephasing gradients. The timing and gradient moments are carefully chosen to avoid echo formation (Wu et al., 2010).
Figure 1.
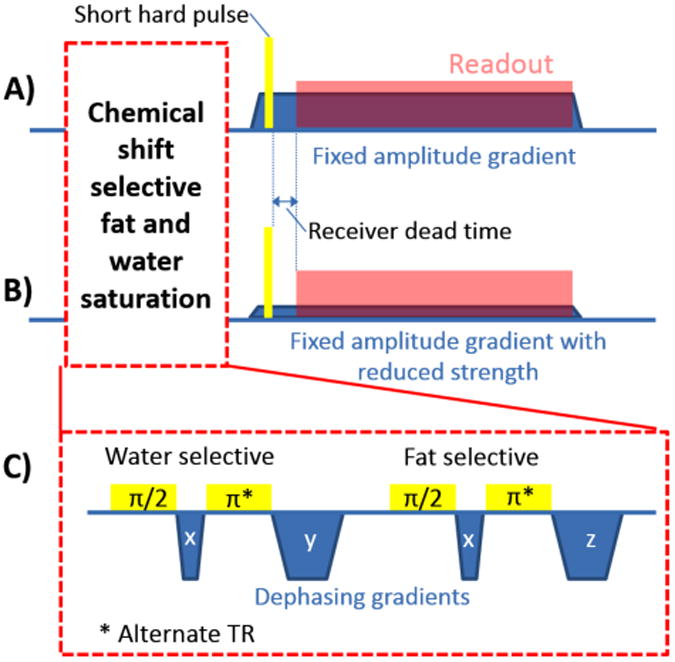
The schematic plot of the WASPI pulse sequences used to acquire (A) the main data set and (B) the second data set for finer sampled k-space centre. (C) The chemical shift selective fat and water saturation.
Special attention was focused on minimizing the receiver dead time between the end of the hard RF pulse and the start of sampling in order to accurately acquire the centre of k-space, which is essential for obtaining quantitatively accurate bone density. To achieve a fast switch from transmitting mode to receiving mode, a home-made cylindrical transmit-receive quadrature RF coil was used (inner diameter = 8.8 cm). A special high speed transmit/receive switch based on a quadrature hybrids and standard silicon switching diodes (rather than PIN diodes) was used to minimize the transmit/receive switching time, reducing it from the order of 100-200 μs to about 10 μs (Wu et al., 2010). To further improve the fidelity of k-space data near the origin, an additional acquisition of a small number of k-space radii are acquired with a reduced gradient strength as shown in Figure 1b, which enables central k-space points to be acquired at times further away from the RF pulse and its switching transients. The RF coil former and coaxial cables were made of Teflon (poly-[tetrafluoroethylene]) to minimize background proton signals from these components which would otherwise appear in the WASPI images.
By completely eliminating echoes, slice selection and time delays following the RF excitation pulse, the WASPI sequence enables the highest fidelity acquisition of very short-T2 signals.
In this work, the gradient strength was fixed at 18.35 mT/m for the main data set, 15972 radii were acquired with 128 points sampling each radius, the bandwidth was 781 Hz/pixel, and the repetition time (TR) was 28 ms. For WASPI, the effective TE is 0. A second data set (44 radii) was acquired with a lower gradient (4.59 mT/m) to recover the data points lost in the receiver dead time. The field of view was 128×128×128 mm3 with 1 mm isotropic spatial resolution. The acquisition time of the non-optimized WASPI acquisition was 7.5 minutes.
2.2 Phantom experiment
In order to obtain realistic bone images, a pig tibia was placed inside a cylindrical glass container 8.5 cm in diameter (Figure 2). The container was then filled with 5% gelatin containing radioactive 18F mimicking soft tissue. The phantom was first scanned on a Siemens Biograph 64 True Point PET-CT scanner (Siemens Healthcare, Erlangen, Germany). PET list-mode acquisition was performed for 10 minutes. CT was conducted with 120 kVp, 66 mAs and reconstructed with 1.37×1.37 mm2 in-plane resolution and 1 mm slice thickness.
Figure 2.
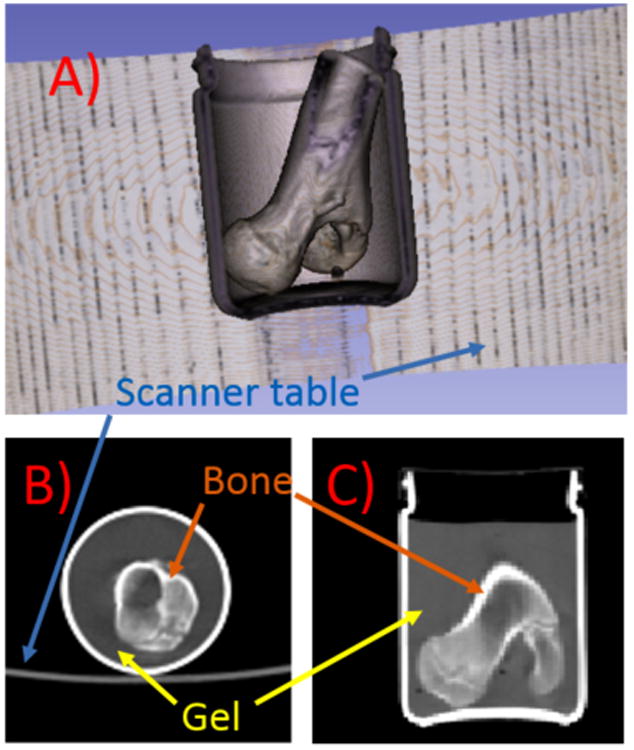
(A) 3D rendering of the phantom CT data with signal from gel removed, (B) a transverse slice and (C) a coronal slice of the CT volume. The 3D rendering was performed using 3D Slicer.
After the PET-CT scan, the MR acquisition was performed on a Siemens Tim Trio 3T MR scanner (Siemens Healthcare, Erlangen, Germany) using WASPI and conventional gradient recalled echo (GRE) imaging. The GRE images were obtained directly from the scanner as DICOM files and the WASPI images were reconstructed using a dedicated in-house reconstruction code from raw measurement data.
2.3 μ-map generation and PET reconstruction
In this work, four different AC strategies were used:
CTAC: AC based on the acquired CT images. The CT image volume was processed using Siemens proprietary software to convert to a reference μmap, which is the same as is done on a clinical PET-CT. We take the CTAC as the reference strategy.
Conventional MRAC: This is the standard MR AC strategy currently available on the Siemens Biograph mMR. In this strategy, bone composition information is not acquired and all bones are assumed to be soft tissue (linear attenuation coefficient μ = 0.095 cm-1). Since glass is not visible on MR, in this study the μ-map of the glass container extracted from the reference μ-map was added to the conventional MRAC μ-map.
WASPI AC: This is the proposed AC strategy using WASPI MR sequence to obtain accurate bone density. The WASPI MR signal intensity was mapped to linear attenuation coefficients via a calibrated linear mapping function. In this study, the linear function was determined by comparing the WASPI MR signal intensity and the reference μmap of two manually drawn regions of interest (ROIs) in the bone. One of the ROIs was selected in the cortical bone, which is highly attenuating, and the other was selected in the spongy bone with lower attenuation coefficient. Other calibration techniques will be further discussed in the Discussion section. Similar to conventional MRAC, the μ-map of the glass container was added separately.
AC with fixed bone attenuation (ACFB): In this approach, the bone density variation in the WASPI AC μ-map was ignored, and all pixels were assigned a linear attenuation coefficient μ = 0.120 cm-1 (Keereman et al., 2010; Ouyang et al., 2013). This is similar to many UTE based segmentation approaches (Keereman et al., 2010; Berker et al., 2012).
For all four μmaps corresponding to these AC strategies, the voxel size was 2.67×2.67×2 mm3. One PET image volume was obtained with each μ-map using the same PET list-mode data. The 3D ordered subset expectation maximization (3D-OSEM) reconstruction was performed using Siemens proprietary software with random, scatter and point spread function corrections. Other reconstruction parameters include: number of iterations = 3, number of subsets = 21. All PET images were smoothed using a Gaussian filter with full-width-at-half-maximum (FWHM) = 2 mm.
3. Results
Figure 3 shows a transverse slice of the CT volume and the corresponding slices of the GRE MR and WASPI MR image volumes. The conventional GRE sequence provides good contrast for soft tissue and bone marrow but no signal from the bone. In contrast, the WASPI MR image exhibits signal from the bone but not soft tissue. More importantly, as can be seen in the figure, the WASPI MR signal intensity is higher for the region of the bone with higher CT HU value, hence more attenuating. Quantitative comparison between the CT HU values and WASPI MR signal intensities was also performed with only bone voxels extracted from the 3D image volumes. The linear correlation coefficient was found to be r = 0.78.
Figure 3.
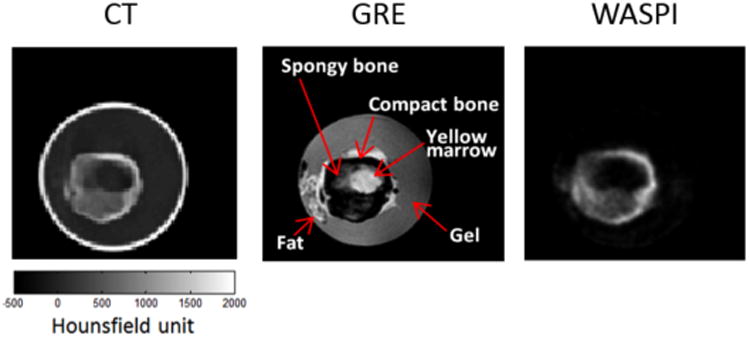
A transverse slice of the CT volume compared with the corresponding slice acquired using a conventional GRE pulse sequence and WASPI. The signal intensity of the bone in the WASPI sequence is similar to the corresponding CT HU values. Note that the phantom is in a glass container, which has no MR signal but high HU values.
Since the interest is to use WASPI MR for accurate bone AC, the μ-maps were further derived from the CT and the WASPI MR images for comparison. Figures 4A and 4B show the same slice of μ-maps derived from the WASPI MR and the CT. These two μ-maps visually have excellent agreement, while the conventional MRAC μ-map does not account for the higher attenuation of the bone as shown in Figure 4C. To quantify the agreement of the WASPI μ-map and the CT-derived μ-map, the joint histogram of the bone μ values in the WASPI AC μ-map and CTAC μ-map is shown in Figure 4D. The linear attenuation coefficients of each voxel of the bone have excellent correlation between these two μ-maps. The linear correlation coefficient is r = 0.86.
Figure 4.
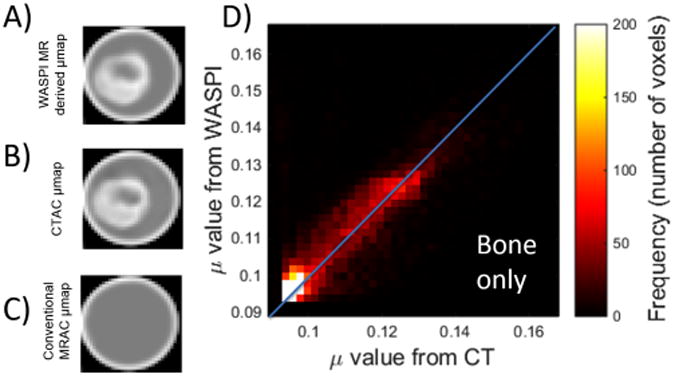
The μ-map generated from (A) the WASPI MR images compared with (B) the CTAC μ-map and (C) the conventional MRAC μ-map. (D) The joint histogram of the linear attenuation coefficient (μ values) of the bone obtained from WASPI and CT. The linear correlation coefficient is r = 0.86.
Attenuation corrected PET reconstruction was performed on the same PET data set with CTAC, WASPI AC and conventional MRAC μ-maps. An additional μ-map ACFB was also included for the reconstruction. Figure 5A shows a transverse slice of the CTAC μ-map as the reference. The PET image reconstructed with CTAC is shown in Figure 5B and Figure 5C in linear and log scales, respectively. Since the radioactivity was only added to the gel, there is little signal inside the bone. Due to the difficulty in visually comparing the reconstructed images, the bias maps are shown instead in Figures 4D, 4E and 4F. These maps show the bias of the PET images reconstructed from the same PET raw data with conventional MRAC, WASPI AC, and ACFB with CTAC as the reference. It can be seen that conventional MRAC leads to large underestimation in the bone, while the bias is considerably reduced in WASPI AC images. When the bone attenuation is set to a fixed value rather than continuous, larger error can be observed comparing to WASPI AC, but still considerably smaller than the error of conventional MRAC.
Figure 5.
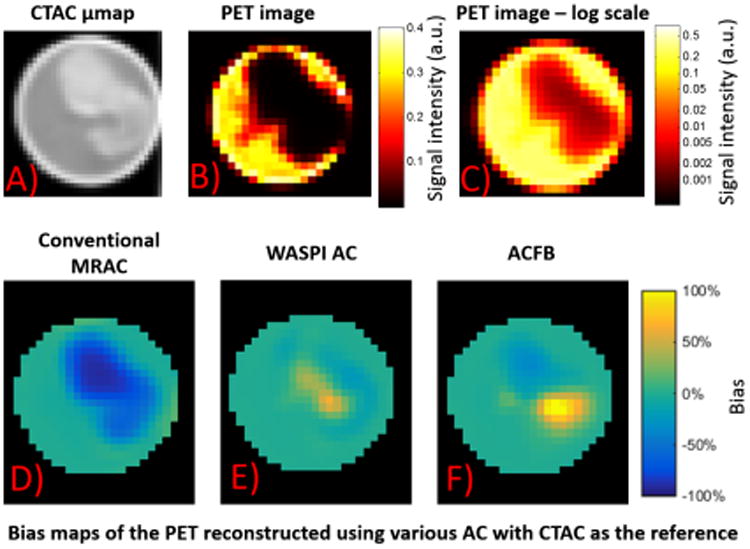
(A) A transverse slice of the CTAC μ-map of the phantom, and the corresponding PET image with CTAC in (B) linear and (C) log scales. The bias map of the slice of the PET image volumes with (D) conventional MRAC, (E) WASPI AC and (E) ACFB, using the PET image volume reconstructed with CTAC as the reference.
The above observation is further confirmed in Figure 6. This figure shows the joint histograms of the PET activity of all the voxels in PET reconstructed with CTAC compared with PET reconstructed with conventional MRAC, WASPI AC and ACFB. It can be seen that among the three PET images reconstructed with various MR-based attenuation correction strategies, WASPI AC provides the best agreement with the image reconstructed with CTAC. The image using ACFB yields some overestimation (arrowhead). However, it is still considerably more accurate than the image reconstructed with conventional MRAC, in which large number of voxels suffers from overestimation (arrow). Table 1 further quantifies these errors. WASPI AC provides the smallest bias and standard deviation. WASPI AC and ACFB yield significantly more accurate PET quantitation, and the difference between these two strategies is small when considering the entire phantom. However, when only studying the bone, WASPI provides significantly better precision and accuracy.
Figure 6.
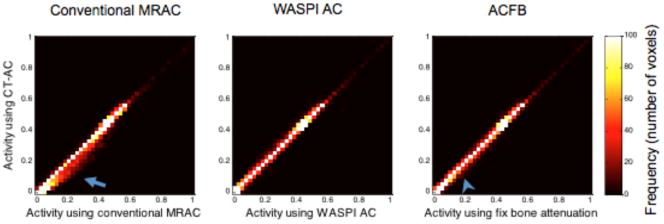
The joint histograms of the PET activities of all the voxels in the PET image volume reconstructed with conventional MRAC, WASPI AC and ACFB compared to the image volume reconstructed using CTAC. The arrow and arrowhead point to the biased pixels, showing the overestimation caused by conventional MRAC and ACFB.
Table 1.
The mean and standard deviation of the errors of each AC strategy in the entire phantom or in the bone only. CTAC was used as the reference.
| Conventional MRAC | WASPI AC | ACFB | |
|---|---|---|---|
| Entire phantom | -14.3%± 25.2% | 1.0% ± 10.07% | -2.77%± 12.43% |
| Bone only | -37.8%± 30.71% | 3.0%± 15.39% | -9.7%± 24.4% |
4. Discussion
In this work, we showed that the WASPI MR signal of the bone correlates with the CT bone density. We used WASPI MR to generate a more accurate μ-map for attenuation correction. The PET images reconstructed with various AC strategies were studied. As demonstrated in Figure 5 and Table 1, WASPI and ACFB both outperform the conventional MRAC. However, when the region of interest is in the bone or close to the bone, accurate bone attenuation provided by WASPI MR could significantly improve the accuracy and precision of the PET estimates.
Due to the non-quantitative nature of MR imaging, calibration is needed for converting the WASPI MR signal to bone density for AC purposes. One limitation of this work is that the calibration was performed using two ROIs in the bone with different bone densities which were compared with the CT-derived reference μ-map. Its accuracy can be further improved by using histogram mapping (Beyer et al., 2008). However, in PET-MR studies, CT images will not be available in practice. The calibration can be performed by including a series of bone and/or synthetic specimens of known density in the field of view to obtain a calibration function mapping WASPI signal intensity to true density as was done in (Cao et al., 2008). Alternatively, similar to absolute quantification in MR spectroscopy (Thulborn and Ackerman, 1983), absolute quantification of immobile proteins in the bone matrix might be obtained by calibrating the proton signal intensity from a reference MR scan obtained without water and fat suppression. The bone density can be derived from this information and the WASPI signal intensity. The methodology of signal calibration warrants further research and is beyond the scope of this work.
As can be seen in Figure 3, the WASPI MR image is relatively noisy under the acquisition conditions used in this work. This is partly responsible for the relatively lower correlation coefficient (r=0.78) between the CT HU values and WASPI MR signal intensity, compared to the correlation coefficient (r=0.86) between the linear attenuation coefficients derived from CTAC and WASPI AC. The voxel size of the WASPI MR acquisition is 1×1×1 mm3 in this work, which is significantly finer than the spatial resolution of the PET camera (∼4×4×4 mm3). The resolution of the μ map in the Biograph mMR is 2.67×2.67×2mm3, as a result, 8 times higher SNR can be expected if the WASPI resolution is reduced to 2.67×2.67×2.67mm3. However, this is assuming the same FOV was used. In reality, the FOV needs to be increased approximately by factors of 2.5 and 4 for head and body imaging, respectively. This also leads to higher thermal noise due to a larger mass visible to the RF coil. Also, different RF coils with different properties from the one shown in this preliminary work need to be used for larger FOV. Moreover, greater RF power is required to uniformly excite a larger FOV with a larger RF coil. The B1 generated by the body RF coils is insufficient for excitation pulses on the order of 10 μs. A head transmit coil may be practical in this application.
Another limitation of the proposed technique is its requirement for a special high speed transmit/receive switch. Silicon diode switches (which are not actively driven by control signals from the scanner) respond directly to the presence of transmitter power, and operate at very high speed. The actively controlled PIN diode-based transmit/receive switches typically used in clinical MRI scanners can handle higher levels of RF power and may have superior on/off ratios, but usually switch far more slowly (on the order of 100 μs), although they can be speeded up with proper design. Using silicon diode switches, or eliminating switches entirely and depending on the transmit/receive isolation of a quadrature hybrid, will shorten the receiver recovery time. The same modification needs to be made to other coils in order to achieve a similar transit/receive switching time. Other limitations on the transmit/receive switching time are the electronic recovery times of the amplifiers in the receiver chain, the Q of the RF coil (high Q coils ring for a long time following the end of the RF pulse), and the nature of the digital signal processing of the scanner (digital filters, like analog filters, will ring following the huge signal spike accompanying the RF pulse).
In this preliminary work, the scan time of the phantom was approximately 8 minutes, which is still too long to be used in a clinical setting. The acquisition time can be reduced by using fewer k-space lines which sacrifices image SNR and spatial resolution. This can be utilized with the help from compressed sensing reconstruction techniques since bone images are intrinsically sparse in the image domain. Further study investigating the trade-off is necessary. In this work, TR = 28 ms was used, which is significantly longer than the ∼3 ms TR for most UTE sequences. The reason for the long TR is to allow full suppression of water and fat signal before the acquisition of each line. Acquisition time can also be reduced if TR can be reduced, such as using a more time-efficient water and fat suppression, or acquiring several k-space lines after each suppression (Wiesinger et al., 2015).
Recently, some advancement on attenuation correction using UTE and ZTE sequences has been reported for head PET/MR. A R2* based continuous attenuation correction strategy using dual-echo UTE was presented (Juttukonda et al., 2015). In that study, the R2* values were estimated from two UTE images with “TE” = 70 μs and 2.46 ms. Because of low SNR, an arbitrary scaling of the short TE image was required to avoid negative R2* estimates, and a 5 parameter fit to an arbitrary function was required to relate this estimated R2* to bone density. As a result, quantitation accuracy for T2* (T2* = 1/R2*) values in the magnitude of 100 μs or less, which corresponds to compact bone with high attenuation effect, will suffer from low SNR. WASPI, which is a zero echo time sequence using short hard pulse excitation, is expected to be superior, especially for dense bone, since it samples data at the earliest possible time after the RF pulse at full gradient. UTE either utilizes ramp sampling or begins sampling at a considerable delay following the end of the RF excitation pulse. Also, a promising proton-density-weighted ZTE segmentation approach has been shown to yield better bone depiction than previously reported methods exploring T2 relaxation differences (Delso et al., 2015; Wiesinger et al., 2015). A similar correlation between ZTE MR signal intensity and CT Hounsfield units was also observed in that work. However, misclassification for regions with dense bone due to insufficient MR signal was also reported (Delso et al., 2015). WASPI is expected to perform better for dense bones since, unlike simple ZTE (which does not suppress fluid signals), WASPI provides better visualization of denser bones. In principle, ZTE and WASPI should yield the same signal for dense bones, but WASPI suppresses the fluid signals and make the dense bones more visible. In practice, the water and fat suppression of WASPI attenuates some of the dense bone signal, so ZTE should yield the strongest dense bone signal.
5. Conclusion
This work provides preliminary evidence in a phantom for the use of WASPI MR to provide continuous bone attenuation for PET-MR attenuation correction, which is capable of accounting for intra- and inter-subject bone density variation. Additional studies in animal and human subjects are required to further assess the performance of WASPI MR.
Acknowledgments
This research was supported in part by NIH grants R03-MH106994, R21-EB012326, R01-CA165221, R01-HL110241, R01-HL118261, the Athinoula A. Martinos Center for Biomedical Imaging, the Imaging Sciences Training Program at the National Institutes of Health, and the Center for Functional Neuroimaging Technologies (funded by NIH grant P41-EB015896).
References
- Ahn S, Shanbhag D, Qian H, Kaushik S, Thiruvenkadam S, Manjeshwar R. Improved attenuation correction in PET/MRI by combining MR image segmentation and joint estimation approaches. Journal of Nuclear Medicine. 2013;54:150. [Google Scholar]
- Berker Y, Franke J, Salomon A, Palmowski M, Donker HC, Temur Y, Mottaghy FM, Kuhl C, Izquierdo-Garcia D, Fayad ZA. MRI-based attenuation correction for hybrid PET/MRI systems: a 4-class tissue segmentation technique using a combined ultrashort-echo-time/Dixon MRI sequence. Journal of Nuclear Medicine. 2012;53:796–804. doi: 10.2967/jnumed.111.092577. [DOI] [PubMed] [Google Scholar]
- Beyer T, Weigert M, Quick H, Pietrzyk U, Vogt F, Palm C, Antoch G, Müller S, Bockisch A. MR-based attenuation correction for torso-PET/MR imaging: pitfalls in mapping MR to CT data. European Journal of Nuclear Medicine and Molecular Imaging. 2008;35:1142–6. doi: 10.1007/s00259-008-0734-0. [DOI] [PubMed] [Google Scholar]
- Bickell M, Koesters T, Boada F, Nuyts J. PET motion correction using MR-derived motion parameters. EJNMMI Physics. 2014;1:1–2. doi: 10.1186/2197-7364-1-S1-A53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bromiley A, Welch A, Chilcott F, Waikar S, McCallum S, Dodd M, Craib S, Schweiger L, Sharp P. Attenuation correction in PET using consistency conditions and a three-dimensional template. Nuclear Science, IEEE Transactions on. 2001;48:1371–7. [Google Scholar]
- Cao H, Ackerman JL, Hrovat MI, Graham L, Glimcher MJ, Wu Y. Quantitative bone matrix density measurement by water - and fat - suppressed proton projection MRI (WASPI) with polymer calibration phantoms. Magnetic Resonance in Medicine. 2008;60:1433–43. doi: 10.1002/mrm.21771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catana C, van der Kouwe A, Benner T, Michel CJ, Hamm M, Fenchel M, Fischl B, Rosen B, Schmand M, Sorensen AG. Toward implementing an MRI-based PET attenuation-correction method for neurologic studies on the MR-PET brain prototype. Journal of Nuclear Medicine. 2010;51:1431–8. doi: 10.2967/jnumed.109.069112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Censor Y, Gustafson DE, Lent A, Tuy H. A new approach to the emission computerized tomography problem: simultaneous calculation of attenuation and activity coefficients. Nuclear Science, IEEE Transactions on. 1979;26:2775–9. [Google Scholar]
- De Vos W, Casselman J, Swennen G. Cone-beam computerized tomography (CBCT) imaging of the oral and maxillofacial region: a systematic review of the literature. International journal of oral and maxillofacial surgery. 2009;38:609–25. doi: 10.1016/j.ijom.2009.02.028. [DOI] [PubMed] [Google Scholar]
- Defrise M, Rezaei A, Nuyts J. Time-of-flight PET data determine the attenuation sinogram up to a constant. Physics in medicine and biology. 2012;57:885. doi: 10.1088/0031-9155/57/4/885. [DOI] [PubMed] [Google Scholar]
- Delso G, Wiesinger F, Sacolick LI, Kaushik SS, Shanbhag DD, Hüllner M, Veit-Haibach P. Clinical Evaluation of Zero-Echo-Time MR Imaging for the Segmentation of the Skull. Journal of Nuclear Medicine. 2015;56:417–22. doi: 10.2967/jnumed.114.149997. [DOI] [PubMed] [Google Scholar]
- Drzezga A, Souvatzoglou M, Eiber M, Beer AJ, Fürst S, Martinez-Möller A, Nekolla SG, Ziegler S, Ganter C, Rummeny EJ. First clinical experience with integrated whole-body PET/MR: comparison to PET/CT in patients with oncologic diagnoses. Journal of Nuclear Medicine. 2012;53:845–55. doi: 10.2967/jnumed.111.098608. [DOI] [PubMed] [Google Scholar]
- Eiber M, Martinez-Möller A, Souvatzoglou M, Holzapfel K, Pickhard A, Löffelbein D, Santi I, Rummeny EJ, Ziegler S, Schwaiger M. Value of a Dixon-based MR/PET attenuation correction sequence for the localization and evaluation of PET-positive lesions. Eur J Nucl Med Mol Imaging. 2011;38:1691–701. doi: 10.1007/s00259-011-1842-9. [DOI] [PubMed] [Google Scholar]
- Fayad H, Schmidt H, Wuerslin C, Visvikis D. Non rigid respiratory motion correction in whole body PET/MR imaging. EJNMMI Physics. 2014;1:1–2. doi: 10.1186/2197-7364-1-S1-A73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fürst S, Grimm R, Hong I, Souvatzoglou M, Casey ME, Schwaiger M, Nekolla SG, Ziegler SI. Motion Correction Strategies for Integrated PET/MR. Journal of Nuclear Medicine jnumed. 2015;114:146787. doi: 10.2967/jnumed.114.146787. [DOI] [PubMed] [Google Scholar]
- Han M, Larson PE, Liu J, Krug R. Depiction of Achilles Tendon Microstructure In-Vivo Using High-Resolution 3D Ultrashort Echo-Time MRI at 7T. Investigative radiology. 2014;49:339. doi: 10.1097/RLI.0000000000000025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofmann M, Bezrukov I, Mantlik F, Aschoff P, Steinke F, Beyer T, Pichler BJ, Schölkopf B. MRI-based attenuation correction for whole-body PET/MRI: quantitative evaluation of segmentation-and atlas-based methods. Journal of Nuclear Medicine. 2011;52:1392–9. doi: 10.2967/jnumed.110.078949. [DOI] [PubMed] [Google Scholar]
- Huang C, Ackerman JL, Petibon Y, Normandin MD, Brady TJ, El Fakhri G, Ouyang J. Motion compensation for brain PET imaging using wireless MR active markers in simultaneous PET–MR: Phantom and non-human primate studies. NeuroImage. 2014;91:129–37. doi: 10.1016/j.neuroimage.2013.12.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Idiyatullin D, Corum C, Park JY, Garwood M. Fast and quiet MRI using a swept radiofrequency. Journal of Magnetic Resonance. 2006;181:342–9. doi: 10.1016/j.jmr.2006.05.014. [DOI] [PubMed] [Google Scholar]
- Jackson J, Meyer CH, Nishimura DG, Macovski A. Selection of a convolution function for Fourier inversion using gridding [computerised tomography application] Medical Imaging, IEEE Transactions on. 1991;10:473–8. doi: 10.1109/42.97598. [DOI] [PubMed] [Google Scholar]
- Juttukonda MR, Mersereau BG, Chen Y, Su Y, Rubin BG, Benzinger TL, Lalush DS, An H. MR-based attenuation correction for PET/MRI neurological studies with continuous-valued attenuation coefficients for bone through a conversion from R2* to CT-Hounsfield units. NeuroImage. 2015;112:160–8. doi: 10.1016/j.neuroimage.2015.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keereman V, Fierens Y, Broux T, De Deene Y, Lonneux M, Vandenberghe S. MRI-based attenuation correction for PET/MRI using ultrashort echo time sequences. Journal of nuclear medicine. 2010;51:812–8. doi: 10.2967/jnumed.109.065425. [DOI] [PubMed] [Google Scholar]
- Keereman V, Mollet P, Berker Y, Schulz V, Vandenberghe S. Challenges and current methods for attenuation correction in PET/MR. Magnetic Resonance Materials in Physics, Biology and Medicine. 2013;26:81–98. doi: 10.1007/s10334-012-0334-7. [DOI] [PubMed] [Google Scholar]
- Keereman V, Van Holen R, Mollet P, Vandenberghe S. The effect of errors in segmented attenuation maps on PET quantification. Medical physics. 2011;38:6010–9. doi: 10.1118/1.3651640. [DOI] [PubMed] [Google Scholar]
- Knoll F, Koesters T, Otazo R, Block T, Feng L, Vunckx K, Faul D, Nuyts J, Boada F, Sodickson DK. Simultaneous MR-PET Reconstruction Using Multi Sensor Compressed Sensing and Joint Sparsity. Proc Intl Soc Mag Reson Med. 2014;22:82. doi: 10.1186/2197-7364-1-S1-A26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Goff-Rougetet R, Frouin V, Mangin JF, Bendriem B. Segmented MR images for brain attenuation correction in PET. Proc SPIE 2167, Medical Imaging 1994: Image Processing. 1994;725 [Google Scholar]
- Li S, Ma L, Chang EY, Shao H, Chen J, Chung CB, Bydder GM, Du J. Effects of inversion time on inversion recovery prepared ultrashort echo time (IR - UTE) imaging of bound and pore water in cortical bone. NMR in Biomedicine. 2015;28:70–8. doi: 10.1002/nbm.3228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez-Möller A, Souvatzoglou M, Delso G, Bundschuh RA, Chefd'hotel C, Ziegler SI, Navab N, Schwaiger M, Nekolla SG. Tissue classification as a potential approach for attenuation correction in whole-body PET/MRI: evaluation with PET/CT data. Journal of nuclear medicine. 2009;50:520–6. doi: 10.2967/jnumed.108.054726. [DOI] [PubMed] [Google Scholar]
- Navalpakkam BK, Braun H, Kuwert T, Quick HH. Magnetic resonance-based attenuation correction for PET/MR hybrid imaging using continuous valued attenuation maps. Investigative radiology. 2013;48:323–32. doi: 10.1097/RLI.0b013e318283292f. [DOI] [PubMed] [Google Scholar]
- Nuyts J, Dupont P, Stroobants S, Benninck R, Mortelmans L, Suetens P. Simultaneous maximum a posteriori reconstruction of attenuation and activity distributions from emission sinograms. Medical Imaging, IEEE Transactions on. 1999;18:393–403. doi: 10.1109/42.774167. [DOI] [PubMed] [Google Scholar]
- O'Sullivan J. A fast sinc function gridding algorithm for Fourier inversion in computer tomography. Medical Imaging, IEEE Transactions on. 1985;4:200–7. doi: 10.1109/TMI.1985.4307723. [DOI] [PubMed] [Google Scholar]
- Ouyang J, Chun SY, Petibon Y, Bonab AA, Alpert N, El Fakhri G. Bias atlases for segmentation-based PET attenuation correction using PET-CT and MR. Nuclear Science, IEEE Transactions on. 2013;60:3373–82. doi: 10.1109/TNS.2013.2278624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petibon Y, Huang C, Ouyang J, Reese T, Kolnick A, Chen YL, El Fakhri G. Cardiac, respiratory motion and point spread function (PSF) compensation in simultaneous PET-MR: A cardiac sarcoma study. Journal of Nuclear Medicine. 2014;55:647. [Google Scholar]
- Polycarpou I, Tsoumpas C, King A, Marsden PK. Quantitative evaluation of PET respiratory motion correction using real-time PET/MR simulated data. EJNMMI Physics. 2014;1:1. doi: 10.1186/2197-7364-1-S1-A62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poynton CB, Chen KT, Chonde DB, Izquierdo-Garcia D, Gollub RL, Gerstner ER, Batchelor TT, Catana C. 2014 Probabilistic atlas-based segmentation of combined T1-weighted and DUTE MRI for calculation of head attenuation maps in integrated PET/MRI scanners. American journal of nuclear medicine and molecular imaging. 4:160. [PMC free article] [PubMed] [Google Scholar]
- Samarin A, Burger C, Wollenweber SD, Crook DW, Burger IA, Schmid DT, von Schulthess GK, Kuhn FP. PET/MR imaging of bone lesions-implications for PET quantification from imperfect attenuation correction. European journal of nuclear medicine and molecular imaging. 2012;39:1154–60. doi: 10.1007/s00259-012-2113-0. [DOI] [PubMed] [Google Scholar]
- Schulz V, Torres-Espallardo I, Renisch S, Hu Z, Ojha N, Börnert P, Perkuhn M, Niendorf T, Schäfer W, Brockmann H. Automatic, three-segment, MR-based attenuation correction for whole-body PET/MR data. European journal of nuclear medicine and molecular imaging. 2011;38:138–52. doi: 10.1007/s00259-010-1603-1. [DOI] [PubMed] [Google Scholar]
- Steinberg J, Jia G, Sammet S, Zhang J, Hall N, Knopp M. Three-region MRI-based whole-body attenuation correction for automated PET reconstruction. Nuclear medicine and biology. 2010;37:227–35. doi: 10.1016/j.nucmedbio.2009.11.002. [DOI] [PubMed] [Google Scholar]
- Thulborn KR, Ackerman JJ. Absolute molar concentrations by NMR in inhomogeneous B 1. A scheme for analysis of in vivo metabolites. Journal of Magnetic Resonance 1969. 1983;55:357–71. [Google Scholar]
- Wagenknecht G, Kaiser HJ, Mottaghy FM, Herzog H. MRI for attenuation correction in PET: methods and challenges. Magnetic Resonance Materials in Physics, Biology and Medicine. 2013;26:99–113. doi: 10.1007/s10334-012-0353-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Fei B. An MR image-guided, voxel-based partial volume correction method for PET images. Medical physics. 2012;39:179–94. doi: 10.1118/1.3665704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Tang W, Zhen Z, Chen H, Xie J, Zhao Q. Improving detection specificity of iron oxide nanoparticles (IONPs) using the SWIFT sequence with long T 2 suppression. Magnetic resonance imaging. 2014;32:671–8. doi: 10.1016/j.mri.2014.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch A, Campbell C, Clackdoyle R, Natterer F, Hudson M, Bromiley A, Mikecz P, Chillcot F, Dodd M, Hopwood P. Attenuation correction in PET using consistency information. Nuclear Science, IEEE Transactions on. 1998;45:3134–41. [Google Scholar]
- Wiesinger F, Sacolick LI, Menini A, Kaushik SS, Ahn S, Veit-Haibach P, Delso G, Shanbhag DD. Magnetic Resonance in Medicine. 2015. Zero TE MR bone imaging in the head. [DOI] [PubMed] [Google Scholar]
- Wollenweber S, Ambwani S, Delso G, Lonn A, Mullick R, Wiesinger F, Piti Z, Tari A, Novak G, Fidrich M. Evaluation of an atlas-based PET head attenuation correction using PET/CT & MR patient data. Nuclear Science, IEEE Transactions on. 2013a;60:3383–90. [Google Scholar]
- Wollenweber S, Ambwani S, Lonn A, Shanbhag D, Thiruvenkadam S, Kaushik S, Mullick R, Qian H, Delso G, Wiesinger F. Comparison of 4-class and continuous fat/water methods for whole-body, MR-based PET attenuation correction. Nuclear Science, IEEE Transactions on. 2013b;60:3391–8. [Google Scholar]
- Wu Y, Ackerman JL, Chesler DA, Graham L, Wang Y, Glimcher MJ. Density of organic matrix of native mineralized bone measured by water - and fat - suppressed proton projection. MRI Magnetic resonance in medicine. 2003;50:59–68. doi: 10.1002/mrm.10512. [DOI] [PubMed] [Google Scholar]
- Wu Y, Hrovat MI, Ackerman JL, Reese TG, Cao H, Ecklund K, Glimcher MJ. Bone matrix imaged in vivo by water - and fat - suppressed proton projection MRI (WASPI) of animal and human subjects. Journal of Magnetic Resonance Imaging. 2010;31:954–63. doi: 10.1002/jmri.22130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J, Lim JCS, Townsend DW. MRI-guided brain PET image filtering and partial volume correction. Physics in medicine and biology. 2015;60:961. doi: 10.1088/0031-9155/60/3/961. [DOI] [PubMed] [Google Scholar]
- Zaidi H, Montandon ML, Meikle S. Strategies for attenuation compensation in neurological PET studies. Neuroimage. 2007;34:518–41. doi: 10.1016/j.neuroimage.2006.10.002. [DOI] [PubMed] [Google Scholar]
- Zaidi H, Montandon ML, Slosman DO. Magnetic resonance imaging-guided attenuation and scatter corrections in three-dimensional brain positron emission tomography. Medical physics. 2003;30:937–48. doi: 10.1118/1.1569270. [DOI] [PubMed] [Google Scholar]
- Zhang X, Chen YL, Huang C, Kolnick A, Lim R, El Fakhri G. Society of Nuclear Medicine Annual Meeting Abstracts. Soc Nuclear Med. 2014;Series 55:1680. [Google Scholar]


