Fast Magnetic Micropropellers with Random Shapes

Abstract

Studying propulsion mechanisms in low Reynolds number fluid has implications for many fields, ranging from the biology of motile microorganisms and the physics of active matter to micromixing in catalysis and micro- and nanorobotics. The propulsion of magnetic micropropellers can be characterized by a dimensionless speed, which solely depends on the propeller geometry for a given axis of rotation. However, this dependence has so far been only investigated for helical propeller shapes, which were assumed to be optimal. In order to explore a larger variety of shapes, we experimentally studied the propulsion properties of randomly shaped magnetic micropropellers. Surprisingly, we found that their dimensionless speeds are high on average, comparable to previously reported nanofabricated helical micropropellers. The highest dimensionless speed we observed is higher than that of any previously reported propeller moving in a low Reynolds number fluid, proving that physical random shape generation can be a viable optimization strategy.

The discovery of the rotation of bacterial flagella nearly 50 years ago¹ seems to suggest that a rotating helical structure could be an optimum shape for propulsion in low Reynolds number fluids. Consequently, attempts to create magnetically driven propellers have focused in particular on helical shapes. Magnetic propellers are a particularly simple and comparatively well understood²⁻⁶ actuation mechanism for artificial microstructures. We understand a magnetic propeller to be a rigid structure, rotated by an external rotating magnetic field.^7,8 Propulsion is achieved if the structure possesses finite rotation-translation coupling. However, which is the optimum shape for magnetic propellers remains unknown and, in addition, there is no estimate for the maximum speed that a propeller of given length could reach if it had an optimal shape. Given the wide range of possible shapes, experimental approaches are difficult. But even modeling approaches were only able to explore possible shape within a narrow range.² Here we devise a combinatorial approach, synthesizing a large number of propellers with random shapes and investigating their dimensionless speeds (that is, speed normalized by length and frequency of rotation). Investigating the histogram of dimensionless speeds in a large population, we propose a lower bound for the highest dimensionless speed that is physically possible. In addition, analyzing the relationship between propeller geometry and dimensionless speed, we aim at determining design principles that make such micropropellers efficient.

Many different approaches have been used to fabricate such magnetic micropropellers. One of the first micropropellers was created by Zhang et al. using self-scrolling thin films.^9,10 These bioinspired “artificial bacterial flagella” are between 30 and 50 μm in size and have been used for micromanipulation tasks.¹¹⁻¹⁶ Smaller propellers were fabricated by Ghosh and Fischer (about 0.25 × 1.5 μm)¹⁷ and recently by Schamel et al. (about 0.1 × 0.4 μm)¹⁸ using glancing angle vapor deposition (GLAD). These have been used to demonstrate the separation of chiral species by magnetic fields⁴ and after applying a cytocompatible coating were able to move through human blood.¹⁹ Because of their small size, special attention has been paid to the effect of thermal noise on these propellers.^6,20,21 Recently Walker et al. used GLAD to produce length optimized helical propellers.²² Using direct laser writing (DLW), helical micropropellers with precisely controlled geometric parameters were fabricated and after coating them with a magnetic material were used for cargo transport and micromanipulation tasks.²³⁻³¹ It has also been shown that the magnetic material can be internalized, by applying DLW to photoresist mixed with superparamagnetic nanoparticles, which were aligned by an external magnetic field during the writing process.³²

The propellers listed above required expensive equipment for their production. Different attempts have been made to reduce the production costs of propellers, by, for example, using self-assembly or templates. Curved nickel nanowires have been assembled into helix-like structures and were used as propellers, actuated by a rotating magnetic field.¹⁶ The metallization of helical liposome scaffolds was also used to create magnetic propellers.³³ Plant-based magnetic helical propellers have been created by coating the spiral xylem vessels of vascular plants with titanium and nickel layers.³⁴ Nickel-coated helical palladium nanosprings were created by a template electrosynthesis method and used as propellers.³⁵ All of these techniques were developed in order to produce helix-shaped propellers, similar to the previously reported nanofabricated micropropeller designs.

Previous investigations of the relationship between propeller shape and dimensionless speed could only explore narrowly limited shape spaces. Several experimental studies investigated variations of helical propellers^23,32,31 and also a theoretical study compared different types of helices.³ In another theoretical study, Keaveny et al. were able to investigate more general shapes and even performed numerical optimization in shape space but remained limited to slender shapes with a single centerline.² Apart from two recent studies on achiral propellers,^36,37 the propulsion properties of alternative morphologies remained unexplored.

Here, we therefore experimentally explore a large shape space by studying the actuation of randomly shaped structures. We recently demonstrated an extremely simple approach to the production of very large quantities of magnetic micro- and nanopropellers, by selecting propellers from a pool of randomly shaped carbon-coated magnetic nanoparticle aggregates.⁵ The reason why this approach worked was already stated by Purcell in his seminal 1976 talk “Life at low Reynolds number”:³⁹ “Turn anything – if it isn’t perfectly symmetrical you’ll swim.” However, how well “anything” swims, remained an open question. Additionally, how big is the subset of randomly shaped structures that can be efficiently actuated by rotating magnetic fields? Surprisingly, we observed that most of the randomly shaped structures can indeed be efficiently actuated. About one in two random shapes we subjected to a rotating magnetic field moved indeed faster than the “artificial bacterial flagella” discussed above,¹¹ when using a dimensionless speed that depends only on the geometry of the actuated structure as a basis for comparison.³⁹

Theoretical Background

We consider a propeller to be a rigid structure rotating with frequency f around a fixed axis of rotation. The propeller is actuated by an external force F and an external torque τ. Because the Reynolds number is low (see the Supporting Information for an estimate), the hydrodynamics of the propeller motion is described by the Stokes equations

1

and

2

where p is the pressure, η is the dynamic viscosity, and u is the speed of the moving fluid. If the propeller is rotating in bulk fluid, the effect of gravity is neglected and we are interested in time scales ≫(1/f), the hydrodynamic problem is on average rotationally symmetric around the axis of rotation of the propeller. Therefore, the translatory propeller movement will be parallel to the axis of rotation and the propeller speed can be described by the scalar quantity v. Assuming a no-slip boundary condition,⁴⁰ it follows from the Stokes equations that the speed v and rotation frequency f of the propeller motion must be linearly related to the applied external force and torque⁴¹

3

L is a size parameter for the propeller and A, C, and D are parameters that depend only on the shape of the propeller for a fixed axis of rotation. The symmetric and positive definite matrix P is called the resistance matrix.⁴² In the case of magnetic propellers, the external force is zero (F = 0). Therefore, the speed of the propeller is related to the frequency of rotation in the following way

4

In order to compare the propulsion properties of propellers of different shapes, it is therefore useful to define a dimensionless speed³⁹ that depends only on the shape of the propeller and the axis of rotation

5

where v is the component of the propeller speed parallel to the vector of rotation of the rotating magnetic field that actuates the propeller. This dimensionless speed corresponds to the number of body lengths a propeller moves during one rotation and can be thought of as an effective screw pitch (see Figure 1a,b). In our experiments, we took care to ensure that the magnetic torque was always sufficient to rotate the propellers with the frequency of the rotating magnetic field. Thus, U_y characterizes the hydrodynamic coupling between rotation and translation for a particular propeller shape and axis of rotation.

Figure 1.

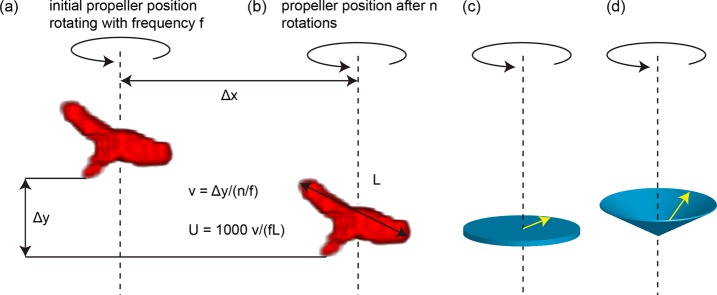
Schematic explanation of the dimensionless speed. (a) The red shape is an example of a 3D reconstruction of a propeller. The dashed black line indicates the axis of rotation. (b) After n (here n = 79 to suit the illustration) rotations, the propeller has moved a certain distance due to rolling (Δx) and a certain distance due to propulsion (Δy). The propeller speed v is the speed parallel to the rotation axis. The length scale L is chosen to be the size of the propeller in the projection in which it appears largest (see methods in Supporting Information). The dimensionless speed is thus the number of body lengths moved per rotation (times 1000) and can be thought of as an effective screw pitch. (c) The net magnetic moment (yellow arrow) of the propeller is likely rotating in the same plane (indicated by the blue shape) as the external magnetic field, perpendicular to the axis of rotation. This corresponds to a precession angle of 90°. (d) The precession angle does not necessarily have to be equal to 90°. Because of the interplay between magnetic and hydrodynamic forces, other precession angles are possible as well.

In our experiments, the axis of rotation is set by the magnetization state of the propeller and the hydrodynamic forces acting on the propeller. Typically, the rotation axis will be perpendicular to the net magnetic moment of the propeller and perpendicular to the plane in which the external magnetic field is rotating. This leaves two degrees of freedom for the position of the propeller relative to the axis of rotation. We observe that the axis of rotation passes through a point in the propeller that seems to be typically close to its center of mass (see Figure 1c). In principle, the net magnetic moment of the propeller does not need to rotate in the plane in which the external magnetic field is rotating. One could imagine that the net magnetic moment rotates (precesses) on a cone around the axis of rotation (see Figure 1d). Therefore, we take the axis of rotation as given and do not make connections to the likely magnetization state of the propeller.

The rotational friction constant c_F of the propeller, defined by the relationship τ = c_Ff, is given by c_F = ηL³(D – C²/A). In the Supporting Information, we show that c_F is always positive, based on the fact that the resistance matrix P is positive definite. Interestingly, the rotational friction constant c_F is reduced when the coupling between rotation and translation is strong (large C). This suggests that arbitrarily shaped structures might have a tendency to rotate around an axis with strong rotation translation coupling.

Synthesized Structures Have Random Shapes

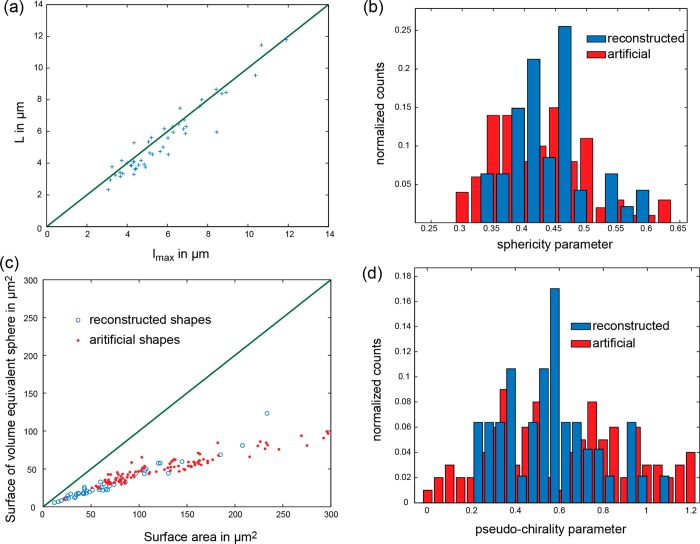
Magnetic microstructures were obtained from a high-throughput synthesis described earlier.⁵ Their dimensionless speeds were measured (512 structures) and their shapes were reconstructed (47 structures, see methods in the Supporting Information). The reconstructed shapes were compared to simulated shapes generated in silico by a random process (spheres are joined in random directions without overlap, see Supporting Information for details) to assess whether the synthesized structures are similarly random. In order to allow a quantitative comparison, several geometric parameters were extracted from the reconstructed, as well as the simulated shapes (see Supporting Information). The general accuracy of the reconstruction method was assessed by comparing a size measure of the reconstructed shape (l_max), to the size of the microstructures as measured in the original video frames (Figure 2a). l_max is the largest distance (in μm) between a pair of voxels belonging to (and forming) the reconstructed shape. The two measures are generally in agreement, although the maximum voxel to voxel distance tends to be a little larger. This was expected, because only five different 2D projections were recorded and the 2D projection in which the propeller would appear largest might not have been one of them. Also, the maximum voxel to voxel distance in the reconstruction might be larger than the true size of the propeller due to overshadowing. The compactness of the reconstructed shapes as well as the artificially generated shapes is characterized by plotting the surface area of the volume equivalent sphere against the actual surface area of the shape (Figure 2c). Similarly, the sphericity is defined as the ratio between the surface area of the volume equivalent sphere to the actual surface area of a shape. The distribution of this dimensionless geometric parameter is broad for both reconstructed as well as generated shapes, indicating that the reconstructed shapes are similarly random (Figure 2b). We also introduce a geometric parameter, which we call pseudochirality. A shape is said to be chiral if it cannot be superposed on its mirror image by rotations and translations. Chirality can be quantified by

6

where A defines the reconstructed shape and A′ its mirror image, V(...) is the volume and the minimization is performed over all rotations and translations.⁴³ The pseudochirality is defined similarly; however, the minimization is done only for one axis of rotation after moving the center of mass (assuming constant density) of the shape and its mirror image to the origin of the coordinate system. For the reconstructed shapes, the rotation is around an axis parallel to the actual axis of rotation of the experimental microstructure. This pseudochirality is easier to calculate and seemingly more useful for the characterization of the propulsion properties of magnetic microstructures. Chirality is independent of the axis of rotation of a shape, whereas pseudochirality is not. It has recently been observed that also achiral shapes can propel, depending on their axis of rotation.^36,37 The distributions of pseudochirality are broad for both reconstructed as well as generated shapes (Figure 2d). We thus conclude that the synthesized structures are indeed random,in the sense that their distributions of geometric parameters are similar to those of shapes generated by a random process.

Figure 2.

(a) Plot of the microstructure size measured in video frames (L) against the maximum voxel to voxel distance in the reconstructed shapes (l_max). The reconstructed shape consists of 3D voxels, thus l_max is a measure of the microstructure size. The green line is a line through the origin with slope one. The good correspondence between the two measures of propeller size is an indication of the quality of the 3D reconstruction. (b) Normalized histograms of the geometric parameter sphericity extracted from reconstructed (blue) as well as artificially generated (red) shapes. (c) The surface area of spheres, equivalent in volume to the reconstructed (blue) or artificially generated (red) shapes, is plotted against the measured surface area of the shapes. This plot is used to characterize the compactness of shapes and again indicates the similarity of reconstructed and generated shapes. (d) Same as (b) but for pseudochirality instead of sphericity.

Random Shapes Have High Dimensionless Speeds

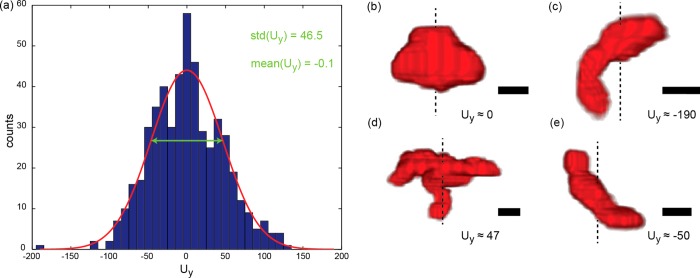
The distribution of the measured dimensionless speed values is shown in Figure 3a. We arbitrarily set the dimensionless speed to be negative for propellers moving away from the observer when rotating clockwise, being viewed along the axis of rotation. A Gaussian fit to the data yields a width of 46.5, which coincides with the standard deviation of the sample. The mean is close to zero as expected for symmetry reasons. The measured distribution of propeller speeds is lower than expected for a Gaussian at |U_y| ≈ 25 and higher than expected at U_y ≈ 0. Whether these deviations from a Gaussian distribution are statistically significant (at the 5% level) depends on the statistical test that is used. While the Lilliefors test does reject the null hypothesis that the measured distribution stems from the normal family, the Anderson-Darling and the Jarque-Bera test cannot reject this null hypothesis. Thus, we do not rule out the possibility of deviations from a Gaussian distribution but use the Gaussian as a phenomenological description.

Figure 3.

Distribution of dimensionless speed for random shapes has a remarkably high standard deviation. (a) The measured values for the dimensionless propulsion speed U_y are displayed as a histogram. The red line is a Gaussian fit to the data. However, Lilliefors test rejects the null hypothesis that the data comes from a normal distribution at the 5% significance level. The pronounced maximum at 0 and the minima at about ±25 are thus potentially no statistical flukes and in fact the distribution might be bimodal. Although a model with one central Gaussian and two symmetrically shifted Gaussians is (trivially) better, we do not include it because we lack a physical argument motivating such a bimodal distribution. The standard deviation of the data and the width of the Gaussian fit is 46.5. The mean of the distribution is −0.1 and thus close to zero as expected for symmetry reasons. (b–e) From all 47 propellers for which the 3D shape was successfully reconstructed, 4 examples were selected according to the following criteria: The absolute value of the dimensionless speed was lowest in (b) (U_y ≈ 1), highest in (c) (U_y ≈ −190), and close to the standard deviation in (d) (U_y ≈ 47) and (e) (U_y ≈ −50). The dashed black lines in (b–e) indicate the approximate position of the rotation axis. The propellers are rotating clockwise when viewed from below. The movement is upward if the dimensionless speed is negative and vice versa (see Supporting Information Figure S1). Scale bars are 1 μm.

As discussed in the introduction, arbitrarily shaped propellers might have a tendency to rotate around an axis for which the rotation translation coupling is strong. Thus, the distribution of dimensionless speeds we measure might not be identical to the dimensionless speed distribution of randomly shaped structures rotating around random axes of rotation in bulk fluid. The dimensionless speeds we measure might be increased by the dependence of the rotational friction constant (c_F) on the rotation translation (C) coupling discussed above, and surface effects might have an influence as well. Measuring the speed close to a surface probably decreases the speed with respect to the bulk propulsion speed (see Supporting Information). However, the propulsion speeds of previously published designs for magnetically actuated propellers have almost always also been measured near a solid surface.^{6,9,11,12,15−17,19,20,22,23,26,28,31,32} Thus, although the dimensionless speeds reported here might not correspond with an idealized theoretical situation, they lend themselves perfectly to comparisons with published propeller designs.

Figure 3b–e shows four examples of reconstructed shapes and their measured dimensionless speeds. The structure in Figure 3c has a dimensionless speed of 190, which is faster than all previously reported magnetic micropropellers moving in low Reynolds number liquid. Interestingly, the shape of this propeller is similar to optimized shapes reported in a theoretical study by Keaveny et al.² The propeller is approximately helical with less than one full helical turn. The optimization performed by Walker et al. arrives at a similar shape as well and they also experimentally verify that this shape moves particularly fast.²² However, the dimensionless speed of their optimal propeller (92) is significantly below the highest dimensionless speed we find here (190).

In contrast, most previous designs for magnetic micropropellers have used screw-like shapes, consisting of many helical turns, a design originally inspired by the shape of bacterial flagella.¹¹Figure 4 compares the dimensionless speeds of all previously reported rigid magnetic micropropeller designs, now with the absolute value of the dimensionless speeds of the random shapes reported here. This comparison shows that the observed standard deviation of σ = 46.5 in the dimensionless speed of random shapes is unexpectedly high. Most previously published propellers have dimensionless speeds below 140 (3 σ). The only propeller reported to have a significantly higher dimensionless speed, moved in a high density solution of microbeads, instead of pure water.¹⁶ This structure might thus have moved more like a screw turning in a solid medium, rather than a propeller moving in low Reynolds number liquid.¹⁶ Some nanofabricated propellers have dimensionless speeds, which are smaller than 46.5 (1 σ). The dimensionless speed of the artificial bacterial flagella, used successfully in many studies, is 33¹¹ and thus 49% of the observed random shapes have a higher dimensionless speed.

Figure 4.

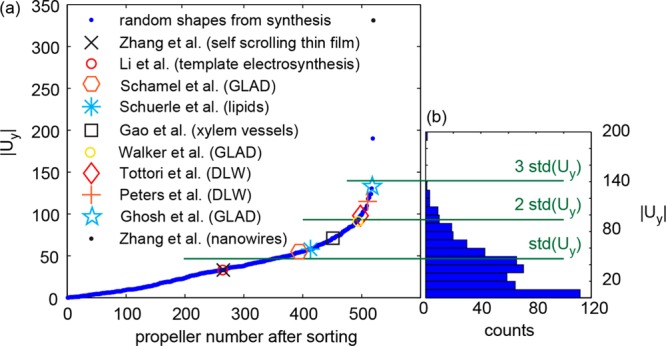
Comparison of randomly shaped propellers from solution synthesis with previously published nanofabricated propellers. The dimensionless speeds of nanofabricated propellers are shown in increasing order as in Supporting Information Figure S3 (Zhang et al.,¹¹ Li et al.,³⁵ Schamel et al.,¹⁸ Schuerle et al.,³³ Gao et al.,³⁴ Walker et al.,²² Tottori et al.,²³ Peters et al.,³² Ghosh et al.,¹⁷ Zhang et al.¹⁶). (a) The absolute value of dimensionless speeds of the random shapes and the dimensionless speed values from the literature are assigned a propeller number, by sorting the values in ascending order. The dimensionless speed of both random shapes and nanofabricated propellers is then plotted against the propeller number. The propeller number of a nanofabricated propeller is thus an indication of how many random shapes (from the set of the 512) have a lower dimensionless speed. (b) The distribution of absolute dimensionless speed values is displayed as a histogram. The scale of |U_y| is the same as in (a). The multiples of the standard deviation of U_y are displayed as horizontal green lines. Assuming a Gaussian distribution, 68% of random shapes have dimensionless speeds lower than the one standard deviation, 95% lower than two, and 99.7% lower than three standard deviations.

In the literature, there are also flexible magnetic structures that can be actuated by rotating magnetic fields (for example, ref (39)). We exclude these from our comparison, as their swimming mechanism is different and does not allow the definition of a dimensionless speed. An exception could be the micropropellers reported by Cheang and Kim,⁴⁴ which consist of chains of flexibly linked magnetic nanoparticles. At least for a fixed actuation frequency, the shape of the structures is constant and a dimensionless speed can be calculated. They report swimming speeds for two micrometer-sized structures moving in salt solution far from a solid interface. The corresponding dimensionless speeds are about 43 and 18 for the bigger and smaller structure, respectively, both below the standard deviation of random shapes we report here.

Chirality Parameter Correlates with Dimensionless Speed

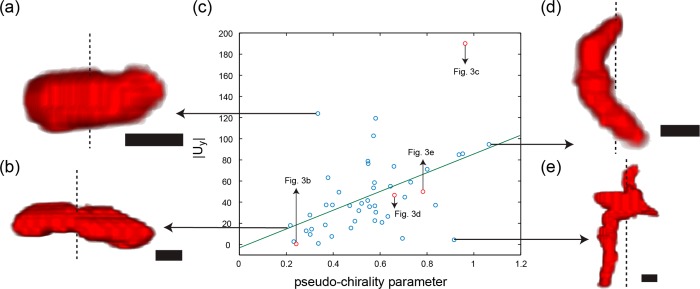
We extracted nine geometric parameters from the reconstructed 3D shapes (see Supporting Information for parameter definitions). The only geometric parameter that correlated significantly with the dimensionless speed is the dimensionless pseudochirality introduced above. The Pearson correlation coefficient is 0.49, with a p-value of 4 × 10^–4, meaning that the null-hypothesis of the pseudochirality being uncorrelated to the dimensionless can be rejected with high confidence. The predictive power of the pseudochirality is limited, but it is already remarkable that a simple geometric parameter can characterize the rotation translation coupling of a particular shape to some extent, the theoretical calculation of which is challenging and involves complex hydrodynamic simulations. If more such geometric parameters could be found, the search for optimal designs of magnetically actuated propellers could be greatly simplified.

Figure 5.

Correlation between the dimensionless speed and the pseudochirality. The absolute value of the dimensionless speed is plotted against the pseudochirality in panel (blue and red circles) (c). The data points corresponding to propellers displayed in Figure 3 are marked in red. The green line is a linear fit to the data. (a) This structure has a high dimensionless speed, despite having a relatively low pseudochirality. This might be because some small but important geometric features could not be resolved in optical microscopy. (b) This structure has a low pseudochirality and also a low dimensionless speed. (d) This structure has a high pseudochirality and also a high dimensionless-speed. (e) This relatively large structure has a very low dimensionless speed, despite having a high pseudochirality. The rotation axes of the propellers are marked by dashed lines, scale bars are 1 μm.

Implications for the Use and Design of Micropropellers

The observation that helical propeller designs are mostly only average when compared to randomly shaped propellers is very surprising. However, randomness per se is not an advantage; we simply use random shape generation to sample a space of possible shapes. The high speeds with which some of our synthesized propellers move depends critically on their specific geometry. The discovery that randomly shaped magnetic micropropellers have high dimensionless speeds has two main implications.

First, it shows that randomly shaped magnetic micropropellers could be used in applications, which do not require particularly high dimensionless speeds. Randomly shaped magnetic nanostructures can be produced cheaply in very large quantities and we have shown previously that propellers can be selected from such nanostructures.⁵ The present work shows that such selection is probably not necessary for certain applications, like micromixing,⁴⁵ environmental remediation tasks,⁴⁶ or catalyst recovery.⁴⁷⁻⁴⁹ The majority of the produced structures have dimensionless speeds comparable to those of nanofabricated propellers and samples of nanofabricated (designed) propellers always contain defective (malformed) structures with reduced speeds as well.

Second, new micropropeller designs could accommodate other design objectives, like ease of fabrication or the incorporation of additional functionalities, without compromising their ability to be effectively actuated by rotating magnetic fields. The range of shapes for which such effective actuation is possible seems to be much larger than was previously assumed. The predominant helical, flagella-like designs are certainly not the only option and might be suboptimal for certain applications, such as particular microassembly tasks or specific envisioned medical procedures.⁵⁰⁻⁵³ Nonetheless, helical propellers with many turns might have specific advantages for certain applications, like pick and place devices.²²

In addition, we identify a structure that has a higher dimensionless speed than any propeller reported previously, showing that random shape generation can be a viable optimization method. The shape of this fastest propeller is similar to theoretically optimized propeller shapes, considering slender bodies with a single centerline.² Future theoretical studies and simulations could be tremendously helpful to better understand the relationship between propeller shape and dimensionless speed. Which geometric shape has the highest possible dimensionless speed remains an intriguing unsolved problem in hydrodynamics, although in practice additional constraints (minimum material thickness, magnetization state, Brownian motion, and so forth) and trade-offs (for example, achievable magnetic moment is also shape-dependent) would need to be considered as well. For biological applications, non-Newtonian and heterogeneous biological fluids pose entirely new challenges.¹⁸ Nonetheless, the fastest propeller we observe sets a lower bound for the highest physically possible dimensionless speed.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b03131.

• Detailed experimental methods, additional theoretical considerations, supporting figures, and author’s contributions. (PDF)

• SI-video_1 (supporting information material number 2): Video showing the movement of the propeller depicted in Figure 3c. The video is slowed down fourfold in comparison to real time. The propeller is rotating with 40 Hz. Horizontal motion (left to right) is rolling, whereas vertical motion is swimming. The video frame size corresponds to an area of 22 (width) by 49 (height) micrometers in real space. (MPG)

• SI-video_2 (supporting information material number 3): Video showing the movement of the propeller depicted in Figure 3d. The video is slowed down fourfold in comparison to real time. The propeller is rotating with 40 Hz. Horizontal motion (left to right) is rolling, whereas vertical motion is swimming. The video frame size corresponds to an area of 83.3 (width) by 46.9 (height) micrometers in real space. (MPG)

• SI-video_3 (supporting information material number 4): Video showing the movement of the propeller depicted in Figure 3e. The video is slowed down fourfold in comparison to real time. The propeller is rotating with 40 Hz. Horizontal motion (left to right) is rolling, whereas vertical motion is swimming. The video frame size corresponds to an area of 21 (width) by 37.8 (height) micrometers in real space. (MPG)

The authors declare no competing financial interest.