A general time-dependent route to Resonance-Raman spectroscopy including Franck-Condon, Herzberg-Teller and Duschinsky effects

Abstract

We present a new formulation of the time-dependent theory of Resonance-Raman spectroscopy (TD-RR). Particular attention has been devoted to the generality of the framework and to the possibility of including different effects (Duschinsky mixing, Herzberg-Teller contributions). Furthermore, the effects of different harmonic models for the intermediate electronic state are also investigated. Thanks to the implementation of the TD-RR procedure within a general-purpose quantum-chemistry program, both solvation and leading anharmonicity effects have been included in an effective way. The reliability and stability of our TD-RR implementation are first validated against our previously proposed and well-tested time-independent procedure. Practical applications are illustrated with some closed- and open-shell medium-size molecules (anthracene, phenoxyl radical, benzyl radical) and the simulated spectra are compared to the experimental results. More complex and larger systems, not limited to organic compounds, are also feasible, as shown for the case of Tris(bipyridine)ruthenium(II) chloride.

I. INTRODUCTION

Vibrational Resonance Raman (RR) is a spectroscopic technique based on a scattering process in which the incident light is set to match an electronic transition. In the last years, it has become a widely used tool for the analysis of complex systems, like molecules of biological interest^1–3 and metal complexes^4,5. The main advantage of tuning the incident light to match the transition energy to an electronic state, which is then called the intermediate state, is an enhancement of the scattered intensity by a factor of 10³-10⁶ with respect to the non-Resonant Raman spectroscopy (nRR). Furthermore, only transitions between vibrational states of the initial and intermediate states corresponding to intense vibronic transitions are enhanced, and this makes RR spectra easier to interpret than nRR ones. As a result, it is possible to study specific regions in complex systems by tuning the incident radiation to match the energy of the electronic transition of interest^3,6,7. For instance, the enhancement can be applied only on the peaks due to the vibrations of a chromophore in a biomolecule, eliminating the interference from the rest of the molecule, present in the nRR spectrum. Of course, the RR spectrum of a molecule changes with the resonant electronic state, and thus, like one-photon absorption spectra, it contains information about excited states. However, the initial and final states for a RR transition are the vibrational levels of the electronic ground state, therefore the resolution of RR spectra is much higher than for one-photon spectra. As a consequence, RR spectroscopy can be used to extract information about excited states while avoiding the problem of low-resolution spectra. The interpretation of RR spectra is far from being straightforward due to the much higher complexity to derive simple selection rules with respect to vibrational spectroscopies (IR and nRR, for instance). Therefore, a theoretical model able to simulate a RR spectrum is essential to identify unequivocally the various contributions to the experimental spectrum and to facilitate its interpretation.

The simulation of RR spectra is related to the calculation of the transition polarizability tensor, as proven by Dirac in his pioneering work⁸. Different methods for the calculation of this tensor have been proposed, which can be divided in two main groups, the time-independent (TI) and the time-dependent (TD) models. Under the Franck-Condon approximation, the polarizability tensor can be written in terms of Franck-Condon integrals (often referred as the A^{V I} Albrecht term in reference to the seminal work of Albrecht^9,10). These integrals can be computed with a TI formulation, using the same metodology as for vibronic spectroscopy^11,12. Analytic formulae have been derived, first explicitly for each transitions^13,14 and later for series of transitions based on the number of simultaneously excited oscillators in the initial and final states^15,16. However, they remain not general enough to be applicable to complex and large systems. Those difficulties can be overcome by using the recursive relations introduced by Ruhoff^17,18, which are based on a few formulae sufficient to obtain all transitions and thus are better suited for general-purpose implementations. The main limitation of the TI method is the a-priori infinite number of integrals to compute, in particular when dealing with large systems. Therefore, in order to limit their computational cost, TI methods must be coupled with appropriate strategies to select the most intense transitions. In a previous work some of us have presented a general TI approach for the calculation of RR spectra¹⁹ with the inclusion of Herzberg-Teller effects relying on a class-based prescreening scheme, which had been previously used for the simulation of one-photon vibronic spectra^20,21.

The shortcomings of TI approaches can be overcome by using the TD formalism introduced by Heller and co-workers in their pioneering works^22,23. By working in the time domain, it is possible to rewrite the components of the polarizability tensor in terms of the half Fourier transform of the dipole moment cross-correlation function, which can be calculated by propagating a wavepacket of the initial state over the potential energy surface (PES) of the intermediate level. Different models have been introduced in order to simulate this propagation. The simplest one is the so-called gradient approximation, in which the wavepacket is propagated over the intermediate state PES only for a short-time and long-time effects are neglected^24–26. This approach is pertinent under a near-resonance condition, but it is ill-suited when high-precision results are needed. Indeed, even if its simplicity reduces significantly the computational cost, the model fully neglects the change in the shape of the PES of the intermediate state and is limited to the Franck-Condon approximation. However, it is possible to overcome these limitations by assuming that the PES of the ground and intermediate levels are harmonic. In fact, under this assumption, the propagation of the initial-state wavepacket over an harmonic potential energy surface is analytic^27,28 even if mode-mixing is present and taken into account. As a consequence, the transition dipole moment cross-correlation function can be computed analytically²⁹ too and the polarizability tensor can be obtained directly from a numerical Fourier-transform algorithm. The expression of the cross-correlation function is simple under the Franck-Condon approximation and if mode-mixing effects are neglected³⁰, since it can be factorized as a product of monodimensional terms. More recently, analytic expressions for the dipole moment cross-correlation function have been derived also with mode-mixing^31–33 present. However, a complete formulation of the TD theory of RR spectroscopy (TD-RR) with the inclusion of both Duschinsky and Herzberg-Teller effects is still lacking. In this work we will extend the TD framework previously developed for the calculation of one-photon vibronic spectra³⁴ to the simulation of RR spectra which is facilitated by the flexibility of our method. Particular care has been devoted to the ease of use of our tool, as well as to its numerical stability. Furthermore, thanks to its implementation in a general-purpose quantum chemical program, it will be possible to investigate both solvent and leading anharmonicity effects.

The paper is organized as follows: the first section describes the general theory of TD-RR with particular attention on the inclusion of Herzberg-Teller, as far as a discussion of the treatment of anharmonicity and solvent effects. The second section presents the computational details regarding the simulation of Resonance-Raman spectra within the TI and TD routes. The reliability of the TD procedure will be validated by comparison with the TI results, using anthracene as a test case. Furthermore, two medium-size radicals, phenoxyl and benzyl, will be used to show the possibility to study open-shell systems and to include environmental and anharmonic effects in order to reproduce correctly the experimental spectra. Finally, support for large-sized systems will be illustrated with Tris(bipyridine)ruthenium(II) chloride.

II. THEORY

A. General theory of Resonance-Raman spectroscopy

The Raman effect is a non-linear optical phenomenon in which a photon is inelastically scattered by a molecular system, which consequently undergoes a transition between two different states ∣ Ψ_i ⟩ and ∣ Ψ_f ⟩. The difference between the incident and the scattered frequency corresponds to the energy separation between those levels.

The experimental quantity, which is usually reported in a Raman spectrum is the differential cross section of the scattering process σ′ = ∂σ/∂Ω, where Ω is the solid angle unit and σ is the cross section. The following equation relates σ′ to the scattered intensity I_s¹⁰:

$${\sigma }^{\prime }({\omega }_I,{\omega }_s)=\frac{I_s({\omega }_I,{\omega }_s,\theta )}{I_{\text{irr}}}$$ (1)

where I_irr is the total irradiance of the incident light. The differential cross section σ′ depends on various parameters. First of all, it is a function of the polarization of the incident and scattered lights and their respective frequencies ω_I and ω_s. Furthermore, it depends on the angle between their directions of propagation. For the sake of simplicity, we will assume that the polarization of the incident light is perpendicular to the direction of scattering. Furthermore, we will assume that the scattered light is unpolarized and orthogonal to the incident one.

Under these approximations, the scattered intensity I_s(ω_I, ω_s, θ) can be expressed in terms of the transition polarizability tensor α^if between the initial and final levels of the transition ∣ Ψ_i ⟩ and ∣ Ψ_f ⟩, as follows:

$$I\left(\frac{\pi }{2};{\Vert }^s{\perp }^s;{\perp }^I{\omega }_I,{\omega }_s\right)=k{{\omega }_s}^2{I}_{\text{inc}}\frac{45a^2+7g^2+5d^2}{45}$$ (2)

In the previous equation, we have introduced the three isotropic invariants a (mean isotropic polarizability), g (symmetric anisotropy) and d (asymmetric anisotropy) which are related to the elements of the transition polarizability tensor:

$$\begin{array}{cc}\hfill a& =\frac{1}{3}\left({\alpha }_{\mathit{xx}}^{\mathit{if}}+{\alpha }_{\mathit{yy}}^{\mathit{if}}+{\alpha }_{\mathit{zz}}^{\mathit{if}}\right)\hfill \\ \hfill g^2& =\frac{1}{2}\left({\mid {\alpha }_{\mathit{xx}}^{\mathit{if}}-{\alpha }_{\mathit{yy}}^{\mathit{if}}\mid }^2+{\mid {\alpha }_{\mathit{xx}}^{\mathit{if}}-{\alpha }_{\mathit{zz}}^{\mathit{if}}\mid }^2+{\mid {\alpha }_{\mathit{zz}}^{\mathit{if}}-{\alpha }_{\mathit{yy}}^{\mathit{if}}\mid }^2\right)\hfill \\ & +\frac{3}{2}\left({\mid {\alpha }_{\mathit{xy}}^{\mathit{if}}+{\alpha }_{\mathit{yx}}^{\mathit{if}}\mid }^2+{\mid {\alpha }_{\mathit{xz}}^{\mathit{if}}+{\alpha }_{\mathit{zx}}^{\mathit{if}}\mid }^2+{\mid {\alpha }_{\mathit{yz}}^{\mathit{if}}+{\alpha }_{\mathit{zy}}^{\mathit{if}}\mid }^2\right)\hfill \\ \hfill d^2& =\frac{3}{4}\left({\mid {\alpha }_{\mathit{xy}}^{\mathit{if}}-{\alpha }_{\mathit{yx}}^{\mathit{if}}\mid }^2+{\mid {\alpha }_{\mathit{xz}}^{\mathit{if}}-{\alpha }_{\mathit{zx}}^{\mathit{if}}\mid }^2+{\mid {\alpha }_{\mathit{yz}}^{\mathit{if}}-{\alpha }_{\mathit{zy}}^{\mathit{if}}\mid }^2\right)\hfill \end{array}$$ (3)

As proposed by Kramers, Heisenberg and Dirac in their pioneering work (KHD formalism)⁸, later proved by Placzek³⁵ in the framework of the second-order time-dependent perturbation theory, the cartesian components of the transition polarizability tensor can be expressed as a sum-over-states in the following way:

$${\alpha }_{\rho \sigma }^{\mathit{if}}=\frac{1}{\hslash }\sum _{m\ne i,f}\left(\frac{\langle {\Psi }_f\mid {\mu }_{\rho }\mid {\Psi }_m\rangle \langle {\Psi }_m\mid {\mu }_{\sigma }\mid {\Psi }_i\rangle }{{\omega }_{\mathit{mi}}-{\omega }_I+i{\gamma }_m}+\frac{\langle {\Psi }_f\mid {\mu }_{\rho }\mid {\Psi }_m\rangle \langle {\Psi }_m\mid {\mu }_{\sigma }\mid {\Psi }_i\rangle }{{\omega }_{\mathit{mi}}+{\omega }_I+i{\gamma }_m}\right)$$ (4)

The sum includes all molecular levels ∣ Ψ_m ⟩, different from ∣ Ψ_i ⟩ and ∣ Ψ_f ⟩, ω_mi is the energy separation between the initial and intermediate levels, γ_m is the lifetime of state m and ω_I is the frequency of the incident light.

The previous KHD formula can be further simplified within the Born-Oppenheimer approximation. Indeed, the wavefunction Ψ_m can then be factorized in an electronic, ϕ_m, and a nuclear components, ψ_m. Then, assuming that the Eckart conditions are met, the latter can be further factorized, and it is possible, with a good approximation, to separate the vibrational part ψ_r(m) from the rotational and translational ones. As a result, the transition dipole moment between molecular states m and n can be rewritten as follows:

$${\mu }_{\mathit{mn}}=\langle {\Psi }_m\mid \mu \mid {\Psi }_n\rangle \approx \langle {\psi }_{r\left(\underset{¯}{m}\right)}\mid {\mu }_{\mathit{mn}}^e\mid {\psi }_{s\left(\underset{¯}{n}\right)}\rangle$$ (5)

where ${\mu }_{\mathit{mn}}^e=\langle {\varphi }_m\mid \mu \mid {\varphi }_n\rangle$ is the electronic transition dipole moment, r is a vibrational state associated to electronic state m corresponding to the molecular state m, and s, n their counterpart for state n.

As mentioned before, in resonance-Raman spectroscopy, the incident frequency ω_I corresponds to the transition energy to an electronic state of the molecule, usually called the intermediate state, ∣ ϕ_m ⟩. This condition implies that ω_mi ≈ ω_I, which means that the first term in equation 4 is dominant with respect to the second one, which can be neglected. Therefore, the second term of the sum is discarded and the sum over all the infinite levels can be restricted to the vibrational levels of the intermediate state. Finally, it is possible to assume that the lifetime, γ_m, is independent of the vibrational states, and thus is a constant labelled γ from here on.

Based on those approximations, we will consider only one intermediary electronic state, m, and carry out the summation over its vibrational states n(m). As a result, equation 4 can be written in a more compact way.

$${\alpha }_{\rho \sigma }^{\mathit{if}}=\frac{1}{\hslash }\sum _{n\left(\underset{¯}{m}\right)}\frac{\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid {\mu }_{m0,\rho }^e\mid {\psi }_{n\left(\underset{¯}{m}\right)}\rangle \langle {\psi }_{n\left(\underset{¯}{m}\right)}\mid {\mu }_{m0,\sigma }^e\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle }{{\omega }_{\mathit{mi}}-{\omega }_I-i\gamma }$$ (6)

where 0 represents the electronic ground state. The main problem of dealing with equation 6 is that no analytic formulae for the electronic transition dipole moment, ${\mu }_{\mathit{mn}}^e$, are known. In order to overcome this limitation, ${\mu }_{\mathit{mn}}^e$ is usually approximated as a Taylor series of the normal coordinates of the initial or intermediate electronic states about their respective equilibrium geometry as follows:

$${\mu }_{\mathit{mn}}^e\left(\mathit{Q}\right)={\mu }_{\mathit{mn}}^e\left({\mathit{Q}}_{\text{eq}}\right)+\sum _{k=1}^N{\left(\frac{\partial {\mu }_{\mathit{mn}}^e}{\partial {\mathrm{Q}}_k}\right)}_{\text{eq}}{\mathrm{Q}}_k+◯\left({\mathit{Q}}^2\right)$$ (7)

In the following derivation, we will consider only terms up to the first order. The zeroth-order terms corresponds to the Franck-Condon approximation, while the inclusion of the first-order terms is known as the Herzberg-Teller approximation.

Finally, in order to calculate the transition polarizability tensor, a relation between the normal modes of the initial and intermediate electronic levels is needed. We will use the following linear transformation proposed by Duschinsky³⁶:

$$\overline{\mathbf{Q}}=\mathit{J}\overline{\overline{\mathbf{Q}}}+\mathit{K}$$ (8)

where $\overline{\mathbf{Q}}$ and $\overline{\overline{\mathbf{Q}}}$ are the normal modes of the electronic initial and intermediate states, respectively, J is the Duschinsky matrix and K is the shift vector. The definition of J and K depends on the approximation of the PES of the intermediate state. A more detailed discussion on those approximations can be found in our previous work²¹.

B. The time-independent approach

At this stage, two different strategies for the calculation of the tensor ${\alpha }_{\rho \sigma }^{\mathit{if}}$ are possible, referred to as the time-independent (TI) and the time-dependent (TD) approaches. We will now describe briefly the former (a more detailed discussion is given in Ref.¹⁹), before focusing on the latter.

By using the Taylor expansion given in equation 7, the sum-over-states formula from eq. 6 can be written in terms of overlap integrals ⟨ ψ_i(m) ∣ ψ_j(0) ⟩ between the vibrational levels of the initial and intermediate electronic states, also called the Franck-Condon integrals. The time-independent method is based on the direct calculation of those overlap integrals by using either analytic or recursive formulae^13,17,18. The main drawback of the time-independent approach is the virtual infinity of integrals to compute, so a prescreening scheme is needed to select a priori the vibrational levels of the intermediate state, that give the most important contributions to the RR spectrum. In our group, we have developed a general time-independent framework for the computation of RR spectra, which relies on a class-based prescreening system to select the most important transitions to include in the actual treatment^19,37. This scheme uses a classification of the intermediate levels according to the number of excited oscillators. For each class, a maximum level of excitation is defined on the basis of an extrapolation process, and all the states over this level are not considered. The reliability of the prescreening system can be assessed by using approximated sum-rules to evaluate the convergence rate for each peak of the RR spectrum between the calculated and analytic intensities.

C. The time-dependent formalism

As highlighted in the previous section, the main disadvantage of the time-independent approach is the requirement of a reliable prescreening system in order to overcome the problem of dealing with an infinite summation and the impossibility to know exactly how much of the intensity is missing from the discarded transitions. Those drawbacks can be overcome by switching to a time-dependent approach.

The transition from the frequency domain to the time domain is done trough the following property of the Fourier transform,

$$\frac{1}{x}=\frac{i}{\hslash }{\int }_0^{+\infty }{e}^{-\mathit{ixt}∕\hslash }\mathrm{d}t$$ (9)

Using the previous relation, Eq. 6 can be rewritten as,

$${\alpha }_{\rho \sigma }^{\mathit{if}}=\frac{i}{{\hslash }^2}\sum _{n\left(\underset{¯}{m}\right)}{\int }_0^{+\infty }\mathrm{d}t\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid {\mu }_{m0,\rho }^e\mid {\psi }_{n\left(\underset{¯}{m}\right)}\rangle \langle {\psi }_{n\left(\underset{¯}{m}\right)}\mid {\mu }_{m0,\sigma }^e\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle e^{-\mathit{it}({\omega }_{\mathit{mi}}-{\omega }_I-i\gamma )}$$ (10)

ω_mi can be rewritten as ω_ad + ω_n(m), where ω_ad is the energy separation between the minima of the electronic ground and intermediate states. ∣ ψ_n(m) ⟩ is an eigenket of the intermediate state vibrational Hamiltonian $e^{-i{\widehat{H}}_{\underset{¯}{m}}^{\mathit{vib}}t∕\hslash }$ with eigenvalue E_n(m). For the sake of readability, we will drop the ”vib” superscript in the following. Therefore, it is possible to introduce the exponential time-evolution operator $e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }$, which satisfies the following property:

$$e^{-{\mathit{iE}}_{n\left(\underset{¯}{m}\right)}t∕\hslash }\mid {\psi }_{n\left(\underset{¯}{m}\right)}\rangle =e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid {\psi }_{n\left(\underset{¯}{m}\right)}\rangle$$ (11)

Equation 11 is then inserted into equation 10. By using the closure relation for the vibrational eigenstates of the electronic state m, it is possible to derive the final time-dependent expression for the RR polarizability tensor;

$${\alpha }_{\rho \sigma }^{\mathit{if}}=\frac{i}{{\hslash }^2}{\int }_0^{+\infty }\mathrm{d}t\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid {\mu }_{m0,\rho }^e{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\mu }_{m0,\sigma }^e\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle e^{-\mathit{it}({\omega }_{\mathit{ad}}-{\omega }_I-i\gamma )}$$ (12)

Under the Franck-Condon approximation, the electronic transition dipole moment is constant and thus can be taken out of the integral. As a consequence, equation 12 can be simplified as follows:

$${\alpha }_{\rho \sigma }^{\mathit{if}}=\frac{i}{{\hslash }^2}{\left({\mu }_{m0,\rho }^e\right)}_{\mathit{eq}}{\left({\mu }_{m0,\sigma }^e\right)}_{\mathit{eq}}{\int }_0^{+\infty }\mathrm{d}t\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle e^{-\mathit{it}({\omega }_{\mathit{ad}}-{\omega }_I-i\gamma )}$$ (13)

For the sake of simplicity, we will introduce some further approximations. First of all, we will ignore temperature effects, so that the only possible initial state is the vibrational ground state of the lower electronic state. Furthermore, we will limit our analysis to fundamental bands, that is transitions to final states with a single quantum of excitation. In the following, the Dirac notation will be adopted, so that the previous statements can be rewritten as $\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle \to \mid \overline{0}\rangle$ and $\mid {\psi }_{f\left(\underset{¯}{0}\right)}\rangle \to \mid {\overline{1}}_f\rangle$

The formulae for the eigenfunctions of the hamiltonian of an harmonic oscillator are well-known. However, in order to use them, the integral in equation 13 must be rewritten in the normal coordinate representation. Moreover, two sets of normal coordinates of the initial electronic state, $\overline{\mathit{Q}}$ and ${\overline{\mathit{Q}}}^{\prime }$, and two sets of normal coordinates of the intermediate state, $\overline{\overline{\mathit{Q}}}$ and ${\overline{\overline{\mathit{Q}}}}^{\prime }$, need to be introduced. For all those coordinates sets, the following closure relation holds,

$${\int }_{-\infty }^{+\infty }d\overline{\mathit{Q}}\mid \overline{\mathit{Q}}\rangle \langle \overline{\mathit{Q}}\mid ={\int }_{-\infty }^{+\infty }d{\overline{\mathit{Q}}}^{\prime }\mid {\overline{\mathit{Q}}}^{\prime }\rangle \langle {\overline{\mathit{Q}}}^{\prime }\mid ={\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}\mid \overline{\overline{\mathit{Q}}}\rangle \langle \overline{\overline{\mathit{Q}}}\mid ={\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }\mid {\overline{\overline{\mathit{Q}}}}^{\prime }\rangle \langle {\overline{\overline{\mathit{Q}}}}^{\prime }\mid =1$$ (14)

By using equation 14, the time-dependent expression of the polarizability tensor given in equation 13 can be rewritten in the following way:

$${\alpha }_{\rho \sigma }^{\mathit{if}}=\frac{i}{{\hslash }^2}{\left({\mu }_{m0,\rho }^e\right)}_{\mathit{eq}}{\left({\mu }_{m0,\sigma }^e\right)}_{\mathit{eq}}{\int }_0^{+\infty }\mathrm{d}t{\int }_{-\infty }^{+\infty }d\overline{\mathit{Q}}{\int }_{-\infty }^{+\infty }d{\overline{\mathit{Q}}}^{\prime }{\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}{\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }\times \langle {\overline{1}}_k\mid {\overline{\mathit{Q}}}^{\prime }\rangle \langle {\overline{\mathit{Q}}}^{\prime }\mid {\overline{\overline{\mathit{Q}}}}^{\prime }\rangle \langle {\overline{\overline{\mathit{Q}}}}^{\prime }\mid e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid \overline{\overline{\mathit{Q}}}\rangle \langle \overline{\overline{\mathit{Q}}}\mid \overline{\mathit{Q}}\rangle \langle \overline{\mathit{Q}}\mid \overline{0}\rangle$$ (15)

The overlap integral $\langle {\overline{1}}_k\mid {\overline{\mathit{Q}}}^{\prime }\rangle$ is the representation of the wavefunction $\langle {\overline{1}}_k\mid$ in the coordinate set ${\overline{\mathit{Q}}}^{\prime }$, while the integral $\langle \overline{\mathit{Q}}\mid \overline{0}\rangle$ is the representation of $\mid \overline{0}\rangle$ in the coordinate system $\overline{\mathit{Q}}$. Both integrals have a closed-form expression:

$$\langle \overline{\mathit{Q}}\mid \overline{0}\rangle =\prod _{i=1}^N{\left(\frac{{\stackrel{‒}{\omega }}_i}{\pi \hslash }\right)}^{1∕4}\exp \left(-\frac{{\stackrel{‒}{\omega }}_i{\overline{Q}}_i^2}{2\hslash }\right)=\frac{\det {\overline{\Gamma }}^{1∕4}}{{\pi }^{N∕4}}\exp \left(-\frac{{\overline{\mathit{Q}}}^T\overline{\Gamma }\overline{\mathit{Q}}}{2}\right)$$ (16)

$$\langle {\overline{1}}_k\mid {\overline{\mathit{Q}}}^{\prime }\rangle =\sqrt{\frac{{\overline{\omega }}_k}{2\hslash }}{\overline{Q}}_k^{\prime }\prod _{i=1}^N{\left(\frac{{\overline{\omega }}_i}{\pi \hslash }\right)}^{1∕4}\exp \left(-\frac{{\overline{\omega }}_i{\overline{Q}}_i^{\prime 2}}{2\hslash }\right)=\sqrt{\frac{{\overline{\Gamma }}_k}{2}}{\overline{Q}}_k^{\prime }\frac{\det {\overline{\Gamma }}^{1∕4}}{{\pi }^{N∕4}}\exp \left(-\frac{{\overline{\mathit{Q}}}^{\prime T}\overline{\Gamma }{\overline{\mathit{Q}}}^{\prime }}{2}\right)$$ (17)

where $\overline{\Gamma }$ is a diagonal matrix whose elements are the reduced frequencies of the initial electronic state.

The key point of the time-dependent formulation of RR spectroscopy is to find an expression for the integrand of equation 15. We will define this function as the cross-correlation function χ_k(t), where the index k refers to the dependence of this cross-correlation function on the excited oscillator of the final state. Analytic formulae for the cross-correlation function χ_k(t) can be derived in the framework of the Feynman path-integral formulation of quantum mechanics³⁸. The starting point is the following expression for the matrix element $\langle {\overline{\overline{\mathit{Q}}}}^{\prime }\mid e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid \overline{\overline{\mathit{Q}}}\rangle$^38,39:

$$\langle {\overline{\overline{\mathit{Q}}}}^{\prime }\mid e^{-\overline{\overline{H}}\overline{\overline{\tau }}}\mid \overline{\overline{\mathit{Q}}}\rangle =\sqrt{\frac{\det \left(\overline{\overline{\mathit{a}}}\right)}{{\left(2\pi \hslash \right)}^N}}\exp \left(\frac{i}{\hslash }\left[\frac{1}{2}{\overline{\overline{\mathit{Q}}}}^{\mathrm{T}}\overline{\overline{\mathit{b}}}\overline{\overline{\mathit{Q}}}+\frac{1}{2}{\overline{\overline{\mathit{Q}}}}^{\prime \mathrm{T}}\overline{\overline{\mathit{b}}}{\overline{\overline{\mathit{Q}}}}^{\prime }-{\overline{\overline{\mathit{Q}}}}^{\prime \mathrm{T}}\overline{\overline{\mathit{a}}}\overline{\overline{\mathit{Q}}}\right]\right)$$ (18)

where we have introduced the auxiliary time variable, $\overline{\overline{\tau }}=\mathit{it}∕\hslash$, and the diagonal matrices $\overline{\overline{\mathit{a}}}$ and $\overline{\overline{\mathit{b}}}$, defined as:

$${\overline{\overline{\mathrm{a}}}}_{\mathit{ij}}=\frac{{\overline{\overline{\omega }}}_i}{\text{sinh}\left(\hslash \overline{\overline{\tau }}{\overline{\overline{\omega }}}_i\right)}{\delta }_{\mathit{ij}}{\overline{\overline{\mathrm{b}}}}_{\mathit{ij}}=\frac{{\overline{\overline{\omega }}}_i}{\text{tanh}\left(\hslash \overline{\overline{\tau }}{\overline{\overline{\omega }}}_i\right)}{\delta }_{\mathit{ij}}$$ (19)

After the introduction of equations 16, 17 and 18 in equation 15 the orthogonality property $\langle \overline{\mathbf{Q}}\mid \overline{\overline{\mathbf{Q}}}\rangle =\delta \left(\overline{\mathbf{Q}}-\mathit{J}\overline{\overline{\mathbf{Q}}}-\mathit{K}\right)$ and $\langle {\overline{\mathbf{Q}}}^{\prime }\mid {\overline{\overline{\mathbf{Q}}}}^{\prime }\rangle =\delta \left({\overline{\mathbf{Q}}}^{\prime }-\mathit{J}{\overline{\overline{\mathbf{Q}}}}^{\prime }-\mathit{K}\right)$ is used to carry out the integrals over the sets of coordinates $\overline{\mathbf{Q}}$ and ${\overline{\mathbf{Q}}}^{\prime }$. As a result, the polarizability tensor can be rewritten as,

$${\chi }_k\left(t\right)=\sqrt{\frac{\det \overline{\overline{\mathit{a}}}}{{\left(2\pi \hslash \right)}^N}}{\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}{\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }\times \langle {\overline{1}}_k\mid {\overline{\mathit{Q}}}^{\prime }\rangle \exp \left(\frac{i}{\hslash }\left[\frac{1}{2}{\overline{\overline{\mathit{Q}}}}^{\prime \mathrm{T}}\overline{\overline{\mathit{b}}}{\overline{\overline{\mathit{Q}}}}^{\prime }+\frac{1}{2}{\overline{\overline{\mathit{Q}}}}^{\mathrm{T}}\overline{\overline{\mathit{b}}}\overline{\overline{\mathit{Q}}}-{\overline{\overline{\mathit{Q}}}}^{\mathrm{T}}\overline{\overline{\mathit{a}}}{\overline{\overline{\mathit{Q}}}}^{\prime }\right]\right)\langle \overline{\mathit{Q}}\mid \overline{0}\rangle$$ (20)

where $\overline{\mathit{Q}}=\mathbf{J}\overline{\overline{\mathit{Q}}}+\mathbf{K}$ and ${\overline{\mathit{Q}}}^{\prime }=\mathbf{J}{\overline{\overline{\mathit{Q}}}}^{\prime }+\mathbf{K}$. It is noteworthy that equation 20 is similar to the time-dependent expression for the absorption cross section, which has been derived in our previous work³⁴. Therefore, in order to calculate the previous integral, it is possible to apply the same strategy by introducing a new set of variables Z and U:

$$\begin{array}{cc}\hfill \mathit{Z}& =\frac{1}{\sqrt{2}}\left(\overline{\overline{\mathit{Q}}}+{\overline{\overline{\mathit{Q}}}}^{\prime }\right)\hfill \\ \hfill \mathit{U}& =\frac{1}{\sqrt{2}}\left(\overline{\overline{\mathit{Q}}}-{\overline{\overline{\mathit{Q}}}}^{\prime }\right)\hfill \end{array}$$ (21)

The integral given in equation 20 is then rewritten in terms of this new set of coordinates, using the expression given in equation 16,

$$\begin{array}{cc}\hfill {\chi }_k\left(t\right)=& \sqrt{\frac{\det \left(\overline{\Gamma }\overline{\overline{\mathit{a}}}\right)}{{\left(2\pi i\hslash \right)}^{2N}}}\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\exp (-{\mathit{K}}^{\mathrm{T}}\overline{\Gamma }\mathit{K}){\int }_{-\infty }^{+\infty }d\mathit{U}{\int }_{-\infty }^{+\infty }d\mathit{Z}{\overline{Q}}_k^{\prime }\times \exp \left(-\frac{1}{2}{\mathit{Z}}^{\mathrm{T}}\mathit{D}\mathit{Z}-\sqrt{2}{\mathit{v}}^{\mathrm{T}}\mathit{Z}\right)\hfill \\ & \times \exp \left(-\frac{1}{2}{\mathit{U}}^{\mathrm{T}}\mathit{C}\mathit{U}\right)\hfill \end{array}$$ (22)

The auxiliary vector, v, is defined as ${\mathit{J}}^T\overline{\Gamma }\mathit{K}$. In order to exploit some intrinsic properties of hyperbolic functions, new matrices, C and D, have been introduced,

$$\mathit{C}=\overline{\overline{c}}+{\mathit{J}}^T\overline{\mathit{c}}\mathit{J}\mathit{D}=\overline{\overline{d}}+{\mathit{J}}^T\overline{\mathit{d}}\mathit{J}$$ (23)

with,

$${\mathrm{c}}_{\mathit{ij}}=\left(\frac{{\omega }_i}{\hslash }\text{coth}\left(\hslash \tau {\omega }_i\right)+\frac{{\omega }_i}{\hslash }\right){\delta }_{\mathit{ij}}{\mathrm{d}}_{\mathit{ij}}=\left(\frac{{\omega }_i}{\hslash }\text{tanh}\left(\hslash \tau {\omega }_i\right)+\frac{{\omega }_i}{\hslash }\right){\delta }_{\mathit{ij}}$$ (24)

Finally, the coordinate element ${\overline{Q}}_k^{\prime }$ must also be expressed in terms of Z and U. This can be done by using first the Duschinsky relation and then the definition given in eq. 21

$${\overline{Q}}_k^{\prime }=\sum _{l=1}^N{J}_{\mathit{kl}}{\overline{\overline{Q}}}_l^{\prime }+K_k=\frac{1}{\sqrt{2}}\sum _{l=1}^N{J}_{\mathit{kl}}(Z_l-U_l)+K_k$$ (25)

The final expression for χ_k(t) is,

$$\begin{array}{cc}\hfill {\chi }_k\left(t\right)=& \sqrt{\frac{\det \left(\overline{\Gamma }\overline{\overline{\mathit{a}}}\right)}{{\left(2\pi i\hslash \right)}^{2N}}}\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\exp (-{\mathit{K}}^{\mathrm{T}}\overline{\Gamma }\mathit{K})\int d\mathit{U}\int d\mathit{Z}\frac{1}{\sqrt{2}}\left(\sum _{l=1}^N{J}_{\mathit{kl}}(Z_l-U_l)+K_k\right)\hfill \\ & \times \exp \left(-\frac{1}{2}{\mathit{Z}}^{\mathrm{T}}\mathit{D}\mathit{Z}-\sqrt{2}{\mathit{v}}^{\mathrm{T}}\mathit{Z}\right)\exp \left(-\frac{1}{2}{\mathit{U}}^{\mathrm{T}}\mathit{C}\mathit{U}\right)\hfill \end{array}$$ (26)

In order to use the same strategy, which has been used for one-photon spectroscopies, we introduce an additional function, χ₀(t). χ₀(t) is the autocorrelation function for the one-photon vibronic spectroscopy under the Franck-Condon approximation.

$$\begin{array}{cc}\hfill {\chi }_0\left(t\right)=& \sqrt{\frac{\det \left(\overline{\Gamma }\overline{\overline{\mathit{a}}}\right)}{{\left(2\pi i\hslash \right)}^{2N}}}\exp (-{\mathit{K}}^{\mathrm{T}}\overline{\Gamma }\mathit{K})\int d\mathit{U}\int d\mathit{Z}\exp \left(-\frac{1}{2}{\mathit{Z}}^{\mathrm{T}}\mathit{D}\mathit{Z}-\sqrt{2}{\mathit{v}}^{\mathrm{T}}\mathit{Z}\right)\hfill \\ & \times \exp \left(-\frac{1}{2}{\mathit{U}}^{\mathrm{T}}\mathit{C}\mathit{U}\right)\hfill \end{array}$$ (27)

As shown in our previous work³⁴, this integral can be computed by using some properties of the multidimensional gaussian-type integrals;

$${\chi }_0\left(t\right)=\sqrt{\frac{\det \left(\overline{\Gamma }\overline{\overline{\mathit{a}}}\right)}{{\left(i\hslash \right)}^{2N}\det \left(\mathit{C}\mathit{D}\right)}}\times \exp \left(-{\mathit{K}}^{\mathrm{T}}\overline{\Gamma }\mathit{K}+{\mathit{v}}^{\mathrm{T}}{\mathit{D}}^{-1}\mathit{v}\right)$$ (28)

The difference between the integrals given in equations 27 and 22 is the presence of the factor ${\overline{Q}}_k^{\prime }$. However, it is possible to express equation 26 in terms of derivatives of equation 27 with respect to the elements of vector v and matrix C. This gives the possibility to use the analytic expression of χ₀(t) given in equation 28 to calculate explicitly the derivatives and to obtain a closed-form expression for the time-dependent polarizability tensor.

As a starting point, let us calculate the derivative of χ₀(t) with respect to a generic element of the vector v:

$$\begin{array}{cc}\hfill -\frac{1}{\sqrt{2}}\frac{\partial {\chi }_0\left(t\right)}{\partial v_l}=& \sqrt{\frac{\det \left(\overline{\Gamma }\overline{\overline{\mathit{a}}}\right)}{{\left(2\pi i\hslash \right)}^{2N}}}\exp \left(-{\mathit{K}}^{\mathrm{T}}\overline{\Gamma }\mathit{K}\right)\int d\mathit{U}\int d\mathit{Z}{Z}_l\hfill \\ & \times \exp \left(-\frac{1}{2}{\mathit{Z}}^{\mathrm{T}}\mathit{D}\mathit{Z}-\sqrt{2}{\mathit{v}}^{\mathrm{T}}\mathit{Z}\right)\exp \left(-\frac{1}{2}{\mathit{U}}^{\mathrm{T}}\mathit{C}\mathit{U}\right)\hfill \end{array}$$ (29)

From this relation, it is possible to express the terms of equation 26 with the scaling factor Z_l as derivatives of χ₀(t) with respect to the elements of the vector v.

By symmetry, the part of equation 26, which depends on U_l, is null. Therefore, it is possible to express χ_k(t) in the following way:

$${\chi }_k\left(t\right)=\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\left[-\frac{1}{\sqrt{2}}\sum _{l=1}^N{J}_{\mathit{kl}}\left(\frac{\partial {\chi }_0\left(t\right)}{\partial v_l}\right)+K_k{\chi }_0\left(t\right)\right]$$ (30)

A closed-form expression for the derivative ∂χ₀(t)/∂v_k can be easily calculated by direct differentiation of equation 28:

$$\frac{\partial {\chi }_0\left(t\right)}{\partial v_l}={\chi }_0\left[\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }^{\ast }\right]$$ (31)

D. Extension to the Herzberg-Teller term

The theoretical framework presented in the previous section can be straightforwardly extended to the calculation of the Herzberg-Teller contribution to the polarizability tensor. Let us start back from equation 12. We now include also the first-order terms from the Taylor expansion of the transition dipole moment, so the polarizability tensor is defined as,

$$\begin{array}{cc}\hfill {\alpha }_{\rho \sigma }^{\mathit{if}}=& \frac{1}{{\hslash }^2}{\left({\mu }_{m0,\rho }^e\right)}_{\text{eq}}{\left({\mu }_{m0,\sigma }^e\right)}_{\text{eq}}{\int }_0^{+\infty }\mathrm{d}t[\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle \hfill \\ & +\frac{i}{{\hslash }^2}\sum _{j=1}^N{\left({\mu }_{m0,\rho }^e\right)}_{\text{eq}}\cdot {\left(\frac{\partial {\mu }_{m0,\sigma }^e}{\partial {\overline{\overline{Q}}}_j}\right)}_{\text{eq}}\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_j\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle \hfill \\ & +\frac{i}{{\hslash }^2}\sum _{j=1}^N{\left(\frac{\partial {\mu }_{m0,\rho }^e}{\partial {\overline{\overline{Q}}}_j}\right)}_{\text{eq}}{\left({\mu }_{m0,\sigma }^e\right)}_{\text{eq}}\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid {\overline{\overline{Q}}}_j{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle \hfill \\ & +\frac{i}{{\hslash }^2}\sum _{j,k=1}^N{\left(\frac{\partial {\mu }_{\mathit{mi},\rho }^e}{\partial {\overline{\overline{Q}}}_j}\right)}_{\text{eq}}\cdot {\left(\frac{\partial {\mu }_{\mathit{mi},\sigma }^e}{\partial {\overline{\overline{Q}}}_k}\right)}_{\text{eq}}\langle {\psi }_{f\left(\underset{¯}{0}\right)}\mid {\overline{\overline{Q}}}_j{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_k\mid {\psi }_{i\left(\underset{¯}{0}\right)}\rangle ]\hfill \end{array}$$ (32)

By limiting our analysis to the fundamental bands, the inclusion of the Herzberg-Teller terms thus requires the calculation of the following additional terms:

$$\begin{array}{cc}\hfill {\chi }_{\mathit{FCHT},1}^{\left(j\right)}\left(t\right)& =\langle {\overline{1}}_k\mid e^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_j\mid \overline{0}\rangle \hfill \\ \hfill {\chi }_{\mathit{FCHT},2}^{\left(j\right)}\left(t\right)& =\langle {\overline{1}}_k\mid {\overline{\overline{Q}}}_j{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }\mid \overline{0}\rangle \hfill \\ \hfill {\chi }_{\mathit{HT}}^{(j,l)}\left(t\right)=& \langle {\overline{1}}_k\mid {\overline{\overline{Q}}}_j{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_l\mid \overline{0}\rangle \hfill \end{array}$$

For the sake of readability, we will drop the explicit reference to the time (t). It should be reminded in the following that χ is always function of the time. The derivation of analytic formulae for those terms can be done by following the same strategy used for the Franck-Condon case. First of all, let us rewrite ${\chi }_{\mathit{FCHT},1}^{\left(j\right)}$ using equation 16,

$${\chi }_{\mathit{FCHT},1}^{\left(j\right)}=\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\langle \overline{0}\mid {\overline{Q}}_k{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_j\mid \overline{0}\rangle$$ (33)

As done for the Franck-Condon approximation, it is possible to relate the initial state normal coordinate ${\overline{Q}}_f$ to the final state normal modes by using the Duschinsky approximation:

$${\chi }_{\mathit{FCHT},1}^{\left(j\right)}\left(t\right)=\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\left[\langle \overline{0}\mid K_k{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_j\mid \overline{0}\rangle +\sum _{s=1}^N{J}_{\mathit{ks}}\langle \overline{0}\mid {\overline{\overline{Q}}}_s{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_j\mid \overline{0}\rangle \right]$$ (34)

The first term of the previous expression is the same as the one, which has been calculated for the Franck-Condon case. The second term is more cumbersome, but can be calculated with the same technique as before, leading to the final expression,

$${\chi }_{\mathit{FCHT},1}^{\left(j\right)}=\sqrt{\frac{{\overline{\Gamma }}_k}{2\hslash }}\left[-\frac{1}{2}{K}_k\frac{\partial {\chi }_0\left(t\right)}{\partial v_j}+\sum _{s=1}^N{J}_{\mathit{ks}}\left(\frac{1}{4}\frac{{\partial }^2{\chi }_{\mathit{FC}}}{\partial v_s\partial v_j}+\frac{\partial {\chi }_0}{\partial C_{\mathit{sj}}}\right)\right]$$ (35)

The calculation of ${\chi }_{\mathit{FCHT},2}^{\left(j\right)}$ is the same as ${\chi }_{\mathit{FCHT},1}^{\left(j\right)}$. The only difference is that the coordinate operator ${\overline{\overline{Q}}}_j$ does not act on the ket $\mid \overline{\overline{\mathbf{Q}}}\rangle$ but on the bra $\langle {\overline{\overline{\mathbf{Q}}}}^{\prime }\mid$. By considering that $\langle {\overline{\overline{\mathbf{Q}}}}^{\prime }\mid$ is an eigenbra of the operator ${\overline{\overline{Q}}}_k$ with eigenvalue ${\overline{\overline{Q}}}_k$, it is easy to derive the following expression:

$${\chi }_{\mathit{FCHT},2}^{\left(j\right)}\left(t\right)=\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\left[-\frac{1}{2}{K}_k\frac{\partial {\chi }_0}{\partial v_j}+\sum _{s=1}^N{J}_{\mathit{ks}}\left(\frac{1}{4}\frac{{\partial }^2{\chi }_{\mathit{FC}}}{\partial v_s\partial v_j}-\frac{\partial {\chi }_0}{\partial C_{\mathit{sj}}}\right)\right]$$ (36)

The last term, ${\chi }_{\mathit{HT}}^{(j,k)}$, is more complex but can be taken out by applying the same strategy as for the previous terms. The Duschinsky transformation is used to rewrite ${\chi }_{\mathit{HT}}^{(j,k)}$ as,

$${\chi }_{\mathit{HT}}^{(j,l)}\left(t\right)=\sqrt{\frac{{\overline{\Gamma }}_k}{2}}\left[K_k\langle \overline{0}\mid {\overline{\overline{Q}}}_j{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_l\mid \overline{0}\rangle +\sum _{s=1}^N\left(J_{\mathit{ks}}\langle \overline{0}\mid {\overline{\overline{Q}}}_s{\overline{\overline{Q}}}_j{e}^{-i{\widehat{H}}_{\underset{¯}{m}}t∕\hslash }{\overline{\overline{Q}}}_l\mid \overline{0}\rangle \right)\right]$$ (37)

By rewriting the final-state normal coordinates in terms of the auxiliary variables Z and U as done before, we obtain the following expression:

$$\begin{array}{cc}\hfill {\chi }_{\mathit{HT}}^{(j,l)}& =\sqrt{\frac{{\overline{\Gamma }}_k}{2}}[K_k\left(\frac{{\partial }^2{\chi }_0}{\partial v_j\partial v_l}-\frac{\partial {\chi }_0}{\partial C_{\mathit{jl}}}\right)+\hfill \\ & \sum _{s=1}^N{J}_{\mathit{ks}}\left(\frac{1}{8}\frac{{\partial }^3{\chi }_0}{\partial v_s\partial v_j\partial v_l}-\frac{1}{2}\frac{{\partial }^2{\chi }_0}{\partial C_{\mathit{jl}}\partial v_s}-\frac{1}{2}\frac{{\partial }^2{\chi }_0}{\partial C_{\mathit{sl}}\partial v_j}+\frac{1}{2}\frac{{\partial }^2{\chi }_0}{\partial C_{\mathit{sj}}\partial v_l}\right)]\hfill \end{array}$$ (38)

The explicit expressions for the second- and third-order derivatives of the autocorrelation function χ₀(t) are the following,

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\chi }_0}{\partial v_k\partial v_l}=& {\chi }_0\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{k\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{k\lambda }{v}_{\lambda }^{\ast }\right)\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }^{\ast }\right)\hfill \\ & +{\chi }_0\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kl}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{lk}}\right)\hfill \end{array}$$ (39)

$$\frac{{\partial }^2{\chi }_0}{\partial {\mathrm{C}}_{\mathit{kj}}\partial v_l}=-\frac{1}{2}{\chi }_0{\left\{{\mathrm{C}}^{-1}\right\}}_{\mathit{kl}}\left[\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{j\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{j\lambda }{v}_{\lambda }^{\ast }\right]$$ (40)

$$\begin{array}{cc}\hfill \frac{{\partial }^3{\chi }_0}{\partial v_k\partial v_l\partial v_j}={\chi }_0& [\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jk}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kj}}\right)\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }^{\ast }\right)\hfill \\ & +\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jl}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{lj}}\right)\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{k\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{k\lambda }{v}_{\lambda }^{\ast }\right)\hfill \\ & +\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kl}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{lk}}\right)\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{j\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{j\lambda }{v}_{\lambda }^{\ast }\right)\hfill \\ & +\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{j\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{j\lambda }{v}_{\lambda }^{\ast }\right)\left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{k\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{k\lambda }{v}_{\lambda }^{\ast }\right)\hfill \\ & \times \left(\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }+\sum _{\lambda =1}^N{\left\{{\mathrm{D}}^{-1}\right\}}_{l\lambda }{v}_{\lambda }^{\ast }\right)]\hfill \end{array}$$ (41)

E. A special case; J=I

The previous formulae can be greatly simplified if we assume that the normal modes in the initial and intermediate states are the same, which means that the Duschinsky matrix is equal to the identity matrix I. Indeed, matrices C and D are then diagonal:

$$C_{\mathit{ij}}=\left(\frac{{\overline{\overline{\omega }}}_i}{\hslash }\text{coth}\left(\hslash \overline{\overline{\tau }}{\overline{\overline{\omega }}}_i\right)+\frac{{\overline{\omega }}_i}{\hslash }\right){\delta }_{\mathit{ij}}{D}_{\mathit{ij}}=\left(\frac{{\overline{\overline{\omega }}}_i}{\hslash }\text{tanh}\left(\hslash \overline{\overline{\tau }}{\overline{\overline{\omega }}}_i\right)+\frac{{\overline{\omega }}_i}{\hslash }\right){\delta }_{\mathit{ij}}$$ (42)

As a consequence, the autocorrelation function becomes,

$$\begin{array}{cc}\hfill {\chi }_0=\prod _{j=1}^N& \sqrt{\frac{{{\overline{\omega }}_j}^2}{\text{sinh}\left(\hslash \overline{\tau }{\overline{\omega }}_j\right)}}\cdot \sqrt{\frac{1}{[{\overline{\omega }}_j+{\overline{\overline{\omega }}}_j\text{tanh}(\hslash \overline{\overline{{\omega }_j}}\overline{\overline{\tau }}\left)\right][{\overline{\omega }}_j+{\overline{\overline{\omega }}}_j\text{coth}(\hslash \overline{\overline{{\omega }_j}}\overline{\overline{\tau }}\left)\right]}}\hfill \\ \hfill & \exp (-{K_j}^2{\overline{\omega }}_j)\exp \left(\frac{v_j^2}{{\overline{\overline{\omega }}}_j\text{tanh}\left(\hslash {\overline{\overline{\omega }}}_j\overline{\overline{\tau }}\right)+{\overline{\omega }}_j}\right)\hfill \end{array}$$ (43)

As done for the general case, the polarizability tensor can be written as a function of derivatives of χ₀ with respect to the elements of the vector v. The expression is further simplified since D is diagonal, so we have,

$$\frac{\partial {\chi }_0}{\partial v_k}=\sqrt{2}\frac{v_k}{{\overline{\overline{\omega }}}_k\text{tanh}\left(\hslash {\overline{\overline{\omega }}}_k\overline{\overline{\tau }}\right)+{\overline{\omega }}_k}\times {\chi }_0$$ (44)

As a result, the polarizability tensor at the Franck-Condon level can be written in the following way:

$$\begin{gathered} {\chi }_k=K_k{\chi }_0+\frac{\partial {\chi }_0\left(t\right)}{\partial v_k}=\left(\sqrt{2}\frac{v_k}{\overline{\overline{{\omega }_k}}\text{tanh}\left(\hslash {\overline{\overline{\omega }}}_k\overline{\overline{\tau }}\right)+{\overline{\omega }}_k}+K_k\right)\prod _{j=1}^N\sqrt{\frac{{{\overline{\omega }}_j}^2}{\text{sinh}\left(\hslash \overline{\tau }{\overline{\omega }}_j\right)}} \\ \times \sqrt{\frac{1}{[{\overline{\omega }}_i+{\overline{\overline{\omega }}}_j\text{tanh}(\hslash {\overline{\overline{\omega }}}_j\overline{\overline{\tau }}\left)\right][{\overline{\omega }}_j+{\overline{\overline{\omega }}}_j\text{coth}(\hslash {\overline{\overline{\omega }}}_j\overline{\overline{\tau }}\left)\right]}}\exp (-{K_j}^2{\overline{\omega }}_j)\exp \left(\frac{v_j^2}{{\overline{\overline{\omega }}}_j\text{tanh}\left(\hslash {\overline{\overline{\omega }}}_j\overline{\overline{\tau }}\right)+{\overline{\omega }}_j}\right) \end{gathered}$$ (45)

The factorization of the cross-correlation function under the Franck-Condon approximation in this simplified case is coherent with the result obtained by Neese and co-workers who neglected the Duschinsky mixing³⁰. This simplified formulation is more stable from a numerical point of view with respect to the general one and more efficient, and thus is well-suited when Duschinsky mixing is negligible. Furthermore, the computational cost is reduced in this second framework because a matrix inversion step and summations over the normal modes are avoided in this case. Herzberg-Teller terms can be included by using the same technique as for the more general case, but the expression for the derivatives of the autocorrelation function is simpler,

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\chi }_0}{\partial v_k\partial v_l}& =\left[{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{ll}}(v_l^{\ast }+v_l)+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kk}}(v_k^{\ast }+v_k)+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kl}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{lk}}\right]\times {\chi }_0\hfill \\ \hfill \frac{{\partial }^2{\chi }_0}{\partial {\mathrm{C}}_{\mathit{kj}}\partial v_l}& =\left[-\frac{1}{2}{\left\{{\mathrm{C}}^{-1}\right\}}_{\mathit{kl}}\cdot \left(v_j^{\ast }{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jj}}+v_j{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jj}}\right)\right]\times {\chi }_0\hfill \\ \hfill \frac{{\partial }^3{\chi }_0}{\partial v_k\partial v_l\partial v_j}& =[{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kk}}\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{lj}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jl}}\right)\cdot (v_k^{\ast }+v_k)+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{ll}}\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kj}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jk}}\right)\hfill \\ & \cdot (v_l^{\ast }+v_l){\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{ll}}\left({\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kj}}+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jk}}\right)\cdot (v_l^{\ast }+v_l)+{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{ll}}{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{kk}}{\left\{{\mathrm{D}}^{-1}\right\}}_{\mathit{jj}}\hfill \\ & \times (v_l^{\ast }+v_l)(v_k^{\ast }+v_k)(v_j^{\ast }+v_j)]\times {\chi }_0\hfill \end{array}$$ (46)

F. Anharmonicity and solvation effects

Proper account of the mode mixing and the shape of the initial- and intermediate-state PESs can be considered as the most elaborate model to simulate RR spectra. In this way, however, two important effects such as the anharmonicity of the PESs and the environmental effects like the solvent are overlooked.

An effective way to include the contribution of the former is by mean of the second-order vibrational perturbation theory (VPT2). A full anharmonic treatment of the vibronic transition would require a more complex derivation of the equations of the cross-correlation function but would remain out of question due to the steep computational cost, which makes it only conceivable for the smallest systems. Since Resonance Raman is a vibrational spectroscopy, a correction of the harmonic frequency can be highly effective, in order to correct the band positions, with no impact on the computational cost required to simulate the RR spectrum itself. In order to compute the anharmonic frequencies, the third and semi-diagonal quartic force constants are generated by numerical differentiation of quadratic force constants along the normal coordinates. The VPT2 is known to suffer from the presence of singularities due to Fermi resonances, which results in unphysical contributions from the anharmonic terms. Resonant terms are identified by mean of ad hoc criteria and treated variationally in the so-called generalized VPT2 scheme^40,41. Those anharmonic frequencies are then used in place of the harmonic ones in the definition of the cross-correlation function, which leads to corrected intensities too. Moreover, anharmonic frequencies can be used to compute accurate partition functions and so abundances of species inside mixtures, when necessary to match experimental conditions^42,43. Regarding the excited electronic state, if analytical force constants are not available, which is the case for most quantum chemical packages, calculation of anharmonic frequencies at the VPT2 level becomes prohibitive. This problem can be overcome by using the mode-specific scaling scheme proposed by some of us and relying on the Duschinsky transformation⁴⁴. It allows the definition of a scaling factor for each excited-state frequency based on the anharmonic corrections obtained for the ground-state frequencies, following the relation,

$${\overline{\overline{\omega }}}_j^{\mathit{anh}}=\left(\sum _i{J}_{\mathit{ji}}^2\frac{{\overline{\omega }}_i^{\mathit{anh}}}{{\overline{\overline{\omega }}}_i^{\mathit{harm}}}\right){\overline{\omega }}_j^{\mathit{harm}}$$ (47)

It should be noted that in Resonance Raman, it is simple to choose a region of interest and only treat anharmonically the contributing modes within it. This is particularly interesting for large systems, since it gives the possibility to reduce dramatically the computational cost with a minimal impact on the accuracy of the anharmonic correction for those modes.

RR spectra are usually recorded in solution, therefore a correct description of solvation effects is needed to reproduce experimental data. Solvation effects, like anharmonicity, affect the vibrational frequencies, leading to a further correction of the peak position, as well as the bands intensity. In this work, solvation effects have been included with the Polarizable Continuum Model (PCM), which has already been used for the simulation of RR spectra with time-independent methods^45–47. Within PCM, the solvent is a polarizable continuum characterized by a dielectric constant. The solute is accomodated in a molecule-shaped cavity inside the continuum. The electrostatic equation is then solved numerically taking into account mutual interaction effects between the density of charge of the solute and the dielectric continuum’s polarization. This is done by including a suitable interaction term in the molecular Hamiltonian⁴⁸. As it has been pointed out, when spectroscopic properties must be simulated with PCM, the correct solvation regime must be used. For example, for the simulation of absorption spectra, a non-equilibrium regime is usually assumed, where the electronic degrees of freedom of the solute are equilibrated with the excited-state electronic density, while the nuclear degrees of freedom stay equilibrated with the ground-state electronic density^49,50. For RR spectroscopy, the definition of the correct solvation regime is far from trivial. In fact, it is evident from the TD picture that RR is a dynamical process and, depending on the time-scales of the time-evolution, some of the nuclear degrees of freedom can be assumed to be static. To simulate this behaviour, vibrational non-equilibrium PCM for excited states should be used, but this approach has never been investigated. To overcome this limitation, three different solvation regimes for the simulation of RR spectra have been proposed¹⁹:

• equilibrium regime: both nuclear and electronic degrees of freedom of the solvent are assumed to be equilibrated for the calculation of the properties of both electronic states.

• fixed cavity regime: the calculations related to the excited-state properties are carried out under the equilibrium regime for the electronic degrees of freedom, while the cavity is kept fixed. In this way, vibrational non-equilibrium effects can be partially reproduced.

• full non-equilibrium regime: in addition to the vibrational non-equilibrium regime, the vertical excitation energy is computed under the electronic non-equilibrium regime.

As it has been pointed out¹⁹, the choice of the solvation regime must be coherent with the model of the PES. For adiabatic models, the equilibrium geometry of the excited state must be optimized, and the PCM cavity is displaced during the optimization process. Therefore the first equilibrium regime is best-suited in this case. For vertical models, the other two regimes are better-suited.

III. COMPUTATIONAL DETAILS

All calculations of electronic structure and the vibronic spectra were done with a locally modified version of the Gaussian suite of quantum chemical programs⁵¹. The electronic calculations have been carried out within the density functional theory (DFT) for the ground states, and its time-dependent extension (TD-DFT), for the excited states. Except when written otherwise, the B3LYP functional⁵² with the double-ζ basis set SNSD⁵³, developed for spectroscopic studies of medium-to-large molecular systems, has been used. This basis set has been built from the polarized double-ζ basis set N07D^54–57 by consistently including diffuse s functions on all atoms, and one set of diffuse polarized functions (d on heavy atoms and p on hydrogens). For benzyl radical, basis set cc-pVTZ was used together with B3LYP, while for Tris(bipyridine)ruthenium(II) chloride, the B3PW91 functional⁵⁸ together with basis set LanL2DZ⁵⁹ has been used.

Solvation effects have been included in the QM calculations by means of the PCM, as described previously. In particular, its integral-equation formulation (IEF-PCM) has been used⁶⁰ and the solute cavity has been built by using a set of interlocking spheres centered on the atoms with the following radii (in Å): 1.443 for hydrogen, 1.926 for carbon and 1.750 for oxygen, each scaled by a factor of 1.1, which is the default value inside Gaussian. The solvent static and dynamic dielectric constant used here are ϵ = 78.36 and ϵ_∞ = 1.78 for water and ϵ = 35.69 and ϵ_∞ = 1.81 for acetonitrile. As mentioned before, different solvation regimes can be chosen for the simulation of RR spectra. In this work, we will use as reference the equilibrium regime for the adiabatic models and the fixed-cavity regime for the vertical models.

As explained in our previous work²¹, the PES of the excited state can be described in different ways and at different level of approximations, giving rise to different definitions of the Duschinsky matrix and the shift vector. In Adiabatic Hessian (AH), the PES of the final state is expanded about its own minimum. From a practical point of view, this model requires the calculation of the optimized geometry of the excited state and, subsequently, of its harmonic frequencies. However, the harmonic PES of the excited state can be also expanded about the equilibrium geometry of the ground state, in the so-called Vertical Hessian (VH) model. Simplified formulations of both AH and VH, respectively named Vertical Gradient (VG) and Adiabatic Shift (AS) have been proposed, in which the PES of the excited state is equal to the ground state’s one. In the first case, only the gradient of the excited-state PES must be computed while, in the second one, only the equilibrium geometry of the excited state is needed. Let us remark that both AS and VG models, in which both Duschinsky mixing and frequency changes are neglected, are usually known as independent-mode displaced harmonic oscillator (IMDHO) models in the field of Resonance-Raman spectroscopy⁶¹. Furthermore, the independent-mode displaced harmonic oscillator with frequency alteration model (IMDHOFA)³³, in which frequency changes are taken into account while Duschinsky mixing is neglected, is equivalent to the AH|FC model by setting the Duschinsky matrix equal to the identity matrix. The AH approach will be used by default. The effects of the different models on RR spectra will be shown for the case of benzyl radical. For a more detailed discussion, see ref.⁶².

As mentioned before, the harmonic frequencies can be replaced by their anharmonic counterparts in order to improve the accuracy of the results. In this work, the latter are computed using the second-order vibrational perturbation theory (VPT2)^41,63,64. The necessary third and semi-diagonal fourth derivatives of the potential energy are obtained by numerical differentiation of the analytic harmonic force constants along the mass-weighted normal coordinates (Q) with the Gaussian default step, $\delta \mathit{Q}=0.01\mathrm{Å}\times \sqrt{\mathrm{amu}}$^40,41. Even if analytic formulae for TD-DFT energy second derivatives have been proposed^65,66, due to the unavailability of them in our TD-DFT calculations and to reduce the computational times, the anharmonic frequencies of the excited state have been calculated by using the extrapolation procedure presented before.

TI RR calculations have been carried out by using the implementation presented in ref.¹⁹. To limit the number of integrals to include in the sum-over-states, an approximated formulation of the class-based prescreening proposed earlier for one-photon absorption and emission^11,37 has been used. This prescreening scheme relies on a categorization of the transitions in so-called classes, which correspond to the number of simultaneously excited oscillators in the excited state. Class 1 (overtones) and class 2 (2-state combinations) are treated up to a specified number of quanta for each oscillator, $C_1^{\max }$ and $C_2^{\max }$, respectively. Overlap integrals and information related to them are stored and used for the prescreening to define the maximum number of quanta for each oscillator in order to choose and compute up to $N_I^{\max }$ transitions, evaluated to be the most significant ones, for each class starting from class 3. In the present work, if not specified otherwise, sum-over-states spectra were computed with the default settings, that is,

$$C_1^{\max }=20,C_2^{\max }=13,N_I^{\max }={10}^8$$

and up to 7 simultaneously exited modes in the final state have been taken into account (class 7).

For all TI and TD calculations, only transitions to fundamental bands will be computed.

For the TD approach, the most time-consuming step is the sampling of the correlation functions. A Gauss-Legendre algorithm has been implemented for the calculation of the half Fourier-Transform in order to reduce the number of sampling points and consequently speedup the calculation. Furthermore, each time-step of the correlation function is independent of the others, and therefore it is possible to speed up further the calculation by carrying out the sampling of this function is parallel. If not specified otherwise, all the TD calculations have been carried out by sampling the Fourier integral on 2¹² points with a time step of 2.44 · 10⁻¹⁶ s. Those parameters result in a satisfactory convergence in all cases we have tested.

When the calculated RR spectra are compared to the experimental ones, the choice of the incident wavelength to use in the calculation is not straightforward. In fact, the calculated vertical energy difference between the ground and excited states can be significantly different from the experimental one. In such cases, the laser wavelength used in the experiment cannot be directly used in the calculation. Following a procedure previously used for TI calculations^19,47, the incident frequency has been set to reproduce the difference between the experimental laser frequency and the measured absorption maximum, using the calculated vertical energy as λ_max.

The damping constant can be extracted from the comparison between the experimental and theoretical one-photon absorption spectra. Indeed, it is related to the HWHM of the Lorentzian broadening to be applied to match the theoretical spectrum to its experimental counterpart. For the sake of simplicity, we have chosen a value of 100 cm⁻¹, in agreement with previous work³⁷. We have also tested higher values of the damping constant with no significant changes. Furthermore, each peak was calculated using equation 2 and then broaden by means of Gaussian or Lorentzian distribution functions, as explained in ref.¹⁹.

IV. EXAMPLES OF APPLICATIONS

A. Anthracene

RR spectroscopy has been used in analytical chemistry as a tool for the detection of different polycyclic aromatic hydrocarbons (PAH) in complex environment like coal liquids^67–69 or DNA derivatives⁷⁰. Even if a lot of high-resolution RR spectra of PAHs are now available thanks to this interest, they have been scarcely studied from a theoretical point of view, except for pyrene^24,47,71. In this work, we will focus on another PAH, anthracene. Thanks to its rigidity, mode mixing and Herzberg-Teller effects are usually negligible for PAHs, which makes it an ideal system to test new methods and implementations. The absence of mode-mixing results in a more efficient prescreening, so there is no risk of convergence issue for the spectrum computed with the TI approach, which can be used as a reference for the TD results.

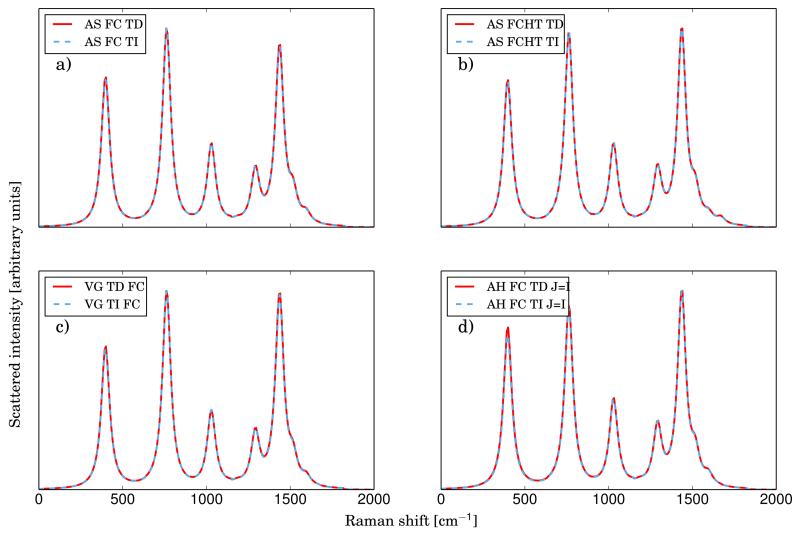
Figure 1 shows the TI and TD spectra calculated in vacuum with different levels of approximations for the PES of the electronic intermediate state. The excitation wavelength has been set to 251 nm (39811 cm⁻¹), which corresponds to the energy difference the vibrational ground states (0-0 transition) of S₀ and S₉. This electronic transition gives an intense band in the UV region⁷². As mentioned before, the time-independent simulation provides a complete convergence of the spectrum (> 99%) with the standard parameters. In all TD and TI calculations, Lorentzian distribution functions with half-widths at half-maximum of 30 cm⁻¹ have been used in order to simulate the broadening effects.

FIG. 1.

Comparison of the RR spectra of anthracene calculated with different models for the PES of the intermediate state (panel a: AS|FC, panel b: AS|FCHT, panel c: VG|FC, panel d: AH| FC with J = I. The excitation wavelength has been set to 251 nm (corresponds to the S₉ state) and Lorentzian functions with HWHM of 30 cm⁻¹ have been used to broaden each peak

The results obtained with the simplified Adiabatic Shift (AS) and Vertical Gradient (VG) models are given in panels (a) and (c) of figure 1. The remarkable agreement proves the reliability of our theoretical derivation when the Duschinsky matrix is assumed to be the identity matrix. The agreement remains excellent with the inclusion of the HT terms, as shown in panel (b). Finally, even under the more general IMDHOFA model³³, which is equivalent to the AH|FC by setting the Duschinsky matrix equal to the identity matrix, the RR spectra simulated at the TD and TI levels are still superimposable, as shown in panel (d). It should be underlined that the bandshape of the RR spectrum is the same independently of the level of approximation of the PES and the transition dipole moment. This is to be expected, since the S₉ ← S₀ transition is fully allowed, thus the HT contribution is negligible, and anthracene does not undergo significant changes upon the transition (so the minima of the PES are almost at the vertical of each other and the mode-mixing is low).

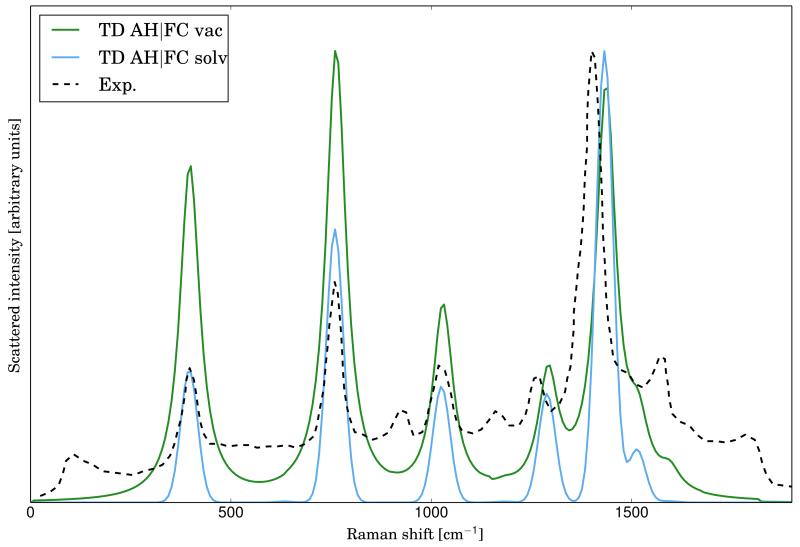
The experimental RR spectrum of anthracene has been measured in a solution of acetonitrile with an excitation wavelength of 251 nm⁶⁸, which corresponds to the transition to S₉ electronic state. Therefore, the previous results can be directly compared with the experimental ones. In figure 2, the experimental RR spectrum, together with the theoretical ones calculated at the AH|FC level both in vacuum and solvent, are reported. Solvent effects have been included by mean of PCM, as reported in the computational details, assuming an equilibrium solvation regime, which is the best-suited one for adiabatic models¹⁹. Comparison between the theoretical and experimental spectra shows that the positions of the most intense bands are already well reproduced in the spectrum calculated in vacuum, even if significant discrepancies are present regarding the peak intensity in the region under 1000 cm⁻¹. Those differences are strongly reduced when solvent effects are taken into account. It should be noted that in this case the solvent does not modify significantly the frequencies, but has a remarkable effect on the intensity.

FIG. 2.

Comparison of the experimental RR spectrum of anthracene (in dashed black, taken from ref.⁶⁸) with the calculated spectra at the AH|FC level in vacuum (solid line, green) and with solvent effect (solid line, clean blue). Lorentzian broadening functions with HWHM of 30 cm ⁻¹ have been used

B. Phenoxyl radical

RR spectroscopy has been also widely applied to the characterization of radical species produced by photochemical reactions on closed-shell systems. Indeed, even if radical species are highly unstable, their lifetime is comparable with the time-scales of the RR scattering process, which is therefore able to detect them. Furthermore, time-resolved RR experiments provide an estimation of the lifetime of the radical. However, a theoretical prediction of the RR spectrum of the radical is usually needed in order to confirm that the RR peaks are due to the radical itself.

Radical species made by photolysis of phenol derivatives have been studied with particular care as prototypes models of photochemical transients of aromatic aminoacids. Those transients have a remarkable interest in biology because they are involved in the UV inactivation of enzymes. RR spectroscopy of aromatic aminoacids has also been used to monitor conformational changes in proteins.

In this section we will analyze the RR spectrum of the phenoxyl radical, which is the product of the photolysis of phenol. The incident wavelength has been set to 368 nm (27151 cm⁻¹), in resonance with the D₃ excited state.

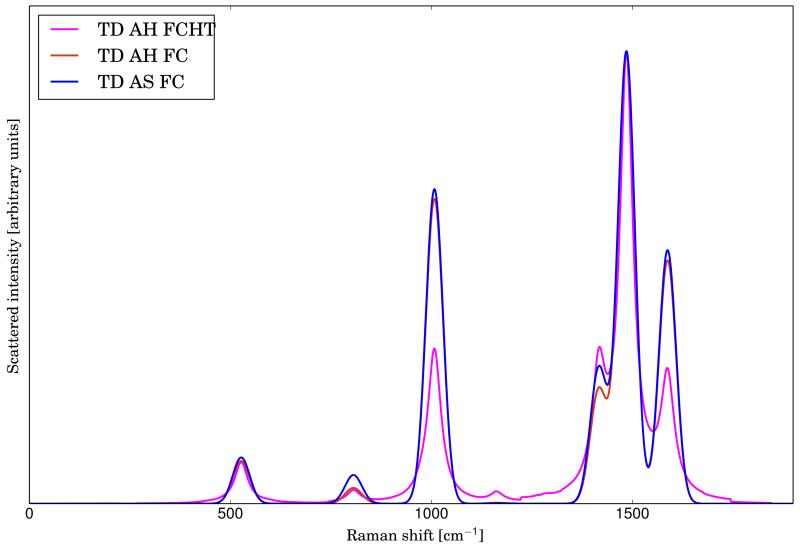
Figure 3 shows the RR spectra of phenoxyl radical simulated within the TD formulation at different levels of approximation for the PES of the intermediate state. All TD calculations have been carried out in vacuum with the default parameters and broadening effects have been simulated with Gaussian functions with HWHM of 20 cm⁻¹. It is noteworthy that the Franck-Condon spectra calculated with the AS and AH models are very similar, which means that, for this system, Duschinsky mixings are negligible. However, the changes caused by the inclusion of the HT terms are remarkable. For example, the intensity of the bands at about 1000 cm⁻¹ is significantly decreased with the inclusion of HT effects. The same behaviour can be seen for the shoulder at 1600 cm⁻¹.

FIG. 3.

Comparison of the RR spectrum of phenoxyl radical calculated with the AS|FC (solid line, blue), AH|FC (solid line, red) and AH|FCHT (solid line, magenta) models. Gaussian broadening functions with HWHM of 20 cm⁻¹ have been used. The excitation wavelength have been set to 368 nm (corresponding to the D₃ electronic level)

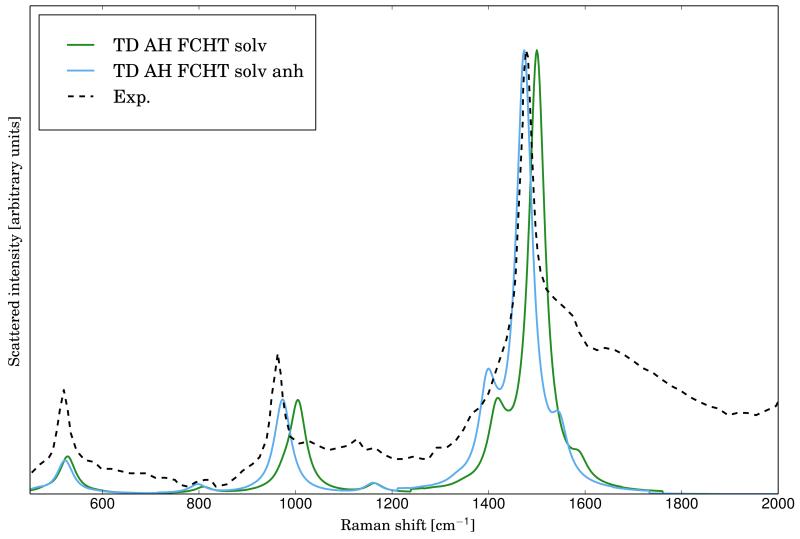
The RR spectra calculated at the AH|FCHT level with the inclusion of solvent effects using harmonic and anharmonic frequencies is reported in figure4, together with the experimental spectrum, taken from ref.⁷³. Solvent effects have been included with PCM in the equilibrium solvation regime, and anharmonicity effects have been included with the scheme presented before. As before, both TD calculations have been carried out with the standard set of parameters and Lorentzian broadening functions with HWHM of 20 cm⁻¹ have been used in order to simulate the broadening effect. The intensities of the three main bands of the experimental spectrum are well reproduced at the harmonic level. However, there is a slight shift of the position of all the main bands, which is caused by the neglect of anharmonicity effects. Indeed, by using the anharmonic frequencies in place of the harmonic ones, the proper band positions are obtained with little changes to the intensities.

FIG. 4.

Comparison of the experimental (taken from ref.⁷³) RR spectrum of the phenoxyl radical with the calculated ones at the AH|FCHT level within the harmonic (solid line, green) and anharmonic (solid line, blue) approximation. The excitation wavelength has been set to 368 nm (transition to the D₃ electronic level). Lorentzian broadening function with HWHM of 20 cm ⁻¹ have been used.

C. Benzyl radical

As for the phenoxyl radical, the benzyl radical has been widely studied with different types of spectroscopy due to its importance as a prototype of aromatic molecules. It can be produced by photolysis of benzene derivatives and can be detected by means of absorption spectroscopy⁷⁴. The electronic excited states involved in the transitions which contribute mostly to the UV-vis spectrum of benzyl radical are D₃ and D₅, corresponding to two intense bands at about 310 and 250 nm, respectively. The RR spectrum with the incident frequency coinciding with the transition energy to D₃ has been measured by Langkilde⁷⁵. However the interpretation of the spectrum is based on a simplified model⁷⁶. A more complete analysis has been done by Schatz and co-workers⁷⁷, but also in this case the agreement with the experimental spectrum is not satisfactory and does not permit an assignment of every band. In the following, we will show how our model, by including different effects, can provide a remarkable support to experimental measurements.

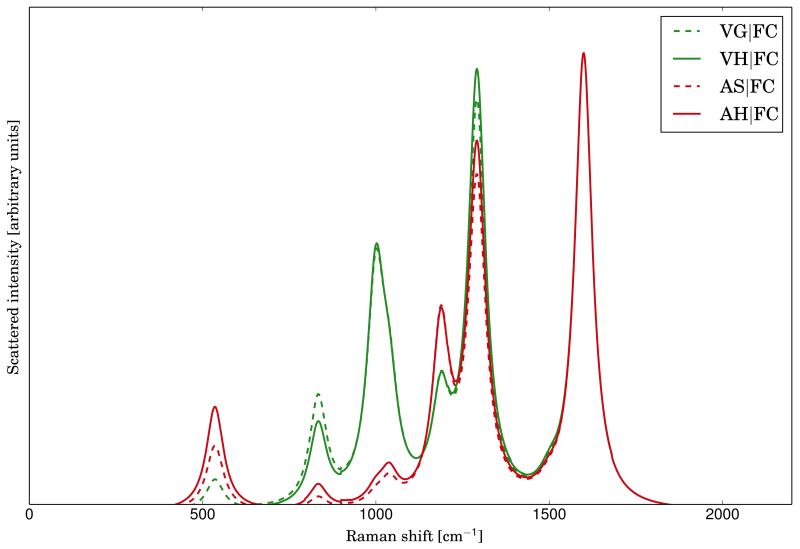
As a first step, the RR spectrum of the benzyl radical has been calculated using both vertical and adiabatic models in order to evaluate the difference between them. The geometry optimization and frequency calculations for the D₀ state, as well as the geometry optimization, force and frequencies calculation for the excited state, have been carried out by using the exchange-correlation functional B3LYP and the cc-pVTZ basis set. The results of the calculations are reported in Figure 5. It is noteworthy that for both adiabatic and vertical models, using the correct excited-state PES does not change significantly the overall bandshape. However, the difference between the spectra calculated with the adiabatic and the vertical models is remarkable, especially in the energy range under 1100 cm⁻¹. For example, the peak at about 1000 cm⁻¹ has a much higher intensity in the VG and VH spectra than in the AS and AH ones. Furthermore, the spectra calculated with the adiabatic models show a peak around 500 cm⁻¹ whose intensity is much lower in the VG spectrum and is nearly vanishing in the VH one^47,62.

FIG. 5.

Simulated TD RR spectrum of the benzyl radical with an excitation wavelength of 320 nm (transition to the D₃ electronic level) with the AH (solid line, red) and the VH (solid line, green) models. The spectra calculated with the simplified AS (dashed line, red) and VG (dashed line, green) are also reported. For all spectra, Lorentzian broadening functions with HWHM of 30 cm⁻¹ have been used.

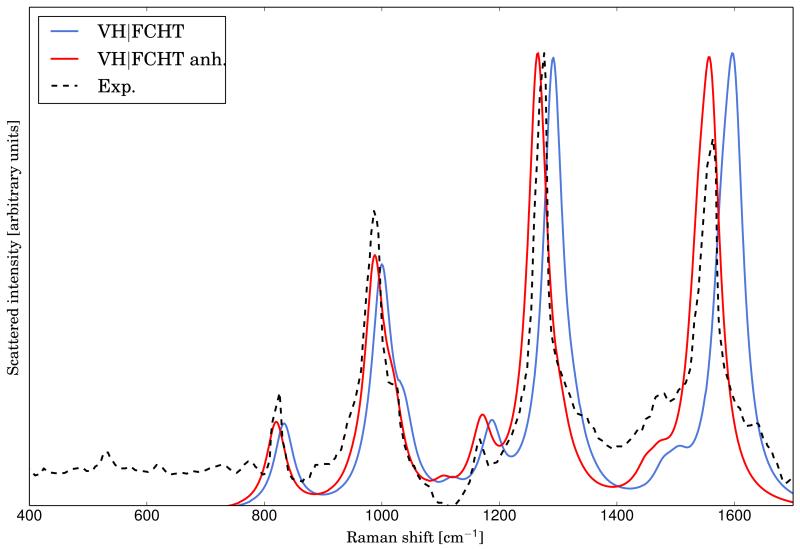
Figure 6 shows the experimental spectrum (taken from ref.⁷⁵) together with the theoretical ones, calculated with both VH and AH models including the Herzberg-Teller terms. It is noteworthy that the overall bandshape over 1100 cm⁻¹ is well reproduced in both VH|FCHT and AH|FCHT spectra, even if slight discrepancies in band positions and intensities are still present. However, for the bands under 1100 cm⁻¹, agreement between the experimental spectrum and the AH|FCHT one is rather poor, while the VH|FCHT model reproduces satisfactorily the intensity of each peak. Therefore, those results tend to confirm that vertical models are better-suited for the description of large-amplitude motions than their adiabatic counterparts.

FIG. 6.

Experimental (dashed line, black) and calculated RR spectra of the benzyl radical with an excitation wavelength of 320 nm (transition to the D₃ electronic level). For the theoretical spectra, Lorentzian broadening functions with HWHM of 30 cm⁻¹ have been used to match the experimental spectrum.

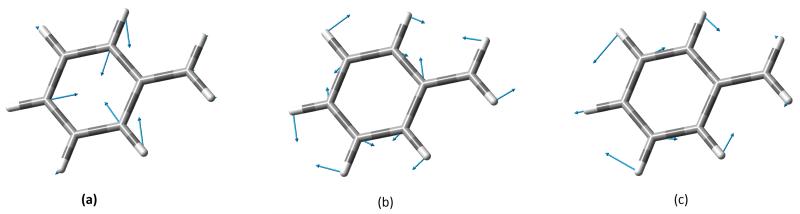
Figure 6 shows also the VH|FCHT spectrum where the anharmonic frequencies have been used in place of the harmonic ones. It is noteworthy that, with our TD approach, the agreement between the calculated and theoretical spectra is significantly improved with respect to the most recent study of the RR spectrum of this molecule⁷⁷. In particular, in the region between 900 and 1400 cm⁻¹ agreement between the experimental and theoretical intensities becomes significantly better and allows a unambiguous assignment of the most intense bands of the spectrum. For example, the intense band at about 1300 cm⁻¹ corresponds to an in-plane deformation of the benzene ring, which can be related to mode 14 in the Wilson notation⁷⁸. Following the same notation, it is easy to assign the band at 1600 cm⁻¹ to mode 8a, and the band at 1000 cm⁻¹ to mode 12. A graphical representation of those three modes is given in figure 7.

FIG. 7.

Graphical representation of the normal modes giving rise to the three main bands in the RR spectrum of the benzyl radical. Following the Wilson notation for the benzene normal modes, (a) corresponds to 12, (b) to 14 and (c) to 8a normal modes.

D. Tris(bipyridine)ruthenium(II) chloride

RR spectroscopy, thanks to the properties mentioned before, is a powerful tool for the study of metal complexes^5,61. In fact, UV-vis spectra of metal complexes usually involve transitions to several excited states and it is far from straightforward to assign each band to a specific electronic transition. However, additional information about the nature of a specific excited state (like for example metal-to-ligand charge transfer or ligand-centered transition) can be obtained from a RR spectrum by tuning the incident frequency to match the transition energy to this state. In fact, the selective enhancement of the bands depends on the transition electron density to the specific excited level.

The simulation of RR spectra of metal complexes is still a challenge for theoretical chemistry because it requires both an accurate description of the PES of the ground and excited electronic states, as well as a reliable method to simulate RR spectra. Some theoretical analysis of RR spectra of metal complexes are present in the literature⁷⁹, but they are usually relying on simplified models. In this section we will show that a complete simulation of RR spectra does not lead to significant additional computational times. Therefore, even if the most accurate model for the simulation of RR spectra is used, it is still not the most expensive step of the whole procedure.

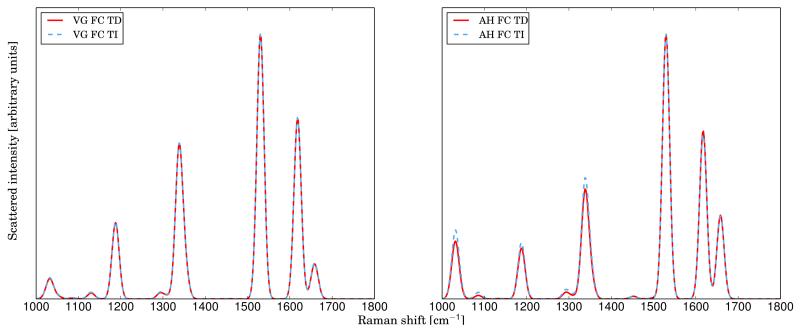
Tris(bipyridine)ruthenium(II) chloride ([Ru(bipy)₃]Cl₂)^80,81 has been chosen as a test-case to demonstrate the reliability of our approach also for larger systems. Following the procedure presented in recent theoretical studies^82,83, geometry optimization, as well as force and frequency calculations have been carried out by using the exchange-correlation functional B3PW91 with the LANL2DZ basis set. The incident wavelength has been set to 458 nm (21834 cm⁻¹), in resonance with the S₅ excited state, which is a metal-to-ligand charge transfer excited state⁸². In the left panel of figure 8 the spectra calculated at the TI and TD levels with the VG|FC model are reported. Both calculations have been done with the standard parameters given in the computational details, which provide a remarkable agreement between the two spectra. The right panel of figure 8 corresponds to the same work, using the AH|FC level. In this case as well, the agreement between the two spectra is remarkable, even if some small discrepancies can be detected for the less intense bands which are due to an incomplete convergence of the TI spectra.

FIG. 8.

Comparison between the VG|FC (on the left) and AH|FC (on the right) spectra of Tris(bipyridine)ruthenium(II) chloride calculated with the TI and TD procedures. The excitation wavelength has been set to 457 nm (transition to the excited state S₅). For all spectra, Gaussian functions with HWHM of 10 cm⁻¹ have been used to simulate the broadening effects.

Figure 9 shows a pictorial comparison of the simulation time of the RR spectrum with respect to the other steps of the calculations of the data directly needed to generate it. For VG|FC, the most expensive step is the harmonic frequency calculation for the ground state, while the time for the simulation of the RR spectrum is negligible thanks to the simplified model derived for the special case in which mode-mixing effects are neglected. In the right panel of figure 9 the same comparison is given for the more accurate AH|FC model. Even if in this case the absolute time of simulation of the RR spectrum increases, because of the more general theoretical formulation, the relative impact of this step on the overall time of computation is still negligible. In fact, for the AH model, the frequencies of the excited state must be calculated, and this becomes the bottleneck of the calculation.

FIG. 9.

Relative weight of the calculation time for each computation step needed to generate input data and simulate the RR spectrum of Tris(bipyridine)ruthenium(II) with VG (on the left) and AH (on the right) models.

CONCLUSIONS

In this work, a new general formulation of the time-dependent theory of Resonance-Raman spectroscopy has been presented, based on an approach previously used for the simulation of one-photon absorption and emission spectra³⁴. The generality and flexibility of the underlying model allow its easy generalization to the inclusion of both Duschinsky mixing and Herzberg-Teller effects, which are usually neglected in the simulation of RR spectra. Furthermore, the implementation is able to include both adiabatic and vertical models of the intermediate-state PES.

The TD-RR theory has been implemented in the Gaussian suite of program, and shares the same framework as our previous implementation of the time-independent theory of RR¹⁹. In this way, the reliability of the TD-RR implementation has been tested by using the previously validated method as a reference. Our tests have shown that, for large-size systems, the computational cost of the calculations needed to generate the input data greatly exceeds that needed for simulating the RR spectrum. Therefore, for a given set of input data, the most accurate and feasible model should always be preferred as the additional computational cost remains always negligible. As a consequence, the reduction of the overall computational cost as to be sought in the generation of input data using approximated strategies (AS and VG). Furthermore, cheaper methods for the computation of harmonic frequencies of excited-state must be found. In our opinion, this goal can be accomplished by using methods where analytical second derivatives are available^65,66. Finally, thanks to the implementation of the TD-RR theory inside Gaussian, it is straightforward to extend it to the study of molecules in solution by using the polarizabile continuum model. Additionally, an approximated model to include anharmonicity effects in both PES of the ground and intermediate states has been presented.

Applications of this procedure to some medium-size molecules have shown that, in order to reach a satisfactory agreement with the experimental spectra, inclusion of Herzberg-Teller terms, as well as the proper description of the excited-state PES is needed. Furthermore, the choice of different harmonic models (adiabatic and vertical) for the excited-state PES can affect significantly the overall bandshape and, in particular, vertical models seem best-suited when large-amplitude motions are present. Finally, when solvation effects are included by mean of the polarizable continuum model, the proper solvation regime must be chosen consistently with the harmonic model of the excited state PES.