PASSIVE BIAXIAL MECHANICAL PROPERTIES AND IN VIVO AXIAL PRE-STRETCH OF THE DISEASED HUMAN FEMOROPOPLITEAL AND TIBIAL ARTERIES

Abstract

Surgical and interventional therapies for atherosclerotic lesions of the infrainguinal arteries are notorious for high rates of failure. Frequently, this leads to expensive reinterventions, return of disabling symptoms, or limb loss. Interaction between the artery and repair material likely plays an important role in reconstruction failure, but data describing the mechanical properties and functional characteristics of human femoropopliteal and tibial arteries are currently not available. Diseased superficial femoral (SFA, n=10), popliteal (PA, n=8), and tibial arteries (TA, n=3) from 10 patients with critical limb ischemia were tested to determine passive mechanical properties using planar biaxial extension. All specimens exhibited large non-linear deformations and anisotropy. Under equibiaxial loading, all arteries were stiffer in the circumferential direction than in the longitudinal direction. Anisotropy and longitudinal compliance decreased distally, but circumferential compliance increased, possibly to maintain a homeostatic multiaxial stress state. Constitutive parameters for a 4-fiber family invariant-based model were determined for all tissues to calculate in vivo axial pre-stretch that allows the artery to function in the most energy efficient manner while also preventing buckling during extremity flexion. Calculated axial pre-stretch was found to decrease with age, disease severity, and more distal arterial location. Histological analysis of the femoropopliteal artery demonstrated a distinct sub-adventitial layer of longitudinal elastin fibers that appeared thicker in healthier arteries. The femoropopliteal artery characteristics and properties determined in this study may assist in devising better diagnostic and treatment modalities for patients with peripheral arterial disease.

1. INTRODUCTION

Peripheral artery disease (PAD) is primarily an atherothrombotic condition reducing blood flow to the lower limbs. It is a major contributor to public health burden and is associated with high morbidity, mortality and impairment in quality of life [1]. The total annual costs of hospitalizations for patients with PAD are in excess of $21 billion per year, and per-patient costs of PAD are higher than those for both coronary artery disease and cerebrovascular disease [2]. The high cost of PAD is partially attributed to higher numbers of peripheral vascular operations and interventions that fail, resulting in poor clinical outcomes and a need for repetitive interventions [3–6]. Specifically, restenosis within 3 years after femoropopliteal bypass occurs in 27% of patients, while occlusion occurs in 19% [7]. The results for angioplasty and stenting in the lower extremity are even worse, with 50–85% of patients developing hemodynamically significant restenosis, and 16–65% developing occlusion within just 2 years after treatment [8], leading to re-intervention in 37–54% of patients [6].

Although the underlying reasons for such alarmingly high rates of treatment failure are still not fully understood, the complex biomechanical forces that occur in the femoropopliteal artery during locomotion are thought to play a significant role [9–12]. These forces create repetitive trauma to both the artery and repair materials. Femoropopliteal artery stents appear to have the highest incidence of fracture [13] as limb-generated movements and forces are capable of crushing and tearing apart metallic stent devices over time. These same movements and forces are also likely culprits in the development of the primary arterial lesion, producing a chronic injury to the artery wall that leads to deleterious cellular and biochemical responses.

Data on the function of the femoropopliteal artery, its mechanical properties, and the conditions of its surrounding local environment are essential for understanding artery-repair device interaction. Surprisingly, the mechanical properties of the infrainguinal arteries, such as the femoropopliteal and tibial arteries, are very poorly studied, perhaps due to difficulties associated with the supply of these tissues. Most existing human studies are limited to the proximal femoral portions of the artery and utilize either duplex ultrasound for non-destructive in vivo testing, or uniaxial tensile testing for excised cadaveric arteries [14–19]. However, in vivo ultrasound and uniaxial tensile experiments are not sufficient to characterize the complex nonlinear anisotropic properties of arterial tissue [20,21]. Biaxial tensile testing is currently the most viable experimental method, although it also has limitations due to its 2D nature [21–23].

The goal of the current work was to measure the passive biaxial mechanical properties of diseased human femoropopliteal and tibial arteries. Apart from measuring the mechanical response of the artery walls, we also calculated the constitutive model parameters and the in vivo axial pre-stretch that allows the artery to eliminate axial work and conserve energy during the pulse cycle [24]. Since in vivo axial pre-stretch cannot be measured directly in aged and diseased arteries as it is not equal to in situ retraction upon transection [25], we present the framework for calculating these values based on the measured arterial mechanical properties.

2. MATERIALS AND METHODS

2.1 Materials

With IRB approval and after informed patient consent, 10 superficial femoral (SFA), 8 popliteal (PA), 3 tibial arteries (TA) and 4 SFA atherosclerotic plaques were harvested from 10 patients (63±8.3 y.o.) after lower extremity amputation for critical limb ischemia. Subject population data are presented in Table 1. All arteries were non-uniformly diseased and were classified into 3 stages of atherosclerotic severity based on visual inspection and manual palpation. Stage one (+) arteries demonstrated no obvious signs of atherosclerotic disease. Stage two (++) vessels demonstrated mild disease severity, consisting of palpable atheromas or thin-cap fibroatheromas that did not contain heavy calcification or result in complete occlusion. Stage two arteries typically contained lesions that would be considered suitable for conservative medical therapy and were not the main reason for amputation. Stage three (+++) arteries demonstrated severe atherosclerotic disease consisting of fissured, ulcerated, hemorrhagic, thrombotic, calcific or fibrotic lesions, often completely occluding the lumen of the vessel. These lesions frequently require angioplasty/stenting or bypass surgery. Severe disease in stage three arteries was the primary cause of amputation.

Table 1.

Demographics of patients used for the study. CAD = coronary artery disease; DM = diabetes mellitus; HTN = hypertension; HLP = hyperlipidemia. Atherosclerotic disease severity ranges from nearly normal tissue (+) to severely diseased (+++) artery as determined by visual inspection and manual palpation.

#	Age	Risk Factors					Indication for amputation	Atherosclerosis Severity
		CAD	DM	HTN	HLP	Smoking
1	55	+		+	+	+	failed bypass, infection	+++
2	76	+	+	+	+	+	N/A	++
3	66	+		+	+	+	N/A	++
4	55	+		+	+	+	thrombosis, gangrene	++
5	55	+		+	+	+	N/A	+
6	55	+		+	+	+	occlusion, gangrene	+++
7	63			+			popliteal aneurysm	+
8	66			+	+		ischemia/reperfusion injury	+
9	76	+	+	+	+	+	gangrene	++
10	60	+	+	+	+	+	N/A	+++

2.2 Mechanical Testing

2.2.1 Specimen Preparation

All tissues were transported to the testing facility in 0.9% NaCl physiological saline solution on ice and testing was done within 4 hours of harvesting to preserve freshness. Prior to testing, an arterial ring of approximately 2 mm in length was cut from each specimen and photographed. The ring was then cut radially to release the residual stresses. Though some dispute is present in the literature as to whether one radial cut is sufficient to release all residual stresses in the tissue [21], this question merits a separate investigation and was beyond the scope of the current study. The opening angle α was measured between two lines drawn from the center of the sector to its outer tips (see APPENDIX) [26]. This definition of the opening angle follows Sommer and Holzapfel [29], and is different from the one in which α is calculated as an angle between two lines drawn from the midpoint of the arc of the inner vessel wall to the outer tips of the open sector [24]. This angle can easily be obtained from our measurements as $\frac{\alpha }{2}$.

After measuring the opening angle, the entire arterial segment was cut longitudinally and spread out into a flat sheet. Grossly disease-free square specimens 13 mm × 13 mm were then cut out of this sheet preserving the in vivo longitudinal and circumferential orientations parallel with the specimen’s square edges. Most specimens opened to initially slightly curved configurations that flattened out either under specimen’s own weight or after application of the 0.01 N tare preload (see 2.2.4 Test protocols section below). Though such flattening may introduce residual stresses to the specimen, these stresses are small compared to those occurring in the sample during testing. Wall thickness was manually measured and averaged at six different locations using a Starrett 1010 Z caliper. Careful measurement technique ensured that the caliper’s lips touched the specimen, but did not compress it. Caliper-measured wall thickness values were corroborated with optical assessment using the photographs of the arterial rings during opening angle measurements. Dimensions of the specimen in the longitudinal and circumferential directions were measured with Mitutoyo Electronic Digital Caliper.

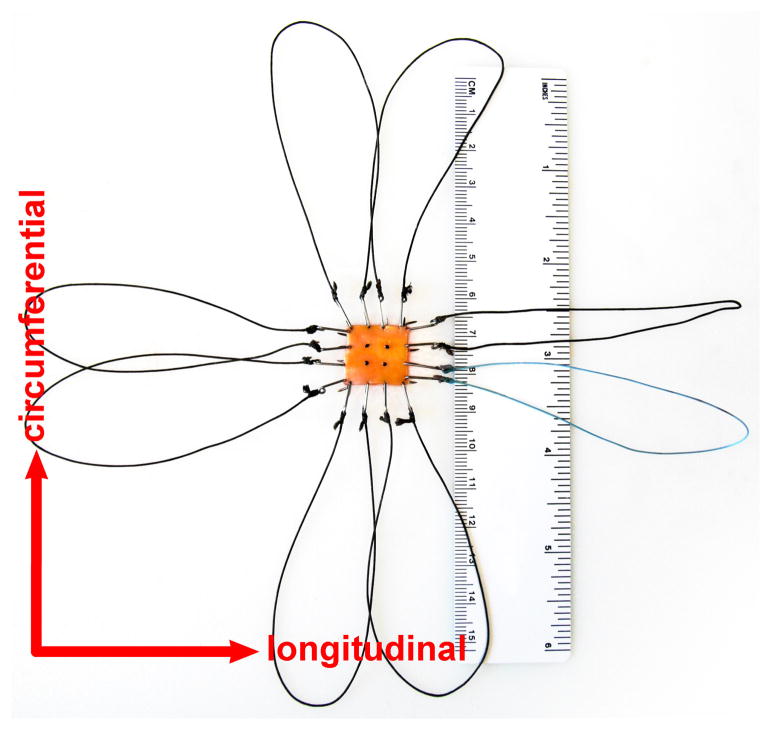
Samples were attached to the biaxial testing device using stainless steel hooks and loops of thick nylon surgical suture [20,27,28]. Hooks were attached to the specimen as close to the edges as possible to minimize the influence of edge effects on strain measurements. Four graphite markers were attached to the arterial intima to track the deformations of the specimen (Figure 1). During testing, specimens were completely immersed in 0.9% NaCl physiological saline solution at 37°C maintained by a Fisher Scientific Isotemp Refrigerated Circulator 9000.

Figure 1.

Specimen prepared for biaxial testing.

2.2.2 Biaxial Device

All tissues were tested quasi-statically using a custom-made soft-tissue biaxial testing device. A detailed device description is given in Sacks [27] and Geest et al [29,30]. Briefly, the device consists of four translation stages (404XR, Parker Hannafin Corp., Irwin, PA) driven by stepper motors (OS22B-SNL10, Parker Hannafin Corp., Irwin, PA). The stages are arranged around the bath that contains the specimen. The spatial resolution of each translation stage is 0.394μm. The translation stages are equipped with carriage arms which are used for specimen attachment. Each arm is free to rotate about its axis and has a pair of stainless steel pulleys. This allows the applied forces to be equally distributed between all suture lines that hold the specimen. The entire biaxial testing system rests on a vibration isolation table to minimize noise caused by stage movements.

To avoid any mechanical interference with the specimen, the deformation gradient F was measured optically by tracking the movements of the four graphite markers with a Sony XCD-X700 video camera [20,21]. In-plane stretch and shear angle were calculated in real time from marker displacements using a four-node finite element technique [20,21]. Specifically, we considered homogeneous biaxial deformation:

$$x_1={\lambda }_1{X}_1+k_1{X}_2,x_2=k_2{X}_1+{\lambda }_2{X}_2,x_3={\lambda }_3{X}_3$$ (1)

where X_i denotes original locations, x_i current locations, λ_i stretches, and k_i are measures of the in-plane shear. We do not use notation z, θ, r here in order to avoid confusion with the cylindrical coordinates used for the calculation of in vivo axial stretch (see APPENDIX). Note that deformation is assumed homogeneous, even though for wall segments with atherosclerotic plaques this may be a questionable assumption that requires further investigation. The deformation gradient then takes the form:

$$\mathbf{F}=\left[\begin{array}{ccc}{\lambda }_1& k_1& 0\\ k_2& {\lambda }_2& 0\\ 0& 0& {\lambda }_3\end{array}\right],$$ (2)

where λ₁, λ₂ are stretches in the longitudinal and circumferential directions and λ₃ is expressed through isochoric motion (i.e. det F = 1) assuming incompressibility (see discussion of incompressibility assumption for young and senior arteries in Boutouyrie et al [31]).

Finite element shape functions fⁿ were used to approximate the displacement field u = x − X within the central region delimited by the four markers. In particular $u_i({\zeta }_1,{\zeta }_2)={\sum }_{n=1}^4{f}^n({\zeta }_1,{\zeta }_2)u_i^n$ where $f^n({\zeta }_1,{\zeta }_2)=\frac{1}{4}(1+{\zeta }_1{\zeta }_1^n)(1+{\zeta }_2{\zeta }_2^n)$ and ζ₁ ∈ [−1,1], ζ₂ ∈ [−1,1] are isoparametric coordinates. The components of F therefore were determined from

$$\left[\begin{array}{cc}{\lambda }_1& k_1\\ k_2& {\lambda }_2\end{array}\right]=\left[\begin{array}{cc}1+\frac{\partial u_1}{\partial X_1}& \frac{\partial u_1}{\partial X_2}\\ \frac{\partial u_2}{\partial X_1}& 1+\frac{\partial u_2}{\partial X_2}\end{array}\right]$$ (3)

and the incompressibility condition.

The applied loads P₁ and P₂ were measured with a pair of tension/compression “250g” (max load 2.5 N) load cells (Honeywell Sensotec) that were calibrated prior to each testing session [32]. These load cells were selected to cover the estimated physiologic loads in the artery as described below in the 2.2.5 Metrics for Compliance and Anisotropy section. Cauchy stresses were then calculated as

$${\sigma }_{11}={\lambda }_1\frac{P_1}{H{L}_2},{\sigma }_{22}={\lambda }_2\frac{P_2}{H{L}_1},{\sigma }_{12}=k_1\frac{P_2}{H{L}_1},{\sigma }_{21}=k_2\frac{P_1}{H{L}_2}$$ (4)

where H is the undeformed thickness, and L_i the undeformed lengths over which the applied loads act. Note that even though loads were applied normal to the edges (and hence 1^st Piola-Kirchhoff stress components T₁₂ = T₂₁ = 0), the Cauchy stress shear components σ₁₂, σ₂₁ are non-zero if shear deformation is present (i.e. k₁, k₂ ≠ 0). Also note that even though the arterial wall is a multi-layered structure with distinct properties for the intima, media and adventitia, these layers were not tested individually. Therefore equation (4) represents average stresses in the longitudinal and circumferential directions.

2.2.3 Testing pre-requisites

In order to formulate the testing protocol and select the appropriate constitutive framework to describe the material behavior, we have conducted several tests investigating the amount of shear and the effects of temperature, loading rate and loading path. These tests were performed using the same parameters (i.e. initial pre-load and max tare loads, preconditioning, etc.) described below in the 2.2.4 Test protocols section.

Our methodology did not allow us to determine the principal orthotropic directions of the specimens prior to mounting them in the biaxial apparatus. However, we aligned the circumferential and longitudinal arterial directions with the test axes. The pulleys of the biaxial device allowed equal application of forces at each tether and permitted the sample to shear freely. If the principal stretch directions did not coincide with the orthotropic directions, the specimens would have demonstrated significant shear. To assess this, we calculated shear angle β in all specimens as:

$$\beta ={sin}^{-1}\left(\frac{2E_{12}}{\sqrt{1+2E_1}\sqrt{1+2E_2}}\right),$$ (5)

where E₁, E₂ and E₁₂ are components of the Green strain tensor $\mathbf{E}=\frac{1}{2}({\mathbf{F}}^T·\mathbf{F}-\mathbf{I})$. We observed no gross evidence of shearing during biaxial loading, and for all tested tissues |β| ≤ 5°, while for most tissues |β| ≤ 3°. We therefore considered shear small and did not account for it in the constitutive model.

The influence of temperature on mechanical property measurement was assessed in five specimens. The temperature of the saline bath containing the specimen was varied from 20–42°C and specimens were loaded equibiaxially to 2 N. At 42°C compared to 20°C, maximum stretch increased by <1.5% in the longitudinal and <3% in the circumferential directions. The difference in maximum stretch at room (25°C) and body (37°C) temperatures was <1% in the longitudinal and <1.5% in the circumferential directions, which is consistent with findings of Kang et al [33]. Even though the difference in mechanical properties measured at room and at body temperatures was not significant, all experiments were conducted at 37°C to more closely match realistic human physiology.

The influence of loading rate was assessed in 14 specimens. Since all tests were load-controlled, the strain rate for each specimen was tuned such that the tissue reached a 2 N load within a set time. The time was varied within a range of 30 sec to 1 sec, with the latter being limited by the frame rate of our camera. Though in vivo loading rates are faster than 1 second, such tests probably cannot be considered within the commonly used quasistatic framework for soft tissues. We have detected stiffening of the tissue with increased loading rate for some specimens, while no changes were observed for the majority of tissues. On average, a reduction of loading time from 30 sec to 1 sec resulted in 0.2±0.6% max stretch decrease in the longitudinal direction, and 1.7±1.9% max stretch decrease in the circumferential direction. Stress-stretch curves at 30 sec and 1 sec were not statistically significantly different. Therefore, the loading rate was chosen such that the length of one cycle was 30 sec, i.e. 15 sec for loading and 15 sec for unloading, in compliance with our previously published experimental protocol [28]. This loading rate resulted in the average strain rate of 0.008±0.004 sec⁻¹.

Dependence of tissue properties on the loading path was assessed in 8 specimens using the following two-step procedure. In step 1, the specimen was first loaded in the longitudinal direction, then in the circumferential direction, and then unloaded while recording marker positions at each load configuration. In step 2, the specimen was first loaded in the circumferential direction, then in the longitudinal direction, followed by unloading, again recording marker positions at each load configuration. Marker positions were then compared for each configuration between steps 1 and 2. Analysis showed no statistically significant difference between configurations, and marker positions varied less than 1%, demonstrating that sequence of loading, i.e. loading path, was not affecting the measured mechanical properties of the tissue.

Finally, we note that all tested tissues exhibited hysteresis that was relatively insensitive to changes in strain rate after approximately 3 cycles of preconditioning. Therefore, the tested tissues were not purely elastic but showed what is termed by Fung as “pseudoelastic” [34] behavior, i.e. when loading and unloading curves are highly repeatable but hysteresis is still present. Pseudoelasticity is not an intrinsic property of the material, but it conveniently allows treatment of the tissue as one elastic material in loading and another elastic material in unloading, without involving the viscoelastic framework [34]. However, the hysteresis observed in the majority of our specimens was relatively narrow; therefore, we present data only for the loading portion of the stress-stretch curve for the sake of brevity. Exceptions were made for those specimens that demonstrated wide hysteresis; they are accompanied by constitutive model parameters for both the loading and the unloading portions of the stress-stretch curves.

2.2.4 Test protocols

Prior to collecting data all specimens were preconditioned with 15 cycles of equibiaxial load at 2 N. Fragile plaques were preconditioned at lower loads to avoid tearing. To ensure consistency from sample to sample, all loading cycles were initiated at a tare load of 0.01 N and all presented stretch data were referenced to the preconditioned tare configuration. For most specimens, a highly repeatable response was observed starting from the 4^th cycle onward. After preconditioning, each artery was subjected to nine different test protocols to cover a wide range of strains and acquire sufficient data density for constitutive modeling [35]. These nine protocols included testing with constant ratio of loads applied in longitudinal and circumferential directions, namely 1:1, 1:2, 1:4, 1:10, 1:1 (stability check), 2:1, 4:1, 10:1, 1:1 (stability check). The maximum load was set at 2N for most arteries. Equibiaxial stability checks were performed twice: in the middle of the testing sequence and at the end, to verify stability of the mechanical response and to ensure that the specimen had not accumulated any damage as it went through the battery of tests. Data collected from the five (1:1, 1:2, 1:4, 2:1, 4:1) protocols were used to find the material constants for the constitutive model, while two 1:10 and 10:1 protocols were used to check the predictive capability of the constitutive relation with determined parameters. We have used 1:10 and 10:1 “boundary” protocols to check predictions because these protocols were the most difficult for the constitutive model to portray accurately.

2.2.5 Metrics for Compliance and Anisotropy

The elastic modulus is not constant for soft tissues; therefore, there is no single parameter that can describe arterial compliance or anisotropy. However, one can define certain levels of stress for which the corresponding stretches in the longitudinal and the circumferential directions can be compared for estimating compliance and anisotropy [28,35]. To estimate these stress levels, we considered an average femoropopliteal artery with diameter of 7 mm and wall thickness of 1 mm under an internal pressure of 80 mmHg (end diastole) and 120 mmHg (peak systole). We note that these values are hypothetical but reasonable, as our SFA, PA and TA specimens had average diameters of 7.3±2.3, 7.1±2.2, 5.2±1.2 mm, and wall thicknesses of 1.5±0.7, 1.3±0.5, 0.9±0.4 mm respectively. Under the assumption of a thin wall, Laplace’s law (σ_θθ = Pd/2h) provides a rough estimate of σ₈₀ = 37 kPa and σ₁₂₀ = 56 kPa for average Cauchy circumferential stress in the arterial wall.

These two stress levels were selected for calculations of anisotropy at both diastole (A₈₀) and systole (A₁₂₀) as the ratio of longitudinal to circumferential stretches. Though use of equibiaxial loading protocols to assess anisotropy is artificial, it is necessitated by the lack of data on the actual in vivo loading conditions of the artery, such as the influence of surrounding structures, flexions of the leg, etc. When these data become available, the constitutive model parameters summarized in this work will facilitate a more accurate physiologic assessment of anisotropy. The change in compliance along the length of the artery was assessed by comparing stretches at σ₈₀ and σ₁₂₀ between the more proximal SFA and the more distal PA and TA.

2.3 Constitutive modeling

2.3.1 Choice of constitutive relation

We assumed that the arterial wall was incompressible and consisted of a mixture of an elastin-dominated amorphous matrix and families of locally parallel collagen fibers [36]. As femoropopliteal arteries also contain significant amounts of smooth muscle in the media, the active stresses from smooth muscle tone might also be considered. However, the active contribution of smooth muscle to the arterial mechanical properties requires further investigation, and for this reason it was not included in the present analysis. The passive contributions by smooth muscle were absorbed by the constitutive model [37].

Following Ferruzzi et al [37] we considered 4 families of collagen fibers, two oriented axially and circumferentially, and two symmetrically along the diagonal. In this regard, we used the strain energy function suggested by Baek et al [36] which was shown to accurately describe the behavior of soft tissues [37,38]. This constitutive model is consistent with the convexity requirements that ensure undesirable material instabilities are precluded [39]. An additional benefit is that this model is motivated by the underlying arterial wall structure, although the relation is phenomenological, i.e. not based on inherent microstructural complexities such as the different types of collagen, cross-linking, physical entanglements or other interactions with extracellular constituents [37]. The selected formulation did not take into account viscoelastic effects because after preconditioning, most of our tissues demonstrated relatively narrow hysteresis. A detailed framework of this constitutive model is given elsewhere [36,37,40], but here we will provide a brief description for clarity of the following discussion.

Consider the following strain energy function

$$W(\mathbf{C},{\mathbf{M}}^{\mathrm{i}})=\frac{c_0}{2}(I_C-3)+{\sum }_{i=1}^4\frac{c_1^i}{4c_2^i}\left\{exp\left[c_2^i{(I_4^i-1)}^2\right]-1\right\},$$ (6)

where c₀, $c_1^i$ and $c_2^i$ are material parameters associated with contributions of elastin and collagen [37], and I_C = tr C is the first invariant of the right Cauchy-Green tensor. Unit vectors Mⁱ define the fiber directions in the reference configuration that make angles γⁱ with the axial direction. With axial and circumferential fibers fixed at γ¹ = 0 and γ² = π/2, and diagonal fibers located at γ³ = −γ⁴ = γ, the square of the stretch of the i-th fiber family $I_4^i={\mathbf{M}}^i·{\mathbf{CM}}^i$ takes the form

$$I_4^1={\lambda }_z^2,I_4^2={\lambda }_{\theta }^2,I_4^{3,4}={\lambda }_z^2{cos}^2\gamma +{\lambda }_{\theta }^2{sin}^2\gamma .$$ (7)

We further assume that diagonal fibers are mechanically equivalent, while axial and circumferential fibers can be mechanically distinct. This results in $c_1^3=c_1^4=c_1^{3,4}$ and $c_2^3=c_2^4=c_2^{3,4}$, therefore function (6) depends on 8 constitutive parameters (c₀, $c_1^1,c_2^1,c_1^2,c_2^2,c_1^{3,4},c_2^{3,4}$, γ). In order for these parameters to be physically realistic, they have to be non-negative, and $0\le \gamma \le \frac{\pi }{2}$ due to the symmetry of the diagonal fibers.

For homogeneous biaxial deformations in the absence of shear, the deformation gradient takes a diagonal form and contains only the principal stretches

$$\mathbf{F}=\text{diag}({\lambda }_z,{\lambda }_{\theta },{\lambda }_r).$$ (8)

Principal Cauchy stresses are found from

$$\overline{{\sigma }_{ii}}={\lambda }_i\frac{\partial W}{\partial {\lambda }_i},i=r,\theta ,z$$ (9)

Note that stress in (9) is the isochoric Cauchy stress (also termed “extra” stress [21]), i.e. ${\sigma }_{ii}=p+\overline{{\sigma }_{ii}}$ where p is the hydrostatic pressure.

Introducing incompressibility, i.e. det F = λ_zλ_θλ_r = 1 we arrive at

$${\lambda }_r=1/({\lambda }_z{\lambda }_{\theta }).$$ (10)

Assuming that during biaxial testing the tissue is in plane stress (i.e. $\overline{{\sigma }_{rr}}=0$), non-zero Cauchy stress components (9) for the strain energy function (6) take the form

$$\begin{array}{l}\overline{{\sigma }_{zz}}=c_0\left({\lambda }_z^2-\frac{1}{{\lambda }_{\theta }^2{\lambda }_z^2}\right)+c_1^1({\lambda }_z^2-1)e^{c\frac{1}{2}{({\lambda }_z^2-1)}^2}{\lambda }_z^2+2c_1^{3,4}(I_4^{3,4}-1)e^{c_2^{3,4}{(I_4^{3,4}-1)}^2}{\lambda }_z^2{cos}^2\gamma \\ \overline{{\sigma }_{\theta \theta }}=c_0\left({\lambda }_{\theta }^2-\frac{1}{{\lambda }_{\theta }^2{\lambda }_z^2}\right)+c_1^2({\lambda }_{\theta }^2-1)e^{c_2^2{({\lambda }_{\theta }^2-1)}^2}{\lambda }_{\theta }^2+2c_1^{3,4}(I_4^{3,4}-1)e^{c_2^{3,4}{(I_4^{3,4}-1)}^2}{\lambda }_{\theta }^2{sin}^2\gamma \end{array}$$ (11)

The two Cauchy stress components in equations (11) are therefore functions of the two principal stretches λ_θ and λ_z, and the 8 constitutive parameters (c₀, $c_1^1,c_2^1,c_1^2,c_2^2,c_1^{3,4},c_2^{3,4}$, γ) that determine the material behavior. These 8 parameters can be found by fitting equations (11) to the experimental data.

2.3.2 Determination of Constitutive Parameters

To find the 8 constitutive model parameters that determine tissue behavior in equations (11), we need to minimize the differences between theoretically calculated (i.e. (11)) and experimentally measured stresses ${\sigma }_{ii}^{\mathit{exp}}$ simultaneously for both directions of stretch in 5 out of 7 protocols (2 unused protocols were utilized to check model prediction). The optimization problem (chi-square minimization) would then be to minimize the objective function

$$e(\omega )={\sum }_{k=1}^5\left\{{\left[\overline{{\sigma }_{zz}}{({\lambda }_{\theta },{\lambda }_z,\omega )}_k-{\left({\sigma }_{zz}^{\mathit{exp}}\right)}_k\right]}^2+{\left[\overline{{\sigma }_{\theta \theta }}{({\lambda }_{\theta },{\lambda }_z,\omega )}_k-{\left({\sigma }_{\theta \theta }^{\mathit{exp}}\right)}_k\right]}^2\right\},$$ (12)

where $\omega =(c_0,c_1^1,c_2^1,c_1^2,c_2^2,c_1^{3,4},c_2^{3,4},\gamma )$.

Minimization was performed using the Levenberg-Marquardt Algorithm in OriginPro 9 (OriginLab Co) with the multi-data global fit mode. Since the weight of each parameter in ω is unclear, we assigned equal weights to all 8 parameters, and 400 iterations were typically sufficient to achieve a tolerance of 10⁻⁹. The traditional coefficient of determination R² ∈ [0,1] was used as a measure of goodness of fit with values R² ≥ 0.9 typically representing a good fit to the experimental data.

In addition to checking the quality of fit, we also checked the quality of model prediction, i.e. the model’s description of the two experimental protocols not used for minimization [21,35,41]. The quality of prediction was also assessed using R².

2.4 Assessment of in vivo Axial Stretch

Healthy arteries in vivo experience stretches and stresses in both the longitudinal and circumferential directions even when they are not loaded with internal pressure. This is demonstrated by retraction following transection in the axial direction and opening of the arterial ring to a sector in a response to a radial cut [21]. Both the axial and the circumferential pre-stretches play important compensatory roles in arterial biomechanics and mechanobiology by equilibrating the homeostatic multiaxial stress state of the artery [24] and homogenizing the stress distributions across the thickness of the arterial wall [42,43].

Circumferential pre-stretch was assessed through the measurement of the opening angle as described above in the 2.2.1 Specimen Preparation section. Measurement of the axial pre-stretch ${\lambda }_z^{\ast }$ was based on the findings of Van Loon et al [44] which were later confirmed by other groups [21,45] and discussed in detail by Humphrey [21]. Van Loon et al [44] have shown that plots of axial force-length data collected in vitro at different fixed pressures reveal a unique cross-over point that reliably estimates the in vivo value of axial pre-stretch ${\lambda }_z^{\ast }$. Therefore, ${\lambda }_z^{\ast }$ can be determined by the standard in vitro pressure-diameter tests with a set (constant) axial stretch λ_z. The desired ${\lambda }_z^{\ast }$ then results in an axial force F_z that is independent of the internal pressure (or alternatively of the circumferential stretch λ_θ) during normal physiologic pressurization [21]. Physiologically, the presence of ${\lambda }_z^{\ast }$ serves to conserve energy such that the artery does no axial work during the pulse cycle. Interestingly, in vivo axial pre-stretch does not always equal the in situ axial pre-stretch, and therefore simple measurement of retraction following transection is insufficient. Though in situ and in vivo arterial pre-stretches were shown to be approximately equal for young animal arteries [44,45], Schulze-Bauer et al [25] have demonstrated that for senior human arteries, this may not be the case and that the axial in situ stretch may be substantially smaller than ${\lambda }_z^{\ast }$.

In this work we focused on the determination of ${\lambda }_z^{\ast }$ to establish the most energy efficient in vivo axial pre-stretch – a characteristic of normal arterial function. In other words, we aimed to determine the in vivo pre-stretch ${\lambda }_z^{\ast }$ that might allow the diseased artery to function in the most energy efficient way. This ${\lambda }_z^{\ast }$ should therefore be distinguished from the in situ retraction, which is appreciably smaller in diseased arteries, such as those we studied here. Therefore, we followed the methodology of Schulze-Bauer et al [25] and calculated ${\lambda }_z^{\ast }$ by studying the axial force F_z as a function of the circumferential stretch λ_θ for each of the fixed axial pre-stretches λ_z = 1 – 1.7. In vivo axial pre-stretch ${\lambda }_z^{\ast }$ then corresponded to the fixed value of λ_z at which F_z was independent of λ_θ. The corresponding mathematical formulation is summarized in the APPENDIX and is provided by equation (29), where the components of the Cauchy stress tensor are given by equations (11).

2.5 Histological evaluation

After biaxial testing, all tissues were fixed in 10% neutral-buffered formalin, embedded in paraffin and sliced 5 μm thick. Standard Verhoeff-Van Gieson (VVG) staining was used to assess elastin and collagen orientation. Images of the stained arteries were captured under 40X bright field magnification.

3. RESULTS

3.1 Mechanical Testing

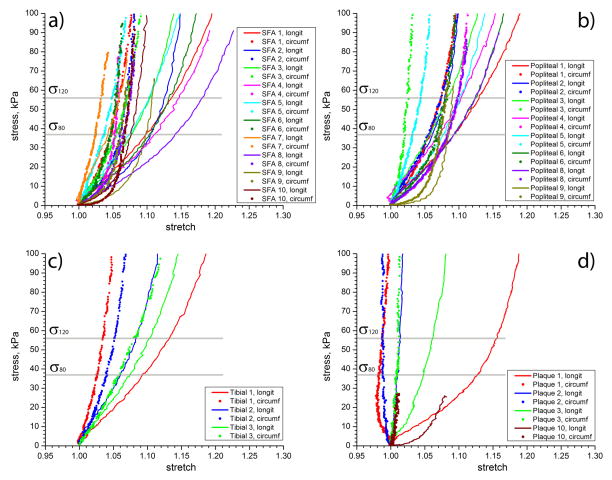
Stress-stretch curves for all arteries, as well as SFA atherosclerotic plaques, are presented in Figure 2. For clarity and brevity, only equibiaxial tests are plotted. All arteries exhibited significant non-linearity and anisotropy. Most specimens demonstrated large deformations in the longitudinal direction even though some of the tissue specimens appeared to be heavily diseased, i.e. specimens #1 and #6.

Figure 2.

Equibiaxial mechanical properties of Superficial Femoral (a), popliteal (a), tibial (c) arteries and SFA atherosclerotic plaques (d). Vertical lines show estimations of diastolic (σ₈₀) and systolic (σ₁₂₀) levels of stress at which compliance and anisotropy (A₈₀, A₁₂₀) metrics were evaluated.

At σ₈₀, the average SFA stretch in the longitudinal direction was 1.09±0.03 (range 1.043–1.145), while in the circumferential direction it was 1.05±0.01 (range 1.025–1.068). At σ₁₂₀, the average SFA stretch in the longitudinal direction was 1.12±0.03 (range 1.059–1.18), while in the circumferential direction it was 1.06±0.01 (range 1.032–1.075).

The more distal PA and TA demonstrated smaller stretches than the SFA at both σ₈₀ and σ₁₂₀ in the longitudinal directions, but higher stretches in the circumferential direction. At σ₈₀, the average PA/TA stretch in the longitudinal direction was 1.08±0.01 (range 1.06–1.097), while in the circumferential direction it was 1.06±0.02 (range 1.02–1.085). At σ₁₂₀, the average PA/TA stretch increased to 1.10±0.02 (range 1.08–1.132) in the longitudinal direction and to 1.07±0.02 (range 1.03–1.098) in the circumferential direction.

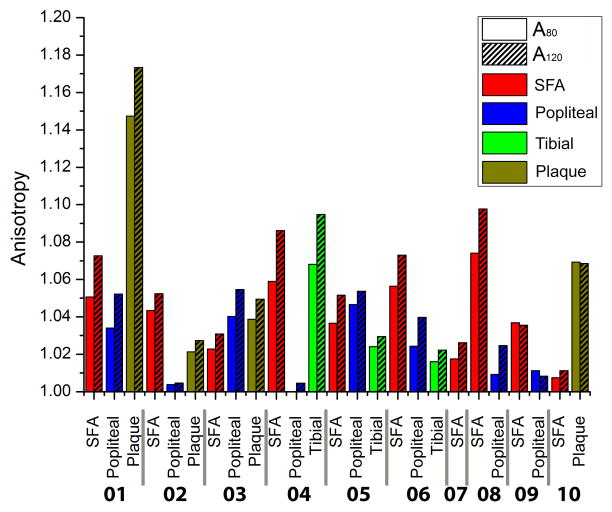
Plaques stretched 1.07±0.05 (range 1.009–1.129) in the longitudinal direction and 0.9975±0.01 (range 0.984–1.01) in the circumferential direction at σ₈₀; and 1.08±0.06 (range 1.014–1.158) in the longitudinal direction and 1.00±0.02 (range 0.987–1.02) in the circumferential direction at σ₁₂₀. Note that in the circumferential direction, atherosclerotic plaques were contracting as the specimen was being stretched in the longitudinal direction. These results demonstrate that all tested tissues, including the atherosclerotic plaques, were more compliant in the longitudinal direction than in the circumferential at both σ₈₀ and σ₁₂₀ (p<0.01) (Figure 3). For the SFA, the average anisotropy ratio A₈₀ calculated at σ₈₀, was 1.04±0.02, and for σ₁₂₀, A₁₂₀ = 1.05±0.03. For the PA and TA both anisotropy ratios were smaller, A₈₀ = 1.02±0.02 and A₁₂₀ =1.04±0.03. The increase in anisotropy at systole compared to diastole, and the lower anisotropy of the PA and TA compared to the SFA, were statistically significant (p<0.05).

Figure 3.

Anisotropy indexes A₈₀ (diastole) and A₁₂₀ (systole) calculated for each arterial specimen.

At both σ₈₀ and σ₁₂₀ stress levels, longitudinal compliance decreased distally (p<0.05), while circumferential compliance increased. The latter was not statistically significant (p=0.35 at σ₈₀ and p=0.23 at σ₁₂₀) but it was observed for 5 out of 8 specimens at diastole and 6 out of 8 at systole. Interestingly, atherosclerotic plaque was significantly stiffer than the arterial tissue only in the circumferential direction (p<0.01), while in the longitudinal direction this result was not statistically significant (p=0.22 and p=0.18 for σ₈₀ and σ₁₂₀ respectively). The small number of plaque specimens and their variable compositions warrant further investigation.

3.2 Constitutive Model Parameters

Constitutive model parameters for each specimen are summarized in Table 2. The coefficient of determination R² ∈ [0,1] is given to demonstrate the quality of fit to the experimental data. Generally R² ≥ 0.9 is usually an indicator of a good fit. Visual demonstration of the representative fit to the multiple experimental protocols for SFA, PA and TA is presented in Figure 4 for patient #5. The selected model was able to accurately portray the complex arterial behavior under different test protocols. Though both the fit and the prediction were generally good for most tissues, experimental data for one atherosclerotic plaque specimen could not be fit with the selected model due to substantial stiffness and compression in one of the directions of stretch during biaxial loading.

Table 2.

Constitutive model parameters for the tested specimens. The coefficient of determination R² is provided to demonstrate the goodness of fit and accurate prediction. Five specimens demonstrated wide hysteresis, therefore both loading (L) and unloading (U) constitutive parameters are provided for these tissues. SFA = Superficial Femoral Artery, PA = Popliteal Artery, TA = Tibial Artery.

Patient	Tissue	c0, kPa	${\mathrm{c}}_1^1$, kPa	${\mathrm{c}}_2^1$	${\mathrm{c}}_1^2$, kPa	${\mathrm{c}}_2^2$	${\mathrm{c}}_1^{3,4}$, kPa	${\mathrm{c}}_2^{3,4}$	γ, deg	$R_{\mathit{fit}}^2$	$R_{\mathit{predict}}^2$
1	SFA	44.32	55.83	2.31	145.43	25.29	27.34	15.78	57.07	0.99	0.97
	PA	34.05	69.80	1.98	99.82	20.64	31.94	8.11	52.13	0.99	0.98
	Plaque	13.86	3.93	14.05	237.13	216.79	649.02	0.00	55.74	0.89	0.85
2	SFA	26.67	0.00	4.18	91.70	42.71	34.81	18.93	29.20	0.98	0.98
	PA	78.25	70.19	0.00	72.71	26.49	5.76	65.79	31.31	0.98	0.95
	Plaque	0.00	859.24	243.31	0.00	0.00	0.00	0.00	47.62	0.34	-
3	SFA (L)	40.03	96.07	5.32	101.90	5.85	26.36	38.31	68.84	0.99	0.99
	SFA (U)	12.83	100.72	5.51	8.82	53.76	52.45	27.40	63.30	0.99	0.99
	PA	80.50	105.67	5.50	493.39	88.92	65.96	70.09	60.32	0.99	0.98
	Plaque	0.00	0.00	653.94	1571.03	103.30	557.35	46.96	42.40	0.97	0.96
4	SFA	27.75	68.58	0.00	52.50	101.46	5.91	63.23	55.26	0.98	0.97
	PA	51.76	77.20	1.07	10.55	33.90	13.11	29.52	58.34	0.99	0.96
	TA	57.18	57.52	1.28	331.67	30.69	19.05	27.55	52.68	0.99	0.97
5	SFA	42.97	126.25	0.53	292.08	22.11	8.80	15.23	26.81	0.99	0.99
	PA (L)	31.87	66.18	7.73	130.16	26.09	136.09	17.72	55.20	0.99	0.99
	PA (U)	0.00	54.90	9.45	25.84	70.26	121.46	27.90	54.75	0.98	0.98
	TA	73.63	59.03	11.33	167.21	29.11	39.99	32.68	48.93	0.99	0.98
6	SFA	14.54	64.27	2.43	76.81	30.96	78.38	20.29	54.42	0.99	0.80
	PA	42.76	46.77	4.43	51.22	12.21	24.02	23.78	53.55	0.99	0.91
	TA (L)	58.97	57.64	4.61	82.69	4.15	33.53	10.15	46.99	0.99	0.86
	TA (U)	0.00	51.96	5.60	8.18	17.89	76.72	8.16	47.84	0.98	0.98
7	SFA (L)	129.98	98.10	22.81	286.45	42.33	0.00	259.25	48.05	0.98	0.99
	SFA (U)	53.82	142.40	22.45	0.00	308.29	95.16	123.29	66.07	0.98	0.96
8	SFA	0.00	77.95	0.63	62.78	38.25	31.40	19.42	62.15	0.99	0.95
	PA (L)	16.12	101.05	1.74	61.61	7.64	24.61	21.09	60.89	0.99	0.97
	PA (U)	1.07	86.77	3.36	13.34	25.25	34.58	20.54	59.55	0.98	0.98
9	SFA	0.00	22.83	12.02	39.46	33.50	32.04	52.18	43.13	0.95	0.99
	PA	0.00	0.00	38.15	28.12	31.70	44.21	50.17	40.69	0.98	0.96
10	SFA	35.60	14.29	44.91	14.81	69.25	13.87	30.22	89.80	0.81	0.79
	Plaque	0.00	36.82	22.90	158.56	47.45	63.68	319.98	58.53	0.91	0.92

Figure 4.

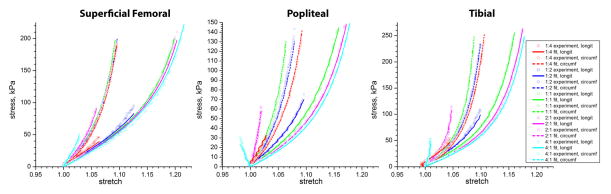
Representative stress-stretch curves for superficial femoral, popliteal and tibial arteries for patient #5. Experimental data and constitutive model fits are presented for different test protocols.

3.3 Opening Angle and In Vivo Axial Stretch

The average opening angle for the SFA was 150°±84° and for the PA and TA it was 177±73°, a difference that was not statistically significant. The average opening angle for the entire femoropopliteal artery was 160°±78°. The opening angle demonstrated strong negative correlation with disease severity (r=−0.64), meaning that more diseased arteries opened less.

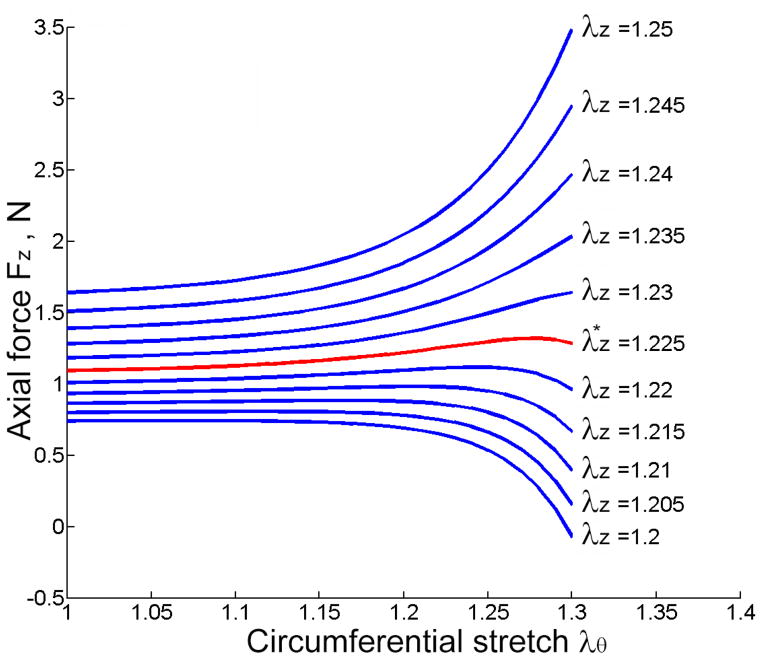
Figure 5 shows the change of axial force F_z as a function of λ_θ for fixed values of λ_z. Note that F_z tends to change little during cyclic pressurization when held near the in vivo axial length (here an extension of ${\lambda }_z^{\ast }=1.225$). The mean value of axial force for the SFA was 2.7±3.0 N, similar to the more distal PA and TA 2.7±2.1 N segments. The value of F_z for atherosclerotic plaques could not be determined, because the graphs did not show the trends presented in Figure 5.

Figure 5.

Representative circumferential stretch (λ_θ) vs. calculated axial force (F_z) response of the tissue stretched with different axial pre-stretches λ_z The graph demonstrates that axial force tends to change little during simulated pressurization when held at the in vivo axial pre-srretch ${\lambda }_z^{\ast }$ (red line).

In vivo axial pre-stretch ${\lambda }_z^{\ast }$ was smaller for the PA and TA than it was for the SFA (p=0.014). The average value of ${\lambda }_z^{\ast }$ for the SFA was 1.33±0.17 (1.62–1.08 range), while for the PA and TA it was 1.25±0.12 (1.43–1.06 range). Axial pre-stretch did not correlate with stiffness of the artery at diastole or systole in either the longitudinal or circumferential directions (r<0.2), nor did it correlate with the anisotropy ratios at diastole or systole (r=0.15, r=0.26). However, ${\lambda }_z^{\ast }$ did demonstrate moderate correlation with the increased anisotropy ratio from diastole to systole (r=0.48), meaning higher axial stretches were observed for the arteries that became more anisotropic as they progressed from diastolic to systolic stresses. Axial pre-stretch demonstrated a moderate inverse correlation with patient age (r=−0.30) and disease severity (r=−0.36), suggesting smaller ${\lambda }_z^{\ast }$ in senior and more diseased arteries.

3.4 Histological evaluation

The structure of the femoropopliteal artery wall exhibited a distinct sub-adventitial layer of elastin fibers oriented in the longitudinal direction (Figure 6). This layer was thicker and denser for arteries with no gross pathology compared to severely diseased arteries.

Figure 6.

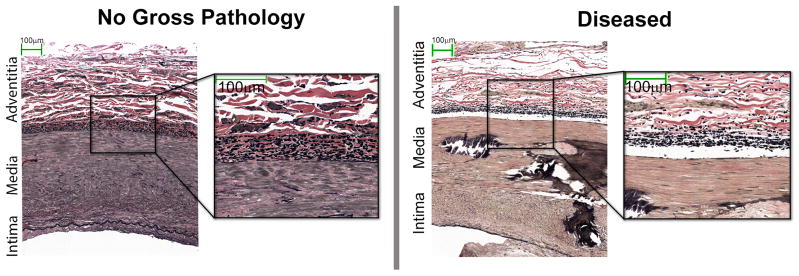
Representative histology of SFA cross-sections with no gross pathology (left) and with severe atherosclerotic disease (right) both stained with Verhoeff-Van Gieson. Cross-sections show a distinct layer of elastin fibers (black) oriented in the longitudinal direction, i.e. perpendicular to the plane of the figure. This layer is thinner for the severely diseased artery. Note that elastin fibers are concentrated at the media/adventitia interface rather than being distributed through the media thickness. Collagen fibers are colored in red.

4. DISCUSSION

Experimental evaluations of femoropopliteal artery mechanical properties are scarce in the literature. Most studies have evaluated uniaxial properties of animal tissue [46–49], while human data are rare [14–19]. To the best of our knowledge, this is the first study that reports the biaxial mechanical properties of human SFA, PA, TA and SFA atherosclerotic plaques stemming from the same patients. In addition, we provide values for constitutive model parameters and in vivo axial pre-stretch that are of interest to biomedical engineers and medical device manufacturers. Though both healthy and the diseased arterial properties are of great interest, this study focuses only on the latter since these are the arteries that typically require surgical treatment. Comparison with healthy control tissue was not performed, as these specimens are rarely available due to the infrequency of amputation for disease-free limbs.

4.1 Mechanical Testing

Our results demonstrate substantial non-linearity in the stress-stretch response characterized by an exponential increase in tissue stiffness with increasing loads. This well-known behavior is explained by the complex multi-layered structure of the arterial wall that among other components contains primarily fibers of collagen and elastin. When the artery is load-free, the stiff collagen fibers are wrinkled and the mechanical response of the vessel is determined largely by elastin. When a normal artery is stretched, collagen fibers straighten, and as they increasingly assume the load, the overall stiffness of the tissue dramatically increases, resulting in the observed stress-stretch response.

Even though many of the specimens were affected with severe disease, the tissues still exhibited large stretch. Interestingly, for the most heavily diseased arteries, large stretches were only observed in the longitudinal direction, while in the circumferential direction the tissues were stiff. Vascular diseases are thought to stiffen the tissue through complex changes that involve both structural and cellular elements of the vessel wall. Resident and migratory cellular elements sense and respond to the arteries environmental conditions and can give rise to calcification, overproduction of collagen, degradation of elastin, and vascular smooth muscle cell tone changes that can all contribute to increased stiffness of the tissue [50]. To regulate lumen diameter and protect the artery from overstretch, collagen fibers and smooth muscle cells have a preferred circumferential orientation [51–53]. Thus, overproduction of collagen and altered smooth muscle tone would most likely stiffen the artery circumferentially rather than longitudinally. This may exacerbate anisotropy and result in higher stiffness of the tissue in the circumferential compared to the longitudinal direction when loaded equibiaxially. This speculation is consistent with findings observed for all arteries in this study.

Another interesting observation was that diseased femoropopliteal arteries were stiffer distally in the longitudinal direction, while becoming more compliant in the circumferential direction. Mechanistically, this could possibly compensate for the increased longitudinal stiffness and serve to maintain a homeostatic multiaxial stress state in the artery wall [24]. Increases in longitudinal stiffness distally may indicate that the structural composition of the artery changes as the collagen fibers could become more axially aligned in the PA and TA segments compared to the more proximal SFA. This reorientation may possibly serve to regulate the axial deformations which are known to be substantial near the adductor hiatus and below the knee [10–12,54,55]. Together, the higher stiffness in the longitudinal direction and the higher compliance in the circumferential direction of the PA and TA compared to the SFA result in decreased anisotropy distally as the stress-stretch curves move closer to each other.

As all tissues tested in this study were affected by different stages of vascular disease, specimens demonstrated appreciable variability in mechanical properties. Though general trends regarding arterial segment location and mechanical properties are described, further investigation of more specimens using more detailed histological examination may shed light on the complex relations between the structure of the artery, its anisotropic response and the composition and severity of the disease.

4.2 Constitutive Modeling

The strain energy function we used was a 4-fiber family constitutive relation [36,37,40] that is an extension of the well-known 2-fiber family model proposed by Holzapfel, Gasser and Ogden (HGO) [56]. Both models are phenomenological in nature, i.e. they do not explicitly account for collagen fibers of different types and diameters or any complex fiber interactions. Nevertheless, in contradistinction to other phenomenological models, these models are motivated by microscopic data on the gross organization of arterial collagen [37,57] reflecting some physical interpretation of model parameters. Both models are formulated using invariants and are objective for non-negative material parameters [58]. The choice of a 4-fiber family model versus the simpler 2-fiber family model was motivated by the explicit inclusion of axially and circumferentially oriented families of fibers demonstrated by femoropopliteal artery histological examination (Figure 6). The inclusion of additional fiber families came at the expense of using 8 constitutive parameters versus 4, and therefore exacerbated the problem of parameter uniqueness. Selection of a large number of different protocols for minimization, i.e. expanding the domain in the strain space, helps to better determine constitutive parameters that adequately describe tissue properties under various loading conditions. However, this does not guarantee uniqueness of these parameters and various sets of values may provide equally good representations of experimental data. Variability and uniqueness can be assessed using non-parametric bootstrapping or jackknife methods described in detail by Yin et al [59], Humphrey [21] or more recently by Ferruzzi et al [37]. However, such detailed statistical assessment was beyond the scope of this study.

Experimental fits to the data using the 4-fiber family model were considerably better than those using the 2-fiber relation. We note that both the 4- and the 2-fiber family models can be augmented with fiber dispersion [52], however, as also reported by Ferruzzi et al [37], addition of rotational fiber dispersion about the primary orientations did not improve the fit enough to justify the further increase in number of structural parameters.

Material parameters for the SFA, PA and TA are summarized in Table 2. The constitutive model provided a good fit to the experimental data for most arteries. Interestingly, contrary to what was reported by Ferruzzi et al [37] for the aortic tissue, we have not observed correlations between age and the model parameter c₀, that was suggested to be associated with the contribution of elastin (r<0.25). This may be due to the effects of vascular disease that overtrumped the effects of age. The collagen-related parameters for SFA, PA and TA however, obeyed $c_1^1>c_2^1$ and $c_1^2>c_2^2$, both statistically significant. Ferruzzi et al [37] reported observing similar inequalities for healthy aortic tissue, changing to the opposite for aneurysmal aortas that contained diminished elastin.

4.3 In Vivo Axial Stretch

The constitutive model parameters we determined allowed calculation of the in vivo axial stretch that would serve to conserve energy such that the artery does no axial work during the pulse cycle. In the femoropopliteal artery, axial pre-stretch also seems to play an important role in preventing buckling during extremity flexion [10]. The structure of the femoropopliteal artery wall facilitates this behavior, exhibiting a distinct layer of elastin fibers oriented in the longitudinal direction – a structural organization not common for larger arteries such as the aorta. This longitudinal layer of elastin fibers appeared thicker and denser in healthier arteries.

As discussed above, in vivo axial pre-stretch and in situ axial pre-stretch are substantially different for aged and diseased arteries [25] suggesting that these arteries have lost their ability to function in an energy efficient way. An appropriate kinematic formulation was therefore developed to calculate that artificial state that might allow the diseased artery to function more efficiently and more closely resemble the characteristics of the normal behavior. We note however that this need for resemblance is purely hypothetical, and it has not been shown by any other studies that axial pre-stretch in the femoropopliteal artery provides any benefits for arterial function or pathophysiology. However, this current work may be the first step towards answering this question, which may eventually lead to development of better treatment techniques and devices for PAD patients.

Our results demonstrate that the in vivo axial pre-stretch decreases with age and disease, and is reduced in the more distal PA and TA compared to the more proximal SFA. In other words, these arteries do not have to be stretched as much to function most efficiently. In general, in cases of sustained alterations in flow or pressure, or when the artery is exposed to sustained mechanical influences, such as mechanical effects of the knee flexion or hypertension, the arterial wall adapts to restore a multiaxial stress state towards homeostatic values [24]. The artery attempts to compensate for high stress in one direction by decreasing the stress (by virtue of decreasing strain) in the other direction [60]. Since arteries have more control over local axial force than local blood flow and pressure, they may employ compensatory mechanisms to reduce the stretch in the axial direction and equilibrate the increased circumferential stress [24]. Such mechanisms may involve remodeling through increased fragmentation or degradation of elastin, increased deposition of collagen, and proliferation or hypertrophy of smooth muscle [24].

Elastin is produced and organized primarily during the perinatal period [24]. Since its half-life is on the order of the lifespan of the organism [61], it matures well before the arteries reach their final diameter. This implies that the elastic laminae stretch as vessel grows, which means that elastin is under considerable tension at maturity [24]. Dobrin et al [62] and Zeller and Skalak [63] reported that in healthy arteries nearly all axial pre-stretch is due to the presence of elastin. Collagen and smooth muscle, on the other hand, turnover continually, which results in collagen being under residual compression [63]. It therefore follows that degradation or fragmentation of elastin and an accompanying increase in collagen deposition likely contributes to a decrease in axial stretch. Recall that increased cyclic stretch induces smooth muscle cells to synthesize more collagen [64], and that the PA is subjected to more severe cyclic loading than the SFA simply by virtue of its anatomic location below the flexing knee [11,12,55,65]. This perhaps contributes to the smaller axial pre-stretch and higher longitudinal stiffness of the PA compared to the SFA as described in our study. Circumferential stretch is also likely affected by collagen deposition, and aged and diseased arteries may have different opening angles compared to those of the healthy arteries. Additional studies are required to investigate this speculation.

The findings of this study should be viewed within the context of its limitations. First and foremost, all mechanical properties were reported under the assumption of homogeneity which clearly is not the case for arteries severely affected with vascular disease. Though alternative methods, such as nanoindentation and elastography with back-calculation, are being currently explored for inhomogeneous tissue characterization, the data obtained with biaxial testing are currently far superior in terms of describing the essential non-linearity and anisotropy of these materials under physiologic and supraphysiologic loads. The second limitation concerns constitutive modeling. As pointed out by Ogden [58], 3D material properties cannot be determined from the 2D biaxial experiments. Though the state of the experimental art at present does not allow full 3D characterization of soft tissues, this limitation should always be kept in mind when using biaxial data for 3D modeling. Finally, the sample size of 10 patients may be too small for adequate statistical analysis, requiring more specimens and experiments to validate the statistical significance of our findings.

In summary, arterial walls are substantially more complex than we can assess with existing testing techniques and describe with current mathematical models. However, the prevalence of peripheral arterial disease and poor outcomes of current treatment methods creates a pressing need for experimental data that can allow a better understanding of the main characteristics of femoropopliteal artery function and pathophysiology. This current work was aimed at elucidating some of these characteristics, which we hope will serve as a starting point towards achieving this challenging goal.

Figure 7.

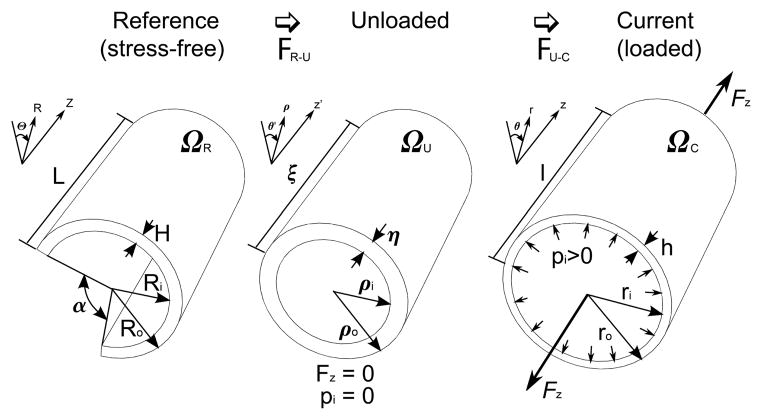
Kinematics of the arterial wall showing an intact artery in the reference (stress-free configuration) Ω_R where the circumferential stress is released by the radial cut resulting in opening of the arterial ring into a sector with angle α. The artery is then transferred to the unloaded configuration via F_R–U, i.e. by closing the sector. In the unloaded configuration Ω_U, the artery contains residual stresses but has no internal pressure or axial force. Finally, the unloaded arterial segment is loaded with an internal pressure p_i and an axial force F_z resulting in the transformation F_U–C to the current (loaded) configuration Ω_C. Note that the dimensions of the arterial segment in all three configurations are different.