Improving z-tracking accuracy in the two-photon single-particle tracking microscope

Abstract

Here, we present a method that can improve the z-tracking accuracy of the recently invented TSUNAMI (Tracking of Single particles Using Nonlinear And Multiplexed Illumination) microscope. This method utilizes a maximum likelihood estimator (MLE) to determine the particle's 3D position that maximizes the likelihood of the observed time-correlated photon count distribution. Our Monte Carlo simulations show that the MLE-based tracking scheme can improve the z-tracking accuracy of TSUNAMI microscope by 1.7 fold. In addition, MLE is also found to reduce the temporal correlation of the z-tracking error. Taking advantage of the smaller and less temporally correlated z-tracking error, we have precisely recovered the hybridization-melting kinetics of a DNA model system from thousands of short single-particle trajectories in silico. Our method can be generally applied to other 3D single-particle tracking techniques.

High-resolution tracking microscopes typically require 4–5 single-photon counting devices to track single particles in the 3D space.^1–3 Recently, we demonstrated a 3D tracking microscope, termed TSUNAMI (Tracking of Single particles Using Nonlinear And Multiplexed Illumination, Fig. 1(a)), that uses only one photomultiplier tube (PMT) to achieve high-resolution 3D single-particle tracking (3D-SPT).^4,5 A two-photon microscope by its nature, TSUNAMI enables multicolor imaging and provides an imaging depth that cannot be achieved by traditional feedback-driven microscopes.^6–8 3D tracking of epidermal growth factor receptor complexes at a depth of ∼100 μm in live tumor spheroids has been demonstrated.⁵ In addition, TSUNAMI can provide particle localization precision as good as 35 nm (at shallow depths) and temporal resolution down to 50 μs (with bright fluorophores).⁵ Whereas SPT is probably the most suitable method for determining whether the tracked particles (here, particles can be single biomolecules such as DNA, membrane receptors, and transcription factors) form dimers or complexes with other particles,^9,10 the current embodiment of TSUNAMI cannot precisely probe binding-unbinding kinetics of the tracked particles for two reasons. First, the z-tracking error of TSUNAMI is considerably larger than its xy-tracking error (nearly 2-fold).^4,5 Second, the z-tracking error is correlated over time, which has made the trajectory analysis tools that assume tracking errors to be white Gaussian noise perform poorly. In this letter, we overcome the above problems by implementing a maximum likelihood position estimator as the tracking algorithm. Precise binding-unbinding kinetics of a model system are recovered from thousands of short single-particle trajectories in silico.

FIG. 1.

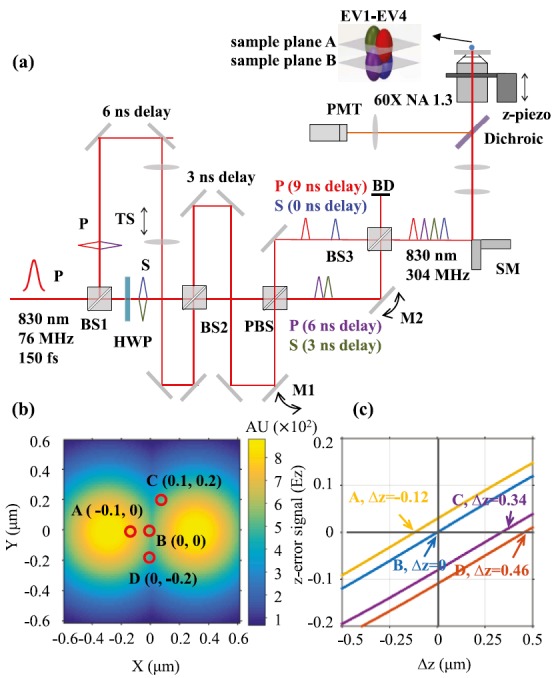
(a) Schematic of the TSUNAMI 3D tracking microscope. P: p-polarized light. S: s-polarized light. HWP: half-wave plate. PBS: polarizing beamsplitter. BD: beam dump. TS: telescope. TSUNAMI uses spatially multiplexed two-photon excitation and temporally demultiplexed detection to achieve 3D single-particle tracking. Spatial multiplexing is enabled through an optical system which utilizes two beam splitters (BS1 and BS2) to generate four beams, which can be quasi-independently controlled via two mirrors (M1 and M2) and a telescope. Physical delay in free space provides temporal separation between these beams. Tracking actuation is performed by raster scanning mirrors (SM) and an objective focusing stage (z-piezo). (b) The heat map displays the illumination intensity distribution of two excitation volumes (EV1 and EV2), at the z = 0 plane. EV1 and EV2 are offset by 0.6 μm in the x axis, and EV3 and EV4 (not shown here) are offset by 0.6 μm in the y axis. (c) The z-error signal functions $E_z(z)$ at four lateral locations: A(−0.1, 0), B(0, 0), C(0.1, 0.2), and D(0, −0.2). $E_z(z)$ at ${\stackrel{\rightharpoonup }{r}}_0$ = ($x_0$, $y_0$) is calculated as follows: $E_z(z)$ = $({\sum }_{i=1}^2{I}_i({\stackrel{\rightharpoonup }{r}}_0,\hspace{0.17em}\mathrm{z})-{\sum }_{i=3}^4{I}_i({\stackrel{\rightharpoonup }{r}}_0,\hspace{0.17em}\mathrm{z}))/{\sum }_{i=1}^4{I}_i({\stackrel{\rightharpoonup }{r}}_0,\hspace{0.17em}\mathrm{z})$. Although the slopes of all four z-error signal functions are identical, their vertical intercepts vary from −0.12 to 0.025. Consequentially, a fluorescent particle at D (0, −0.2, 0) will be misinterpreted by the error signal analysis as below the z = 0 plane (i.e., Δz < 0) as E_z < 0, while a particle at A (−0.1, 0, 0) will be misinterpreted as above the z = 0 plane (i.e., Δz > 0) as E_z > 0.

In TSUNAMI, multiplexed illumination is achieved by splitting the pulsed laser beam from a 76 MHz Ti-sapphire oscillator into four beams, with each beam delayed by 3.3 ns relative to the preceding one (Fig. 1(a)). These beams are focused through a 60 × 1.3 N.A. objective (UPLSAPO 60XS, Olympus) at slightly offset xyz positions, generating four barely overlapped two-photon excitation volumes. These four excitation volumes form a tetrahedral geometry in the sample space (colored oval balls in Fig. 1(a) inset), and they receive laser pulses at different time frames (Fig. S1¹¹). With time-correlated single photon counting (TCSPC) analysis, each detected photon can be assigned to a 3.3 ns-wide time gate (G1-G4 in the fluorescence decay histogram, Fig. S1¹¹), and therefore attributed to a specific excitation volume (EV1-EV4 in Fig. 1(a) and Note S1¹¹).

When the tracked particle (which is also called the “emitter” below) is right at the center of the excitation tetrahedron, photon counts in the four time gates are about equal (i.e., I₁ = I₂ = I₃ = I₄). Any xyz displacement (Δx, Δy, and Δz) of the emitter from the tetrahedron center can be estimated via the normalized differences of photon counts in the four time gates (Figs. S1(c) and S1(d)¹¹), namely, the error signals (Ex, Ey and Ez)¹²

$$\begin{array}{c}\Delta x=k_x{E}_x=k_x\frac{I_1-I_2}{I_1+I_2},\\ \Delta y=k_y{E}_y=k_y\frac{I_3-I_4}{I_3+I_4},\\ \Delta z=k_z{E}_z=k_z\frac{(I_1+I_2)-(I_3+I_4)}{(I_1+I_2)+(I_3+I_4)},\end{array}$$ (1)

where k_x, k_y, and k_z are proportional gains (constants in unit of μm) that have been previously determined and optimized.³

Once the particle's displacement is determined, a feedback loop steers the galvo mirrors and the objective z-piezo stage to lock the tetrahedral excitation volumes on the particle (Note S1¹¹). The particle's 3D trajectory is given by the xy location of the excitation beams (xy) and the z translation of the piezo stage (z) in each time step.

In the error signal analysis (ESA, Eq. (1)), the responsivities of the tracking system (i.e., the change of x-, y-, z-error signal per micron displacement of the tracked particle) are determined by the gradient of the square of excitation intensity.³ Due to the elongated excitation volume, tracking responsivity is considerably smaller in the z direction (Fig. S2¹¹), resulting in a much worse z-tracking accuracy. Other than this native tracking responsivity issue, we experimentally found that the dependence of E_z on emitter's xy position (Fig. S3¹¹) could also deteriorate the z-tracking accuracy. In our optical modeling (see Note S2¹¹ for details), we can clearly see that the resulting z-error signal functions $E_z(z)$ at the four lateral locations A-D are not identical—they have the same slope but distinct intercepts (Fig. 1(c)). When E_z is zero, ESA will simply interpret the situation as perfect z-locking on the tracked particle (Eq. (1)). However, the actual z displacement of the emitter (Δz) can be −0.12 μm (A, yellow line), 0 μm (B, blue line) or +0.34 μm (C, purple line). As a result, a false Δz interpretation leads to a false objective stage response (piezo stage does not move when E_z is zero, Fig. S4(a)¹¹), which not only increases tracking errors but also reduces tracking duration (easier to lose the tracked particle). A straightforward way to fix the problem is to compensate the z-error signal functions in Fig. 1(c) by taking emitter's estimated lateral position ($\widehat{x}$, $\widehat{y}$) into account (Note S3¹¹). However, our Monte Carlo simulations indicate that only a marginal improvement (∼10%) in the z-tracking accuracy can be achieved by this remedy (Note S3¹¹).

An algorithm that can significantly increase the z-tracking accuracy is maximum likelihood estimation (MLE). Using MLE for particle position estimation, Sahl and coworkers have previously achieved 2D single-particle tracking with xy-localization error as small as 10–20 nm.¹³ MLE finds the most likely position of the emitter by comparing the recorded photon counts in the four time gates $\overrightarrow{I}=[I_1,\hspace{0.17em}{I}_2,\hspace{0.17em}{I}_3,\hspace{0.17em}{I}_4]$ with a 3D reference map $\overrightarrow{R}(x,y,z)=[R_1(x,y,z),R_2(x,y,z),R_3(x,y,z),R_4(x,y,z)]$, where $R_i(x,y,z)$ denotes the photon counts in the i-th time gate when the reference emitter is located at position $(x,y,z)$. Such a 3D reference map $\overrightarrow{R}(x,y,z)$ can either be established by optical modeling (Note S4¹¹), or established experimentally by raster scanning the excitation tetrahedron with an immobilized fluorescent nanoparticle (i.e., the reference emitter) while recording the four signal intensities as a function of the particle's position. $\overrightarrow{R}(x,\hspace{0.17em}y,\hspace{0.17em}z)$ is further normalized such that ${\sum }_{i=1}^4{R}_i(x,\hspace{0.17em}y,\hspace{0.17em}z)=1$. For a given emitter position $(x,y,z)$, the probability of detecting $I_i$ photons in the $i$-th time gate follows Poisson distribution (where $R_i\hspace{0.17em}$ is the expected value and the variance)

$$p_i\left(I_i;R_i|x,\hspace{0.17em}y,\hspace{0.17em}z\right)=\frac{(R_i(x,y,z\left)\right){\hspace{0.17em}}^{I_i}}{I_i!}\text{exp}(-R_i(x,y,z)).$$ (2)

The likelihood of detecting $\overrightarrow{I}$ photons at a position $(x,y,z)$ with $\overrightarrow{R}(x,y,z)$ expected photons on average is given by the product of the above probabilities

$$L(\overrightarrow{I};\overrightarrow{R}|x,y,z)=\underset{i=1}{\overset{4}{\Pi }}{p}_i(I_i;R_i|x,y,z).$$ (3)

The most likely position of the emitter is thus the location where this likelihood $L$ is maximized, or equivalently where the log-likelihood is maximized¹⁴

$$(\widehat{x},\widehat{y},\widehat{z})=\underset{(x,y,z)}{\text{argmax}}\left[\sum _{i=1}^4{I}_i\ln (R_i(x,y,z))\right].$$ (4)

In each time step, we search for a position $(x,y,z)$ that maximizes the log-likelihood $[{\sum }_{i=1}^4{I}_i\text{ln}(R_i(x,y,z))$] and uses that to represent the emitter's position (Note S4¹¹).

By virtue of MLE, the z-tracking accuracy is enhanced by 1.7 fold (Table I, also see Note S3¹¹ for details of this simulation). While the z-tracking error is still larger than the xy-tracking error, their relative difference is reduced from 129 $\pm$ 23% to 33 $\pm$ 4%. Besides, the relative error for the calculated diffusion coefficient is decreased from 14 $\pm$ 1% to less than 2%. The improvement of the z-tracking accuracy can be clearly seen in the z-tracking error histograms (Figs. S5(b) and S5(d)¹¹). Both histograms could be well described by a Gaussian distribution, with mean approximately equal to zero. Comparing the two tracking schemes, MLE clearly gives a narrower z-tracking error distribution (σ = 50.2 nm vs. 93.9 nm) and a better diffusion coefficient estimate ($\widehat{D}$ = 0.50 μm²/s vs. 0.47 μm²/s).

TABLE I.

Comparison of tracking errors from four different position estimation algorithms. $\widehat{D}$ is the estimation of true diffusion coefficient $D$, ESA: error signal analysis, and MLE: maximum likelihood estimator.

	Method	XY (nm)	Z (nm)	$\widehat{D}$ ($\mu {\mathrm{m}}^2/\mathrm{s}$)
$D$ = 0.5 $\mu {\mathrm{m}}^2/\mathrm{s}$	ESA	42.9	87.6	0.42 $\pm 0.06$
	MLE	38.7	50.7	0.51 $\pm$ 0.06
$D$ = 1.0 $\mu {\mathrm{m}}^2/\mathrm{s}$	ESA	53.4	123.8	1.14 $\pm$ 0.13
	MLE	55.6	72.8	1.00 $\pm$ 0.11
$D$ = 1.5 $\mu {\mathrm{m}}^2/\mathrm{s}$	ESA	65.7	164.7	1.76 $\pm$ 0.20
	MLE	69.0	95.5	1.53 $\pm$ 0.18

In single-particle tracking, the localization errors are often modeled as time-independent white Gaussian noise when studying the effects of localization errors on the particle behavior interpretation (e.g., free diffusion or confined diffusion).^15–17 While the white Gaussian noise model greatly simplifies mathematical analysis of localization errors, the white Gaussian noise assumption may not be true in the real tracking experiments. Indeed, with close examination, we found many of the published single-particle trajectories show notable temporal correlation in their tracking errors^{2,6,7,18–20} (Fig. S6¹¹). Below we demonstrate that temporally correlated tracking errors make the current trajectory analysis tools perform poorly and the MLE tracking scheme alleviates this problem by generating temporally uncorrelated tracking errors.

To investigate the temporal properties of tracking errors, we plotted the autocorrelation functions C(τ)²¹ of white Gaussian noise, ESA z-tracking error and MLE z-tracking error in Fig. 2(a), and fitted them with a single exponential decay model²² ($A{e}^{-t/{\tau }_0})$. As expected, the autocorrelation function of zero-mean white Gaussian noise (C_GAU) asymptotically approaches a delta function, showing no temporal correlation at all. Similar to C_GAU, the autocorrelation function of the MLE z-tracking error (C_MLE) decays rapidly, with a temporal correlation length ${\tau }_0\hspace{0.17em}$ = 0.36 (in units of time steps). On the contrary, C_ESA decays slowly with ${\tau }_0\hspace{0.17em}$ = 2.06. To understand the whiteness of the z-tracking errors, their power spectral densities²³ (PSD) were plotted and compared (Fig. 2(b)). Ideal white noise has a constant PSD. Both autocorrelation and PSD analyses indicate that the z-tracking error from the MLE scheme is a better approximation of white Gaussian noise.

FIG. 2.

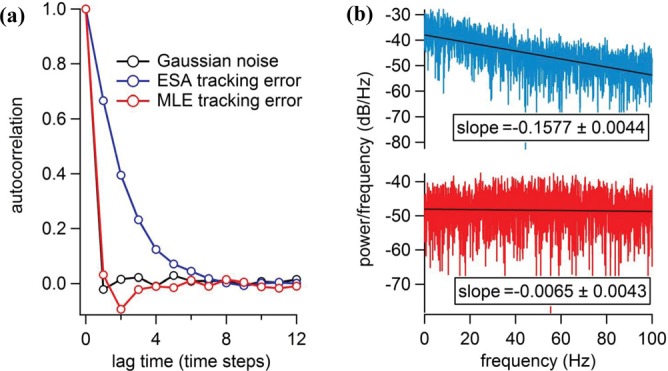
(a) Normalized autocorrelation functions of zero-mean white Gaussian noise (C_GAU, black), ESA z-tracking error (C_ESA, blue) and MLE z-tracking error (C_MLE, red). The autocorrelation function C(τ) of error e(t) is defined as: $C(\tau )={⟨\delta e(t)\cdot \delta e(t+\tau )/e(t)⟩}^2$, where $\hspace{0.17em}⟨⟩$ represents averaging over time and $\delta e(t)=e(t)-⟨e(t)⟩.$ (b) Power spectral densities of ESA z-tracking error (blue) and MLE z-tracking error (red). The fitted slopes are also shown in inset (coefficient value $\pm$ one standard deviation). A constant power spectral density is the characteristic of white noise. In this simulation, the diffusive particle (D = 0.5 μm²/s) is tracked for 20 s. Each time step is 5 ms.

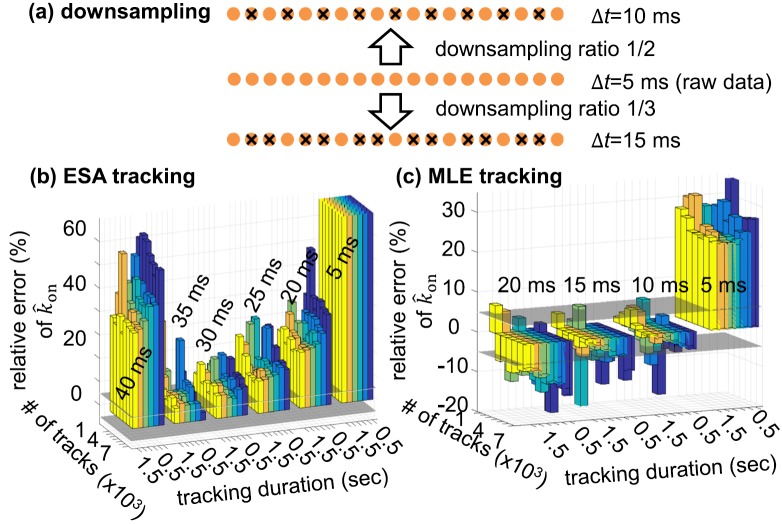
Temporally uncorrelated tracking errors can be crucial for the reliable recovery of molecular kinetics from 3D-SPT data. We have verified this hypothesis using DNA hybridization and melting kinetics as a model system (see details in Fig. S7¹¹). In our simulations, transition between the hybridized state (D_h = 0.15 μm²/s) and the melted state (D_m = 0.30 μm²/s) is a memoryless process, with a rate constant $k_{\text{on}}$ = 2.99 $\times$ 10⁵M⁻¹s⁻¹ for hybridization and a constant $k_{\text{off}}$ = 0.7 s⁻¹ for melting.²⁴ The tracking duration varies from 0.5 s to 1.5 s, limited by the photostability of the fluorescent tag. A hidden Markov model (HMM) is adopted to model the random switch between the two diffusive states,^24–26 and a 3D variational Bayes method (vbSPT)²⁷ is used to determine the hybridization-melting kinetics (i.e., $k_{\text{on}}$ and $k_{\text{off}}$) from downsampled 3D trajectory data. Here, downsampling of the raw trajectory data (time step δt = 5 ms) is just an additional step to further decorrelate tracking errors at the expense of worse effective temporal resolution.

The relative errors of ${\widehat{k}}_{\text{on}}$ and ${\widehat{k}}_{\text{off}}$ (estimates of rate constants) are a function of effective temporal resolution (Δt = N δt, 1/N is the downsampling ratio), number of tracks, and tracking duration (Figs. 3 and S8¹¹). Consistent with previous reports,²⁷ the relative errors of ${\widehat{k}}_{\text{on}}$ and ${\widehat{k}}_{\text{off}}$ monotonically decrease with increasing number of tracks and tracking duration. Without any downsampling (Δt = 5 ms), the relative errors of ${\widehat{k}}_{\text{on}}$ are over +70% for ESA tracking (Fig. 3(b)) and in a range of +20% to +40% for MLE tracking (Fig. 3(c)). These large positive relative errors are predominantly caused by the temporal correlation of the tracking errors, which can be reduced by downsampling. Using a downsampling ratio of 1/2 (Δt = 10 ms), the relative errors of ${\widehat{k}}_{\text{on}}$ fall within ±5% for MLE tracking. On the other hand, even though a downsampling ratio 1/7 is used (Δt = 35 ms), the relative errors of ${\widehat{k}}_{\text{on}}$ are still biased and over +12% for ESA tracking. In other words, MLE tracking offers both better molecular kinetics estimation and higher effective temporal resolution.

FIG. 3.

(a) Downsampling of the raw trajectory data. Raw trajectory data have a temporal step size Δt = 5 ms. Downsampling ratios of 1/2 and 1/3 result in Δt = 10 ms and Δt = 15 ms, respectively. Downsampled trajectories are then analyzed by the 3D variational Bayes method (vbSPT)²⁷ in order to discern the binding-unbinding kinetics (${\widehat{k}}_{\text{on}}$ and ${\widehat{k}}_{\text{off}}$) of the tracked particle. (b) Relative error of ${\widehat{k}}_{\text{on}}$ derived from ESA-based trajectories. (c) Relative error of ${\widehat{k}}_{\text{on}}$ derived from MLE-based trajectories. In this simulation, the number of tracks and track duration are varied to assess the convergence of vbSPT. Each bar represents one vbSPT analysis of 1,000-7,000 trajectories, with bar height showing the relative error of ${\widehat{k}}_{\text{on}}$ and bar color encoding tracking duration (0.5 s—purple, 0.7 s—dark blue, 0.9 s—light blue, 1.1 s—green, 1.3—orange, and 1.5 s—yellow). The horizontal grey planes are where the relative error equals $\pm$ 5%. The 6 bar groups in (b) correspond to ${\widehat{k}}_{\text{on}}$ obtained from 6 different downsampling ratios, whose Δt are integer multiples of 5 ms. Similarly, the 4 bar groups in (c) correspond to ${\widehat{k}}_{\text{on}}$ obtained from 4 different downsampling ratios.

Both enhanced z-tracking accuracy and less temporally correlated z-tracking errors can contribute to the improved molecular kinetics estimation shown in Fig. 3(c). To understand their relative importance, we have tested two scenarios in our simulations (Note S5¹¹): (a) the z-tracking errors are kept small, but they are temporally correlated; (b) the z-tracking errors are large, but they are temporally uncorrelated. By comparing the relative errors given by the MLE-based tracking and the scenario (a), we have found that more precise kinetics estimation in MLE-based tracking cannot be solely explained by better z-tracking accuracy (Note S5¹¹). On the other hand, by comparing the relative errors given by the ESA-based tracking and the scenario (b), we have found that the quality of kinetics characterization can be dramatically improved solely by making the tracking error less correlated over time, even when the tracking error amplitude remains the same. Therefore, decorrelation of z-tracking error plays a critical role in reliable recovery of molecular kinetics.

In conclusion, we have developed a maximum likelihood estimator (MLE) that can improve the z-tracking accuracy of TSUNAMI microscope by 1.7 fold, without sacrificing the xy-tracking accuracy. MLE outperformed the traditional ESA tracking scheme mainly because ESA has a fundamental flaw in its z-position estimate—the cross-talk between the lateral and axial direction is not accounted for. MLE, on the other hand, uses all the information available for position estimate (including any possible cross-talk), therefore resulting in a much smaller z-tracking error. We believe that the less temporally correlated z-tracking error found in MLE tracking is also a result of its better position estimate in each time step. With less temporally correlated tracking error, precise hybridization-melting kinetics of a DNA model system have been recovered from thousands of short trajectories in silico. Our preliminary implementation of the MLE algorithm on a quad-core Windows PC suggests that MLE can be run in quasi real time (<1 ms), and potentially can be further accelerated by dedicated field-programmer gate array (FPGA). Our approach can be readily applied to other feedback-driven SPT techniques which suffer from the large z-tracking error and the temporally correlated-tracking-error issues.⁷ This work demonstrates that temporally uncorrelated tracking error is as important as small tracking error, and binding-unbinding kinetics cannot be correctly characterized without first examining the temporal properties of tracking/localization errors.