Abstract
Purpose:
The work presented here demonstrates an application of diffuse optical tomography (DOT) to the problem of breast-cancer diagnosis. The potential for using spatial and temporal variability measures of the hemoglobin signal to identify useful biomarkers was studied.
Methods:
DOT imaging data were collected using two instrumentation platforms the authors developed, which were suitable for exploring tissue dynamics while performing a simultaneous bilateral exam. For each component of the hemoglobin signal (e.g., total, oxygenated), the image time series was reduced to eight scalar metrics that were affected by one or more dynamic properties of the breast microvasculature (e.g., average amplitude, amplitude heterogeneity, strength of spatial coordination). Receiver-operator characteristic (ROC) analyses, comparing groups of subjects with breast cancer to various control groups (i.e., all noncancer subjects, only those with diagnosed benign breast pathology, and only those with no known breast pathology), were performed to evaluate the effect of cancer on the magnitudes of the metrics and of their interbreast differences and ratios.
Results:
For women with known breast cancer, simultaneous bilateral DOT breast measures reveal a marked increase in the resting-state amplitude of the vasomotor response in the hemoglobin signal for the affected breast, compared to the contralateral, noncancer breast. Reconstructed 3D spatial maps of observed dynamics also show that this behavior extends well beyond the tumor border. In an effort to identify biomarkers that have the potential to support clinical aims, a group of scalar quantities extracted from the time series measures was systematically examined. This analysis showed that many of the quantities obtained by computing paired responses from the bilateral scans (e.g., interbreast differences, ratios) reveal statistically significant differences between the cancer-positive and -negative subject groups, while the corresponding measures derived from individual breast scans do not. ROC analyses yield area-under-curve values in the 77%–87% range, depending on the metric, with sensitivity and specificity values ranging from 66% to 91%. An interesting result is the initially unexpected finding that the hemodynamic-image metrics are only weakly dependent on the tumor burden, implying that the DOT technique employed is sensitive to tumor-induced changes in the vascular dynamics of the surrounding breast tissue as well. Computational modeling studies serve to identify which properties of the vasomotor response (e.g., average amplitude, amplitude heterogeneity, and phase heterogeneity) principally determine the values of the metrics and their codependences. Findings from the modeling studies also serve to clarify the influence of spatial-response heterogeneity and of system-design limitations, and they reveal the impact that a complex dependence of metric values on the modeled behaviors has on the success in distinguishing between cancer-positive and -negative subjects.
Conclusions:
The authors identified promising hemoglobin-based biomarkers for breast cancer from measures of the resting-state dynamics of the vascular bed. A notable feature of these biomarkers is that their spatial extent encompasses a large fraction of the breast volume, which is mainly independent of tumor size. Tumor-induced induction of nitric oxide synthesis, a well-established concomitant of many breast cancers, is offered as a plausible biological causal factor for the reported findings.
Keywords: mammography, cancer, image processing in medical imaging, biological signal processing, modeling of biomedical systems
1. INTRODUCTION
Evidence of increased tissue stiffness,1,2 structural malformations,3 altered perfusion of the vascular bed,4 and changes in molecular expression5 have all served as phenotypic markers for the presence of breast cancer. While examinations of these have resulted in the development of improved strategies for the assessment and management of breast cancer, the determination of which methods are preferred is influenced by a host of unrelated factors. An ideal endpoint would be an economical sensing methodology that has high patient comfort and that, owing to its simplicity and robustness, can be used by nondomain experts and outside of complex, costly environments. However, experience with many sensing strategies has shown that these considerations frequently lead to conflicting requirements.
For instance, one principled approach to developing improved assessment and management strategies is to adopt methods that are sensitive to the increasingly well-understood molecular environment changes that accompany tumorigenesis. An example of this is in vitro examination of various molecular markers. This is highly useful for diagnosing disease and guiding treatment,6 but it is also invasive, costly, and not suitable for use by nondomain experts, among other limitations.
A growing number of functional assessment tools represent a bridge between direct assays of molecular markers and observation of structural changes. Within this category, one class of markers that has been considered is noninvasive measures of tissue stiffness.7,8 Among these are tactile sensing methods,8,9 as well as stiffness-sensitive varieties of ultrasound10 and MR imaging.11 In its simplest form, tactile sensing, as incorporated in the clinical breast exam (CBE),12 meets many of the aims listed above. Unfortunately, while this technique has high specificity in the case of palpable tumors, it is poorly suited for the nonpalpable tumors that commonly are present in early stage disease.
Various optical inspection methods also hold potential to fill the gap, while retaining the desirable elements of low cost and reduced complexity. One of the most frequently considered strategies is use of near-infrared methods, which are sensitive to the hemoglobin (Hb) signal.7,13–18 Other elements of tissue composition, such as tissue fat and water content, can be additionally considered by NIR methods.19 There are strong phenomenological grounds for expecting correlations between cancer and abnormal levels of one or more of these tissue constituents,5 and studies have been carried out to evaluate their diagnostic utility.18,20
An alternative to the preceding, mainly static, examination methods is techniques that explore the naturally occurring dynamics of the hemoglobin signal that accompany modulation of the vascular tree and its interactions with tissue.7,13,21 Similar to other time-varying measures of tissue function (e.g., measures of tissue bioelectric properties), these can be obtained either under conditions of rest or in response to controlled provocations.7 To this end, our group has developed several different instrumentation platforms that are suitable for exploring tissue dynamics while a simultaneous bilateral exam is performed.7,13,21 In one form, and following the spirit of the CBE procedure, we have implemented a system design that combines optical measures with tactile sensing and controlled articulations.7 In keeping with the disease phenotype-independent considerations outlined above, one factor guiding this approach was the aim of leveraging the clinical expertise and other factors associated with the CBE procedure while augmenting them in a quantitative manner.
While we have succeeded in developing a robust device,7 the dimensionality of the information space that could be examined in pursuit of identifying suitable biomarkers has prompted us to also explore more limited data-collection conditions. One such consideration is a simple resting-state measure, wherein time-series optical measures are obtained from both breasts simultaneously under defined conditions of optode contact. Our initial aim was to compare such baseline measures to responses evoked by controlled provocations in the expectation that findings of interest would align mainly with the latter. However, as evidenced by the results reported here, notably promising findings have been obtained based solely on examination of the resting-state responses.
1.A. Strategy for identifying suitable biomarkers for cancer detection
A key assumption underlying efforts to identify suitable biomarkers is the expectation that the impact of disease on measured quantities exceeds the natural variance inherent in the subject population. Here, our attention is drawn to elements of spatiotemporal behavior obtained from resting-state vascular dynamics. Obvious factors that can add to variance are the wide range in breast sizes and in breast composition (e.g., ratio of adipose to glandular tissue), and the presence of common comorbidities (e.g., atherosclerosis). One approach to minimizing intersubject variance is to adopt some form of referencing scheme wherein subject-dependent differences are substantially canceled out. Depending on how this is implemented, additional data-collection requirements may arise. Here, we have systematically explored elements of spatiotemporal behavior, ranging from simple univariate metrics obtained from individual breasts to various metrics derived from simultaneous bilateral measurements.
Our analysis approach has been to divide the information space into different principal domains and then to identify levels of statistical significance in comparisons between the affected and unaffected groups, as a prelude to receiver-operator characteristic (ROC) analysis. The domains considered are elements of the Hb signal (e.g., total, oxygenated component, deoxygenated component), measures of central tendency derived from the reconstructed image time series, and use of elementary variance reduction methods to minimize intersubject variance arising from measurement issues (e.g., variations in skin-optode contact in different measurement sessions) and from biological factors that are not related to the presence of cancer (e.g., the previously noted variations in breast size and composition). Apart from identifying promising metrics, one aim of this approach has been to determine factors that influence the robustness of a given metric (see Sec. 4).
2. METHODS
2.A. Data collection
Data reported here were obtained from the first-13 and second-generation7 simultaneous bilateral, high density, time-series optical tomographic imaging systems developed by our group. One of the guides to system design was the hypothesis that the hemodynamic response evoked by a controlled provocation may yield useful biomarkers stemming from the presence of the aberrant vascular bed that is produced by tumor angiogenesis.7,13,22
For both systems, following the initial setup, data collection included a baseline measurement lasting 5–10 minutes with subjects resting comfortably, followed by a series of controlled provocations. For the scans conducted using the first-generation system, subjects were asked to perform a quantitative Valsalva maneuver13 while lying prone with breasts in the pendent position. While the optical system performance was excellent,13 the ability of patients to perform the respiratory maneuvers proved disappointing.23 This prompted us to develop a second-generation device that eliminated the need for active participation on the part of the subject. Instead, vascular responses are evoked by using a feedback-controlled articulating device upon a supported breast, with subjects examined while comfortably seated.7
Thus, while our principal aim has been to explore evoked responses, measures obtained under resting-state conditions have been available from studies conducted with both imaging systems.
2.B. Summary of system functionality
2.B.1. First-generation imager
This unit performed simultaneous bilateral measures (31 sources × 31 detectors per breast) with subjects lying in the prone position and breasts hanging pendent.13 The sensor heads have a cup-like geometry and contain spring-loaded optodes uniformly spaced over the breast surface. The measuring cups are positioned beneath the subject and carefully translated to achieve contact.
2.B.2. Second-generation imager
This unit also performed simultaneous bilateral measures, but with a higher sensor density (32 sources × 64 detectors per breast) and with subjects in the seated position.7 Another innovation was the introduction of active articulating elements with embedded optodes and the ability to perform concurrent viscoelastic measures under conditions of controlled articulation. Each sensing head is attached to a multi-axis articulating arm that supports stable optode contact with a breast. Because measures reported here are restricted to the resting-state, the latter sensing capabilities were not explored.
Each system has an image sampling rate of 1.8 Hz and performs simultaneous dual-wavelength measures (760, 830 nm). Additionally, the geometry of the sensing heads assured that most of the breast volume was explored to within the limits of optical penetration. Also common to both systems is the ability to accommodate a range of breast sizes (larger range for the articulating system), while imposing substantially symmetric external boundary conditions.
2.C. Processing of optical data
Because of the wide range of breast sizes among subjects, appreciable variability can be expected in the noise level for any given optical channel associated with full tomographic measures. To limit effects of breast size on signal quality, a noise threshold was imposed, restricting data for subsequent processing to only those channels having coefficients of variation (CV) of less than 15%. Additionally, to avoid biases in interbreast comparisons, a symmetry restriction was imposed, such that channels deleted from one breast were also deleted from the other, yielding bilaterally symmetric data sets. Also, while either instruments could accommodate a range of breast sizes (greater size range with the second-generation system), experience showed that an excessive number of channels were excluded from women who had either very large breasts, due to poor signal quality, or very small breasts, due to limited optode contact. To minimize undersampling effects, only data sets in which at least 60% of the optode channels satisfied the CV-threshold criterion were used for subsequent processing.
2.D. Extraction of biometrics
Collected time series data were processed in two principal steps. First, following the exclusion of excessively noisy channels, a linear detrending operation was performed and then 4D (three spatial and one temporal) image time series were computed for various components of the Hb signal for each breast, using a previously described algorithm.13,25 Derived measures included individual [i.e., deoxyhemoglobin (deoxyHb) and oxyhemoglobin (oxyHb)] and composite [i.e., total hemoglobin (totalHb = deoxyHb + oxyHb), hemoglobin oxygen extraction efficiency (O2effHb = deoxyHb − oxyHb24), and hemoglobin oxygen saturation (HbSat = 100*oxyHb/totalHb)] components of the Hb signal. That is, all of the commonly considered Hb-signal components were examined, as prior studies have emphasized that the sensitivity of optical tomography for breast cancer detection is dependent on which component is examined.18,20–23 Second, for each Hb-component image time series, various subsequently described spatial, temporal, and spatiotemporal indices were explored, both as unilateral scalar quantities and as bilateral quantities where values from the two breasts were compared to each other.
2.D.1. Unilateral breast metrics
In an effort to limit the size of the data space, we have derived a set of scalar quantities from descriptive statistics computed over the baseline time period, integrating first over one domain (spatial or temporal) and then the other. Thus, a 4D image time series can be reduced to a 1D time series by computing either the spatial mean (SM) or the spatial standard deviation (SSD) across the image volume, at every time frame,
| (1) |
where the generic symbol x(r, t) is used to denote a function of position and time, such as a time series of volumetric Hb-concentration images, and Nv is the number of FEM mesh nodes. Alternatively, the image time series can be reduced to a single 3D image by computing either the temporal mean (TM) or the temporal standard deviation (TSD) in each voxel, over the baseline time interval,
| (2) |
where Nt is the number of baseline time frames. However, owing to the normalization method used in image recovery (i.e., for every measurement channel, individual data values are referenced to the baseline-period temporal mean25), TM(r) is identically zero. In contrast, TSD(r) is a nontrivial (e.g., see Fig. 3) and diagnostically useful (see Sec. 3.B) quantity, and its formulation simplifies to
| (3) |
FIG. 3.
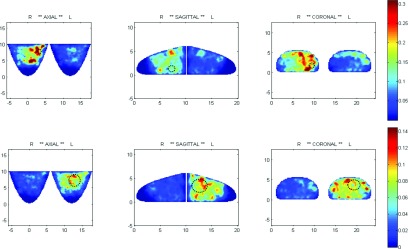
Spatial maps of the TSD metric. Top: right-breast tumor (Grade-2 IDC, ER+), 1 cm, 4 o’clock; HbSat; second-generation imager; subject is 34 yo, BMI 29, size D. Bottom: left-breast tumor (Grade-3 IDC, ER+), 4 cm, 1 o’clock, HbSat; second-generation imager; subject is 50 yo, BMI 44, size C. Dotted black circles superimposed on the spatial maps indicate approximate locations and sizes of the tumors.
The SM and SSD time series can be further reduced to scalar metrics by computing either the mean or standard deviation over time, and the TSD image can be reduced to scalar metrics by computing either the mean or standard deviation across the image volume. While this would appear to net a total of six numerical values, the temporal mean of SM(t) (TMSM) must be equal to zero, since averaging is a commutative operation, which guarantees that TMSM = SMTM, and TM(r) = 0. In all, then, five nontrivial scalar parameters are extracted from the image time series: the spatial mean of the temporal standard deviation (SMTSD), spatial standard deviation of the temporal standard deviation (SSDTSD), temporal mean of the spatial standard deviation (TMSSD), temporal standard deviation of the spatial mean (TSDSM), and temporal standard deviation of the spatial standard deviation (TSDSSD). The formulas for these quantities are
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
The five metrics were calculated for each component of the Hb signal (deoxyHb, oxyHb, totalHb, HbSat, and O2effHb), for a total of 25 values for each breast for all subjects.
Mathematically, SMTSD and SSDTSD are the first two moments of the TSD(r) distribution, while TMSSD and TSDSSD are the first two moments of the SSD(t) distribution. It should be noted that pairwise comparisons between the parameters reveal instances of commutations applied to both the operator and domain (SMTSD and TSDSM), or to the operator only (TSDSM and TMSSD), or to the domain only (SMTSD and TMSSD, SSDTSD, and TSDSSD). In light of the noted differences in mathematical definitions, one motivation for considering this group of quantities is the expectation that they will be differently influenced by different aspects of biological modulation (see Sec. 4 and the Appendix).
With the same goal of probing different modulatory elements, we have examined three additional metrics, each of which is a ratio of two of those defined in Eqs. (4)–(8),
| (9) |
These were calculated for each of the five Hb-signal components, yielding an additional 15 values for each breast for all subjects. The first two quantities in Eq. (9) are the CV in the spatial and temporal domains, respectively; because it is a scale-independent measure of variability, use of the CV can aid in comparisons among data from multiple subjects if there is a broad range of mean values. The last quantity in Eq. (9), a ratio of two operator-and-domain commuted metrics, is an index of coordination among different spatial locations within a breast (SCI = spatial coordination index). The reason for this is that TSD(r), and hence SMTSD, is independent of the phase of the time-varying Hb signal in any of the image voxels, but the amplitude of SM(t), of which TSDSM is a measure, definitely is affected by phase shifts. Consequently, SCI is necessarily ≥1, with larger values implying more loss of coordination among different locations within the image volume, and approaching 1 in the limit of perfectly synchronized temporal variability throughout the breast volume (see the Appendix).
All metric values were binned in four of the subject categories indicated in Table I: “left-breast active cancer” (LC), “right-breast active cancer” (RC), “benign breast pathology” (BP), and “no breast pathology” (NP, healthy subjects). A fifth category, “all noncancer” (NC), was subsequently formed by combining data for the BP and NP groups. For tests of discriminability between cancer and benign pathologies in the same breast, data for subjects having diagnosed benign pathologies restricted to one breast also were binned in “left-breast benign” (LB) and “right-breast benign” (RB) subcategories. Comparisons indicated in the upper half of Table I are intended to evaluate the diagnosability of cancer in the absence of prior knowledge, while the comparisons in the lower half are intended to evaluate the distinguishability of malignant from benign lesions. For all subsequently described analyses, data for the first- and second-generation imager subjects were not combined but were considered separately, owing to concerns about the possibility of confounds resulting from the subject-posture difference. Also, unequal-variance t-tests were applied to the combinations of breast and subject category indicated in Table I, to assess the diagnostic potential of each of the 40 metrics (8 formulations × 5 Hb signal components) defined in Eqs. (4)–(9), and to evaluate the same metrics’ potential to distinguish breast cancer from benign breast pathologies.
TABLE I.
Subject/breast pairings considered, for unilateral tests of: breast-cancer discovery in the absence of prior knowledge (upper half); specificity for breast cancer in partial-knowledge cases (lower half). LC = left-breast active cancer, RC = right-breast active cancer, BP = benign breast pathology, and NP = no breast pathology, NC = all noncancer (= BP + NP), LB = leftbreast benign, RB = right-breast benign.
| Breast-cancer subject category | ||||||
|---|---|---|---|---|---|---|
| LC | RC | |||||
| Noncancer subject category | Left | Right | Left | Right | ||
| NP | Left | ✓ | ✓ | |||
| Right | ✓ | ✓ | ||||
| NC | Left | ✓ | ✓ | |||
| Right | ✓ | ✓ | ||||
| BP | LB | Left | ✓ | |||
| Right | ✓ | |||||
| RB | Left | ✓ | ||||
| Right | ✓ | |||||
2.D.2. Bilateral breast metrics
Quantities representing interbreast differences between, and interbreast ratios of, metric values were evaluated in the expectation that such bilateral metrics will have lower intersubject variances than the metric values for individual breasts. Bilateral metrics that yield statistically significant differences, when values for affected and unaffected groups are compared, have potential to serve as biomarkers sensitive to the presence of cancer. It deserves emphasis that these comparisons do not invoke prior knowledge of whether or not a subject has cancer, or of which breast is affected if cancer is present (and do not need to employ specific information such as metrics associated with a region of interest18). Rather, the expectation is that metric values will be bilaterally similar in unaffected women, while the presence of disease will produce ratios that are either greater or less than one and differences that are greater or less than zero. By adhering to a fixed convention in calculating the differences (i.e., always left-breast minus right-breast metric value) and ratios (i.e., always left-breast divided by right-breast metric value), an indication of which breast is affected is provided by the algebraic sign of the difference or the magnitude of the ratio.
As with the analyses of unilateral breast metrics, data obtained from the two instruments were treated separately and were explored in accordance with the comparisons listed in Table I for each of the 40 metrics.
2.D.3. ROC analysis
Results of the preceding tests for differences between group means allow exclusion from further consideration of metrics that do not have appreciably different distributions in cancer-positive and cancer-negative subject groups. However, a statistically significant group-mean difference is not sufficient to guarantee that the associated metric will perform well as a diagnostic indicator for individual subjects. For that second level of characterization, ROC analyses were carried out,26 using the “perfcurve” function of matlab 7.11.0.584 (R2010b), upon the sets of individual-subject metric values for affected and unaffected [healthy only (NP) or healthy plus benign disease (NC)] groups. The diagnostic-accuracy parameters resulting from these calculations were area-under-curve (AUC), which is a convenient single-number index of overall performance (AUC also can be interpreted as the percentage of cases in which the metric correctly assigns two subjects to the correct categories, for a pair consisting of one selected at random from the each of the two groups being compared), sensitivity (Sn), or the percentage of breast-cancer subjects who are correctly categorized, and specificity (Sp), or the percentage of noncancer subjects who are correctly categorized. In general, Sn and Sp are functions of the metric value chosen as the diagnostic threshold, with each parameter tending to fall as the other increases; for results reported here, the threshold that minimizes the total number of incorrect classifications was used. Also, in light of the relatively small numbers of subjects in some of the groups, which increases the widths of the Sn and Sp confidence intervals, results are reported in terms of the absolute numbers of true positives and true negatives, along with subject-group sizes.
2.E. Subject groups
The study population for the first-generation instrument was recruited from women who visited the Kings County Hospital Center (Brooklyn, NY) breast clinic (66 subjects overall). The study population for the second-generation instrument was recruited from women who visited breast clinics at SUNY Downstate Medical Center (Brooklyn, NY) and The Brooklyn Hospital Center (63 subjects overall). Subject recruitment protocols were approved by the institutional review board (IRB) of each center (KCHC: HHC#01-343, DMC: IRB#99-093, THBC: IRB#599) and informed consent was obtained from every participant. In accordance with the terms of the informed-consent document, subjects’ medical records were examined to obtain information on age, BMI, breast-cancer status (positive or negative); tumor type, stage, size, location; and results of assays for estrogen receptor (ER), progesterone receptor (PR), and human epidermal growth factor receptor 2 (HER2/neu), for the cancer-positive subjects and the presence of benign breast pathologies, for the cancer-negative subjects. The subjects were age- and BMI-matched, both between the first- and second-generation imager groups and among the active-cancer, benign breast pathology, and no breast pathology categories within each group. Subject age, BMI, and tumor-size information is summarized in Table II.
TABLE II.
Subject-group descriptive information.
| Active breast cancer | |||||
| Device | Group-level parameter | Left | Right | Benign breast pathology | No breast pathology |
| n | 11a | 17b,c | 19 | 19 | |
| First-generation imager | Age [yr, mean (SD)] | 47.5 (12.3) | 51 (11.9) | 45.6 (7.6) | 43.3 (9.1) |
| Tumor size [cm, min–max (mean)] | 0.8–7 (4.1) | 0.8–11 (3.9) | n/a | n/a | |
| n | 12d | 6e,f | 23 | 22 | |
| Second-generation imager | Age | 53.9 (9.5) | 53.7 (14.1) | 48.1 (10.7) | 51.5 (11.7) |
| Tumor size | 0.5–6 (2.8) | 1–5 (2.7) | n/a | n/a | |
Includes nine cases of invasive ductal carcinoma (IDC), one of invasive mucinous carcinoma (IMuC), and one of metastatic breast cancer of unspecified type.
Includes one case where a recurrence of prior cancer was diagnosed six months after NIRS study; analysis of the NIRS data, placed her in the right-breast active cancer category.
Includes 15 cases of IDC, 1 of invasive mammary carcinoma (IMaC), and 1 of occult breast carcinoma presenting as an axillary lymph-node adenocarcinoma and right-breast hyperplasia.
Includes 10 cases of IDC, 1 of invasive lobular carcinoma (ILC), and one of IMaC.
Includes one equivocal case: subject had a right-breast lumpectomy two years prior to NIRS study, and subsequent radiological scans indicate a recurrence.
Includes four cases of IDC, one of IMaC and one of IMuC.
3. RESULTS
3.A. Resting state frequency response
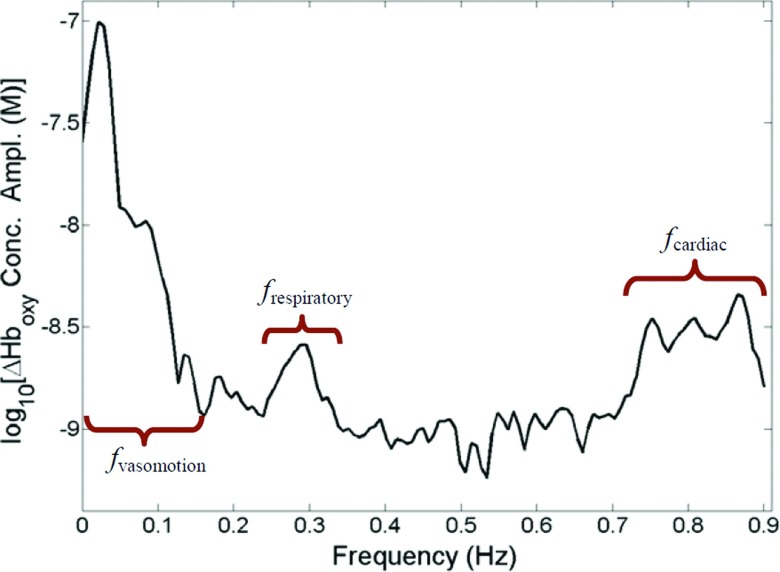
A simple and informative means for characterizing dynamic phenomena is to explore its frequency structure. Shown in Fig. 1 is a typical oxyHb amplitude spectrum, obtained from one breast of a subject in the NP group, who was examined while at rest. Three prominent features are observed, which correspond to oscillations generated by the principal elements of the vascular tree. The low frequency response (∼0.02–0.10 Hz) is produced under control of autonomic and autoregulatory factors and involves mainly microvascular structures, especially arterioles. Oscillations produced by movement of the diaphragm, which cause a periodic systemic venous congestion, are seen at intermediate frequencies (∼0.3 Hz). Oscillations originating from the pulsatile cardiac activity have the highest frequency. Typically, this last response occurs at ∼1 Hz, but owing to aliasing produced by the limited sampling rate (1.8 Hz), it is shown here as occurring in the range of 0.75–0.9 Hz.
FIG. 1.
Representative amplitude spectrum (logarithmic scale) computed from the spatially averaged oxyHb resting-baseline time series for a healthy breast (second-generation instrument). The expected physiological peaks and relative amplitudes are seen.
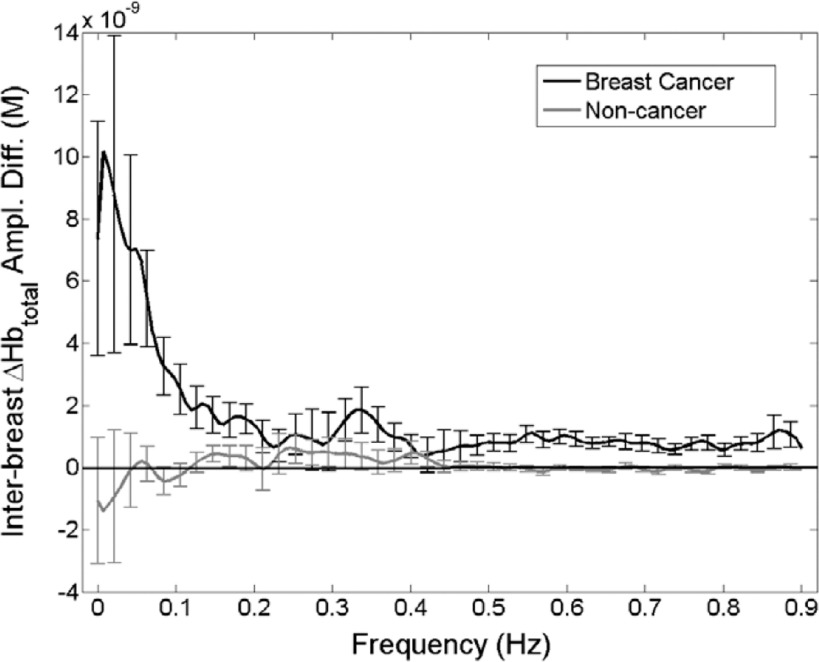
Spectra shown in Fig. 2 are the group mean ±SD values obtained when the amplitude spectrum for one breast is subtracted from that for the corresponding contralateral breast, for individuals known to have breast cancer (dark curve) and those who do not (i.e., healthy individuals and those with benign disease, light curve). Inspection reveals that the net value is essentially zero in the case of noncancer subjects but is notably elevated in the vasomotor region for subjects with breast cancer.
FIG. 2.
Group-averaged (error bars = ± 1 standard deviation) intrasubject differences between totalHb amplitude spectra for the two breasts. Spectra were computed from the spatially averaged totalHb time series for subjects with (dark curve) and without (light curve) breast cancer (second-generation instrument). For the first group, interbreast differences were computed as affected breast minus unaffected breast; for the second, as left breast minus right breast.
3.B. Spatial dependence of enhanced resting-state modulation of the Hb signal
It is instructive to use the available tomographic image information to explore the spatial dependence of the enhanced vasomotor response observed in Fig. 2. We have encoded temporal behavior within spatial maps by computing 3D images that reveal the position-dependent temporal standard deviation of the resting-state hemoglobin-signal response. Examples of such images are shown in Fig. 3, in the form of mutually orthogonal 2D transects for two women having tumors of different sizes (top: 1 cm diameter; bottom: 4 cm diameter). Also shown are the corresponding views for the unaffected contralateral breast. The color scale reveals differences in the amplitude of resting-state behavior. Inspection of the spatial maps shows that the amplitude of the temporal dynamics is notably elevated in the affected breast and that the region exhibiting the enhanced amplitude extends well beyond the expected border of the tumor.
To more fully characterize this behavior and to identify simplified biomarkers that are sensitive to it, in Sec. 3.C we report findings obtained from the different instrument systems used to collect simultaneous bilateral measures applied to the different subject groups.
3.C. Group-level enhanced modulation response
3.C.1. Unilateral metrics
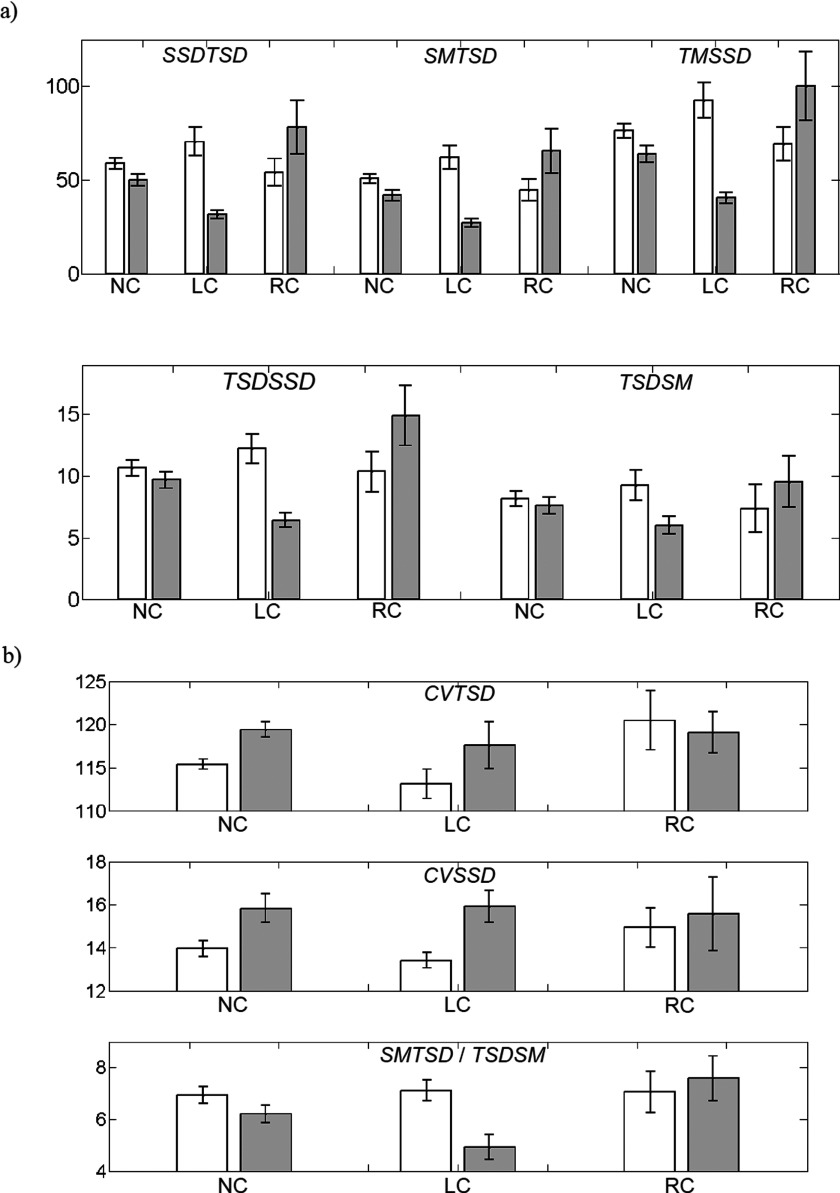
To explore the three-domain information space described in the Introduction, we began by computing the eight scalar quantities [Eqs. (4)–(9)] for each of the five components of the hemoglobin signal considered, for both breasts of subjects in the LC, RC, and NC groups. Representative findings (mean ±SEM) obtained from examination of the HbSat image time series, for subjects examined with the second-generation instrument, are shown in Fig. 4. Note that the left (white) and right (gray) bars in each pair represent results for the left and right breasts, respectively. Results of statistical analyses (unequal-variance t-tests) comparing the metric values shown in Fig. 4 for affected and unaffected subject groups, for each metric and all hemoglobin components, are given in Table III. Note that tabulated numbers are p-values corresponding to a weighted average of t-statistics for ipsilateral comparisons of the affected breast in cancer subjects to the corresponding breast of the unaffected subjects.
FIG. 4.
Unilateral group means (error bars = ± 1 SEM) for the 8 bidomain metrics computed from HbSat image time series (second-generation imager), for both the left (white bars) and right (gray bars) breast, for the NC, LC, and RC subject groups. (a) For the {SSDTSD, SMTSD, TMSSD, TSDSSD, and TSDSM} set of metrics, the largest single-breast group mean overall was arbitrarily set to 100, and all other group means and all SEMs were rescaled to that unit. (b) The units for the dimensionless metrics have not been rescaled; however, the displayed vertical-axis ranges have been chosen to optimize the within- and between-group visual contrasts. Results of statistical analysis are reported in the text and Tables III (unpaired analysis) and V (paired analysis).
TABLE III.
t-test p-values for comparison of single-breast metric values in the breast-cancer and noncancer subject groups; second-generation—nCa = 18, nNonCa = 45, (first-generation—nCa = 28, nNonCa = 38) imager. Statistically significant results are italicized.
| SSDTSD | SMTSD | CVTSD | TSDSSD | TMSSD | CVSSD | TSDSM | SCI | |
|---|---|---|---|---|---|---|---|---|
| deoxyHb | 0.18 | 0.12 | 0.24 | 0.55 | 0.15 | 0.063 | 0.59 | 0.34 |
| (0.046) | (0.11) | (0.40) | (0.27) | (0.029) | (0.36) | (0.26) | (0.69) | |
| oxyHb | 0.80 | 0.51 | 0.12 | 0.16 | 0.52 | 0.056 | 0.82 | 0.18 |
| (0.079) | (0.092) | (0.19) | (0.18) | (0.027) | (0.90) | (0.38) | (0.29) | |
| totalHb | 0.57 | 0.99 | 0.056 | 0.15 | 0.84 | 0.14 | 0.90 | 0.47 |
| (0.024) | (0.0042) | (0.35) | (0.090) | (0.011) | (0.23) | (0.20) | (0.50) | |
| O2effHb | 0.21 | 0.15 | 0.52 | 0.75 | 0.17 | 0.078 | 0.88 | 0.079 |
| HbSat | 0.15 | 0.11 | 0.39 | 0.20 | 0.12 | 0.37 | 0.42 | 0.57 |
While there are many features identifiable in Fig. 4 (and in corresponding results, not shown owing to space limitations, for the other Hb-signal components), two findings stand out. One is the substantial bilateral similarity of group-mean values across the various metrics obtained for the NC subjects. Examination of only the NP or BP fractions of the NC group’s results yielded similar findings (not shown). Also, equivalent treatment applied to other components of the Hb signal showed that the left- and right-breast group-mean values are more nearly equal still, with totalHb showing the smallest interbreast differences. The other principal finding is that in most cases (>90%), the presence of a tumor does not produce statistically significant differences between the group-mean metric values for the cancer and noncancer subjects (see Table III), but an unmistakable trend in the data is nevertheless evident. Namely, we observe that in comparison to NC, the LC subjects have larger differences between the left- and right-breast group means in every case. A qualitatively similar trend is seen for the RC subjects, but with the algebraic sign of the interbreast difference reversed, in comparison to NC, for seven out of eight of the quantities.
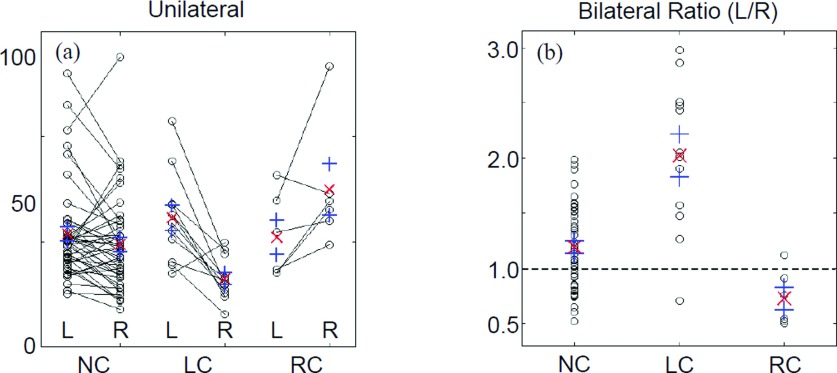
To gain a better understanding of factors that might be affecting the discriminatory power of unilateral comparisons, the primary data comprising the central tendencies shown in Fig. 4 have been replotted as shown in Fig. 5(a) (corresponding results for the other metrics are qualitative similar to the representative TSDSSD results shown). This type of plot, which highlights bilateral differences, immediately reveals the reason for the overall negative discriminatory findings seen in Fig. 4 and Table III: the range of metric values spanned by the NC subjects [and by only the NP subset (not shown)] is large and fully overlaps the ranges of values in the affected breasts of the LC and RC subjects.
FIG. 5.
Individual-subject TSDSSD values derived from HbSat image time series (second-generation imager). “○” = individual-subject data values; “×” = group mean value; and “+” = mean ±SEM. The largest individual data value overall was arbitrarily set to 100, and all other values were rescaled in proportion. “L” = left breast, “R” = right breast, “NC” = noncancer subjects, “LC” = subjects having left-breast cancer, and “RC” = subjects having right-breast cancer.
A closer examination of Fig. 5(a) reveals an important difference between the subjects who do and do not have breast cancer. The NC group is about evenly divided between cases having the larger metric value in the left breast and cases having it in the right. In marked contrast, in both the LC and RC groups, all but one subject have the larger metric value in the affected breast. This finding provides the insight that performing intrasubject, interbreast comparisons is the key to reducing variance in the selective manner described in Sec. 3.C.2.
3.C.2. Bilateral metrics
As noted in the Introduction, it can be expected that metrics of the type considered here will be affected by factors unrelated to the presence of cancer (e.g., comorbidities, differences in breast size). This consideration emphasizes the potential value of using variance reduction techniques that serve to reveal group differences that may otherwise be obscured. In order to enhance intergroup differences, an adopted technique would somehow need to have a selective effect, reducing variance specific to the cancer/noncancer distinction to a smaller extent than that arising from the other factors. The key to achieving this goal is an appreciation that the expected influences of the clinically irrelevant factors should be nearly the same in both breasts for any selected subject, while the impact of unilateral breast cancer should be strongly asymmetric. Then, a simple means for producing the desired selectivity is to compute the intrasubject, interbreast difference (or some equivalent) value for each of the considered quantities.
In Fig. 5(b), we show the left-over-right bilateral ratios for the same subjects, metric, and Hb-signal component as in Fig. 5(a). Inspection reveals that only one LC subject has a ratio smaller than the mean value for the NC group, while no RC subjects have ratios greater than the NC-group mean. Qualitatively, similar results were obtained based on interbreast differences values (not shown); overall, however, the ratio was found to have marginally better breast-cancer diagnostic ability than bilateral metric difference values.
To place the preceding observation on more quantitative footing, we performed a second round of between-groups t-tests, comparing bilateral-difference and -ratio metric values for the affected group to those for the NC group. In contrast to the Table III results, the p-values for the bilateral-ratio comparisons reported in Table IV show that there are significant or highly significant differences for most combinations of metric and Hb-signal component.
TABLE IV.
t-test p-values for comparison of bilateral ratios of metric values in the breast-cancer and noncancer subject groups; second-generation—nCa = 18, nNonCa = 45, (first-generation—nCa = 28, nNonCa = 38) imager. Composite t-scores computed the same way here as for the unilateral comparison case (Table III).
| Metric | ||||||||
|---|---|---|---|---|---|---|---|---|
| Hb signal component | SSDTSD | SMTSD | CVTSD | TSDSSD | TMSSD | CVSSD | TSDSM | SCI |
| deoxyHb | 0.0019 | 0.0015 | 0.44 | 0.0056 | 0.0017 | 0.32 | 0.014 | 0.0018 |
| (0.024) | (0.013) | (0.014) | (0.021) | (0.026) | (0.17) | (0.51) | (0.087) | |
| oxyHb | 0.0070 | 0.0042 | 0.33 | 0.058 | 0.0050 | 0.013 | 0.037 | 0.016 |
| (0.010) | (0.0031) | (0.43) | (0.016) | (0.0043) | (0.96) | (0.14) | (0.34) | |
| totalHb | 0.012 | 0.0053 | 0.47 | 0.21 | 0.0079 | 0.0097 | 0.040 | 0.23 |
| (0.063) | (0.0031) | (0.38) | (0.0018) | (0.059) | (0.14) | (0.13) | (0.29) | |
| O2effHb | 0.0028 | 0.0025 | 0.28 | 0.0037 | 0.0024 | 0.15 | 0.036 | 0.0079 |
| HbSat | 0.0015 | 0.0013 | 0.38 | 0.0021 | 0.0014 | 0.36 | 0.0063 | 0.0011 |
A more careful inspection of Table IV reveals that these combinations can be divided into three principal groupings based on their discriminatory power. Showing the most consistent response across all hemoglobin components are the metrics SSDTSD, SMTSD, and TMSSD. Next are the metrics TSDSM, TSDSSD, and SCI, and those having the smallest number of significant findings are the metrics CVTSD and CVSSD. This empirical observation aligns closely with the finding that the metrics in the first group are strongly correlated with each other (r > 0.98, averaged over all Hb components), those in the second group are less strongly correlated with the first group and with each other (r = 0.63–0.85), and the third group are the least strongly correlated with each other and with the metrics in the first and second groups (r < 0.53). Taken together, to some readers these findings may suggest a form of codependence, and hence informational redundancy, between the metrics with the best performance as diagnostic indicators for breast cancer. However, the mathematical analysis summarized in the Appendix shows that any such codependence is not a trivial or inevitable consequence of the metrics’ mathematical definitions, and this implies that it must instead have a biological origin. Further, the analysis provides a basis for determining which primitive elements of spatiotemporal behaviors are most closely aligned with the clinical performance.
Shown in Table V are results from ROC analysis applied to the same data used to generate Table IV, reordered in accordance with the preceding metric groupings. For each group, the specific Hb components that have the best and worst overall performance (i.e., highest and lowest AUCs, respectively) are included, along with the overall average for all Hb components. Inspection reveals that AUCs are highest for O2effHb (86%), with similar values for sensitivity and specificity across the first grouping and with mainly lower performance for totalHb. A similar trend is seen for the second grouping of metrics, with HbSat having the best performance. Results obtained for metrics in the third grouping have a more variable and generally poorer performance. A mainly similar pattern of results was obtained from data collected using the first-generation imager, with AUC, sensitivity, and specificity values trending 3%–5% lower in most categories, indicating that postural changes do not strongly affect clinical performance.
TABLE V.
ROC analysis: All breast-cancer subjects; second-generation instrument; nCa = 18, nNonCa = 45.
| Metrics | Hb signal componenta | AUC (%) | Sensitivity | Specificity | # FPs | # FNs |
|---|---|---|---|---|---|---|
| SMTSD, SSDTSD, | O2effHb | 86.3–86.9 | 83.3–88.9 | 87.4–88.1 | 5.3–5.7 | 2–3 |
| TMSSD | totalHb | 76.9–81.2 | 66.7–72.2 | 84.4–91.1 | 4–7 | 5–6 |
| All (avg.) | 83.5–84.9 | 80.0–83.3 | 85.3–86.8 | 5.9–6.6 | 3.3–4.0 | |
| TSDSM, TSDSSD, | HbSat | 76.5–85.1 | 77.8 | 74.8–80.7 | 8.7–11.3 | 4 |
| SCI | totalHb | 61.4–73.5 | 55.6–72.2 | 60.7–74.8 | 11.3–17.7 | 5–8 |
| All (avg.) | 73.4–76.8 | 68.9–74.4 | 75.4–79.0 | 9.5–11.1 | 5.0–5.5 | |
| CVSSD, CVTSD | oxyHb | 58.5–74.0 | 55.6–77.8 | 64.4–72.6 | 12.3–16 | 4–8 |
| deoxyHb | 59.4–62.1 | 55.6–83.3 | 48.9–63.7 | 16.3–23 | 3–8 | |
| All (avg.) | 59.7–66.9 | 57.8–73.3 | 64.9–68 | 14.4–15.8 | 4.8–7.6 |
Note: “# FPs” = number of false positives, “# FNs” = number of false negatives. These may have fractional values when averaged over multiple Hb components or when left- and right-breast cancer results are pooled.
The individual Hb signal components included are the ones that have the best and worst overall performance for breast-cancer diagnosis, as quantified by averaging AUC values over all the metrics specified in the first column.
Overall, we find that the diagnostic performance seen for the first category of metrics appears quite promising, especially when considering that active participation on the part of the subject is not required and that the measurement data can be recorded while subjects are comfortably seated.7 We also note that there is a positive correspondence between the degree of intercorrelation among the metrics in each group and the diagnostic performance (i.e, range of AUC values) for that same group. Owing to this correspondence, we subsequently refer to these groups—initially defined on the basis of intermetric correlations, without regard to diagnostic performance—as the “excellent,” “good,” and “poor” categories.
The ranges shown for the diagnostic performance indices in Table V were not substantially different when the ROC analyses were performed by contrasting metric values for the breast-cancer subjects with those for the NP subject group (n = 22) instead of the NC group. This finding is indirect evidence that the metrics considered here are highly specific for breast cancer. For a more direct evaluation, we performed additional ROC analyses contrasting the LC group with LB, and RC with RB (see Table I). These comparisons do make use of a certain amount of prior knowledge, namely, that some type of pathology is present and the affected breast is known, thus modeling a hypothetical clinical application wherein a clinical breast exam or a structural imaging study (for example) detects an abnormality but cannot determine whether it is cancer or a benign lesion.12 Using second-generation instrument data and combining results for left- and right-breast disease, the overall number of false positives [i.e., benign disease (n = 16) misdiagnosed as breast cancer] was 2 and the overall number of false negatives [i.e., breast cancer (n = 18) misdiagnosed as benign disease] was 2–3, for metrics in the excellent performance category.
3.D. Dependence of metric response on tumor size
An unexpected finding suggested by results shown in Fig. 3 is that the observed enhanced modulatory behaviors, which are associated with the vasomotor response, are mainly independent of tumor size. If substantiated, this finding appears qualitatively different from previous NIRS-based studies involving subjects with breast cancer, whose measures are sensitive to the content of hemoglobin, a finding consistent with enhanced angiogenesis.18,19
To explore this further, we have correlated tumor size to each of the eight metrics across all five hemoglobin components. Contrary to the results presented above, which show that many combinations of metric and Hb component are sensitive to the presence of a tumor, here we observe just two instances (out of 40) where metric values have a statistically significant correlation with tumor size (note that 2/40 = 5%, suggesting that even the few statistically significant correlations that were found may be spurious). Having the largest correlation (r = 0.58) is the SCI left-over-right ratio for HbSat. While this is statistically significant, only 33% of the intersubject variance is accounted for by the regressor. Additional evidence that the observed correlations may be spurious comes from calculations in which we correlated tumor size with metric values obtained from only the affected breast (i.e., not from a bilateral comparison). In this case, we observed that none of the metric-component combinations were significantly correlated with tumor size. Additionally, as a control the same analysis was applied to the unaffected, contralateral breast. This analysis yielded significant correlations for two of the forty combinations, further indicating that the statistically significant correlations between tumor size and affected-breast metric are likely spurious.
To summarize, findings presented to this point demonstrate that there are many bilateral spatiotemporal metrics, corresponding to a range of components of the hemoglobin signal which have notable diagnostic performance. Surprisingly, however, these metrics are mainly uncorrelated with tumor burden and are not strongly localized to the spatial limits of the tumor.
3.E. Influence of tumor phenotype on scalar metric values
Clinical experience shows that prognosis and preferred treatments for breast cancer are functions of the tumor markers present in a particular case. Therefore, while the preceding demonstrations of diagnostic performance are encouraging, the clinical applicability of the data analysis considered here could be substantially greater if it could be shown to provide information regarding the type of cancer present. However, owing to the small numbers overall of breast-cancer subjects enrolled in the study, we have no expectation that any trends revealed will achieve statistical significance in a convincing way, only that they may yield suggestive and intuitively reasonable answers that can be further explored in future studies involving larger populations.
Mean values of the relative percent differences between interbreast metric ratios for subjects whose tumors do and do not have the indicated biomarkers are presented in Tables VI (ER-PR) and VII (HER2/neu), for the different components of the Hb signal. As in our evaluation of the metrics’ diagnostic performance, we have examined the marker effects on single-breast measures and on the bilateral ratios. Findings obtained from the latter analysis are included in Tables VI and VII.
TABLE VI.
Average percent differencea between L/R ratio for ER(+) (n = 13) and ER(−) (n = 5) subjects. The subset of the subject population considered is all breast-cancer subjects imaged with the second-generation instrument.
| Hb signal component | Excellent | Good | Poor |
|---|---|---|---|
| deoxyHb | −29.7 | −12.5 | 21.1b |
| O2effHb | −40.4 | −26.0 | 6.9 |
| oxyHb | −25.2 | −9.2 | 22.5c |
| HbSat | −34.3 | −18.5 | 12.7d |
| totalHb | −4.8 | 5.1 | 20.3b |
| Average across components | −26.9 | −12.2 | 16.7 |
100(xER(+) − xER(−))/[(xER(+) + xER(−))/2], where x is the L/R ratio for a selected metric.
p < 0.02 for CVSSD.
p < 0.004 for CVSSD.
p ≤ 0.07 for CVSSD and CVTSD.
TABLE VII.
Average percent difference between L/R ratio for HER2(+) (n = 9) and HER2(−) (n = 9) subjects.
| Hb signal component | Excellent | Good | Poor |
|---|---|---|---|
| deoxyHb | 21.9 | 7.4 | −17.6a |
| O2effHb | 23.6 | 11.2 | −10.7b |
| oxyHb | 12.5 | 2.1 | −13.5 |
| HbSat | 26.6 | 11.5 | −13.5b,c |
| totalHb | 0.5 | −5.8 | −12.3 |
| Average across components | 17.0 | 5.3 | −13.5 |
p < 0.06 for both metrics.
p ≤ 0.03 for CVSSD.
p < 0.07 for CVTSD.
Inspection of Table VI reveals a consistent directionality in the difference between interbreast metric ratios of the ER(+) and ER(−) subjects, for the metrics in the excellent and poor diagnostic categories, and a mixed response for the good category. Statistical (t-test) analysis of individual combinations of metric and Hb component showed that significant differences were limited to metrics in the poor category. A similar trend was observed for PR results, but with smaller relative percent differences and with only two of the individual metric-Hb combinations reaching statistical significance (CVTSD-HbSat, p ≤ 0.05).
Inspection of Table VII reveals a grossly similar trend as seen in Table VI, but notably with reversed directionality. Also similar was the restriction of statistical significance to metrics in the poor diagnostic category.
Inspection of results of individual-breast comparisons were less consistent across the metric categories for the different cellular biomarkers, with the exception of the ER-CVSSD combination, where statistically significant (p < 0.02) relative percent differences were obtained for all Hb components except totalHb. The apparent sensitivity of Hb components other than totalHb to marker status is consistent with the pattern seen in the diagnostic-performance results, and with a report by Brown et al., who observed that HbSat, but not totalHb, was significantly different in tumor tissue than in other tissue types.27
While it is tempting to regard the preceding findings as informative, we are aware that the large numbers of comparisons performed makes the analysis susceptible to spurious findings. To control for this possibility, we have applied the individual-breast comparison to metric values for the unaffected breast in tumor-bearing subjects. Results of this analysis were inconclusive. Some spurious statistically significant differences were obtained, but these appear more randomly distributed across the different diagnostic-performance categories and are more limited in the number of Hb components involved (primarily O2effHb).
4. DISCUSSION
Most previously reported approaches to exploring the diagnostic potential of NIRS measures for detecting breast cancer have sought to leverage the features of enhanced angiogenesis that are common to most solid tumors.18,19 However, there are other elements of the tumor phenotype that can serve as a basis for disease detection. One example is the fact that on a macroscopic level solid tumors tend to have increased stiffness compared to surrounding tissue.1,2 This finding forms the basis of tactile sensing as used during a clinical breast exam.12 On a finer spatial scale are features discernible using high-resolution imaging methods such as MR,11 ultrasound,10 or x-ray mammography.28 Finer still are features that occur on a cellular or molecular level, but excepting the use of radiotracer methods, features closely tied to the tumorigenic state have resisted detection using noninvasive macroscopic sensing methods such as diffuse optical tomography (DOT). On initial review, the findings presented here present an explanatory challenge: how can a tool having good sensitivity to the hemoglobin signal and associated angiogenesis be found to detect cancer with high accuracy, but in a manner that is not highly correlated with tumor size or location? To be sure, careful benchmarking of system performance7,13 rules out any concerns regarding the technical performance of the developed imaging systems or the developed reconstruction algorithms.25,29
4.A. Implications regarding the biological origin of reported findings
Among the various features that have been recognized as contributing to the tumorigenic state—including sustained proliferative signaling, evasion of growth suppressors, resistance to cell death, replicative immortality, induction of angiogenesis, and activation of invasion and metastasis—the establishment of a generalized inflammatory state is now widely appreciated as a requirement for tumor development and growth.5,30,31 Common to this process, and to many elements associated with the mentioned phenotypes, is a central role played by nitric oxide production and its metabolites31 in promoting and maintaining the cancerous state.30
Nitric oxide is produced under the control of three distinct isoenzyme forms of nitric oxide synthase (NOS). NOS1 and NOS3 are found in neural and endothelial tissues and are thought to produce nitric oxide episodically.30 In contrast, NOS2 is constitutively activated in cancer and is closely associated with inflammatory processes.30 This understanding, coupled with the fact that NO is a highly diffusible gas, leads us to plausibly suggest that the initially unexpected findings presented here are likely attributable to the actions of NO in sustaining a generalized inflammatory state and an associated erythema. While the sensing tools used here cannot confirm this suspicion, corroborating evidence from prior studies involving dynamic infrared sensing, wherein time series of thermographic measurements of the cancerous breast were acquired, reinforces the plausibility of this conjecture. We take particular note of a report by Button et al.,35 who observed a frequency response in the vasomotor region substantially similar to that shown in Fig. 2. Also noteworthy were the reported findings that when xenografts of excised tumors were grown in rodents, treatment of these animals with a specific inhibitor of NOS eliminated the enhanced vasomotor response.35 Our interpretation, therefore, is that the combination of good clinical performance with relatively poor ability to localize a tumor and limited sensitivity to tumor burden is consistent with well-known tendency of tumors to produce such generalized inflammatory responses. The latter is observable by dynamic optical tomography because an effect of the inflammatory state is to produce an environment having enhanced vasoreactivity.
4.B. Extending interpretability of clinical findings by computational modeling of dynamic behavior
The reported performance of dynamic sensing methods developed by our team,32–34,36 combined with a recognition that a wealth of understanding of otherwise hidden relationships can be derived from accurate measures of such systems,37 led us to wonder if the empirical measures explored can be examined in ways that give us a more in-depth understanding of the reported clinical findings. To pursue this, we have modeled spatiotemporal behavior in a simplified system and computed the same metric quantities as were derived from the clinical data. A mathematical description of the approach used to define relationships between primitive elements of spatiotemporal behavior and the corresponding metric responses is presented in the Appendix.
Simply described, our approach has been to calculate response profiles for the various metrics under parameter sweeps of the elements of spatiotemporal behavior, in the hope that these profiles would contain trends that would allow us to determine which combinations of primitive features best align with the clinical findings. It is also appreciated that the process of reducing high-dimensional information to scalar quantities, which is the approach adopted for this report, might raise concerns about information being overly compressed, thereby blurring key features of the system under study. Were the computational studies to show that the methods employed here have the effect of obscuring key information, the conclusion that those methods are not clinically viable would seemingly be unavoidable.
We begin by noting that in a causal inspection of Eqs. (4)–(9), it is not obvious what relationships exist between the metrics and the elementary features of spatiotemporal behavior. In the computational study, we explored a linear model whose behaviors are determined by three independent parameters: Average amplitude of hemodynamic fluctuations, spatial heterogeneity and asymmetry of the amplitude fluctuations, and degree of temporal coordination among different parts of the medium (i.e., phase heterogeneity). Our aim was to derive a first-order understanding of the importance of the intrinsic behaviors and their influence on clinical performance, in full knowledge that such comparisons are only approximate owing to the simplicity of the model and the fact that no details of true breast dynamics were explored. Nevertheless, operating under the principle that useful models should be as simple as possible but not simpler, we do note that all of the principal dependencies and codependencies between metric values and clinical responses apparently are entirely consistent with similar trends identified in the modeling study results (see Sec. 4.C and the Appendix).
4.C. Dependence of clinical performance on modeled behavior and metric
Shown in Table VIII is a summary of clinical performance for the various metrics as a function of the type of modeled behavior. Clinical performance assignments were made using the same criteria as were applied to the results in Tables IV and V.
TABLE VIII.
Relation between the scalar metrics’ performance as diagnostic indicators of breast cancer, and the parameters of the tissue dynamics model that influence them.
| Metric | Ability to distinguish LC/RC subject groups from NC | Number of parameter dependences |
|---|---|---|
| SSDTSD | Excellent | 2 |
| SMTSD | Excellent | 1 (average amplitude) |
| CVTSD | Poor | 1 (amplitude heterogeneity) |
| TSDSSD | Good | 3 |
| TMSSD | Excellent | 3 |
| CVSSD | Poor | 2 |
| TSDSM | Good | 2 |
| SCI | Good | 1 (phase heterogeneity) |
Inspection reveals that among the three metrics having excellent performance (SMTSD, SSDTSD, and TMSSD), all are influenced by the average amplitude. The latter two metrics also exhibit sensitivity to amplitude heterogeneity (SSDTSD and TMSSD) and phase heterogeneity (TMSSD). Evidence that the influence of amplitude heterogeneity on clinical performance is less than that of the average amplitude comes from a comparison of the effectiveness of CVTSD (amplitude heterogeneity only, poor performance) and SSDTSD (average amplitude and amplitude heterogeneity, excellent performance) as diagnostic indicators for breast cancer. Reinforcing this assignment is the excellent performance of SMTSD, which is sensitive to average amplitude only.
A similar comparison can be made to assess the importance of phase heterogeneity. Measures sensitive to phase heterogeneity include all those for which the first mathematical operation is applied to the spatial domain (TSDSSD, TMSSD, CVSSD, TSDSM, and SCI). Of these, only the TMSSD metric exhibited clinical performance in the excellent category. Having an assignment in the poor category was the CVSSD metric, which includes sensitivities to heterogeneity both in amplitude and in phase. Contrasting with this is performance of the SCI metric (good category), for which the sensitivity to medium dynamics is limited to phase heterogeneity only, suggesting that sensitivity to amplitude heterogeneity does not improve a metric’s clinical performance and may even degrade it. Inspection of the remaining metrics that are sensitive to phase heterogeneity (i.e., TSDSSD and TSDSM), and which have clinical performance in the good category, identifies that both include sensitivity to average amplitude. Thus, it would seem that there is a consistent correlation between observed clinical performance and different elementary forms of modeled dynamic behaviors. Having the greatest impact on clinical performance is sensitivity to average amplitude, followed by sensitivity to phase heterogeneity and finally to amplitude heterogeneity.
It is noteworthy that these findings may have implications regarding the strategies used for data collection. For instance, a simple consideration is the fact that DOT is a low-resolution technique. It follows that it could prove difficult to access useful discriminating information from measures that require some degree of resolution of possible tumor-induced spatial differences in amplitude dynamics. Also worth considering is the experimental techniques required to reliably measure phase heterogeneity. The instrumentation used here employs a time-multiplexing approach to illumination, thereby limiting sampling rates to ∼2 Hz. Clinical experience with measures of hemodynamic phase delays (e.g., time delays between pulse recordings in the foot compared to the neck) indicates that these occur on a much faster time scale for any local tissue type. An alternative approach to data collection would be to employ a full frequency-encoding scheme, wherein all sources are illuminated simultaneously but are encoded with different modulation frequencies. While having a more limited dynamic range compared to time-multiplexing schemes, this approach is well suited for fast imaging (e.g., 100 Hz), which could better support measures of phase heterogeneity.
Findings from the modeling studies would also appear to yield additional information regarding features inherent to the breast. For instance, as noted in the Appendix, values for CVTSD obtained from the clinical studies are always greater than 100% (see Fig. 4). Similar values were obtained from the modeling study only in the case where the model medium properties were nonuniform and asymmetric (NA), which is a feature consistent with the known heterogeneity of breast anatomy.
Turning to the other scalar metrics, we find information in some of them that permits the drawing of inferences regarding the relative magnitude of the tumor effect. For example, the model computations suggest two possible causes for the empirical finding that SSDTSD value is larger in the affected breast: greater average amplitude or increased asymmetry in the nonuniform amplitude distribution. However, the second possibility is ruled out by the CVTSD result (Fig. 4), which implies that amplitude heterogeneity is lower in affected breasts. Additionally, since an increase in average amplitude and decrease in amplitude asymmetry have opposing effects on SSDTSD, the fact that the metric is seen to increase implies that the magnitude of the first effect is sufficient to more than overcome the second. In similar fashion, the observed increase in TSDSM in the affected breast could be a consequence of either greater average amplitude or lower phase heterogeneity, but the second possibility is ruled out by the SCI result; further, since the increases in average amplitude and in phase heterogeneity have opposing effects on TSDSM, the fact that the metric is seen to increase implies that the magnitude of the first effect is sufficient to more than overcome the second.
4.D. Comparisons of results for different Hb-signal components
As identified by the results presented in Tables III and IV, evaluation of metric values as diagnostic indicators of breast cancer considered all five components of the Hb signal (see Sec. 2). In the following, we highlight findings that point to differential information that may prove useful from evaluation of these components. While the HbSat component yielded the easily interpreted TSD maps (see Fig. 3), individual-subject SSDTSD values (see Fig. 5) and group-mean metric values (see Fig. 4) selected for display here, corresponding results that are comparably striking were obtained for most of the other components. However, the metrics derived from totalHb image time series appeared, overall, to hold the lowest discriminatory potential. This is supported by ROC findings in Table V, which indicate that across nearly all of the tabulated clinical indices, for the metrics in the excellent and good categories totalHb had reduced performance compared to the other hemoglobin components. A similar outcome is observed in the t-test results in Table IV, showing that of the group comparisons made, where totalHb has the greatest number of nonsignificant findings, for either instruments.
4.E. Relevance of disease phenotype and signal variance to instrumentation design
Development of useful diagnostic measures is guided by an appreciation of factors that contribute to disease discrimination, combined with adoption of methods that are sensitive to these factors in a manner that minimizes signal variance. Ideally, the measuring system deployed would be one that is not limited by factors associated with system design or signal quality, but only by intrinsic factors that discriminate affected from nonaffected individuals. Experience has shown that methods intended to explore macroscopic properties of tissue, even those methods having high spatial resolution, must be capable of distinguishing among multiple sources of contrast in order to achieve good clinical performance. While added contrast features can be discerned using NIRS based on spectroscopic differences in the hemoglobin signal, in the absence of prior knowledge,18,27 the low spatial resolution of the method limits its clinical utility.
A well-established approach to improve on this situation is to artificially enhance contrast by use of injectable agents.38 While this can be effective, its avoidance is often desirable. An alternative scheme is to consider ways to capture additional contrast features, and the natural variability of the hemoglobin signal makes consideration of dynamic measures an obvious choice. This has the appeal of introducing an additional contrast domain (i.e., temporal features), but the influence of posture-dependent gravitational pooling of blood and details of soft-tissue contact could potentially make such measures problematic. Indeed, as seen from our analyses of individual-breast data, extraction of simplified dynamic metrics may not be useful. However, in this report, we have shown that disease-independent sources of variance can be effectively canceled by considering measures obtained from a simultaneously bilateral measure. To emphasize this point and to document that these features are weakly dependent on the details of the data-collection process, we have intentionally not combined data from the different measuring systems. This overall similarity of findings emphasizes that even gross changes in hemoglobin content arising from postural shifts, with concomitant changes in signal attenuation, do not obscure the capacity to observe distinguishing dynamic responses.
Returning to intrinsic contrast features of cancer, we believe, as noted above, that the existence of a generalized inflammatory state is the likely origin of the temporal features identified. Because these rhythms are not observable using static imaging methods,18,19 and are likely obscured when methods intended to provoke responses are applied,14,22,23 it is not overly surprising that the phenomenology reported here has previously gone unrecognized when using the NIRS method. It is less clear at this time if metrics sensitive to this behavior are also associated with the clinical biomarkers used to guide treatment decisions. Nevertheless, because NO is known to modulate a host of cellular mechanisms modified by the tumorigenic state,30,31 including these factors,39,40 their further consideration appears warranted. Further, the general understanding that NO is a key factor in sustaining and promoting the tumor state makes the finding of high discriminatory power between breast cancer and benign breast pathologies particularly encouraging.
Finally, we point out that that if our observation that the phenomenology considered in this report is broadly dispersed in the affected breast holds up in further studies, it would imply that use of simplified instrumentation having notably lower sensor density than used here should prove equally suitable for breast-cancer diagnosis.
ACKNOWLEDGMENTS
This research was supported by the National Institutes of Health (NIH), Grant No. R41CA096102; the U.S. Army, Grant No. DAMD017-03-C-0018; Susan G. Komen for the Cure, Grant No. IMG0403022; the New York State Department of Health, Empire Clinical Research Investigator Program; the New York State Foundation for Science, Technology and Innovation—Technology Transfer Incentive Program (NYSTAR-TIPP), Grant No. C020041; and NIRx Medical Technologies. For their assistance with recruiting subjects, obtaining informed consent, acquiring and reading medical records, and collecting fNIRS measurement data, the authors wish to acknowledge Michael S. Katz, MD; Rosemarie E. Hardin, MD; Nelson A. Franco, MD; Paul L. Toubas, MD; David P. Klemer, MD, PhD; Alessandro D. Smeraldi, MD; Frank A. Tarantini, MD; Georges Khoury, MD; David J. Naar, MD; Mark B. Farber, MD, PhD; O. Raphael Nwanguma, MD; Begum R. Noor, MD; and Zaw Bo, MD.
APPENDIX: NUMERICAL EVALUATION OF BIDOMAIN METRIC RESPONSE TO INTRINSIC SPATIOTEMPORAL BEHAVIORS
1. Specification of model parameters
The data format of each modeled image time series is an Nt × Nv array, where Nt is the number of image time frames and Nv is the number of voxels [see Eqs. (1) and (2)]. The term “voxel” is used here for consistency with the description in Sec. 2.D, but the model does not actually include any particular spatial structure. Modeling of spatial structure is superfluous, because such information is lost when spatial means and standard deviations are computed. In order to mirror subject-data format, here we used Nt = 500, with a sampling rate of 2 Hz, and Nv = 1000. These quantities were selected because they have the same order of magnitude as their experimental counterparts, and results of the model computations are not sensitively dependent on the particular values chosen for Nt, Nv, or the sampling rate.
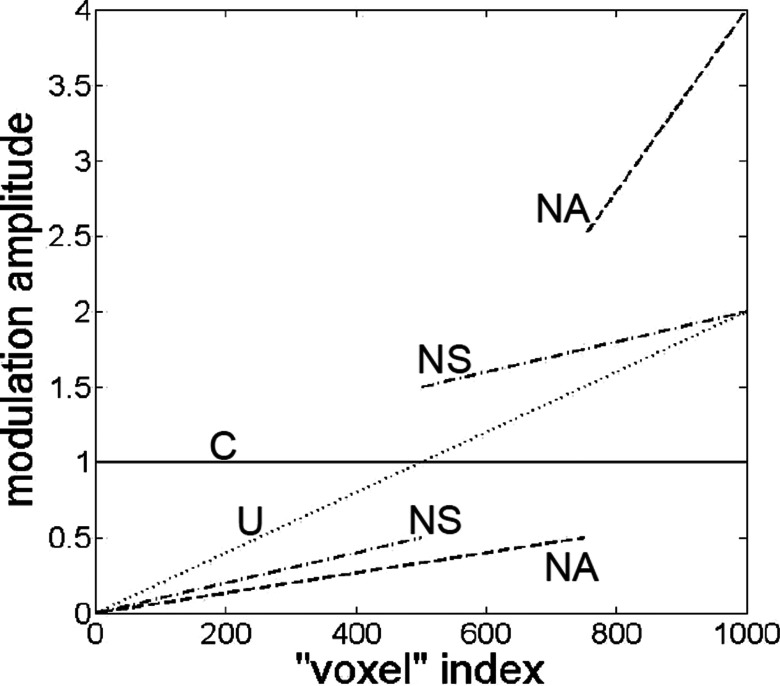
In the place of experimental data, the model time series in each voxel (i.e., each column of the Nt × Nv data array) was a pure sinusoid having an AC amplitude in the range of 0–2, zero DC offset, and a frequency of ∼0.1 Hz. (The exact value, π/32 ≈ 0.0982 Hz, by design is incommensurable with the sampling frequency, which guarantees that different function values are sampled in each cycle.) The column-specific parameters were the amplitude and phase of the sinusoid. The spatial distributions of amplitude considered were (see Fig. 6) as follows:
-
1.
Constant (C): The AC amplitude (c) was 0.5, 1, or 2 in all columns of the data array. (Three sets of computations.)
-
2.
Uniformly varying (U): The AC amplitude ranged linearly from 1 − k to 1 + k, with k = 0.1, 0.2, …, 0.9, 1. Thus, the spatial mean amplitude was 1 in every case. (Ten sets of computations.)
-
3.
Nonuniform but symmetric (NS): The AC amplitude ranged linearly from 0 to 1 − k in columns 1 through Nv/2, and from 1 + k to 2 in columns (Nv/2) + 1 through Nv, with k = 0.1, 0.2, …, 0.9, 1. Thus, the spatial mean amplitude was 1 in every case. (Ten sets of computations.)
-
4.
Nonuniform and asymmetric (NA): The AC amplitude ranged linearly from 0 to 0.5 in columns 1 through 3Nv/4, and from 2.5 to 4 in columns (3Nv/4) + 1 through Nv. Thus, the spatial mean amplitude was 1. (One set of computations.)
FIG. 6.
Graphical illustration of the four types of sinusoidal-rhythm amplitude modeled: “C” = constant; “U” = uniformly varying; “NS” = nonuniformly but symmetrically varying; “NA” = nonuniformly and asymmetrically varying. In each of the four cases depicted, the average value of the amplitude across all voxels is unity.
In the U, NS, and NA cases, the smallest amplitude was assigned to column 1, the second smallest to column 2, etc.
In each run, the Nv phase offsets ranged linearly from 0 to m degrees, with m = 0, 1, …, 359, 360 (361 sets of computations). Thus, the model considers spatial heterogeneity in two medium properties (amplitude and phase) simultaneously, which raises the question of whether their effects interact in producing the ultimately computed metric values. To evaluate this, the following procedure was adopted. First, the phase shifts were randomly assigned to the columns of the data array, in order to maximize the independence the amplitude- and phase-heterogeneity effects. Next, the Nt × Nv array of sinusoidal-function values corresponding to the assigned amplitudes and phases was generated, and metric values for the SSDTSD, SMTSD, CVTSD, TSDSSD, TMSSD, CVSSD, TSDSM, and SCI metrics were computed using Eqs. (4)–(9). The proceeding steps of randomly assigning phase shifts, generating the data array, and computing the scalar metrics was performed 100 times, for each modeled distribution of amplitudes, thereby allowing us to explicitly compute relevant parameters (e.g., mean, minimum, and maximum) of the distributions of metric values that each combination of amplitude and phase heterogeneities can produce.
While it is possible to include more elaborate and realistic model parameters (e.g., more than one frequency, nonlinear amplitude, and phase distributions), as described subsequently, results obtained from the simplified model qualitatively reproduce the clinically relevant trends seen in the experimental data. Our expectation—borne out by computational results—that a simple one-frequency model would suffice as an approximation for hemodynamic fluctuations followed from the experimental data showing that the most significant difference between affected and unaffected breasts occurs in relatively narrow vasomotor-frequency band (see Fig. 2). Computational results also show that the type of amplitude distribution (e.g., NA vs NS) is more important than the quantitative details (e.g., k = 0.1 vs k = 0.9) within a class, implying that use of nonlinear amplitude models in place of the linear trends shown in Fig. 6 also would have a relatively small impact.
2. Codependence of metric values on simplified dynamics
A first-order understanding of the influence of model parameters on the scalar metrics is indicated by check marks in Table IX. Here, we simply identify if a metric is sensitive to the variations modeled as per Fig. 6. Not explicitly shown is the additional finding that only trivial variations were found in the values of all metrics, across the sets of 100 randomized assignments of phase shifts to voxels, indicating that details of fine structure within the medium are unimportant in terms of their influence on metric values. Also included in the table is a division of the metrics into two primary subgroups, temporal and spatial. A common property for the temporal subgroup is that the initial step in generating the bidomain metric is computation of the TSD, separately for each voxel, while for the spatial subgroup, the initial step is computation of the SM or SSD, separately for each time frame. Phase differences among the voxels are irrelevant in the first category, so it was expected that these metrics would have no phase-heterogeneity dependence. In contrast, phase differences do affect the particular set of sinusoidal-function values that are present at a given time frame, and consequently, they have an impact on the spatial mean and standard deviation. Accordingly, all five metrics in the second category have phase-heterogeneity dependences.
TABLE IX.
Dependence of the eight scalar metrics on the three model parameters. A checkmark in a table cell indicates that the model parameter in the corresponding column influences the numerical value of the metric in the corresponding row.
| Model-parameter dependence | ||||
|---|---|---|---|---|
| Metric | Average amplitude | Amplitude heterogeneity | Phase heterogeneity | First dimension considered |
| SSDTSD | ✓ | ✓ | Temporal | |
| SMTSD | ✓ | |||
| CVTSD | ✓ | |||
| TSDSSD | ✓ | ✓ | ✓ | |
| TMSSD | ✓ | ✓ | ✓ | |
| CVSSD | ✓ | ✓ | Spatial | |
| TSDSM | ✓ | ✓ | ||
| SCI | ✓ | |||
In Table X, we expand on Table IX results, to include information about the manner in which the metrics vary as the parameter values (i.e., c, k, m) are increased. In every case where a dependence on the average amplitude exists, it takes the form of direct proportionality, as examination of Eqs. (1)–(8) had led us to expect. The absence of amplitude dependence in the other cases follows directly, as it cancels out when the ratio of two metrics having the same amplitude dependence is computed [Eq. (9)].
TABLE X.
Functional forms of the scalar-metric dependences on the model parameters.
| Model-parameter dependence | |||
|---|---|---|---|
| Metric | Average amplitude | Amplitude heterogeneity | Phase heterogeneity |
| SSDTSD | Linear | Monotonic increase | |
| SMTSD | Linear | ||
| CVTSD | Monotonic increase | ||
| TSDSSD | Linear | Multiphasic | Nonlinear, multiphasic |
| TMSSD | Linear | Monotonic increase | Nonlinear, monotonic increase |
| CVSSD | Multiphasic | Nonlinear, multiphasic | |
| TSDSM | Linear | Nonlinear, monotonic decrease | |
| SCI | Nonlinear, monotonic increase | ||
The average amplitude and phase heterogeneity properties of the model are each governed by a single parameter (c and m, respectively). Therefore, the corresponding dependences can be categorized as either linear or nonlinear in Table X. In contrast, there are two dimensions to the amplitude heterogeneity properties, the qualitative C → U → NS → NA progression (Fig. 6) and the quantitative sweep across values of k within the U and NS cases. In the “amplitude heterogeneity” column of Table X, the response described as “monotonic increase” is for fixed values of c and m, the metric value increases as the fluctuations becomes qualitatively more heterogeneous, NA > NS > U > C; within the U and NS cases, the metric value increases monotonically with increasing k, for fixed values of c and m.
Selected model-computation results are shown in Figure 7. These illustrate the dependences on amplitude heterogeneity and phase heterogeneity that are reported in Table X. The parameter m is plotted on the horizontal axis. As the largest phase shift between different voxels increases, we would expect to see an increase in SSD on average, but the temporal variability of the increasing spatial variability would concomitantly decrease. Thus, it is not surprising that TMSSD [Fig. 7(a)] is a monotonically increasing function of m, while the dependence of TSDSSD [Fig. 7(b)] is more complex but ultimately decreases to a value near zero. It is seen that TMSSD and CVTSD [Fig. 7(d)] monotonically increase with increasing k. In addition, the transitions from U to NS, and from NS to NA, are associated with larger-magnitude increases in the values of both metrics (not shown). The NA case is the only one for which we obtain CV TSD > 100%, and since values of CVTSD in excess of 100% are obtained from the experimental data for all subject groups (see Fig. 4), we can conclude that the spatial distribution of hemodynamic fluctuations in the breast is nonuniform and asymmetric, a finding consistent with the known heterogeneity in tissue composition of the breast.
FIG. 7.
Combined dependence of the (a) TMSSD, (b) TSDSSD, (c) CVSSD and (d) CVTSD metrics on amplitude and phase heterogeneity of the model medium, for the C (i.e., k = 0) and U (i.e., k > 0) amplitude-distribution cases. The average value of the AC amplitude is 1 in all cases. Each plotted curve is the average across the 100 random assignments of phase shifts to the voxels. For the metrics that are not explicitly shown here owing to space limitations: the SSDTSD plot is qualitatively the same as CVTSD (only difference is the y-axis unit); SMTSD is a single zero-slope straight line; the shape of the TSDSM curve (which has no k-dependence) is similar to the TMSSD curve for k = 0, reflected about m = 180; and SCI is a single nonlinear curve (no k-dependence) that is equal to 1 at m = 0 and increases without bound as m approaches 360.
Model-computation results also aid in interpreting the experimental findings that CV SSD < CV TSD for all groups and Hb signal components, and that CVSSD is never as large as 50% (e.g., CVSSD values derived from totalHb are approximately twice as large as the HbSat-based result in Fig. 4). The observations are consistent with Fig. 7(c) model result, which shows that the upper limit for CVSSD is approximately 50%. The same upper limit is found in the NS and NA cases and agrees with analytical calculations that give as the largest possible value.
REFERENCES
- 1.Lu P., Weaver V. M., and Werb Z., “The extracellular matrix: A dynamic niche in cancer progression,” J. Cell Biol. 196, 395–406 (2012). 10.1083/jcb.201102147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kumar S. and Weaver V. M., “Mechanics, malignancy, and metastasis: The force journey of a tumor cell,” Cancer Metastasis Rev. 28, 113–127 (2009). 10.1007/s10555-008-9173-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Andreea G. I., Pegza R., Lascu L., Bondari S., Stoica Z., and Bondari A., “The role of imaging techniques in diagnosis of breast cancer,” J. Curr. Health Sci. 37, 55–61 (2011), available at https://scholar.google.com/citations?view_op=view_citation&hl=en&user=AdPhtXAAAAAJ&citation_for_view=AdPhtXAAAAAJ:d1gkVwhDpl0C. [Google Scholar]
- 4.Vaupel P., “Tumor blood flow,” in Blood Perfusion and Microenvironment of Human Tumors: Implications for Clinical Radiooncology, edited by Molls M. and Vaupel P. (Springer, Berlin, 1998), pp. 41–45. [Google Scholar]
- 5.Hanahan D. and Weinberg R. A., “Hallmarks of cancer: The next generation,” Cell 144, 646–674 (2011). 10.1016/j.cell.2011.02.013 [DOI] [PubMed] [Google Scholar]
- 6.Sidransky D., “Emerging molecular markers of cancer,” Nat. Rev. Cancer 2, 210–219 (2002). 10.1038/nrc755 [DOI] [PubMed] [Google Scholar]
- 7.Al abdi R., Graber H. L., Xu Y., and Barbour R. L., “Optomechanical imaging system for breast cancer detection,” J. Opt. Soc. Am. A 28, 2473–2493 (2011). 10.1364/JOSAA.28.002473 [DOI] [PubMed] [Google Scholar]
- 8.Egorov V., Kearney T., Pollak S. B., Rohatgi C., Sarvazyan N., Airapetian S., Browning S., and Sarvazyan A., “Differentiation of benign and malignant breast lesions by mechanical imaging,” Breast Cancer Res. Treat. 118, 67–80 (2009). 10.1007/s10549-009-0369-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wellman P. S., Dalton E. P., Krag D., Kern K. A., and Howe R. D., “Tactile imaging of breast masses,” Arch. Surg. 136, 204–208 (2001). 10.1001/archsurg.136.2.204 [DOI] [PubMed] [Google Scholar]
- 10.Evans A., Whelehan P., Thomson K., Mclean D., Brauer K., Purdie C., Jordan L., Baker L., and Thompson A., “Quantitative shear wave ultrasound elastography: Initial experience in solid breast masses,” Breast Cancer Res. 12, R104 (11pp.) (2010). 10.1186/bcr2787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Manduca A., Oliphant T. E., Dresner M. A., Mahowald J. L., Kruse S. A., Amromin E., Felmlee J. P., Greenleaf J. F., and Ehman R. L., “Magnetic resonance elastography: Non-invasive mapping of tissue elasticity,” Med. Image Anal. 5, 237–254 (2001). 10.1016/S1361-8415(00)00039-6 [DOI] [PubMed] [Google Scholar]
- 12.McDonald S., Saslow D., and Alciati M. H., “Performance and reporting of clinical breast examination: A review of the literature,” Ca-Cancer J. Clin. 54, 345–361 (2004). 10.3322/canjclin.54.6.345 [DOI] [PubMed] [Google Scholar]
- 13.Schmitz C. H., Klemer D. P., Hardin R. E., Katz M. S., Pei Y., Graber H. L., Levin M. B., Levina R. D., Franco N. A., Solomon W. B., and Barbour R. L., “Design and implementation of dynamic near-infrared optical tomographic imaging instrumentation for simultaneous dual-breast measurements,” Appl. Opt. 44, 2140–2153 (2005). 10.1364/AO.44.002140 [DOI] [PubMed] [Google Scholar]
- 14.Fang Q., Carp S. A., Selb J., Boverman G., Zhang Q., Kopans D. B., Moore R. H., Miller E. L., Brooks D. H., and Boas D. A., “Combined optical imaging and mammography of the healthy breast: Optical contrast derived from breast structure and compression,” IEEE Trans. Med. Imaging 28, 30–42 (2009). 10.1109/tmi.2008.925082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhu Q., Hegde P. U., Ricci A., Kane M., Cronin E. B., Ardeshirpour Y., Xu C., Aguirre A., Kurtzman S. H., Deckers P. J., and Tannenbaum S. H., “Early-stage invasive breast cancers: Potential role of optical tomography with US localization in assisting diagnosis,” Radiology 256, 367–378 (2010). 10.1148/radiol.10091237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brooksby B., Pogue B. W., Jiang S., Dehghani H., Srinivasan S., Kogel C., Tosteson T., Weaver J. B., Poplack S. P., and Paulsen K. D., “Imaging breast adipose and fibroglandular tissue molecular signatures using hybrid MRI-guided near-infrared spectral tomography,” Proc. Natl. Acad. Sci. U. S. A. 103, 8828–8833 (2006). 10.1073/pnas.0509636103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu R. X., Young D. C., Mao J. J., and Povoski S. P., “A prospective pilot clinical trial evaluating the utility of a dynamic near-infrared imaging device for characterizing suspicious breast lesions,” Breast Cancer Res. 9, R88(12pp.) (2007). 10.1186/bcr1837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Choe R., Konecky S. D., Corlu A., Lee K., Durduran T., Busch D. R., Pathak S., Czerniecki B. J., Tchou J., Fraker D. L., DeMichele A., Chance B., Arridge S. R., Schweiger M., Culver J. P., Schnall M. D., Putt M. E., Rosen M. A., and Yodh A. G., “Differentiation of benign and malignant breast tumors by in-vivo three-dimensional parallel-plate diffuse optical tomography,” J. Biomed. Opt. 14, 024020 (2009). 10.1117/1.3103325 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pogue B. W., Jiang S., Dehghani H., Kogel C., Soho S., Srinivasan S., Song X., Tosteson T. D., Poplack S. P., and Paulsen K. D., “Characterization of hemoglobin, water, and NIR scattering in breast tissue: Analysis of intersubject variability and menstrual cycle changes,” J. Biomed. Opt. 9, 541–552 (2004). 10.1117/1.1691028 [DOI] [PubMed] [Google Scholar]
- 20.Nioka S. and Chance B., “NIR spectroscopic detection of breast cancer,” Technol. Cancer Res. Treat. 4, 497–512 (2005). 10.1177/153303460500400504 [DOI] [PubMed] [Google Scholar]
- 21.Flexman M. L., Khalil M. A., Al abdi R., Kim H. K., Fong C. J., Desperito E., Hershman D. L., Barbour R. L., and Hielscher A. H., “Digital optical tomography system for dynamic breast imaging,” J. Biomed. Opt. 16, 076014 (2011). 10.1117/1.3599955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Carp S. A., Selb J., Fang Q., Moore R., Kopans D. B., Rafferty E., and Boas D. A., “Dynamic functional and mechanical response of breast tissue to compression,” Opt. Express 16, 16064–16078 (2008). 10.1364/OE.16.016064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schreiter N. F., Volkwein N., Schneider P., Maurer M. H., Piper S., Schmitz C., and Poellinger A., “Optical imaging of breast cancer using hemodynamic changes induced by Valsalva maneuver,” Fortschr. Geb. Roentgenstr. Ver. Roentgenprax. 184, 358–366 (2013). 10.1055/s-0032-1330446 [DOI] [PubMed] [Google Scholar]
- 24.Yoshino K., Oka N., Yamamoto K., Takahashi H., and Kato T., “Functional brain imaging using near-infrared spectroscopy during actual driving on an expressway,” Front. Hum. Neurosci. 7, 882 (16pp.) (2013). 10.3389/fnhum.2013.00882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pei Y., Graber H. L., and Barbour R. L., “Influence of systematic errors in reference states on image quality and on stability of derived information for DC optical imaging,” Appl. Opt. 40, 5755–5769 (2001). 10.1364/AO.40.005755 [DOI] [PubMed] [Google Scholar]
- 26.Metz C. E., “Basic principles of ROC analysis,” Semin. Nucl. Med. 8, 283–298 (1978). 10.1016/S0001-2998(78)80014-2 [DOI] [PubMed] [Google Scholar]
- 27.Brown J. Q., Wilke L. G., Geradts J., Kennedy S. A., Palmer G. M., and Ramanujam N., “Quantitative optical spectroscopy: A robust tool for direct measurement of breast cancer vascular oxygenation and total hemoglobin content in vivo,” Cancer Res. 69, 2919–2926 (2009). 10.1158/0008-5472.CAN-08-3370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gershon-Cohen J., Atlas of Mammography (Springer, Berlin, 2012). [Google Scholar]
- 29.Pei Y., Graber H. L., Farber M., Schmitz C. H., Xu Y., Toubas P., Patel N., Katz M. S., Solomon W. B., and Barbour R. L., “Tumor detection by simultaneous bilateral diffuse optical tomography (DOT) breast imaging,” in Poster No. 82 at Fifth Inter-Institute Workshop on Optical Diagnostic Imaging from Bench to Bedside, National Institutes of Health, Bethesda, MD, September 25-27 (2006). [Google Scholar]
- 30.Choudhari S. K., Chaudhary M., Bagde S., Gadbail A. R., and Joshi V., “Nitric oxide and cancer: A review,” World J. Surg. Oncol. 11, 118(11pp.) (2013). 10.1186/1477-7819-11-118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cheng R., Glynn S., Flores-Santana W., Switzer C., Ridnour L., and Wink D. A., “Nitric oxide and redox inflammation in cancer,” Adv. Mol. Toxicol. 4, 158–176 (2010). 10.1016/s1872-0854(10)04005-1 [DOI] [Google Scholar]
- 32.Barbour R. L., Graber H. L., Schmitz C. H., Pei Y., Zhong S., Barbour S.-L. S., Blattman S., and Panetta T., “Spatio-temporal imaging of vascular reactivity by optical tomography,” in Proceedings of Inter-Institute Workshop onIn Vivo Optical Imaging at the NIH, edited by Gandjbakhche A. H. (Optical Society of America, Washington, DC, 1999), pp. 161–166. [Google Scholar]
- 33.Barbour R. L., Graber H. L., Pei Y., Zhong S., and Schmitz C. H., “Optical tomographic imaging of dynamic features of dense-scattering media,” J. Opt. Soc. Am. A 18, 3018–3036 (2001). 10.1364/JOSAA.18.003018 [DOI] [PubMed] [Google Scholar]
- 34.Graber H. L., Pei Y., and Barbour R. L., “Imaging of spatiotemporal coincident states by DC optical tomography,” IEEE Trans. Med. Imaging 21, 852–866 (2002). 10.1109/TMI.2002.801154 [DOI] [PubMed] [Google Scholar]
- 35.Button T., Li H., Fisher P., Rosenblatt R., Dulaimy K., Li S., O’Hea B., Salvitti M., Geronimo V., Geronimo C., Jambawalikar S., Carvelli P., and Weiss R., “Dynamic infrared imaging for the detection of malignancy generated nitric oxide,” Phys. Med. Biol. 49, 3105–3116 (2004). 10.1088/0031-9155/49/14/005 [DOI] [PubMed] [Google Scholar]
- 36.Schmitz C. H., Löcker M., Lasker J. M., Hielscher A. H., and Barbour R. L., “Instrumentation for fast functional optical tomography,” Rev. Sci. Instrum. 73, 429–439 (2002). 10.1063/1.1427768 [DOI] [Google Scholar]
- 37.Barbour R. L., Graber H. L., Xu Y., Pei Y., Schmitz C. H., Pfeil D. S., Tyagi A., Andronica R., Lee D. C., Barbour S.-L. S., Nichols J. D., and Pflieger M. E., “A programmable laboratory testbed in support of evaluation of functional brain activation and connectivity,” IEEE Trans. Neural Syst. Rehabil. Eng. 20, 170–183 (2012). 10.1109/TNSRE.2012.2185514 [DOI] [PubMed] [Google Scholar]
- 38.Schneider P., Piper S. K., Schmitz C. H., Schreiter N. F., Volkwein N., Lüdemann L., Malzahn U., and Poellinger A., “Fast 3D near-infrared breast imaging using indocyanine green for detection and characterization of breast lesions,” Fortschr. Geb. Roentgenstr. Ver. Roentgenprax. 183, 956–963 (2011). 10.1055/s-0031-1281726 [DOI] [PubMed] [Google Scholar]
- 39.Glynn S. A., Boersma B. J., Yi M., Yfantis H. G., Ridnour L. A., Martin D. N., Switzer C. H., Hudson R. S., Wink D. A., Lee D. H., Stephens R. M., and Ambs S., “Increased NOS2 predicts poor survival in estrogen receptor-negative breast cancer patients,” J. Clin. Invest. 120, 3843–3854 (2010). 10.1172/JCI42059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rashad Y. A., Elkhodary T. R., El-Gayar A. M., and Eissa L. A., “Evaluation of serum levels of HER2, MMP-9, nitric oxide and total antioxidant capacity in Egyptian breast cancer patients: Correlation with clinico-pathological parameters,” Sci. Pharm. 82, 129–145 (2014). 10.3797/scipharm.1306-18 [DOI] [PMC free article] [PubMed] [Google Scholar]