A new approach for detecting riboswitches in DNA sequences

Abstract

Motivation: Riboswitches are short sequences of messenger RNA that can change their structural conformation to regulate the expression of adjacent genes. Computational prediction of putative riboswitches can provide direction to molecular biologists studying riboswitch-mediated gene expression.

Results: The Denison Riboswitch Detector (DRD) is a new computational tool with a Web interface that can quickly identify putative riboswitches in DNA sequences on the scale of bacterial genomes. Riboswitch descriptions are easily modifiable and new ones are easily created. The underlying algorithm converts the problem to a ‘heaviest path’ problem on a multipartite graph, which is then solved using efficient dynamic programming. We show that DRD can achieve ∼88–99% sensitivity and >99.99% specificity on 13 riboswitch families.

Availability and implementation: DRD is available at http://drd.denison.edu.

Contact: havill@denison.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The regulation of gene expression is a critical process that dictates the ability of cells to function properly, to establish cellular identity, and to respond to changes in environmental conditions. Gene regulation is manifested in a variety of ways, ranging from the action of transcriptional activators and repressors through cis-acting regulatory binding sites, DNA accessibility via chromatin structure, and localization of DNA within the cellular/nuclear confines. In addition to these mechanisms, RNA has surfaced as a player in gene regulation (Mondal and Kanduri, 2013). Specific forms of RNA, such as microRNAs, small interfering RNAs and many others, have been identified and characterized as important components of gene regulation.

One specific manner by which RNA molecules serve as regulators of gene expression is in the form of riboswitches. Riboswitches are short sequences (∼50–250 nt in length) located in the non-coding portions of specific messenger RNAs (mRNAs) that regulate the expression of the coding sequences contained within the mRNA (Miranda-Rios, 2007; Montange and Batey, 2008). They function via their ability to fold into distinct secondary structures that influence the ability of the mRNA to be transcribed, processed or translated. Riboswitches consist of two specific components: an aptamer region that binds to a specific organic molecule, often some type of metabolite; and an expression platform that produces a change in structural conformation as a result of binding to the aptamer (Winkler and Breaker, 2003). The aptamer region is generally a highly conserved sequence, capable of binding to a number of organic molecules with high specificity (Nahvi et al., 2007). Binding to the aptamer triggers changes in the intramolecular base pairing within the expression platform, leading to changes in secondary and tertiary structure of the RNA. The change in conformation in turn influences the ability of the mRNA to be expressed in a variety of different ways, depending on the specific riboswitch. The activation of some riboswitches results in premature termination of transcription, ending synthesis of the mRNA before the coding region. Others act by directly blocking translation of the mRNA by restricting access to the ribosomal binding site (Nudler and Mironov, 2004). In eukaryotes, riboswitch folding may also influence expression via regulation of mRNA splicing.

There are currently about 20 known families of riboswitches that bind to a variety of nucleobases, amino acids, metal ions and other organic compounds (Batey, 2012). Many of the more extensively studied riboswitches serve as part of a feedback regulatory system for genes that participate in cellular metabolism (Miranda-Rios, 2007). The metabolites that bind to the aptamer serve as indicators of the relative activity of specific metabolic pathways, and upon binding, influence expression of genes that participate in the pathway. For example, certain genes involved in the synthesis of vitamin ${\text{B}}_1$ (thiamin) are regulated by a riboswitch that binds thiamin pyrophosphate (TPP), the biologically active form of thiamin. TPP binds to a conserved RNA sequence known as a THI-box, which represses transcription of genes possessing this sequence in the 5′ untranslated region. The THI-box is a particularly intriguing example of a riboswitch, as it is found in a wide range of bacteria, archaea and eukaryotes and functions in a variety of contexts. The TPP riboswitch is the only known eukaryotic riboswitch identified to date (Bocobza and Aharoni, 2008).

Given the importance of riboswitches in gene regulation in the context of whole-genome regulation, methods to identify such sequences are needed. A variety of efforts have been previously undertaken to develop bioinformatics tools to predict the presence of riboswitches in RNA sequences (Bengert and Dandekar, 2004; Chang et al., 2009, 2013; Freyhult et al., 2007; Veksler-Lublinsky et al., 2007). Most programs that have been developed operate on the principle of sequence alignment to identify conserved sequences in previously identified riboswitches, coupled with RNA structural folding algorithms. Programs that are currently available are generally limited to the identification of a specific subset of known riboswitch types, and are only able to search modest sized sequence inputs. To date, few programs have been developed to take advantage of the abundance of completed full genome sequences.

To address the need for riboswitch prediction on the whole-genome scale, we have developed a new computational tool with a Web interface that can identify putative riboswitches in DNA sequences, called the Denison Riboswitch Detector (DRD). DRD can quickly (typically <1 min) process complete bacterial genomes and achieve ∼90% sensitivity and almost 100% specificity. DRD’s description of a riboswitch is simple and easily modifiable, based on the highly conserved motifs found in all known riboswitches. To identify an optimal sequence of short motifs, DRD transforms the search into a path-finding problem on a directed multipartite graph, which is then solved by an efficient dynamic programming algorithm. DRD can be accessed at http://drd.denison.edu. Researchers interested in using the program as a stand-alone tool may also contact the first author.

2 RELATED RESEARCH

There are three primary approaches currently used to detect riboswitches. The first approach compares conserved stem-loop features in the secondary structure, determined by an algorithm like mFold (Zuker, 2000). For example, RiboSW (Chang et al., 2009) and RegRNA (Chang et al., 2013) focus on the characteristic secondary structures of 12 different riboswitches. Riboswitch Finder (Bengert and Dandekar, 2004) searches for the characteristic secondary structure of purine riboswitches. RNAMotif (Macke et al., 2001) defines a general descriptor language, allowing one to search for any desired structure.

The second approach takes advantage of the fact that the aptamer regions of riboswitches are highly conserved for the metabolite that they bind to. Thus, it is possible to recognize motif sequences that are specific to a certain family of riboswitches. To detect a riboswitch, the input is first scanned for the motif sequence(s), and then the optimal secondary structure is predicted. If the predicted structure matches the known structure of the riboswitch, it may be considered a putative riboswitch. This approach is also incorporated into Riboswitch Finder (Bengert and Dandekar, 2004) and the unpublished SequenceSniffer algorithm (Sudarsan et al., 2003). Motif search is used exclusively by RibEx (Abreu-Goodger and Merino, 2005), which also searches for translational attenuators.

The third, more recent, approach is to characterize a riboswitch family using a probabilistic model. Singh, et al. (2009) consider using profile hidden Markov models and Infernal (Nawrocki et al., 2009), upon which Rfam (Gardner et al., 2011) is based, uses a covariance model. RiboSW (Chang et al., 2009) also uses HMMER (Eddy, 1998) after it performs a search for conserved structural characteristics.

Our technique primarily falls into the second category. DRD is designed to be fast, working quickly on entire bacterial genomes, with conveniently modifiable definition files. Although this approach sacrifices some of the accuracy of the more comprehensive probabilistic models, it still achieves ∼90% specificity, compared with Rfam, in our comprehensive tests.

3 METHODS

Here we will give an overview of our algorithm, followed by a more detailed description and a discussion of its implementation.

3.1 The DRD algorithm

To detect instances of a particular riboswitch with n known motifs in a long DNA sequence, we first break the sequence and its reverse complement into short overlapping segments of a few hundred nucleotides each. We assume that at most one riboswitch can occur in each segment. In each segment, we identify all matches for each of the n motifs. If at least one match is found for each motif, we then find the highest scoring sequence of matches in the segment that conforms to given ordering and spacing requirements. This step is accomplished by transforming the problem into a heaviest path problem on an n-partite graph, and using an efficient dynamic programming algorithm to find the best path. (This is described in detail in Section 3.2.) If such a path exists and its weight exceeds a given threshold, we then fold the corresponding putative riboswitch using mFold (Zuker, 2000). Finally, we align the resulting Vienna (dot-bracket) string, with motifs inserted to guide alignment, with a given consensus Vienna string. If the number of identities in this alignment exceeds another given threshold, we display the result with a graphical representation of its secondary structure.

DRD accepts the following parameters describing a riboswitch:

• a maximum length of the riboswitch M;

• a segment length l and segment overlap length $p\ge M$;

• n motifs $m_1,m_2,\dots ,m_n$ (may contain degenerate symbols);

• minimum motif identity scores (By ‘identity score’, we mean the number of nucleotide matches in a local alignment between a motif and a portion of the query sequence with the same length. An indel subtracts one from the score in the local alignment algorithm but is not counted in the final motif identity score.) ${\mu }_1,{\mu }_2,\dots ,{\mu }_n$, where μ_i is the score corresponding to motif m_i;

• maximum inter-motif distances $D_0,D_1,D_2,\dots ,D_n$, where D_i, $i=1,2,\dots ,n-1$, is the maximum distance between motifs m_i and $m_{i+1}$, and D₀ and D_n are distances on the 5′ side of the first motif and the 3′ side of the last motif, respectively, that are used to define the 5′ and 3′ boundaries of a reported riboswitch;

• minimum inter-motif distances $d_1,d_2,\dots ,d_{n-1}$, where d_i, $i=1,2,\dots ,n-1$, is the minimum distance between motifs m_i and $m_{i+1}$;

• minimum total motif identity score $S_1\ge {\displaystyle {\sum }_{i=1}^n{\mu }_i}$;

• consensus secondary structure representations F and $F\prime$ (in Vienna notation), where F is the consensus secondary structure, and $F\prime$ is the consensus secondary structure with motifs inserted in their appropriate locations; and

• minimum total Vienna identity score S₂.

DRD begins by cutting the input sequence and its reverse complement into short segments of l ($\approx 700$–1000) nucleotides that overlap each other in p ($\approx 200$) nucleotides. The overlap length should exceed the expected maximum length of the riboswitch. For each segment, our approach consists of the following steps:

1. Use the Smith–Waterman local alignment algorithm to locate, for each specified motif m_i, all matches with identity score at least μ_i. Indels subtract one from the alignment score. For the $j^{\text{th}}$ discovered match for motif m_i, record both its starting position $b_{i,j}$ and its identity score $s_{i,j}\ge {\mu }_i$. If not all motifs are found, abort and continue with the next segment.

2. Construct a directed n-partite graph $G=(V,A)$ in which each layer i contains a node $v_{i,j}$ for each match to motif m_i found in the previous step. Connect a node $v_{i,j}$ in layer i to a node $v_{i+1,k}$ in layer i + 1 if $b_{i+1,k}>b_{i,j}$ and $|m_i|+d_i\le b_{i+1,k}-b_{i,j}\le D_i$. Each node is given a weight equal to the associated motif’s Smith–Waterman identity score.

3. Find the maximum weight path $\langle v_{1,j_1},v_{2,j_2},\dots ,v_{n,j_n}\rangle$ from a node in Layer 1 to a node in Layer n, using a dynamic programming algorithm described below. If no such path exists, abort and continue with the next segment. Otherwise, this path corresponds to a subsequence containing matches to all the motifs, and its weight ${\displaystyle {\sum }_{i=1}^n{s}_{i,j_i}}$ is the sum of the identify scores of the corresponding motifs. If ${\displaystyle {\sum }_{i=1}^n{s}_{i,j_i}}\ge S_1$, consider the subsequence between positions $b_{1,j_1}-D_0$ and $b_{n,j_n}+|m_n|+D_n$ to be a putative riboswitch. Otherwise, abort and continue with the next segment.

4. Optionally, check whether the putative riboswitch discovered in the previous step overlaps with any sufficiently long open reading frames (ORFs). If so, abort and continue with the next segment.

5. Fold the putative riboswitch using the mFold algorithm (Zuker, 2000) and convert it to a Vienna string in dot-bracket notation.

6. Insert the discovered motifs into the Vienna string at their correct locations and perform a global alignment of the resulting Vienna string and the modified consensus string $F\prime$. If the resulting identity score is at least S₂, output the sequence as a putative riboswitch.

7. Also, for informational purposes only, perform a global alignment of the unmodified Vienna strings, convert the Vienna representations of both the putative and consensus riboswitches to shape notation (Giegerich et al., 2004; Lorenz et al., 2008), and perform a global alignment of the two shape strings.

3.2 Heaviest path problem

We will illustrate the heaviest path problem described in Steps 2–3 with a small example. Consider a search for a short fictitious riboswitch with only three conserved motifs m₁ = AAAA, m₂ = CCCC, and m₃ = TTTT; threshold identify scores ${\mu }_1={\mu }_2={\mu }_3=3$; and minimum and maximum distances $d_1=d_2=d_3=2$ and $D_1=D_2=D_3=20$. Suppose our current segment is the following, with matches for each motif underlined (single for AAAA, double for CCCC and triple for TTTT). (There are more overlapping matches, but we will ignore them here.)

With these matches, we construct the directed tripartite graph below. In the first layer are vertices representing matches for motif AAAA, in the second layer are matches for motif CCCC and in the third layer are matches for motif TTTT. Each vertex is connected to all vertices in the next layer corresponding to motifs between distance 2 and 20 downstream.

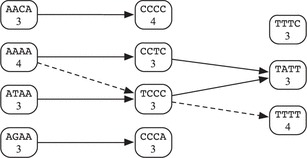
We now wish to find a path connecting a vertex in Layer 1 with a vertex in Layer 3 with the maximum total vertex weight. The unique maximum weight path in this case is shown with dashed lines. This path corresponds to the subsequence indicated below with the chosen motifs still underlined.

The heaviest path problem is solved using a dynamic programming algorithm based on the following recurrence. Let $H_{i,j}$ denote the weight of the heaviest path from a node in Layer 1 to node $v_{i,j}$ in Layer i. Then we can define $H_{i,j}$ recursively as follows:

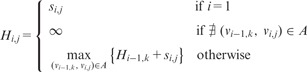Then, we ultimately want the heaviest path, satisfying

$$H^{*}=\underset{j}{\max }{H}_{n,j}.$$

The associated dynamic programming algorithm has time complexity $\Theta (n{m}^2)$, where m is the maximum number of matches for a motif.

3.3 Implementation as a Web tool

We implemented DRD as a multithreaded C++ program for the Linux operating system and placed it behind a PHP Web interface, shown in the top half of Figure 1. The interface allows one to input a query sequence in FASTA format and choose one or more query riboswitch types. Each riboswitch is represented by a text definition file containing the parameters outlined in Section 3.1. Clicking on the name of the riboswitch displays the corresponding file. One may also supply their own definition file (or a modified version of one of the given files) by selecting the ‘Other’ option. Finally, one may opt to have the program disregard any motifs that overlap ORFs (by checking ‘ORF Search?’). An ORF is defined to be a sequence of codons that starts with the start codon ATG and ends with one of three stop codons (TAA, TAG, TGA), with no stop codons in between. Only ORFs containing at least the number of codons given by the user in the ‘Minimum ORF Length’ box (120 by default) impact the search.

Fig. 1.

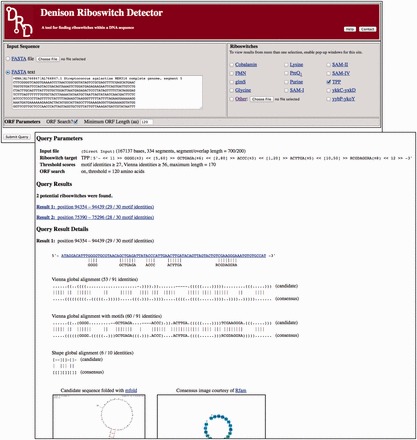
The Web interface of DRD (above) and a sample result (below)

The format of the description file is straightforward; one example is shown in Figure 2. Line 1 contains the values of l and p. Line 2 contains n, the number of motifs, followed by a motif m_i and its minimum identity score μ_i on each of the following n lines. After the motifs (on Line 8 in the example in Fig. 2), are the maximum inter-motif distances $D_0,D_1,D_2,\dots ,D_n$. These are followed on the next line by the minimum inter-motif distances $d_1,d_2,\dots ,d_{n-1}$. On the next line are the values of S₁, S₂ and M. Finally, we have the Vienna string for the consensus secondary structure and the same Vienna string with motifs inserted.

Fig. 2.

The TPP riboswitch definition file, with the last two lines truncated

When Submit is pressed, work begins and a results window, describing the progress so far, appears for each selected riboswitch. The pages will refresh every 3 s, leading ultimately to the final results, like those in Figure 1, listed in the order of motif identity score, then Vienna identity score. In our tests, matches to previously annotated riboswitches were virtually always displayed on top. Clicking on a result sets up a BLAST query. Below the alignments and scores, optimal and suboptimal secondary structures computed by mFold are displayed with the Rfam consensus image.

4 RESULTS

We tested DRD on 13 riboswitch families, using definition files derived from multiple sequence alignments of the families’ Rfam-designated seed sequences. These definition files may be viewed in Supplementary Table S1 or in the Web interface by clicking on the riboswitch name. For each riboswitch, we performed two types of tests. First, to obtain robust sensitivity results for each riboswitch family, we tested DRD on all known riboswitch sequences predicted for each family in the Rfam database at http://rfam.xfam.org. The sensitivity, or true-positive rate (TPR), is TP/(TP+FN), where TP is the number of true-positive findings, and FN is the number of false-negative findings. Second, to measure the corresponding false-positive rate (FPR) for each family in genome-scale sequences, we randomly selected a small number of Rfam-predicted riboswitch sequences and tested DRD on the set of GenBank sequence records in which they are contained. The false-positive rate is 1-specificity; specificity is defined to be TN/(TN + FP), where TN is the number of true-negative findings, and FP is the number of false-positive findings. We discuss each of these tests in detail below.

4.1 Sensitivity

We used a specialized front-end program to test how well DRD detects Rfam-predicted riboswitches in isolation. The number of sequences assigned to a family in Rfam ranges from 356 (SAM-II) to 11 197 (TPP). For each riboswitch family, we set $S_1=0$ in the definition file to ascertain the sensitivity over the full range of possible S₁ values. The results, displayed in Figure 3 and Table 1, show that, with the exception of the cobalamin riboswitch, we get a sensitivity of ∼90% or better for each riboswitch family when S₁ is set to be ∼95% of the maximum possible motif identify score. The data in the left half of Table 1 show the detailed sensitivity results for the default values of S₁ in DRD. Higher values of S₁ allow for too little deviation from the given motifs, and therefore, the sensitivity drops off quickly. Sensitivity for the cobalamin riboswitch on the full set of 9056 Rfam sequences reaches a maximum of ∼83%. However, sensitivity for the smaller set of 430 seed sequences easily exceeds 90%. Looking at the multiple sequence alignment for the full set of cobalamin riboswitch sequences reveals much less consensus than the seed sequences, especially at the 5′ end.

Fig. 3.

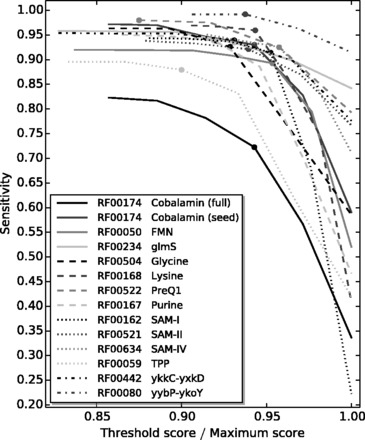
Sensitivity values for each riboswitch family over a range of S₁ values. To display the results on a common x-axis, S₁ values are normalized by the maximum possible motif identity score for each family. The filled circle on each curve marks the value of S₁ in that riboswitch’s default definition file

Table 1.

Sensitivity and $1-\text{specificity}$ when S₁ is the default value

Family		Sensitivity tests				Specificity tests			Default $S_1$/ Maximum
		Seed		Full
Name	Rfam ID	Number of sequences	Sensitivity	Number of sequences	Sensitivity	Number of nucleotides	Number of segments	$1-Specificity$
Cobalamin	RF00174	430	0.93	9056	0.72	26 954 544	67 385	0.000178	33 / 35
FMN	RF00050	144	0.97	4516	0.89	78 082 630	173 519	0.000161	41 / 43
glmS	RF00234	18	0.94	842	0.93	12 042 233	30 104	0.000266	27 / 29
Glycine	RF00504	44	0.93	6875	0.93	27 624 292	2 762 348	0.000001	26 / 28
Lysine	RF00168	47	0.96	2422	0.96	22 451 184	52 213	0.000038	50 / 53
preQ1	RF00522	41	0.95	894	0.98	13 487 486	23 256	0.000086	21 / 24
Purine	RF00167	133	0.96	2427	0.94	80 376 637	146 145	0.000363	34 / 37
SAM-I	RF00162	433	0.89	4757	0.91	13 752 571	28 651	0.000140	40 / 42
SAM-II	RF00521	40	1.00	356	0.92	18 875 429	49 672	0.000000	31 / 33
SAM-IV	RF00634	40	0.98	468	0.93	26 737 655	53 476	0.000056	45 / 47
TPP	RF00059	115	0.89	11 197	0.88	62 623 450	125 251	0.000453	27 / 30
ykkC-yxkD	RF00442	109	0.99	741	0.94	18 698 253	38 955	0.000077	27 / 29
yybP-ykoY	RF00080	17	1.00	1882	0.99	23 704 402	49 385	0.000162	30 / 32

Note: The last column contains the default S₁ values, relative to the maximum motif identities.

We find that, upon closer inspection, when DRD fails to identify an Rfam-predicted riboswitch, it is commonly due to missing one or two identities in one or two motifs. By reducing individual minimum motif identity scores μ_i and the value of S₁, we can easily generate higher sensitivity values. However, we also found that this will result in much lower specificity values when DRD is applied to genome-scale input files. We discuss these results next.

4.2 Specificity

To contextualize these sensitivity results, we would ideally compute corresponding specificity values for every GenBank sequence record containing an Rfam-predicted riboswitch. Because this is infeasible, we instead estimated sensitivity by randomly selecting a small set of Rfam-predicted sequences from each riboswitch family and running DRD on their corresponding GenBank sequence records. For each family, we selected records that covered at least five organisms and totaled at least 12 million nt. In the case of three riboswitch families—flavin mononucleotide (FMN), purine and TPP—we conducted tests on a larger set of 30 GenBank records. To derive specificity values over a range of S₁ values, we set S₁ to be three less than the maximum possible identity score for each family.

Because DRD searches for a riboswitch in each segment, we considered each segment to be an individual trial. If a segment contained a riboswitch that has been annotated in either Rfam or GenBank, it was considered a true positive when DRD detected the riboswitch and a false negative otherwise. If a segment did not contain an annotated riboswitch, it was considered to be a false positive when DRD detected a riboswitch and a true negative otherwise. We note that this may not be a perfect classification because either (i) a segment may actually contain a previously unannotated riboswitch or (ii) two overlapping segments may both contain the same annotated riboswitch, but DRD will report only one hit. In the first case, the reported specificity may be too low. In the second case, the reported specificity will be too high. However, because the number of annotated riboswitches is so small relative to the number of segments, these errors are negligible.

Our results, displayed in Figure 4 and Table 1, show that DRD achieves very high specificity while generally maintaining sensitivity at least 90%. The data in the right half of Table 1 show the detailed specificity results for the default values of S₁ in DRD. The raw data for these experiments can be found in Supplementary Tables S2–S14.

Fig. 4.

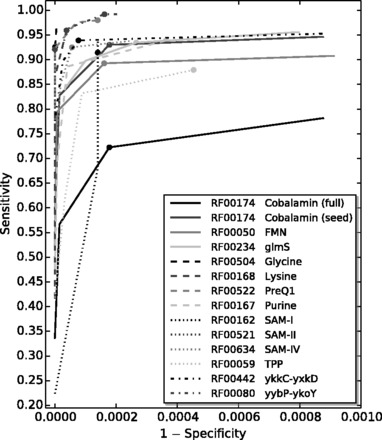
The receiver-operator characteristic curve for each riboswitch family correlating sensitivity values from Section 4.1 to $1-\text{specificity}$ on a representative sample of GenBank sequence records. The filled circle on each curve marks the value of S₁ in that riboswitch’s default definition file

4.3 Other observations

While we found that the default ORF threshold length (120 codons) worked well for a variety of inputs, we also found that, in some cases, especially with cobalamin and ykkC-yxkD, it was necessary to increase the ORF threshold to locate a riboswitch reported by Rfam. Some examples of this are annotated in Supplementary Tables S2–S14. In many cases, increasing the ORF threshold did not introduce many more false-positive results, but in a very few cases it did.

Because DRD defines the ends of its reported riboswitches with respect to distances on either side of the first and last motif (D₀ and D_n, respectively), the accuracy of these predicted positions is better when there are defined motifs close to the 5′ and 3′ ends. Because this is true in almost all of the tested families, the bounds reported by DRD are very close to those in Rfam. One exception is the cobalamin riboswitch. While a multiple sequence alignment of the cobalamin seed sequences predicts a well-conserved short GGT motif near the 5′ end, we eliminated this motif from our definition file because it resulted in an even lower hit rate for the full set of sequences. (An inspection of the multiple sequence alignment for the full set of sequences reveals significantly more variability than the seed sequences and no clear consensus on the 5′ end.) The leaves the first motif 40–50 bases from the 5′ end, resulting in more variability in the predicted 5′ boundary.

To detect glycine riboswitches, which tend to appear as two similar structures in tandem, DRD must have contiguous segments overlap significantly. Therefore, in our definition files, we set each segment length to be 150, with a 140 bp overlap, resulting in a 150 bp ‘window’ that shifts down by 10 bp in each iteration. This significantly slows the search, but it still completes within a few minutes on genome-scale sequences.

Riboswitches are most commonly found in bacterial genomes, but the TPP riboswitch has also been identified in eukaryota and archaea. Therefore, in the TPP riboswitch specificity tests, we included three archaeal organisms from the Thermoplasma genus and two eukaryotic organisms [Arabidopsis thaliana and Glycine max (soybean)]. The results on this small sample were comparable with those on bacterial genomes. (See Supplementary Table S12.)

4.4 Comparison with existing tools

Table 2 compares the functionality of DRD with some other recently developed riboswitch search tools discussed in Section 2. As discussed previously, DRD is able to scan genome-scale files for riboswitches, whereas other tools have relatively constraining input size limits. Like RiboSW (Chang et al., 2009), DRD also allows a user to define new riboswitch definition files, but the format of DRD’s files is significantly more straightforward.

Table 2.

A basic comparison of the main features of each tool

Feature	Riboswitch finder	RibEx	RiboSW	DRD
Maximum input length	3 Mb	40 kb	10 kb	none
Number of riboswitches	1	≥17	12	13
New user definitions	No	No	Yes	Yes

We compared the sensitivities of DRD and RiboSW (Chang et al., 2009) on all riboswitch families but SAM-IV, which RiboSW does not consider. For the purine riboswitch, we also compared the sensitivities of DRD and Riboswitch finder (Bengert and Dandekar, 2004). We chose to omit RibEx because a similar comparison with RiboSW was already undertaken by Chang et al. (2009).

For these comparisons, we randomly selected up to 50 Rfam seed sequences for each family. If the number of seed sequences was <50, we used the entire seed set. We chose to test on this reduced set because of RiboSW’s size constraints and computation times. The results, summarized in Table 3, show that DRD’s sensitivity at least rivals that of RiboSW for all riboswitch families, and significantly exceeds it in four cases (glycine, TPP, ykkC-yxkD and yybP-ykoY) (For TPP and ykkC-yxkD, we used the most favorable results for RiboSW over four random sets to validate these more significant differences.). Over all sequences, RiboSW achieves sensitivity of 0.85, whereas DRD achieves sensitivity of 0.95. Overall, there were 12 instances in which RiboSW detected a riboswitch that was not detected by DRD, and 64 instances in which the opposite was true. Complete results can be found in Supplementary Tables S15–S26.

Table 3.

Test results illustrating the relative sensitivity (TPR) of each tool

Family		Riboswitch finder		RiboSW		DRD
Name	Number of sequences	Number of hits	TPR	Number of hits	TPR	Number of hits	TPR
Cobalamin	50	–	–	44	0.88	46	0.92
FMN	50	–	–	48	0.96	49	0.98
glmS	18	–	–	16	0.89	17	0.94
Glycine	44	–	–	24	0.55	41	0.93
Lysine	47	–	–	45	0.96	45	0.96
preQ1	41	–	–	36	0.88	39	0.95
Purine	50	48	0.96	47	0.94	48	0.96
SAM-I	50	–	–	45	0.90	44	0.88
SAM-II	40	–	–	37	0.93	40	1.00
TPP	50	–	–	32	0.64	45	0.90
ykkC-yxkD	50	–	–	42	0.84	49	0.98
yybP-ykoY	17	–	–	13	0.76	17	1.00
Totals	507	–	–	429	0.85	480	0.95

Because of the input size constraint and the different way in which RiboSW searches a sequence, it was not possible to compute comparable specificity values for RiboSW. Such a comparison was omitted by Chang et al. (2009) as well.

In conducting this comparison, we found the response time of RiboSW to be mostly comparable with that of DRD on inputs with similar sizes (but searches for a single cobalamin riboswitch sometimes took up to a few minutes). RiboSW’s limited input size prevented comparisons on larger inputs.

5 CONCLUSIONS

We have designed a new Web-based tool for identifying putative riboswitches on a whole-genome scale. To efficiently identify high-quality strings of short conserved motifs, DRD transforms the problem into a heaviest path problem on a directed multipartite graph and solves the transformed problem with an efficient dynamic programming algorithm. We have shown that this technique is both fast and can achieve relatively high sensitivity and specificity.

There are several directions that could be pursued in the future to improve DRD. First, we could enhance our motif model to include site-specific characterizations of motifs, akin to a profile hidden Markov model, with a likely increase in computation time. Second, we could consider replacing our somewhat crude method for secondary structure in comparison with an alternative method, such as that used by Macke et al. (2001).

Funding: This work was performed by C.B., S.M.J. and J.D.S. while they were students at Denison University.

Conflict of Interest: none declared.