ASP-G: an ASP-based method for finding attractors in genetic regulatory networks

Abstract

Motivation: Boolean network models are suitable to simulate GRNs in the absence of detailed kinetic information. However, reducing the biological reality implies making assumptions on how genes interact (interaction rules) and how their state is updated during the simulation (update scheme). The exact choice of the assumptions largely determines the outcome of the simulations. In most cases, however, the biologically correct assumptions are unknown. An ideal simulation thus implies testing different rules and schemes to determine those that best capture an observed biological phenomenon. This is not trivial because most current methods to simulate Boolean network models of GRNs and to compute their attractors impose specific assumptions that cannot be easily altered, as they are built into the system.

Results: To allow for a more flexible simulation framework, we developed ASP-G. We show the correctness of ASP-G in simulating Boolean network models and obtaining attractors under different assumptions by successfully recapitulating the detection of attractors of previously published studies. We also provide an example of how performing simulation of network models under different settings help determine the assumptions under which a certain conclusion holds. The main added value of ASP-G is in its modularity and declarativity, making it more flexible and less error-prone than traditional approaches. The declarative nature of ASP-G comes at the expense of being slower than the more dedicated systems but still achieves a good efficiency with respect to computational time.

Availability and implementation: The source code of ASP-G is available at http://bioinformatics.intec.ugent.be/kmarchal/Supplementary_Information_Musthofa_2014/asp-g.zip.

Contact: Kathleen.Marchal@UGent.be or Martine.DeCock@UGent.be

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Gene Regulatory Networks (GRNs) consist of genes, proteins and other regulatory molecules that undergo complex and dynamic interactions, which drive gene expression, and ultimately, complex cellular behavior. To be able to understand and predict this behavior, various mathematical models have been developed that describe the dynamics of these GRNs. Different model formalisms have been used, as reviewed in De Jong (2002). One of the earliest models to describe GRNs are Boolean network models (Kauffman 1993). Boolean network models are attractive because of their simplicity (Shmulevich et al., 2002): by reducing the complexity of GRNs to qualitative logical models, Boolean network models are able to cope with the largely incomplete kinetic information of biological networks. Despite their highly simplified representation of biological reality, Boolean network models were shown to still grasp the important dynamic properties of GRNs, such as the networks’ attractors. An attractor represents a stable set of states toward which the transiently changing gene expression values converge to. Evolving toward an attractor thus corresponds to reaching a specific developmental stage (cell types, development stages of cells, etc.) or functional mode (De Jong and Page, 2008; Kauffman, 1993), and the analysis of attractors in a regulatory network thus hints toward the functional modes of the regulatory network (De Jong and Page, 2008).

Current knowledge regarding GRNs is generally incomplete (Rottger et al., 2012). Comparing simulated with observed attractors (states, e.g. developmental stages) of a certain network model can thus aid in evaluating existing network models and/or predict missing information in the current knowledge. For instance, Mendoza and Alvarez-Buylla (1998); Mendoza et al. (1999) and more recently, Espinosa-Soto et al. (2004) and Sanchez-Corrales et al. (2010) studied flower development in Arabidopsis thaliana using Boolean network models of which the network attractors corresponded to stable gene expression levels during the different stages of flower development. These models helped predicting mutant phenotypes and the existence of a yet uncharacterized gene involved in the transition from the non-flowering to the flowering state. Davidich and Bornholdt (2008) and Li et al. (2004) used a Boolean network model and its steady states to describe the different stages in yeast cell cycle, where the stages of the cycle correspond to the strong attractors of the network. Kaufman et al. (1985) explained the various states of the immune system with Boolean network models and Albert and Othmer (2003); González et al. (2008) and Sánchez and Thieffry (2001) used Boolean network models and their attractors to describe the cellular development of Drosophila melanogaster.

Key to simulating GRNs with Boolean network models is the choice of the proper assumptions. These assumptions refer to the activation rules and update scheme. Activation rules determine the way the activation state of each gene depends on the activation states of its interactors in the previous transition step. The update scheme determines how these activation states are updated, i.e. either synchronously or asynchronously. The exact choice of these assumptions largely determines the number and characteristics of the attractors. As in most cases, the true biological activation rules and update scheme are not known, one should be able to easily test different activation rules and schemes, as this allows to have an idea on the conditions under which the simulated network model would be able to capture an observed biological phenomenon (boundary conditions).

Several computational tools have been developed to perform the computation of attractors in Boolean network models. Garg et al. (2007) developed genYsis, which uses techniques involving binary decision diagrams (BDD) to compute attractors. Arellano et al. (2011) used techniques based on Temporal Logic model checking in Antelope. Ay et al. (2009) used state space pruning and randomized state space traversal methods to improve the scalability of the attractor computation. Dubrova and Teslenko (2011) used a Boolean Satisfiability (SAT) solver, typically used for combinatorial modeling and problem solving, to compute attractors of GRNs and obtained a better computational time and space efficiency compared with the BDD-based approach. More recently, Zheng et al. (2013) developed geneFatt based on the reduced-order BDD (ROBDD) data structure, which further improves the efficiency of the attractor computation.

Most of the aforementioned systems to simulate Boolean network models in principle can perform simulations with different assumptions. However, changing these assumptions would require tedious modifications on these systems. For instance, using the SAT approach (Dubrova and Teslenko, 2011), modifying the structure of the network and the updating rules would require updating the truth tables in the cnet format.

To allow for a more flexible simulation framework, we developed ASP-G, which makes use of the declarative programming paradigm Answer Set Programming (ASP; Lifschitz, 2008). The declarative nature of ASP allows one to specify and modify the domain-specific logic (here the definition of the network interactions, activation rules and update schemes) required to represent and solve the computational problem at hand (here dynamical modeling and attractor calculation) in an intuitive and modular way (Eiter et al., 2009). To illustrate the flexibility of our approach, we applied it to calculate attractors of previously published Boolean network models of GRNs of different sizes and complexity, and different simulation assumptions. By trying to mimic previous results under diverse settings, we can show that the main advantage of our approach consists of making the modeling more flexible and less error-prone, and therefore helps delineate the boundary conditions under which the biological conclusions based on simulations of Boolean network models are valid. At the same time, we also show that, with the use of fast and efficient ASP solvers, the computational efficiency of our method is in the same range as that of the most efficient dedicated methods for the simulation of Boolean network models and the calculation of their attractors.

2 METHODS AND MODELS

2.1 Boolean network modeling of GRNs

In our work, we adopt the definition of Boolean networks as described in Kauffman (1993): a Boolean network model consists of network elements (nodes, here representing structural and regulatory genes/proteins), which can either be active (ON) or inactive (OFF), and interactions between these elements (edges, which represent the directed regulatory interactions between the genes). We define two types of regulatory interactions between interacting nodes, i.e. activation (upregulation) and inhibition (downregulation). The activation state of a certain node at a certain time step is determined by a logical function of the activation states at the previous time step of its interactors (where the interactors of a node are defined as the incoming edges of a certain network node).

Formally, a Boolean network model G(V, F) is defined by a set of nodes $V=\{x_1,\dots ,x_n\}$ and a list of Boolean functions $F=(f_1,\dots ,f_n)$. Each $x_i\in \{0,1\},i=1,\dots ,n$ is a binary variable and its value at time t + 1 can be determined by the values of some other nodes $x_{j_1(i)},x_{j_2(i)},\dots ,x_{j_{k_i}(i)}$ at time t by means of a Boolean function $f_i\in F$. That is, there are k_i nodes assigned to x_i that determine its state. The activation state of every node x_i changes over time according to

$$x_i(t+1)=f_i\left(x_{j_1\left(i\right)}\left(t\right),x_{j_2\left(i\right)}\left(t\right),\dots ,x_{j_{k_i}\left(i\right)}\left(t\right)\right)$$

A state s of a Boolean network is an assignment of $\{0,1\}$ to each node x_i. Its successor state is the state resulting of applying f_i to each node x_i. The dynamics of the network consists of transitions between network states. An example of a Boolean network is given in Figure 1. This network has three nodes, denoted by x₁, x₂ and x₃, and interactions between these nodes, represented by the edges. The dynamics of the network can be described using a state-transition graph (STG) as given in the Supplementary Figure S1.

Fig. 1.

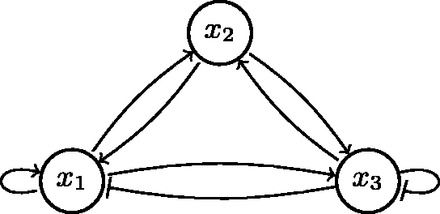
A Boolean network model with three genes. Edges with arrowed tips are activating interactions and edges with blunt tips are repressing (inhibiting) links

Attractors in a Boolean network model are defined as in Ay et al. (2009) and Garg et al. (2007).

Definition 1 —

Let S be a set of states of a Boolean network model. S is an attractor if and only if the following conditions are satisfied:

1. The set of the successor states of all the states in S is equal to S.

2. For each $s_i\in S$, once it is visited, the probability of revisiting s_i in a finite number of state transitions is equal to 1.

2.2 Representing Boolean network models of GRNs and computing their attractors using ASP

ASP-G framework

Our framework for modeling GRNs and computing attractors, called ASP-G, uses ASP. ASP is a declarative programming paradigm (Lifschitz, 2008), which is typically used to solve combinatorial search problems (Eiter et al., 2009). The architecture of ASP-G is shown in Figure 2. ASP-G consists of four main modules/parts of the system: the network description, the update scheme, the activation rules and the attractor computation algorithm. The following describes each of these modules:

Fig. 2.

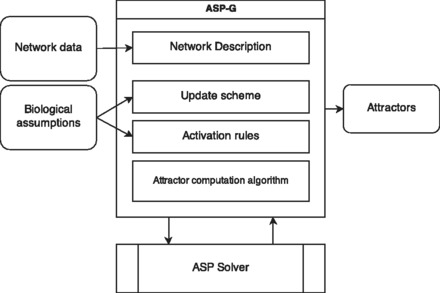
Architecture of ASP-G

Network description module

This module contains the description of the structure of the network, encoded in a set of facts provided by the user. Because of the declarative nature of ASP, such a description can be written succinctly in an intuitive format. For example, the following set of facts is used to describe the network depicted in Figure 1:

$$\begin{array}{l}gene(x_1).gene(x_2).gene(x_3).\\ activates(x_1,x_1).activates(x_1,x_2).activates(x_1,x_3).\\ activates(x_2,x_1).activates(x_2,x_3).inhibits(x_3,x_1).\\ activates(x_3,x_2).inhibits(x_3,x_3).\end{array}$$

To compare the declarative specification of the network with the more classically used SAT notation (Dubrova and Teslenko, 2011), we give the network specification corresponding to the Boolean network depicted in Figure 1 in cnet format, as follows:

.n 1 3 1 2 3	.n 2 2 1 3	.n 3 3 1 2 3
––1 0	1- 1	––1 0
1-0 1	-1 1	1-0 1
-10 1	00 0	-10 1
000 0		000 0

Each gene in the network is written with its label, e.g. .n 1 for node x₁, followed by the number of regulators and then their labels, e.g. (3 1 2 3). Next, a truth table follows that determines the behavior of the network (e.g. - -1 0 in the truth table for x₁ means that whenever x₃ is active then x₁ will be inhibited irrespective of the values of x₁ and x₂).

Activation rules

This module determines the activation rules used to update the activation state of each gene at each transition step, based on the intended assumption by the user. We implemented two frequently used activation rules:

1. A gene will be active in a subsequent time step t + 1 if at time step t at least one active interactor is an activator and no active interactors that act as inhibitors are present.

2. A gene will be active in a subsequent time step t + 1 if there are more active activators than active inhibitors among its interactors at time step t.

In ASP-G this first type of activation rule is encoded as follows:

$$r_1^{+}:active(X,T)\leftarrow A>0,I=0,\#act(X,A,T-1),$$

$$\#inh(X,I,T-1),gene(X),$$

$$T>0.$$

$$r_2^{+}:inhibited(X,T)\leftarrow \mathrm{not}active(X,T),gene(X),$$

$$T>0.$$

The second type of activation rule is encoded as follows:

$$r_1^{*}:active(X,T)\leftarrow A-I>0,\#act(X,A,T-1),$$

$$\#inh(X,I,T-1),gene(X),$$

$$T>0.$$

$$r_2^{*}:inhibited(X,T)\leftarrow I-A\ge 0,\#act(X,A,T-1),$$

$$\#inh(X,I,T-1),gene(X),$$

$$T>0.$$

To illustrate the flexibility of ASP to express nearly any possible activation rule, we implemented more specific type of rules in which the activation of a certain gene is expressed as a free-form gene-specific Boolean function of all the interactors of that gene, such as the one used in González et al. (2008) and Sanchez-Corrales et al. (2010). For example, the activation rule of a gene G1 might be expressed as a Boolean function of the form:

$$\mathtt{G1=G1}\mathtt{and}\mathtt{(not}\mathtt{G2\; or}\mathtt{not}\mathtt{G3)}$$

where G2 and G3 are two other genes involved in the network. In this case, G1 has a self-activating interaction, while G2 and G3 act as inhibitors for G1. To accommodate such an activation rule in ASP-G, we first convert the Boolean function into a disjunctive normal form. For example, the activation rule given above is rewritten into the following:

$$\mathtt{G1=G1}\mathtt{and}\mathtt{not}\mathtt{G2}$$

$$\mathtt{G1=G1}\mathtt{and}\mathtt{not}\mathtt{G3}$$

and then encoded in ASP as follows:

$$active(G1,T)\leftarrow T>0,active(G1,T-1),$$

$$inhibited(G2,T-1)$$

$$active(G1,T)\leftarrow T>0,active(G1,T-1),$$

$$inhibited(G3,T-1)$$

Update scheme

Two update schemes were adopted in ASP-G: synchronous and asynchronous updates. In the synchronous update scheme, we assume that all genes in the network are updated simultaneously per evaluated time step. This implies that the transitions between the network states are deterministic, i.e. for every state visited over time, only one possible successor state exists. In the asynchronous update, no assumptions of synchronicity are made, and genes may be updated at different time steps. Therefore, transitions are non-deterministic: there may be several possible next states after a certain transition. As illustrated in the Supplementary Figures S1 and S2, an asynchronous update scheme can result in a drastically different STG and can lead to different attractors.

Both the synchronous and the asynchronous updating were implemented in ASP-G. For the synchronous update scheme, we use the following rules to generate initial activation states of the genes:

$$active(X,0)\leftarrow gene(X),inhibited(X,0).$$

$$inhibited(X,0)\leftarrow gene(X),active(X,0).$$

We then use the following rules (in relation with the activation rules described previously) to determine the activation state of each gene at each time step t:

$$active(X,t)\leftarrow active(X,t-1),inhibited(X,t).$$

$$inhibited(X,t)\leftarrow inhibited(X,t-1),active(X,t).$$

For the asynchronous update scheme, we need to add the following rules, in addition to the previously described rules:

$$changed(X,T)\leftarrow active(X,T),inhibited(X,T-1),$$

$$gene(X),T>0.$$

$$changed(X,T)\leftarrow inhibited(X,T),active(X,T-1),$$

$$gene(X),T>0.$$

$$\leftarrow \#changed(N,X,T),N\ge 2,$$

$$gene(X),T>0.$$

To obtain a better performance in the asynchronous case, we apply the STG reduction technique, as explained in the Supplementary Figure S2.

Computing the attractors

The attractor computation in ASP-G is performed by Algorithm 1, which is based on the algorithm by Dubrova and Teslenko (2011). The main idea used in Algorithm 1 is to identify attractors by looking at identical states in transition paths of certain lengths in the STG of the network. Because there are exponentially many possible states in an STG (in relation to the number of nodes in the network), explicit enumeration of all the states in an STG is unfeasible for larger networks. ASP-G avoids this explicit enumeration by implicitly simulating the dynamics of the network. Furthermore, once a state is identified as part of an attractor, it can be removed from the STG to prune the search space. An illustration on how the algorithm works is given in Supplementary Figure S4. Path generation and state removal are being done using ASP rules and ASP constraints, respectively, as shown in Supplementary Figure S5. To further increase the efficiency of the computation, we use the incremental ASP approach described in Gebser et al. (2008) and the clasp solver from the Potassco ASP suite (Gebser et al., 2011b).

Algorithm 1 Algorithm to compute attractors in ASP-G.

1: {P is the ASP program with the rules of the network}

2: k = n

3: attractor_is_found = False

4: $attractors=\pi$

5: while ASP finds a path of length k as an answer set in P do

6:  {$s=\langle s_1,s_2,\dots ,s_k\rangle$ is the path found}

7:  for $j=k-1$ to 1 do

8:  if s_j = s_k then

9:   $attractors=attractors{\displaystyle \cup \{\langle }{s}_{j+1},\dots ,s_k\rangle \}$

10:   attractor_is_found = True

11:   {The attractors already found are forbidden in P}

12:   for s in $\{s_k,\mathrm{...},s_{j+1}\}$ do

13:   {The states are added as constraints for the next path}

14:   $P=P{\displaystyle \cup \{\leftarrow active(}{X}_1,T),inhibited(X_2,T),\dots |X_i\in s\}$

15:   end for

16:   break

17:  end if

18:  end for

19:  if attractor_is_found then

20:  attractor_is_found = False

21:  else

22:  $k=2·k$

23:  end if

24: end while

25: return attractors

3 RESULTS

3.1 ASP-G: a novel framework for the simulation and attractor computation of GRNs with Boolean network models

Simulating Boolean network models implies that activation rules have to be defined to decide how a gene is activated by its interactors. The exact choice of the assumptions largely determines the outcome and the number and characteristics of the attractors. Supplementary Figures S1–S3 show that, for example, Boolean network in Figure 1, the choices of activation rules and update scheme can result in a different network behavior and thus different sets of attractors. As it is often not known in advance which assumptions best match the biological reality of the modeled GRN, testing different assumptions is advisable.

To have a generic framework that allows testing different assumptions, ASP-G implements three different activation rules: the first one adopted by Ay et al. (2009); Davidich and Bornholdt (2008) and Li et al. (2004)in which a gene is considered to be activated if the majority of its active incoming interactors (interactors that are themselves active) have an activating role. Otherwise, the gene will become inactive. This is referred to as the $r^{*}$ rule in ASP-G. A second one adopted by Garg et al. (2007) and Pedicini et al. (2010) assumes that a gene is activated only when there is at least one active activator among its active incoming interactors and no inhibitor. This is referred to as the r⁺ rule in ASP-G. In addition, we implemented a third more detailed activation rule in which the activation for each gene is expressed as a free-form Boolean function of its activators and inhibitors. These types of rules better grasp the complexity of true biological interactions and include more detailed information on the specifics of the interactions. It was used, for instance, in Albert and Othmer (2003); González et al. (2008) and Sanchez-Corrales et al. (2010).

Related to the update scheme, a choice has to be made between updating the network elements simultaneously (synchronously) versus at different points (asynchronously). Earlier work by Kauffman (1993) and Thomas (1973) assumed synchronicity in their modeling, mainly because of computational efficiency reasons. However, the assumption of synchronicity was challenged in Harvey and Bossomaier (1997) and Thomas (1991), who argued that, for many biological systems, assuming an asynchronous update scheme is more realistic. Subsequent work on Boolean network models (Ay et al., 2009; Garg et al., 2007, 2008; González et al., 2008 and Naldi et al., 2007) mainly applied asynchronous update schemes. Therefore, in ASP-G we implemented both the synchronous and the asynchronous update scheme.

3.2 Simulation results

To test the correctness of ASP-G in simulating Boolean network models and computing attractors, we applied ASP-G on previously published Boolean network models of GRNs and compared the obtained attractors with the originally published ones. Like any other formalism to find attractors in Boolean network models, ASP-G detects exhaustively all attractors of the network. Therefore, a correct result corresponds to an exact match in the attractor set identified by ASP-G and that present in the reference publications.

First, we tested ASP-G on the relatively small GRNs involved in budding and fission yeast cell cycle analyzed in Ay et al. (2009); Davidich and Bornholdt (2008) and Li et al. (2004), as well as on the network model of the GRN from the T-helper (Th) cell differentiation described in Garg et al. (2007). We used the activation rules and update schemes that were also applied in the original studies, except for the dataset of Garg et al. (2007), in which we applied also the synchronous update scheme in addition to the originally applied asynchronous one (Table 1).

Table 1.

ASP-G results and running times for common GRNs found in the literature

Network	Reference	Genes	Attractors	Update mechanism	Activation rules	Time
Yeast cell cycle	Li et al. (2004)	11	7	Synchronous	r*	1.507
	Ay et al. (2009)	11	7	Asynchronous	r*	0.134
Fission Yeast	Davidich and Bornholdt (2008)	10	13	Synchronous	r*	1.653
	Ay et al. (2009)	10	15	Asynchronous	r*	0.371
Th cell differentiation	–	23	3	Synchronous	r+	0.270
	Garg et al. (2007)	23	3	Asynchronous	r+	0.206

Note. Network: describes the original network model. Genes: number of genes present in the network; Attractors: number of detected attractors; Update mechanism: synchrounous versus asynchrounous updating was used as described in the methods section; Activation rules: r* activation rules indicates that a gene becomes active when it has more active activating interactors than active inhibiting ones, whereas the r⁺ activation rules indicate that a gene becomes active if it has at least one active activating gene and no inhibiting ones. Time: running time on a Dell Latitude D820 notebook.

As expected for each of these results, the attractors found by ASP-G match exactly the ones found by the reference papers (data not shown). The table also shows that ASP-G performs relatively fast for these small networks. We also observe that the attractors in the synchronous case often coincide with those in the asynchronous case. This is because of the fact that simple attractors (i.e. attractors that have only one state) are more commonly found, and that they are shared between synchronous and asynchronous update schemes. Only for the fission yeast cell network under the r* activation rules there is a difference in the number of synchronous attractors (13) and asynchronous attractors (15). The fact that there are more attractors in the asynchronous case might seem counter-intuitive, as the reduced STG used to calculate these attractors contains at most as many nodes as the synchronous STG, and often less. However, the original STG for the asynchronous case typically contains more edges than in the synchronous case, and these additional edges can account for more attractors.

To show the flexibility of ASP-G in expressing different types of activation rules, we also encoded the Boolean network model of the GRN involved in A.thaliana flower development originally described in Sanchez-Corrales et al. (2010), with our ASP-G framework. This network model consists of 13 genes and uses gene-specific update rules as described in Section 2.2 Activation rules. As in the original publication, we applied a synchronous update scheme. ASP-G correctly recapitulated all 10 attractors of the network as described in the original paper Sanchez-Corrales et al. (2010). The computation took only 0.479 s.

To test ASP-G on a larger network, we use the network data from the Th cell differentiation described by Pedicini et al. (2010). The purpose of the study was to find evidence supporting (or contradicting) the traditional view that the genes involved in the regulation of the two types of Th cells, Th1 and Th2, have counter-regulatory interaction. Similar to what has been done in Pedicini et al. (2010), we first computed the attractors of the original network in the presence of all genes and then searched for attractors in different single-gene knockout networks in silico to test the effect of knocking out intracellular genes toward the attractors of the network. To show the added value of using different simulation assumptions, we also performed the computations using an asynchronous update mechanism, as opposed to only synchronous update scheme, as performed by Pedicini et al. (2010). The results are presented in the Supplementary Table S6.

In terms of computational efficiency, the result shows that ASP-G is able to perform relatively well for the moderately sized Th cell network. For the asynchronous case, attractor computation required 0.6 s on average. For the synchronous case where more attractors were found, the computation times took 71.9 s on average. When applying the synchronous update scheme as used in Pedicini et al. (2010), ASP-G reproduced the four attractors: Th0, Th1, Th2 and ThX, as in the original paper. However, when trying to reproduce the attractors in the gene knockout setting, we found discrepancies with the results reported by Pedicini et al. (2010). These discrepancies were caused by mistakes in the SAT-based truth table used in the original publication. Supplementary Table S6 shows the corrected results for completeness. Note that these mistakes do not affect the biological conclusions made in the original publication. However, it illustrates that specifying larger networks with rather complicated behavior becomes cumbersome and error-prone in paradigms like SAT, whereas this is much less the case for a declarative approach such as ASP-G.

The existence of the ThX attractor and the observed pattern of gene activities in the attractors of the knockout networks caused the authors of Pedicini et al. (2010) to conclude that the active genes in Th1 and Th2 cells do not play counter-regulatory roles with each other, contrary to what is traditionally believed. However, when using the asynchronous update scheme, we noted that the attractor ThX is no longer obtained. A similar pattern occurs for the knockout networks, where the use of the asynchronous update scheme drastically changes the set of detected attractors compared with those detected using a synchronous update scheme: the number of attractors found with the asynchronous update scheme for the knockout networks ranges only between 2 and 5, whereas the number of attractors found in the synchronous case ranged between 286 and 1154. This finding suggests that the occurrence of the ThX attractor and the existence of a large number of attractors in the knockout networks as found in Pedicini et al. (2010) are only valid under the synchronous update scheme. It thus defines the boundary conditions under which the conclusions of Pedicini et al. (2010) are valid and highlights the relevance of performing modeling under different scenarios, as offered by ASP-G, to put biological conclusions in perspective.

4 CONCLUSION

In this article, we presented ASP-G, a modular system to simulate Boolean network models of GRNs and to subsequently compute their attractors. ASP-G is based on the declarative ASP programming paradigm, which has already been previously applied in the context of biological network data analysis and modeling (see, e.g. Corblin et al., 2012; Dworschak et al., 2008; Gebser et al., 2008, 2010a and b, 2011). Recently, Inoue (2011) showed in a theoretical comparison between Boolean networks and the underlying semantics of ASP, that a strong mathematical relation exists between the attractors/steady states of Boolean networks and the notion of stable models commonly used in ASP. We built on this earlier result in our proposed method, ASP-G.

The main added value of ASP-G is in its declarativity and modularity: it allows users to easily test different update schemes and activation rules when simulating the dynamics of their Boolean network model by selecting and modifying the appropriate modules. In addition, the fact that ASP-G is based on a declarative language makes it less error-prone than other approaches such as SAT, which depend on the definition of difficult to interpret and tedious to construct truth tables. Using an underlying declarative programming paradigm also makes ASP-G easily extendable to other parameter settings. Decoupling the problem definition from its solution thus allows for a greater flexibility compared with other ad hoc systems such as genYsis (Garg et al., 2007) and geneFAtt (Zheng et al., 2013), where assumptions such as update scheme and activation rules are already built into the system.

We showed the correctness of ASP-G in simulating Boolean network models and obtaining attractors under different assumptions by successfully recapitulating the detection of attractors of previously published studies. Relying on a modular and flexible declarative programming paradigm definitely comes at the expense of being slower than the more dedicated systems to compute attractors, such as genYsis (Garg et al., 2007) and geneFAtt (Zheng et al., 2013). However, in terms of computational efficiency, ASP-G proved to be fast (for small networks, i.e. up to 23 genes, computations are below a second, for larger networks, i.e. up to 51 genes, the longest computation time took <4.5 min). Also, ongoing research in ASP solvers (Gebser et al., 2011a) will make it possible for ASP to reach a point where it outperforms other logic paradigms. This is definitely the case when comparing ASP with Binary (or multiple) decision diagrams (Lee, 1959) used to calculate attractors in Boolean Networks models for GRNs (Arellano et al., 2011; Naldi et al., 2007) as they suffer from memory explosion when the size of the network starts to become large (Clarke et al., 2001).

For larger-sized networks, any exhaustive method will face a challenge, as the state space of the network increases exponentially with respect to the number of nodes in the network. When dealing with such larger networks, methods that avoid an exhaustive search as in Ay et al. (2009) might become more suitable under these conditions. Conclusively, ASP-G is tailored to simulate Boolean network models of GRNs and to compute attractors in a diagnostic mode, where one wants to test different update schemes and activation rules to find the setting that best matches experimental data or to correctly delineate the boundary conditions under which the biological conclusions based on these simulations are valid.

Funding: This work was supported by the Ghent University Multidisciplinary Research Partnership ‘Bioinformatics: from nucleotides to networks’ and the Interuniversity Attraction Poles Programme [IUAP P6/25], initiated by the Belgian State, Science Policy Office (BioMaGNet) and by the IWT: SBO-NEMOA; FWO: G.0428.13N fund.

Conflict of Interest: none declared.