Monte Carlo algorithms for Brownian phylogenetic models

Abstract

Motivation: Brownian models have been introduced in phylogenetics for describing variation in substitution rates through time, with applications to molecular dating or to the comparative analysis of variation in substitution patterns among lineages. Thus far, however, the Monte Carlo implementations of these models have relied on crude approximations, in which the Brownian process is sampled only at the internal nodes of the phylogeny or at the midpoints along each branch, and the unknown trajectory between these sampled points is summarized by simple branchwise average substitution rates.

Results: A more accurate Monte Carlo approach is introduced, explicitly sampling a fine-grained discretization of the trajectory of the (potentially multivariate) Brownian process along the phylogeny. Generic Monte Carlo resampling algorithms are proposed for updating the Brownian paths along and across branches. Specific computational strategies are developed for efficient integration of the finite-time substitution probabilities across branches induced by the Brownian trajectory. The mixing properties and the computational complexity of the resulting Markov chain Monte Carlo sampler scale reasonably with the discretization level, allowing practical applications with up to a few hundred discretization points along the entire depth of the tree. The method can be generalized to other Markovian stochastic processes, making it possible to implement a wide range of time-dependent substitution models with well-controlled computational precision.

Availability: The program is freely available at www.phylobayes.org

Contact: nicolas.lartillot@univ-lyon1.fr

1 INTRODUCTION

Brownian models have a long history in macroevolutionary studies. The first likelihood approaches to phylogenetic reconstruction based on allele frequencies (Edwards and Cavalli-Sforza, 1967), or for formalizing the comparative method (Felsenstein, 1985; Martins and Hansen, 1997), all assume that the variables of interest undergo continuous-time changes along the lineages of the phylogeny according to a Brownian motion. Later on, Brownian models have been recruited for relaxing the molecular clock (Thorne et al., 1998). Beyond variation in absolute rate, different types of substitutions, synonymous or non-synonymous, from or to G or C, occur at different relative rates in different regions of the phylogeny. Following the work of Thorne et al. (1998), it seems natural to formalize this heterogeneity in substitution patterns among lineages in terms of a two-level model, in which some of the parameters of the substitution model are themselves evolving through time according to a Brownian process (Seo et al., 2004). These generalized Brownian substitution models can then be naturally integrated with the classical comparative method, by considering the correlated variation of the substitution parameters and the directly observable quantitative traits as one single multivariate Brownian process running over the phylogeny (Lartillot and Poujol, 2011).

Beyond Brownian models, a larger family of stochastic processes, not even necessarily Gaussian, have more recently been explored in the context of the comparative method, as good candidates for describing the evolution of traits undergoing directional, stabilizing or punctuated evolution (Harmon et al., 2010; Landis et al., 2013; Monroe and Bokma, 2010; Slater et al., 2012). Such non-Brownian continuous-time stochastic processes could ultimately be recruited to model variation in substitution patterns and, more generally, to describe the joint evolution of genetic sequences and quantitative traits in the context of an integrative modeling framework for macroevolutionary studies (Lartillot and Delsuc, 2012).

However, in contrast to their nice analytical properties in a comparative context, the application of Brownian processes for modeling sequence evolution raises important computational issues. In the context of the classical comparative method, exact likelihood calculation under Brownian models is straightforward. The detailed Brownian path taken by the process along each branch is irrelevant for the calculation of the likelihood, and conditioning on observed values of the quantitative traits at the leaves only involves the net jump probability densities over entire branches, thus implicitly and analytically integrating over all possible paths.

In contrast, for Brownian relaxed clocks, likelihood calculation involves the total substitution rate along each branch. This total rate is the integral of the instant rate at all times along the branch and therefore depends on the exact trajectory of the process. Mathematically, the total rate is a random variable, whose probability distribution conditional on the values of the process at both ends of the branch is typically unavailable in closed form (Lepage et al., 2007). The situation is even more complicated in the case of generalized Brownian substitution models in which other aspects of the substitution process (such as the equilibrium GC content) undergo continuous-time variation. In that case, the rate matrix itself is time-dependent, and the finite-time substitution probabilities over the branch are given by the exponential of the integral of the matrix over the trajectory of the Brownian process, which is again a (now matrix-valued) random variable whose distribution is not directly computable.

Exact likelihood calculation under Brownian substitution models therefore appears to be computationally intractable. As a result, implementations of these models have thus far relied on rather crude approximations. Typically, the Brownian process is explicitly sampled only at the internal nodes of the phylogeny, corresponding to cladogenetic events (Lepage et al., 2007; Thorne et al., 1998) or at the midpoints along the branches (Rannala and Yang, 2007). The total rate along each branch is then approximated by the average of the instant rates at both ends or by the midpoint value. Similar approximations have been used for more general substitution models (Lartillot and Poujol, 2011; Seo et al., 2004).

Such approximate strategies appear to yield qualitatively reasonable results when tested on simulations (Lartillot and Poujol, 2011). However, the quality of the approximation could deteriorate for particular rate variation patterns across phylogenies or for particular configurations of time-dependent substitution parameters. More fundamentally, these approximations ignore the fact that the integrated substitution probabilities across branches are themselves random, even conditional on the values of the Brownian process at the nodes. In practice, the additional dispersion induced by this specific level of randomness will be buffered by other aspects of the model, in particular by the Brownian process itself, thus potentially resulting in artifactually increased variance in trait or rate evolution. This phenomenon could have important consequences in a comparative context, where the covariance between substitution rates and quantitative traits is of direct interest. All these arguments suggest that current approximation schemes fundamentally lack robustness. In a long-term perspective, as ever more complex time-dependent substitution models are being contemplated, the reliability of the approach will become increasingly questionable, potentially compromising the idea of a principled model-based approach to the molecular comparative method.

The approximation resulting from sampling the trajectories of the Brownian process at a finite number of time points could easily be controlled by explicitly sampling the process over a sufficiently fine-grained discretization grid along each branch. Doing so, however, raises several computational problems. First, it results in a high-dimensional space of possible model configurations, many of which have a similar fit to the data. Efficient Monte Carlo sampling methods therefore need to be developed to mix over this large set of possible model configurations. Obviously, simple Metropolis–Hastings schemes updating one instantaneous value at a time will not scale properly in this context, and therefore, direct resampling of entire paths, either along or across branches, is necessary. Second, in the context of complex Brownian substitution models, for a given branch and a given trajectory of the Brownian process, efficient methods are needed to approximate the substitution probabilities over the branch implied by this trajectory.

In this article, an integrated solution to these computational challenges is introduced, in the form of a Markov chain Monte Carlo (MCMC) framework for calculating the likelihood and sampling from the posterior distribution over Brownian substitution models. The approach combines a discretization scheme along the lines just suggested with path-resampling and data-augmentation MCMC algorithms, so as to achieve approximate sampling from the posterior distribution in a time that scales reasonably well with the level of discretization.

2 MATERIALS AND METHODS

2.1 Models and priors

The models considered here have been introduced earlier (Lartillot and Poujol, 2011; Lartillot, 2013a). The first model is time-homogenous. It assumes a general time-reversible nucleotide substitution process, homogeneous across sites and along the phylogeny (measured in time, relative to the age of the root), except for the overall substitution rate r(t), which is time-dependent, log-normal Brownian and correlated with a vector of L quantitative traits, denoted C_l, $l=\mathrm{1..}L$. Thus, the Brownian process X(t) has dimension $M=L+1$:

$$\begin{array}{c}{X}_1(t)=\ln r(t)\\ l=\mathrm{1..}L,X_{l+1}(t)=\ln C_l(t)\end{array}$$

The second model is time-heterogeneous. It assumes correlated variation of the substitution rate and the equilibrium GC content with quantitative traits. Specifically, the nucleotide substitution process is parameterized as follows (see also Lartillot, 2013a):

$$Q(\gamma )=\left(\begin{array}{cccc}-& {\rho }_{AC}\frac{\gamma }{2}& {\rho }_{AG}\frac{\gamma }{2}& {\rho }_{AT}\frac{1-\gamma }{2}\\ {\rho }_{AC}\frac{1-\gamma }{2}& -& {\rho }_{CG}\frac{\gamma }{2}& {\rho }_{CT}\frac{1-\gamma }{2}\\ {\rho }_{AG}\frac{1-\gamma }{2}& {\rho }_{CG}\frac{\gamma }{2}& -& {\rho }_{GT}\frac{1-\gamma }{2}\\ {\rho }_{AT}\frac{1-\gamma }{2}& {\rho }_{CT}\frac{\gamma }{2}& {\rho }_{GT}\frac{\gamma }{2}& -\end{array}\right)$$ (1)

where γ is the equilibrium GC frequency, and ρ_XY is the relative exchangeability between nucleotides X and Y. Then, variation in r, γ and C is modeled as a Brownian process of dimension $M=L+2$:

$$\begin{array}{c}{X}_1(t)=\ln r(t)\\ X_2(t)=\ln \frac{\gamma (t)}{1-\gamma (t)}\\ l=\mathrm{1..}L,X_{l+2}(t)=\ln C_l(t)\end{array}$$

For the two models, the Brownian process X(t) is parameterized by an M × M covariance matrix Σ, endowed with an inverse Wishart prior of parameter ${\Sigma }_0=Diag({\eta }_1,\dots ,{\eta }_M)$, and with M degrees of freedom, where η_m, $m=\mathrm{1..}M$ are themselves from a truncated Jeffrey’s prior, on $[{10}^{-3},{10}^3]$. The prior distribution of X at the root is truncated uniform, on $[-100,100]$. The phylogeny is fixed, and a uniform prior is used for divergence times. All other aspects of the model, including the priors, are as in Lartillot (2013a).

2.2 Discretization scheme

As illustrated in Figure 1, a global discretization grid is defined by a series of P + 1 regularly spaced absolute sampling times between the root and the tips of the phylogeny, defining P time intervals of length $\delta t=1/P$ (times are relative to the age of the root). The Brownian process is sampled at all points where the tree and the grid intersect, as well as at the bifurcating nodes. In the following, superscripts will index branches, while subscripts will index successive discretization points along each branch. Note that the branchwise approximation classically used (Lartillot and Poujol, 2011; Lepage et al., 2007; Thorne et al., 1998) corresponds to P = 1.

Fig. 1.

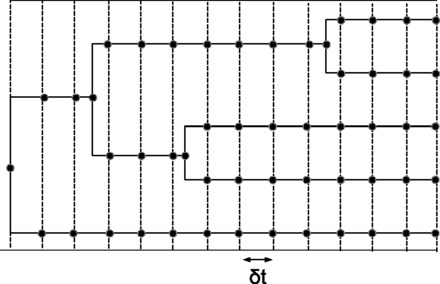
Discretization strategy. The Brownian process is explicitly sampled at all time points represented by black dots. Substitution rates and matrices are then approximated within each small time interval by the average of the values at both ends. See text for details

For a given branch j, let $n^j+1$ denote the total number of discretization points along the branch, ${(t_i^j)}_{i=\mathrm{0..}{n}^j}$ the corresponding sampling times and $X^j(t_i^j)$ the value of the Brownian path at time $t_i^j$. Note that, for each $i=\mathrm{0..}{n}^j,X^j(t_i^j)$ is a vector of dimension M, whose entries are denoted $X_k^j(t_i^j)$, for $k=\mathrm{1..}M$. The joint probability of the Brownian path is given by the following chain rule:

$$X^j(t_{i+1}^j)\sim N\left(X^j(t_i^j),(t_{i+1}^j-t_1^j)\Sigma \right)$$

2.3 Likelihood computation

The main idea proposed here is to approximate the continuous trajectories of the instant substitution rate, r(t), and equilibrium GC, $\gamma (t)$, such as defined by the Brownian process, by trajectories that are piecewise constant within each time interval defined by the discretization. The values of r(t) and $\gamma (t)$ within each interval are taken as the average of the values at both ends of the interval. Once this is done, integrating the substitution rates over the branch can proceed as usual. The overall error induced by this approximation is proportional to the resolution δt, and can therefore be made arbitrarily small by using sufficiently fine-grained discretizations.

In the case of the time-homogeneous model, for branch j, the total rate (which is the substitutional length of the branch) is approximated by

$$l^j={\displaystyle \sum _{i=1}^{n^j}}(t_i^j-t_{i-1}^j)\frac{e^{X^j(t_i^j)}+e^{X^j(t_{i-1}^j)}}{2}.$$

and the matrix giving the substitution probabilities over branch j is simply

$$R^j=e^{l^{j}Q}$$ (2)

In the case of the time-heterogeneous substitution model, the rate matrix also depends on time, through the second entry of the Brownian process, describing the logit of the instant equilibrium GC. Specifically, for each time point $i=\mathrm{0..}{n}^j$, the instant equilibrium GC at $t_i^j$ is given by

$${\gamma }^j(t_i^j)=\frac{e^{X_2^j(t_i^j)}}{1+e^{X_2^j(t_i^j)}}$$

The equilibrium GC over the ith time interval is then assumed to be constant and equal to the average of the instantaneous values at both ends:

$${\overline{\gamma }}_i^j=\frac{{\gamma }^j(t_{i-1}^j)+{\gamma }^j(t_i^j)}{2}$$

A rate matrix $Q_i^j=Q({\overline{\gamma }}_i^j)$ is then calculated by setting $\gamma ={\overline{\gamma }}_i^j$ in Equation 1. Finally, the matrix giving the substitution probabilities over the entire branch is given by

$$R^j={\displaystyle \prod _{i=1}^{n^j}}{e}^{(t_i^j-t_{i-1}^j)Q_i^j}.$$ (3)

Equation 3 requires efficient computation of matrix exponentials of the form $e^{\delta tQ}$ for small δt and for arbitrary Q. This exponentiation can be done by repeated squaring, i.e. by relying on the fact that

$$e^{\delta tQ}={\left(e^{\frac{\delta t}{2^s}Q}\right)}^{2^s}\simeq {\left(I+\frac{\delta t}{2^s}Q\right)}^{2^s}$$

This approximation requires a total of s matrix products. The accuracy is controlled by choosing s dynamically, such that ${\max }_k\frac{\delta t}{2^s}|Q_{kk}|$ is less than some predefined threshold. Here, a threshold of 0.01 is used. In practice, for moderately fine-grained discretization schemes ($\delta t=0.01$), s is most often equal to 1, and therefore, the overall calculation of R^j requires a total of $\overline{s}{n}^j\simeq n^j$ matrix products.

2.4 Markov chain Monte Carlo

The fine-grained discretization scheme introduced here results in a high dimensional model configuration, with strong correlations between the values of the Brownian process at neighboring time points. Simple MCMC procedures updating one instantaneous value of X at a time will be extremely inefficient in this context, and alternative algorithms should therefore be developed. An efficient approach to this problem is to rely on a combination of several general strategies for updating the Brownian paths, possibly in combination with other components of the model (in particular, the divergence times and the covariance matrix).

The first strategy is to add a Brownian bridge to the current Brownian path along a branch. Brownian bridges are Brownian paths conditioned on starting and ending at 0. Adding a bridge to a path therefore results in an update of the entire path that leaves the two end points unchanged (Fig. 2A). The amplitude of the Brownian bridge can be set to any desired level, thus leading to flexible tuning of the proposal.

Fig. 2.

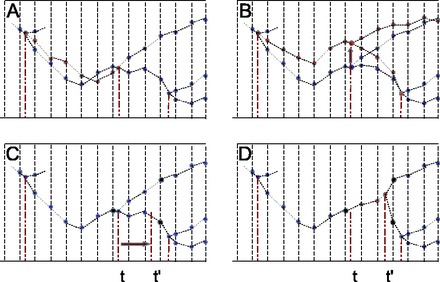
(A) MCMC proposals. Current and proposed configurations represented in red and blue, respectively. A. OnePathMove adds a Brownian bridge to the path along the focal branch. (B) ThreePathMove shifts the instantaneous value at an internal node (vertical arrow) and propagates the shift linearly across the three surrounding branches. (C and D) TimePathMove shifts the time of a node by a random amount and resamples the paths within the smallest window bracketing the move (here defined by the three black filled circles). See text for details

The second strategy aims at simultaneously resampling the three Brownian paths surrounding an interior node of the tree. Here, this is done by applying a simple uniform sliding move proposal to the value of X at the focal node and propagating this change linearly over the three surrounding paths, such that their other end points remain constant (Fig. 2B).

The third strategy proposes a local resampling of the current Brownian path on a small time-interval, conditional on the values of the path at the endpoints. This strategy is useful in a context where the local time configuration itself is being updated (Fig. 2C and D).

An important basic tool for devising all these path resampling proposals is to sample Brownian paths conditional on the end points. Consider for instance a Brownian path ${(X(t))}_{t=\mathrm{0..}T}$ of generator Σ. We wish to sample a discretized realization of X(t) along an arbitrary sequence of time points between 0 and T: $0=t_0<t_1<\dots <t_n=T$, and such that $X(0)=a$ and X(T) = b. This can be done by iteratively sampling $x_{i+1}|x_i,x_n$, for $i=\mathrm{1..}n-1$. At each step, one can use the conjugate normal relation:

$$\begin{array}{c}{x}_{i+1}|x_i\sim N(x_i,(t_{i+1}-t_i)\Sigma )\\ x_n|x_{i+1}\sim N(x_{i+1},(t_n-t_{i+1})\Sigma )\end{array}$$

so that

$$x_{i+1}|x_i,x_n\sim N\left({\overline{x}}_i,{\overline{t}}_i\Sigma \right)$$

where

$${\overline{x}}_i=\frac{(t_{i+1}-t_i)x_n+(t_n-t_{i+1})x_i}{t_n-t_i}$$

and

$${\overline{t}}_i=\frac{(t_{i+1}-t_i)(t_n-t_{i+1})}{t_n-t_i}.$$

This sampling algorithm can be generalized to bifurcating Brownian paths. Consider three paths, ${(X^u(t))}_{t=\mathrm{0..}{T}^u}$, ${(X^l(t))}_{t=\mathrm{0..}{T}^l}$ and ${(X^r(t))}_{t=\mathrm{0..}{T}^r}$ (indexed by u for up, l for left and r for right), all of generator Σ and connected at the bifurcation point $Z=X^u(T^u)=X^l(0)=X^r(0)$. We wish to sample from this bifurcating configuration, conditional on the end points $X^u(0)=a,X^l(T^l)=b$ and $X^r(T^r)=c$. This can be done by first sampling

$$Z|X^u(0)=a,X^l(T^l)=b,X^r(T^r)=c$$

and then sampling each path independently, conditional on its end points. To sample $Z|a,b,c$, the argument is the same as above, although now with three factors in the conjugate normal relation.

$$\begin{array}{c}z|a\sim N(a,T^u\Sigma )\\ b|z\sim N(z,T^l\Sigma )\\ c|z\sim N(z,T^r\Sigma )\end{array}$$

so that

$$z|a,b,c\sim N\left(\overline{z},\overline{T}\Sigma \right)$$

where

$$\overline{z}=\frac{{(T^u)}^{-1}a+{(T^l)}^{-1}b+{(T^r)}^{-1}c}{{(T^u)}^{-1}+{(T^l)}^{-1}+{(T^r)}^{-1}}$$

and

$${\overline{T}}^{-1}={(T^u)}^{-1}+{(T^l)}^{-1}+{(T^r)}^{-1}.$$

With these basic building blocks, the following series of update mechanisms can be proposed:

• OnePathMove (Fig. 2A). Choose a branch at random. Along this branch, sample a Brownian bridge of covariance matrix $\delta \Sigma$, where δ is a tuning parameter. Add this Brownian bridge to the current Brownian path along the branch, recompute the likelihood and apply the Metropolis–Hastings decision rule. By symmetry of the undirected Brownian motion, the Hastings ratio of this proposal is 1. Letting the tuning parameter δ go to 0 results in arbitrarily small moves.

• ThreePathMove (Fig. 2B). Take an interior node at random; propose a small random change to the value of the process z at this node: $z\prime =z+\delta m$, where $m\sim N(0,\Sigma )$ and δ is a tuning parameter. Propagate the change linearly over the three surrounding branches; recompute the likelihood and apply the Metropolis–Hastings decision rule. Hastings ratio is 1.

• TimePathMove (Fig. 2C). Updating divergence times: take an interior node at random, shift the divergence time by a random amount drawn uniformly in $[-\delta /2,\delta /2]$, where δ is a tuning parameter. Reflect divergence time within allowed interval if necessary. Define the smallest on-grid window around the focal node encompassing both the current and the proposed dates for the focal node. Within this window, resample the Brownian path over the three branches, conditional on the three end points. For this move, the Hastings ratio exactly compensates for the probability of the Brownian path in the window, and therefore, the Metropolis–Hastings ratio is simply equal to the ratio of the likelihoods of the final and the initial configurations.

The three update proposals just mentioned are conditional on the current covariance matrix Σ. This covariance matrix can in turn be resampled conditional on the current configuration of Brownian paths across branches. This can be done using conjugate Gibbs sampling (as in Lartillot and Poujol, 2011). However, this simple alternation between updates of X conditional on Σ and updates of Σ conditional on X turn out to be inefficient for large P (small δt, see Section 4). Thus, an additional joint update of the matrix and the Brownian paths was devised, simply consisting of applying the same linear transformation to all paths and to the covariance matrix:

• LinearBrownianSigmaMove. Construct a random M × M matrix by drawing each entry i.i.d. from a standard normal distribution: $M_{ij}\sim N(0,1)$. Set $G=e^{\delta M}$, where δ is a tuning parameter. Note that exponential matrices are always invertible and that a value of δ close to 0 will result in a matrix G close to the identity matrix. Apply the transformation $X\prime =GX$ uniformly across all instantaneous values of the Brownian process across the phylogeny (including the root). Simultaneously, set $\Sigma \prime =G\Sigma G^t$, where G^t is the matrix transpose of G. Recompute the probability of the entire model and apply the Metropolis–Hastings rule. The Hastings ratio of this move is equal to $|G{|}^{N+2}$, where $|G|$ is the determinant of G and N is the number of instantaneous values of the Brownian process instantiated over the entire tree.

Note that most of the Hastings ratio in fact cancels out with the ratio of the probability of the new and the old configuration of the Brownian process. For a generic instantaneous value X (except the root):

$$\frac{p(X\prime |\Sigma \prime )}{p(X|\Sigma )}=\frac{|\Sigma \prime {|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}{\mathrm{X\text{'}}}^t\Sigma {\prime }^{-1}X\prime }}{|\Sigma {|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}{X}^t{\Sigma }^{-1}X}}=\frac{|\Sigma \prime {|}^{-\frac{1}{2}}}{|\Sigma {|}^{-\frac{1}{2}}}=|G{|}^{-1}.$$

There are N − 1 such values, which will therefore compensate for all but three occurrences of $|G|$ in the Hastings ratio. This point is important, allowing the Hastings ratio to remain under control even for high-dimensional models.

2.5 Data augmentation

To improve computational efficiency, the MCMC proposals described above are used in combination with data augmentation. The data augmentation strategy developed here is different from the one most often used (such as described in Lartillot, 2006; Lartillot and Poujol, 2011; Mateiu and Rannala, 2006; Nielsen, 2002), in that it does not rely on a detailed substitution history along the branches of the tree. Instead, the augmentation at each site consists only of the ancestral nucleotide sequences at the interior nodes of the tree. Sampling ancestral sequences conditional on current parameter values can be done independently for each site, using a standard backward–forward algorithm (Nielsen, 2002). Then, for each branch and for the root, the following sufficient statistics are collected across sites: the number of sites going from nucleotide a at the beginning of branch j to nucleotide b at the end of the branch, ${(n_{ab}^j)}_{a,b=A,C,G,T}$, and the number of sites in each possible nucleotide state in the ancestral sequence at the root, ${(m_a)}_{a=A,C,G,T}$. Conditional on this data augmentation, when applying one of the Metropolis–Hastings proposals described above, only local probability factors, corresponding to those branches on which Brownian paths have changed, need to be recomputed. The probability factor contributed by branch j is given by ${(R_{ab}^j)}^{n_{ab}^j}$, which can be calculated in a time independent of the length of the genetic sequences. The main rate-limiting step of the overall procedure therefore lies either in the resampling of the Brownian path or in the recalculation of the R matrix, depending on the exact model settings. The ancestral sequences are refreshed regularly, conditional on the current parameter configuration. This update is the only one requiring dynamic programming methods classically used for likelihood computation (Felsenstein, 1981).

The overall MCMC schedule is organized in long cycles, each starting with a resampling of the ancestral sequences conditional on the current parameter values, followed by a complex series of calls (of the order of 10 000 in total) to each of the update mechanisms described above and to standard Metropolis–Hastings updates of the global parameters of the model (Lartillot and Poujol, 2011). A typical chain is run for 1100–5100 cycles, discarding the first 100 cycles (burn-in). Convergence was checked visually and then quantitatively assessed by estimating the discrepancy between independent runs and the effective sample size associated to key parameters of the model (in particular, the entries of the covariance matrix). Typical effective sample sizes are of the order of 300 independent points drawn from the posterior distribution for a nominal sample size of 1000.

2.6 Data and simulations

Empirical data were gathered from several previous studies: a placental nuclear dataset of 16 concatenated genes in 73 taxa (Lartillot and Delsuc, 2012), another placental nuclear dataset of 180 concatenated exons from 33 placental taxa (Lartillot, 2013b; Ranwez et al., 2007), a mitochondrial dataset obtained by concatenating the 13 mitochondrial protein-coding genes from 273 placental mammals (Nabholz et al., 2013), another similar concatenation restricted to 201 Cetartiodactylia (Figuet et al., 2014) and an alignment of ribosomal RNA sequences (only the stem regions) from 33 Archaea and an outgroup of 12 Eubacteria (Groussin and Gouy, 2011). In each case, the tree topology was obtained from the corresponding publication and was used in all subsequent analyses.

Simulations were conducted using the placental nuclear dataset with 73 taxa as a template: a first MCMC chain was run under the time-heterogeneous model to estimate the global parameters of the model (the divergence times, the diagonal matrix ${\Sigma }_0$ used as a constant parameter for the inverse Wishart prior, the nucleotide exchangeabilities, the value of the substitution rate and the equilibrium GC composition at the root of the tree). Simulation replicates were then produced conditional on these parameter values, each time drawing a covariance matrix, a Brownian history along the tree and a multiple sequence alignment, and using P = 5000 to effectively approximate a true Brownian motion. The Brownian process is here of dimension 3 (substitution rate, equilibrium GC and one quantitative trait). True (simulated) values of each of these components were set aside for later comparison, and the resulting simulated data (the aligned sequences and the quantitative trait) were used as an input for the MCMC sampler under various model configurations.

3 RESULTS

3.1 MCMC mixing

Convergence and mixing of the MCMC is achieved across a wide spectrum of discretization levels, ranging from P = 25 to P = 1600 discretization points along the entire depth of the tree, both under the time-homogeneous model (Table 1) and the time-heterogeneous settings (Table 2). The time spent per cycle of the MCMC is significantly longer under the time-heterogeneous than under the time-homogeneous model, representing a 6-fold difference between the two settings. This difference reflects the substantially more complex matrix computation implied by models where the substitution matrix itself, and not just the overall substitution rate, is time-dependent (compare Equations 2 and 3). Under both models, however, the time per cycle is approximately linear in P, illustrating the linear complexity of all of the algorithmic developments introduced here, whether for proposing new Brownian paths or for recalculating the likelihood once a new path has been proposed (see Section 2).

Table 1.

MCMC statistics for the time-homogenous model

			Acceptance rates
P	Timea	Eff.sizeb	Onec	Timed	Threee	Linf
25	54	1000	86	90	31	86
50	63	1000	81	90	31	86
100	81	779	74	87	31	86
200	128	861	64	82	31	86
400	173	462	53	75	31	86
800	366	745	39	66	31	86
1600	688	554	26	55	31	86

^aTime per saved point (in seconds). ^bEffective sample size (measured over 1000 points saved after burn-in). ^cOnePathMove. ^dTimePathMove. ^eThreePathMove. ^fLinearBrownianSigmaMove.

Table 2.

MCMC statistics for the time-heterogenous model

			Acceptance rates
P	Timea	Eff.sizeb	Onec	Timed	Threee	Linf
25	114	901	88	83	22	40
50	160	794	88	77	22	40
100	295	930	85	68	22	40
200	538	748	79	58	22	40
400	1016	782	71	45	22	40
800	2053	333	60	31	22	40
1600	4142	412	48	19	23	38

^aTime per saved point (in seconds). ^bEffective sample size (measured over 1000 points saved after burn-in). ^cOnePathMove. ^dTimePathMove. ^eThreePathMove. ^fLinearBrownianSigmaMove.

Acceptance rates remain stable across the entire range for most proposals, except for OnePathMove and for TimePathMove, for which the acceptance rate declines as a function of the discretization level, albeit remaining sufficiently high to provide good mixing even under the finest discretization scheme. Note that acceptance rates given in Tables 1 and 2 are given only for one reference value of the tuning parameter. During the MCMC, a wider range of tuning parameters is used, so as to cover the entire range of acceptance rates, from 10 to 90%. Finally, mixing rate, such as measured by the empirical effective sample size, remains stable when measured per cycle, decreasing somewhat for large P. Because time per cycle increases linearly, the overall efficiency of the Monte Carlo sampling procedure decreases approximately linearly in real time, as a function of the discretization level P.

Importantly, LinearBrownianSigmaMove was essential for obtaining good mixing. Without this proposal, mixing quickly degrades as a function of the discretization level, to the point that the Monte Carlo completely breaks down for more than P = 400 discretization points (not shown). The main rate-limiting aspects causing this breakdown are discussed below.

3.2 Accuracy

Data simulated under a Brownian model were reanalyzed using either the classical branchwise approximation (P = 1) or the fine-grained discretized Brownian model introduced here (P = 100). Compared with the discretized Brownian implementation, the branchwise approximation results in less accurate point estimates of the instant substitution rate and the equilibrium GC content at ancestral nodes of the phylogeny, with a root mean square error (rmse) of 0.41 under P = 1 versus 0.36 under P = 100. The reconstruction of the quantitative trait itself, on the other hand, appears to be less affected by the branchwise approximation (rmse of 0.32 versus 0.30). Similarly, the estimates of divergence times appear to be robust to the specific approximation scheme (rmse of 0.042 versus 0.039).

The inaccuracies at the level of the instantaneous values of the substitution parameters result in inflated estimates of the corresponding entries of the covariance matrix. Diagonal entries are systematically overestimated (rmse = 1.26 versus 0.69). Similarly, covariance parameters are inflated in absolute values (rmse = 0.66 versus 0.29, Fig. 3). This bias is accompanied by a greater uncertainty about the estimation of the variance and covariance parameters, by ∼50% (Fig. 3). This error incurred on the estimation of the covariance matrix can be explained by the fact that the variance contributed at the levels of branch-specific rates or substitution patterns by the randomness of the Brownian paths, which is ignored under the branchwise approximation, is absorbed by the values taken by the Brownian process at the nodes of the phylogeny. This artifactually increased variance is then naturally reflected in the estimated generator of the Brownian process.

Fig. 3.

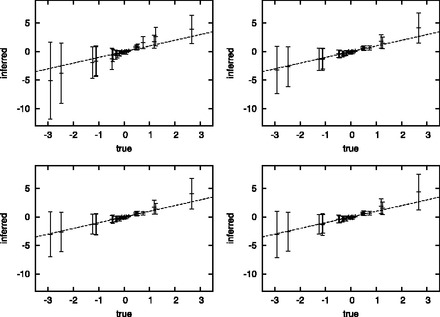
Estimated versus inferred covariances (non-diagonal entries of the covariance matrix), under the branchwise approximation (top left) or using the discretization strategy with P = 25 (top right), P = 100 (bottom left) and P = 200 (bottom right). Error bars are proportional to posterior standard deviation

Of note, the accuracy was found to be nearly the same under all values of $P\ge 25$ explored here (between 25 and 200, Fig. 3), suggesting that even moderate levels of discretization are sufficient to achieve good precision in the reconstruction of Brownian substitution models.

3.3 Empirical data

The model was applied to a series of real datasets spanning a broad range of taxon sampling and sequence length. The time-heterogeneous model was used in all cases, leading to an estimation of the correlation of the variation in substitution rate (Table 3) and equilibrium GC content (Table 4) with a quantitative trait (body mass in the case of mammals and optimal growth temperature for the archaeal ribosomal RNA sequences). The overall reconstructions obtained with P = 100 are globally consistent with previously reported results on the same datasets. In particular, substitution rate decreases with body mass in mammals and with temperature in Archaea (Table 3). The relation between equilibrium GC and body mass in mammals is estimated to be negative in nuclear genomes but positive in mitochondrial genomes (Table 4), probably reflecting a biased gene conversion effect in the nuclear case (Lartillot, 2013b; Romiguier et al., 2010) and a body-size–dependent mutation bias in the mitochondrial compartment (Nabholz et al., 2013). Finally, a strong positive correlation between GC and growth temperature is found in Archaea, possibly the result of an adaptative tuning of RNA stem composition induced by thermodynamic stability constraints (Galtier and Lobry, 1997; Groussin and Gouy, 2011).

Table 3.

Correlation between substitution rate and trait in empirical data

			P = 100			Branchwise (P = 1)
Dataset	Taxa	Sites	cova	Rb	ppc	cov	R	Pp
Plac nuc	73	15 117	−1.38	−0.57	<0.01	−1.43	−0.53	<0.01
Plac nuc	33	112 089	−1.68	−0.60	<0.01	−1.29	−0.45	0.01
Cet mit	201	11 355	−0.37	−0.28	0.01	−0.18	−0.13	0.16
Plac mit	273	3843	−0.27	−0.17	0.02	−0.10	−0.06	0.25
Arch RNA	43	1801	−28.1	−0.64	<0.01	−33.1	−0.62	<0.01

^aCovariance. ^bCorrelation coefficient. ^cPosterior probability of a positive correlation.

Table 4.

Correlation between equilibrium GC and trait in empirical data

			P = 100			Branchwise (P = 1)
Dataset	Taxa	Sites	cova	Rb	ppc	cov	R	pp
Plac nuc	73	15 117	−1.11	−0.37	0.01	−1.43	−0.35	0.01
Plac nuc	33	112 089	−1.89	−0.49	0.04	−1.73	−0.36	0.08
Cet mit	201	11 355	0.92	0.28	0.90	0.98	0.25	0.90
Plac mit	273	3843	1.06	0.24	0.97	1.19	0.24	0.96
Arch RNA	43	1801	70.0	0.78	>0.99	72.0	0.62	>0.99

^aCovariance. ^bCorrelation coefficient. ^cposterior probability of a positive correlation.

These correlation patterns are globally robust to the choice of the specific approximation scheme. On the other hand, some differences in the quantitative results are present between the branchwise (P = 1) and the fine-grained (P = 100) approaches, mirroring what was already observed on simulated data. Globally, the branchwise approach leads to larger estimated covariance parameters. This additional dispersion in turn results in weaker correlations. For instance, body size explains 36 versus 18% of the variation in substitution rate in placental nuclear genomes in the case of the 33 taxon dataset. Similarly, growth temperature explains $R^2=61\%$ of the variation in equilibrium GC content in Archaea according to the discretized model, versus $R^2=42\%$ under the branchwise method. The use of even a moderately fine-grained discretization scheme (typically P = 100) therefore appears to result in a moderate gain in statistical power for detecting and measuring correlations between substitution patterns and quantitative traits.

4 DISCUSSION AND CONCLUSION

In this work, the details of an MCMC method for sampling fine-grained discretizations of stochastic time-dependent substitution models have been worked out and presented. While confirming earlier observations that the classical branchwise approximation of Brownian substitution models gives qualitatively acceptable results (Lartillot and Poujol, 2011), the present simulations nevertheless suggest that a more fine-grained computational approach leads to increased accuracy in the estimation of those features of the model, ancestral rates and covariance matrix, that are of more direct relevance in a comparative perspective. As suggested by the application of this new framework to empirical data, this increased accuracy results in a gain in statistical power when assessing the strength of correlated variation in substitution patterns and quantitative traits along phylogenies.

Beyond these relatively modest short-term gains, the main contribution of the present work is primarily algorithmic and computational. Fundamentally, the present methodological developments represent an important first step toward a general framework for addressing the specific challenges raised by stochastic time-heterogenous substitution models. Ultimately, the promising results obtained here on Brownian models open the way to the implementation of a much wider class of stochastic processes.

4.1 Fine-grained discretizations and MCMC

Among the specific challenges raised by fine-grained time-dependent substitution models, the most critical one encountered in this work has been to obtain a MCMC whose mixing behavior scales acceptably with the level of discretization of the model. Even for a stochastic process as simple as a Brownian motion, good MCMC update proposals that do not become extremely inefficient for fine-grained discretization settings turn out to be difficult to find.

The fundamental reason behind this difficulty is that the subset of model configurations significantly contributing to the posterior distribution, and which the MCMC should therefore efficiently visit, is large in the absolute but small relative to the space of all possible configurations. The data provide only limited constraint for determining which paths are acceptable, so that the relative size of the subset of acceptable configurations is primarily determined at the level of the Brownian process itself. Technically, the Brownian process acts as a regularizer, selecting only those paths that have globally consistent correlation patterns (i.e. whose successive increments along the discretization grid look all i.i.d. from the same multivariate normal distribution). In the limit of large P, these paths are all in the vicinity of a subspace of much lower dimension than the total configuration space. In this regime, the proposed updates are likely to be rejected, unless they are based on good prior guesses.

Practically, these fundamental limitations manifest themselves in several indirect ways. First, while the data provide limited information about the covariance matrix Σ, and thus the marginal posterior on Σ is relatively broad, the conditional posterior density on Σ given the current configuration of the Brownian process X, on the other hand, is highly peaked in the vicinity of the empirical correlation matrix defined by the current paths across branches. As a result, resampling Σ conditional on X and then X conditional on Σ becomes highly inefficient under fine-grained discretization.

Integrating out the covariance matrix, which is possible in the present case because the inverse-Wishart is conjugate to the normal distribution, does not really improve the situation for the following reason: the independent Brownian paths instantiated over distinct branches still have to match in their correlation patterns, to be jointly considered as acceptable under any given covariance matrix. Thus, updating one branch-specific path at a time, conditional on all other paths, while important for mixing paths under the current correlation structure, will not result in a good mixing across correlation structures. This suggests that the only possibility to mix over the correlation structure of the Brownian process is to update all paths simultaneously. Even in that case, however, the update will be accepted only if the final paths are all typical Brownian-looking paths, all with similar empirical correlation structures, which is what LinearBrownianSigmaMove is meant to achieve.

All these difficulties are certainly not specific to Brownian models. Instead, they merely betray a more fundamental curse of dimensionality inherent to the project of implementing fine-grained implementations of doubly stochastic substitution models. On the other hand, the solutions proposed here, while not totally satisfactory (some of the MCMC updates used here do seem to ultimately fail for sufficiently fine-grained discretization schemes, see Table 1 and 2), are good enough for reasonably large values of P. In addition, they should generalize well to other types of processes.

Other specific challenges are also worth mentioning. In particular, alternative discretization schemes have been explored but did not prove robust in the face of the other constraints of the model. Branchwise discretization schemes, for instance, in which each branch is subdivided into segments of equal size, were not found to be satisfactory, raising problems of consistency of the overall approximation procedure or inducing non-local changes when divergence times are modified. The global discretization grid developed here, in contrast, is globally consistent and allows for local-only proposals, which can then be flexibly tuned to target any desired acceptance rate. It should also be noted that the solution developed here could easily be generalized to proposals that would modify the topology of the tree. Paths would then be resampled in the neighborhood of the pruning and the regrafting points, directly from the distribution defined by the stochastic process and conditional on the end points.

The main computational bottleneck under time-heterogeneous models is the calculation of the matrix giving the substitution probabilities across branches (Equation 3). Currently, this rate-limiting step is still prohibitive for larger state spaces, such as implied in particular by codon models. On the other hand, given that the underlying algorithmics entirely consists of iterated series of matrix–matrix products, all of identical dimensions, standard vectorization or parallelization methods could certainly be recruited here. In its current form, the present program typically allows for comparative analyses using datasets with up to a few hundred taxa and a few hundred thousand aligned positions (Tables 3 and 4), achieving effective sample sizes of 100–300 after a few days of computation on a single core, reaching up to one or two weeks for the largest datasets and under time-heterogeneous models (180 h for the placental mitochondrial dataset, 273 taxa).

4.2 Long-term applications

Beyond the specific case of Brownian models, the approach introduced here delineates a general framework for developing fine-grained implementations of a large spectrum of time-dependent substitution models. In principle, it could easily be adapted to more general Gaussian processes, such as the Ornstein–Uhlenbeck process (Hansen, 1997), or to other more complex models such as Levy processes (Landis et al., 2013).

In fact, the main properties of the process used here for developing path sampling algorithms (see Section 2) are (i) the Markov property, (ii) the possibility of efficiently calculating and sampling from conditional finite-time probability distributions and (iii) the possibility of applying a joint transformation to the paths and the generator of the process that leaves the prior invariant. Most Markovian stochastic processes used in the comparative method today meet these requirements and could therefore now be recruited as alternative models for the evolution of the substitution rate or any other parameter of the substitution process.

On the other hand, by relying on a fixed discretization grid, the current approach may possibly not be ideal for processes that make rare but large jumps at arbitrary time points. Although the approximation would still be controlled with an error proportional to δt even in the presence of jumps, for the sake of accuracy, it might be more convenient to adapt the sampling grid so as to match the actual positions of the jumps. In this direction, compound Poisson processes (Huelsenbeck et al., 2000) could represent a promising avenue of research.