Compression and fast retrieval of SNP data

Abstract

Motivation: The increasing interest in rare genetic variants and epistatic genetic effects on complex phenotypic traits is currently pushing genome-wide association study design towards datasets of increasing size, both in the number of studied subjects and in the number of genotyped single nucleotide polymorphisms (SNPs). This, in turn, is leading to a compelling need for new methods for compression and fast retrieval of SNP data.

Results: We present a novel algorithm and file format for compressing and retrieving SNP data, specifically designed for large-scale association studies. Our algorithm is based on two main ideas: (i) compress linkage disequilibrium blocks in terms of differences with a reference SNP and (ii) compress reference SNPs exploiting information on their call rate and minor allele frequency. Tested on two SNP datasets and compared with several state-of-the-art software tools, our compression algorithm is shown to be competitive in terms of compression rate and to outperform all tools in terms of time to load compressed data.

Availability and implementation: Our compression and decompression algorithms are implemented in a C++ library, are released under the GNU General Public License and are freely downloadable from http://www.dei.unipd.it/~sambofra/snpack.html.

Contact: sambofra@dei.unipd.it or cobelli@dei.unipd.it.

1 INTRODUCTION

A genome-wide association study (GWAS) measures a large set of common genetic variants, mainly in the form of single nucleotide polymorphisms (SNPs), across different individuals to see whether any variant is associated with a phenotypic trait. Promising examples of GWAS findings that may soon be translated into clinical care are starting to emerge, including variants that provide strongly predictive or prognostic information or that have important pharmacological implications (Manolio, 2013).

GWASs, however, have brought insight on what is known as the missing heritability problem: almost without exception, only a small part of the genetic variance estimated from the data can actually be explained with association results of GWASs (Manolio et al., 2009). Apart from environmental and epigenetic interactions, the genetic component of phenotypic traits is now believed to be attributed to larger numbers of small-effect common variants, large-effect rare variants or, probably, to a combination of the two (Gibson, 2012).

This has induced an increase in both the number of required samples (Lango Allen et al., 2010) and the number of measured markers (1000 Genomes Project Consortium, 2012) in a GWAS, often resorting to new technologies such as next-generation sequencing. This, in turn, is leading to a compelling need for new methods for effective compression and fast retrieval of SNP data. For this purpose, the widely used whole-genome analysis tool PLINK has introduced the Binary PED (BED) format, which requires only 2 bits to store the information on one genotype (Purcell et al., 2007). However, the achieved compression rate is often not sufficient, with large datasets still requiring several gigabytes for storage on disk.

BED files can be further processed with all-purpose compression tools, like 7ZIP or GZIP, which often achieve rather high compression rates. The drawback of this solution, however, is the need to fully decompress the files before accessing the data, thus requiring both additional computational time and additional disk space for the temporary storage of uncompressed data.

The majority of the methods proposed in the literature for the storage and retrieval of DNA data are designed to compress the entire genome of a small number of subjects and rely on the presence of a reference genome and/or of a reference variation map (Brandon et al., 2009; Christley et al., 2009; Wang and Zhang, 2011). Such methods, however, are unfit for GWAS data, where the number of subjects is much higher and the proportion of identical base pairs between subjects is much lower. Durbin (2014) proposes an efficient algorithm for compressing collections of haplotypes, which, however, requires genetic sequences to be phased.

Deorowicz et al. (2013) propose a software tool, TGC, for compressing collections of SNPs and indels by positively exploiting similarities in the whole collection. However, the tool still requires genetic data to be fully decompressed before accession and, together with the aforementioned methods, it suffers from the large overhead required for storing a reference genome.

To the best of our knowledge, the problem of compressing GWAS data has only been directly addressed by Qiao et al. (2012) with the SpeedGene software tool. The authors propose an algorithm for compressing each SNP according to the most effective among three types of coding algorithms, or codes, designed to exploit the peculiar properties of the genotype distribution of each SNP in the compression process. By compressing one SNP at a time, however, the SpeedGene approach does not take into account the strong local similarity typical of SNP data (linkage disequilibrium).

The object of this work is to develop a novel algorithm for the compression and fast retrieval of SNP data, decomposing the problem in two tasks: (i) summarizing linkage disequilibrium (LD) blocks of SNPs in terms of differences with a common nearby SNP, and (ii) compress such SNPs exploiting information on their call rate and minor allele frequency. The latter task is accomplished by means of five compression codes, two of which are inspired by some ideas from Qiao et al. (2012) but are designed with a more compact representation.

We test our algorithm on two datasets, namely a set of 11 000 subjects from the Wellcome Trust Case Control study (Wellcome Trust Case Control Consortium, 2007) and the 38 millions of SNPs genotyped by the 1000 Genomes Project (1000 Genomes Project Consortium, 2012). Compared with the widely used analysis tool PLINK, the SpeedGene software for SNP compression and retrieval, the general compression tool GZIP and the specific genetic compression tool TGC, our algorithm is shown to outperform the two former tools in terms of storage space and all considered tools in terms of time to load the data.

2 MATERIALS AND METHODS

In this section, we first briefly review the three codes introduced by the SpeedGene algorithm. We then present our improvements of the SpeedGene codes and our novel strategy for compressing LD blocks. The pseudo-code and the description of our final algorithm conclude the section.

2.1 The SpeedGene algorithm

We start by defining code as an algorithm for storing, in a compressed form, the genotype of an SNP for all the subjects in a dataset. The SpeedGene algorithm compresses the SNP data by storing each locus with the best performing among three codes, defined as follows.

• Code 1. For each SNP and each subject, code 1 uses 2 bits to represent the number of copies of the minor allele (0, 1 or 2) or a missing genotype. The genotype of four subjects can thus be stored on 8 bits, equalling one byte on disk. This format is similar to the one adopted by the PLINK software for the Binary PED files and requires the same disk space.

• Code 2. Code 2 is designed for SNPs with low minor allele frequency (MAF) and records only the subjects with the heterozygous and rare homozygous genotype, plus the ones with missing genotype. If n is the number of subjects, code 2 requires $\lceil {\log }_2(n)\rceil$ bits to store the index of each rare homozygous, heterozygous and missing subject, plus $3\times \lceil {\log }_2(n)\rceil$ bits to store the number of subjects in each of the three categories.

• Code 3. Code 3 is designed for SNPs exhibiting a large number of heterozygous subjects. For these subjects, code 3 uses a binary array of n digits: the i-th element of the array is 1 if the i-th subject is heterozygous and 0 otherwise. Rare homozygous and missing subjects are stored as in code 2.

For each SNP, the number of storage bytes required by each code can be computed beforehand, based on the allelic frequencies in the dataset, and the code requiring less space can be selected. SpeedGene stores an additional byte for each SNP to identify the selected code. Furthermore, the algorithm stores the initial position in bytes of each SNP at the beginning of the compressed file, to reduce the time needed for decompression by simplifying the access to each saved SNP.

2.2 Improvements of the SpeedGene codes

The first improvement we propose concerns SpeedGene codes 2 and 3 and reduces the space needed for storage. In fact, rather than storing each time the entire indices of the subjects, requiring $\lceil {\log }_2(n)\rceil$ bits each, we store, for each subject category (rare homozygous, heterozygous and missing), the first index, followed by the differences between all pairs of consecutive indices. For each index in each SNP, thus, it is enough to store a number of bits equal to bdiff_aa, bdiff_aA and bdiff_miss, i.e. the number of bits required to represent both the first index and a difference between consecutive indices of rare homozygous, heterozygous and missing subjects, respectively.

The schematics of the new codes are presented in Figure 1a. As it is clear from the figure, the first 3 bits are used to save a unique identifier for each code. Code 1, then, ignores the subsequent 5 bits and proceeds unmodified storing in the subsequent bytes the genotype of four subjects for each byte.

Fig. 1.

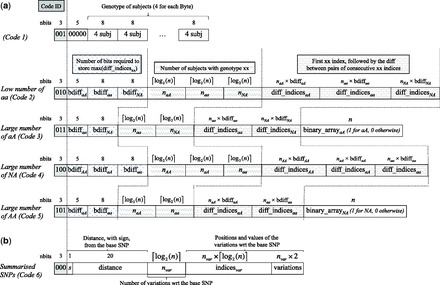
Schematics of the five codes for compressing reference SNPs (a), plus the code for compressing summarized SNPs by storing their variations with respect to a reference SNP (b). For each code, we report the sequence of stored values and, on top of them, the number of allocated bits. (a) Code 1 contains the code ID (3 bits) followed by five 0 bits and the genotype of the subjects (four subjects per byte). The remaining codes report the code ID followed by bdiff_xx, i.e. the number of bits for representing the first index and the difference between consecutive indices of the subjects in category xx, where xx can be aa, aA, AA or NA for homozygous rare, heterozygous, homozygous frequent or missing subjects, respectively. Then codes 2–5 contain the number of subjects with genotype xx (n_xx) followed by the first xx index and the differences between the indices of consecutive subjects in category xx. In addition, codes 3 and 5 contain binary_array_aA and binary_array_NA, respectively with 1 in position i if the i-th subject is in category aA (or NA) and 0 otherwise. (b) Code 6, used to compress summarized SNPs, contains the code ID (3 bits) followed by 21 bits coding the distance, with sign (upstream or downstream), from the reference SNP; the number of variations wrt the reference SNP (n_var), the positions (indices_var) and values (variations) of the variations wrt the reference SNP

Code 2, on the other hand, exploits the 5 bits of the first byte, together with the two subsequent bytes, to store bdiff_aA, bdiff_aa and bdiff_miss. The code, then, stores the number of rare homozygous, heterozygous and missing subjects, each requiring $\lceil {\log }_2(n)\rceil$ bits, and then stores, for each of the three sets of indices, the first index, followed by the differences between pairs of consecutive indices.

Similarly, code 3 stores bdiff_aa and bdiff_miss in the first 2 bytes, followed by the numbers of rare homozygous and missing subjects and by the two sets of indices. Code 3 terminates with a binary array of n digits, with a 1 for each heterozygous subject and a 0 otherwise.

For each SNP, we measure a separate bdiff for each subject category, rather than simply taking the maximum of the three, because we observed that it greatly varies across the three categories. This is to be expected, as the indices of rare homozygous and missing subjects will be, on average, more sparsely distributed than the indices of heterozygous subjects; the latter, thus, will generally require less bits to code the difference between two consecutive indices.

Compared with the original SpeedGene codes, our modified versions add a fixed overhead of 2 bytes to code 2 and of 1 byte to code 3. However, the overhead is almost always compensated by a gain of several bits for each of the stored indices, as shown in Section 3.

The second improvement we propose is the introduction of code 4 and 5, especially useful for SNPs with many missing values. The schematics of the new codes are represented in Figure 1a.

Code 4 is similar to code 2, but swaps the role of missing values with the one of frequent homozygous subjects: the code records explicitly the indices of frequent homozygous, rare homozygous and heterozygous subjects, assuming the majority of subjects to be missing for the SNP.

Code 5 is less extreme than code 4 and is similar to code 3, but swaps the role of missing values with the one of heterozygous subjects: the code records explicitly the indices of rare homozygous and heterozygous subjects, exploiting a binary array of n digits to record missing values.

2.3 Compression algorithm

The DNA is known for exhibiting regions of strong local similarity, known as LD blocks, separated by small regions with high recombination rates (Wall and Pritchard, 2003). In a population, SNPs in high LD have identical genotypes for the majority of subjects. When compressing an LD block, thus, it suffices to store one of the SNPs in its entirety and use it as a reference to summarize the other SNPs in the block, storing just their variations with respect to the common SNP. In what follows, we will call the former reference SNP and the latter summarized SNPs.

We stem from this intuition to design our compression algorithm, whose pseudo-code is reported in what follows.

Compress-Snps

1 load SNP data

2 for each SNP i

3   $cost[i]=$ Byte size of the best code for i

4 for each SNP i

    //useful neighbours, i.e. SNPs worth being summarised by i

5   $uN[i]=\varnothing$

6   for each SNP $j\in N[i]$//Neighbourhood of i

7     compute genotype variations between i and j

      // partial gain

8     $pg[i,j]=cost[j]-$ cost of summarising j with i

9     if $pg[i,j]>0$

10       $uN[i]=uN[i]\cup j$

11   $gain[i]=\sum _{j\in uN[i]}pg[i,j]$

12 $m={\text{argmax}}_i(gain[i])$

13 while $gain[m]>0$

14   $summary[uN[m]]=m$

15   $gain[m]=0$

16   $gain[uN[m]]=0$

17   for each $j\in uN[m]$

18     for each k such that $j\in uN[k]$

19       $gain[k]-=pg[j,k]$

20   $m={\text{argmax}}_i(gain[i])$

21 write data to disk according to summary

The algorithm starts by computing the best of the five codes for each SNP and the corresponding cost in bytes (lines 2–3).

For each SNP i, then, the algorithm searches its neighbourhood $N[i]$ for SNPs j that could be effectively summarized by i, by computing their partial gain, i.e. by subtracting the cost of summarizing j with i from the cost of storing j. For the moment, consider the neighbourhood of an SNP simply as its flanking region in the DNA; the concept would be more clearly defined in what follows. SNPs with positive partial gains are added to the set of useful neighbours of i, $uN[i]$, and their partial gains are summed to compute the total byte gain of using SNP i as a reference for summarizing its useful neighbours (lines 4–11).

Once the gain of each SNP has been computed, the algorithm proceeds by building the summary, i.e. by either assigning to an SNP the role of reference or by indicating for the SNP which reference should summarize it, in a greedy fashion (lines 12–20). The algorithm, in fact, iteratively selects SNP m with the largest gain and sets it as the reference of its useful neighbours. The gain of m and of its useful neighbours is set to zero and, for each SNP j in $uN[m]$, the algorithm updates the gain of all SNPs that have j as useful neighbour (as each SNP can be summarized by at most one reference).

The depth of the summary is limited to 1, i.e. summarized SNPs are not allowed to be reference for other SNPs. This design choice is meant to limit the complexity of the decompression phase, as it will be further clarified in the next section.

Finally, the algorithm writes the data to disk according to the summary, using the five aforementioned codes to store the reference SNPs and a sixth code, named Summarized SNPs in Figure 1b, to store the summarized SNPs. As it is clear from the figure, this latter code uses the first three bits to save a unique identifier. The subsequent 21 bits are used to identify the relative index of the reference SNP, with one bit for the sign and 20 bits for the index distance. The code, then, reports the number of genotype variations with respect to the reference SNP and lists their indices and values.

The computational complexity of the algorithm is dominated by two operations: the computation of genotype variations between each SNP and the SNPs in its neighbourhood (line 7) and the iterated computation of the maximum element of the vector gain (line 20). If n is the number of subjects, p is the number of SNPs and $|N|$ is the number of SNPs in a neighbourhood, the former has complexity $\text{O}(pn|N|)$ and the latter $\text{O}(p^2)$.

Both to limit the complexity of computing genotype variations and to cope with the variable patterns of LD throughout the genome, we designed a heuristic procedure for adaptively setting the size of the neighbourhood of an SNP. The procedure incrementally grows the neighbourhood, independently up and downstream of the SNP, starting from 10 SNPs and doubling the number as long as at least one of the newly added SNPs turns out to be a useful neighbour, or when the maximum extension w, received as input from the user, is reached. Such a procedure lets the algorithm reach the desired neighbourhood extension in regions with low recombination, while halting the search for useful neighbours when recombination hotspots are encountered.

As no LD is to be expected between the borders of two consecutive chromosomes, we run the algorithm separately on each chromosome: this allows us to reduce both memory occupation and the complexity of the argmax operation in line 20, which becomes quadratic in the number of SNPs in a chromosome.

Finally, to exploit the embarrassing parallelism of our compression task, after loading a chromosome and computing the SNP costs (lines 1–3), we further split the chromosome into chunks of equal size and assign each chunk to a separate thread, which is responsible to compute both the gain of each SNP in the chunk (lines 4–11) and the portion of the summary corresponding to the chunk (lines 12–20). The threads are distributed on the available computational cores, and the computation is joined before writing the compressed chromosome on disk. Apart from the improvement in computational time owing to parallelism, this also has the positive side effect of further reducing both memory occupation and the complexity of the argmax operation on line 20, of a factor equal to the number of chunks. The drawback of this choice is a loss in compression performance at the borders of the chunks. The loss is, however, limited if the number of chunks is reasonably low, as shown in Section 3.

Before each chromosome, we write to disk the byte size of the entire compressed chromosome, followed by the byte size of each of its SNPs. This results in an overhead in the file size, but it is useful for accelerating the decompression phase.

2.4 Decompression

Decompression is carried out separately on each chromosome, to limit memory occupation. For each chromosome, the decompression procedure loads the entire chromosome (whose compressed size is stored in our compressed file), allocates memory to hold decompressed data and scans the loaded chromosome twice. A first pass reads and decodes the reference SNPs, interpreting codes 1 to 5. A second pass, then, reconstructs the summarized SNPs from the decoded reference SNPs.

A depth of the summary limited to 1 ensures that only two passes are needed to fully decompress a chromosome, thus limiting decompression time.

2.5 Implementation and file formats

Our compression and decompression algorithms are implemented in C++, with parallelism handled by OpenMP directives. The code, licensed under the GNU General Public License, is structured as a library, so to make it easily usable by other software.

Input data are required to be in the standard PLINK binary format, consisting of a triplet of .bim, .fam and .bed files. The .bim and .fam files hold information on the genotype and pedigree in text format, whereas the .bed file holds genetic data in the binary format already described, similar to code 1. Our library, thus, does not require additional data preprocessing or unnecessary large disk space to hold the input files in text format.

The output of our library is a binary .pck file, containing the compressed genetic data. The library requires the same .fam and .bim files received as input for decompression. We made this design choice to retain the readability of the pedigree and genotype information typical of the PLINK binary format, often familiar to genetic data analysts. This comes at the cost of a larger disk occupation because of the uncompressed nature of the .bim and .fam text files.

3 EXPERIMENTAL RESULTS

In this section, we present two SNP datasets, and we exploit them to assess several aspects of our compression algorithm, namely:

• The improvements of the newly defined codes over the SpeedGene codes in terms of storage space,

• The effect on the performance of the two tunable parameters of the algorithm, i.e. the maximum neighbourhood extension and the number of chunks used for parallelization,

• The global performance of our algorithm, in terms of time and peak memory occupation for compression, of compressed file size and of time to load the compressed file,

• The relative utility of LD blocks compression.

All experiments are run on an Intel® Core™2 Quad CPU Q6700 with 8 GB of RAM and a Linux operative system.

3.1 Datasets

The first dataset we adopt originates from the Wellcome-Trust Case Control Study (Wellcome Trust Case Control Consortium, 2007) and consists of 10 992 subjects, either healthy or affected by type 1 diabetes, type 2 diabetes, hypertension or coronary artery disease. Each subject was genotyped on the Affymetrix GeneChip 500K Mapping Array Set, which measures 490 294 SNPs. Given that the information on the physical position of each SNP is essential for our compression algorithm, we updated it to reference assembly GRCh37.

The second dataset is the 1000G Phase I Integrated Release Version 3 of the 1000 Genomes Project (1000 Genomes Project Consortium, 2012), consisting of 37 888 420 SNPs typed for 1092 individuals.

The two datasets can be considered fairly complementary in terms of the number of subjects and of measured SNPs.

3.2 Effectiveness of the new codes

To assess the effectiveness of the new versions of code 2 and 3, compared with the original SpeedGene codes, together with the addition of codes 4 and 5, we randomly sampled 20 sets of 1000 SNPs from each of the two datasets, applied the two sets of codes and compared the distribution and the disk occupation of the best code for each SNP.

Figure 2 reports the median amount of disk space over the 20 sampled sets, in bytes and summed by code, needed for storing the SNPs from the WTCCC (left) and 1000g (right) datasets, with the SpeedGene and new codes. Whiskers extend from the first to the third quartile of the total byte size. As it is clear from the figure, for both datasets the application of the new codes results in a decrease in the number of SNPs for which code 1 is the best, in favour of the best-performing codes 2–5. The effectiveness of codes 4 and 5 is limited for the WTCCC dataset (no SNPs with code 4 and one SNP with code 5), while the two are by far the most effective for the 1000g dataset. The new codes lead to a decrease in the compressed file size of more than 12% for the WTCCC dataset and 40% for the 1000g dataset, statistically significant in both cases (Wilcoxon signed-rank test P-value $<5\times {10}^{-5}$).

Fig. 2.

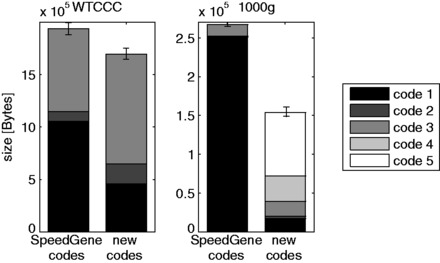
Median byte size, separately for each code, over 20 randomly sampled sets of 1000 SNPs from the WTCCC (left) and the 1000g (right) datasets. Whiskers extend from the first to the third quartile of the total byte size

3.3 Parameter tuning

The two major tunable parameters of our algorithm are the maximum extension of the neighbourhood, w, and the number of chunks in which the chromosomes are split for parallelizing the computation.

Figure 3 shows the trade-off between the computational time for compression and the output file size for different values of w, ranging from ±10 to ±200 kilobases, for the WTCCC (Fig. 3a) and 1000g datasets (Fig. 3b).

Fig. 3.

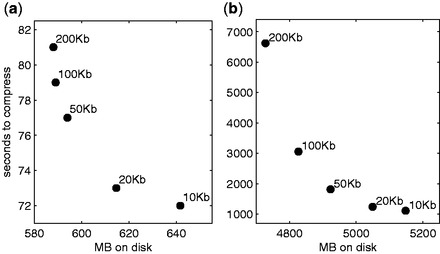
Time in seconds for compression versus size in MB of the compressed files on disk for different values of the maximum neighbourhood size, for the WTCCC (a) and the 1000g (b) datasets

As it is clear from the figure, varying w between 20 and 100 kb is an effective means for trading computational time for smaller file size. In all the following experiments, we set w to 100 Kb for the WTCCC dataset, as no apparent gain can be obtained with a larger neighbourhood, while we set it to 50 kb for the 1000g dataset, favouring a lower compression time.

Concerning the other tunable parameter, we recall that parallelism is obtained in our software by splitting each chromosome into several chunks, each containing the same number of SNPs, and by processing in parallel a number of chunks equal to the number of available cores. To assess the effectiveness of such a procedure, we measure the computational time and peak memory usage for compression and the final size of the compressed file, for the number of chunks varying between 1 and 32. The results are represented in Figure 4.

Fig. 4.

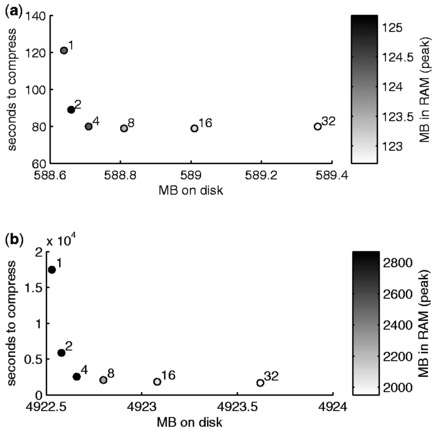
Time in seconds for compression, MB of the compressed files on disk and peak MB of RAM occupation during compression when splitting the computation for each chromosome in different numbers of chunks (between 1 and 32), for the WTCCC (a) and the 1000g (b) datasets

Please recall that all experiments are run on a quad-core machine: as expected, thus, most of the gain in computational time is obtained for up to 4 chunks. A further increase in the number of chunks, however, still results in a decrease in computational time, more evident on the 1000g data (Fig. 4b), owing to the reduced complexity of the argmax operation explained in Section 2.3. For the WTCCC dataset, however, the temporal overhead owing to the parallelization procedures becomes detrimental for >16 chunks. Increasing the number of chunks above four also results in a consistent decrease in peak memory occupation for both datasets.

The benefits of parallelism come at the cost of an increase in the file size, albeit limited: given that the file size obtained with 1 chunk is the minimum achievable by varying the number of chunks, the size achieved with 32 chunks is <0.12% larger than the minimum for the WTCCC dataset and <0.02% larger for the 1000g dataset.

From the results, thus, we can conclude that 16 is an overall good choice for the number of chunks on a quad-core machine and will be adopted in all the following experiments.

3.4 Global performance

The entire compression algorithm is then applied to both datasets. The performance of our software library and file format, in terms of time and peak memory occupation for compression, of compressed file size and of time to load the compressed file, is compared with the ones of the widely used PLINK binary format, of the SpeedGene format, of the general compression tool GZIP applied to PLINK binary files and of the specific genetic compression tool TGC. For the latter two methods, time to load is computed as time to decompress plus time to load decompressed data with the adequate data analysis tool, thus PLINK for the former and VCFtools (Danecek et al., 2011) for the latter. To compute the output file size of each format, we also take into account the size of the file descriptors, i.e. the .bim and .fam files for our format and for the binary PLINK format, the file with additional information on SNPs and subjects for the SpeedGene format and the GZIPped human reference genome required by TGC to fully decompress the genetic data. Tables 1 and 2 report the results of the comparison for the WTCCC and 1000g datasets, respectively.

Table 1.

Performance measures of our new format versus the PLINK binary format and the SpeedGene format on the WTCCC dataset

Format	Time to compress	RAM [MB] to compress	Output size [MB]	Time to load
Text file	–	–	21 564	–
PLINK binary format	–	–	1636	0:02:52
SpeedGene format	3:16:40	77	962	0:01:56
New format	0:01:19	123	589	0:00:17
GZIPped PLINK binary format	0:01:36	<1	546	0:03:06
TGC format	NAa	$>8000$	$403+900$	0:03:46

^aNot reported, too much RAM required.

Table 2.

Performance measures of our new format vs. the PLINK binary format and the SpeedGene format on the 1000g dataset

Format	Time to compress	RAM [MB] to compress	Output size [MB]	Time to load
Text file	–	–	166 000	–
PLINK binary format	–	–	11 500	0:25:24
SpeedGene format	3:57:48	4100	10 850	NAa
New format	0:30:02	2050	4923	0:02:38
GZIPped PLINK binary format	0:05:47	<1	1150	0:27:54
TGC format	2:04:53	2400	$1036+900$	0:38:56

^aNot reported, too much RAM required.

Starting from the PLINK binary format, our algorithm achieves a compression rate of ∼2.8 for the WTCCC dataset and of 2.3 for the 1000g dataset. The compressed file size is also consistently better than the one obtained with the SpeedGene tool, as is the time needed for compression. Concerning the peak memory occupation, our library requires almost twice as much RAM as the one required by SpeedGene for the WTCCC dataset, but the opposite is true for the 1000g dataset.

Compared with the GZIP software, our compression algorithm is faster on the WTCCC dataset and slower on the 1000g dataset. However, the amount of memory used and the output file size obtained by the GZIP software are better than the ones of our algorithm.

The compression rate of the TGC tool, when considering the 900 MB of the GZIPped human reference genome, is better than the one of our algorithm on the 1000g dataset and worse on the WTCCC dataset. On both datasets, the TGC tool requires higher RAM and computation time, actually reaching the 8 GB memory limit of our testing machine on the WTCCC dataset: the time measurement in this case is not reported, as it would be biased by the system’s paging operations.

When comparing the time to load the compressed data, one can observe that our library always requires at least one order of magnitude less time than all the other methods. For the 1000g dataset, the time to load is not reported for the SpeedGene tool, because its internal representation requires too much RAM on our testing machine.

As final notes, we point out that the input formats required by the SpeedGene and TGC tools are ad hoc textual formats, derived from the PLINK PED and from the Variant Call Format (VCF), respectively. As it is clear from the first line of the two tables, considerable disk space is required to store text inputs and additional effort is needed to convert data from standard formats to the required input formats. Our library, directly processing data in the PLINK binary format, requires 16 times less space and no effort for conversion. Finally, one should note that neither SpeedGene nor TGC accomplish lossless compression, with the former losing information on chromosome and position of each SNP and the latter losing SNP IDs in the compression process.

3.5 Effectiveness of LD blocks compression

We study the effectiveness of LD blocks compression by analysing, for each dataset, the number of SNPs selected as reference or summarized (Table 3, first two columns) and the size occupied by reference SNPs, by summarized SNPs, by the overhead in the compressed file (described at the end of Section 2.3) and by the .bim and .fam files (Table 3, last two columns). Both measures are presented in Table 3 as percentages, to directly compare the results on the WTCCC and 1000g datasets.

Table 3.

Percentage of the number of SNPs coded as reference or summarized (first two columns) and percentage of the total file size occupied by reference SNPs, by summarized SNPs, by the overhead in the compressed file and by the .bim and .fam files (last two columns)

	No. of SNPs [%]		File size [%]
	WTCCC	1000g	WTCCC	1000g
reference SNPs	59.37	55.02	76.45	51.68
Summarized	40.63	44.92	20.53	23.22
Overhead	–	–	0.33	3.02
.bim, .fam	–	–	2.69	22.08

As expected, the fraction of summarized SNPs over the total depends on the density of the SNP measurements along the DNA, which is roughly proportional to the number of measured SNPs. Around 40% of the SNPs are summarized in the WTCCC dataset and 45% in the denser 1000g dataset.

It is even more interesting to analyse the relative sizes of reference and summarized SNPs in the output files. In the WTCCC dataset, summarized SNPs are 40% of the total but occupy a little more than 20% of the output files size. The effect is consistent in the 1000g dataset (45% of the SNPs are summarized, but they occupy 23% of the file size).

Considering the relative weight of the overhead and of the .bim and .fam files on the output file size, one can observe that it depends on the ratio between the number of SNPs and the number of subjects in the dataset, being thus negligible for the WTCCC dataset but significant (>25% of the total output size) for the 1000g dataset.

Finally, to gain further insights on LD-blocks compression, we studied the distribution of the neighbourhood extension among the reference SNPs: log counts for the WTCCC and 1000g datasets are reported in Figure 5. As it can be seen from the figure, in both cases, many reference SNPs have neighbourhood extension equal to zero, meaning no summarized SNPs. The neighbourhood frequency tends in general to decrease with the extension, up to the maximum value 2w (200 kb for the WTCCC dataset and 100 kb for the 1000g). However, while for the WTCCC data the decrease is steady and the proportion of SNPs with maximum extension is quite low, the effect is less evident for the 1000g dataset. This is in line with the results from Figure 3: increasing the maximum size of the neighbourhood above the chosen value, in fact, results in a significant increase in compression rate only for the 1000g dataset.

Fig. 5.

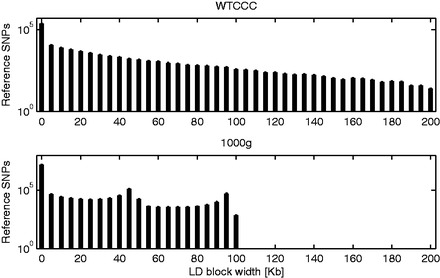
Histogram (log counts) of the neighbourhood extension of reference SNPs, for the WTCCC (top) and 1000 g (bottom) datasets

4 DISCUSSION

In this article, we presented a novel algorithm and file format for the compression and fast retrieval of SNP data. Our algorithm is based on two main ideas: summarize LD blocks in terms of differences with a reference SNP and compress reference SNPs with the best among five types of codes, designed to exploit the information on the call rate and minor allele frequency of the SNPs.

We compared our algorithm with one of the most widely adopted tools for genetic data analysis, the PLINK software, with the state of the art in GWAS data compression and retrieval, the SpeedGene software, with the general compression tool GZIP and with the specific genetic compression tool TGC. Our algorithm was shown to outperform the two former tools in terms of storage space and all the other tools in terms of time to load the data on two representative datasets. Furthermore, among the analysed tools only our algorithm and GZIP accomplish truly lossless compression and were able to process both datasets within the 8 GB memory limit.

The algorithm has been implemented as an open-source C++ software library, to facilitate its integration into newly developed genetic analysis software. Tools based on our library could sit in the GWAS analysis pipeline right after variant calling and implement, for example, data quality control or association analysis, effectively exploiting the reduction in storage space and time to load the data granted by our library and file format.

The library directly processes SNP data in the widely used PLINK binary format, and thus does not require additional effort for preprocessing. The output of our software consists in a .pck file, containing compressed SNP data, and in a pair of .bim and .fam text files, identical to the ones of the PLINK binary format.

Rather than extreme compression, we decided to favour the readability of our file format and the speed of data retrieval. This has motivated several design choices:

• retain the familiar .bim and .fam text files in the output;

• save the byte size of each compressed SNP at the beginning of the .pck file, thus adding a size overhead to facilitate data access;

• limit to one the depth of the summary in the compression algorithm, thus allowing data decompression with only two passes of the entire file.

The creation of the summary, i.e. the choice of which SNPs should be coded as reference and of which SNPs should be summarized by each reference is at the core of our compression algorithm. In general, finding the optimal summary is an NP-complete problem. The current version of our algorithm solves the problem with a greedy approach, which performs sufficiently well thanks to the strong locality of genetic information. However, we intend to further study the problem from an optimization point of view, to understand whether more advanced solutions could be designed.

Another future direction will be to extend our compression framework to more expressive file formats, such as the GEN format used by the analysis tools SNPTEST and IMPUTE (Howie et al., 2012) and the VCF, together with its binary counterpart (BCF2) (Danecek et al., 2011). The former format, particularly effective for complex meta analysis problems where data are aggregated from multiple genotyping platforms and several SNPs are imputed, allows one to assign probability values to the three genotypes of each SNP in each subject. The latter format, on the other hand, is the current standard for representing genetic variation in the form of SNPs, indels and larger structural variants, together with additional quantitative information originating from next-generation sequencing technologies, such as read depth. The seminal idea will be to exploit the redundancy of neighbouring variants across a collection of individuals to effectively store reduced representations of both allele probability distributions and read counts.

Funding: The research was supported by the European Union’s Seventh Framework Program (FP7/2007-2013) for the Innovative Medicine Initiative under grant agreement n IMI/115006 (the SUMMIT consortium) and by the University of Padova's strategic project AACSE.

Conflict of interest: none declared.