Inter-method Performance Study of Tumor Volumetry Assessment on Computed Tomography Test-retest Data

Abstract

Rationale and objectives

Tumor volume change has potential as a biomarker for diagnosis, therapy planning, and treatment response. Precision was evaluated and compared among semi-automated lung tumor volume measurement algorithms from clinical thoracic CT datasets. The results inform approaches and testing requirements for establishing conformance with the Quantitative Imaging Biomarker Alliance (QIBA) CT Volumetry Profile.

Materials and Methods

Industry and academic groups participated in a challenge study. Intra-algorithm repeatability and inter-algorithm reproducibility were estimated. Relative magnitudes of various sources of variability were estimated using a linear mixed effects model. Segmentation boundaries were compared to provide a basis on which to optimize algorithm performance for developers.

Results

Intra-algorithm repeatability ranged from 13% (best performing) to 100% (least performing), with most algorithms demonstrating improved repeatability as the tumor size increased. Inter-algorithm reproducibility determined in three partitions and found to be 58% for the four best performing groups, 70% for the set of groups meeting repeatability requirements, and 84% when all groups but the least performer were included. The best performing partition performed markedly better on tumors with equivalent diameters above 40 mm. Larger tumors benefitted by human editing but smaller tumors did not. One-fifth to one-half of the total variability came from sources independent of the algorithms. Segmentation boundaries differed substantially, not just in overall volume but in detail.

Conclusions

Nine of the twelve participating algorithms pass precision requirements similar to what is indicated in the QIBA Profile, with the caveat that the current study was not designed to explicitly evaluate algorithm Profile conformance. Change in tumor volume can be measured with confidence to within ±14% using any of these nine algorithms on tumor sizes above 10 mm. No partition of the algorithms were able to meet the QIBA requirements for interchangeability down to 10 mm, though the partition comprised of the best performing algorithms did meet this requirement above a tumor size of approximately 40 mm.

I. Introduction

Lung tumor volume change assessed with computed tomography (CT) has potential as a quantitative imaging biomarker to improve diagnosis, therapy planning, and monitoring of treatment response [1, 2]. Tumor volume change as a predictor of outcome has been of interest for some time [3-5].

To establish confidence in algorithmic analysis for CT volumetry as a rigorously defined assay useful for clinical and research purposes, volume measurement algorithms need to be characterized in terms of both bias and variability. Measurement error on serial CT scans can be affected by a number of inter-related factors, including imaging parameters, tumor characteristics, and/or measurement procedures [6-8]. These effects must be understood and quantified. A number of technical studies have been performed toward that goal [9-32].

The Quantitative Imaging Biomarker Alliance (QIBA) [33] has defined standard procedures for reliably measuring lung tumor volume changes in a document called a Profile. The CT Volumetry Profile is based in part by available literature, as well as “groundwork” studies conducted by QIBA itself [34]. Groundwork studies of algorithm performance organized as public challenges have been conducted under the moniker of “3A.” The first 3A study was conducted to estimate intra- and inter-algorithm bias and variability using phantom data sets (manuscript under review). Algorithms utilized by participating groups were applied to CT scans of synthetic lung tumors in anthropomorphic phantoms. While such a study design was effective for estimating bias since ground truth was known, phantom studies are likely to underestimate the biological variability typically seen in clinical data sets. More recently, QIBA has undertaken studies on the analysis of clinical data. The QIBA “1B” study was undertaken to compare two reading paradigms, independent readings at both time points vs. locked sequential readings, using a test-retest design [35]. Readers in the QIBA 1B study used a single algorithm. The current study, known as the “second” 3A, combines the algorithm performance challenge approach established by the first 3A study using the same clinical data as was used in 1B. The goal of the current study was to quantify the error when a tumor with no biological change in size was imaged twice and each image was measured by the same or multiple algorithms.

Intra- and inter-algorithm variability was analyzed using data from twelve diverse tumor segmentation algorithms from eleven academic and commercial participating groups for measuring volume. The algorithms included semi-automated algorithms with and without post-segmentation manual correction. The analysis of algorithm performance conducted in this study complements the other groundwork studies in establishing performance claims for the QIBA Profile.

In section 2 we describe the statistical methods and open-source informatics tool used to conduct the study as a challenge problem. The estimated intra-algorithm repeatability and inter-algorithm reproducibility are presented in section 3. Section 3 also describes a comparison of the segmentation boundaries themselves for the subset of algorithms where tumor segmentations were submitted.

II. Materials And Methods

Data Collection

Thirty-one subjects with non-small cell lung cancer were evaluated in a test-retest design. The cases were contributed to the RIDER database from Memorial Sloan Kettering Cancer Center, acquired in a previously conducted study [36]. Each patient was scanned twice within a short period of time (< 15 minutes) on the same scanner and the image data was reconstructed with thin sections (< 1.5 mm). Since the time interval between repeat scans is small, the actual volume of the tumor is the same in each scan (a zero-change scenario).

CT scans were obtained with a 16–detector row (LightSpeed 16; GE Healthcare, Milwaukee, Wisconsin) or 64–detector row (VCT; GE Healthcare) scanner. Parameters for the 16–detector row scanner were as follows: peak voltage across the X-ray tube, 120 kVp; tube current, 299– 441 mA; detector configuration, 16 detectors × 1.25-mm section gap; and pitch, 1.375. Parameters of the 64–detector row scanner were as follows: tube voltage, 120 kVp; tube current, 298–351 mA; detector configuration, 64 detectors × 0.63-mm section gap; and pitch, 0.984. The thoracic images were obtained without intravenous contrast material during a breath hold. Since the second scan was considered as a separate scan, its field of view was set given the patient's second scout image. Adjustment was allowed owing to the patient's position in the scanner. Thin-section (1.25 mm) images were reconstructed with no overlap by using filtered back projection with the lung convolution kernel and transferred to the research picture archiving and communication system server where Digital Imaging and Communications in Medicine (DICOM) images were stored.

One tumor per subject was selected for measurement by the clinical staff at Memorial Sloan Kettering. Among them, most were primary lung cancers but three were metastatic tumors (used because the primary tumors were non-measureable, as defined by the Response Evaluation Criteria in Solid Tumors criteria). The data set includes tumors that are distinct and solitary as well as others with attachment to various structures including bronchus, chest wall, and mediastinum. The approximate tumor diameters ranged from 8 mm to 65 mm, as calculated by the equivalent diameter were a sphere to include the same volume.

The shapes of the selected tumors ranged from simple and isolated to complex and cavitated. To facilitate comparison of results with the prior QIBA 1B study, the tumors were further subdivided according to whether they met the following “measurability” criteria defined in the Profile: tumor margins were sufficiently conspicuous and geometrically simple enough to be recognized on all images, and the longest in-plane diameter of the tumor was 10 mm or greater (see Figure 1).

Figure 1.

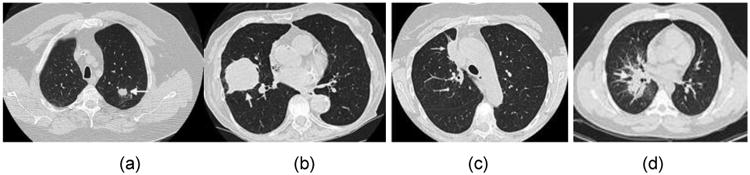
Examples of tumors from our study. (a) and (b) are examples of tumors that were judged to have met the QIBA measurability criteria, while (c) and (d) were not found to meet the criteria. Image (c) was excluded because it demonstrates a large attachment to other pulmonary structures and (d) was excluded because it demonstrates a highly invasive structure where the boundary between tumor and non-tumor is not well demarcated.

Eleven groups from a diverse set of industry and academic groups participated in the challenge by submitting results from twelve algorithms (one group made two submissions). The participating groups downloaded the images, including the raw image data and location points. The location (“seed”) points were defined to lie within the tumor margin. Groups were allowed to select different or multiple seed point(s) for their individual algorithms, provided they utilized the tumor identification scheme provided. Some of the groups submitted data from the algorithm without any post-segmentation modifications (semi-automated without editing), others submitted data with adjustments made to varying degrees by a reader (semi-automated with editing), and one group submitted both. Each group then uploaded their results using an open-source informatics tool called QI-Bench [37]. To establish and maintain anonymity of participants, all communications were handled through the QIBA staff at RSNA. The participants are as follows (listed alphabetically rather than according to the IDs used in reporting the results of the study):

• Fraunhofer MEVIS

• GE Healthcare

• ICON Medical Imaging

• KEOSYS

• MEDIAN Technologies

• Mirada Medical

• Perceptive Informatics

• Siemens AG

• UCLA

• University of Michigan

• Vital Images

See the appendix for detailed algorithm descriptions for each of the participating groups.

Statistical Methods

Estimation of Variability

The repeatability coefficient (RC, was used to characterize the intra-algorithm variability [6]. The RC was defined as:

$$\mathit{\text{RC}}=1.96\sqrt{2{\sigma }_{\epsilon }^2}=2.77{\sigma }_{\epsilon }$$

where ${\sigma }_{\epsilon }^2$ is the within-tumor variance. The range in which two measurements on the same tumor were expected to fall for 95% of replicated measurements was given by [-RC, +RC] [38]. In this study we computed the within-tumor variance and thus RC based on the difference of the test and retest measurements for each algorithm respectively.

Two calculation methods were used, one using log transformed data and the other a root mean square approach. The root mean square approach proceeds by calculating the square root of the mean of squared tumor-based RC values. Additionally, the within-tumor coefficient of variability (wCV_intra) was calculated as a measure of precision for single measurements [6]. It was calculated in an analogous fashion, but dividing each tumor-based ${\sigma }_{\epsilon }^2$ by the square of the mean of the two measurements and without use of the 2.77 factor. The percent RC (% RC) for an algorithm was determined by multiplying wCV_intra by 2.77. In the logarithmic approach, the % RC is determined by taking an inverse transform. Both wCV_intra and % RC are relative measures proportional to the magnitude of the tumor's size. We verified the equivalence of these two methods in a manner described by Bland [39], with the equivalence strongest when the % metrics were small. Since we were interested in how the metrics changed for differing tumor sizes, we plotted the percentage metrics as a function of tumor size.

The reproducibility coefficient (RDC), as well as its percentage counterpart percent RDC (% RDC), and wCV_inter, were used to characterize inter-algorithm variability [6]. The RDC, similar to RC, was calculated from the variance across different algorithms' measurements of the same tumor [6]. In this study [-RDC, +RDC] described the range within which approximately 95% of the differences in measurements between two algorithms lie. We reported the reproducibility results in three partitions of algorithms, partitioned based on the intra-algorithm repeatability results. One partition included all algorithms minus the lowest performing algorithm. Another partition included the set of algorithms with % RC less than 30%. A third partition was formed by only including those algorithms with a % RC less than 15%.

A linear mixed effects (LME) model using transformed data was fitted to estimate the relative contributions of different factors to the total variability. The dependent variable in the model was the measured tumor volume. Volume estimation is considered a fixed effect in this model. The independent variables were tumor, algorithm, and tumor-by-algorithm interactions. Model assumptions were evaluated with Q-Q (quantile-quantile) and observed-versus-fitted plots.

Comparison of Segmentation Boundaries

Five groups provided segmentation data in addition to tumor volume measurements, four of which were compatible for analysis (the data from the fifth was submitted with different orientation and scaling). To compare algorithms' segmentation boundaries, we produced a reference segmentation using the Simultaneous Truth And Performance Level Estimation (STAPLE) method [40] on 3D volumes. This method performs a voxel-wise combination of an arbitrary number of input images, which in our case consisted of the segmentations extracted by the four participant algorithms. Each input segmentation to STAPLE was weighted based on its “performance” as estimated by an expectation-maximization algorithm, described in detail in [41]. This algorithm used all input segmentations to create “consensus” results according to the level of overlap among input segmentations. We then compared each individual segmentation result to this reference data. We computed voxel-wise accuracy, based on the number of voxels segmented with a particular algorithm compared with the reference data by tabulating counts of true positives (TP, where both the algorithm and the reference contained that voxel), true negative (TN, where neither the algorithm and the reference contained that voxel), false positive (FP, where the algorithm contained the voxel but the reference did not), and false negative (FN, where the reference contained the voxel but the algorithm did not). These were used in the calculation of two spatial overlap measures, the Jaccard index [42], and Sørensen–Dice coefficients [43, 44] defined as:

$$\mathit{\text{Jaccard}}=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FP}}+\mathit{\text{FN}}}$$

$$\mathit{\text{SørensenDice}}=\frac{2\times \mathit{\text{TP}}}{2\times \mathit{\text{TP}}+\mathit{\text{FP}}+\mathit{\text{FN}}}$$

The Jaccard index includes a penalty for false positive voxels, i.e., when the candidate segmentation is larger than the reference segmentation. The Sørensen– Dice coefficient also penalizes false positives, but penalizes more strongly segmentations that have missed true positives. We computed and presented both types of overlap metrics to allow easier and wider comparison with results from other studies.

Excel was used for RC, wCV, and RDC estimation, the R statistical software was used for the mixed-effects model, and Matlab was used for overlap metrics.

III. Results

1. Precision of Volume Measurements

The total number of possible readings was 744, with each of twelve participating groups submitting both test and retest readings for each of 31 tumors. Of these, 740 were actually submitted, with the following cases missing:

• One group only submitted readings on 30 tumors (rather than 31).

• One group only submitted test readings (without retest readings) for two tumors.

Basic descriptive statistics on submitted measurements are given in Table 1, based on the 740 submitted readings. The distribution is skewed due to a very few large reading values, where the mean is much higher than the median.

Table 1. Basic Descriptive Statistics for measured tumor volume.

	Volume (mm3)	Equivalent Sphere Diameter (mm)
Arithmetic Mean	24,100	36
Geometric mean	8,320	25
Median	9,110	26
Range	160,000	67

Detailed review of these 740 submitted readings exposed 34 presumably anomalous readings (leaving 706):

• The unpaired readings were judged anomalous due to having no retest readings.

• Four test/retest reading pairs from three groups differed by log-orders of magnitudes from the rest of the data, suggesting data transcription errors.

• One tumor was particularly challenging for all groups, as judged by the differences in volume measurements being log-orders of magnitudes from each other (whereas other tumors, even other ones which did not otherwise meet the measurability criteria established by QIBA did not exhibit this behavior).

Intra-algorithm repeatability analyses were performed and presented here with and without the readings judged as anomalous. Inter-algorithm reproducibility was assessed with these values excluded. These were removed from the analyses.

Intra-algorithm Repeatability Across Test-Retest Repetitions Within Groups

Repeatability results assessed separately for each group are presented in Table 2. Tumors were judged to be “Small” if they had a volume of less than 4189 mm³, an equivalent diameter of less than about 20 mm for a sphere, and “Large” otherwise (as judged by algorithms individually). Since the algorithm measurements were not normally distributed and did not have constant variance, a log-transformation was applied, reshaping the distribution of the data into a usable form. These summary metrics apply across the large range of tumor volumes included in the study. Figure 2 depicts how the percentage metrics, wCV_inter and % RC, changed based on the difference in the two measurements for differing tumor sizes, stratified by algorithm performance. Moderately performing algorithms are plotted in the upper panel. In general, these algorithms perform at levels less than 20 % RC over the majority of the range, and would be generally understood as being capable of conforming with QIBA repeatability performance requirements. The lower panel depicts the results for the best performing algorithms which not only provide the best repeatability, but which could also be considered for interchangeability were they to be utilized in certain clinical trial designs or clinical use cases.

Table 2. Intra-algorithm repeatability results.

	Using all 740 Readings	34 Anomalous Readings Excluded
		All Tumors Pooled			Small	Large
Group	RC (mm3)	RC (mm3)	% RC	wCVintra	RC (mm3)	RC (mm3)
Group02	7,557	1,871	13%	5%	141	1,866
Group03	14.060	13,568	100%	36%	1,321	13,501
Group04	1,801	1,830	14%	5%	175	1,825
Group05	3,007	2,177	14%	5%	245	2,163
Group06	3,418	3,472	20%	7%	160	3,469
Group07	3,495	3,551	20%	7%	210	3,545
Group08	2,935	2,982	13%	5%	147	2.979
Group11	41,411	39,885	50%	18%	441	39,883
Group12	43,101	37,868	48%	18%	601	37,863
Group14	11,081	11,259	21%	7%	161	11,257
Group15	2,226	2,261	24%	9%	321	2,238
Group10/161	7,522	7,643	22%	8%	215	7,639

¹Volume results submitted under ID Group16 and segmentation objects submitted under ID Group10.

Figure 2.

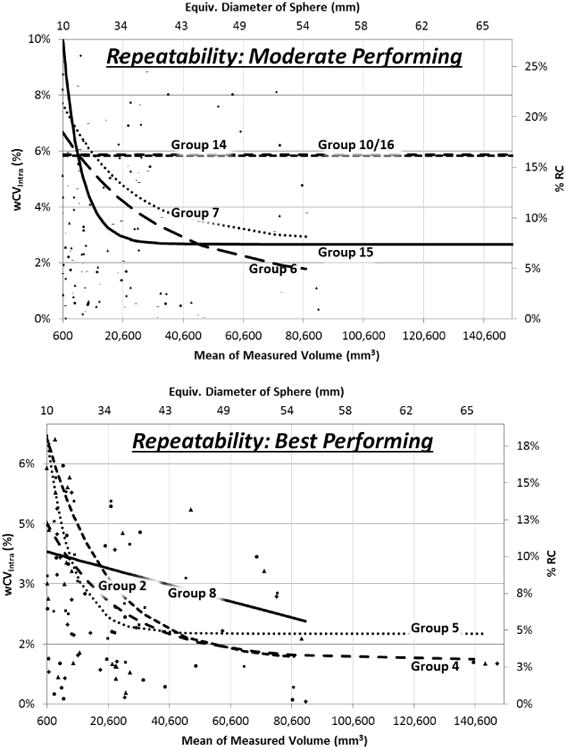
Results of intra-algorithm repeatability analysis plotted as a function of measured tumor size. The line fits follow exponential functions. Fits for the least performing algorithms could not be made given highly variable results from tumor to tumor. Upper panel shows performance with fit lines for moderate performing algorithms, and lower panel for best performing algorithms. The fit lines are truncated where they would imply better performance than the sparse set of points at high tumor volumes actually suggest.

Inter-algorithm Reproducibility Across Groups

Three separate reproducibility partitions were analyzed. One partition included all groups but Group 3 which demonstrated multiple discrepancies from the behavior exhibited by the other algorithms and had a % RC well above other groups. Another partition included the set of groups that would be considered to conform to QIBA's requirements as judged by a % RC less than 30%. A third partition was formed by only including those algorithms with a % RC less than 15%. Reproducibility results across all groups are presented in Table 3. Figure 3 depicts how the percentage metrics changed for differing tumor sizes.

Table 3. Inter-algorithm reproducibility results.

Partition	RDC	% RDC
All but Group 3	25,284 mm3	84%
Conforming Groups	16,057 mm3	70%
Best Performers	9,290 mm3	58%

Figure 3.

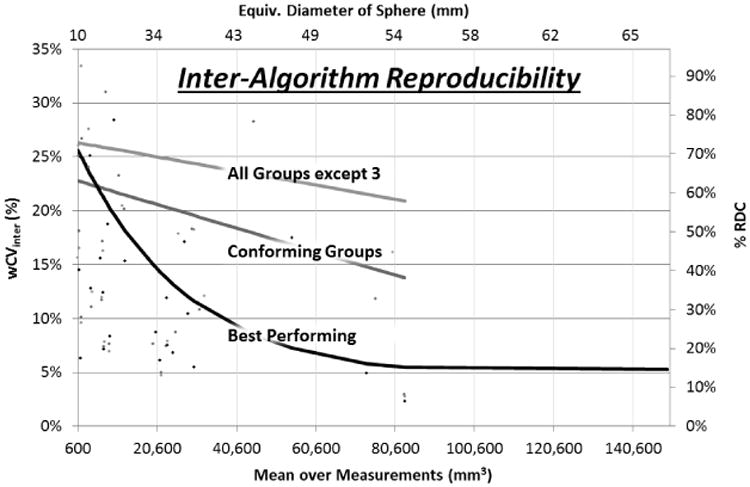
Results of inter-algorithm reproducibility analysis plotted across tumor size range. Line fits follow exponential functions. The fit lines are truncated where they would imply better performance than the sparse set of points at high tumor volumes actually suggest.

Linear Mixed Effects Model for Estimating Algorithm vs. Other Sources of Error

Results of the Linear Mixed Effects (LME) are presented in Figure 4 which illustrates the weights of the four different variables on overall volume variability. The variables included in the LME model are: tumor, algorithms, and tumor-by-algorithm interactions. Residual error relates to factors not included in the model.

Figure 4.

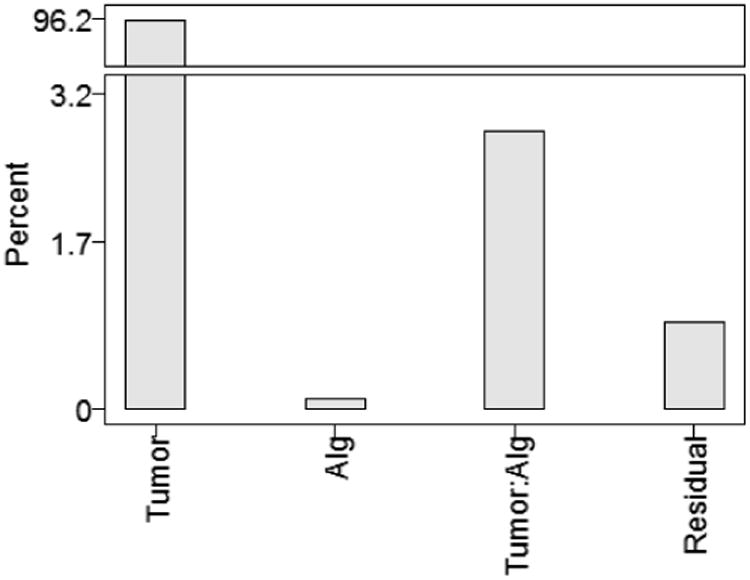
Results of LME for overall reproducibility analysis, illustrating the percent of total variation captured by each model factor.

Tumor variation between patients dominates with 96% of total variation, which is expected as this is the component which is due to true differences in the object being measured. Tumor-by-algorithm interaction variance comprises the next highest variance, accounting for 3% of the variance, indicating that tumors were measured differently by different algorithms, which is the primary reproducibility result. Residual variance of 1% accounts for factors not attributable to the algorithm performance, e.g., hardware variations or scanning technique.

Stratified Reproducibility Analyses

Four other stratified analyses of reproducibility were carried out, for various combinations of the tumors outlined in Table 4. (For these analyses, definition of Small and Large was judged based on the average volume estimate for a tumor across the algorithms and using the same 4189 mm³ threshold as used in the repeatability analyses.)

Table 4.

Number of tumors analyzed in each strata. Profile=Yes or No indicates whether the tumor met the measurability requirements as described above. With/without editing defines whether post-segmentation contours could be adjusted by a user.

Analysis	Strata	N
Overall	All	31
	Small	8
	Large	23
Profile=Yes	All	20
	Small	7
	Large	13
Profile=No	All	11
	Small	0
	Large	11
With editing	All	31
	Small	8
	Large	23
Without editing	All	31
	Small	8
	Large	23

Results for the stratified analyses are summarized in Table 5. The reproducibility of volumetric measurements was better for tumors meeting the QIBA Profile (Profile=Yes) compared to those tumors that did not (Profile=No). This was also reflected in the reduced ratio of algorithm/residual variance for those two analyses. Reproducibility was better when editing was not allowed, indicated by smaller RDC, and smaller algorithm/residual variance in the factors model.

Table 5.

Summary of reproducibility results for stratified subgroups of tumors and algorithms. “Alg/Residual Variance” indicates the relative contributions of the two factors to the total variability.

	RDC of Small Tumors	RDC of Large Tumors	Alg/Residual Variance (all tumors)
Combined	1,290 mm3	28,205 mm3	3:1
Profile=Yes	1,290 mm3	6,369 mm3	2:1
Profile=No	(none in sample)	41,074 mm3	10:2
With Editing	1,343 mm3	26,760 mm3	4:1
Without editing	1,234 mm3	33,004 mm3	2:1

2. Analysis of Segmentation Boundaries

Figure 5 shows an example of a reference standard segmentation based on the STAPLE algorithm applied to the segmentation results. A reference segmentation was created for each test-retest repetition and each individual tumor. As indicated in the methods section, the reference segmentations were formed using an expectation-maximization algorithm applied to the four compatible submissions. Figure 6 shows an example slice for a single algorithm (Group08) overlapping with the corresponding reference segmentation. Full evaluation of individual segmentation methods is beyond the scope of the present study but the detailed maps are provided to the groups who contributed segmentation boundaries for their own analysis.

Figure 5.

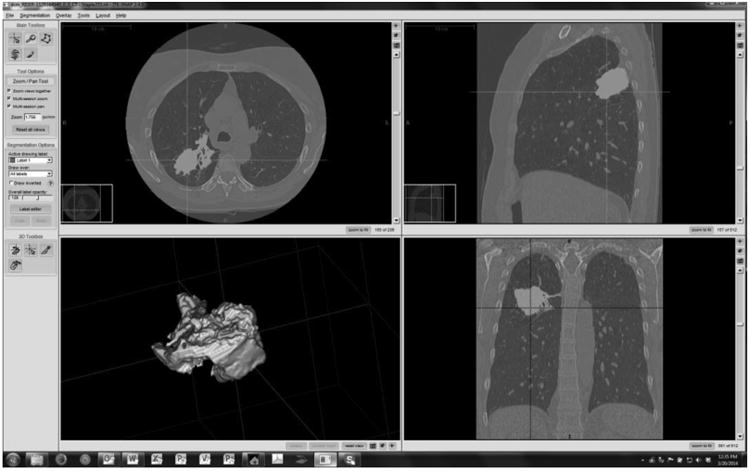
Example of a reference truth segmentation. (RIDER-1129164940, first repetition, Group08)

Figure 6.

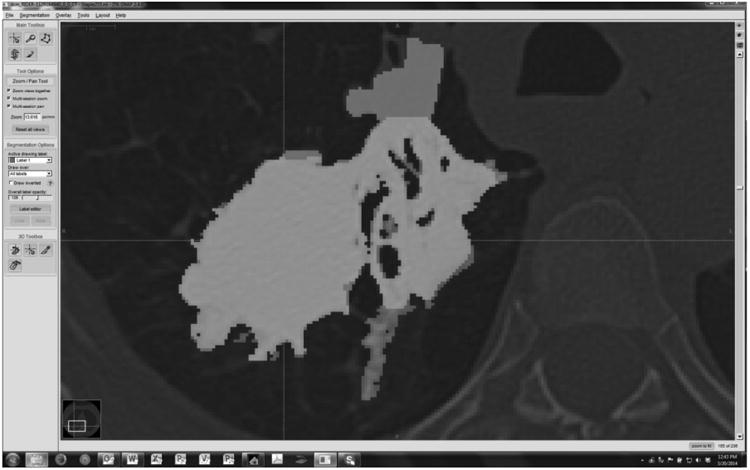
Example of a group's result superimposed on to the reference. True positive (TP) voxels are rendered as light grey, False Negative (FN) voxels as dark grey, and False Positive (FP) as medium grey. True Negative (TN) pixels are displayed as reduced intensity background image. (RIDER-1129164940, first repetition, Group08)

Merging and Plotting of Histograms by Metric and Group

Figure 7 illustrates the histograms of the results created for each group and merged onto a plot that compares the relative segmentation performance of each. The higher numbers of Sorensen-Dice results above 0.8 compared with Jaccard results suggests that over-segmentation (resulting in larger volume measurements) may have been a larger issue than under-segmentation (relative to the imperfect reference standard). Group10/16 performs best, Group03 was the least performing algorithm (consistent with its poor computed volume performance), and Groups 04 and 08 depend on the metric used.

Figure 7.

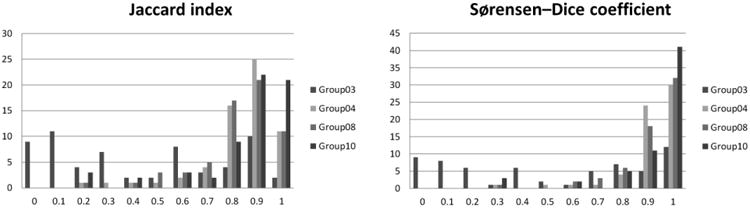
Merged histograms for each of three overlap metrics. The x axis represents the relevant index value (0-1). The y axis represents the number of tumors with the corresponding index value. Results from 4 algorithms are plotted with separate colors but combined on each plot to facilitate comparison.

IV. Discussion

This study was setup to simulate actual practice in the field vs. what might be considered from a more controlled academic setting, consistent with QIBA's role of engaging the multiple stakeholders, notably industry, in the practice of quantitative imaging biomarkers such as CT volumetry. In this setting, the information identified in the appendix is similar to what would be available for methods that are used in practice. Through studies such as ours, we document the performance available and through the Profile writing effort we seek to identify and reduce sources of variable performance where studies like the present one highlight variability. The goal was not to determine the best algorithm but rather the range in performance across diverse algorithms. This is important to the QIBA Profile because the profile describes the performance not of any one algorithm but of a diverse group of algorithms.

Intra-algorithm %RC ranged from 13% (best performing) to 100% (least performing), with most algorithms demonstrating better percentage performance as the tumor size increased. The four algorithms with the smallest RCs (Groups 2, 4, 5, 8) were self-identified as semi-automated without editing while the ones with the highest RCs tended to be semi-automated with editing algorithms (Groups 3 and 11: semi-automated with editing) as described in the Appendix. Semi-automated with editing algorithms allow the clinician to correct for egregious segmentation boundaries that can occur when segmenting low-contrast, large or complex tumors, but this can also introduce the variability often observed from individual perception. One interpretation of these results would be that poorly performing algorithms need editing due to egregious results without it, but once an algorithm is refined to avoid these then editing actually makes the results inferior as they may be best left alone. The algorithms generally show a marked tendency to have smaller percentage metrics (less variability) for larger tumors which is consistent with related literature findings [11, 45, 46]. Algorithms were also fairly consistent across tumor sizes in that the algorithms with the highest wCVs for small tumors also tended to have the highest wCVs for large tumors. The data shows some differences, however; for example Group 8 has a lower disparity in wCVs between small and large tumors compared with the other best performers.

The RC and wCV results indicate good overall repeatability performance for at least a subset of algorithms, possibly suggesting that some algorithms may also have the potential to be used interchangeably as tumor volume measurement tools for use cases where it is not possible to use a single algorithm. By itself, RC is not sufficient comparing algorithms with unknown truth, motivating the reproducibility analysis which is a measure of the dispersion in values across algorithms. If the multiple algorithms are individually repeatable but each comes up with (widely) varying measurements, RDC is large (poor) and the algorithms would not be deemed interchangeable. The only way for RDC to come out small is if the algorithms measurements are similar among them, and if both the test and retest measurements from each algorithm are included in the calculation of RDC, then it may suffice as a test of interchangeability, hence our approach. Previously reported repeatability results are widely varied across projects and authors; our results demonstrate a range of results as experienced in practice to help account for some of these differences.

The RDC and % RDC was determined in three partitions; 58% for the four best performing groups, 70% for an expanded set of algorithms on the basis of their intra-algorithm repeatability being less than 30%, and 84% when all groups but one that was excluded due to erratic behavior. This analysis of the RDC values shows that across all algorithms, the reproducibility performance was low and that in general, interchanging of all algorithms is not appropriate. This is not surprising because of the low repeatability for some algorithms including Groups 3 and 11 among others. When we evaluated the reproducibility for the subset of algorithms with the best repeatability (e.g., Groups 2, 4, 5 and 8) we found that reproducibility improved to 7%. This provides initial evidence that some tumor volume measurement tools might be appropriate for interchangeable use across patient scans acquired at different times. However, this appears to be only possible for a small subset of the algorithms evaluated in this study, and even with these only on tumors with equivalent diameter exceeding 40 mm. For the other algorithms, or for tumors less than 40 mm, care should be taken that the same algorithm is applied at each subsequent time point to eliminate inter-algorithm variability as part of the overall measurement error.

The reproducibility results of Table 5 show that RDC is lowest when algorithms were applied on tumors meeting the measurability criteria defined in the Profile as expected. Editing helps performance on larger tumors but no editing is better for small tumors. This may be intuitive, in that larger tumors often include more complex structure, such as larger vessel attachments, and more variation in structure within the tumor whereas smaller tumors might be more easily segmented without need for editing and actually more variable if users try to do so.

Another consideration concerns the extent to which the algorithm may be considered “the end of the line” with respect to variability of the entire process of evaluating tumor size. Our LME analysis showed that over 96% of the variation is associated with the tumor, leaving just 4% related to other factors. Of this remaining 4%, one-fifth to one-half of this variability comes from sources independent of the algorithms. The ratio of the size of the effect due to algorithm (plus algorithm-tumor interaction) versus the residual informs an “error budget” that may be used for specifying allowable variability due to algorithm versus other parts of the processing chain, so that the system as a whole meets the QIBA claim. On this basis, using results summarized in Table 5, no more than two-thirds of the overall variability claim of the system can be allocated to analysis software if the overall system is to be meet the QIBA Profile claims. By this measure, conforming algorithms are those with RC less than two-thirds of the overall QIBA profile claim of 30%, or 20%. Eight of the twelve algorithms assessed in this study met this criterion. If the scanner and acquisition parameters are not controlled, demands on algorithms would be much higher. Hence, the QIBA approach is to define performance requirements as means to reduce this variability, even though it cannot be eliminated completely.

An additional consideration in characterizing and comparing segmentation algorithms is the segmentation boundaries themselves. We utilized the Jaccard Index and Sørensen-Dice coefficient for this task. The Jaccard Index and Sørensen-Dice coefficient are consistent across Groups 4 and 8 indicating that the segmentations are generally consistent in both volume and edge profiles for these high RC algorithms. This provides stronger evidence that these two algorithms, and potentially Group 5 as well, could be used interchangeably when evaluating CT tumor progression. Groups 3 and 10/16 did not agree with each other or with Groups 4 and 8 in regard to the Jaccard Index and Sørensen-Dice coefficient indicating that they likely could not be used interchangeably with any other algorithm and may in fact have divergent performance.

The reference standard segmentation was based on the STAPLE algorithm defined across all of the four algorithms that provided segmentation results (Groups 3, 4, 8 and 10/16). This is the maximum likelihood segmentation for the tumor based on the segmentations. It may be appealing to think of the reference standard as an estimate for the borders of the true tumor. However, this is generally not appropriate because the segmentation algorithms likely over- or under-segment the true tumor, globally or within local regions. Either case would produce a bias in the true boundaries. Even with this limitation, the reference standard can be useful when comparing a set of algorithms because it will show which algorithms have substantial deviation from the norm. This information is likely very helpful in determining which subsets of algorithms can potentially be used interchangeably as discussed above.

The greatest utility of this work, and public algorithm challenges in general, from a group's point of view, or a company seeking to commercialize analysis software for tumor volumetry, may be the performance of their algorithm compared with other similar algorithms. Individualized reports inclusive of raw data and intermediate analysis results have been provided to participants in the challenge. The value of the results is highest to those who contributed actual segmentation boundaries, given the ability to distinguish true positive and negatives from false positives and negatives at a level of granularity allowing algorithm optimization. This data is instrumental to inform the definition of a performance standard for CT tumor volumetry algorithms. Participating groups also benefit in that algorithm weaknesses are identified.

Our study has limitations. The degree and extent of editing applied to semi-automated algorithms was not held constant between replicates (test-retest measurements) which could have contributed to the overall variability and associated measures of repeatability and reproducibility. Also, our analyses did not account for differences in experience between algorithm operators in terms of interacting with radiological findings or in terms of familiarity/training with the software. Another limitation stems from an explicit determination for this study that workflow not be constrained, but the related QIBA 1B study suggests that workflow considerations are of substantial importance. In this case, workflow refers to how the repeat scans were processed. In our study, all of the scans were processed independently while in part of the QIBA 1B study scans were process in a locked sequential fashion. We had originally thought that semi-automated without editing algorithms (no post-segmentation correction) would not differ in their performance based on workflow, but found that this does not always hold true because ROI and seed placements may be affected. Additionally, the data used in this study were relatively limited, thus only an early version of the QIBA Profile claim specification can be made. Although the data contained an assortment of clinical cases, they did not fully represent the claimed clinical context of use for the corresponding QIBA Profile. Definitive reference data sets that adequately represent the target patient population according to formally assessed statistical criteria should include patients representing a range of common co-morbidities, disease characteristics, and imaging settings (e.g. sedated vs. non-sedated patients). Finally, the manner in which these tests are run and the data collected has implications regarding the interpretation and use of metrics computed and reported. For example, execution of these tests by a trusted third-party on sequestered data sets may increase their utility.

VI. Appendix: Algorithm Descriptions

Eleven groups participated in the challenge by submitting volume readings for twelve algorithms and five submitted segmentation boundaries, four of which were compatible for analysis. Algorithms from each participating group are described below.

Participating Group	Description / Workflow
Group02 (volume readings and segmentation boundaries1) Moderate image/boundary modification (on less than 50% of the tumors)	Volumetric analysis was determined using a segmentation approach employing a Z-score on the highest conspicuity post-contrast volumetric image set. A cylinder is placed around the highest conspicuity slice and around all slices above and below this slice in which the tumor is seen. A kernel defined within the region of interest (ROI) is then propagated to other slices using connectivity algorithms. The search is constrained by the predefined cylinder to accelerate the search algorithm.
Group03 (volume readings and segmentation boundaries) Editing not allowed	One-click user-seeded segmentation. Utilizes shape and boundary information to delineate the tumor. The workflow for segmenting lung tumors involves a single click at a seed-point roughly centered in the tumor. The algorithm uses the seed point in combination with a thresholded ROI in order to extract the most probable shape of the tumor.
Group04 (volume readings and segmentation boundaries) Limited image/boundary modification (on less than 15% of the tumors)	Utilize a trained non-radiologist technician and trained radiologist. As the images would be of chest and the tumors would be in lung parenchyma, all the volume assessment were made using a fixed lung window/level display setting of 200HU (window) and -1400HU (level). Trained non-radiologist opens the images in and uses the tumor location to identify the tumors on images. Trained non-radiologist outlines/ROIs of the identified tumors using automated algorithms. Trained non-radiologist evaluates the quality of the segmentation and adjusts outlines with additional semi-automated tools as necessary. Finally, that image data is submitted to trained radiologist for final assessment of outlines/ROIs. The trained radiologist evaluates the quality of the segmentation and adjusts outlines with automated & semi-automated tools as necessary. Once trained radiologist is satisfied with all the outlines/ROIs of the respective tumors, the automated volume assessment tool is used to calculate volume as volume = (Image Position Interval1 * Area1) + (Image Position Interval2 * Area2)…+…+ (Image Position Interval n * Area n). The images with ROI is processed, re-colored and converted in to .nii file.
Group05 (volume readings) Moderate editing allowed (on less than 50% of the tumors).	Modelization of the heat-flow between the inside and outside of the tumor. Based on intensity gradients, in 3D. User clicks on a tumor, or draws a diameter joining the boundaries of the tumor => software computes a segmentation of the tumor, and displays its contours. User can then refine the segmentation by the means of a slider => software adjusts the segmentation accordingly, and displays in real-time the new contours. If needed, user can manually edit any contour by drawing it. User finally validates the segmentation => software “locks” the segmentation and extracts the statistics: volume, long axis, short axis, and all intensity-based numbers (average value, standard deviation, etc.)
Group06 (volume readings) Editing not allowed; (uses only seed points and ROI information)	This algorithm combines the image analysis techniques of region-based active contours and level set approach in a unique way to measure tumor volumes. It may also detect volume changes in part solid and Ground Glass Opacity tumors. The user clicks and drags to define an elliptical/circle ROI to initiate the segmentation. The computer then carries out the segmentation, and tumor measurements are saved. The algorithm is an edge-based segmentation method that uniquely combines the image processing techniques of marker-controlled watershed and active contours. An operator initializes the algorithm by manually drawing a region-of-interest encompassing the tumor on a single slice and then the watershed method generates an initial surface of the tumor in three dimensions, which is refined by the active contours. The volume, maximum diameter and maximum perpendicular diameter of a segmented tumor are then calculated automatically.
Group07 (volume readings) Editing not allowed; (uses only seed points and ROI information)	An initialization sphere is drawn from the center of the mass, on the slice with its largest boundaries, such that it covers the entire extent of the mass. The user determines the center and radius in a single click-drag action, and this initialization circle imposes hard constraints on the maximum boundaries of the three dimensional segmentation. The employed algorithm is part of a commercial software package for multimodal oncology treatment assessment and review. Thus the workflow mimics the typical workflow a user has with this tool: Select the desired CT data set and load it into any review mode Select the lung window-level setting Navigate to the tumor center using the pixel and slice locations from the MSKCC Coffee Break study Locate the slice where the tumor has the greatest boundaries Select the algorithm, and initialize the segmentation by clicking in the approximate center of the mass and dragging the mouse to set the radius of the spherical region of interest. The spherical region of interest contains a fixed inner sphere and the outside sphere which is set by the mouse dragging motion. The radius is chosen such that the inner circle encompasses most of the mass to be segmented, and the outer sphere can be used as a constraint to prevent any leakage into the chest wall or heart if the mass is attached/abducting to these organs. The computation takes a few seconds (single digit numbers) to compute the result. User may retry the segmentation a few times if the result is unsatisfactory. With each try the previous result is erased, and does not influence the result of preceding try. In this experiment, the user has in overall three tries to get a satisfactorily result. Once the segmentation has been determined, the user reads off the volume from the region statistics, which are automatically computed and displayed as soon as the segmentation has been defined. (The volume measurement algorithm counts all voxels whose centroid lies within the segmented contour and multiplies this number with voxel volume) To document the segmentation result, save the segmentation as a RT-structure set to the data repository
Group08 (volume readings and segmentation boundaries)Moderate editing allowed (on less than 50% of the tumors)	Semi-automatic segmentation based on thresholds, growing region and mathematical morphology processing DICOM images are downloaded and imported into a database. Image data are converted to a proprietary optimized format before the insertion into the database. Tumors coordinate are downloaded and reformatted by our data manager. Relying on a proprietary Validation Framework System, landmarks are automatically inserted into the database. The software is allowed then to display the repeated images side by side with the correct landmarks identifying the tumors to segment. The first repetition was edited as a single image. The side-by-side displayed was available only for the repetition when the first scan edit was locked. Three reviewers are involved, each in charge of segmenting approximately a third of the dataset. The data manager made available to the reviewers a commercial semi-automated algorithm dedicated to Lung tumors. Another manual tool can be enabled if semi-automatic segmentations were not fully satisfactory. The data manager recommended using different window level to better assess tumors boundary, pulmonary window level being the major window level to refer to. The data manager recommended correcting semi-automated segmentation as long as the segmentation was not fully satisfactory. Once the whole dataset segmented, an additional reviewer was involved to check the whole coherency of the measurements: Total number of tumors, no obvious incoherency, correct recording of the data, etc. A complete report was extracted. The same Validation Framework System allowed automatic extraction of tumors mask as .mhd format. A third party software as SLICER was used to convert masks to NIFTI format.
Group11 (volume readings) Editing not allowed (uses only seed points and ROI information)	Method is completely automatic and consists of three steps. First, a region of interest is extracted and the tumor is classified as solid or subsolid. In the second step, a binary segmentation mask is computed by an algorithm based on thresholding and morphological postprocessing, using slightly different procedures for the two classes. Finally, the volume of the tumor is determined by adaptive volume averaging correction. Preprocessing: a stroke is generated from the given center and bounding box by shortening the bounding box diameter to 40%. The segmentation is performed in a cubic region of interest (ROI), whose edge length is twice the stroke length. The ROI is smoothed with a 3 × 3 Gaussian filter and resampled to isotropic voxels and a maximum size of 100 × 100 × 100 voxels. For detecting the tumor type, the local maximum in a 5 × 5 × 5 neighborhood of the ROI center is identified. If its value is greater than -475 HU, the tumor is treated as solid, otherwise as subsolid. The ROI center is used as a seed point for region growing. The lower threshold is derived from the 55% quantile of the histogram of the dilated stroke by applying an optimal elliptic function yielding values between -780 and -450 HU. The resulting mask contains the complete tumor, but may also leak into adjacent vasculature or, in case of juxtapleural tumors, into structures outside the lungs. In order to remove vessels, an adaptive opening is applied, where the erosion threshold is chosen such that the segmentation has no connection to the ROI boundary anymore. A slight overdilation allows a final refinement of the mask. In order to avoid leakage outside the lungs, a convex hull of the lung parenchyma is computed within a minimal elliptical region that is fitted to the shape of the tumor. The convex hull is then used as a blocker for the segmentation. Due to the limited spatial resolution of CT and partial volume effects, the volume of a segmented tumor cannot be determined exactly by voxel counting. Instead, voxels in a tube around the segmentation boundary are weighted according to their estimated contribution to the tumor volume. The weight depends on the relation of a voxel's value to the typical tumor and parenchyma densities.
Group12 (volume readings) Moderate editing allowed (on less than 50% of the tumors)	We start with an automatic method (submitted Group11) and correct results interactively if necessary. The user draws partial contours which are included in the segmentation in the edited slice. Additionally, the correction is automatically propagated to a set of neighboring slices by sampling the contour, matching points to the next slice and connecting them with a live-wire method. Interactive correction: Our interactive correction tool provides an efficient way to fix segmentation results which are mostly correct but need some refinement. The user draws partial contours indicating the desired segmentations which are then automatically propagated into 3d. Seed points calculated from the user contour are moved to adjacent slices by a block matching algorithm and the seed points are connected by a live-wire algorithm. For the submission, correction was performed by two experienced developers in consensus. Volumetry: The volumetry used for automatic results is integrated in the segmentation algorithm. To ensure consistency after interactive correction, the change in the number of voxels is computed and multiplied with the (partial-volume-corrected) volume of the initial result.
Group14 (volume readings) Editing not allowed (uses only seed points and ROI information)	The system is fully automated after manual input of an approximate bounding box for the tumor of interest. Within the bounding box, the system automatically processes the images in 3 stages-preprocessing, initial segmentation, and 3D level-set segmentation. In the first stage, a set of smoothed images and a set of gradient images are obtained by applying 3D preprocessing techniques to the original CT images. Smoothing, anisotropic diffusion, gradient filtering, and rank transform of the gradient magnitude are used to obtain a set of edge images. In the second stage, based on attenuation, gradient, and location, a subset of pixels is selected, which are relatively close to the center of the tumor and belong to smooth (low gradient) areas. The pixels are selected within an ellipsoid that has axis lengths one-half of those of the inscribed ellipsoid within the bounding box. This subset of pixels is considered to be a statistical sample of the full population of pixels in the tumor. The mean and SD of the intensity values of the pixels belonging to the subset are calculated. The preliminary tumor contour is obtained after thresholding and includes the set of pixels falling within 3 SDs of the mean and with values above the fixed background threshold. A morphologic dilation filter, a 3D flood fill algorithm, and a morphologic erosion filter are applied to the contour to connect the nearby components and extract an initial segmentation surface. The size of the ellipsoid and the remaining parameters are selected experimentally in a way that enables segmentation of a variety of tumors, including necrotic tumors. In the third stage, the initial segmentation surface is propagated by using a 3D level-set method. Four level sets are applied sequentially to the initial contour. The first three level sets are applied in 3D with a predefined schedule of parameters, and the last level set is applied in 2D to every section of the resulting 3D segmentation to obtain the final contour. The first level set slightly expands and smooths the initial contour. The second level set pulls the contour toward the sharp edges, but at the same time, it expands slightly in regions of low gradient. The third level set further draws the contour toward the sharp edges. The 2D level set performs final refinement of the segmented contour on every section
Group15 (volume readings) Moderate editing allowed (on less than 50% of the tumors)	The software used is essentially a semi-automated contouring method. The user clicks on a voxel located inside the tumor of interest and then drag a line to the outside of the tumor (to the background). The voxels along that line are sampled and a histogram of intensities (Hounsfield Units) is created. A statistical method is employed to determine the threshold that best separates the two distributions (tumor and background) in that histogram. Once that threshold is determined, the software employs a 3-D (or if selected a 2-D) seeded region growing using the initial voxel selected as the point inside the tumor and the threshold determined from the histogram analysis. The tool also provides several user editing tools such as adding and erasing voxels from the contour, etc. The workflow description: Each contour is automatically stored in a database linked to the experiment along with meta data such as patient id, contouring individual's id, etc. Each contoured object has a unique id that is linked to the series uid to maintain its identity. Once the contour is completed and accepted, the volume of the contoured object is calculated. This is done essentially by counting the number of voxels within the boundaries of the contoured object and multiplying that by the voxel size (as derived from DICOM header data).
Group10/16 (volume readings and segmentation boundaries2) Limited editing allowed (on less than 50% of the tumors)	As the input for the algorithm, the user has to draw a stroke being favorably the largest diameter in the axial orientation or click a point in the given lung tumor. Usually, the decision to use a stroke or a single click point depends on the size of the tumor to be segmented (for bigger tumors, a stroke is preferable, while for small tumors, a single click is sufficient). In the next step, a Volume of Interest (VOI) around the tumor is estimated. In the case where the algorithm has been initialized with stroke, the size of the VOI depends on the length of the stroke. 3D region growing is conducted in a VOI starting from seeds generated along the stroke or around the click point, depending on the initialization. Adjacent structures of similar density (pleura, vessels) are separated by a set of interchanging morphological operations (erosion, dilation, convex hull and binary combination with region growing mask.) Finally, a plausibility check between the resulting segmentation mask and the position of the initial stroke or click point is conducted. If necessary, initial thresholds are readjusted and the whole procedure (steps 2-5) is repeated. For the case when the semi-automatic results are not satisfactory, the software provides the possibility of correcting the results by drawing contours in selected slices and then propagating the contours in an automatic manner onto the whole 3D segmentation. The algorithm performs best optimally for the resolution up to 2 mm, though it still works reasonably well for thicker slices such as 5 mm.

¹Alignment issues prevented inclusion in the segmentation boundary analysis.

²Volume results submitted under ID Group16 and segmentation objects submitted under ID Group10.

Three groups (Group01, Group09, and Group13) initially applied but did not submit results.