Laboratory studies have demonstrated a satisfaction of search (SOS) effect in chest radiography, with reduced accuracy in detecting native abnormalities on chest radiographs in the presence of simulated pulmonary nodules (1, 2). Various abnormalities were missed when a pulmonary nodule was present (SOS condition), but detected when the nodule was absent (non-SOS condition). The original experiment on SOS effects in chest radiography (1) was conducted 25 years ago and the most recent replication (2) 15 years ago. Both of those studies demonstrated a reduction in detection accuracy as a function of SOS. The practice of radiology has changed significantly in the last two decades. Film has given way to digital imaging. The utilization of CT and MR examinations has dramatically increased and advanced imaging is often the preferred initial examination. Resolution and quality of those modalities have improved significantly. There have been corresponding changes of emphasis in the training of radiologists.
The purpose of the current investigation is to test for SOS effects in computed radiography (CR) of the chest. A new set of test cases acquired with CR were read by a new sample of resident, fellow, and faculty radiologists. Results of the earlier studies (1, 2) were subjected to additional analyses of decision thresholds to better understand current results.
MATERIALS AND METHODS
Experimental Conditions
We used the same two conditions used in previous SOS demonstrations: presentation of each chest radiograph with and without a simulated pulmonary nodule. The detection accuracy for native, subtle lesions was assessed with and without the addition of a digitally added simulated pulmonary nodule. This created two cases with the same background anatomy and actual lesions perfectly matched for the two conditions (Figure 1). Simulated and native lesions were not spatially superimposed, and the native abnormalities were physically identical with and without the nodules.
Figure 1. Constructs for the experimental conditions.
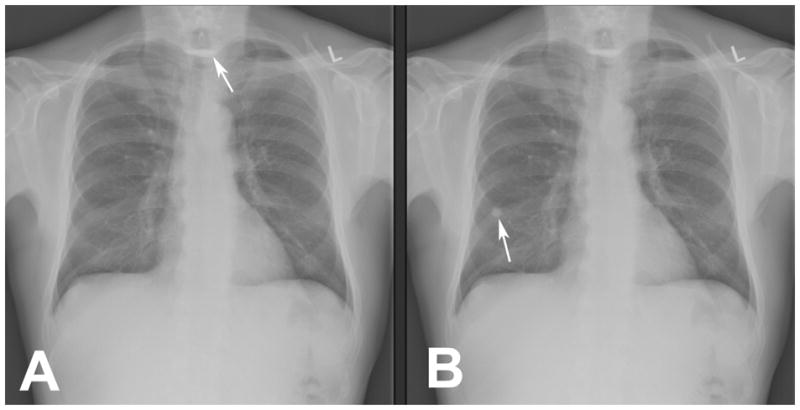
The non-SOS condition presents without a pulmonary nodule (A) and the SOS condition presents with a pulmonary nodule (B). The same native abnormality, a Zenker’s diverticulum with residual barium, appears in both A (white arrow) and B. A simulated pulmonary nodule has been digitally placed in B (white arrow). In all other respects the two images are identical.
Cases and Readers
Sixty-four new CR chest cases were obtained from clinical studies with approval by our local institutional review board. Verification of the lesions and disease state was through follow-up studies, surgery, clinical course, laboratory tests, and autopsy reports that were part of the patient medical record. All patient identifiers were removed from the studies to ensure patient confidentiality. Thirty-three cases presented subtle, native abnormalities (Table 1) and thirty-one had no native abnormalities. The versions for the SOS treatment condition were generated by adding simulated pulmonary nodules to the original 64 examinations (described below).
Table 1.
Native Abnormalities in Case Sample
| Native Abnormality | Number |
|---|---|
| Aneurysm, chest | 3 |
| Aortic calcification | 1 |
| Asbestosis | 1 |
| Cardiomegaly | 1 |
| Cervical ribs | 2 |
| Clavicle fracture | 1 |
| Dilated esophagus | 1 |
| Free air hemidiaphragm | 2 |
| Gallstones | 1 |
| Gastric air shadow compressed | 1 |
| Hiatal hernia | 2 |
| Middle lobe collapse | 1 |
| Morgagni hernia | 1 |
| Pneumonia | 1 |
| Pneumothorax | 2 |
| Renal stone | 1 |
| Rib fractures | 2 |
| Right-sided aortic arch | 2 |
| Scapula fracture | 1 |
| Tracheal deviation, neck mass | 4 |
| Tuberculosis | 1 |
| Zenker’s diverticulum | 1 |
The observers saw each case twice in sessions separated by about 2 months to reduce the likelihood that the study images and the responses to them would be remembered. The presentation of non-SOS and SOS trials were intermixed to counterbalance the effect of whether examinations were seen for the first or second time by ensuring that effects of repeated presentation were equal in both treatment conditions. Each session had 64 examinations. Half of the cases presented in each session contained a single added nodule (a different nodule and nodule placement for each case) and half did not. Thus, in the course of the two sessions, each examination appeared twice, once with and once without an added nodule. If the examination appeared with an added nodule in the first session, it appeared without in the second session, and vice-versa. Within each session, examinations were presented in a random order.
Twenty radiologists from the University of Arizona who had no prior knowledge of the examinations used in the experiment agreed to participate in the experiment and included: 2 senior faculty members; 8 fellows; 4 fourth-year residents; 3 third-year residents, 3 second-year residents. None of these participants was an author of this report. All were given and signed an informed consent document approved by their institutional review board for human subject use. Each radiologist received $200 for his or her participation.
Simulation of Pulmonary Nodules on Chest Radiographs
The use of simulated pulmonary nodules in perception research in diagnostic radiology has a long history (3). It is one of the few abnormalities that it is possible to simulate on x-ray or computed radiography images with any degree of realism. The methods developed at Henry Ford Hospital (4) allow better simulation of lung nodules than have been available before. This work informed our own approach.
Pulmonary nodules were simulated using Gaussian distributions of greyscale levels to simulate x-ray attenuating lesions and placed in the 64 cases, with and without the native abnormalities. One author who is a medical physicist [MTM] developed an algorithm to place simulated nodules in computed radiographs allowing an operator to select the position as well as to adjust the radius, contrast, and kernel density. The operator was directed to place and adjust the nodules by an author who is senior faculty radiologist [EAF] with the goal of producing natural-appearing pulmonary nodules on the radiographs. Because the method of creating the nodules differed slightly from the method used to display the cases, a second opinion was sought from independent radiologist authors with extensive experience reading chest radiographs [ATL, BHT, BFM]. Adjustments to the gain were made and reviewed again. This iterative review and improvement process relying on radiologists’ judgment was similar to that used in the original demonstration of SOS in chest x-ray (1).
We checked realism and level of detectability using pre-readers who where residents at a different university (not readers participating in the reported experiment). These readers reported on the examinations with added nodules using a free response format in which they described findings in their own words. None of these reports gave any indication that the nodules looked other than native. Likewise, using the somewhat different reporting scheme of the experiment reported here, none of the 20 readers indicated that any of the 64 occasions presentations of a simulated nodule appeared to be other than a reportable nodule. We take this lack of comment as confirmation that we succeeded in developing natural-looking nodules.
Authors of the original demonstration of SOS in chest radiography (1) noted that their simulated nodules may not have been entirely realistic:
“Simulated nodules sometimes may have had steeper edges than native nodules rendering them more detectable. This was not a problem for the current investigation because we measured only the detection of target lesions.” – Page 136
They used the simulated nodule to evoke the SOS effect, but detecting the nodules played no role in measured ROC performance. They documented a satisfaction of search effect with reduced detection accuracy for native abnormalities in the presence of the simulated nodules. As in the original demonstration of SOS (1), we measured only detection of the native abnormalities: the simulated nodules were an experimental manipulation. Therefore, we believe that we duplicate their procedure by using natural-appearing nodules even though we do not show that the simulated nodules are indistinguishable from real nodules.
Image Display
The cases were displayed on a NEC MultiSync LCD 2490WUXi color display (maximum luminance 400 cd/m2; contrast ratio 800:1; resolution 1920 × 1200; screen size 24.1″) that was calibrated to the DICOM (Digital Imaging and Communications in Medicine) Grayscale Standard Display Function (GSDF). WorkstationJ software, (copyright 2011, the University of Iowa, http://perception.radiology.uiowa.edu), was used to emulate the clinical displays in radiology reading rooms, and additionally, record responses, such as time on image, time to make a response, location of response, confidence in response, and display operations such as window and level adjustment (5).
Procedure
Prior to the start of the experiment, each reader was given instructions and presented with a practice case to provide an opportunity to understand how responses would be recorded. The reader was informed that each case might contain one, several, or no abnormalities and that the image set contained a wide range of abnormalities. No special mention was made of the frequency of types of abnormality that might be seen. The reader sat in front of a display with room light set to 30 lux. An abnormality could be identified by clicking a mouse cursor on the abnormality, describing it in a pop-up text box, and giving a confidence that the feature was abnormal using a subjective probability scale: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100% (no response to an abnormality was treated as “definitely normal” and 0% confidence).
Scoring
In most of the previous SOS experiments using Receiver Operating Characteristic (ROC) methodology and chest radiographs, false positive (FP) responses on examinations without native abnormalities were counted in scoring regardless of whether they were focal lung abnormalities or not (1, 2). In recent SOS experiments using chest CT examinations and simulated nodules as added abnormalities, focal lung abnormalities have not been included in scoring detection of the native abnormalities (6, 7).
Some care is needed in deciding how to score false positive responses. Whether a difference in ROC area between experimental conditions is observed or a shift in decision thresholds may come down to what happens to FP response rates in the ROC points. If a decrease in true positive (TP) responses is not accompanied by a decrease in FP responses at each ROC point, an ROC area reduction will be observed. If however a decrease in TP responses is accompanied by a decrease in FP responses, a threshold shift is observed. In either case, the same missed abnormalities owing to the SOS manipulation will be present. Therefore, to be consistent with the earlier research on SOS in chest radiography, we present results from scoring all false-positive responses on examinations without native abnormalities. However, results from scoring only FP responses other than focal abnormalities of the lung were similar leading to the same conclusions.
Statistical Analysis
Detection Accuracy
In our research, it has been uncommon for readers to provide operating points beyond a false positive fraction of 0.25. When ROC points are only available for a narrow range of FP fractions like this, trustworthy measurement of detection accuracy can be achieved by measuring ROC curve height in the region that contains ROC points. This measure does not attempt to generalize to tradeoffs between sensitivity and specificity that readers refuse to make. This can be done using partial area under the ROC curve within a given range of specificity, sensitivity at a given fixed specificity, or specificity at a fixed specificity (8). We used the empirical ROC method with detection accuracy measured using true-positive fraction (TP fraction = sensitivity) at the FP fraction of 0.1 (1 – specificity = 0.9) because this index focuses on a part of the ROC curve well-supported with empirical ROC points. For generality, we repeated the analysis using the contaminated binormal model (CBM) [9]. We also checked whether the same results were obtained for TP fractions at other FP fractions across the range of FP fractions for which readers provided operating points.
The multireader multicase (MRMC) ROC methodology developed by Dorfman, Berbaum, and Metz (DBM) [10, 11] has recently been extended in software (DBM MRMC 2.4, available from http://perception.radiology.uiowa.edu). Because SOS affects readers rather than patients, generalization to the population of readers is fundamental. Therefore, reader was treated as a random factor and patient and treatment as fixed factors. To accomplish this we selected DBM Analysis 3 (Obuchowski-Rockette Analysis): Random Readers and Fixed Cases (results apply to the population of readers).
Shift in Decision Thresholds
Shifts in decision thresholds are associated with SOS effects found in traditional radiographic contrast studies of the abdomen (12–14) and in computed tomography examination of the chest (6). These shifts reflect reductions in TP fractions accompanied by reductions in FP fractions: the ROC points move downward along the ROC curve. These reductions in both types of response to abnormalities visible without contrast indicate that the radiologists tend to focus on the area of the contrast when it is introduced to the exclusion of areas without contrast. In the current experiment, we studied decision thresholds using the FP fraction associated with each ROC point, perhaps the best and simplest index of decision threshold (15). In our scoring, a report of abnormality at a location other than the simulated nodule was considered a false positive if it occurred on a case with no native abnormality. See Appendix B for additional details of the decision threshold analysis.
For each reader-treatment combination, the midpoint of the FP range of ROC points was computed as the average of most and least conservative ROC points. As such we get an array of midpoint values consisting of the two SOS conditions X 20 readers (40 values). Likewise, the width of the FP range of ROC points was computed as least conservative minus the most conservative ROC point. Similar arrays were obtained for TP responses.
Response Time
We computed median response times within each treatment condition for each reader. This gives an array of median values consisting of the two SOS conditions X 20 readers (40 values). Analyses of Variance (ANOVA) with within-subject factors for SOS treatment condition and case type (native abnormality absent or present) were used to analyze median reading time (16).
RESULTS
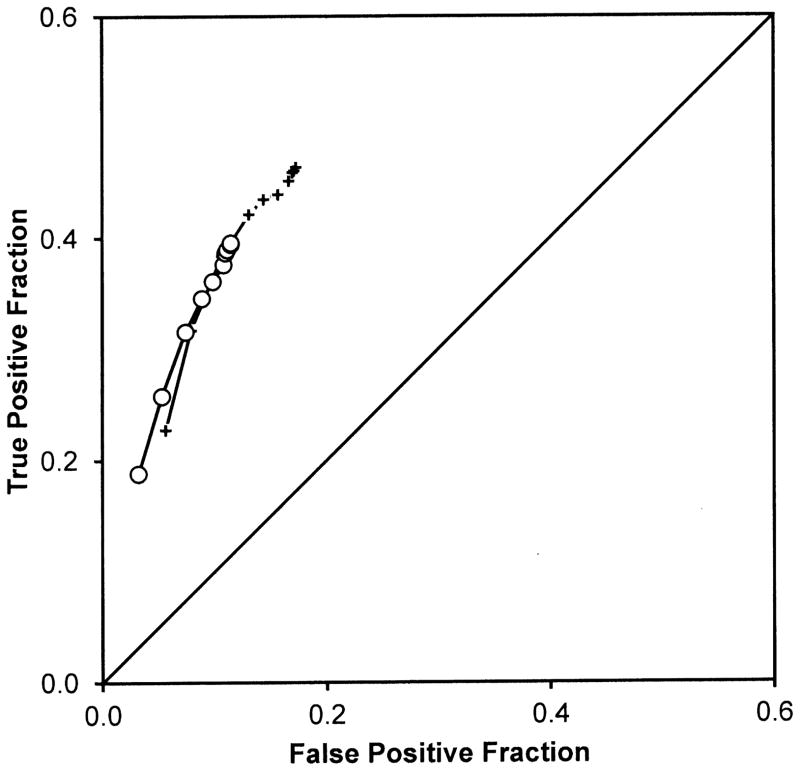
Figure 2 presents the observed ROC points averaged over readers for detecting the native test abnormalities. Each ROC point is the average of 20 readers. Comparing crosses to open circles provides a visual comparison of the non-SOS and SOS conditions.
Figure 2.
Figure 2A. Each point is the average of 20 readers. Cross symbols represent ROC points from the non-SOS condition and open symbols represent ROC points from the SOS condition. These points suggest that detection accuracy as measured by ROC curves through the points would not differ between the conditions.
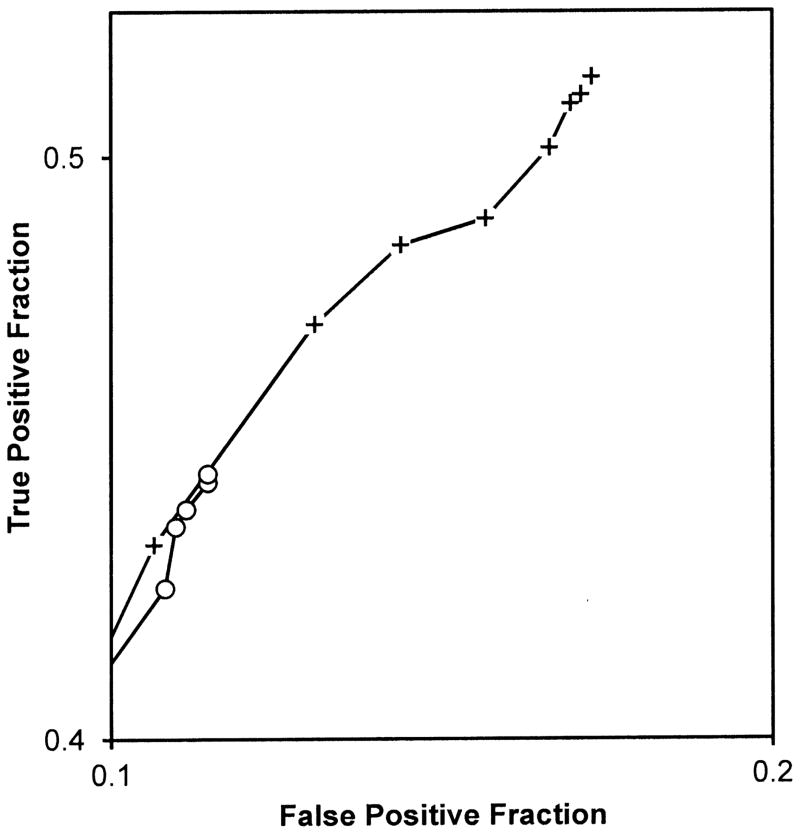
Figure 2B provides a magnified view of the most lenient operating points in Figure 2A to highlight differences in those points between the treatment conditions. Each point is the average of 20 readers. Cross symbols represent ROC points from the non-SOS condition and open circle symbols represent ROC points from the SOS condition. These points suggest a major threshold shift toward more conservative reporting in the SOS condition. (Note that the chance line shown in the other figures is not visible in this Figure because the ranges of true and false positive fractions do not overlap in the magnified view).
Diagnostic Accuracy
Table 2 provides a summary of the ANOVA analysis performed on rating data scored using either all FP responses or just non-nodule FP responses and applying either empirical ROC method or fitting the contaminated binormal model (9). None of the approaches shown in the Table indicate a difference in the TP fraction measured at FP fraction = 0.1 for the SOS condition compared with the non-SOS condition. For example, for the empirical method applied to the data that included all FP responses, for a FP fraction of 0.1, the TP fraction was 0.329 for the non-SOS condition and 0.326 for the SOS condition, (F(1,19) = 0.01, p = 0.93). Other choices of FP fraction for measurement of TP fraction yield similar conclusions.
Table 2.
ROC Accuracy
| Using All False Positive Responses | Non-SOS Condition | SOS Condition | Difference | F(1,19) | P |
|---|---|---|---|---|---|
| Empirical ROC TP@FP=0.1 | 0.329 | 0.326 | 0.003 | 0.01 | 0.9272 |
| Contaminated Binormal Model ROC Curve TP@FP=0.1 | 0.332 | 0.330 | 0.002 | 0.01 | 0.9380 |
| Using Only Non-Nodule False Positive Responses | Non-SOS Condition | SOS Condition | Difference | F(1,19) | P |
|---|---|---|---|---|---|
| Empirical ROC TP@FP=0.1 | 0.362 | 0.376 | -0.014 | 0.21 | 0.6525 |
| Contaminated Binormal Model ROC Curve TP@FP=0.1 | 0.382 | 0.390 | -0.008 | 0.05 | 0.8211 |
Decision Thresholds
From Figure 2 it is clear that FP fractions associated with the averaged operating points were reduced in the SOS condition (open circles) relative to the non-SOS condition (crosses). Thus, there was more conservative reporting in the SOS condition.
The first section of Table 3 shows the results of analyses of the TP fractions associated with most and least conservative ROC operating points and with the midpoint and range of the operating points. The most and least conservative operating points had lower TP fractions in the SOS condition (more misses, P < 0.05). Similarly the TP fraction at center of the TP range of the operating points is also significantly reduced in the SOS condition (P < 0.001), though the width of the TP range of the operating points was no different in the SOS condition.
Table 3.
Analysis of Thresholds
| True Positive Fractions | Non-SOS Condition | SOS Condition | F(1,18) | P | Significance Level |
|---|---|---|---|---|---|
| Most Conservative Threshold | 0.225 | 0.186 | 5.70 | 0. 0282 | * |
| Most Lenient Threshold | 0.467 | 0.395 | 12.18 | 0. 0026 | ** |
| Center of Range | 0.346 | 0.290 | 15.60 | 0. 0009 | *** |
| Width of Range | 0.242 | 0.209 | 1.87 | 0. 1888 |
| False-Positive Fractions Reporting Non-Nodule Abnormality | Non-SOS Condition | SOS Condition | F(1,18) | P | Significance Level |
|---|---|---|---|---|---|
| Most Conservative Threshold | 0.056 | 0.033 | 5.86 | 0.0263 | * |
| Most Lenient Threshold | 0.174 | 0.116 | 6.71 | 0.0185 | * |
| Center of Range | 0.115 | 0.075 | 9.66 | 0.0061 | ** |
| Width of Range | 0.118 | 0.083 | 2.45 | 0.1350 |
| False-Positive Fractions Reporting Any Abnormality | Non-SOS Condition | SOS Condition | F(1,18) | p | Significance Level |
|---|---|---|---|---|---|
| Most Conservative Threshold | 0.073 | 0.046 | 7.81 | 0.0120 | * |
| Most Lenient Threshold | 0.263 | 0.172 | 11.38 | 0.0034 | ** |
| Center of Range | 0.168 | 0.109 | 13.25 | 0.0019 | ** |
| Width of Range | 0.190 | 0.126 | 6.93 | 0.0169 | * |
indicates P < 0.05;
indicates P < 0.01;
indicates P < 0.001.
The second section of Table 3 shows the results of analyses of the FP fractions from only non-nodule responses associated with most and least conservative ROC operating points and with the midpoint and range of the operating points. The most and least conservative operating points had lower FP fractions in the SOS condition (fewer overcalls, P < 0.05). Similarly the center of the FP range of the operating points is also significantly reduced in the SOS condition (P < 0.01), though the width of the FP range of the operating points was no different in the SOS condition.
The third section of Table 3 shows the results of analyses of the FP fractions from both nodule and non-nodule responses associated with most and least conservative ROC operating points and with the midpoint and range of the operating points. The results were very similar to those on non-nodule FP responses and TP responses, though for all FP response types, the width of the FP range of operating points was also reduced in the SOS condition (P < 0.05).
Inspection Time
Median inspection times were computed for each reader for each experimental condition for examinations with and without test abnormalities. The two median times per reader were analyzed with an ANOVA with within-subject factors for SOS condition and examination type (with or without test abnormality). The only statistically significant effect was for presence of test abnormality (36.0 seconds without test abnormality vs. 49.8 seconds with test abnormality, F(1,19) = 117.41, p < 0.0001. The SOS manipulation did not affect inspection time (43.4 seconds without added nodules vs. 42.4 seconds with added nodules, F(1,19) = 0.40, p = 0.53). The interaction of factors was not statistically significant.
DISCUSSION
The SOS effect observed in this experiment differs from that previously reported for chest radiography (1, 2). The previous experiments reported a decrement in detection accuracy of detecting test abnormalities with the addition of nodules. In contrast, there was no accuracy difference in the current study with the addition of the nodules. Instead, there were reduced FP fractions of the ROC points and reduced TP fractions of the ROC points, indicating a threshold shift toward more conservative reporting.
It is noteworthy that the earlier demonstrations of SOS in chest radiography (1, 2) did not explicitly study decision threshold shifts. However, the figures in those reports (Figures 5 and 6 in reference 1; and Figures 1, 2 and 3 in reference 2) all suggest rather obvious shifts particularly in the most lenient decision thresholds. Subsequent studies (17) did report some analyses of individual response frequencies and probabilities, but did not touch on the question of thresholds shifts. Although analysis of decision thresholds was briefly introduced to the radiology audience (15), it has never received much attention. To our knowledge the first time an analysis of decision thresholds was used in the radiology literature was not until 1994 (12) several years after the first demonstration of SOS in 1990. There have been analyses of single, “important” operating points such as those associated with decision to biopsy. This may be because differences in detection accuracy are viewed as outside a reader’s control whereas decision thresholds reflect a readiness to report which can be influenced by the reader. Of course, both accuracy and threshold reductions involve missed diagnoses.
The authors of the original SOS papers (1, 2) graciously shared their data (Berbaum personal communication, 2014) so that we could examine the results of applying our analysis. We expected that the SOS accuracy reduction observed in earlier studies using area under the ROC curve would also be found if we applied the technique used for the current experiment which is insensitive to the vagaries of ROC curve fitting. Appendix A presents this analysis, confirming the SOS effect on area. Next, to examine decision threshold shifts associated with the SOS manipulation in the earlier data, we performed analyses similar to those used for the current data. A previously unrecognized shift in decision thresholds was revealed that is similar to the reluctance to report SOS effect found in the current experiment. In the earlier experiments, the SOS effect on detection accuracy and the SOS effect on threshold to report abnormality are superimposed.
We attempted to make the procedures of the current experiment comparable to those of the earlier studies (1, 2). An uncontrolled factor is that our readers may be more aware of SOS effect than the readers in the earlier studies. Assuming that the findings of both the current and earlier experiments were representative of practice at these time periods, we should try to explain the lack of SOS on detection accuracy in the present study.
Radiographic imaging has changed from film-based to computer-based, allowing greater flexibility in tuning window-level setting to optimize search for specific abnormalities. In addition, a greater proportion of the radiology workload has shifted to cross-sectional modalities. The original experiment on SOS effects in chest radiography (1) was conducted 25 years ago and the most recent replication (2) 15 years ago. Between then and now, the utilization of CT and MR examinations has dramatically increased and advanced imaging is often the preferred initial examination. Resolution and quality of those modalities have advanced remarkably as well. Given this change in the practice of radiology, there have been corresponding changes of emphasis in the training of radiologists. Relative to radiologists and residents tested between 15 and 25 years ago, current radiologists and residents may approach the interpretation of radiographs differently.
Two types of SOS effects have been distinguished. Type I SOS effects appear to be the result of faulty pattern recognition (6). Decreases in ROC accuracy result from decreases in TP probability without changes in FP probability for each ROC point. Type I SOS is not generally related to changes in search behavior or inspection time (17). Type II SOS effects are based on reductions in visual search. Reductions in TP rates are accompanied by reductions in FP rates: ROC points move downward along the ROC curve. The cause of reluctance to report an abnormality in Type II SOS has been identified as reduced inspection. In this taxonomy, the SOS effect in chest radiography reported in 1990 through 2000 would be called Type I SOS, whereas the SOS effect of the current experiment might be considered to be Type II SOS. A new finding of the current experiment is more conservative reporting but no reduction in inspection time. In other words, the addition of simulated nodules shifted decision thresholds but not inspection time, which is consistent with neither Type I nor Type II SOS effects.
Acknowledgments
Supported by USPHS Grant R01 EB 00145 from the National Institute of Biomedical Imaging and Bioengineering (NIBIB), Bethesda, Maryland.
Appendix A: 1990 and 2000 SOS Experiments Reconsidered
The first experiment demonstrating the SOS effect in the laboratory, Berbaum et al. (1), included 8 readers. Ten years later, Berbaum et al. (2) using essentially the same set of chest radiographs added another 11 readers. The combined data was analyzed using a variety of ROC models including several proper ROC models, all of which demonstrated significant reduction detection accuracy as measured by ROC area.
To directly compare the earlier data with those of the current experiment, we reanalyzed the data of earlier 19 readers using the same methods we have used to analyze the current data. DBM MRMC analysis was performed on TP fractions at the FP fraction of 0.1. For the empirical ROC curves, the average non-SOS TP fraction was 0.509 and the average SOS TP fraction was 0.437 for a FP fraction of 0.1; the difference was statistically significant (F(1,17) = 11.67, P = 0.0033). For the contaminated binormal ROC curves, the average non-SOS TP fraction was 0.513 and the average SOS TP fraction was 0.441 for a FP fraction of 0.1; the difference was statistically significant (F(1,17) = 14.57, P = 0.0014). Therefore, our method of ROC analysis of detection accuracy finds the same reduction in detection of test abnormalities with nodules added as was originally reported.
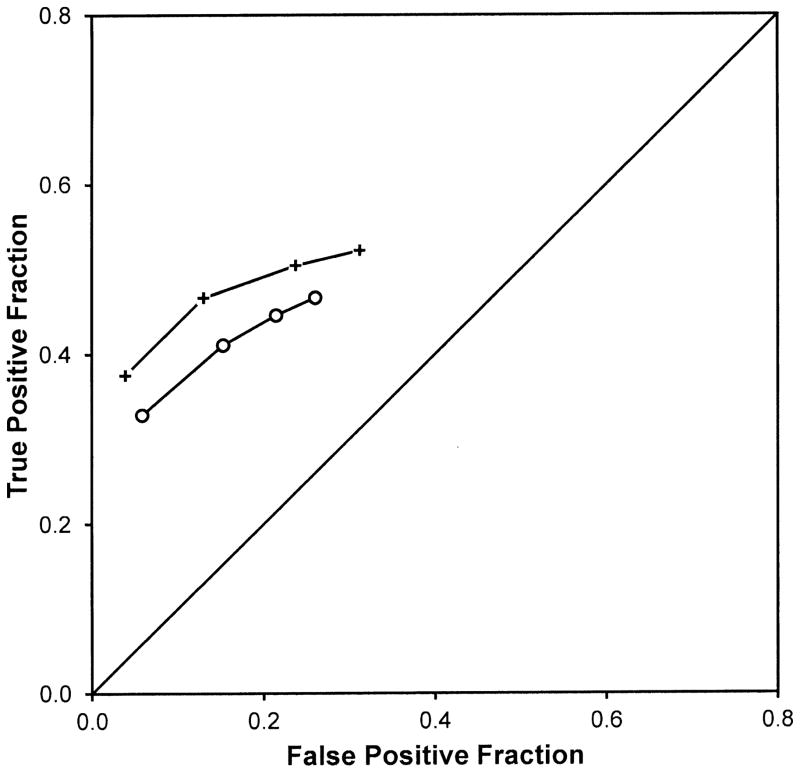
Figure 3 shows the average of the 19 readers operating points for each experimental condition. There are only 4 operating points per condition because a five-category rating was used in the earlier experiments. The points for the SOS condition are far enough below those of the non-SOS condition that it is clear that any method of fitting the points would demonstrate reduced accuracy.
Figure 3.
Average empirical ROC points from Berbaum et al. (1990) and (2000). Crosses are the non-SOS condition without added nodules; open circles are the SOS condition with added nodules.
Table 4 presents our analysis of the thresholds used by readers in Berbaum et al. (2). The first part of the table shows reduced true positive fractions for the most conservative and most lenient thresholds and for the center of the range of thresholds. The second part of the table shows reduced false positive fractions only for the most lenient threshold and for both the center and width of the range of thresholds. These effects can be seen most clearly in the most lenient two thresholds in Figure 3. Therefore, although the earlier results are indicative of larger reductions in TP fractions than FP fractions yielding reduced detection accuracy, there is also a previously unrecognized shift in decision thresholds in the earlier data that is similar in kind if not magnitude to that found in our current experiment.
Table 4.
Analysis of Thresholds from 1990 and 2000
| True Positive Fractions | Non-SOS Condition | SOS Condition | F(1,18) | P | Significance Level |
|---|---|---|---|---|---|
| Most Conservative Threshold | 0.443 | 0.389 | 9.47 | 0.0068 | ** |
| Most Lenient Threshold | 0.597 | 0.519 | 19.81 | 0.0004 | *** |
| Center of Range | 0.520 | 0.454 | 18.67 | 0.0005 | *** |
| Width of Range | 0.154 | 0.130 | 2.03 | 0.1727 |
| False Positive Fractions Reporting Non-Nodule Abnormality | Non-SOS Condition | SOS Condition | F(1,18) | P | Significance Level |
|---|---|---|---|---|---|
| Most Conservative Threshold | 0.043 | 0.053 | 0.87 | 0.3636 | |
| Most Lenient Threshold | 0.328 | 0.247 | 8.37 | 0.0101 | * |
| Center of Range | 0.185 | 0.150 | 5.52 | 0.0311 | * |
| Width of Range | 0.285 | 0.195 | 9.52 | 0.0067 | ** |
indicates P < 0.05;
indicates P < 0.01;
indicates P < 0.001.
Appendix B: Note on Analysis of Decision Thresholds
Even when a reader never uses a rating category, there are no missing observed ROC points. The rating categories do not have to be combined, as is typically the case in fitting smooth curves to ROC data in order to preclude points on the boundaries of the ROC space or the same ROC point being obtained for successive category boundaries. This is illustrated in Table 5 which shows the rating data from one observer in one experimental condition. Where the reader never used a response category for normal or abnormal patients, the observed response probability for that cell of the rating data matrix would be zero (indicated by the borders on those cells). However, the TP and FP probabilities (or fractions) for each response category is the sum of that category and all of more conservative response categories. As indicated by the grey cells in Table 5, for unused categories, the TP and FP probabilities are “inherited” from the next more conservative ROC point so that some of zero cells for response frequencies and probabilities become non-zero in the ROC points. This “inheritance” demonstrates the dependence of successive more lenient ROC points on the more conservative ones. Because the ROC points are not independent, we do not use thresholds, FP fractions associated with individual ROC points, as a repeated measure. Instead we analyze the midpoint and widths of FP ranges of ROC points for treatment-reader combinations in separate ANOVAs. For these analyses, FP or TP fractions of zero do not compromise any assumptions of the method.
Table 5.
Illustration of Inheritance of Response Probability from More Conservative Operating Points
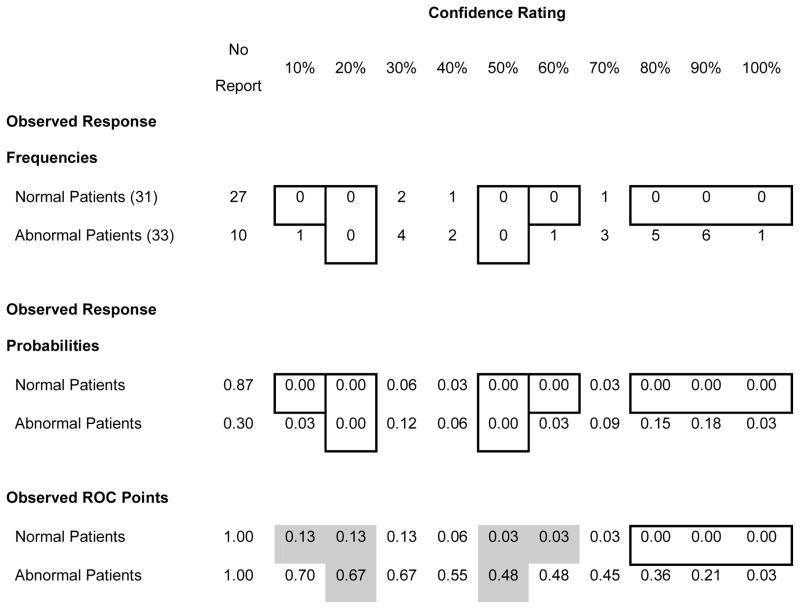
|
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Berbaum KS, Franken EA, Dorfman DD, et al. Satisfaction of search in diagnostic radiology. Invest Radiol. 1990;25:133–140. doi: 10.1097/00004424-199002000-00006. [DOI] [PubMed] [Google Scholar]
- 2.Berbaum KS, Dorfman DD, Franken EA, Jr, Caldwell RT. Proper ROC analysis and joint ROC analysis of the satisfaction of search effect in chest radiography. Acad Radiol. 2000;7:945–958. doi: 10.1016/s1076-6332(00)80176-2. [DOI] [PubMed] [Google Scholar]
- 3.Samei E, Flynn MJ, Eyler WR. Simulation of subtle lung nodules in projection chest radiography. Radiology. 1997;202:117–124. doi: 10.1148/radiology.202.1.8988200. [DOI] [PubMed] [Google Scholar]
- 4.Samei E, Flynn MJ, Eyler WR. Detection of subtle lung nodules: relative influence of quantum and anatomical noise on chest radiographs. Radiology. 1999;213:727–734. doi: 10.1148/radiology.213.3.r99dc19727. [DOI] [PubMed] [Google Scholar]
- 5.Schartz KM, Berbaum KS, Caldwell RT, Madsen MT. WorkstationJ as ImageJ plugin for medical image studies. Annual Meeting of the Society for Imaging Informatics in Medicine (SIIM) – 9th Annual SIIM Research & Development Symposium; Charlotte, NC. June 6, 2009; ( http://www.siimweb.org/assets/FCBE219A-C30B-4003-9892-FACA9230AB91.pdf) [Google Scholar]
- 6.Berbaum KS, Schartz KM, Caldwell RT, et al. Satisfaction of search from detection of pulmonary nodules in computed tomography of the chest. Acad Radiol. 2013;20:194–201. doi: 10.1016/j.acra.2012.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schartz K, Berbaum K, Madsen M, et al. Multiple diagnostic task performance in computed tomography examination of the chest. Br J Radiol. 2013;86:20110799. doi: 10.1259/bjr/18244135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jiang Y, Metz CE, Nishikawa RM. A receiver operating characteristic partial area index for highly sensitive diagnostic tests. Radiology. 1996;201:745–750. doi: 10.1148/radiology.201.3.8939225. [DOI] [PubMed] [Google Scholar]
- 9.Dorfman DD, Berbaum KS. A contaminated binormal model for ROC data - Part II. A formal model. Academic Radiology. 2000;7:427–437. doi: 10.1016/s1076-6332(00)80383-9. [DOI] [PubMed] [Google Scholar]
- 10.Dorfman DD, Berbaum KS, Metz CE. Receiver operating characteristic rating analysis: Generalization to the population of readers and patients with the jackknife method. Invest Radiol. 1992;27:723–731. doi: 10.1097/00004424-199209000-00015. [DOI] [PubMed] [Google Scholar]
- 11.Hillis SL, Berbaum KS, Metz CE. Recent developments in the Dorfman-Berbaum-Metz procedure for multireader ROC study analysis. Acad Radiol. 2008;15:647–61. doi: 10.1016/j.acra.2007.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Franken EA, Jr, Berbaum KS, Lu CH, et al. Satisfaction of search in detection of plain film abnormalities in abdominal contrast examinations. Invest Radiol. 1994;29:403–409. doi: 10.1097/00004424-199404000-00001. [DOI] [PubMed] [Google Scholar]
- 13.Berbaum KS, Franken EA, Jr, Dorfman DD, et al. The cause of satisfaction of search effects in contrast studies of the abdomen. Acad Radiol. 1996;3:815–826. doi: 10.1016/s1076-6332(96)80271-6. [DOI] [PubMed] [Google Scholar]
- 14.Berbaum KS, Franken EA, Jr, Dorfman DD, Caldwell RT, Lu CH. Can order of report prevent satisfaction of search in abdominal contrast studies? Acad Radiol. 2005;12:74–84. doi: 10.1016/j.acra.2004.11.007. [DOI] [PubMed] [Google Scholar]
- 15.Swets JA, Pickett RM. Evaluation of diagnostic systems: methods from signal detection theory. New York: Academic Press; 1982. p. 39. [Google Scholar]
- 16.BMDP2V, release: 8.0. Copyright 1993 by BMDP Statistical Software, Inc. Statistical Solutions Ltd; Cork, Ireland: ( http://www.statsol.ie) [Google Scholar]
- 17.Berbaum KS, Franken EA, Dorfman DD, et al. Time course of satisfaction of search. Invest Radiol. 1991;26:640–648. doi: 10.1097/00004424-199107000-00003. [DOI] [PubMed] [Google Scholar]