Relative sound localisation abilities in human listeners

Abstract

Spatial acuity varies with sound-source azimuth, signal-to-noise ratio, and the spectral characteristics of the sound source. Here, the spatial localisation abilities of listeners were assessed using a relative localisation task. This task tested localisation ability at fixed angular separations throughout space using a two-alternative forced-choice design across a variety of listening conditions. Subjects were required to determine whether a target sound originated to the left or right of a preceding reference in the presence of a multi-source noise background. Experiment 1 demonstrated that subjects' ability to determine the relative location of two sources declined with less favourable signal-to-noise ratios and at peripheral locations. Experiment 2 assessed performance with both broadband and spectrally restricted stimuli designed to limit localisation cues to predominantly interaural level differences or interaural timing differences (ITDs). Predictions generated from topographic, modified topographic, and two-channel models of sound localisation suggest that for low-pass stimuli, where ITD cues were dominant, the two-channel model provides an adequate description of the experimental data, whereas for broadband and high frequency bandpass stimuli none of the models was able to fully account for performance. Experiment 3 demonstrated that relative localisation performance was uninfluenced by shifts in gaze direction.

I. INTRODUCTION

Psychophysical investigations of sound localisation abilities generally fall into one of two classes: Absolute localisation studies determine the accuracy with which human listeners can localise the source of a sound, generally by requiring subjects to indicate the perceived origin of the source (Stevens and Newman, 1936; Makous and Middlebrooks, 1990; Carlile et al., 1999). In contrast, other studies seek to determine the spatial resolution of the subject by measuring the minimum discriminable difference in source location that a listener can reliably discern; results generate what is termed the minimum audible angle (MAA) (Mills, 1958). MAA tasks are well suited to standard psychophysical techniques, such as two-alternative forced-choice (2AFC) procedures. This is advantageous if one wants to combine behavioural investigations with neuronal recordings, as established methods facilitate “neurometric” approaches (Parker and Newsome, 1998). However, measurement of the MAA can be time consuming, especially if one is interested in exploring how spatial resolution varies throughout space. In contrast, an absolute localisation task allows relatively rapid assessment of localisation abilities throughout auditory space. However, because an absolute localisation task has many response options (i.e., at least as many as there are source locations), analysis of simultaneously recorded neural activity is considerably more complicated. We therefore developed a 2AFC relative localisation task using signal detection theory to estimate sensitivity (d′) at a fixed angular separation to enable efficient measurement of spatial localisation abilities throughout azimuth.

Very few studies have investigated the ability of either human or non-human listeners to judge the relative location of two sequential sources outside of the MAA context (Recanzone et al., 1998; Maddox et al., 2014). Determining the relative location of two sound sources, or the direction of movement of a single source, is an ethologically relevant task. For example, the relative location of two voices could help a person pick out a voice in a crowded room, or for a wild animal, being able to follow the direction of a moving sound, be it prey or predator, could be important for survival. Real-world hearing frequently entails listening in noisy environments composed of multiple sound sources. Therefore movement discrimination is distinct from, but closely related to, relative sound localisation—especially at adverse signal-to-noise ratios (SNRs) where the target sound may only be intermittently audible. In the paradigm reported here, listeners were required to determine whether a target stimulus originated from the left or from the right of a preceding reference stimulus. The target and reference were always separated by a fixed interval of 15° and both were embedded in a continuously varying noisy background which was independently generated for each of the 18 speakers in the testing arena. This required that subjects both detect and segregate the sources in order to determine their relative location.

The spatial location of a sound source must be computed centrally using sound location cues, including binaural cues that can be extracted by comparing the signal at the two ears; i.e., interaural timing differences (ITDs) and interaural level differences (ILDs), as well as monaural or spectral cues, which arise as a result of interaction of sound waves with the torso, head, and with the folds of the external ear (Middlebrooks and Green, 1991). While cues for sound localisation are extracted in the brainstem (reviewed in Grothe et al., 2010), auditory cortex is required for accurate sound localisation performance (Neff et al., 1956; Jenkins and Merzenich, 1984; Kavanagh and Kelly, 1987; Heffner and Heffner, 1990; Malhotra et al., 2004, 2008; Malhotra and Lomber, 2007). However, the means by which the activity of neurons within auditory cortex is readout to support sound source localisation remains controversial. Several models have been proposed that account for the neural basis of sound localisation (Jeffress, 1948; Stern and Shear, 1996; Harper and McAlpine, 2004; Stecker et al., 2005).

The topographic model posits that space is represented by a number of neural channels, each of which is tuned to a particular region of space. Together, these spatial channels encompass and encode all of auditory space. Such a representation was first proposed for the representation of ITD cues in the auditory midbrain (Jeffress, 1948). Modified versions of the topographic model include a greater number and/or more tightly tuned channels near the midline in order to account for the superior spatial resolution observed there (Stern and Shear, 1996) and the decline in localisation ability that occurs away from the midline (Middlebrooks and Green, 1991). In contrast, the two-channel or opponent channel model (Stecker et al., 2005), proposes that two broadly tuned channels exist to represent azimuth. This model was first proposed for the encoding of ITD in small mammals (McAlpine et al., 2001) and was adapted to the auditory cortex following the observation that neural tuning in auditory cortex was typically broad and contralateral (Stecker et al., 2005). While such a model is likely an over-simplification, recent human imaging studies have suggested that both sound localisation cues and auditory space might be represented in human auditory cortex by this kind of “hemifield code” (Salminen et al., 2009; Salminen et al., 2010; Magezi and Krumbholz, 2010; Briley et al., 2013).

In this study the relative sound localisation abilities of subjects were first measured at different supra-detection-threshold SNRs. Bandpass noise (BPN) stimuli were then used to compare performance when listeners were tested with stimuli in which localisation cues were dominantly ITDs or ILDs with broadband stimuli in which all localisation cues were present. A combination of modeling and empirical methods was used to predict performance in this task with different models of sound localisation, and these predictions compared with the observed data. Finally, the influence of gaze direction was measured by estimating performance while subjects fixated at ±30° while maintaining a constant head position.

II. METHODS

A. Participants

This experiment received ethical approval from the University College London (UCL) Research Ethics Committee (3865/001). Twenty normal hearing adults between the ages of 18 and 35 participated, 8 in Experiment 1 and 16 (4 of whom were subsequently excluded for poor performance, see below for details) in Experiment 2, with 4 participants taking part in both. All participants had no reported hearing problems or neurological disorders.

B. Testing chamber

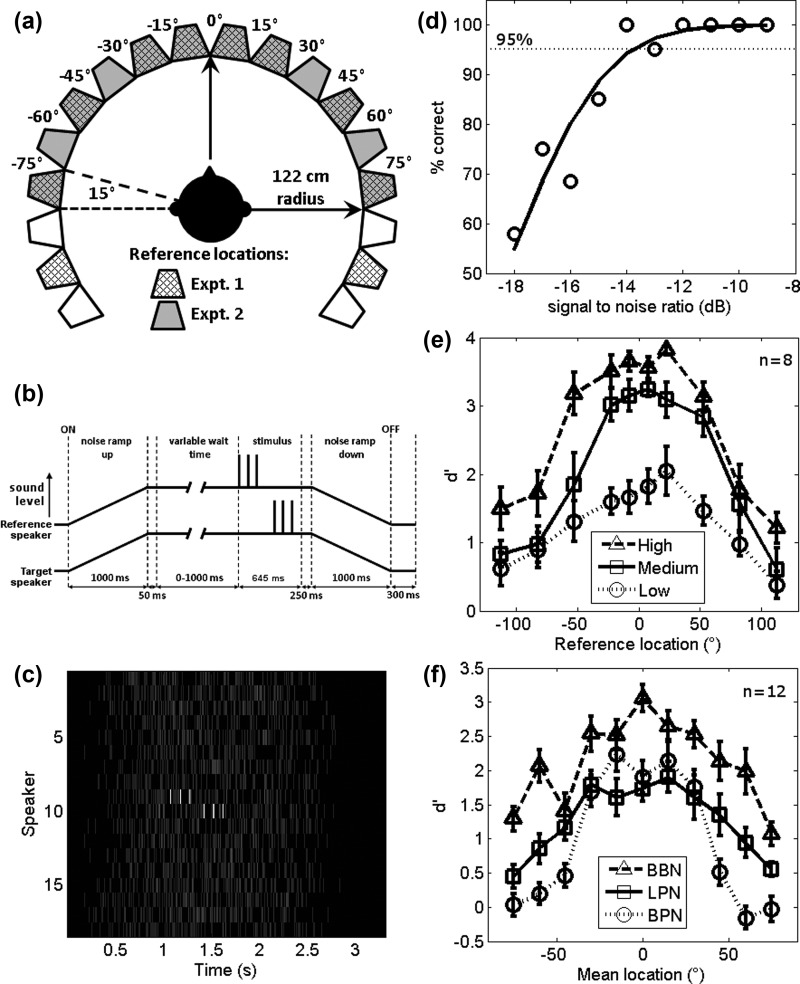
For testing, subjects sat in the middle of an anechoic chamber (3.6 × 3.6 × 3.3 m (width × depth × height) with sound attenuating foam triangles on all surfaces (24 cm triangular depth and total depth of 35 cm) and a suspended floor) surrounded by a ring of 18 speakers (122 cm from the centre of the subject's head and level with the ears) arranged at 15° intervals from −127.5° to +127.5° [Fig. 1(a)]. The subject's head was maintained in a stationary position in the centre of the speaker ring throughout testing with the aid of a chin rest. Subjects were asked to fixate on a cross located at 0° azimuth, unless otherwise instructed.

FIG. 1.

Experimental setup, thresholds, and discrimination results: (a) Speaker Arrangement: The subject's head was positioned in the centre of a ring of 18 speakers, each separated by 15°. Hatched speakers were reference locations in Experiment 1, gray speakers were reference locations in Experiment 2. Mean stimulus locations for Experiment 2 are labeled. (b) Schematic of the stimulus showing the reference and target speakers. The background noise (independently generated for each speaker) is ramped up to full intensity over 1 s. The reference stimulus starts between 50 and 1050 ms after this. The reference stimulus is presented from a pseudo-randomly selected speaker from those defined in the different experiments. One hundred ms after, the target is presented from a speaker 15° to the left or the right of the reference speaker. The noisy background continues for a further 250 ms after the stimulus presentation before being ramped down to zero over 1 s. (c) Example stimulus. This diagram shows all speakers in an example stimulus. The reference stimulus comes from speaker 9 and the target speaker 10; all speakers presented independently generated noise. Lighter colours indicate a greater intensity. Reference and target stimuli have been shown at a higher SNR than was used in testing for visualisation purposes. (d) Example threshold from a single participant: The dotted black line indicates the 95% correct mark. The solid line is the binomial fit. A person's threshold was taken as the 95% correct point of the binomial fit. (e) Effect of SNR: Mean d′ of all subjects showing discriminability of the direction of the target sounds relative to the reference at three different SNRs, which were specific to each participant. Low was defined as their 95% threshold SNR, with medium and high being the threshold plus 3 and 6 dB, respectively. (f) Mean d′ of the mean stimulus location for all participants in Experiment 2 in each condition; BBN, low-pass filtered (<1 kHz, LPN) and bandpass filtered (3–5 kHz, ILD). These experiments were all performed at the subject's 95% threshold plus 1.5 dB.

C. Stimuli

All stimuli were generated and presented at a sampling frequency of 48 kHz. In the broadband noise (BBN) conditions, 3 pulses of white noise were presented from a reference speaker, followed by 3 pulses of white noise from a target speaker. Noise pulses were 15 ms in duration which included cosine ramping with 5-ms duration at the beginning and end of each pulse. Pulses were presented at a rate of 10 Hz with 130-ms delay between the end of the final reference pulse and the first target pulse in order to aid perceptual segregation of the reference and the target. Preliminary work showed that a delay of this order helped listeners to segregate the reference and the target such that they were perceived as separate sound sources within the noisy background. The sequence of reference and target pulses occurred at an unpredictable interval from trial onset [see Fig. 1(b)]. The pulses were embedded in a noisy background generated by presenting white noise whose amplitude was varied every 15 ms with amplitude values drawn from a distribution whose mean and variance could be controlled, this control over the noise statistics being the main rationale for using such a background noise (adapted from Raposo et al., 2012). The reference and target pulses were also 15 ms in duration and were superimposed onto this background of on-going amplitude changes [see Fig. 1(c) where the high amplitude white noise pulses are visible for the reference (speaker 9) and target (speaker 10) locations]. Each noise source was generated independently for each speaker on every trial [Fig. 1(c)] while the overall level of noise was simultaneously ramped on and off with a linear ramp over 1 s for all 18 noise sources according to the schematic in Fig. 1(b). The reference and target pulses could occur any time between 50 and 1050 ms after the noise levels reached their maximum (i.e., 1050–2050 ms after trial onset). In these experiments the mean noise level when all speakers were presenting the background noise was 63 dB sound pressure level (SPL) [calibrated using a CEL-450 sound level meter (Casella CEL Inc., NY, USA)]. Stimuli in the low-pass noise (LPN) and BPN conditions were also brief noise pulses but were filtered at so they contained power below 1 kHz and between 3 and 5 kHz, respectively. Except for threshold measurements (see below), the target speaker was always 15° to the left or right of the reference speaker [see Fig. 1(a) for speaker locations] and subjects were oriented such that their head faced a fixation point located at 0° [Fig. 1(a)]. Stimuli were presented by Canton Plus XS.2 speakers (Computers Unlimited, London) via a MOTU 24 I/O analogue device (MOTU, Cambridge, MA) and two Knoll MA1250 amplifiers (Knoll Systems, Point Roberts, WA). The individual speakers were matched for level using a CEL-450 sound level meter and the spectral outputs were checked using a Brüel and Kjær 4191 condenser microphone placed at the centre of the chamber where the subject's head would be during the presentation of a stimulus. The microphone signal was passed to a Tucker Davis Technologies System 3 RP2.1 signal processor via a Brüel and Kjær 3110–003 measuring amplifier. All speakers were matched in their spectral output which was flat from 400 to 800 Hz, with a smooth, uncorrected 1.2 dB/octave drop off from 400 to 10 Hz, and a smooth uncorrected drop off of 1.8 dB/octave from 800 Hz to 25 kHz. The MOTU device was controlled by Matlab (MathWorks, Natick, MA) using the Psychophysics Toolbox extension (Brainard, 1997; Kleiner et al., 2007).

D. Threshold estimation

In order to determine the SNR at which subjects were able reliably to detect the pulse train within the noise, they first performed a threshold test. In this task, subjects were oriented to face a speaker at the frontal midline (0° azimuth). The reference sound was always presented from this speaker, and the target was presented from a speaker at either −90° or +90°. Subjects reported the direction in which the stimulus moved using the left and right arrows on a keyboard to indicate −90° and +90°, respectively. Stimuli were presented at 10 different SNRs by varying the signal attenuation in 1 dB steps over a 10 dB range. Subjects performed ten trials for each direction and SNR combination, presented pseudo-randomly, over a single testing block. Percentage correct lateralisation scores were fit using binomial logistic regression and the threshold value, selected to be 95% correct, was extracted from the fitted function. Since a 180° difference in location is well above localisation threshold (Mills, 1958), it follows that failure to localise a sound accurately in this condition was because the subject was unable to detect the sound in the noise and hence a correct lateralisation response was used to determine the detection threshold. Indeed, pilot studies demonstrated that the threshold for a yes/no detection task at 90° was within 0.1 dB of the threshold estimated using the left–right choice. A threshold value of 95% was taken because the aim was to present stimuli at a level that was clearly audible, but difficult enough to be challenging for the subsequent relative localisation task. Difficulty was matched across subjects and task conditions by determining individual threshold values for each subject and in each task condition. The resulting threshold value determined three SNRs for Experiment 1; a “low” SNR which was equal to the 95%-correct threshold (mean SNR ± standard deviation; −6.8 ± 1 dB, n = 8), a “medium” and a “high” SNR, equivalent to the threshold value +3 and +6 dB, respectively. For Experiment 2, a single SNR was chosen, intermediate to the low and medium SNRs in Experiment 1; defined as the 95%-correct point +1.5 dB. The SNR of the thresholds of each subject taking part in Experiment 2 ranged from −9.4 to −7.4 dB (mean ± standard deviation = −8.3 ± 0.7 dB, n = 12, Table I). Four subjects were excluded from Experiment 2 as their detection thresholds were more than three standard deviations from the group mean. Threshold estimations were performed for each testing condition (see Experiment 2 testing). An example threshold test of a single participant is shown in Fig. 1(d): at the lowest SNR tested (−18 dB) the subject is at 58% correct (chance being 50%) indicating that they could barely discriminate the direction the signal moved. This subject's low SNR threshold was defined as −14 dB since this was the point at which the fitted function crossed the 95% correct point.

TABLE I.

Threshold testing results for Experiment 2.

Stimulus	Mean threshold SNR (dB)	Standard deviation (dB)	Range (dB)
			min	max
Broadband	−8.3	0.8	−9.4	−7.4
Low-pass filtered	−13.9	1.3	−16	−12
Bandpass filtered	−12.5	1.2	−15.5	−10.5

E. Testing

During testing, on each trial the reference sound was presented from one of the speakers in the ring (speaker selected pseudo-randomly from the set of speakers used in that experiment, see Secs. II F, II G, and II H for speakers used) and the target was presented from an adjacent speaker, either to the left or right (a 15° change in location). The participants were instructed to report which way the target had moved relative to the reference using the left and right arrows on a keyboard. Each trial began automatically 1 s after the subject made a response in the preceding trial. Testing runs were divided into blocks lasting approximately 5 min. At the end of each block the subject could take a break and choose when to initiate the next block.

F. Experiment 1: Effect of SNR on relative sound localisation

In this task, BBN pulses were presented to the participants at the three individually determined SNRs (see Sec. II D). The reference locations were −112.5°, −82.5°, −52.5°, −22.5°, −7.5°, 7.5°, 22.5°, 52.5°, 82.5°, and 112.5°, and targets were the speakers to the right and left of these locations [e.g., −127.5° and −97.5° for a reference of −112.5°, see Fig. 1(a)]. Subjects performed 20 trials for each direction/SNR combination across 3 testing runs, each divided into 5 blocks of approximately 6 min. Eight subjects completed Experiment 1. Of these, two subjects performed three testing runs with a mix of all three SNRs and six performed two runs with a mix of the low and medium SNRs and one run with the high SNR only.

G. Experiment 2: Effect of spectral band on relative sound localisation

BBN pulses were presented to the participants at a single SNR (95% + 1.5 dB) determined by the threshold testing and intermediary to the low and medium SNR in Experiment 1. In this experiment, reference locations were restricted to the frontal hemifield but tested all possible speaker positions within it. The reference positions were therefore: −97.5°, −82.5°, −67.5°, −52.5°, −37.5°, −22.5°, −7.5°, 7.5°, 22.5°, 37.5°, 52.5°, 67.5°, 82.5°, and 97.5°. In the LPN condition, the white noise pulses were low-pass filtered (<1 kHz, implemented in Matlab, low-pass finite-duration impulse response (FIR) filter, 70 dB attenuation at 1.2 kHz) while in the BPN condition, the white noise pulses were bandpass filtered (3–5 kHz, implemented in Matlab with a bandpass FIR filter, 70 dB attenuation at 2.6/5.4 kHz). Threshold estimates were made for each stimulus type (BBN, LPN, BPN) for each subject immediately before testing the relevant stimulus type. Subjects performed a total of 480 trials (20 trials per direction per reference location) in 1 testing run divided into 5 blocks of approximately 6 min each.

H. Experiment 3: Effect of eye fixation position on relative sound localisation ability

In Experiment 3, subjects were asked to focus their gaze on points 30° to the left or right of the midline while maintaining a 0° azimuth head position and perform the same task as in Experiment 2 with BBN stimuli in order to see the effects of eye position on the accuracy of relative localisation. Subjects performed 20 trials at each speaker location (10 left moving, 10 right moving) at each eye position, a total of 720 trials in 1 testing run divided in 6 blocks of approximately 7 min each.

I. Modeling localisation performance

Three simple models were created: a two-channel model, a topographic model, and a modified topographic model. In each case the model was used to predict the performance that an observer would make in the relative localisation task. The two-channel model, based on the opponent-channel model (McAlpine et al., 2001; Stecker et al., 2005), was estimated by modeling two spatial channels as cumulative Gaussians with a mean of 0° and standard deviation of 46°, as found by Briley et al. (2013) [Fig. 2(a)]. The peak of this model occurs at 90° reflecting the fact that the largest interaural time difference cue values occur at this point. Changing the standard deviation effectively altered the slope of the two channels and the extent to which tuning overlapped across the midline. To determine performance, the model of neural tuning was convolved with a representation of the stimulus based upon the actual sound level (the SNR value was selected as the across-subject mean BBN threshold of −8.3 dB SPL from Experiment 2). From this, the amount of neural activity was estimated as the ratio of the area under the resulting activity pattern of the two channels and the resulting change in activity between the reference and target was used as a measure of discriminability.

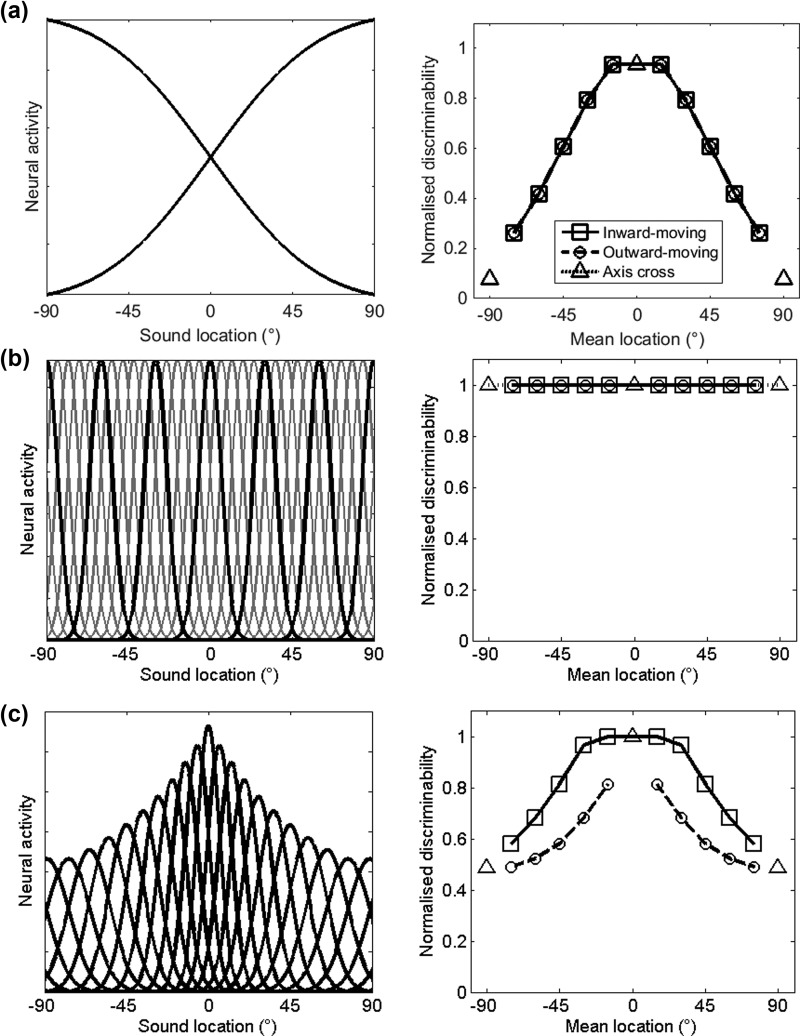
FIG. 2.

Models of sound location coding: The left-hand column shows representations of the models in terms of neural activity that would be expected for a given sound source location. The two-channel model (a) is represented by two Gaussians with means of −90° and 90° and standard deviation of 46°. The topographic model (b) is represented by multiple Gaussian curves located 6° apart with a standard deviation of 6. The modified topographic model (c) is represented by multiple Gaussian curves, with the midline represented by more and more narrowly tuned channels, the narrowest being 6° and the broadest, 12°. In (b) the channels are shown in gray with every tenth channel in black for visualisation purposes. The right-hand column shows the normalised discriminability (where 0 is chance and 1 is maximum performance) of the direction of the stimulus at the mean stimulus location based on the models. The two-channel model (a) discriminability is calculated as the change in the ratio of activity of each channel between the reference and target stimuli. In topographic (b) and modified topographic (c) discriminability is estimated by calculating the difference in Euclidean distance between the peak population activity generated by the reference and target sounds.

For the topographic model, tuning functions were constructed as a series of Gaussians with a standard deviation of 6° spread across 360° of azimuth with 50% overlap between adjacent channels [Fig. 2(b)]. The width of 6° was chosen based upon Carlile et al. (2014). The modeled neural channels were convolved with the acoustic stimulus as described for the two-channel model above to determine the activity elicited in each channel. The activity elicited by the reference and target sounds were therefore described by two vectors, each representing the activity elicited in each channel. Discriminability was calculated as the Euclidean distance between the two population vectors: a large value indicates that the two sounds activate different patterns of activity across the neural population.

The modified topographic model used a similar approach but rather than channels of equal width and spacing, channels increased in width from 6° to 12° from the midline to 72°. A 50% overlap was maintained so that as channels became more narrowly tuned they were also more closely spaced [Fig. 2(c)]. Again, the choice of channel widths was estimated from Carlile et al. (2014).

J. Analysis

Overall performance was assessed by calculating sensitivity index (d′) for subjects' ability to discriminate whether a target sound moved left or right at each reference or target speaker location and bias was calculated by estimating the criterion (Green and Swets, 1974). Using d′ as a sensitivity index implies the subject is using a model with two possible stimulus classes represented by normal distributions with different means. The distance between these distributions determines a subject's sensitivity (estimated d′) in the task. The subject is assumed to decide which class has occurred by comparing each observation with an adjustable criterion. The location of this criterion with no bias would be in the middle of the two stimulus class means, whereas any bias would be indicated by the criterion shifting closer to one or the other mean, thus increasing the likelihood of a response for that stimulus class (Macmillan and Creelman, 2004). Data were further analysed by separating trials into those where the target sound moved toward the midline and those where it moved away from the midline and calculated % correct performance for each SNR with respect to the reference location in Experiment 1. In Experiment 2, data were considered relative to the mean location of the reference and target location rather than either in isolation as this meant that inward and outward-moving sounds at this location elicited equivalent changes in localisation cues. This was not possible in Experiment 1 because the fixed set of reference locations and their respective targets did not make a full set of overlapping reference-target pairs. Statistical analyses were performed with SPSS software (IBM SPSS, NY, USA) and are described in the relevant sections in the text. For comparison of the data to the predicted spectral cues available, we estimated the ITD of the stimuli using Rayleigh's formula (Rayleigh, 1907); ITD = r/c * [theta + sin(theta)], where r is the radius of the head (9 cm was used here), c is the speed of sound (343 m/s), and theta is the angle of incidence of the sound in radians. For estimation of ILDs available in the stimuli we used the information provided by Shaw and Vaillancourt (1985).

III. RESULTS

Participants performed a single interval 2AFC task where they were asked to report whether a target sound was presented to the left or right of a preceding reference. The reference and target stimuli each consisted of three 15-ms pulses of noise presented in a background of noise generated and presented independently from each of the 18 speakers in the ring. Prior to completing the main experiments, each participant performed a threshold task to estimate the SNRs over which testing took place.

A. Thresholds

Each subject completed a threshold task to determine their individual threshold for detecting the stimuli embedded in the background noise. Subjects performed a modified task whereby reference sounds were presented from a speaker at 0°, and target sounds from ±90°. Since a location shift of this magnitude was well above perceptual threshold, it follows that if the subject could correctly discriminate the relative location, then the target was audible above the noise. Figure 1(d) shows an example of a threshold for a single participant. At high SNRs (−9 to −12 dB) the participant is able to identify correctly the direction the target has moved, but as the SNR decreases, performance decreases toward chance (50%). The 95% correct threshold was at a SNR of −14 dB. Each participant performed an independent threshold experiment for the BBN (Experiments 1–3), low-pass, and bandpass filtered stimuli (Experiment 2). Table I shows the summary of threshold values for participants.

B. Experiment 1: Effect of SNR

Experiment 1 aimed to determine how SNR influenced spatial sensitivity assessed with signal detection theory. Figure 1(e) plots the across-subject discriminability index [mean d′ ± standard error of the mean (SEM)] for discrimination of the direction of the target at the three SNRs. Sensitivity (d′) values are higher for judgments made in frontal space than in the periphery. Subjects' best performance was at the highest SNR followed by the medium SNR and then lowest SNR. A two-way repeated measures analysis of variance (ANOVA) (dependent variable: d′, independent variables: reference location and SNR) revealed a main effect of reference location (F_(9,63) = 29.81, p < 0.001) and SNR (F_(2,14) = 82.85, p < 0.001) and a significant interaction between these factors (F_(18,126) = 2.95, p < 0.001). Post hoc pairwise comparisons (Tukey-Kramer, p < 0.05) showed that subjects tended to be worse at the peripheral speakers than the central speakers (speaker 1 was significantly different from speakers 4–8, speakers 2 and 10 from speakers 3–8, speaker 3 from speakers 2 and 10, speakers 4–8 from speakers 1, 2, and 10, speaker 7 from speakers 1, 2, 9, and 10 and speaker 9 from speaker 7) and that performance at each SNR was different from the other two. While Experiment 1 demonstrated a clear effect of SNR and reference speaker location on performance, some subjects were confused at the most lateral speaker locations (which were behind them) and our speaker selection did not allow us to test left–right discriminations across pairs of speakers with equal changes in localisation cues. In Experiment 2, testing was therefore restricted to frontal space [−82.5° to +82.5°, Fig. 1(a)], and all possible reference-target speaker pairs were tested thus allowing us to compare left– right discriminations with equal changes in localisation cues [Fig. 1(a)].

C. Experiment 2: Effect of spectral band

In Experiment 2, all speaker locations in frontal space were tested using three types of acoustic stimulus: BBN (as in Experiment 1) and two types of narrowband (NB) stimulus designed to restrict the dominant sound localisation cues to either ITDs (low-pass filtered noise <1 kHz, LPN) or ILDs excluding spectral cues (bandpass filtered noise 3–5 kHz, BPN). Figure 1(f) shows the effects of varying the spectral band on sensitivity measures, plotting data according to the mean reference-target location such that left- and rightwards moving stimuli elicited changes in localisation cues that were identical in magnitude. Qualitatively, it is clear that performance is best in the BBN condition relative to LPN and BPN. Generally, performance is better centrally than peripherally, although the decrement in peripheral performance is particularly marked in the BPN condition. A two-way repeated measures ANOVA (independent variables—target location and task condition, and dependent variable d′) revealed main effects of spectral band condition (F_(2,22) = 17.63, p < 0.001) and speaker location (F_(10,110) = 43.08, p < 0.001) and the task condition showed an interaction with mean location (F_(20,220) = 5.56, p < 0.001). Post hoc pairwise comparisons (Tukey-Kramer, p < 0.05) revealed that the BBN condition was significantly different from the LPN and BPN conditions but the BPN and LPN conditions were not different from each other. Post hoc analysis of mean stimulus location revealed that the main differences were between peripherally located stimuli and those located around the midline [mean locations −75° to −45° vs −30° to 30°, −30° to −15° vs −75° to −45° & 60° to 75°, 0° to 30° vs −75° to −45° & 45° to 75°, 45° vs −15° to 30° & 60° to 75°, 60° vs −30° to 30°, and, 75° vs −30° to 45°, see Fig. 1(a) for mean stimulus locations].

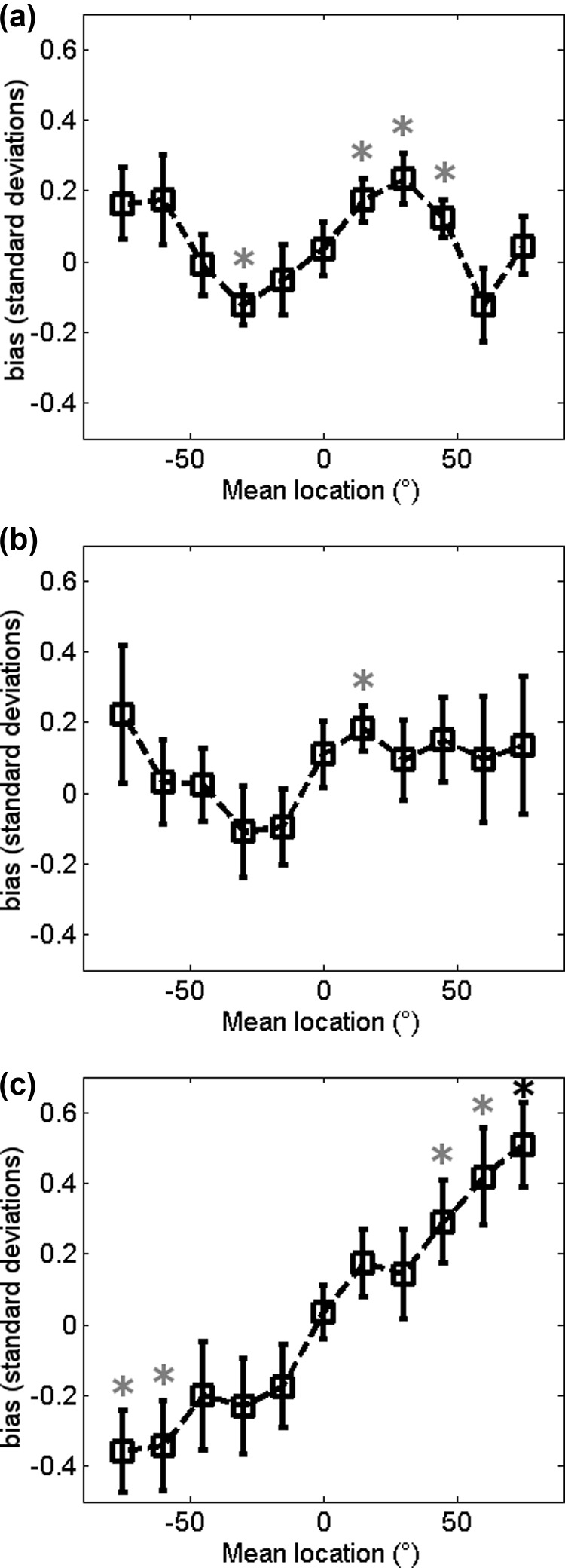
As well as exploring sensitivity we also estimated bias (Fig. 3) for performance in each of the three conditions. A positive bias value indicates subjects were more likely to report that the target was right of the reference, and a negative value indicates subjects were more likely to report that the target was left of the reference. A two-way repeated measures ANOVA examining the influence of stimulus condition and speaker location on bias showed a main effect of speaker location (F_(10,110) = 2.64, p = 0.006) and an interaction between speaker location and condition (F_(20,220) = 3.01, p < 0.001), indicative of conditions having different patterns of bias; for example, the BPN condition shows a bias favouring the target on the side peripheral to the reference. However, analysis to determine whether the bias was significantly different from zero (t-tests, p-values Bonferroni corrected for multiple comparisons) suggest that the across-subject bias is relatively modest; only in the BPN case was any bias value significantly non-zero (mean location 75°, p = 0.0013).

FIG. 3.

Bias at the mean stimulus location across conditions: Mean bias ± SEM of all participants at the mean locations of the stimuli in the BBN (a), LPN (b), and BPN (c) conditions. Gray asterisks indicate p < 0.05 in a t-test to check for difference from zero. The black asterisk in (c) indicates significance in the t-test after Bonferroni correction (p < 0.0045).

D. Models

Previous neuroimaging studies have measured the change in neural activity elicited by a change in sound source location following a brief adapting stimulus in order to compare two-channel and topographic models of sound localisation and have demonstrated that predictions generated from a two-channel model best match the observed data (Salminen et al., 2009; Salminen et al., 2010; Magezi and Krumbholz, 2010; Briley et al., 2013). In order to compare our observed behavioural performance to that predicted by different models of auditory space, relative localisation abilities were modeled using three different approaches: a two-channel model, with two channels broadly tuned to ipsi- and contra-lateral space, a topographic model with equally spaced equal-width channels spanning all of auditory space, and a modified topographic model, with channels that were both narrower and more closely spaced near the midline [see Sec. II, Figs. 2(a)–2(c) first column]. For each model a representation of the stimulus, including the background noise, was convolved with the spatial channels and the discriminability of the reference and target sounds was estimated, computing measures for inward and outward changes in spatial location separately, throughout frontal space (see Sec. II). The models, and the resulting normalised discriminability measures (where 0 is equal to chance and 1 to maximum performance), are plotted in Fig. 2, second column. Note that the models are only intended to provide a qualitative impression of the characteristics one might observe as the measures of “discriminability” are not necessarily equivalent across models. Each model produces a different predicted pattern of discriminability: First, in the two-channel model [Fig. 2(a)], performance is best around the midline, and inward- and outward-moving targets elicit equivalent measures of discrimination. Second, in the topographic model [Fig. 2(b)], inward- and outward-moving targets again elicit overlapping discriminability measures; however, in this case performance does not change across auditory space. Finally, in the modified topographic model [Fig. 2(c)], performance is best at the midline, with a drop in performance peripherally and inward-moving sounds always having a higher discriminability than outward-moving sounds, i.e., this model predicts that subjects should be better at detecting location shifts toward the midline. The models generated two testable predictions relating to whether (a) there was a change in performance across space (as in the two-channel and modified topographic model) and (b) whether there was a difference between inward- and outward-moving sounds, as the modified topographic model predicts a benefit for inward- over outward-moving sounds.

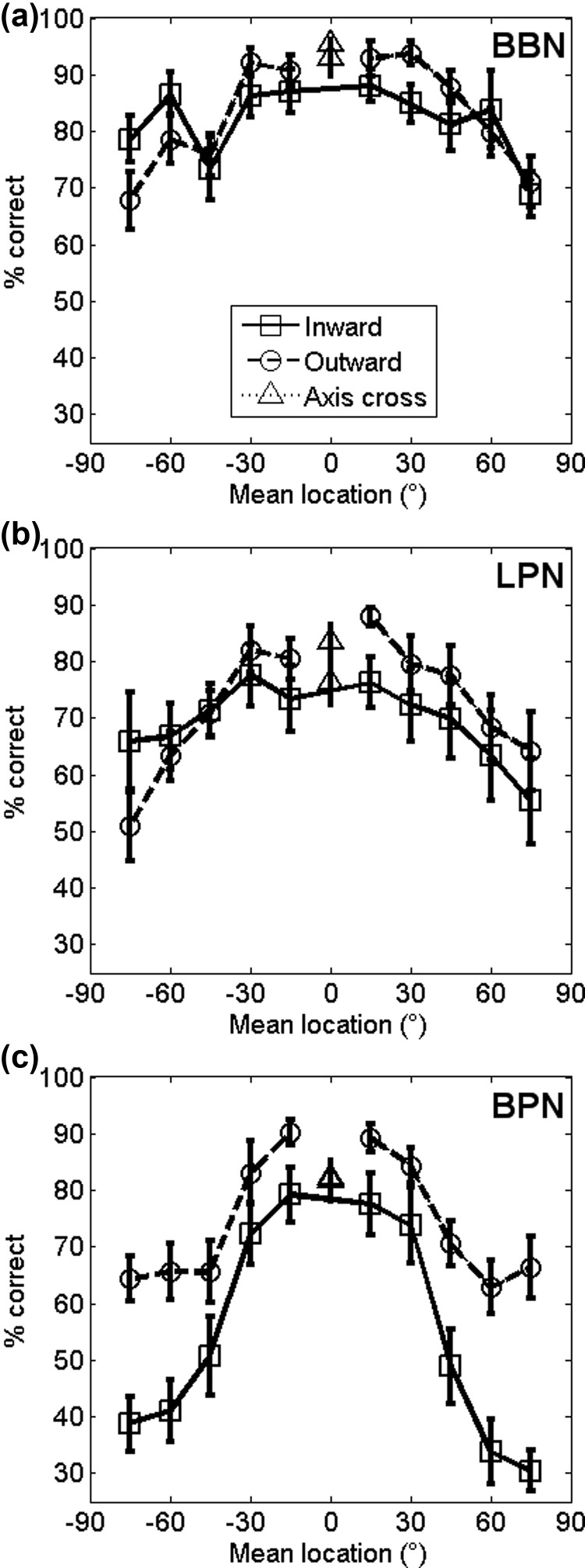
The data from Experiment 2 was therefore analysed according to whether the target sound moved toward or away from the midline to address the hypotheses above. Each point in Fig. 4 therefore represents a pair of reference-target sounds that share the same mean location (and therefore localisation cues) and differ only in the direction of movement. Figure 4 shows the resulting mean (±SEM) performance scores of all participants in each of the three spectral band conditions. Two-way repeated measures ANOVAs on each condition revealed main effects of speaker location in all conditions but only in the BPN condition was there a significant effect of direction of target (Table II). There was also an interaction between direction and speaker location in the BBN condition (F_(4.11,45.25) = 2.57, p = 0.049, Greenhouse-Geisser corrected for sphericity). The LPN condition is consistent with the two-channel model, in that there is a significant effect of location, but not a statistically significant difference between inward- and outward-moving sounds. None of the models is consistent with the BBN condition, where there is a significant location—direction interaction or the BPN condition where there is a significant main effect of direction but showing higher performance for outward-moving sounds.

FIG. 4.

Effect of low and bandpass filters: (a) Mean percent correct of all participants separated into the direction of the target relative to the reference in the BBN condition. Circles/dashed lines show targets that moved away from the midline (0°) relative to the reference location, squares/solid lines show sounds that moved toward the midline relative to the reference and triangles show targets that crossed the midline. (b) Mean percent correct for all participants in the LPN condition. (c) Mean percent correct for all participants in the BPN condition.

TABLE II.

Post hoc analysis looking at significant differences between the mean stimulus locations, see Fig. 1(a) for locations, of a two-way repeated measures ANOVA on individual bandwidth conditions with dependent variable percent correct and independent variables speaker location and direction the target moved.

Independent variable	Degrees of freedom	Total degrees of freedom	Task condition	F	p	Post hoc pairwise comparisons (Tukey-Kramer, p < 0.05)
Speaker location	9	99	Broadband	9.98	<0.001	Location −75° vs Locations −60°, −30° and 30°
						Location −60° vs Locations −75° and 75°
						Location −45° vs Locations −30°, −15°, 15° and 30°
						Locations −30° and 30° vs Locations −75°, −45° and 75°
						Locations −15° and 15° vs Locations −45° and 75°
						Locations 75° vs Locations −60°, −30°, −15°, 15° and 30°
			Low-pass filtered	10.97	<0.001	Location −75° vs Locations −30°, −15° and 15°
						Location −60° vs Locations −15° and 15°
						Location −45° vs Location −30°
						Location −30° vs Locations −75°, −45° and 75°
						Location −15° vs Locations −75° and −60°
						Location 15° vs Locations −75°, −60°, 60° and −75°
						Location 60° vs Location 15°
						Location 75° vs Locations −30° and 15°
			Bandpass filtered	37.42	<0.001	Locations −75° to −45° and 45° to 75° vs Locations −30°, −15°, 15° and 30°
Direction target moved	1	11	Broadband	0.20	0.663a
			Low-pass filtered	0.21	0.657a
			Bandpass filtered	8.66	0.013a

^aGreenhouse-Geisser correction for sphericity.

E. Assessing the relationship between performance and binaural cue values

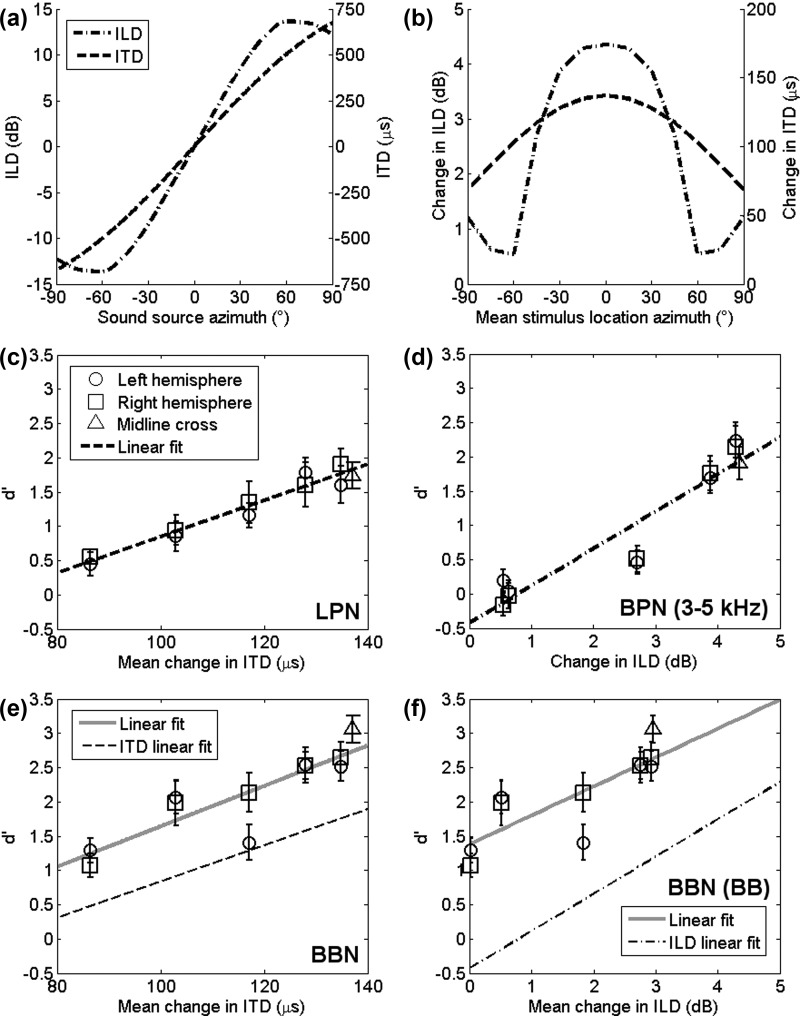
Since a 15° shift in azimuth does not produce an equal change in localisation cues across all spatial locations, the change in ITD and ILD cues that would be elicited for each reference-target pair were estimated. The estimated cue values were then used to analyse the relative-localisation abilities according to the magnitude of the change in ITD or ILD each stimulus pair produced. ITD values were estimated using a spherical head of diameter 18 cm (Rayleigh, 1907) and ILD values were estimated using data from Shaw and Vaillancourt (1985) weighted to reflect the spectra of the speakers and the bandwidth of the stimuli used in the current study. Figure 5(a) shows the resulting ITD and ILD values for the range of space tested. Figure 5(b) converts these values into the change in cue value between reference and target sounds at each mean location. Figures 5(c) and 5(d) plot sensitivity (d′) measures from Experiment 2 according to the change in ITD and ILD values, respectively, in each of the NB conditions. For the LPN condition this shows that d′ decreases for smaller changes in ITD, and that performance is well fit with a linear regression line (R² = 0.95, p < 0.0001). The BPN data show that performance also declines with decreasing ILD change. Regression analysis was also used to yield a linear fit of these data, although the fit was marginally worse (R² = 0.90, p < 0.0001) possibly due to a floor effect in performance. The resulting regression coefficients were used to compare performance in the BBN condition to that in both NB conditions. Figures 5(e) and 5(f) show the discriminability index with change in ITD and ILD for the BBN condition. Performance in the BBN condition is higher than performance in either of the spectrally restricted cases and is less well fit with a linear regression line (LPN: R² = 0.77, p < 0.001, BPN: R² = 0.69, p < 0.01) in both cases. While performance in the BBN case is superior to either NB case, the slopes of the regression lines in each condition are very similar when comparing the BBN and NB conditions (NB ITD: 0.0264 d′ μs⁻¹ and BBN ITD: 0.0295 d′ μs⁻¹, NB ILD: 0.5427 d′ dB⁻¹ and BBN ILD: 0.4214 d′ dB⁻¹). The decrease in performance from BBN to NB is more marked in the BPN condition (∼2 d′) than in the LPN condition (∼0.5 d′).

FIG. 5.

Real world changes in the binaural cues: (a) Changes in ITD and ILD cues as sound source azimuth varies. Dashed line shows changing ITD cues. Dashed-dotted lines show changing ILD cues [ILD values calculated using data from Shaw and Vaillancourt (1985)]. (b) Shows the change in ILD and ITD cues at the mean stimulus locations. (c) Shows the mean d′ values from the LPN condition plotted as a function of the change in ITD a stimulus elicited. The dashed line shows a linear fit of the data. (d) Shows the mean d′ values from the BPN condition plotted as a function of the change in ILD (frequency weighted to reflect the bandpass filter of 3–5 kHz) a stimulus elicited. The dashed-dotted line shows a linear fit of the data. (e) Shows the mean d′ values from the BBN condition plotted as a function of the change in ITD a stimulus elicited. The gray solid line shows a linear fit of this data. The dashed line shows the linear fit of the LPN data from (b). (f) Shows the mean d′ values from the BBN condition plotted as a function of the change in ILD (frequency weighted to reflect the broadband stimulus presented at 48 kHz) a stimulus elicited. The gray solid line shows a linear fit of this data. The dashed-dotted line shows the linear fit of the BPN data from (c).

F. Experiment 3: Effect eye fixation position on relative localisation

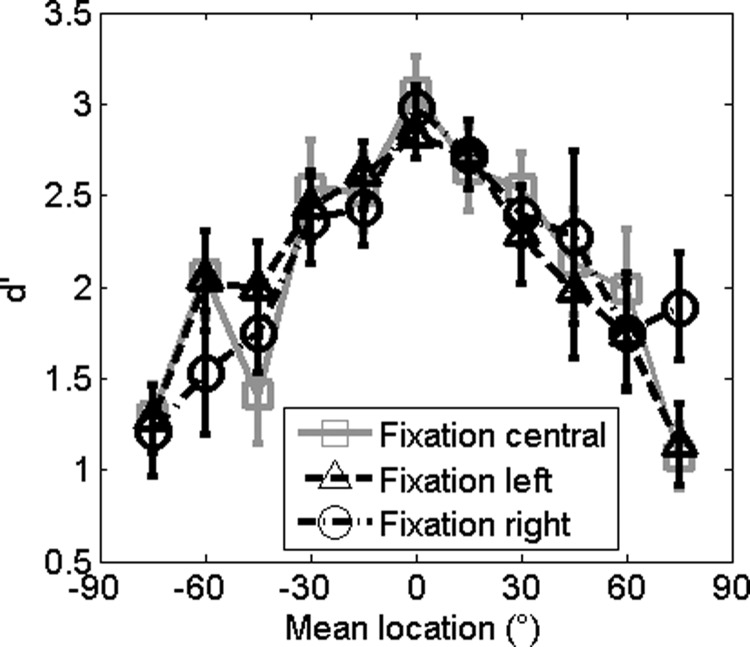
Since Experiments 1 and 2 demonstrated that performance is superior at the midline, Experiment 3 aimed to test whether this was a consequence of head or gaze direction by requiring that subjects fixate either centrally, as in Experiments 1 and 2, or 30° to the left or 30° right while maintaining the head fixed at 0° azimuth. Figure 6 shows the discriminability at each fixation point, with central fixation in gray for comparison. A two-way repeated measures ANOVA with dependent variable d′ and independent variables mean speaker location and direction of gaze (central, left, or right) showed a main effect of speaker location (F_(3.39,37.31) = 11.69, p < 0.001, Greenhouse-Geisser corrected for sphericity) but not direction of gaze (F_(1.23,13.48) = 0.32, p = 0.9, Greenhouse-Geisser corrected for sphericity).

FIG. 6.

Effect of eye position: Mean d′ of all participants in the broadband condition with a fixation of 30° left (triangles and dashed line) or 30° right (circles and dashed-dotted line). The d′ from the central fixation point (0°) is shown for comparison (gray squares and solid line).

IV. DISCUSSION

The goal of this study was to develop a 2AFC task to allow the efficient measurement of spatial acuity throughout auditory space. A relative localisation task was developed that facilitated measurement of spatial resolution at fixed 15° intervals throughout auditory space by requiring human listeners to discriminate the relative location of two sequentially presented sound sources. In order to simulate more real-world listening conditions stimuli were presented in the presence of multiple independent noise sources. Experiment 1 demonstrated that decreasing the SNR impaired performance throughout auditory space. Experiment 2 tested the ability of listeners to perform this task with bandpass stimuli and compared performance to broadband stimuli containing ITD, ILD, and spectral cues. Subjects were able to perform the relative localisation task at a high level of accuracy across the frontal hemifield in the broadband condition with performance reduced relative to this in the low-pass and bandpass conditions. Predictions generated from models of three common theories of how auditory space is encoded by the brain showed that the low-pass data were compatible with a two-channel model but that data from the bandpass and broadband conditions were incompatible with any of the model predictions. The differences in discrimination abilities observed across space were well described by the underlying acoustic cues available to listeners. Experiment 3 determined that eye position did not impact upon behavioural performance in this task.

Auditory performance in a variety of tasks declines with decreasing SNR with single masker noise sources (Good and Gilkey, 1996; Lorenzi et al., 1999) and multiple noise sources (Lingner et al., 2012). Experiment 1, which tested ability in the task across three SNRs (all of which were above subjects' detection thresholds), demonstrated that listeners were less able to perform this task at adverse SNRs, consistent with results obtained in an absolute localisation task (Good and Gilkey, 1996). There was an interaction between the SNR and the performance across auditory space, indicating that increasing the SNR improved performance differently throughout space—this may partly be explained by ceiling effects in the highest SNR and/or floor effects in the lowest SNR.

When stimuli were presented at equivalent audibility but bandpass filtered, in order to restrict localisation cues to predominantly ITD or ILD cues, subjects could still perform the task but showed weaker performance in each condition compared with the broadband stimuli, notably in the BPN condition, consistent with absolute localisation studies (Carlile et al., 1999; Freigang et al., 2014). This finding is also consistent with data from Recanzone et al. (1998), who measured the ability of listeners to detect changes in source location and demonstrated that performance declined when subjects were given spectrally limited vs BBN stimuli. The data from Experiment 2 also demonstrate that listeners were substantially more biased in the BPN condition than in the other two. This bias could be a “response bias” which shifts the decision criterion in the direction of the hemisphere in which the sound is presented (Hartmann and Rakerd, 1989). In order to exclude monaural spectral cues, the BPN stimuli were restricted in their spectral band, with the consequence that the spectral bandwidth differed between the LPN and BPN conditions potentially accounting for some of the observed decrement in performance between BPN and the other conditions. The spectral band chosen also limited listeners to relatively small ILD cues [Figs. 5(a) and 5(b)] with which to perform the task and it has been previously shown that performance is poor for localising pure tones in the region of 3–5 kHz (Stevens and Newman, 1936). Listeners may also have been able to utilise envelope ITDs in the BPN condition (Bernstein and Trahiotis, 1994). Future experiments are necessary to explore the contribution of spectral bandwidth, as well as both envelope and temporal fine structure cues, to performance in this task. Performance was best in the broadband condition, when both binaural and monaural spectral cues were available, although it is likely that subjects mainly relied on binaural cues to perform the task even when spectral cues were available since spectral cues contribute little information when normal binaural cues are available in an absolute localisation task in azimuth (Macpherson and Middlebrooks, 2002).

Analysis of the underlying cues available to listeners in the bandpass conditions allowed us to compare performance in the task with available cues. For pairs of speakers at peripheral locations, the change in the available ILD cue was <1 dB and since Mills (1960) reported a just noticeable difference of approximately 1.6 dB ILD about the midline for pure tones of 3–5 kHz, it is perhaps unsurprising that subjects performed poorly at these locations in the BPN condition. In contrast to the limited availability of ILD cues at peripheral locations, ITD cues did not decline as sharply in the periphery and behavioural performance reflected this. For tones of 1 kHz or less, presented in silence at 75° azimuth, the MAA corresponds to an ITD change of approximately 70 μs (Mills, 1958). In the present study, the most peripheral location the change in ITD corresponded to only ∼86 μs, a value fractionally higher than the measured corresponding MAA.

Previous studies have demonstrated a role for spectral cues in absolute localisation studies (Musicant and Butler, 1985; Yost and Zhong, 2014). In Experiment 2, the slopes of the regression lines estimated from the available cues in the BBN case were broadly similar to those in the spectrally restricted cases (Fig. 5), however, the intercept was higher in the broadband case than both LPN (BBN: −1.31 d′, LPN: −1.80 d′) and BPN (BBN: 1.38 d′, BPN: −0.43 d′) cases. This suggests that listeners integrate the available binaural and spectral cues in the BBN condition to allow better relative localisation than either cue alone, just as they do during absolute localisation studies (Hebrank and Wright, 1974; Macpherson and Middlebrooks, 2002).

An open question is how these cues are integrated to form a perception of auditory space within the brain. Three simple models were developed where auditory space was represented as a two-channel model, a topographic model, or a modified topographic model, based on recent non-behavioural imaging studies that tested brain responses to shifts in sound source locations (Salminen et al., 2009; Salminen et al., 2010; Magezi and Krumbholz, 2010), and predictions were generated for psychophysical performance in this task. Specifically, the two-channel and modified topographic model predicted that performance should be better around the midline than in the periphery, while only the modified topographic model, predicted that performance should differ (specifically should be superior) for inward- as compared to outward-moving sounds. Statistical analysis of our behavioural data demonstrated that in all three-cue conditions (LPN, BPN, and BBN) performance varied throughout space, and that midline performance was superior to that in the periphery. Additionally, in the LPN condition where ITDs are the dominant localisation cue, performance for outward- and inward-moving sounds was statistically indistinguishable lending support to the two-channel model, which was originally developed for ITD processing. In contrast, the data for the BBN and BPN conditions were not satisfactorily explained by any of the models.

While recent neuroimaging studies have lent support to a two-channel model of sound location in human auditory cortex (Salminen et al., 2009; Salminen et al., 2010; Magezi and Krumbholz, 2010; Briley et al., 2013), alternative models of the neural representation of sound location propose that space may be represented by a three-channel model (Dingle et al., 2010, 2012, 2013) or that an optimal model would change according to both frequency and head size such that, for humans, coding is predicted to be two-channel at low frequencies and labeled line/topographic at higher frequencies (Harper et al., 2014). Recent physiological findings from auditory cortex are also consistent with a labeled-line code for sound localisation cues (Belliveau et al., 2014; Moshitch and Nelken, 2014). It may also be the case that different localisation-based tasks tap into different levels of the auditory brain in which different coding schemes operate. For example, a recent behavioural study using multiple auditory objects to probe the representation of auditory space is consistent with there being multiple, narrowly tuned, spatial channels (Carlile et al., 2014), while neurophysiological studies support a coding transformation for ITDs from two-channel to labeled line from midbrain to cortex (Belliveau et al., 2014)

Experiment 3 explored whether eye position influenced performance in the relative localisation task by asking subjects to fixate 30° to the left or 30° to the right of the midline while maintaining a central head-position. We found that gaze location had no effect on the discriminability of left and right moving sounds for our subjects, indicating that the superior performance in the midline in Experiments 1 and 2 is relative to head position rather than eye position or attentional focus, or some combination of the these factors. This is in contrast to previous work on absolute sound localisation, which has shown that gazing toward a visual stimulus can alter sound localisation abilities, for short periods of time sound localisation is biased away from the point of gaze (Lewald and Ehrenstein, 1996) and for longer periods of time, sound localisation is biased toward the point of gaze (Razavi et al., 2007). However, it is not clear that this would necessarily affect the accuracy of comparing the location of two sounds. In another study looking at acuity of localisation cue discrimination (Maddox et al., 2014), a short gaze cue that informed subjects about the location of the sound they were about to listen to improved performance in an auditory relative localisation task. Our results do not show a difference in performance but this could be because our subjects had their gaze fixed for minutes at a time in one location, which in itself offered no information about the likely origin of the upcoming sound. When Maddox et al. (2014) used uninformative cues there was no improvement in performance. Thus, the present data are consistent with auditory space being represented relative to the orientation of the head, rather than the direction of gaze.

We measured individual thresholds for each signal type using a modified version of the task which required that listeners report whether a target sound originated from ±90° left or right of the midline. Signals at 90° eccentricity presented in noise will be more audible than those presented at the midline due to a combination of the better ear effect (Zurek, 1993) and spatial release from masking (Blauert, 1997). Pilot experiments demonstrated that 95% detection thresholds were on average 0.4 dB lower at +90° than at 0°. If audibility was limiting performance at central locations we might predict that localisation performance would also decrease toward the midline whereas the data in Experiments 1–3 suggest the opposite. Nevertheless, it is possible that at the lowest SNR, where performance at the midline is substantially poorer than the medium and high SNRs, audibility differences might be imposing a limit on performance.

In conclusion, we have developed a 2AFC localisation task that provides a rapid way of assessing spatial sensitivity throughout auditory space. Rather than collecting thresholds for spatial discrimination at multiple locations, or requiring that subjects make some sort of absolute localisation judgment, we tested listeners in a task that measured localisation abilities at fixed 15° intervals in the frontal hemisphere. Such a test provides a robust, sensitive, and flexible method that could prove useful both in clinical settings for examining the precision of localisation in hearing impaired listeners and for testing in animal models. For invasive neurophysiological studies that must necessarily be performed in animal models, this task represents an ideal way to explore the neuronal correlates of sound localisation in animals actively engaged in a localisation task. Unlike an approach to target task this paradigm reduces the response options to two, thus allowing more powerful neurometric analysis.