Problems of Robustness in Poisson–Boltzmann Binding Free Energies

Abstract

Although models based on the Poisson–Boltzmann (PB) equation have been fairly successful at predicting some experimental quantities, such as solvation free energies (ΔG), these models have not been consistently successful at predicting binding free energies (ΔΔG). Here we found that ranking a set of protein–protein complexes by the electrostatic component (ΔΔG_el) of ΔΔG was more difficult than ranking the same molecules by the electrostatic component (ΔG_el) of ΔG. This finding was unexpected because ΔΔG_el can be calculated by combining estimates of ΔG_el for the complex and its components with estimates of the ΔΔG_el in vacuum. One might therefore expect that if a theory gave reliable estimates of ΔG_el, then its estimates of ΔΔG_el would be reliable. However, ΔΔG_el for these complexes were orders of magnitude smaller than ΔG_el, so although estimates of ΔG_el obtained with different force fields and surface definitions were highly correlated, similar estimates of ΔΔG_el were often not correlated.

Introduction

Classical molecular dynamics (MD) methods^1,2 have been fairly successful at predicting a wide variety of biophysical quantities, including solvation free energies (ΔG),³⁻⁵ but computing binding free energies (ΔΔG) with such methods is computationally expensive. Implicit solvent models, such as the Poisson–Boltzmann (PB) equation (PBE),⁶⁻¹⁰ that average over the degrees of freedom of the solvent have therefore been developed to predict these quantities more quickly. The basic strategy of PB methods is to model the effects of the solvating waters by treating the molecule as a set of point charges in a low-dielectric region with a surrounding high-dielectric medium and to replace the surrounding ions with a continuous charge distribution outside the molecule that changes self-consistently in response to the electric field generated by the fixed charges in the molecule. These models have been fairly successful at predicting many biophysical quantities, including ΔG of small molecules^3,5,11−15 and the salt dependences of ΔΔG.¹⁶⁻²²

If estimates of ΔΔG could be obtained quickly from implicit solvent models, drug development and discovery could be accelerated. However, although implicit solvent models, including PB methods, have been successful at predicting ΔG,^3,5,11−15 they have been less successful at predicting ΔΔG.²³⁻³⁰ At first glance, this statement appears to be self-contradictory because the electrostatic component (ΔΔG_el) of ΔΔG can be computed from

1

where ΔG_el^comp is the electrostatic component (ΔG_el) of ΔG of the complex, ΔG_el and ΔG_el² are the ΔG_el of the two components of the complex, and ΔΔG_el is the electrostatic binding free energy of the complex in vacuum. One might therefore initially think that if implicit solvent models can accurately rank molecules by ΔG, then they should be able to similarly rank complexes by ΔΔG, but, as shown in the Results, this assumption is not necessarily true.

One potential explanation of this apparent contradiction is explored in the present work. In this study, ΔG_el was orders of magnitude larger than ΔΔG_el. Therefore, estimates of ΔG_el with small relative errors combined to yield estimates of ΔΔG_el that contained large relative errors. All of the methods examined led to estimates of ΔG_el that were highly correlated with each other, but the individual estimates of ΔG_el could differ by hundreds of kJ/mol. These differences did not affect the rankings of these molecules by ΔG_el because ΔG_el covered a range of tens of thousands of kJ/mol, but the rankings by ΔΔG_el were affected because ΔΔG_el only covered a range of hundreds of kJ/mol.

One possible source of these errors is uncertainty in the force field used to specify the atomic charges and radii. These parameters were taken from the AMBER 94³¹ and CHARMM 27³² force fields, which were both created for classical MD simulations. Partly because these force fields were not designed specifically for implicit solvent models, using them could introduce errors into the calculations.³³⁻³⁵ The choice of force field led to large absolute changes in ΔG_el (ranging from 39–2640 kJ/mol), but these changes did not lead to significant changes in the rankings of the molecules by ΔG_el because of the large range of ΔG_el. The rankings of complexes by ΔΔG_el were also not strongly affected by the choice of force field, but the large absolute errors in these free energies (ranging from 0.3–112 kJ/mol) could cause problems for applications, such as drug development, where complexes may differ in ΔΔG_el on the order of 1 kJ/mol.

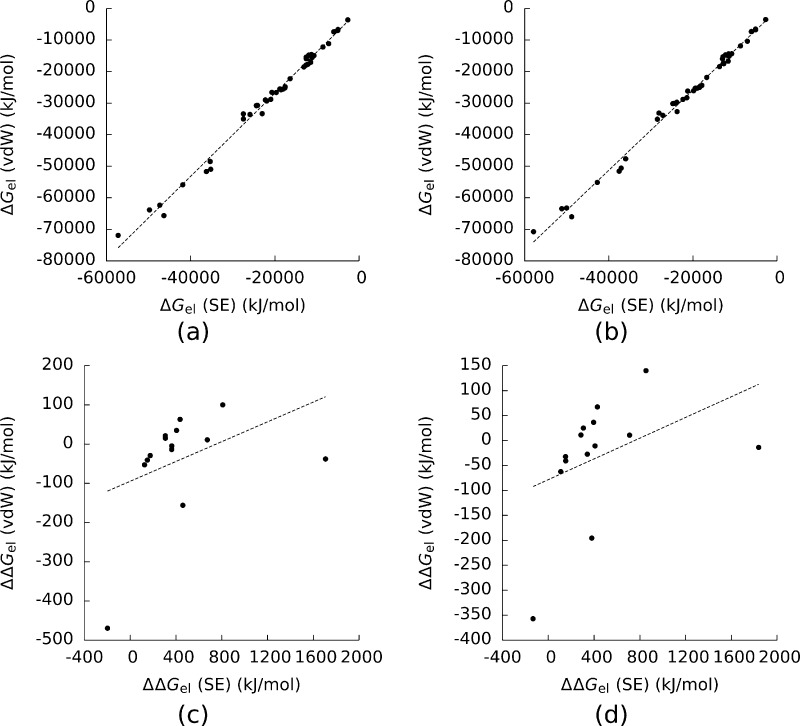
Another potential source of error is the method chosen to define the boundary between the molecular interior and exterior. Several surface definitions have been used in implicit solvent models. The most common choice is the solvent-excluded (SE) surface,^36,37 but other surfaces are advocated by some researchers, including the van der Waals (vdW) surface,³⁸⁻⁴⁰ Gaussian surfaces,^41,42 and self-consistent surfaces.⁴³⁻⁴⁷ No consensus has yet emerged about which of these surfaces is most realistic or best matches experimental data. For the complexes in the present study, although the SE surface produced predictions of ΔG_el that were highly correlated with those given by the vdW surface, the predictions of ΔΔG_el by these two surfaces were not strongly correlated. To further explore the uncertainties in these free energies generated by the uncertainties in the surface definition, we used a modified version of the vdW surface⁴⁸ (mvdW) to examine how these free energies changed as the definition of the surface was gradually changed. As the gaps and crevices inside the vdW surface were filled in as the radius of the probe used to define the mvdW surface was increased, ΔG_el increased smoothly and monotonically. These increases in ΔG_el probably reflected the losses of the favorable interactions between these regions of high dielectric constant and the nearby charges. However, the dependence of ΔΔG_el on probe radius was less predictable and nonmonotonic. Because ΔG_el changed smoothly and monotonically with probe radius, the rankings of these complexes by ΔG_el were not strongly sensitive to the choice of probe radius, but the complicated dependences of the ΔΔG_el on probe radius made the rankings by ΔΔG_el sensitive to the choice of probe radius.

If the results presented here are transferable to other molecular complexes, they could help explain why PB models have been less successful at ranking complexes by ΔΔG than at ranking them by ΔG. Perhaps the predictions of ΔΔG by PB methods could be improved by obtaining better force fields and by determining what surface definition best matches experimental data. However, trying to do so by comparing the predictions of ΔG given by PB methods to experimental measurements may be difficult. In addition to ΔG_el and ΔΔG_el, ΔG and ΔΔG contain nonelectrostatic components that are also somewhat uncertain.⁴⁹⁻⁵² Therefore, most of these comparisons are performed by determining whether the predictions of the PB methods are correlated with the experimental measurements, not by comparing the absolute values of these free energies. Because the uncertainties in the force field and molecular surface definition did not significantly change the rankings of these complexes by ΔG_el but did change the rankings by ΔΔG_el, such experimental data would not have provided enough information to improve the predictions of ΔΔG_el. Attempting to improve the predictions of ΔG given by PB models may not provide enough information to improve their predictions of ΔΔG.

Methods

We chose 14 complexes from the RCSB Protein Data Bank⁵³ by searching for high-resolution X-ray structures of protein–protein complexes where the components of the complex had a wide variety of interfacial shapes and charges. The pdbids and chains used as the binding components were as follows: 1acb chains E and I, 1atn chains A and D, 1avx chains A and B, 1b6c chains A and B, 1beb chains A and B, 1brs chains A and D, 1buh chains A and B, 1h1v chains A and G, 1he8 chains A and B, 1kxp chains A and D, 1sbb chains A and B, 1ysl chains A and B, 2hp0 chains A and B, and 2uy1 chains A and B. The coordinates of the protein atoms in these chains were taken from the structure files. The atomic partial charges were taken from the CHARMM 27³² and AMBER 94³¹ force fields. The radii were taken to be half the distance to the Lennard-Jones potential energy minimum between two atoms of the type in question. These charges and radii were added to the structures with the pdb2pqr utility.^54,55 All protein residues were assumed to be in their standard ionization states at pH = 7. All PB calculations were performed with the Cartesian PB (CPB) solver.⁵⁶ The locations of the atoms were fixed at the coordinates given in the structure files. No attempt was made to model conformational changes. All of these calculations used an interior dielectric constant of 1, an exterior dielectric constant of 80, a temperature of 298.15 K, a 1:1 salt concentration of 0.1 M, a grid that extended 2 times the largest dimensions of the complex, a finest grid spacing of 0.02 nm, and charge-conserving boundary conditions.⁵⁷

The vdW surface defines the interior of the molecule to be the interiors of the set of spheres centered at the charge sites with radii equal to the vdW radii in the force fields. The SE surface defines the exterior of the molecule as the regions that can be contained within a probe sphere that does not overlap any of the vdW spheres. We used a probe radius of 0.14 nm to define the SE surface. The mvdW surface⁴⁸ is similar to the vdW surface, but any spheres that would not have solvent-accessible surface area in a SE surface with a given probe radius have their vdW radii increased by the probe radius. The internal crevices present in the vdW surface are therefore filled in as the probe radius used to define the mvdW surface is increased.

Results

Convergence with Respect to Grid Spacing

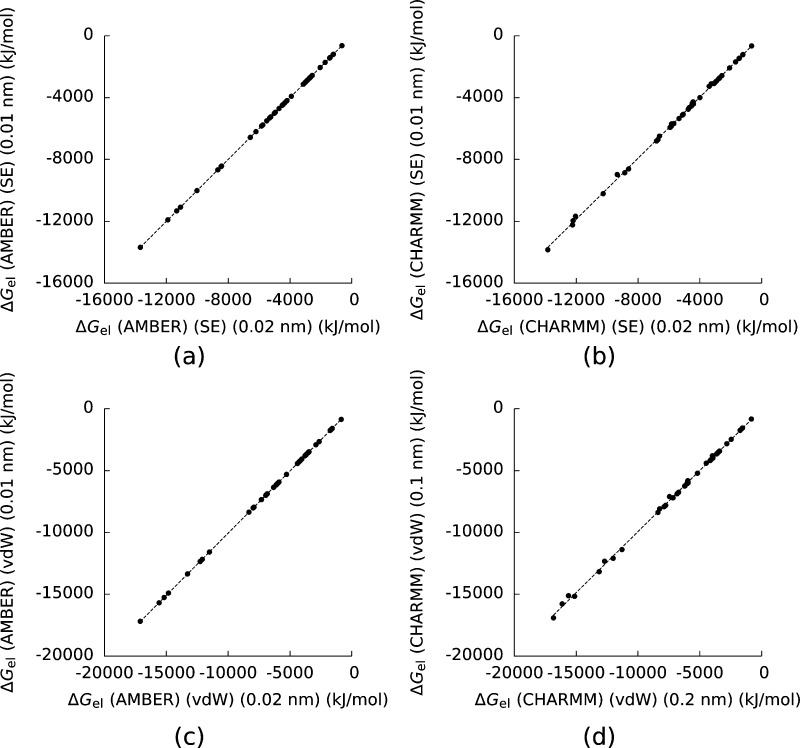
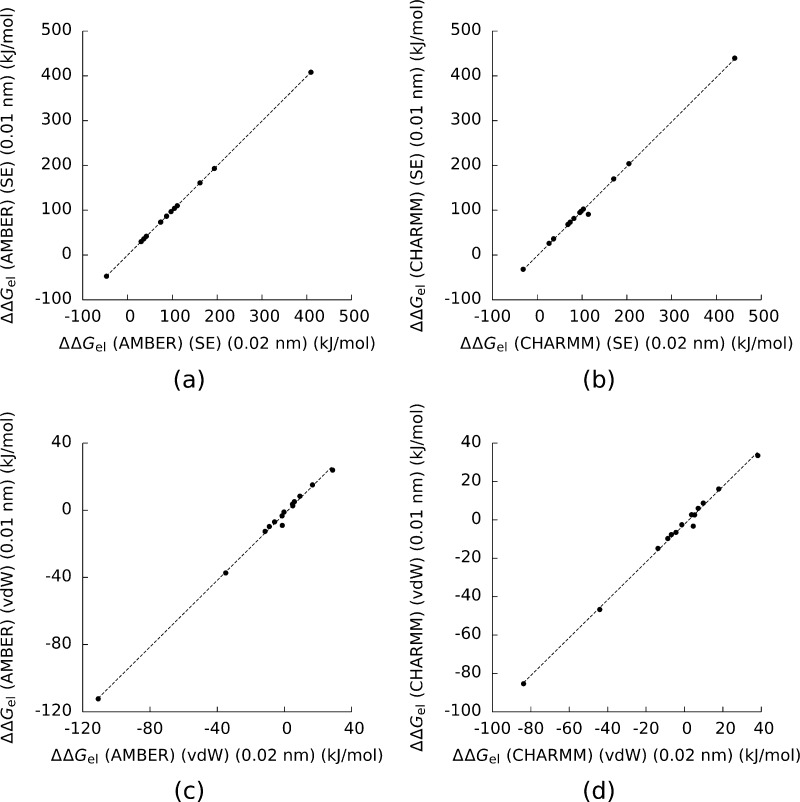
Ensuring that PB results are converged is necessary in any PB application.^58,59 To this end, we recomputed ΔG_el and ΔΔG_el with both the AMBER and CHARMM force fields and with both the SE and vdW surfaces with a mesh spacing of 0.01 nm and compared the results to those obtained with a mesh spacing of 0.02 nm (Figure 1 and Figure 2). The results obtained at 0.01 nm were in good agreement with those we obtained with a grid spacing of 0.02 nm. For the remainder of the paper, we will only consider results obtained with a grid spacing of 0.02 nm.

Figure 1.

a) The electrostatic solvation free energy (ΔG_el) for the complexes and their components computed with the AMBER force field, the solvent-excluded (SE) surface, and a mesh spacing of 0.01 nm plotted against the same numbers computed with a mesh spacing of 0.02 nm. b), c), and d) are the same figures using the CHARMM force field and the SE surface, the AMBER force field and the van der Waals (vdW) surface, and the CHARMM force field and the vdW surface. The dotted lines are least-squares fits to the data. For a) the square of the Pearson correlation coefficient (R²) is 0.99999996, for b) R² = 0.9993, for c) R² = 0.999997, and for d) R² = 0.9991.

Figure 2.

a) The electrostatic binding free energy (ΔΔG_el) for the complexes and their components computed with the AMBER force field, the solvent-excluded (SE) surface, and a mesh spacing of 0.01 nm plotted against the same numbers computed with a mesh spacing of 0.02 nm. b), c), and d) are the same figures using the CHARMM force field and the SE surface, the AMBER force field and the van der Waals (vdW) surface, and the CHARMM force field and the vdW surface. The dotted lines are least-squares fits to the data. For a) the square of the Pearson correlation coefficient (R²) is 0.999997, for b) R² = 0.997, for c) R² = 0.997, and for d) R² = 0.996.

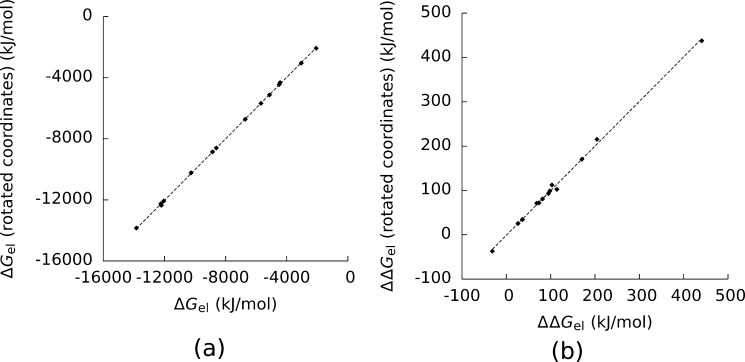
To further test that our results had reached convergence, we recomputed ΔG_el and ΔΔG_el with a grid spacing of 0.02 nm, the CHARMM force field, and the SE surface after rotating the coordinates of the molecules around the x-axis by 45 deg. Figure 3 shows that these new values were highly correlated with our original data. (The square of the Pearson correlation coefficient (R²) was 0.99992 for ΔG_el and R² = 0.999 for ΔΔG_el.) We can therefore conclude that for those plots where R² ≪ 1 this lack of correlation was not caused by numerical errors.

Figure 3.

a) The electrostatic solvation energy (ΔG_el) for the complexes and their components computed with the CHARMM force field, the solvent-excluded surface, and coordinates rotated around the x-axis by 45 deg plotted against the same values computed with nonrotated coordinates. b) The same plot for the electrostatic binding free energy (ΔΔG_el. For a) the square of the Pearson correlation coefficient (R²) was equal to 0.99992, and the square of the Spearman correlation coefficient (R_S²) was equal to 0.996. For b) R² = 0.999, and R_S = 0.996.

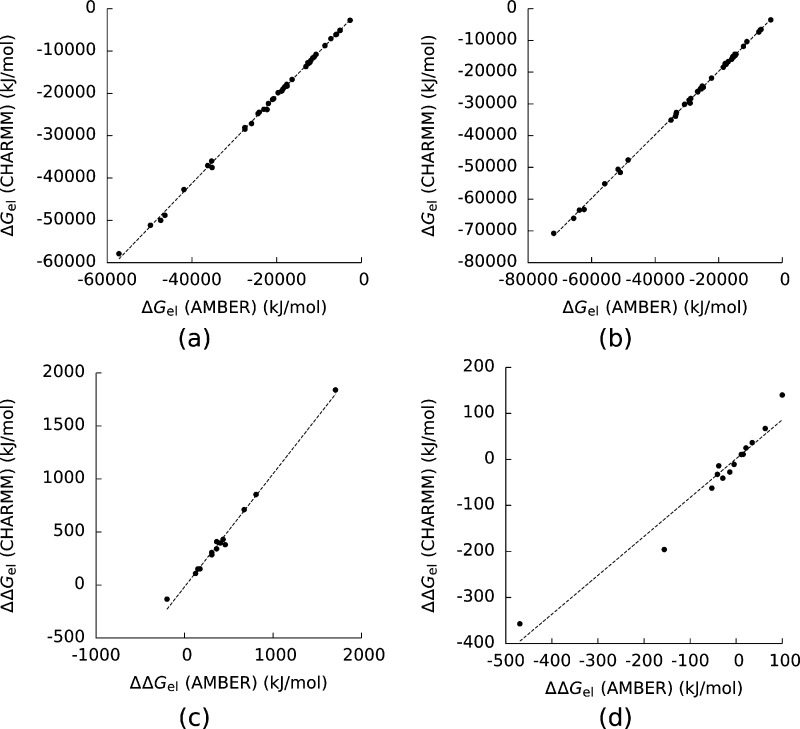
Force Field Choice

The choice of force field did not strongly affect the ordering of the molecules by ΔG_el (Figure 4), as the Spearman correlation coefficients (R_S²) were large. The R² between the ΔG_el computed with the AMBER force field and those computed with the CHARMM force field was greater than 0.99999 when either the vdW or SE surface was used. However, these R² were this large partly because ΔG_el covered a relatively large range, and simply using these correlation coefficients to judge the accuracy of this method would obscure some large uncertainties for individual molecules. The individual ΔG_el given by the AMBER force field differed from those given by the CHARMM force field by between 39 and 2640 kJ/mol when the SE surface was used and 8 and 1180 kJ/mol when the vdW surface was used. These estimates were still accurate enough to generate large R² because the ΔG_el of these molecules covered a range of more than 50000 kJ/mol.

Figure 4.

Electrostatic solvation free energies (ΔG_el) for the complexes and their components computed with the CHARMM force field plotted against those with the AMBER force field created with (a) a solvent-excluded surface and (b) a van der Waals surface. (c) and (d) show the same plots for the electrostatic binding free energies (ΔΔG_el). For (a) and (b) the Pearson correlation coefficient (R²) of the least-squares line was greater than 0.99999, and the Spearman correlation coefficients (R_S²) were 0.998 and 0.998. For (c) and (d) R² = 0.99 and 0.95, and R_S = 0.965 and 0.978. The dashed lines are least-squares lines drawn through the data.

The rankings of the complexes by ΔΔG_el, like the rankings of the molecules by ΔG_el, were not strongly sensitive to the choice of force field, as a plot of the results given by the CHARMM force field versus those given by the AMBER force field had R² = 0.99 and R_S² = 0.965 when the SE surface was used and R² = 0.95 and R_S = 0.978 when the vdW surface was used (Figure 4). However, the differences between the predictions given by the two force fields ranged from 0.15–127 kJ/mol when the SE surface was used and from 0.3–112 kJ/mol when the vdW surface was used.

Surface Definition

Figure 5 shows the ΔG_el computed with the SE surface plotted against those computed with the vdW surface for both the AMBER and CHARMM force fields. For both force fields, the vdW surface predicted consistently larger magnitudes of ΔG_el. The slopes of the least-squares lines in the first two plots in Figure 5 were 0.75 and 0.78, but this difference did not affect the ranking of the complexes by ΔG_el. (For both of these plots R² > 0.99 and R_S² > 0.99.)

Figure 5.

Electrostatic solvation free energies (ΔG_el) for the complexes and their components computed with the van der Waals (vdW) surface plotted against those with the solvent-excluded (SE) surface created with (a) the AMBER force field and (b) the CHARMM force field. (c) and (d) show the same plots for the electrostatic binding free energies (ΔΔG_el). For (a) and (b) the Pearson and Spearman correlation coefficients (R² and R_S²) of the least-squares line were greater than 0.99. For (c) and (d) R² = 0.16 and 0.17, and R_S = 0.45 and 0.63. The dashed lines are least-squares lines drawn through the data.

In contrast, the rankings of these complexes by ΔΔG_el (Figure 5) were very sensitive to the choice of surface definition. (R² = 0.16 and 0.17 and R_S² = 0.45 and 0.63.) The predictions of ΔΔG_el given by the two surface definitions differed by between 177 and 1745 kJ/mol.

Gradually Varying the Surface Definition

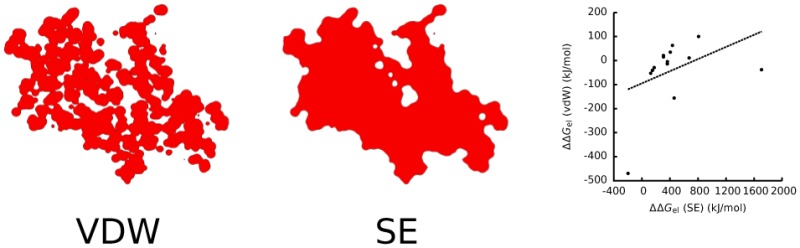
As shown in the previous section, the estimates of ΔΔG_el given by the SE surface differed substantially from those given by the vdW surface. Although both the SE and vdW surfaces agree that the region contained within the vdW radii of the solute atoms should be treated as interior to the solute, the charges in the vdW surface are more solvent exposed than those in the SE surface because the vdW surface contains gaps and crevices of high dielectric inside the molecule, whereas the SE surface does not (Figure 6).

Figure 6.

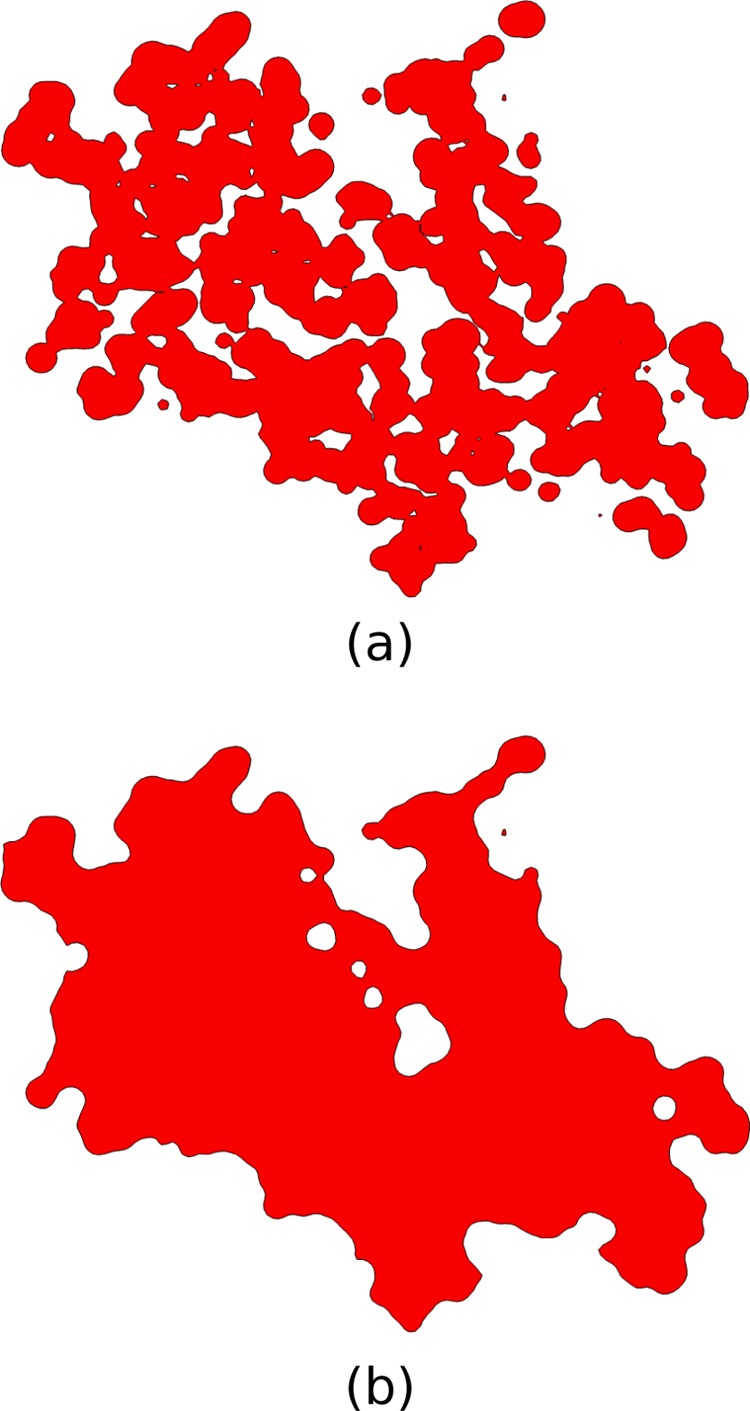
Slices through chain A of the 1he8 complex. The contours trace the boundary between the molecular interior and exterior for a) the van der Waals and b) the solvent-excluded surfaces.

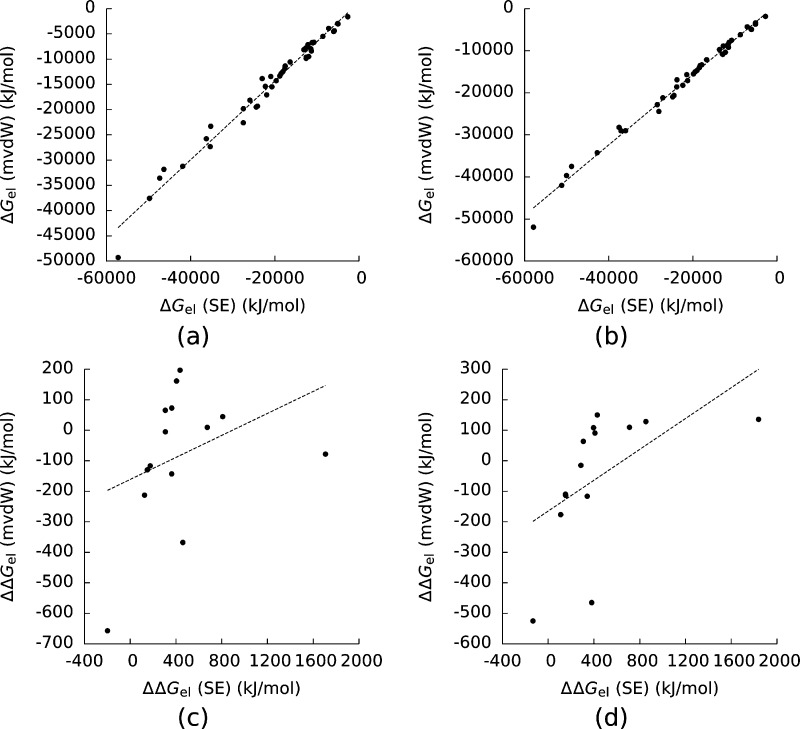
Whether these crevices should be considered to be solvated is still an active area of research,³⁸⁻⁴⁰ and we wanted to know how the PBE’s predictions of ΔG_el and ΔΔG_el changed as these crevices were gradually filled. To this end, we considered the mvdW surface. The mvdW surface was originally designed to mimic the SE surface when the probe radius was set to 1.4 Å,⁴⁸ and its predictions of ΔG_el were indeed highly correlated with those of the SE surface (Figure 7). (R² = 0.98 for the AMBER force field and 0.99 for CHARMM.) However, its predictions of ΔΔG_el were not. (R² = 0.13 for the AMBER force field and 0.30 for CHARMM.) Once again, that a surface definition produced estimates of ΔG_el that were highly correlated with those given by the SE surface did not guarantee that its predictions of ΔΔG_el would be similarly highly correlated with those of the SE surface.

Figure 7.

Electrostatic solvation free energies (ΔG_el) for the complexes and their components computed with the modified van der Waals (mvdW) surface plotted against those with the solvent-excluded (SE) surface created with (a) the AMBER force field and (b) the CHARMM force field. (c) and (d) show the same plots for the electrostatic binding free energies (ΔΔG_el). For (a) and (b) the Pearson correlation coefficients (R²) of the least-squares lines were 0.98 and 0.99. For (c) and (d) R² = 0.13 and 0.30. The dashed lines are least-squares lines drawn through the data.

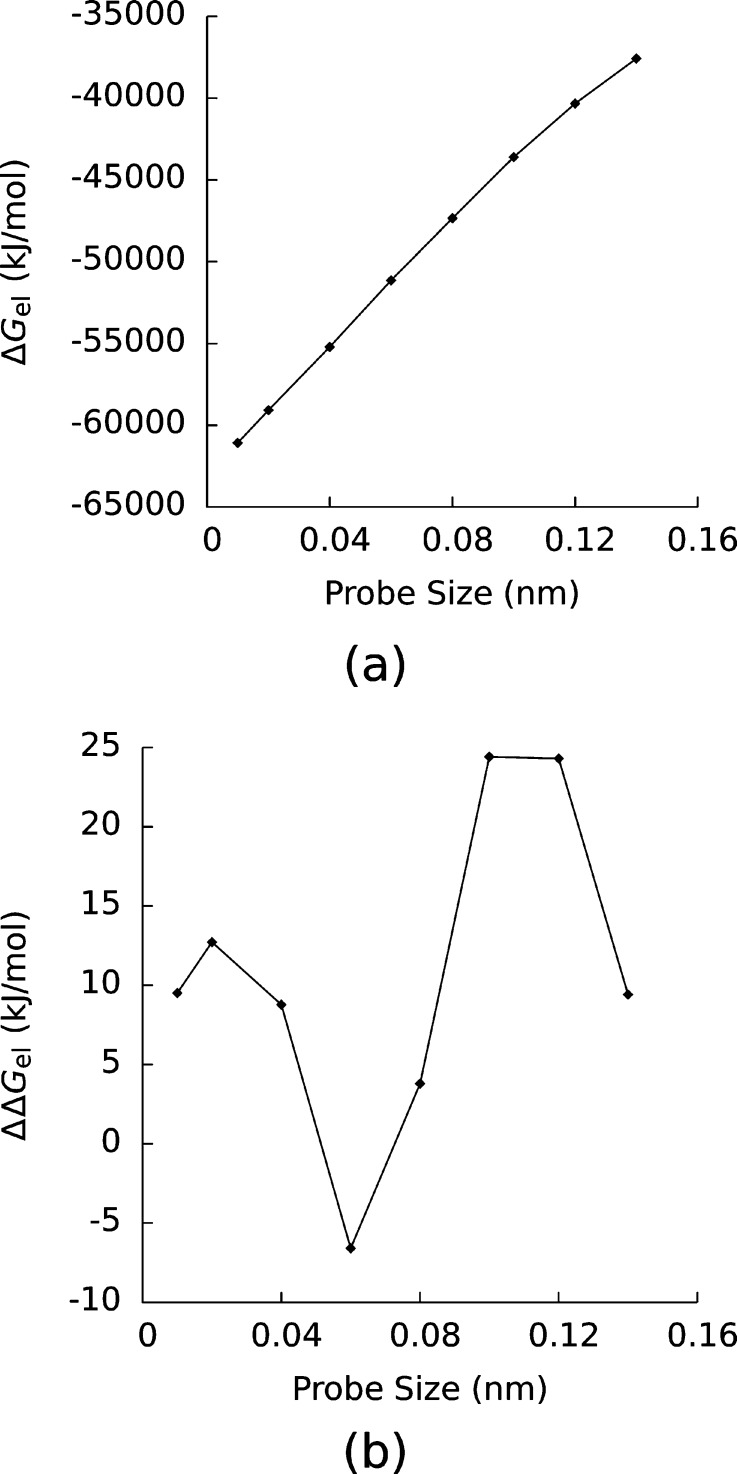
In Table 1, the ΔG_el of the complexes and the ΔΔG_el are shown as functions of the probe radius in the mvdW surface. Possibly because the charges in the molecules were less solvent exposed as the probe radius was increased, ΔG_el increased monotonically with probe radius. A typical example is shown in Figure 8, where ΔG_el for the complex with the pdbid 1kxp is shown as a function of probe radius. However, the dependence of ΔΔG_el on probe radius is more complex. In Figure 8 ΔΔG_el for 1kxp is displayed, and unlike ΔG_el for this complex, ΔΔG_el did not vary monotonically with probe radius. Although ΔΔG_el^C did not depend on probe radius and the ΔG_el all increased monotonically with surface area, ΔΔG_el = ΔG_comp – ΔG₁ – ΔG₂ + ΔΔG_el had no simple dependence on probe radius and was instead a complicated function of the molecular shape and charge distribution.

Table 1. Electrostatic Solvation (ΔG_el) and Binding (ΔΔG_el) Free Energies for the Complexes in This Study Computed with the Modified van der Waals Surface and the AMBER Force Field As Functions of Probe Radius^a.

		probe radii (nm)
complexes		0.01	0.02	0.04	0.06	0.08	0.1	0.12	0.14
1acb	ΔGel	–16941	–16107	–14482	–12847	–11387	–9987	–8781	–7810
	ΔΔGel	–39	–37	–39	–30	–41	–70	–102	–130
1atn	ΔGel	–45796	–43720	–40084	–36851	–34123	–31514	–29228	–27330
	ΔΔGel	–53	–48	–59	–73	–103	–144	–181	–213
1avx	ΔGel	–23678	–22504	–20272	–18115	–16272	–14552	–13066	–11846
	ΔΔGel	–474	–473	–487	–497	–529	–566	–613	–657
1b6c	ΔGel	–27210	–26020	–23682	–21188	–18952	–16858	–15001	–13440
	ΔΔGel	20	21	23	26	33	38	50	65
1beb	ΔGel	–32291	–31412	–29810	–28156	–26631	–25147	–23792	–22603
	ΔΔGel	–32	–20	–28	–57	–71	–91	–107	–117
1brs	ΔGel	–11592	–11121	–10126	–9055	–8060	–7082	–6209	–5491
	ΔΔGel	–9	4	–4	–38	–69	–96	–121	–143
1buh	ΔGel	–23443	–22389	–20309	–18157	–16226	–14363	–12722	–11367
	ΔΔGel	–4	–3	0	10	30	40	61	73
1h1v	ΔGel	–53147	–50968	–46929	–43069	–39649	–36404	–33593	–31214
	ΔΔGel	65	76	78	92	94	114	146	197
1he8	ΔGel	–61945	–59048	–53460	–47992	–43215	–38849	–35058	–31823
	ΔΔGel	12	11	7	9	27	14	–5	–5
1kxp	ΔGel	–61074	–59078	–55212	–51137	–47334	–43605	–40331	–37577
	ΔΔGel	10	13	9	–7	4	24	24	9
1sbb	ΔGel	–31396	–29839	–26757	–23646	–20853	–18146	–15783	–13853
	ΔΔGel	40	43	50	56	80	110	135	161
1ysl	ΔGel	–69136	–67038	–63300	–59813	–56728	–53866	–51382	–49291
	ΔΔGel	–21	–3	7	12	35	7	–38	–78
2hp0	ΔGel	–48480	–46080	–41773	–37751	–34226	–30989	–28172	–25779
	ΔΔGel	119	139	173	201	202	156	103	45
2uy1	ΔGel	–59581	–57517	–53323	–48714	–44448	–40334	–36703	–33576
	ΔΔGel	–158	–146	–159	–177	–220	–267	–328	–368

^aBoth ΔG_el and ΔΔG_el are in units of kJ/mol.

Figure 8.

Electrostatic (a) solvation and (b) binding free energies (ΔG_el and ΔΔG_el) of one of the complexes in this study (pdbid: 1kxp) as functions of the probe radius used to define the modified van der Waals surface.

Conclusions

Implicit solvent methods based on the PBE⁶⁻¹⁰ have been fairly successful at predicting a wide range of biophysical quantities, including ΔG^3,5,11−15 and the salt dependence of ΔΔG.¹⁶⁻²² Because these methods eliminate the need to consider the degrees of freedom of the solvent by integrating over them, they are a fast alternative to methods, such as MD methods,^1,2 that explicitly account for those degrees of freedom. In particular, if PB methods could be used to obtain fast and accurate estimates of ΔΔG, they could complement slow, expensive experimental screening of compound libraries in drug-development studies, potentially revolutionizing drug development and discovery. Unfortunately, PB methods have been less successful at predicting ΔΔG than ΔG.²³⁻³⁰

At first glance, the idea that PB methods could be successful at predicting ΔG but fail to predict ΔΔG seems self-contradictory. As shown in eq 1, ΔΔG_el can be computed by combining estimates of ΔG_el with estimates of ΔΔG_el^C. Part of the reason for this seeming contradiction may be that ΔΔG_el, as in the present study, is sometimes orders of magnitude smaller than ΔG_el, and therefore estimates of ΔG_el that have reasonably small relative errors can lead to estimates of ΔΔG_el with large relative errors. In the present study ΔG_el covered a range of tens of thousands of kJ/mol, whereas ΔΔG_el only covered a range of hundreds of kJ/mol. Rankings of these molecules by ΔG_el were almost independent of surface definition and choice of force field, whereas rankings of these complexes by ΔΔG_el were very sensitive to these details.

One reason that ΔΔG_el is difficult to compute may be its sensitivity to the choice of force field. Modern force fields, such as the AMBER³¹ and CHARMM³² force fields, use approximate classical energy functions to model the underlying quantum mechanical interactions, and whether these methods can accurately predict ΔΔG, even when the degrees of freedom of the solvent are included, is unclear. The results presented here are consistent with those of other studies that show that current force fields are accurate enough to accurately rank small molecules by ΔG.³⁻⁵ Additionally, the rankings of these complexes by ΔΔG_el were not much affected by changing the force field, but although the rankings of the complexes examined here did not change significantly when different force fields were used, the absolute differences in ΔΔG_el were large enough that they could cause problems for applications where the differences in ΔΔG_el between different complexes were smaller.

Another potential source of uncertainties in ΔΔG_el is the uncertainty in how the interface between the interior and exterior of the molecule should be defined. Many different surface definitions have been created (e.g., the SE surface,^36,37 the vdW surface,³⁸⁻⁴⁰ Gaussian surfaces,^41,42 and self-consistent surfaces⁴³⁻⁴⁷), and no clear consensus has emerged on which of these surface definitions is most realistic. In the present study both the SE and vdW surfaces produced consistent rankings of these molecules by ΔG_el, although the absolute differences in ΔG_el between these two surface definitions could be quite large. In contrast, the estimates of ΔΔG_el produced by these two surface definitions were not correlated. (R² = 0.16 for the AMBER force field, and 0.17 for CHARMM.) Even the mvdW surface, which was designed to mimic the SE surface, produced estimates of ΔΔG_el that were uncorrelated with those given by the SE surface. (R² = 0.13 for the AMBER force field and 0.30 for CHARMM.) Until the question of how to define the molecular surface is more settled, the PBE will not be able to produce estimates of ΔΔG_el accurate enough to be useful for the systems considered here. Of course, only a small number of complexes were considered here and the PBE may be more reliable for other systems, but the data shown here indicate that the sensitivity of ΔΔG_el to the exact method that is used to define the molecular surface may help explain why PBE methods have not been uniformly successful at predicting ΔΔG.

In conclusion, explaining why PB methods have been fairly successful at predicting ΔG but have been much less successful at predicting ΔΔG appears to be difficult at first glance because ΔΔG_el can be computed by combining estimates of ΔG_el with ΔΔG_el^C. However, ΔG_el is typically orders of magnitude larger than ΔΔG_el, and therefore estimates of ΔG_el must be very accurate if they are to combine to give accurate estimates of ΔΔG_el. For these reasons, studies that compare the predictions of ΔG by PB methods to experimental results will probably not be sufficient for improving the predictions of ΔΔG given by these methods because the ability of a particular model to predict consistent estimates of ΔG_el does not guarantee that it will produce consistent estimates of ΔΔG_el.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States