Discovering Genetic Ancestry Using Spectral Graph Theory

Abstract

As one approach to uncovering the genetic underpinnings of complex disease, individuals are measured at a large number of genetic variants (usually SNPs) across the genome and these SNP genotypes are assessed for association with disease status. We propose a new statistical method called Spectral-GEM for the analysis of genome-wide association studies; the goal of Spectral-GEM is to quantify the ancestry of the sample from such genotypic data. Ignoring structure due to differential ancestry can lead to an excess of spurious findings and reduce power. Ancestry is commonly estimated using the eigenvectors derived from principal component analysis (PCA). To develop an alternative to PCA we draw on connections between multidimensional scaling and spectral graph theory. Our approach, based on a spectral embedding derived from the normalized Laplacian of a graph, can produce more meaningful delineation of ancestry than by using PCA. Often the results from Spectral-GEM are straightforward to interpret and therefore useful in association analysis. We illustrate the new algorithm with an analysis of the POPRES data [Nelson et al., 2008].

INTRODUCTION

Human population structure and ancestry are of interest when investigating fundamental questions in evolution and practical questions such as studies to detect association of disease status with genotypes from specific loci in the genome. If association studies rely on the unrealistic assumption of population homogeneity, then spurious associations can arise in the presence of population heterogeneity and differential prevalence of disease by ancestry.

Genetic ancestry can be estimated based on allele counts derived from individuals measured at a large number of SNPs. A dimension reduction tool known as principal component analysis (PCA [Cavalli-Sforza et al., 1994; Patterson et al., 2006; Price et al., 2006]), or principal component maps (PC maps), summarize the genetic similarity between subjects at a large numbers of SNPs using continuous axes of genetic variation. These axes are inferred from the dominant eigenvectors of a data-based similarity matrix and define a “spectral” embedding, also known as an eigenmap, of the original data. Typically a small number of ancestry dimensions are sufficient to describe the key variation. For instance, in Europe, eigenvectors displayed in two dimensions often reflect the geographical distribution of populations [Heath et al., 2008; Novembre et al., 2008]. The number of dimensions required to capture the key features in the data vary, depending on the nature of the structure. If the sample consists of k distinct subpopulations, typically k−1 axes will be required to differentiate these subpopulations. If a population has a gradient or cline, then an axis is required for this feature.

Heterogeneous samples collected from numerous continents present an additional challenge in the successful construction of an eigenmap. For instance, analysis of the four core HapMap samples [International-HapMap-Consortium, 2005] using the classical PC map produced by the software smartpca [Patterson et al., 2006] does not reveal substructure within the Asian sample; however, an eigenmap constructed using only the Asian samples discovers an additional substructure [Patterson et al., 2006]. Another feature of PCA is its sensitivity to outliers [Luca et al., 2008]. Due to outliers, numerous dimensions of ancestry appear to model a statistically significant amount of variation in the data, but in actuality they function to separate a single observation from the bulk of the data. This feature can be viewed as a drawback of the PCA method.

For population-based genetic association studies, such as case-control studies, the confounding effect of genetic ancestry can be controlled for by regressing out the eigenvectors [Price et al., 2006], matching individuals with similar genetic ancestry [Luca et al., 2008; Rosenbaum, 1995], or clustering groups of individuals with similar ancestry and using the Cochran-Mantel-Haenszel test. In each situation, spurious associations are controlled better if the ancestry is successfully modeled, but power is reduced if extra dimensions of ancestry are included.

To overcome some of the challenges encountered in constructing a successful eigenmap of the genetic ancestry, we propose a spectral graph approach. These methods are more flexible than PCA and allow for the different ways of modeling structure and similarities in data. Our alternative approach utilizes a spectral embedding derived from the so-called normalized Laplacian of a graph. We proceed by making the connection between PCA, multidimensional scaling (MDS) and spectral graph theory. We conclude with a presentation of the new algorithm, which is illustrated via an analysis of the POPRES data [Nelson et al., 2008].

METHODS

LOW-DIMENSIONAL EMBEDDING BY EIGEN-ANALYSIS

Record the minor allele count ϒ_ij for the ith subject and the jth SNP in a matrix ϒ, for i = 1,…, N and j = 1,…, L. Center and scale the allele counts by subtracting the column mean and dividing by the standard deviation of each entry to update ϒ. The elements of the ith row of ϒ represent the genetic information for subject i, y_i = (y_i1, …, y_iL). The similarity between individuals i and j is computed using the inner product h_ij = L⁻¹〈y_i, y_j〉. The corresponding inner product matrix H = L⁻¹ϒϒ^t associated with standard PCA is positive semi-definite. Traditionally, in PC maps, the ancestry vectors are estimated by embedding the data in a low-dimensional space using the eigenvectors of the matrix H, the kernel of the PC map. To find the embedding compute the eigenvectors (u₁,u₂,…, u_N) and eigenvalues (λ₁≥λ₂≥ ⋯ ≥λ_N) of H. Typically the large eigenvalues correspond to eigenvectors that reveal important dimensions of ancestry.

Since we are using the low-dimensional embeddings for clustering it is important to know what the distances in the embedding space represent. An analysis shows that the kernel H induces a natural Euclidean distance m(i,j) between individuals:

$$m{(i,j)}^2=L^{-1}{\Vert y_i-y_j\Vert }^2=h_{ii}+h_{jj}-2h_{ij},i,j=1,\dots ,N.$$ (1)

If the objective is to preserve these distances, using only d dimensions, classical MDS theory says to use the N × d-dimensional matrix with row i

$$({\mathrm{\lambda }}_1^{1/2}{u}_1(i),\dots ,{\mathrm{\lambda }}_d^{1/2}{u}_d(i))$$ (2)

representing the ith individual. Let m̂ (i, j) be the Euclidean distance between individuals i and j in this low-dimensional configuration. To measure the discrepancy between the Euclidean distances in the full and low-dimensional space, let δ = ∑_i,j (m(i, j)² − m̂(i, j)²). This quantity is minimized over all d-dimensional configurations by the top d eigenvectors of H, weighted by the square root of the eigenvalues (Equation 2) [Mardia et al., 1979]. Thus PC mapping is a type of classical MDS. It provides the optimal embedding if the goal is to preserve the pairwise distances m(i,j) with H = L⁻¹ϒϒ^t as closely as possible.

MDS was originally developed to visualize high-dimensional data. The downside of using PCA for a quantitative analysis is that the associated metric is highly sensitive to outliers, which diminishes its ability to capture the major dimensions of ancestry. Our goal in this paper is to develop a spectral embedding scheme that is less sensitive to outliers and that is better, in many settings, at clustering observations similar in ancestry. We note that the choice of eigenmap is not unique: Any positive semi-definite matrix H defines a low-dimensional embedding and associated distance metric according to Equations 1 and 2. Hence, we will use the general framework of MDS and PC maps but introduce a different kernel for improved performance. Below we give some motivation for the modified kernel and describe its main properties from the point of view of spectral graph theory and spectral clustering.

SPECTRAL CLUSTERING

In recent years, spectral clustering [von Luxburg, 2007] has become one of the most widely used clustering algorithms. It is more flexible than traditional clustering algorithms such as the k-means algorithm and can be solved efficiently using standard linear algebra. Spectral clustering has not been, heretofore, fully explored in the context of a large number of independent genotypes, such as is typically obtained in genome-wide association studies. The eigendecomposition of H can be viewed from the point of view of spectral clustering. In this framework the decomposition of ϒϒ^t in PCA corresponds to an unnormalized clustering scheme. Such schemes tend to return embeddings where the principle axes separate outliers from the bulk of the data. On the other hand, an embedding based on a normalized matrix (the graph Laplacian) identifies directions with more balanced clusters.

To introduce the topic, we require the language of graph theory. For a group of n subjects, define a graph G where {1, 2, …, n} is the vertex set (composed of subjects in the study). The graph G can be associated with a weight matrix W, that reflects the strength of the connections between pairs of subjects: the higher the value of the entry w_ij, the stronger the connection between the pair (i,j). Edges that are not connected have weight 0. The weight matrix W is symmetric with non-negative entries.

Laplacian eigenmaps [Belkin and Niyogi, 2002] decompose a function of the weight matrix known as the graph Laplacian to obtain a new representation of the data. Inspired by MDS, we consider a rescaled variation of standard eigenmaps. The Laplacian matrix S of a weighted graph G is defined by

$$S(i,j)=\{\begin{array}{cc}\hfill -w_{ij}\hfill & \hfill \text{if}i\ne j,\hfill \\ \hfill d_i-w_{ii}\hfill & \hfill \text{if}i=j,\hfill \end{array}$$

where d_i = ∑_j w_ij is the so-called degree of vertex i. In matrix form,

$$S=D-W,$$

where D = diag(d₁,…, d_n) is a diagonal matrix. The normalized graph Laplacian is a matrix defined as

$$ℒ=D^{-1/2}S{D}^{-1/2}.$$

Entries in the kernel matrix, h_ij, measure the similarity, or correlation, between subjects, making it a good candidate for a weight matrix: the larger the entry for a pair (i,j), the stronger the connection between the subjects within the pair. For a weight matrix, 0 indicates an unconnected pair. Negative values in H correspond to negative correlations, hence motivating the choice of 0 for these pairs. We define the weights as

$$w_{ij}=\{\begin{array}{cc}\sqrt{h_{ij}}\hfill & \text{if}{h}_{ij}\ge 0,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

In other words, a simple transformation of the PCA kernel. Directly thresholding H at 0 guarantees nonnegative weights but creates a skewed distribution of weights. To address this problem, we have added a square-root transformation for more symmetric weight distributions.

Let ν_i and u_i be the eigenvalues and eigenvectors of ℒ. We index these {i = 0, 1, …, N − 1} in reference to the first “trivial” eigenvector u₀ associated with eigenvalue ν₀ = 0. We replace H with I − ℒ, where I is the identity matrix, and map the the ith subject into a lower dimensional space according to Equation 2, where u_i and λ_i = max{0, 1 − ν_i}, respectively, are the eigenvectors and truncated eigenvalues of I − ℒ. In Results, we show that estimating the ancestry from the eigenvectors of ℒ (which are the same as the eigenvectors of I − ℒ) leads to more meaningful clusters than ancestry estimated directly from ϒϒ^t. Some intuition as to why this is the case can be gained by relating eigenmaps to spectral clustering and “graph cuts.” In graph-theoretic language, the goal of clustering is to find a partition of the graph so that the connections between different groups have low weight and the connections within a group have high weight. For two disjoint sets A and B of a graph, the cut across the groups is defined as cut(A, B) = ∑_i∈A,j∈B w_ij. Finding the partition with the minimum cut is a well-studied problem; however, the minimum cut criterion favors separating individual vertices or “outliers” from the rest of the graph [Shi and Malik, 1997]. The normalized cut approach by Shi and Malik circumvents this problem by incorporating the volume or weight of the edges of a set into a normalized cost function Ncut(A, B) = cut(A, B)/vol(A) + cut(A, B)/vol(B), where vol(A) = ∑_i∈A d_i and vol(B) = ∑_i∈B d_i. This cost function is large when the set A or B is small. Our Spectral-GEM algorithm (below) exploits the fact that the eigenvectors of the graph Laplacian provide an approximate solution to the Ncut minimization problem. Smartpca [Patterson et al., 2006] and standard GEM [Luca et al., 2008], on the other hand, are biased toward embeddings that favor small, but tight, clusters in the data. For further exposition on this topic an excellent review is available [von Luxburg, 2007].

NUMBER OF DIMENSIONS

When using the eigenmap based on ϒϒ^t a formal test for the number of significant dimensions can be based on the theoretical results concerning the Tracy-Widom distribution of eigenvalues of a covariance matrix [Johnstone, 2001; Patterson et al., 2006]. Tracy-Widom theory does not extend to the eigenvalues of the graph Laplacian. Instead we introduce a different approach, known as the eigengap heuristic, based on the difference in magnitude between successive eigenvalues.

The graph Laplacian has several properties that make it useful for cluster analysis. Both its eigenvalues and eigenvectors reflect the connectivity of the data. Consider, for example, the normalized graph Laplacian where the sample consists of d distinct clusters. Sort the eigenvalues 0 = ν₀ ≤ ν₁ ≤ ⋯ ≤ ν_N−1 of ℒ in ascending order. The matrix ℒ has several key properties [Chung, 1992]: (i) The number d of eigenvalues equal to 0 is the number of connected components S₁, …, S_d of the graph. (ii) The first positive eigenvalue ν_d reflects the cohesiveness of the individual components; the larger the eigenvalue ν_d the more cohesive the clusters. (iii) The eigenspace of 0 (i.e., the vectors corresponding to eigenvalues equal to 0) is spanned by the rescaled indicator vectors D^1/21_Sk, where 1_Sk = 1 if i ∈ S_k, and 1_Sk = 0 otherwise. It follows from (iii) that for the ideal case where we have d completely separate populations (and the node degrees are similar), individuals from the same population map into the same point in an embedding defined by the d first eigenvectors of ℒ. For example, if d = 3, the N − d embedding matrix for N = 6 individuals could have the form

$$U=[D^{1/2}{\mathbf{1}}_{S_1},D^{1/2}{\mathbf{1}}_{S_2},D^{1/2}{\mathbf{1}}_{S_3}]=\left(\begin{array}{ccc}\hfill d_1^{1/2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill d_2^{1/2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill d_3^{1/2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill d_4^{1/2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill d_5^{1/2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill d_6^{1/2}\hfill \end{array}\right)\approx \left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$

In a more realistic situation the between-cluster similarity will not be exactly 0 and all components of the graph will be connected. Hence only the trivial eigenvalue (ν₀) will be zero corresponding to the null eigenvector $u_0={(d_1^{1/2},\dots ,d_6^{1/2})}^t$. Nevertheless, if the clusters are fairly distinct, we can still use the eigenvalues of the graph Laplacian to determine the number of significant dimensions. Heuristically, choose the number of eigenvectors d+1 such that the eigengaps δ_i = |ν_i − ν_i−1| are small for i≤d but the eigengap δ_d+1 is large. One can justify such an approach with an argument from perturbation analysis [Stewart, 1990]. The idea is that the matrix ℒ for the genetic data is a perturbed version of the ideal matrix for d disconnected clusters. If the perturbation is not too large and the “non-null” eigengap δ_d is large, the first d eigenvectors will be close to the ideal indicator vectors and a spectral clustering algorithm will separate the individual clusters well. The question then becomes: How do we decide whether an eigengap is significant (non-null)?

In this work, we propose a practical scheme for estimating the number of significant eigenvectors for genetic ancestry that is based on the eigengap heuristic and hypothesis testing. By simulation, we generate homogeneous data without population structure and study the distribution of eigengaps for the normalized graph Laplacian. Because there is only one population, the first eigengap δ₁ is large. We are interested in the first null eigengap, specifically the difference δ₂ = |ν₂−ν₁| between the first and second eigenvalues. If the data are homogeneous, this difference is relatively small. Based on our simulation results, we approximate the upper bound for the null eigengap with the 99th quantile of the sampling distribution as a function of N and L. We choose the number of dimensions d in the eigenvector representation according to

$$d=\text{max}\{i;{\mathrm{\delta }}_i>-0.00016+2.7/N+2.3/L\}-1.$$

The eigengap heuristic applies regardless of the true number of dimensions needed to describe the structure in the data because it relies on a comparison of the first null eigengap with the simulated null eigengap.

ALGORITHM FOR SPECTRAL-GEM

• Center and scale the allele counts and compute ϒϒ^t. This is a computationally intensive calculation.

• Compute W from ϒϒ^t.

• Find the eigenvector decomposition of D^−1/2WD^−1/2.

• Compute the eigengaps δ_i = |ν_i − ν_i−1|.

• Determine the number of significant dimensions d in the eigenvector representation

  $$d=\text{max}\{i:{\mathrm{\delta }}_i>-0.00016+2.7/N+2.3/L\}-1.$$

• Let U = [u₀,…, u_d] be the matrix having as columns the first d+1 eigenvectors.

• Using the NJW algorithm [Ng et al., 2001] normalize the rows in U to have squared length one. Call the resulting matrix V.

• Compute the distance between subjects i and j using ${\sum }_{\ell =0}^d{(v_{i\ell }-v_{j\ell })}^2$.

• Obtain homogeneous clusters of individuals using k-means clustering via Ward’s algorithm [Luca et al., 2008].

• For regression analysis include u₀,…, u_d as regressors to remove the effect of confounding due to ancestry.

• For analysis of matched case-control data, perform the following additional steps:

  • ◦
    Rescale the data as described in the GEM algorithm and determine if any subjects are unmatchable.
  • ◦
    Remove unmatchable subjects prior to analysis.
  • ◦
    Recompute the eigenvectors, and match cases and controls based on the Euclidean distance using the (d+1)-dimensional NJW representation.
  • ◦
    Perform conditional logistic regression.

RESULTS

DATA ANALYSIS OF POPRES

To assess the performance of spectral embeddings we use the POPRES database [Nelson et al., 2008]. This resource includes a large sample of individuals of European ancestry, and smaller samples of African Americans, E. Asians, Mexicans, and Asian Indians. Demographic records include the individual’s country of origin and that of his/her parents and grandparents.

Of the 4,079 samples with labeled ethnicity and genotypes that passed the POPRES quality control (their QC2 procedure) we removed 38 close relatives and 280 samples with greater than 5% missing genotypes. The remaining data included 346 African Americans, 49 E. Asians, 329 Asian-Indians, 82 Mexicans, and 2,955 Europeans. Of the 457,297 SNPs passing POPRES QC2, we removed those with missingness greater than 5%, with minor allele frequency less than 0.01, or with Hardy Weinberg P-value less than 0.005 (the latter two calculations were performed using sample of European ancestry only). From the remaining 326,129 SNPS, we reduced the list to 48,529 SNPs separated by at least 10 Kb which had missingness less than 1%. From these we chose 21,743 tag SNPs using H-clust, set to pick tag SNPs with squared correlation less than 0.04 [Rinaldo et al., 2008].

For the sample of European ancestry we assigned the country of origin by the following strategy. For an individual, ideally the country of origin is recorded for six immediate ancestors. If at least five out of six of these list the same country, then it was assigned as the country of origin. If no ancestry information was recorded then we used the self-reported country of origin. Otherwise the individual’s country of origin was not assigned.

We construct three scenarios from POPRES to illustrate the differences between PCA as implemented in the smartpca software [Patterson et al., 2006] and Spectral-GEM. For smartpca, by default any observation that exceeds 6 standard deviations in any of the top 10 eigenvectors is removed prior to the estimation of the ancestry vectors.

Scenario 1

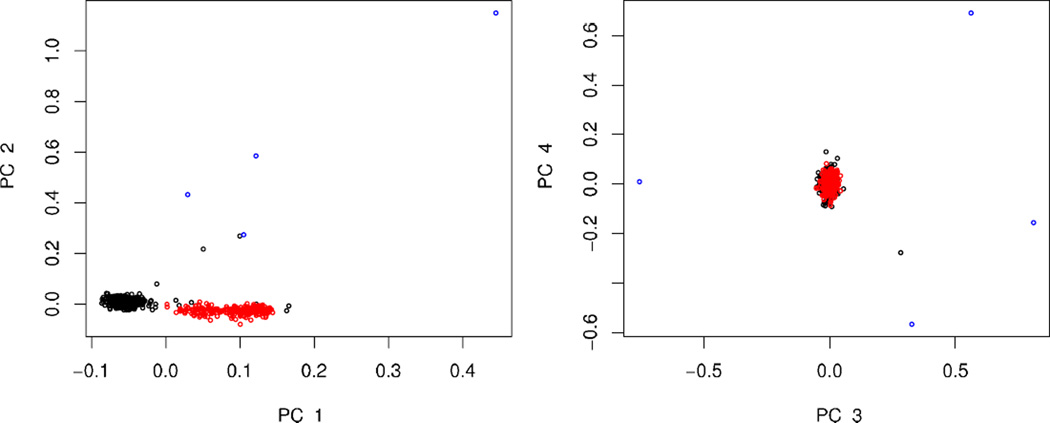
In our simulations and data analyses using PCA [Luca et al., 2008] we found that outliers can interfere with discovery of the major axes of ancestry and greatly increase the number of dimensions of ancestry discovered. To illustrate the effect of outliers we created a subsample from POPRES including 580 Europeans (all self-identified Italian and British subjects), 1 African American, 1 E. Asian, 1 Indian, and 1 Mexican. Smartpca removes the four outliers prior to analysis and discovers two significant dimensions of ancestry. If the outliers are retained, five dimensions are significant. The first two eigenvectors separate the Italian and British samples and highlight normal variability within these samples. Ancestry vectors 3–5 isolate outliers from the majority of the data, but otherwise convey little information concerning ancestry (Fig. 1). This example highlights our previous results [Luca, 2008], which show that outlier removal is an essential stage in PCA analysis to determine ancestry.

Fig. 1.

Principal components from PCA for Scenario 1. Subjects are self-identified as UK (black), Italian (red), and non-European (blue).

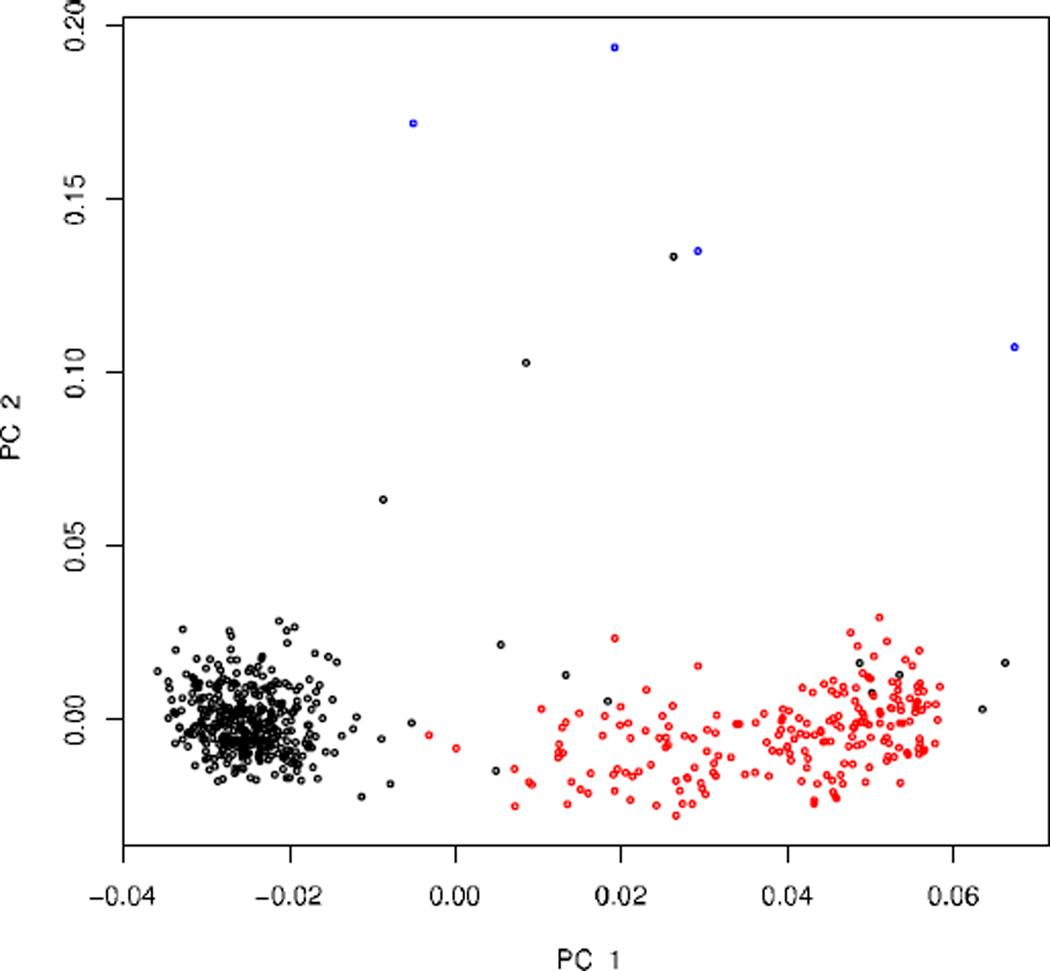
With Spectral-GEM, leaving the outliers in the data has no impact. The method identified two significant dimensions that are nearly identical to those identified by PCA (Fig. 2). In our cluster analysis we identified four homogeneous clusters: 1 British cluster, 2 Italian clusters, and 1 small cluster that includes the outliers and six unusual subjects from the self-identified British and Italian samples.

Fig. 2.

Principal components from the Spectral-GEM analysis of data from Scenario 1. Subjects are self-identified as UK (black), Italian (red), and non-European (blue).

Scenario 2

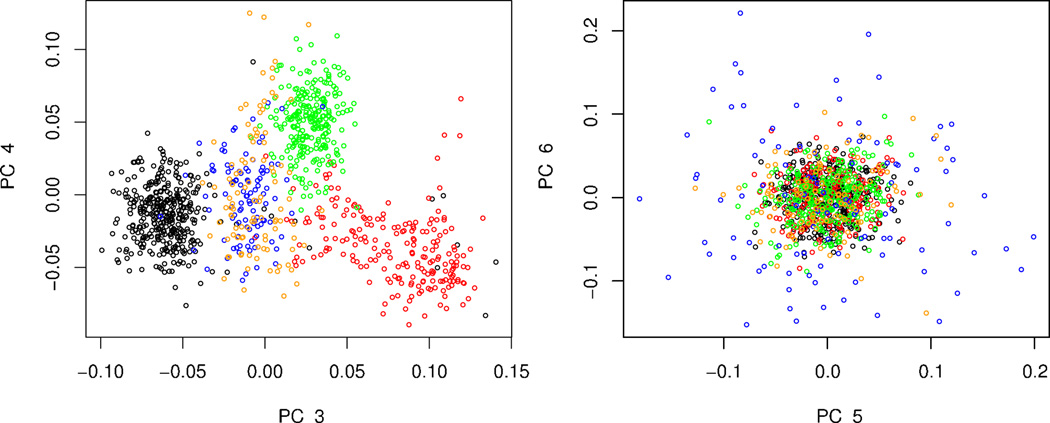
The ancestral composition of samples for genome-wide association can be highly variable. Often, however, the majority of the data come from one continent, but a sizable fraction of the sample derives from other continents. To mimic this scenario we created a subsample from POPRES including 832 Europeans (all self-identified British, Italian, Spanish, and Portuguese subjects), 100 African Americans and 100 Asian-Indians. Using smartpca, seven dimensions of ancestry are significant. The first two eigenvectors separate the continental samples. The third and fourth eigenvectors separate the Europeans roughly into three domains (Fig. 3). The three European populations cluster, but they are not completely delineated. The other continental groups generate considerable noise near the center of the plot. The remaining three significant dimensions reveal little structure of interest.

Fig. 3.

Principal components 3–6 for data from Scenario 2. PC 1 and PC 2 are quite similar to the eigenvectors shown in Fig. 4. Subjects are self-identified as UK (black), Italian (red), Iberian Peninsula (green), African American (blue), and Indian (orange).

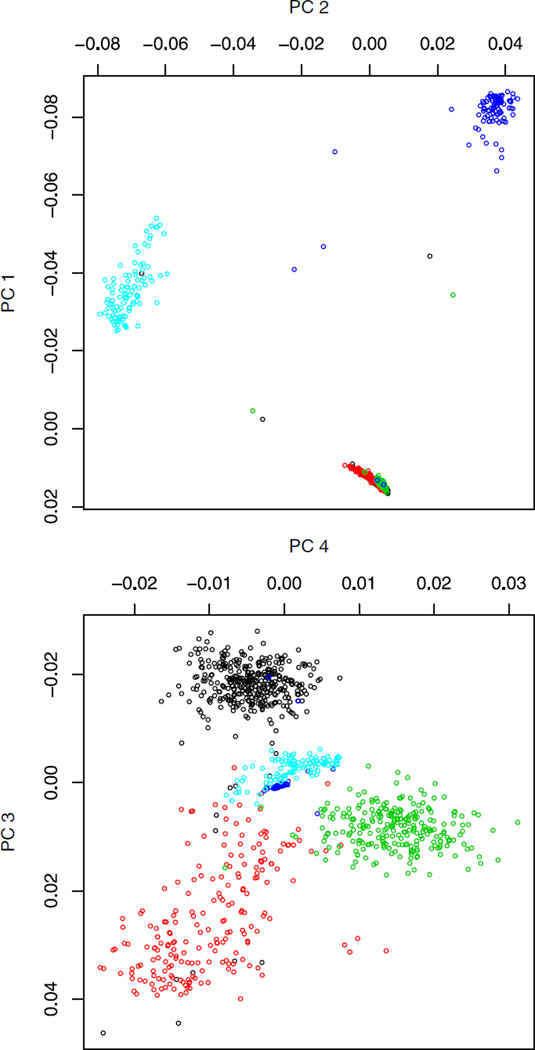
Using Spectral-GEM four dimensions are significant (Fig. 4). The first two dimensions separate the continental clusters, similar to PCA. In the third and fourth dimensions, the European clusters separate more distinctly than they did for PCA. For these higher dimensions, the samples from other continents plot near to the origin, creating a cleaner picture of ancestry. Six homogeneous clusters are discovered, three European clusters, an African American cluster, and two Indian clusters.

Fig. 4.

Principal components from the spectral graph approach for Scenario 2. Subjects are self-identified as UK (black), Italian (red), Iberian Peninsula (green), African American (blue), and Indian (orange).

Scenario 3

In this example we analyze the full POPRES sample. Smartpca’s six standard deviation outlier rule removes 141 outliers, including all of the E. Asian and Mexican samples. If these “outliers” were retained, PCA finds 12 significant dimensions: the first four dimensions separate the five continental populations (African, European, Latin American, E. Asian, and S. Asian). Other ancestry vectors are difficult to interpret. Moreover, based on this embedding, Ward’s clustering algorithm failed to converge; thus no sensible clustering by ancestry could be obtained.

Spectral-GEM produces clearer results. No outliers are removed prior to analysis. The number of significant dimensions of ancestry is eight. The first four dimensions separate the major continental samples; the remaining dimensions separate the European sample into smaller homogeneous clusters.

Applying the clustering algorithm based on this eight dimensional embedding we discover 16 clusters and 3 outliers. Four of these clusters group the African American, E. Asian, Indian, and Mexican samples. These clusters conform with near perfect accuracy to self-identified ancestry; greater than 99% of the subjects in a cluster self-identified as that ancestry, and only a handful of subjects who self-identified as one of those four ancestries fall outside of the appropriate cluster.

The remaining 12 clusters separate the individuals of European ancestry. For ease of interpretation, we removed the samples obtained from Australia, Canada, and the US, and focus our validation on 2,302 European samples, which can be more successfully categorized by ancestry based on geographic origin. These individuals could be classified to one of the 34 European countries represented in the database (Table I). Sample sizes varied greatly across countries. Switzerland is represented by 1,014 individuals. Some countries are represented by only one subject. Seven countries had samples of size 60 or more. Countries with smaller samples were combined to create composite country groupings based on region; see Table I for definition of country groupings.

TABLE I.

Counts of Subjects from Each Country Classified to Each Cluster

			Cluster label
Country	Subset	Count	A	B	C	D	E	F	G	H	I	J	K	L
Switzerland	CHE	1,014	871	36	3	2	32	39	1	0	9	14	5	2
England	GBR	26	0	22	0	0	1	0	0	0	1	0	2	0
Scotland	GBR	5	0	5	0	0	0	0	0	0	0	0	0	0
United Kingdom	GBR	344	20	300	0	3	8	0	3	0	1	1	5	1
Italy	ITA	205	8	0	1	124	1	60	0	4	1	2	4	0
Spain	ESP	128	3	0	122	0	1	1	0	0	0	0	1	0
Portugal	PRT	124	1	0	119	0	0	2	0	0	0	0	0	0
France	FRA	108	39	34	15	0	5	6	0	0	3	2	3	1
Ireland	IRL	61	0	61	0	0	0	0	0	0	0	0	0	0
Belgium	NWE	45	21	19	0	0	3	0	0	0	1	1	0	0
Denmark	NWE	1	0	1	0	0	0	0	0	0	0	0	0	0
Finland	NWE	1	0	0	0	0	0	0	1	0	0	0	0	0
Germany	NWE	71	16	22	0	0	22	1	3	0	3	0	2	2
Latvia	NWE	1	0	0	0	0	0	0	1	0	0	0	0	0
Luxembourg	NWE	1	0	0	0	0	1	0	0	0	0	0	0	0
Netherlands	NWE	19	3	15	0	0	1	0	0	0	0	0	0	0
Norway	NWE	2	0	2	0	0	0	0	0	0	0	0	0	0
Poland	NWE	21	0	1	0	0	3	0	16	0	1	0	0	0
Sweden	NWE	10	0	7	0	0	2	0	0	0	0	1	0	0
Austria	ECE	13	3	1	0	0	6	0	0	0	2	0	0	1
Croatia	ECE	8	0	0	0	0	5	0	2	1	0	0	0	0
Czech	ECE	10	1	0	0	0	6	0	3	0	0	0	0	0
Hungary	ECE	18	0	0	0	0	10	0	4	1	2	1	0	0
Romania	ECE	13	0	0	0	0	5	0	2	4	1	1	0	0
Russia	ECE	7	1	0	0	0	0	0	6	0	0	0	0	0
Serbia	ECE	3	0	0	0	0	0	0	1	0	2	0	0	0
Slovenia	ECE	2	0	0	0	0	2	0	0	0	0	0	0	0
Ukraine	ECE	1	1	0	0	0	0	0	0	0	0	0	0	0
Albania	SEE	2	0	0	0	1	0	0	0	1	0	0	0	0
Bosnia	SEE	7	0	0	0	0	3	0	4	0	0	0	0	0
Cyprus	SEE	4	0	0	0	4	0	0	0	0	0	0	0	0
Greece	SEE	5	0	0	0	2	0	0	0	3	0	0	0	0
Kosovo	SEE	1	0	0	0	0	0	0	0	1	0	0	0	0
Macedonia	SEE	3	0	0	0	0	0	1	0	2	0	0	0	0
Turkey	SEE	6	0	0	0	2	0	0	0	3	0	0	0	0
Yugoslavia	SEE	17	0	0	0	1	6	0	2	6	0	2	0	0
Total		2,302	988	526	260	139	123	110	49	26	27	25	22	7

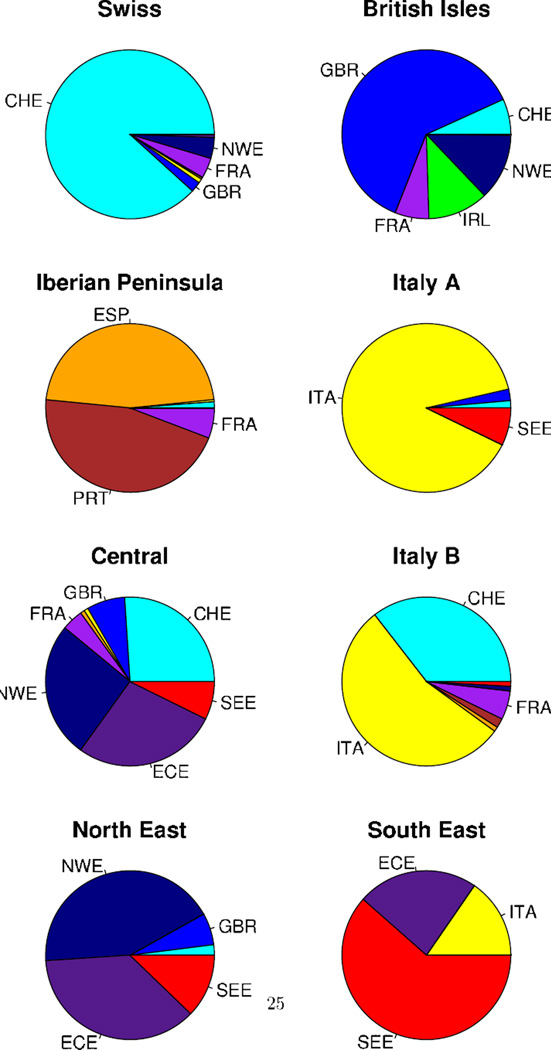
Labels in column two create country groupings where necessary due to small counts of subjects in many individual countries. Country groupings NWE, ECE, and SEE include countries from north west, east central, and south east Europe, respectively. Eight clusters (A–H) were given descriptive cluster labels based on the majority country or country grouping membership: (A) Swiss, (B) British Isles, (C) Iberian Peninsula, (D) Italian A, (E) Central, (F) Italian B, (G) North East, and (H) South East. The remaining four clusters are labeled as I, J, K, and L.

By using Ward’s clustering algorithm based on the spectral embedding, all but 81 of the European sample were clustered into one of eight relatively large European clusters (labeled A–HH, Table I). Figure 5 illustrates the distribution of country groupings within each cluster (i.e., the conditional probability of country grouping given cluster). Clusters tend to consist of individuals sampled from a common ancestry, or likewise, people of common ancestry tend to be clustered together. Labeling the resulting clusters in Figure 5 by the primary source of their membership highlights the results: (A) Swiss, (B) British Isles, (C) Iberian Peninsula, (D) Italian A, (E) Central, (F) Italian B, (G) North East, and (H) South East. The remaining four small clusters show a diversity of membership and are simply labeled I, J, K, and L. Cluster L has only seven members who could be classified by country of origin and is not considered further.

Fig. 5.

Country membership by cluster for Scenario 3. Cluster labels and country groupings are defined in Table I. Cluster labels were derived from the majority country or country grouping membership.

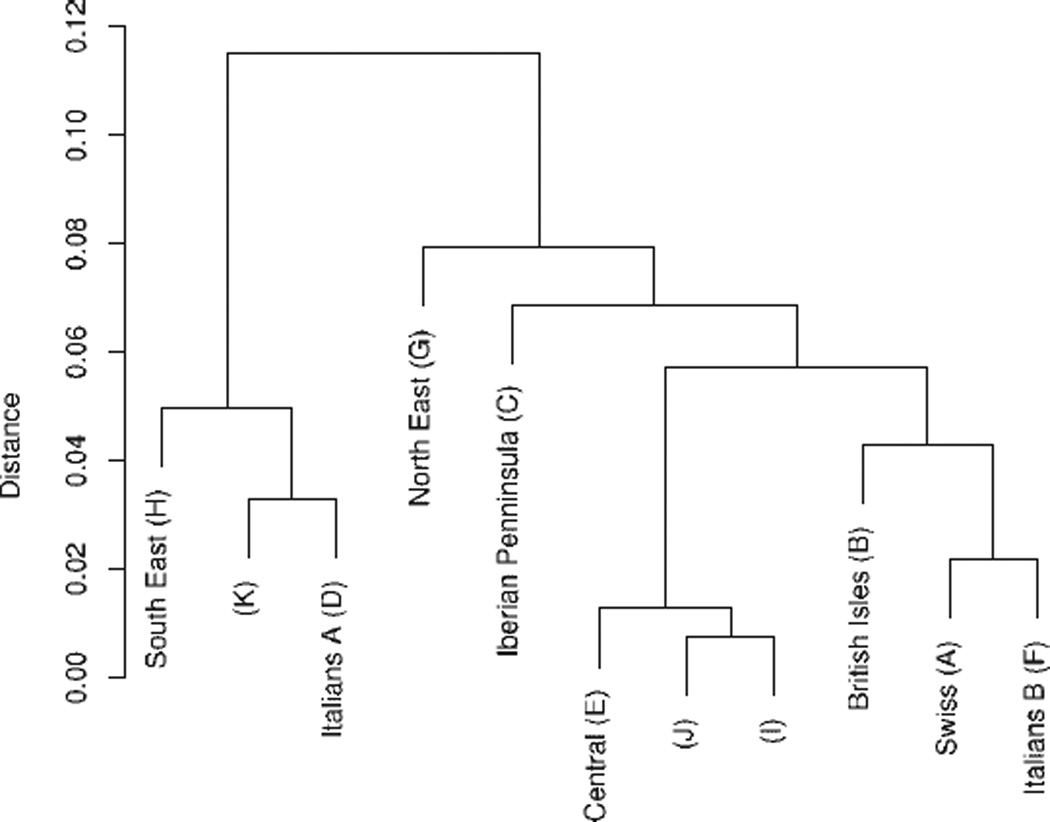
A dendrogram shows that the clusters are related to varying degrees (Fig. 6). For instance, it appears that the Italian A and B clusters represent Southern and Northern Italy, respectively. Clusters I and J are similar to the Central cluster, whereas Cluster K represents a more Southern ancestry. It is likely that one or more of the smaller clusters consists of Ashkenazi Jews.

Fig. 6.

Dendrogram for European clusters from Scenario 3.

Deeper examination of Table I reveals some interesting patterns. As in other studies of European populations [Heath et al., 2008], we found that large, centrally located countries such as France and Germany appear in several clusters indicating their complex history. Multilingual countries such as Switzerland and Belgium split into clusters which might correlate with distinct lingual groups [Novembre et al., 2008]. With the exception of Bosnia, Russia, Poland, and Romania, nearly all of the Central Europeans fell into cluster E. From South East Europe, although a handful fell in cluster E, the majority fell into cluster H. Finally several subjects from Cyprus, Greece, and Turkey appear in cluster D with the Southern Italians.

DISCUSSION

Large, genetically heterogeneous data sets are routinely analyzed for genome-wide association studies. These samples exhibit complex structure that can lead to spurious associations if differential ancestry is not modeled. Numerous approaches for handling this issue are now available in the literature [Epstein et al., 2007; Pritchard et al., 2000; Purcell et al., 2007; Zhang et al., 2003]. Due to computational challenges encountered in genome-wide association studies much interest has focused on estimating ancestry using computationally efficient methods such as PCA. These methods are based on an eigenvector decomposition of a matrix that reflects genetic similarity between pairs of individuals.

While often successful in describing the structure in data, PCA has some notable weaknesses, as illustrated in our exploration of POPRES [Nelson et al., 2008]. Part of the challenge faced by PCA from POPRES is the disproportionate representation of individuals of European ancestry combined with individuals from multiple continents. To obtain results more in keeping with knowledge about population demographics, Nelson et al. [2008] supplement POPRES with 207 unrelated subjects from the four core HapMap samples. In addition, to overcome problems due to the dominant number of samples of European descent, they remove 889 and 175 individuals from the Swiss and the UK samples, respectively. Because PCA is sensitive to outliers, it performs a careful search for outliers, exploring various subsets of the data iteratively. After making these adjustments they obtain an excellent description of the ancestry of those individuals in the remaining sample. From this analysis we see that with careful handling, PCA successfully reveals ancestry. Likewise, when analysis is restricted to individuals of European ancestry, PCA again works very well [Novembre et al., 2008]. Less nuanced application of the approach leads to much less useful insights as we showed above.

In many settings the proposed spectral graph approach, Spectral-GEM, is more robust and flexible than PCA. It determines eigenvectors that separate the data into meaningful clusters. In contrast, smartpca sometimes finds a large number of significant dimensions. For instance in a study of nearly 6,000 individuals of European ancestry smartpca identified 110 significant dimensions with two dominant axes [Heath et al., 2008]. Spectral-GEM’s embedding is not notably affected by outliers (e.g., Scenario 1 of Results). It can detect fine ancestral structure even in very heterogeneous data (Scenarios 2 and 3 of Results). Finally in a large sample of complicated ancestry, such as Scenario 3, it can successfully delineate the relatively discrete and relatively continuous ancestral components. Axes of ancestry can be used to control for structure following any of the standard epidemiological approaches: regressing out the effects of ancestry [Price et al., 2006]; matching cases and controls of similar ancestry [Luca et al., 2008]; or analyzing the homogeneous clusters using the Cochran-Mantel-Haenszel test. For most situations these approaches are likely to lead to similar results. Successfully finding the hidden structure using a small number of eigenvectors is the key to controlling for the effects of ancestry. Spectral-GEM should be a useful addition to the tools used to analyze genome-wide association data and other data sets in which ancestry is of interest.

Successful implementation of Spectral-GEM benefits from careful choice of the SNP panel. A thoughtful choice of SNPs leads to more robust discoveries of eigenvectors that are more interpretable. In the analysis of POPRES described in Results we use less than 5% of the available SNPs, but we believe we are retaining essentially all of the available information about ancestry. In the process of chosing the SNPs for ancestry analysis we suggest a number of edits. First, we remove any SNPs with missingness rate greater than 0.2%. This edit removes artificial correlations between individuals due to imputed missing values. Second, we reduce the panel to include only tag SNPs. Including SNPs in LD leads to discoveries of axes that describe local LD structure rather than true axes of ancestry. For instance using all of the SNPs, we found d = 16, a representation that includes eight more dimensions than reported in our analysis. Through experience we have found that applying an initial screen that selects a grid of SNPs separated by 10 Kb approximates a tag SNP selection fairly well. Next we apply a formal tag SNP selection process to remove any remaining SNPs with r²>0.04. Using the tag SNPs reported in our analysis we found d = 8, a result that is quite robust to slight variations in the SNP selection. For instance, using various choices of tag SNPs ranging in number from 15,000 to 80,000 yielded similar results. But using 10,000 SNPs we find only d = 5 dimensions. This suggests that there is an inflection point in the information content of the SNP panel.

The distribution of the eigengap statistic used to determine the number of significant axes of ancestry is well approximated by a function of the sample size, provided the number of tag SNPs is relatively large (L>10,000). For a genome-wide association study we expect to have at least this number available. For smaller numbers of SNPs the distribution also depends on L. Consequently the cutoff value provided herein for the test does not apply. For smaller numbers of SNPs it is necessary to simulate the distribution of the eigengap statistic. Further study will be required to obtain an asymptotic theory such as applied to eigenvalues of ϒϒ′ [Patterson et al., 2006].

The choice of weight matrix W is also open for further investigation. We selected a simple kernel derived from the traditional kernel employed in PCA analysis; however any matrix that measures the non-negative genetic similarity between pairs of individuals is a candidate. A natural choice with roots in both genetics [Purcell et al., 2007] and spectral graph theory is based on IBS sharing. For individuals i and j, let s_ij be the fraction of alleles shared by the pair identical by state across the panel of SNPs. Define the corresponding weight as w_ij = exp{−(1 − s_ij)/ε}. In this formulation ε is a tuning parameter. Preliminary investigation suggests this kernel has good properties, but further study is required to develop a data-dependent choice of the tuning parameter.