Applying mathematical concepts with hands-on, food-based science curriculum

Abstract

This article addresses the current state of the mathematics education system in the United States and provides a possible solution to the contributing issues. As a result of lower performance in primary mathematics, American students are not acquiring the necessary quantitative literacy skills to become successful adults. This study analyzed the impact of the FoodMASTER Intermediate curriculum on fourth-grade student’s mathematics knowledge. The curriculum is a part of the FoodMASTER Initiative, which is a compilation of programs utilizing food, a familiar and necessary part of everyday life, as a tool to teach mathematics and science. Students exposed to the curriculum completed a 20-item researcher-developed mathematics knowledge exam (Intervention n=288; Control n=194). Overall, the results showed a significant increase in mathematics knowledge from pre- to post-test. These findings suggest that students engaged in food-based science activities provided them with the context in which to apply mathematical concepts to an everyday experience. Therefore, the FoodMASTER approach was successful at improving students’ mathematics knowledge while building a foundation for becoming quantitatively literate adults.

Introduction

American students are falling behind other countries in science, technology, engineering, and mathematics (STEM) disciplines. Statistics from international tests such as Trends in International Mathematics and Science Study (TIMMS) and the Program for International Student Assessment (PISA) have ranked the United States (US) students well below students from other countries, particularly in mathematics (Ornstein, 2010; Preston, 2010; Provasnik, et. al., 2012). Many efforts have been made to improve student competency in mathematics; however, these attempts have made little to no impact on scores (Preston, 2010).

Numerous reasons have been considered to explain the low-test scores. One of the more notable causes may be that students lack the ability to put mathematics concepts into context. They are aware of the usefulness of mathematics; however, they are not able to fully comprehend its nature or apply their knowledge to everyday life (Dacey & Polly 2012; Wilkins, 2000; Piatek-Jimenez, Marcinek, Phels, Dias, 2012). This application of mathematics knowledge is referred to as quantitative literacy. Many adults in the US lack basic quantitative literacy skills, which can lead to greater issues as a society (Wilkins, 2000; Wilkins, 2010; Piatek-Jimenez, et. al., 2012; Madison & Steen, 2008).

The purpose of this article is to address the implications of American students’ lack of quantitative literacy and discuss one possible method to increase their quantitative literacy. To do this, authors will discuss the impact of the FoodMASTER¹ Intermediate science curriculum on fourth-grade students’ mathematics knowledge gains and its possible usefulness for teaching students how to apply mathematics content to everyday situations.

Literature Review

Mathematics Education

Applying mathematical concepts to everyday situations is essential for success, making competency in mathematics important for daily functions. To assess students’ mathematics competence in the K-12 education system, international assessments are conducted. The TIMSS is one of the more widely accepted assessments, which measures achievement based on a scale from 0 to 1,000, with an average of 500 and standard deviation of 100 (Kasterburg, Ferraro, Lemanski, Roey & Jenkins, 2012). Unfortunately, according to the most recent TIMSS assessment (2011), US fourth-grade students’ scores ranked below 10 other countries in mathematics assessments. Since 1995, the US has improved its score by 23 points indicating a move in the right direction; however, the US is still 65 points below the number one country, Signapore (Kasterburg et. al., 2012; TIMSS, 2011).

Some researchers have found application-based instruction to be successful in improving student scores on international tests (Dacey & Polly, 2012). In addition to changes in instructional practices, modifications to current mathematics curricula and the implementation of a centralized education system through standards also have been identified as areas of improvement (Lee & Wassel, 2012). In 2010, the Common Core State Standards for Mathematics (CCSSM) were released in hopes of improving these areas. The CCSSM attempts to provide centralized education standards as well as emphasize the importance of making significant changes to what is being taught and how the information is being presented (National Governors Association Center for Best Practices [NGACBP] & Council of Chief State School Officers [CCSSO], 2010). One of the many goals of CCSSM is to challenge teachers to educate and engage students using real-world situations (Dacey & Polly, 2012).

Due in-part to curricula encouraging teaching methods such as skill-and drill or watch-and-learn, many students are unable to apply mathematical concepts to everyday life resulting in diminished quantitative literacy across the lifespan (Wilkins, 2010; Steen, 2001; Wilkins, 2000; Richland, Stigler, & Holyoak, 2012). Children and adults need quantitative literacy skills to function as well-informed citizens in today’s society. Skills such as making informed decisions and solving real-world problems are of upmost importance. Employers expect workers to identify problems, analyze and interpret information, and make a decision that will solve the identified problem. This type of reasoning is not based on one’s ability to solve mathematical problems, rather one’s ability to apply mathematical concepts to real-world situations (Wilkins, 2010; Wilkins, 2000; Madison & Steen, 2008; Richland et. al., 2012).

Before quantitative literacy can be achieved, students must have a meaningful connection with mathematics. Students need to visualize the importance of mathematics and apply its concepts in daily life (Steen, 2001; Wilkins, 2000; Madison & Steen, 2008). They must also value its usefulness before they can become quantitatively literate. A quantitative literate person has the ability to understand the true nature of mathematics through problem solving, which is necessary for success at home and work (Wilkins, 2010; Madison & Steen, 2008).

Researchers, practitioners, and educators have explored numerous methods to ensure American students are able to become quantitatively literate. As a result of their efforts, the utilization of other subjects as context has been found to be an effective method. Health and nutrition are among the topics suggested as beneficial for this method (James & Adams, 1998; Hyman, 2012). In an effort to engage students with topics such as health and nutrition, some researchers have successfully utilized mathematics as a method to complete this task. While their primary purpose may have not been to improve mathematics performance, they were still successful at increasing the students’ mathematics knowledge. For example, James and Adams (1998) connected mathematics concepts and procedures with nutrition. They proposed the use of nutrition as a context to present mathematics concepts to elementary children. These concepts included (a) statistics and probability; (b) number sense; (c) fractions; (d) measurement; (e) whole numbers; and (f) numeration. With this model, students used applicable concepts (the study of food and its impact on the body) to construct knowledge related to the topic as well as build mathematical skills.

The Nutrition Facts Label has been used as a tool to present mathematical and health-related concepts to students. This approach provided the students with context to everyday life. The students were required to utilize mathematical concepts to analyze food label information and make an informed decision based on their findings (Hymam, 2012). Research suggests building on fundamental life skills requiring the use of mathematical concepts, such as the examples mentioned above, will allow children to become better informed adults (Wilkins, 2000; Madison & Steen, 2008).

The purpose of this study was to use a researcher-developed 20-question exam to determine mathematics knowledge gains of students exposed to the FoodMASTER Intermediate curriculum and compare results to control classrooms. While the FoodMASTER Initiative is a compilation of several science and mathematics focused curricula, the FoodMASTER Intermediate Grade 3-5 curriculum is science curriculum that uses food as a teaching tool. The FoodMASTER Intermediate Grade 3-5 lessons provided students an opportunity to engage in a hands-on, minds-on approach to learning science along with crosscutting mathematics concepts.

Methods

Design

A partnership between a nutrition science faculty and an elementary school teacher initiated the first drafts of food-based activities. These initial lessons led to the creation of the FoodMASTER Initiative, which is a compilation of activities aimed at using food as a tool to teach mathematics and science. During the 2007-2008 academic year, 45 one hour, food-based science lessons were piloted in 10 third-grade classrooms in Southeast Ohio (Duffrin et. al., 2010). Formative feedback collected from pilot teachers and content experts provided researchers with the means to modify and complete final development on the intermediate curriculum. Fourth-grade classrooms were then selected for intervention after informal discussions with teachers in both states revealed that 4^th grade would be the most appropriate to introduce the concepts covered in the FoodMASTER curriculum.

The curriculum used for this study, FoodMASTER Intermediate, is a 10-chapter curriculum consisting of 24 hands on food-based science lessons geared towards students in grades three to five. In the 2009-2010 academic year, the curriculum was implemented in 18 fourth-grade classrooms. A pre- and post-test method was utilized to assess the impact of the FoodMASTER Intermediate curriculum on mathematics knowledge among fourth-grade students. University East Carolina University’s Institutional Review Board approved all study protocol and instruments prior to implementation.

Participants

Researchers recruited 18 intervention (I) and 16 control (C) fourth-grade classrooms in Ohio (I=9; C=8) and North Carolina (I=9; C=8) during the 2008-2009 academic year. Intervention teachers were selected based on location, interest, and recommendation by school administrators (e.g. principles, curriculum coordinators). Once intervention classrooms were identified, similar classrooms were recruited to serve as control classrooms. Control classrooms followed the same pre- and post-test protocol as intervention classrooms while continuing normal curricular activities. Teachers in both groups maintained normal curricular activities; however, intervention classrooms included FoodMASTER lessons during instructional time. FoodMASTER Directors visited intervention teachers on at least one implementation day to provide support and offer teachers an opportunity to ask questions or make comments. Teachers could also contact Directors at any time if additional support was needed.

Classrooms across both states were selected to obtain a mixture of rural, urban, and suburban settings, which would provide a better representation of classrooms across the states. These states were chosen based on the Principle Investigators’ affiliation with Ohio University and East Carolina University. Participating teachers took part in a 2-3 hour content training session prior to intervention. Teachers provided researchers with demographic information including gender, date of birth, and ethnicity for participating students can be found in Table 1².

Table 1.

Student Demographic Information

	Intervention (n=288)	Control (n=194)
Male	135	84
Female	153	95
White	221	138
Black/African American	46	20
Asian	4	3
Hispanic or Latino	13	11
Other Race	4	6
Missing	0	16

Researchers enrolled 762 students in the study (NC=330; OH=432). Students in both the intervention and control classrooms completed the same mathematics knowledge exam at pre- and post-intervention. Of the larger sample, researchers included only data from students who completed both baseline and post-intervention questionnaires (n=482). The primary reason for students not completing the mathematics knowledge questionnaire at both pre-test and post-test was primarily due to absenteeism on the day of survey administration.

Curriculum

Prior to pilot-testing the FoodMASTER Intermediate curriculum was reviewed by a team of seven experts including nutrition and education faculty, a nutrition scientist, an elementary teacher, and a pediatrician. During the FoodMASTER Intermediate pilot both teachers and students enjoyed the curriculum indicating it was meaningful and engaging. Feedback from participating teachers was used to revise and further develop the intermediate curriculum (Duffrin, et. al., 2010). The final curriculum consisted of 24 lessons organized into 10 chapters, each chapter focusing on food topics: Measurement; Food Safety; Vegetables; Fruit; Milk and Cheese; Meat, Poultry, and Fish; Eggs; Fats; Grains; and Meal Management. One to three lessons were included in each chapter. The lessons focused on chapter-specific topics and included proficiency questions to assess overall comprehension. The lessons were comprised of an introduction to provide background information, a hands-on lesson, and an optional extension of the lesson to be completed at home. The background portion highlighted Doodle Bugs, which promoted reading comprehension. The next portion, Scientific Inquiry, which is considered the bulk of the lesson, guided students through an activity using food to explore the concepts of the lesson. For example, in lesson one students prepared liquid and dry ingredients to make chocolate chip oatmeal cookies to learn more about measurement and fractional math. The last portion contained Try this at Home pages, which included a recipe and fun facts about food and nutrition. Students could share with this information with their friends and family. Proficiency questions were also included at the end of each chapter. A teacher’s manual was created to provide background information; answers; and a reference to link curriculum content to the National Science Education Standards (NRC, 1996) and the National Mathematics Standards (National Council of Teachers of Mathematics [NCTM], 2000). Teachers were not prescribed an implementation plan for the lessons; rather FoodMASTER lessons could take place anytime during one academic year.

The FoodMASTER activities used for this study were science focused; however, each chapter incorporated varying amounts of crosscutting mathematics concepts throughout the lessons. For example, in the first chapter students were required to make conversions, utilize deductive reasoning skills, and work with fractions. Many of the NCTM National Mathematics (2000) standards were addressed in each chapter. Using the chapter example provided above, expectations under Number and Operations, Measurement, Problem Solving, and Connections standards were addressed. See Figure 1 for an example lesson.

Figure 1.

Example Lesson – Milk

Measurement

A researcher-developed 20-question exam was used at pre-and post-test to measure fourth-graders mathematics knowledge. Sample Ohio proficiency test questions were used as a model for formatting the exam. Additionally, all questions were written using the National Council of Teachers of Mathematics: Standards for Grades 3-5 as a guide (2000). Once complete, the FoodMASTER research team reviewed the exam and then sent questions to the expert team to review for content. While the content of the questions were focused on food-related subject matter, the mathematics questions were developed to measure a range of 4^th grader mathematics problem-solving abilities.

In 2010, the Common Core State Standards for Mathematics (CCSSM) were released replacing the previous standards set aside by individual states and enhancing the NCTM (2000) standards. Therefore, researchers categorized the exam questions into four CCSSM content areas: seven questions in Operations and Algebraic Thinking, two questions in Number and Operations in Base Ten, two questions in Number and Operations with Fractions, and eight questions in Measurement and Data. Researchers instructed teachers on how to administer the exams at the beginning (pre-test) and near the end of the academic year (post-test). Scores were calculated using a one-point scale; therefore, a total score of 20 points was possible and scores for domains were determined on the amount of questions in each domain category (e.g. a total of seven points were possible for Operations and Algebraic Thinking).

Statistical Analysis

Descriptive statistics were used to describe percent correct at pre-and post-test for the intervention and control groups. Independent sample t-test were used to examine mean score differences (p<.05) between intervention and control at pre-and post-test for the four content areas and for total scores. Independent sample t-tests revealed no significant differences between the intervention and control group at pre-test. This made it appropriate to analyze independent sample t-tests on post-test scores without adjusting for pre-test scores. Statistical analyses were performed using Statistical Package for the Social Sciences 20.0 (SPSS).

Results

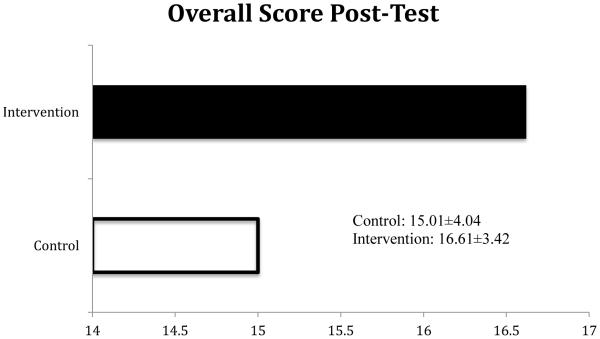
The mean age and standard deviation (SD) of the sample was I = 10.05±0.57 years and C = 9.93±0.81. Pre-test frequencies revealed that 4 out of 7 items in the domain Operations and Algebraic Thinking, 1 out of 2 items in the domain Number and Operations in Base Ten, and 3 out of 8 items in the domain Measurement and Data received correct responses from 80% or more of the students indicating some existing competency in these content areas. Many of the items receiving lower percentages at pre-test were more complex, application-based questions; all items in the domain Number and Operations with Fractions were considered as such. Percent correct responses for each item at pre- and post-test are located in Table 2. Frequency of correct responses to each item provides a good illustration students’ prior knowledge. At post-test, significant differences in mean scores were found between the intervention and control group in all domains as illustrated in Table 3. A significant difference was observed between intervention and control group on the overall 20-item exam as illustrated in Figure 1.

Table 2.

Percentage of Correct Responses at Pre-and Post-Test

Questions	Pre-test		Post-test
Operations & Algebraic Thinking	Intervention	Control	Intervention	Control
1. If there are 120 spaghetti noodles in a box of   spaghetti and there are 6 servings in a box, then how   many noodles are in each serving of spaghetti?	59%	58%	80%	71%
2. There are 8 hotdogs in a package. How many   packages of hotdogs do you need to buy to serve   hotdogs to 24 people?	81%	76%	90%	88%
3. Which cereal has the least amount of fiber?	88%	88%	94%	89%
4. Whole-wheat pasta has 6 grams of fiber per serving.   How many servings of pasta do you need to eat to   get 25 grams or more of fiber?	46%	45%	66%	51%
5. Rita needs to double her recipe. What should she   do?	81%	78%	81%	71%
6. Select the answer that lists the ice creams from least   to most grams of total fat.	83%	84%	91%	97%
7. One serving of French salad dressing has 6 grams of   fat and there are 9 calories per gram of fat. Chris ate   1 serving of French salad dressing. How many   calories from fat did Chris eat?	43%	46%	65%	54%
Number & Operations: Base Ten
8. You buy an apple, carrots, milk, and a turkey   sandwich for lunch. How much does lunch cost?	70%	61%	78%	69%
9. Whose lunch costs the most?	93%	93%	95%	92%
Number & Operations: Fractions
10. Which measuring cup is the smallest?	57%	55%	82%	72%
11. What fraction of the cookies are chocolate chip?	74%	76%	92%	84%
12. If you don’t have a one-cup dry measure, how can   you measure 1 cup of flour?	65%	64%	81%	71%
Measurement and Data
13. Amber is measuring the weight of a carrot. What   unit of measurement should she use?	64%	64%	74%	71%
14. The first step of a recipe says, “Add 2 of brown   sugar and 3 of flour to a large bowl.” What piece of   information is missing?	69%	65%	81%	78%
15. Which is the best example of circumference?	51%	47%	83%	56%
16. You measured 1 cup of flour. What did you   measure?	38%	33%	65%	51%
17. James needs to measure 1 teaspoon of salt. Which   measuring tool should he use?	76%	73%	89%	81%
18. Based on the Venn diagram, what are two ways   apples and oranges are alike?	86%	82%	92%	87%
19. The bar graph shows the number of students who   voted for each fruit as their favorite fruit. How many   more people voted for apples than bananas?	84%	81%	89%	85%
20. Which graph matches the data table?	84%	78%	87%	78%

Table 3.

T-Test Comparison of Mean Scores and Standard Deviation of Domains Between Control and Intervention Groups

Content Area	Total Score	Intervention	Control	Significance	Intervention	Control	Significance
Operations & Algebraic Thinking	7	4.81±1.72	4.76±1.75	0.77	5.76±1.42	5.27±1.57	0.00*
Number Operations: Base Ten	2	1.63±0.56	1.54±0.58	0.10	1.73±0.48	1.61±0.60	0.02*
Measurement and Data	3	1.95±0.99	1.95±1.08	0.98	2.69±0.58	2.48±0.75	0.00*
Number Operations: Fractions	8	5.52±1.83	5.23±1.82	0.10	6.60±1.41	5.87±1.74	0.00*

Discussion

The purpose of this study was to assess the effectiveness of the hands-on, food-based science curriculum on fourth-grade student’s mathematics knowledge. As measured by the researcher-developed mathematics knowledge exam, the food-based science curriculum increased fourth-graders’ overall mathematics knowledge. The exam also provided baseline data describing existing student mathematics knowledge. Baseline data can be used to identify starting points for educators (Moreno et. al., 2004). Teachers in Ohio and North Carolina might find the results to be particularly helpful selecting subject matter requiring more attention.

Pre-test frequency results revealed students demonstrated difficulty in correctly answering complex application-based questions (e.g. “One serving of French salad dressing has 6 grams of fat and there are 9 calories per gram of fat. Chris ate 1 serving of French salad dressing. How many calories from fat did Chris eat?”). The example above was considered a complex application-based question because it required students to apply the information being presented rather than directly answering a question such as “Which cereal has the least amount of fiber?”. When comparing post-test frequencies to pre-test, both groups showed gains in knowledge; however, the intervention group showed larger percent gains for the more complex application-based questions. Other studies combining nutrition and mathematical concepts have seen similar improvements (James & Adams 1998; Hyman 2012). Similarly, when comparing post-test mean scores, the intervention group showed significant gains over the control group in all domain areas and overall exam score. When analyzing the effectiveness of a curriculum that requires students to apply mathematics to everyday situations, it is important to note that all questions in the domain Number and Operations with Fractions required more complex application of skills to real-life situations. This indicates that the food-based science curriculum, FoodMASTER Intermediate, was more effective than the control classroom curriculum in increasing students’ ability to correctly respond to application-based questions. Other studies utilizing similar curricula or instruments to assess student performance have seen similar performance improvements (James & Adams, 1998; Hyman, 2012; Wood & Sellers, 1996).

The data from this study provides evidence to suggest that students engaged with a curriculum using food-based science concepts as a context to teach mathematics through student engagement will show greater gains in mathematics knowledge (as measured by the research exam) when compared to students exposed to other curricula. The utilization of curricula encouraging skill-and-drill or watch-and-learn has been found to produce frustration and anxiety in students (Brady & Bowd, 2005; Woodward, 2004). To improve this situation, teachers could choose to supplement such curricula with student-centered lessons encouraging engagement (Cotabish, Dailey, Robinson & Hughes, 2013; Lee & Wassel, 2012; Stonewater, 2005; Slavin & Lake, 2008; Furner & Kumar, 2007).

Conclusion

Considering the current state of the US mathematics education system today, changes need to be made in order to improve student performance. To do this, research shows that building a foundation for mathematics knowledge is essential and should be achieved through student engagement using everyday situations as a context (Wilkins, 2000; Bodovoski & Farkas, 2007; Slavin & Lake, 2008; Woodward, 2004). The potential for teaching mathematical concepts using real-life situations allows for alignment with the CCSSM while also demonstrating knowledge acquisition through standardized testing (Dacey & Polly, 2012; Schwols & Miller, 2012 Wood & Sellers, 1996).

The FoodMASTER Intermediate curriculum encompasses a majority of the elements suggested by researchers that support applied mathematics as essential for promoting quantitative literacy and improving mathematics performance. As food is an effective teaching tool for engaging students in retaining information about multidisciplinary concepts (Duffrin, et. al., 2010; Hovland, et.al., 2013), findings from this study suggest FoodMASTER Intermediate utilized effective methods for increasing student mathematics knowledge. Additionally, this study supports the crosscutting concept potential of science and mathematics to allow K-12 students to demonstrate achievement in knowledge without compromising classroom instruction time. Teachers using this curriculum will be able to help their students develop quantitative literacy skills during primary years. These skills are considered indispensible for success in today’s society (Wilkins, 2000; Wilkins, 2010; Piatek-Jimenez, et. al., 2012; Madison & Steen, 2008). Continued discussion and research across mathematics education disciplines is warranted to determine further ways to utilize an application-based curriculum.

Figure 2.

T-Test Comparison of Mean Scores and Standard Deviation of Overall Score between Control and Intervention Groups