Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Oct 21.
Published in final edited form as: Phys Med Biol. 2015 Sep 25;60(20):7877–7891. doi: 10.1088/0031-9155/60/20/7877

Estimation of optimal b-value sets for obtaining apparent diffusion coefficient free from perfusion in non-small cell lung cancer

Kishor Karki 1,‡, Geoffrey D Hugo 1, John C Ford 1, Kathryn M Olsen 2, Siddharth Saraiya 1, Robert Groves 3, Elisabeth Weiss 1
PMCID: PMC4610399  NIHMSID: NIHMS726893  PMID: 26406921

Abstract

The purpose of this study was to determine optimal sets of b-values in diffusion-weighted MRI (DW-MRI) for obtaining monoexponential apparent diffusion coefficient (ADC) close to perfusion-insensitive intravoxel incoherent motion (IVIM) model ADC (ADCIVIM) in non-small cell lung cancer. Ten subjects had 40 DW-MRI scans before and during radiotherapy in a 1.5T MRI scanner. Respiratory triggering was applied to the echo-planar DW-MRI with TR ≈ 4500 ms, TE = 74 ms, eight b-values of 0–1000 µs/µm2, pixel size = 1.98×1.98 mm2, slice thickness = 6 mm, interslice gap = 1.2 mm, 7 axial slices and total acquisition time ≈ 6 min. One or more DW-MRI scans together covered the whole tumour volume. Monoexponential model ADC values using various b-value sets were compared to reference-standard ADCIVIM values using all eight b-values. Intra-scan coefficient of variation (CV) of active tumour volumes was computed to compare the relative noise in ADC maps. ADC values for one pre-treatment DW-MRI scan of each of the 10 subjects were computed using b-value pairs from DW-MRI images synthesized for b-values of 0–2000 µs/µm2 from the estimated IVIM parametric maps and corrupted by various Rician noise levels. The square root of mean of squared error percentage (RMSE) of the ADC value relative to the corresponding ADCIVIM for the tumour volume of the scan was computed. Monoexponential ADC values for the b-value sets of 250 and 1000; 250, 500 and 1000; 250, 650 and 1000; 250, 800 and 1000; and 250–1000 µs/µm2 were not significantly different from ADCIVIM values (p > 0.05, paired t-test). Mean error in ADC values for these sets relative to ADCIVIM were within 3.5%. Intra-scan CVs for these sets were comparable to that for ADCIVIM. The monoexponential ADC values for other sets- 0–1000; 50–1000; 100–1000; 500–1000; and 250 and 800 µs/µm2 were significantly different from the ADCIVIM values. From Rician noise simulation using b-value pairs, there was a wide range of acceptable b-value pairs giving small RMSE of ADC values relative to ADCIVIM. The pairs for small RMSE had lower b-values as the noise level increased. ADC values of a two b-value set- 250 and 1000 µs/µm2, and all three b-value sets with 250, 1000 µs/µm2 and an intermediate value approached ADCIVIM, with relative noise comparable to that of ADCIVIM. These sets may be used in lung tumours using comparatively short scan and post-processing times. Rician noise simulation suggested that the b-values in the vicinity of these experimental best b-values can be used with error within an acceptable limit. It also suggested that the optimal sets will have lower b-values as the noise level becomes higher.

Keywords: DW-MRI, diffusion, ADC, IVIM model, Rician noise, lung cancer

1. Introduction

Diffusion-weighted magnetic resonance imaging (DW-MRI) is increasingly being investigated for radiotherapy treatment planning and response assessment in a variety of tumour sites (Eccles et al 2009, Lambrecht et al 2014, Haack et al 2010). It utilizes physiological and microstructural properties to differentiate between normal and abnormal tissues. Diffusion-weighted signal is related to the random motion of water molecules in tissue. In pure water at human body temperature of 37°C, the average displacement of water molecules due to diffusion in 1 ms is approximately 4 µm since the diffusion coefficient at this temperature is approximately 3.0 µm2/ms (Hagmann et al 2006).However, the observed average displacement of the molecules in tissues is much less than that in pure water due to interaction with cells and their hydrophobic membranes and macromolecules (Padhani et al 2009, Kallehauge et al 2010). Thus, the apparent diffusion of the water molecules in tissues is greatly influenced by the cellularity or cell sizes, organization and packing density. This property makes DW-MRI a strong candidate as an imaging biomarker for various diseases including cancer.

Although the intravoxel incoherent motion (IVIM) model, which is biexponential, has the potential to provide useful information about both cellularity and perfusion in tumours without contrast agent injection (Le Bihan and Turner 1992, Federau et al 2014), the monoexponential model is more widely used in DW-MRI to compute the apparent diffusion coefficient (ADC) due to computation simplicity, and reduced scanning and post-processing times. The incorporation of low b-values in computation of a monoexponential model ADC can result in a measurable contribution from perfusion, representing microvascular flow effects (Le Bihan et al 1988, Taouli and Koh 2010). ADC values of substantial variability are reported from different institutions for the same tissue type and pathology due to use of different b-values (Zhang et al 2010, Colagrande et al 2006). A consensus is needed to establish correct selection of a limited number of b-values in DW-MRI to ensure comparability across clinical ADC data and to avoid systematic error (Padhani et al 2009, Zhang et al 2010, Colagrande et al 2006). For monoexponential assessments of ADC values, the use of two b-values (>100 and between 500 and 1000 µs/µm2) has been recommended to avoid perfusion effects and to obtain accurate ADC values (Padhani et al 2009). In this respect, there have been a number of studies of normal tissues from various body sites such as kidney (Freiman et al 2012), liver (Freiman et al 2012), and spleen (Freiman et al 2012) as well as malignant tumours such as cervix cancer (Kallehauge et al 2010) to establish opt imal b-value sets to obtain the monoexponential ADC values close to reference-standard perfusion-insensitive IVIM model ADC (ADCIVIM). Malignant tumours have in general higher cellularity and therefore less diffusion compared to normal tissue of similar density. In addition, tumour cells originate from tissue-specific cells and therefore display characteristic properties that vary between tissues. Lung cancers, in particular, originate from various lung-specific cells, extend in air-filled spaces and display heterogeneous consistency that is expected to affect water diffusion. The purpose of this study is to estimate the effect of various b-value sets on ADC values and determine optimal b-value sets for obtaining monoexponential ADC close to reference-standard perfusion-insensitive ADCIVIM value for non-small cell lung cancer which so far has not been analyzed before.

2. Methods and materials

2.1. Patients

Ten subjects (6 men and 4 women, age 49–73 (mean 58±7) yrs), diagnosed with non-small cell lung cancer and receiving radiation therapy were included in this study after informed consent on an institutional review board-approved study. In addition to DW-MRI, other MRI protocols such as pre- and post-Gd-DTPA T1-weighted ultrafast gradient echo volume interpolated breath-hold examination (VIBE), diagnostic PET/CT with 2-deoxy-2-(18F)fluoro-D-glucose (FDG) and diagnostic CT with intravenous contrast were performed to assist with identification of the tumour margins.

2.2. DW-MRI Data Acquisition

Forty DW-MRI scans were acquired in the ten subjects before and during radiotherapy at about 3 and 6 weeks in a 1.5T MRI scanner (Magnetom Avanto, Siemens Medical Solutions, Erlangen, Germany). Diffusion-weighted images were acquired using an echo-planar imaging (EPI) pulse sequence with TR ≈ 4500ms, TE = 74 ms, number of excitations (NEX) = 2, fat saturation on, FOV ≈ 380×285 mm2, inplane image matrix size = 192×144 (115 phase encode steps), pixel bandwidth = 1736 Hz/pixel, pixel size ≈ 1.98×1.98 mm2, slice thickness = 6 mm, interslice gap = 1.2 mm, 7 axial slices and total acquisition time ≈ 6 min. One or more DW-MRI scans together covered the whole tumour volume. For respiratory triggering, prospective acquisition correction (PACE) was used (Barnwell, Smith, and Castillo 2007). Data were acquired in the end-expiratory phase. Body transmit coil and the 8-channel body array matrix receive coil were used. Diffusion gradients were applied to all three orthogonal axes producing trace-weighted images with eight b-values of 0, 50, 100, 250, 500, 650, 800 and 1000 µs/µm2.

2.3. Image Processing and Analysis

The IVIM, i.e. biexponential, model of signal decay proposed by Le Bihan et al (1988) is

S=S0[fe−b(D*+D)+(1−f)e−bD], (1)

and the monoexponential model of decay (Stejskal and Tanner 1965) is

S=S0e−γ2G2δ2(Δ−δ3)D=S0e−bD. (2)

In Eq. (1) and (2), S is the signal intensity of a voxel or volume of interest corresponding to b-value ‘b’; γ = gyromagnetic ratio; G = gradient strength; δ = diffusion gradient duration; Δ = time between diffusion gradient pulses; S0 is the baseline signal (without any diffusion attenuation); f is the perfusion fraction; D is the apparent diffusion coefficient; and D* is the perfusion or pseudo-diffusion coefficient. The monoexponential model D is denoted by ADC in the text. The IVIM model D, which represents the perfusion-insensitive diffusion compartment, is considered as the reference-standard ADC and is denoted by ADCIVIM, which will be used here.

MATLAB software package (R2012b version; MathWorks, Natick, MA), ImageJ and MIM Software (MIM Software Inc., Cleveland, OH) were used for image processing and analysis. The monoexponential model ADC was obtained, on a voxel-by-voxel basis, as the negative of the slope of the straight line fit to the measured signal intensity (in logarithmic scale) vs b-value: ln(S) = −ADC*b + ln(S0). The IVIM model parametric maps were obtained by fitting the data on a voxel-by-voxel basis using the Levenberg-Marquardt algorithm (Levenberg 1944, Marquardt 1963) implemented in MATLAB. Lung tumours usually are heterogeneous including areas of active tumour, normal tissue structures, such as bronchi, and necrotic tissue. The presumed active primary tumour margins were contoured manually, excluding regions of necrosis, on all DW-MRI images for highest b-value = 1,000 µs/µm2 or next highest b-value, i.e. 800 µs/µm2, in consensus by a radiation oncologist (EW) and a thoracic radiologist (either KMO or RG).

2.4. Simulation of the Effect of Noise

DW-MRI signal intensity images were synthesized on voxel-by-voxel basis for one DW-MRI scan obtained before radiation treatment of each of the ten subjects included in this study from the estimated IVIM parametric maps using Eq. (1) with b-values in the following ranges: 0–500 µs/µm2 with the increment of 50 µs/µm2, and 650–2000 µs/µm2 with the increment of 50 µs/µm2. Images were corrupted by Rician noise distribution (Rice 1944, Gudbjartsson and Patz 1995) with σ = 0, 5, 10 and 15. In our experimental respiratory triggered DW-MRI scans of lung cancer, σ is approximately 5, with a mean SNR on the b = 0 µs/µm2 image of approximately 25. ADC of a voxel can be computed using a 2-point estimation method in the monoexponential model represented by Eq. (2) as:

ADC=−ln(S2)−ln(S1)b2−b1, (3)

where S1 and S2 are the signal intensity of the voxel corresponding to the b1 or low b-value (blow) and b2 or high b-value (bhigh), respectively. The blow and bhigh were taken in the ranges of 0–500 µs/µm2, and 650–2000 µs/µm2, respectively. The square root of the mean of the squared error percentage (RMSE) of the ADC value relative to the corresponding reference-standard ADCIVIM for the tumour volumes of the ten scans was computed to determine the two b-value sets giving ADC close to ADCIVIM for each of the noise level.

To study the effect of inclusion of data at very high b-values at noise floor, the signal intensity vs b-value data were synthesized from the simulation of a subject’s tumour volume having comparatively high mean values of ADCIVIM, D* and f using Eq. (1). Then the synthesized data were corrupted with Rician noise of σ = 5.0. The synthesized data were obtained for the b-values of 1200, 1400, 1600, 1800, and 2000 in addition to the eight b-values - 0, 50, 100, 250, 500, 650, 800 and 1000 µs/µm2 used in the actual DW-MRI scans.

2.5. Statistical Analysis

Monoexponential model ADC values of active tumour from DW-MRI scans using various b-value sets were compared to reference-standard ADCIVIM using all b-values using two-tailed paired Student t-test. Intra-scan coefficient of variation (CV) was computed to compare the relative noise in ADC maps for the different b-value sets. Normalized mean and normalized standard deviation (SD) of the ADC values of tumour volume of each scan were obtained by dividing the mean and SD of the ADC values, respectively, by the corresponding mean ADCIVIM value of the tumour volume of the scan. The intra-scan CV was computed as the mean of the normalized SD divided by the mean of the normalized mean ADC values. The details of the method of computing intra (within) and inter (between) coefficient of variation can be found in Rodbard (1974). The intra-scan CVs for the b-value sets of the individual scans were also compared to that for IVIM using two-tailed paired Student t-test. The intra-scan CV will provide the information on the noise superimposed on the heterogeneity within the tumour volumes. F test was used to compare goodness of fit of the active tumour volume S vs b-value for the IVIM and monoexponential models.

3. Results

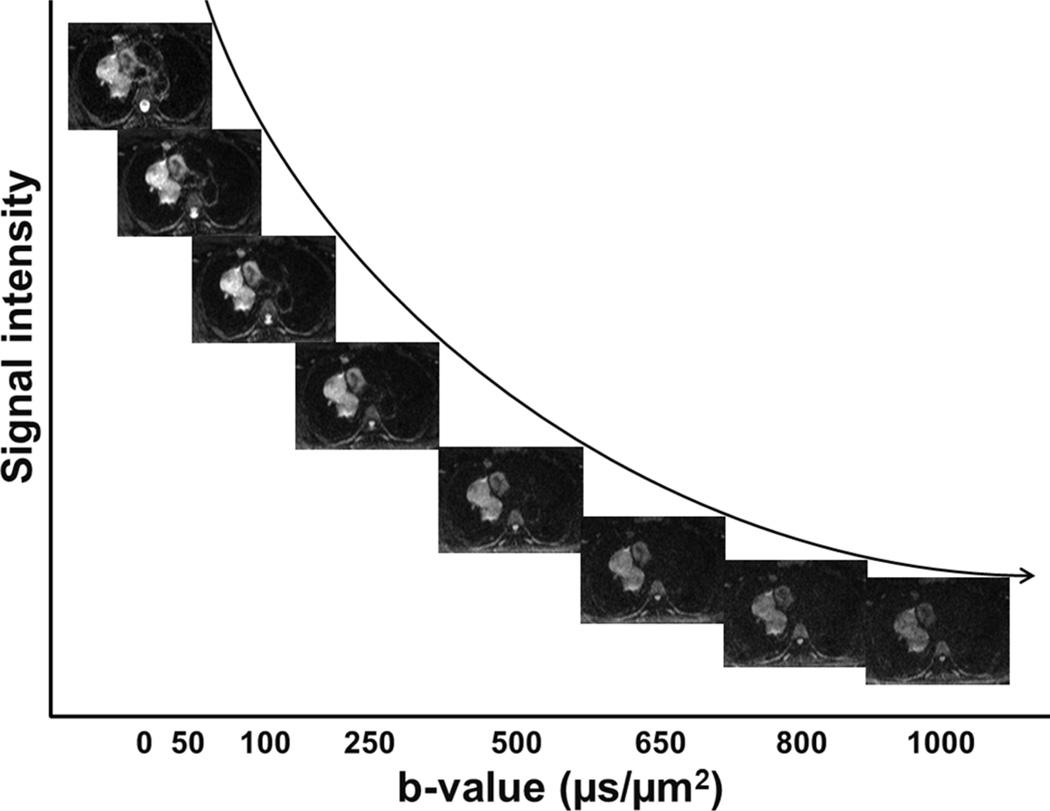
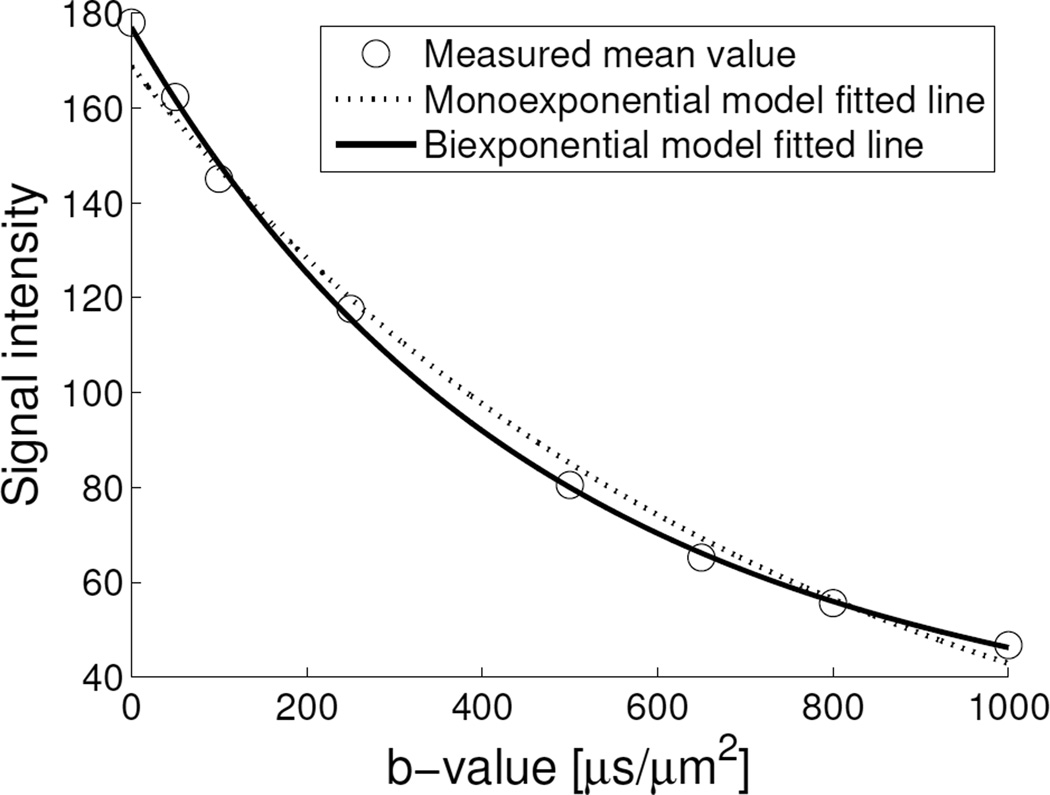
An example of the decay of signal with respect to b-value is shown in Fig. 1. The tissues with faster decay have greater ADC values. The tumour regions can be delineated on high b-value DW-MRI images. F test was done to examine whether the IVIM model gives, in general, a lower residual fit error to the active tumour volume S vs b-value than the monoexponential model. One pretreatment DW-MRI scan data of active tumour volume of each of the ten subjects were fitted by monoexponential and IVIM models. Using F test, we observed a significantly lower fit error by IVIM model to the active tumour volume S vs b-value than the monoexponential model for seven subjects at 5% significance level, marginally significant for one subject at 5–10% significance level, and not significant for two subjects (see an example in Fig. 2). Using all eight b-values, adjusted R2 for the IVIM and monoexponential model fittings for all 40 scans were 0.911±0.065 and 0.891±0.070, respectively. The IVIM model removes the effect of perfusion or pseudo-diffusion on diffusion. Hence, the ADC value obtained from IVIM fitting was considered as the reference-standard although IVIM assessment is commonly not performed in clinical settings.

Figure 1.

Figure 1

Open in a new tab

Illustration of DW-MRI signal decay of various types of tissues with respect to b-value. The labels in x-axis correspond to the b-values of the DW-MRI image above them. The curve represents the exponential decay of mean signal of the tumour region in arbitrary unit (not to scale) with respect to b-value.

Figure 2.

Figure 2

Open in a new tab

Plot of an active tumour volume mean signal intensity (S) vs b-value fitted by monoexponential (adjusted R2 = 0.9860) and biexponential, i.e. IVIM (adjusted R2 = 0.9977) models. Using F test, the IVIM model gave a significantly lower residual fit error to the signal vs b-value data of active tumour volume of this subject’s DW-MRI scan than the monoexponential model at 5% significance level. At low b-values, the signal decay originates from both perfusion (fast component) and diffusion (slow component), whereas at high b-values, mainly from diffusion.

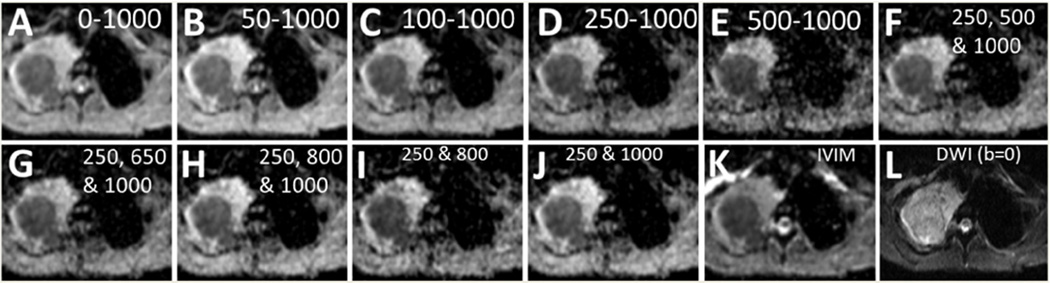
In addition to the values of the parameters S0 (baseline signal without decay due to diffusion) and D (i.e. ADC) that can be obtained by the monoexponential model, IVIM model fitting gives the values of f and D* by separating the perfusion and diffusion compartments as shown in the parametric maps in Fig. 3. The tumour region within the right lung is shown by the arrows in the ADCIVIM map. The lymph nodes near the primary tumour are also visible. Fig. 4 depicts an example of tumour, surrounded by non-malignant conditions likely atelectasis, normal lung tissues and other tissues in an axial slice seen in IVIM and monoexponential model ADC maps obtained by using various combinations of b-values, and a DW-MRI image for b = 0 µs/µm2. While all of the ADC maps shown are able to delineate the tumour and the surrounding atelectasis regions in the slice, the monoexponential maps starting with b-value = 500 µs/µm2 (panel E) and ending with 800 µs/µm2 (panel I) have high n oise compared to ADCIVIM which is also indicated by the intra-scan CV in Table 1.

Figure 3.

Figure 3

Open in a new tab

ADCIVIM, D*, f, S0 and coefficient of determination, R2, maps of an axial slice (from left to right) using IVIM model. Large value of R2 in tumour region (shown by white arrows in panel A) indicates that the IVIM model fits well the exponential DW-MRI signal decay with respect to b-values in the region. In normal lung tissues, the values of all parameters are generally low.

Figure 4.

Figure 4

Open in a new tab

ADC maps of an axial MRI slice showing active tumour using monoexponential model for 0–1000 (A), 50–1000 (B), 100–1000 (C), 250–1000 (D), 500–1000 (E), 250, 500 and 1000 (F), 250, 650 and 1000 (G), 250, 800 and 1000 (H), 250 and 800 (I), 250 and 1000 µs/µm2 b-value sets (J), and using IVIM model for the set of all eight b-values- 0, 50, 100, 250, 500, 650, 800 and 1000 µs/µm2 (K), and b 0 mage (no diffusion weighting) (L). High intra-slice CV within the tumour is observed n panels (E) and (I).

Table 1.

Comparison of apparent diffusion coefficient (ADC) values.

b-value seta Mean error relative
to ADCIVIMb (%)		 p-valuec Intra-scan
CVd (%)
0–1000 18.6 <0.001 18.6
50–1000 13.0 <0.001 19.1
100–1000 9.4 <0.001 19.8
250–1000 2.2 0.564 22.4e
500–1000 −7.8 <0.001 29.4
250, 500 and 1000 −0.13 0.402 23.1e
250, 650 and 1000 1.6 0.805 22.6e
250, 800 and 1000 3.5 0.113 21.9e
250 and 800 12.5 <0.001 24.9e
250 and 1000 1.3 0.994 22.7e
0–1000 (IVIM) - - 24.1
Open in a new tab
a

The b-value (in µs/µm2) sets were used for the monoexponential model except the last row which used IVIM model;

b

ADCIVIM represents the IVIM model ADC;

c

Two-tailed paired t-test with ADCIVIM mean values of the active tumour volumes of the scans;

d

CV, coefficient of variation;

e

Not significantly different intra-scan CV of ADC values of the active tumour volumes compared to that of IVIM (two-tailed paired t-test).

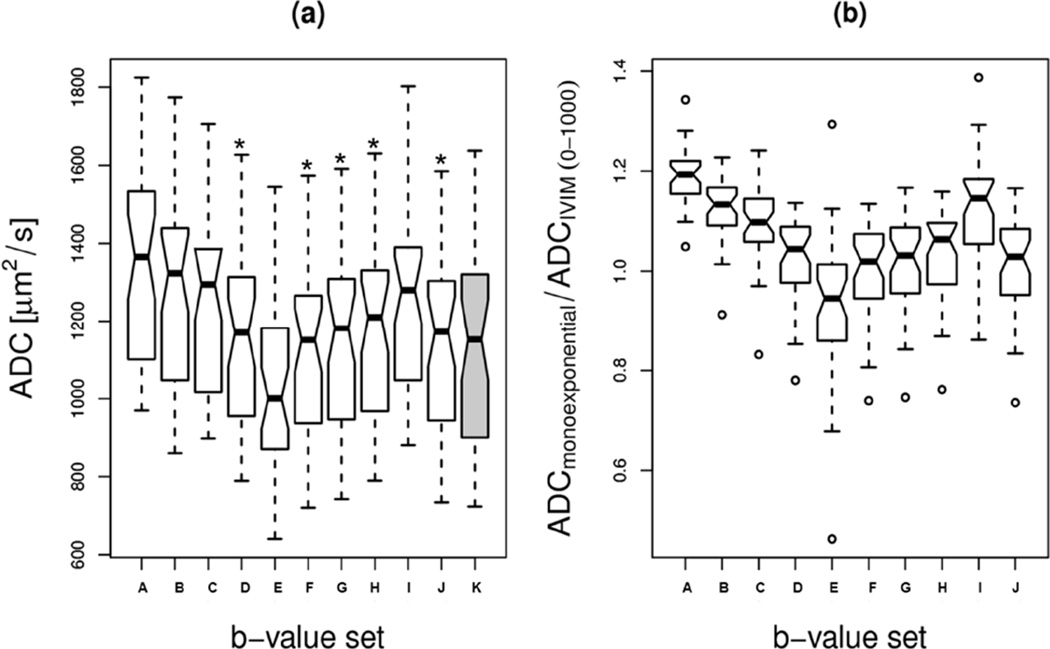
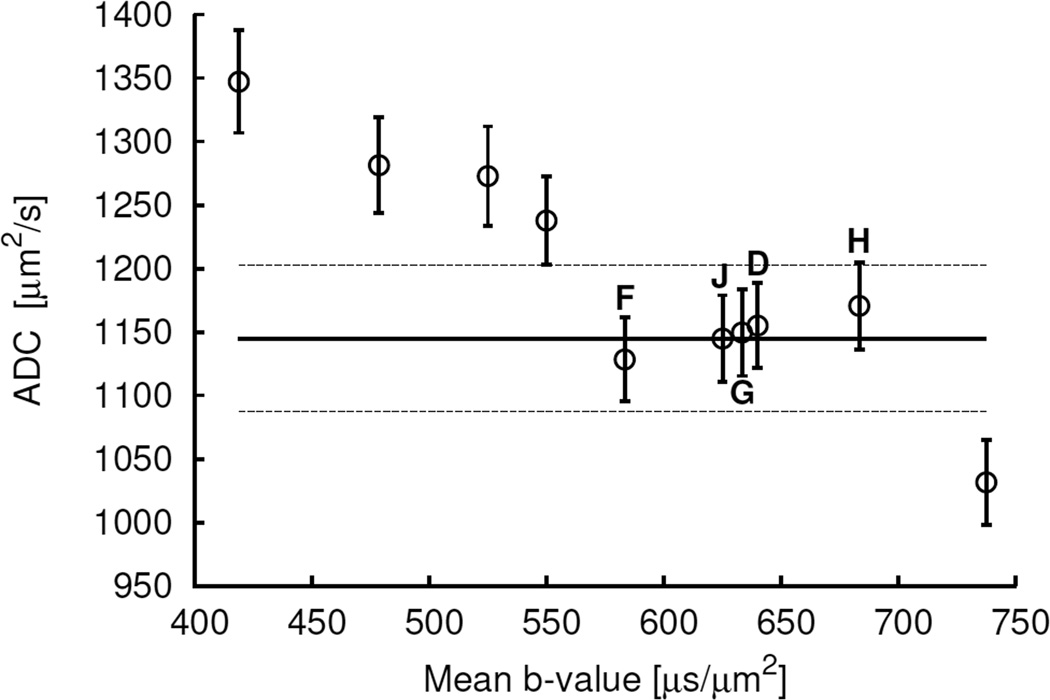
Mean ADCIVIM, D*, f, and D*/ADCIVIM values for active tumour volumes of the scans were in the range of 723–1,637 µm2/s, 6,983–45,143 µm2/s, 16.2–33.9%, and 6.3–38.6, respectively. The volume of the tumour within each of the DW-MRI scans had the range of 2.5–143.8 cm3. ADC values using monoexponential model for the b-value sets of 250 and 1000; 250, 500 and 1000; 250, 650 and 1000; 250, 800 and 1000; and 250–1000 µs/µm2 only shown in Fig. 5(a) were not significantly different from ADCIVIM (p > 0.05, paired t-test) (Table 1). The intra-scan CV values for them were comparable to that for IVIM (Table 1). The monoexponential mean ADC values for the b-value sets of 250–1000; 250 and 1000; 250, 500 and 1000; 250, 650 and 1000; 250, 800 and 1000 µs/µm2 were within 5% of the reference-standard ADCIVIM (Fig. 6). The mean monoexponential ADC value decreased with the increase of the mean b-value used to compute ADC (Fig. 6). The intra-scan variation of ADC values for 500–1000 µs/µm2 set relative to ADCIVIM was particularly high due to computation from comparatively low signal-to-noise ratio (SNR) data sets. From a sample of 19 DW-MRI scans, the mean ADC value of the necrotic region for the set of all eight b-values was 11.3% greater than the corresponding mean ADC value of the active tumour region, whereas that for the two b-value set- 250 and 1000 µs/µm2 was 11.7% greater than the corresponding mean ADC value of the active tumour region. However, the mean values of the normalized ADC values (obtained by dividing by the corresponding IVIM values) of the necrotic regions for these two sets of b-values differed by 0.6 and 0.1%, respectively from the mean of normalized ADC value for the active tumour. These values indicate that the features shown in Fig. 5(b) may robustly apply to the necrotic region or whole tumour including both active and necrotic regions also.

Figure 5.

Figure 5

Open in a new tab

ADC values (a), and normalized ADC values relative to ADCIVIM (b) of active tumours from 40 DW-MRI scans of (A) 0–1000, (B) 50–1000, (C)100–1000, (D) 250–1000, (E) 500–1000, (F) 250, 500 and 1000, (G) 250, 650 and 1000, (H) 250, 800 and 1000, (I) 250 and 800, (J) 250 and 1000 µs/µm2 b-value sets. The b-value set (K) corresponding to gray shaded box in panel (a) represents the 0–1000 µs/µm2 set for reference-standard ADCIVIM values. The star symbol represents the ADC values that were not significantly different from the ADCIVIM values (p > 0.05, paired t-test). The small open circles in panel (b) represent the individual data points that are either below Q1 − 1.5×IQR or above Q3 + 1.5×IQR, where “interquartile range (IQR)” is the width of the box, i.e., IQR = third quartile (Q3) - first quartile (Q1).

Figure 6.

Figure 6

Open in a new tab

Plot of the mean (±SE) values of the monoexponential ADC values of active tumour volumes of scans versus mean b-values. The horizontal solid line represents the mean of the reference-standard IVIM ADC values. The horizontal dashed lines represent ±5% values of the mean IVIM ADC value. The data points within the dashed lines from left to right represent the values corresponding to the b-value sets of 250, 500 and 1000; 250 and 1000; 250, 650 and 1000; 250–1000; and 250, 800 and 1000 µs/µm2, i.e. the b-value sets F, J, G, D and H, respectively in Fig. 4 and 5.

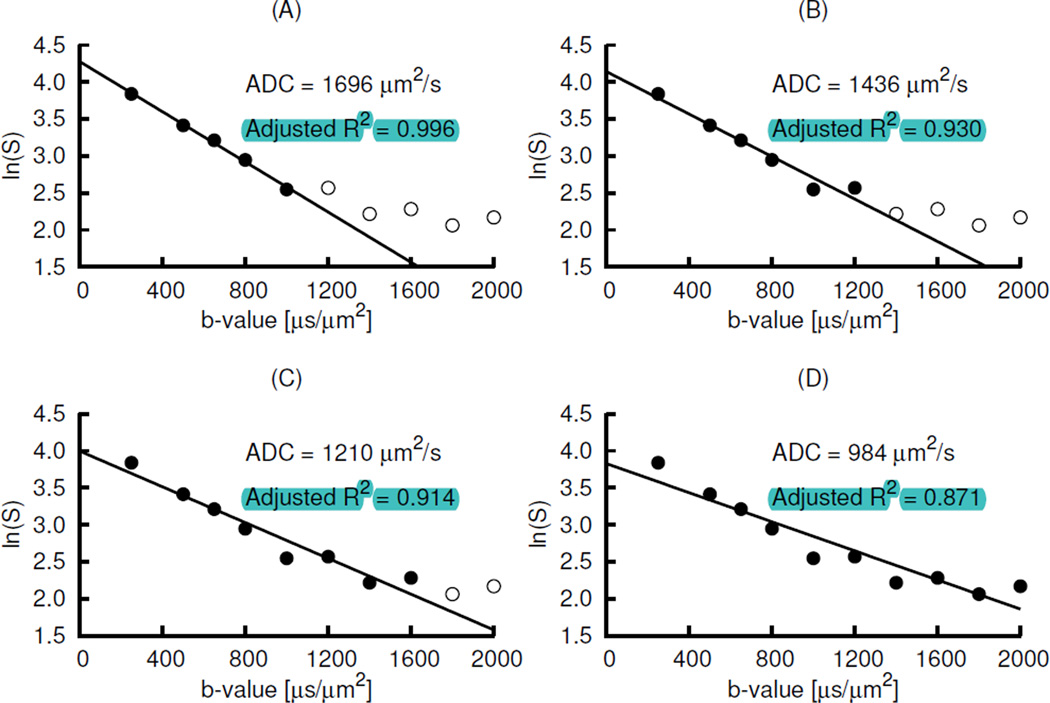
An example of the effect of high b-values in the noise floor on the ADC computation is shown in Fig. 7. The natural logarithm of signal intensity (ln(S)) of 3 × 3 tumour region voxels with the total volume of ~ 6 × 6 × 6 mm3 of the synthesized data from the simulation of a subject’s tumour volume having comparatively high mean values of ADCIVIM, D* and f, and corrupted with Rician noise distribution of σ = 5, was plotted against b-value. In the panels of the figure, the data represented by the filled circles were fitted by using monoexponential diffusion model for b-values ≥250 µs/µm2. As shown in Fig. 7, the higher the highest b-value used, the lower were the ADC values. The inclusion of the signal intensity vs b-value at or near noise floor lowered both ADC value and adjusted R2 for the fitting. In this example of very high decay rate, the b-value of 1000 µs/µm2 was above the noise floor. It indicate d that the highest b-value of 1000 µs/µm2 is acceptable for the lung tumour avoiding the effect of noise floor on ADC computation.

Figure 7.

Figure 7

Open in a new tab

An example of the effect of the signal intensity (S) vs b-value data below or near noise floor. In the panels of the figure, the data represented by the filled circles of a data set obtained by the Rician noise simulation were fitted by using monoexponential diffusion model for b-values ≥ 250 µs/µm2. The ADC value is the negative of the slope. Panel D has much lower ADC than panel A. Similarly, panel D has lower adjusted R2 than panel A. The data represented by the open circles in panel B are almost below the noise floor.

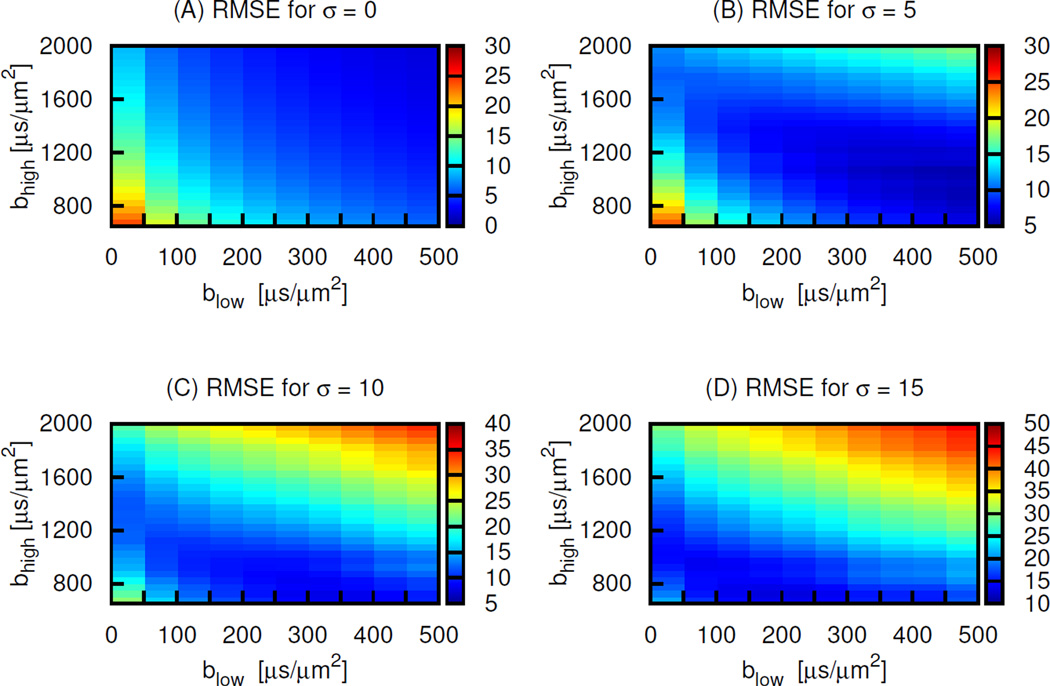
Using 2 b-value sets for various levels of Rician noise distribution, there were wide ranges of b-value sets giving small RMSE of ADC value relative to the ground truth ADCIVIM (Fig. 8). The band of sets with small errors moved from high values of both blow and bhigh for the lowest noise level towards the lower values with the increase of the noise levels. The minimum error corresponding to the optimal sets increased with the noise level. The range of RMSE for σ = 5 in panel (B) was approximately 5–30 % whereas that for σ = 15 in panel (D) was approximately 10–50 %. The RMSE for the pair of 250 and 1000 µs/µm2 in panel B, which represents approximately our imaging noise level, is ~8 % and fell in the low RMSE region.

Figure 8.

Figure 8

Open in a new tab

Plots of the RMSE of the ADC values from the simulated DW-MRI data with Rician noise distribution with (A) σ = 0, (B) 5, (C) 10 and (D) 15 relative to the reference-standard ADCIVIM vs the blow (x-axis) and bhigh (y-axis) for the b-value pairs used for the estimation of the ADC. The color depths represent the values of RMSE in percent.

4. Discussion

To the best of our knowledge, this is the first study to determine the optimal combinations of b-values to obtain ADC free from perfusion in lung tumours in the clinical setting. Malignant tumours are usually characterized by increased cellularity, larger nuclei with more abundant macromolecular proteins, a larger nuclear/cytoplasmic ratio and less extracellular space relative to normal tissue. Because of these characteristics, the diffusion of water molecules in malignant tumours is restricted, resulting in decreased ADC (Henzler et al 2010). Accordingly, ADC values for benign tumours have been reported as higher than that for malignant tumour in various sites such as liver (Taouli et al 2003, Filipe et al 2013), prostrate (Kitajima et al 2012), ovary (Uehara et al 2012), and thyroid (Ilica et al 2013). As shown in Fig. 4, we observed the ADC values of non-malignant conditions neighboring the tumour (e.g., atelectasis, pneumonia, mucoid impaction) higher than that of the active tumour region. There was also a good contrast between tumour and normal lung parenchyma in ADC maps with tumour ADC values several times greater. The ADC values of the necrotic region were higher than that of the active tumour region, possibly due to larger extracellular space in the necrotic region. DW-MRI may assist in target definition in the treatment planning. DW-MRI also has the potential to provide a surrogate biomarker of treatment response in lung cancers (Weiss et al 2013). ADC values within tumour volume increase after radiation treatment, likely due to increase in extracellular space and therefore increased diffusion as a result of cell killing (Lambrecht et al 2014).

The microscopic motion within a voxel in tissue includes not only restricted molecular diffusion of water but also microcirculation of blood (perfusion). Due to the random organization of the capillaries in a voxel, the microcirculation of blood is considered as incoherent motion (Le Bihan et al 1986, Colagrande et al 2006). The IVIM model in DW-MRI considers both types of motion, and has the potential to provide information about both the cellularity and perfusion of tumours (Le Bihan and Turner 1992, Federau et al 2014, Le Bihan et al 1988, Chenevert et al 1991). Although our signal attenuation data for lung tumours vs b-value is better fitted by the IVIM model, the monoexponential model is desirable in the clinical setting due to simplicity and shorter time period of acquisition and post-processing. This study focused on diffusion (slow component) which has a potential as a biomarker for tumour cellularity.

There are a number of previous DW-MRI studies for optimizing b-values for purposes different from our study. Kingsley and Monahan (2004) studied the b-values for the optimization of the CNR for both diffusion-weighted signal intensity and ADC when evaluating ischemic stroke. Bernardin et al (2014) studied intra- and inter-observer repeatability of ADCs acquired from free-breathing DW-MRI in malignant lung tumours delineated on the DW-MRI images of b = 800 µs/µm2 with assumed high CNR. Peng et al (2014) investigated the effect of b-values on ADC values to differentiate the prostate tumour from normal tissue, but did not compare the monoexponential ADC values with perfusion-insensitive ADCIVIM. Using linearized simplified equation derived by approximation for high b-values from IVIM model, Pang et al (2013) computed the IVIM parmeters- f and D for prostate cancer detection. Their results showed that both f and D depended heavily on the b-values, and those derived without the highest b-value of 750 µs/µm2 in the study correlated best with the results from DCE-MRI studies. Tamura et al (2014) recommended a b-value of approximately 1400–1500 µs/µm2 for optimizing breast tumour detectability. Tang et al (2007) found 300 µs/µm2 as the optimized b-value for the differential diagnosis of benign and malignant vertebral fractures by comparing the ADC values between them. None of these studies investigated optimal b-values selection for obtaining the monoexponential ADC values that are comparable to ADCIVIM. Our study attempted to obtain the ADC values of heterogeneous lung tumours with high accuracy, whereas the non-tumour studies by Brihuega-Moreno et al (2003), Alexander (2008) and Caan et al (2010) focused mainly on other topics such as the precision of the ADC values or other related parameters by adopting mainly Cramér-Rao lower bound on the variance of the model parameters.

The decrease of the tumour ADC values in lung tumour with the increase of the mean b-value is in agreement of the values reported by Colagrande et al (2006) for different types of tissues in liver, and by Zhang et al (2010) for whole renal parenchyma, cortex and medulla. The substantial variability among the reported monoexponential ADC values of a tissue type, due mainly to the b-values that were used, compels the investigation and standardization in selection of b-values. Sensitivity to diffusion-based contrast is primarily controlled by the b-value with the appropriate b-value range dependent on tissue diffusion properties, SNR, and the need to suppress perfusion effects effectively at low b-values(Padhani et al 2009). The calculation of the tissue ADC can be more accurate when starting with even higher b-values to omit the contribution of flow and microvascular effects. Blood flow signal is rapidly attenuated at low b-values (e.g., b < 100–150 µs/µm2) and may be mistakenly attributed to diffusion. The calculation of ADC from very high b-values only will be susceptible to significant amount of noise, and lack of leverage in fitting. The ADC maps obtained from the sets with lowest b-value = 500 µs/µm2 were substantially noisy in our study. By choosing the lower b-value of 250 µs/µm2 and the upper b-value of 1000 µs/µm2 rather than 800 µs/µm2, the monoexponential ADC value was close to ADCIVIM in this study. Intra-scan CVs of ADC values for these b-value sets were comparable to that of ADCIVIM, and hence the noise superimposed on the heterogeneity of the active tumour volumes on the ADC maps for these sets were comparable to that of ADCIVIM. For lung tumours, this result refines the suggestion of b-values set in Padhani et al (2009).

The Rician noise simulation study suggested that the b-values of optimal sets may change across the different regions and subjects. It also suggested that the b-values in the vicinity of these experimental best b-values can be used with error within an acceptable limit. In addition, optimal sets will have lower values of both blow and bhigh as the noise level increases. The b-value pairs for the minimum errors of the computed ADC of active tumour region appear to cluster, whilst necrotic region results are more diffuse. Thus, active tumour and necrotic regions should be segmented for using a pair of b-values to calculate ADC. Considering our simulation results together with the simulation results in Freiman et al (2012), we will include the b-values greater than 1000 µs/µm2 for further analysis in our future DW-MRI scans. In general, very low values of blow (close to 0 µs/µm2) are not desirable to avoid the effect of perfusion, and very high values of bhigh (close to 2000 µs/µm2) are not desirable to avoid the effect of noise floor. The maximum b-value should be set such that the signals recorded at that b-value are adequately above the noise floor. This maximum b-value to be used depends on the SNR achievable for the target tissues and the water diffusion coefficient of these tissues - the lower the diffusion value, the higher the b-value achieved before the signal approaches the noise floor (Thoeny and Ross 2010).

The inclusion of data for b-values beyond the noise floor lowers both the computed ADC value and adjusted R2 for monoexponential diffusion model fitting. In this study, the signals in the tumour region for the maximum b-value of 1000 µs/µm2 were above the noise floor. With EPI, integrated parallel imaging, NEX = 2, TR = 1200 ms, TE = 74 ms, 2 b-values of 250 and 1000 µs/µm2, and other parameters just like in this study, it may be feasible to perform DW-MRI in a single breat h-hold with total scan time of ~21 s, reducing the scan time in comparison to respiratory triggered free breathing, and potentially reducing the impact of free-breathing artifacts on ADC calculation. This study suggests robust and clinically feasible sets of b-values for reducing the contribution of perfusion. The effect of varying static magnetic field strengths, protocol variables, and systems from different vendors was not investigated, but is anticipated to be small especially if SNR is close to that of this study, i.e., if potential SNR increase due to using 3T is traded for increased scan speed rather than increased image quality.

5. Conclusions

ADC values of a two b-value set- 250 and 1000 µs/µm2, and the three b-value sets with 250, 1000 µs/µm2 and an intermediate value all approached the perfusion-insensitive reference standard ADCIVIM value, with a relative noise level comparable to that of ADCIVIM. Any of these sets can be used to obtain the perfusion-insensitive ADC values in non-small cell lung tumours using comparatively short scan and post-processing times. The Rician noise simulation suggested that the b-values in the vicinity of these experimental best b-values can be used with error within an acceptable limit. Very low b-values introduce bias (due to the effect of perfusion that is not modeled by the monoexponential model) whereas very high b-values are not desirable since signals recorded at high b-values have a low SNR (leading to a low precision). The optimal set of b-values depends on many factors, including the noise level. The sets of b-values recommended should therefore be interpreted with care. This study provides some insight and guidelines to choose optimal b-value sets. This study aids to establish DW-MRI as a sensitive imaging method to detect structural and functional changes in lung cancer. The results of this study will help guide future use of DW-MRI in lung cancer treatment.

Acknowledgments

This work was supported by Virginia Commonwealth University Massey Cancer Centre pilot project A35242 (EW). Disclosures: Varian Medical Systems and Philips Oncology Systems, UpToDate (EW); NIH grant R01 CA166119 (GDH and EW).

The authors thank Nitai D. Mukhopadhyay, Ph.D. for useful suggestions regarding statistical analysis and fitting of the MRI data of our study. The authors thank Linda Walker also for her valuable support for arrangement of MRI scans.

Footnotes

This work was presented in part at the American Association of Physicists in Medicine (AAPM) 56th Annual Meeting in 2014, Austin, TX, USA, and at AAPM 57th Annual Meeting in 2015, Anaheim, CA, USA.

There are no conflicts of interest.

References

  1. Alexander DC. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue-microstructure features. Magn. Reson. Med. 2008;60:439–448. doi: 10.1002/mrm.21646. [DOI] [PubMed] [Google Scholar]
  2. Barnwell JD, Smith JK, Castillo M. Utility of navigator-prospective acquisition correction technique (PACE) for reducing motion in brain MR imaging studies. AJNR, Am. J. Neuroradiol. 2007;28:790–791. [PMC free article] [PubMed] [Google Scholar]
  3. Bernardin L, Douglas NH, Collins DJ, Giles SL, O’Flynn EA, Orton M, deSouza NM. Diffusion-weighted magnetic resonance imaging for assessment of lung lesions: repeatability of the apparent diffusion coefficient measurement. Eur. Radiol. 2014;24:502–511. doi: 10.1007/s00330-013-3048-y. [DOI] [PubMed] [Google Scholar]
  4. Brihuega-Moreno O, Heese FP, Hall LD. Optimization of diffusion measurements using Cramer-Rao lower bound theory and its application to articular cartilage. Magn. Reson. Med. 2003;50:1069–1076. doi: 10.1002/mrm.10628. [DOI] [PubMed] [Google Scholar]
  5. Caan MW, Khedoe HG, Poot DH, den Dekker AJ, Olabarriaga SD, Grimbergen KA, van Vliet LJ, Vos FM. Estimation of diffusion properties in crossing fiber bundles. IEEE Trans. Med. Imaging. 2010;29:1504–1515. doi: 10.1109/TMI.2010.2049577. [DOI] [PubMed] [Google Scholar]
  6. Chenevert TL, Pipe JG, Williams DM, Brunberg JA. Quantitative measurement of tissue perfusion and diffusion in vivo. Magn. Reson. Med. 1991;17:197–212. doi: 10.1002/mrm.1910170123. [DOI] [PubMed] [Google Scholar]
  7. Colagrande S, Carbone SF, Carusi LM, Cova M, Villari N. Magnetic resonance diffusion-weighted imaging: extraneurological applications. Radiol. Med. 2006;111:392–419. doi: 10.1007/s11547-006-0037-0. [DOI] [PubMed] [Google Scholar]
  8. Eccles CL, Haider EA, Haider MA, Fung S, Lockwood G, Dawson LA. Change in diffusion weighted MRI during liver cancer radiotherapy: preliminary observations. Acta Oncol. 2009;48:1034–1043. doi: 10.1080/02841860903099972. [DOI] [PubMed] [Google Scholar]
  9. Federau C, Meuli R, O’Brien K, Maeder P, Hagmann P. Perfusion measurement in brain gliomas with intravoxel incoherent motion MRI. AJNR, Am. J. Neuroradiol. 2014;35:256–262. doi: 10.3174/ajnr.A3686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Filipe JP, Curvo-Semedo L, Casalta-Lopes J, Marques MC, Caseiro-Alves F. Diffusion-weighted imaging of the liver: usefulness of ADC values in the differential diagnosis of focal lesions and effect of ROI methods on ADC measurements. Magma. 2013;26:303–312. doi: 10.1007/s10334-012-0348-1. [DOI] [PubMed] [Google Scholar]
  11. Freiman M, Voss SD, Mulkern RV, Perez-Rossello JM, Callahan MJ, Warfield SK. In vivo assessment of optimal b-value range for perfusion-insensitive apparent diffusion coefficient imaging. Med. Phys. 2012;39:4832–4839. doi: 10.1118/1.4736516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995;34:910–914. doi: 10.1002/mrm.1910340618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Haack S, Pedersen EM, Jespersen SN, Kallehauge JF, Lindegaard JC, Tanderup K. Apparent diffusion coefficients in GEC ESTRO target volumes for image guided adaptive brachytherapy of locally advanced cervical cancer. Acta Oncol. 2010;49:978–983. doi: 10.3109/0284186X.2010.500619. [DOI] [PubMed] [Google Scholar]
  14. Hagmann P, Jonasson L, Maeder P, Thiran JP, Wedeen VJ, Meuli R. Understanding diffusion MR imaging techniques: from scalar diffusion-weighted imaging to diffusion tensor imaging and beyond. Radiographics. 2006;26(Suppl 1):S205–S223. doi: 10.1148/rg.26si065510. [DOI] [PubMed] [Google Scholar]
  15. Henzler T, Schmid-Bindert G, Schoenberg SO, Fink C. Diffusion and perfusion MRI of the lung and mediastinum. Eur. J. Radiol. 2010;76:329–336. doi: 10.1016/j.ejrad.2010.05.005. [DOI] [PubMed] [Google Scholar]
  16. Ilica AT, Artas H, Ayan A, Gunal A, Emer O, Kilbas Z, Meric C, Atasoy MM, Uzuner O. Initial experience of 3 Tesla apparent diffusion coefficient values in differentiating benign and malignant thyroid nodules. J. Magn. Reson. Imaging. 2013;37:1077–1082. doi: 10.1002/jmri.23913. [DOI] [PubMed] [Google Scholar]
  17. Kallehauge JF, Tanderup K, Haack S, Nielsen T, Muren LP, Fokdal L, Lindegaard JC, Pedersen EM. Apparent Diffusion Coefficient (ADC) as a quantitative parameter in diffusion weighted MR imaging in gynecologic cancer: Dependence on b-values used. Acta Oncol. 2010;49:1017–1022. doi: 10.3109/0284186X.2010.500305. [DOI] [PubMed] [Google Scholar]
  18. Kingsley PB, Monahan WG. Selection of the optimum b factor for diffusion-weighted magnetic resonance imaging assessment of ischemic stroke. Magn. Reson. Med. 2004;51:996–1001. doi: 10.1002/mrm.20059. [DOI] [PubMed] [Google Scholar]
  19. Kitajima K, Takahashi S, Ueno Y, Yoshikawa T, Ohno Y, Obara M, Miyake H, Fujisawa M, Sugimura K. Clinical utility of apparent diffusion coefficient values obtained using high b-value when diagnosing prostate cancer using 3 Tesla MRI: comparison between ultra-high b-value (2000 s/mm2) and standard high b-value (1000 s/mm2) J. Magn. Reson. Imaging. 2012;36:198–205. doi: 10.1002/jmri.23627. [DOI] [PubMed] [Google Scholar]
  20. Lambrecht M, Van Herck H, De Keyzer F, Vandecaveye V, Slagmolen P, Suetens P, Hermans R, Nuyts S. Redefining the target early during treatment. Can we visualize regional differences within the target volume using sequential diffusion weighted MRI? Radiother. Oncol. 2014;110:329–334. doi: 10.1016/j.radonc.2013.09.023. [DOI] [PubMed] [Google Scholar]
  21. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168:497–505. doi: 10.1148/radiology.168.2.3393671. [DOI] [PubMed] [Google Scholar]
  22. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161:401–407. doi: 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
  23. Le Bihan D, Turner R. The capillary network: a link between IVIM and classical perfusion. Magn. Reson. Med. 1992;27:171–178. doi: 10.1002/mrm.1910270116. [DOI] [PubMed] [Google Scholar]
  24. Levenberg K. A method for the solution of certain non-Linear problems in least squares. The Quarterly of Applied Mathematics. 1944;2:164–168. [Google Scholar]
  25. Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Indust. Appl. Math. 1963;11:431–441. [Google Scholar]
  26. Padhani AR, Liu G, Koh DM, Chenevert TL, Thoeny HC, Takahara T, Dzik-Jurasz A, Ross BD, Van Cauteren M, Collins D, Hammoud DA, R ustin GJ, Taouli B, Choyke PL. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: consensus and recommendations. Neoplasia. 2009;11:102–125. doi: 10.1593/neo.81328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pang Y, Turkbey B, Bernardo M, Kruecker J, Kadoury S, Merino MJ, Wood BJ, Pinto PA, Choyke PL. Intravoxel incoherent motion MR imaging for prostate cancer: an evaluation of perfusion fraction and diffusion coefficient derived from different b-value combinations. Magn. Reson. Med. 2013;69:553–562. doi: 10.1002/mrm.24277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Peng Y, Jiang Y, Antic T, Sethi I, Schmid-Tannwald C, Eggener S, Oto A. Apparent diffusion coefficient for prostate cancer imaging: impact of B values. AJR, Am. J. Roentgenol. 2014;202:W247–W253. doi: 10.2214/AJR.13.10917. [DOI] [PubMed] [Google Scholar]
  29. Rice SO. Mathematical analysis of random noise. Bell. System. Tech. J. 1944;23:282. [Google Scholar]
  30. Rodbard D. Statistical quality control and routine data processing for radioimmunoassays and immunoradiometric assays. Clin. Chem. 1974;20:1255–1270. [PubMed] [Google Scholar]
  31. Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time Dependent Field Gradient. J. Chem. Phys. 1965;42:288–292. [Google Scholar]
  32. Tamura T, Murakami S, Naito K, Yamada T, Fujimoto T, Kikkawa T. Investigation of the optimal b-value to detect breast tumours with diffusion weighted imaging by 1.5-T MRI. Cancer Imaging. 2014;14:11. doi: 10.1186/1470-7330-14-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tang G, Liu Y, Li W, Yao J, Li B, Li P. Optimization of b value in diffusion-weighted MRI for the differential diagnosis of benign and malignant vertebral fractures. Skeletal Radiol. 2007;36:1035–1041. doi: 10.1007/s00256-007-0358-7. [DOI] [PubMed] [Google Scholar]
  34. Taouli B, Koh DM. Diffusion-weighted MR imaging of the liver. Radiology. 2010;254:47–66. doi: 10.1148/radiol.09090021. [DOI] [PubMed] [Google Scholar]
  35. Taouli B, Vilgrain V, Dumont E, Daire JL, Fan B, Menu Y. Evaluation of liver diffusion isotropy and characterization of focal hepatic lesions with two single-shot echo-planar MR imaging sequences: prospective study in 66 patients. Radiology. 2003;226:71–78. doi: 10.1148/radiol.2261011904. [DOI] [PubMed] [Google Scholar]
  36. Thoeny HC, Ross BD. Predicting and monitoring cancer treatment response with diffusion-weighted MRI. J. Magn. Reson. Imaging. 2010;32:2–16. doi: 10.1002/jmri.22167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Uehara T, Takahama J, Marugami N, Takahashi A, Takewa M, Itoh T, Kitano S, Nakagawa H, Kichikawa K. Visualization of ovarian tumours using 3T MR imaging: diagnostic effectiveness and difficulties. Magn. Reson. Med. Sci. 2012;11:171–178. doi: 10.2463/mrms.11.171. [DOI] [PubMed] [Google Scholar]
  38. Weiss E, Ford JC, Olsen K, Hugo GD. Diffusion-weighted MRI for response assessment during radiation therapy of lung cancer. Int. J. Radiat. Oncol. Biol. Phys. 2013;87:S15–S16. [Google Scholar]
  39. Zhang JL, Sigmund EE, Chandarana H, Rusinek H, Chen Q, Vivier PH, Taouli B, Lee VS. Variability of renal apparent diffusion coefficients: limitations of the monoexponential model for diffusion quantification. Radiology. 2010;254:783–792. doi: 10.1148/radiol.09090891. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES