Single-Isocenter Multiple-Target SRS: Risk of Compromised Coverage

Abstract

Purpose

To determine the dosimetric effects of rotational errors on target coverage using volumetric modulated arc therapy (VMAT) for multi-target stereotactic radiosurgery (SRS).

Methods and Materials

This retrospective study includes 50 SRS cases, each with 2 intracranial planning target volumes (PTVs). Both PTVs were planned for simultaneous treatment to 21 Gy using a single-isocenter, non-coplanar VMAT SRS technique. Rotational errors of 0.5°, 1.0°, and 2.0° were simulated about all axes. The dose to 95% of the PTV (D95) and the volume covered by 95% of the prescribed dose (V95) were evaluated using multivariate analysis to determine how PTV coverage is related to PTV volume, PTV separation, and rotational error.

Results

At 0.5° rotational error, D95 values and V95 coverage rates were ≥ 95% in all cases. For rotational errors of 1.0°, 7% of targets had D95 and V95 values below 95%. Coverage worsened substantially when the rotational error increased to 2.0°: D95 and V95 values were > 95% for only 63% of the targets. Multivariate analysis showed that PTV volume and distance to isocenter were strong predictors of target coverage.

Conclusions

The effects of rotational errors on target coverage were studied across a broad range of SRS cases. In general, the risk of compromised coverage increases with decreasing target volume, increasing rotational error and increasing distance between targets. Multivariate regression models from this study may be used to quantify the dosimetric effects of rotational errors on target coverage given patient-specific input parameters of PTV volume and distance to isocenter.

Introduction

Volumetric modulated arc therapy (VMAT) has been used for linac-based stereotactic radiosurgery (SRS), allowing for multiple targets to be treated simultaneously using a single plan with one isocenter [1, 2]. VMAT is able to achieve highly conformal dose distributions through the use of non-coplanar arcs and the simultaneous variation of MLC leaf positions, dose rate, and gantry rotation speed during treatment delivery [1, 2]. These prior studies have investigated the treatment planning aspects of multi-target single-isocenter VMAT SRS. An advantage of treating multiple targets simultaneously is the shortened treatment time, which may reduce adverse dosimetric effects due to intra-fraction motion [3]. The ability to track and correct for intra-fraction motion may reduce dosimetric errors for situations where an unacceptable level of patient motion is detected; however, not all clinics have this technology and this approach involves the tradeoff of additional treatment time. In general, reduced treatment times are advantageous provided that quality is not compromised. For many busy clinical departments, the reduced treatment time of VMAT is a substantial advantage when compared to traditional IMRT treatments [4]. Increased efficiency allows for a greater number of patients to be treated in a fixed amount of time or conversely the same number of patient to be treated in a shorter amount of time.

However, there is a tradeoff to treating multiple targets simultaneously as opposed to treating each target independently with a separate plan. When targets are treated independently, each plan isocenter is centered on a target and imaging-based alignment can focus primarily on that region of interest. Under these conditions, rotational errors up to a few degrees typically have a minimal dosimetric effect [3]. This robustness against rotational errors means that acceptable patient positioning may be achieved by translating the couch in three dimensions, which is advantageous given that many radiation therapy couches can only correct for a rotation about the couch vertical axis, commonly referred to as the yaw, but not for rotations such as pitch, the rotation about the lateral couch axis, and roll, the rotation about the longitudinal couch axis. In contrast, multi-target, single-isocenter SRS treatments are not as robust against rotational errors because at least one target is necessarily offset from the point of rotation. The amount of target displacement increases in proportion to its distance from the point of rotation, which results in a greater dosimetric effect.

Setup errors are important considerations in both framed-based and frameless SRS, and setup errors may vary between the two techniques [5]. This current study is based on the rotational errors observed in frameless SRS patients at several instances during the treatment process. Pretreatment imaging prior to rotational corrections in one frameless SRS study showed that the largest rotational error about any one axis was 1.7° ± 0.8°, maximum 3° [3]. Immediately after using in-room imaging in conjunction with a custom mount for six degree-of-freedom alignment to correct for initial setup errors, confirmation imaging has shown residual rotational errors about each axis of 0.3° ± 0.2°, maximum 1.3° [6]. Intra-fraction rotations about each axis were within 0.3° at one standard deviation, though outliers > 1.0° have been reported [7]. These findings are consistent with a prior study that specifically evaluated setup errors of non-isocentric stereotactic treatments. The dosimetric effects of rotational errors were evaluated for only two test cases, and the authors point out that the dosimetric results are not generalizable because of confounding factors including the size of the lesion [8].

The purpose of the current study is to determine the dosimetric effects of rotational errors on multi-target single-isocenter VMAT frameless SRS treatments. A retrospective multivariate analysis was performed across a large patient cohort to characterize target coverage as a function of target size, distance from the point of rotation, and the degree of rotational error. From this analysis, models of target coverage were developed that may be used to quantify the dosimetric consequences of rotational errors.

Methods and Materials

Fifty consecutive patient cases, each with at least two intracranial lesions, were selected retrospectively from our radiosurgery program with approval from the institutional review board. Only two lesions per case were evaluated in this study. Cases were anonymized. In total there were 100 planning target volumes (PTVs). All PTVs had been treated to ≥ 21 Gy. PTV volumes and the distance between PTV centroids were recorded for each case.

Single-isocenter VMAT plans were created in Eclipse Version 10 [Varian, Palo Alto, CA, USA] by a board certified medical physicist who previously planned over 100 SRS cases. For each case, the plan isocenter was positioned midway between PTV centroids. The midpoint was defined as the average of coordinate of the PTV centroids. Non-coplanar arcs spanning > 300° in total arc length were spread over the superior 2π. The principles of island blocking were considered when designing gantry and collimator angles to improve plan conformity and minimize normal tissue dose [2]. Normal tissues were further spared within the optimization using the normal tissue objective function and organ specific penalties. Maximum dose was kept below 12 Gy to the brainstem and 8 Gy to the optical apparatus. Maximum lens dose was < 2 Gy. The prescription dose of 21 Gy covered > 99% of each PTV while keeping the maximum PTV dose < 120% of the prescription. Dose was calculated on a 1 mm grid using the analytical anisotropic algorithm (AAA) with heterogeneity corrections [9].

Rotational errors were simulated about the plan isocenter using Velocity AI [Velocity Medical, Atlanta, GA, USA]. Rotations of 0.5°, 1.0°, and 2.0° were applied uniformly about three orthogonal axes. PTV dose metrics were obtained by sampling the rotated dose distribution. D95 - the percent isodose line relative to the prescription dose that covers 95% of the PTV -was recorded for each target and degree of rotation. Also recorded was V95, the volume of the PTV covered by 95% of the prescription dose. The D95 and V95 estimates from Velocity were compared with estimates from a dose calculation in Eclipse for 10 cases at the worst case scenario of a 2° rotation about each axis. For these 10 cases, the CT was rotated by 2° about each axis. Dose was calculated on the rotated CT in Eclipse using the same parameters as in the original VMAT plan. D95 and V95 values from Velocity and Eclipse were evaluated for agreement using the concordance correlation coefficient (CCC), which is consistent with the subsequent statistical analysis using Generalized estimating equations (GEE) [10-12].

Coverage rates were analyzed with respect to the target volume and distance to isocenter. GEEs were used to account for intra-patient correlations, e.g., dosimetric cross talk between PTVs in close proximity. At rotations of 0.5°, 1.0°, and 2.0°, the effects of volume and distance on D95 were characterized by multivariate linear regression:

$$\mathrm{D}95=a\cdot \text{PTV volume}[\text{cc}]+b\cdot \text{Distance to Isocenter}[\text{cm}]+c$$ (1)

Confidence intervals and p-values were calculated for the parameter estimates. The identity link for normally distributed outcome data, i.e. the linear model, was evaluated using a Kolmogorov-type supremum test applied to simulated realizations of the cumulative sum of residuals as a measure of goodness-of-fit [13].

V95 data were categorized at levels above and below 95%. For the data with a rotational error of 1.0° and 2.0°, multivariate logistic regression models were fit using GEE, modeling the probability of V95 coverage exceeding 95% given inputs of target volume and distance to isocenter:

$$log\left(\frac{p}{1-p}\right)=A\cdot \text{PTV volume}[cc]+B\cdot \text{Distance to Isocenter}[\text{cm}]+c$$ (2)

Odds ratios, 95% confidence intervals (CIs), and p-values were reported to determine the association between target size and separation distance on V95. Receiver operating characteristic (ROC) curves were generated, which represent the model sensitivities and specificities for an assortment of cut-points in the model probabilities. The area under the ROC curve (AUC) was estimated. The analysis was performed using SAS 9.3 [SAS Institute, Cary, NC, USA] and R 2.15.1 [R Foundation for Statistical Computing, Vienna, Austria], and statistical significance was assessed at the 0.05 level. Figures were plotted in Matlab R2013b [MathWorks, Natick, MA, USA].

Results

Across the 50 cases and 100 lesions studied, the mean and standard deviation in PTV volumes were 0.96 ± 1.25 cc. Distances from the PTV centroid to the plan isocenter varied from a relatively small separation of 0.6 cm to 7.3 cm when targets were on opposite sides of the brain; mean distance and standard deviation were 3.53 ± 1.61 cm.

Dose estimates were investigated between Velocity and Eclipse. For the 10 cases where dose was estimated in both Velocity and Eclipse at the 2° rotation, D95 and V95 values were marginally higher in Velocity by 0.67 ± 1.3% and 0.67 ± 0.96% respectively. In a case with PTVs on opposite sides of the brain, each 7.3 cm from isocenter, the agreement of V95 values between Velocity and Eclipse was well within 1% for both PTVs: 71.2% vs 70.9% and 65.4% vs 65.0%. D95 values also agreed within 1% between Velocity and Eclipse for both PTVs: 70.0% vs 70.5% and 71.9% vs 71.4%. A statistical analysis of all D95 and V95 paired data points in Velocity and Eclipse demonstrated that for V95 the CCC was 0.995, and for D95 the CCC was 0.990. CCC values over 0.990 suggest almost perfect agreement [14]. Because of the agreement found between dose estimates from Velocity and Eclipse, the estimates from Velocity were used in subsequent analyses, which require far less computational time and effort.

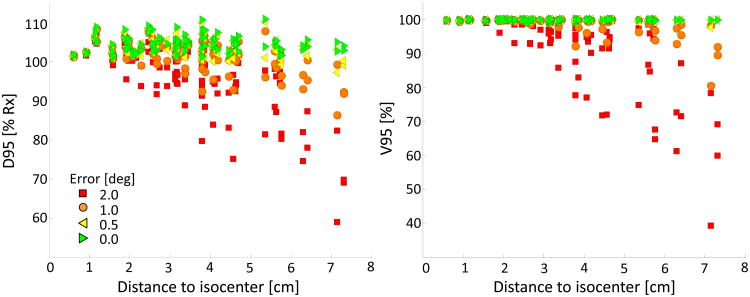
Target coverage was characterized at uniform rotations of 0.5°, 1.0° and 2.0° about all axes. D95 and V95 values are plotted as a function of distance to isocenter in Figure 1. When rotational errors were small, target coverage was similar to the ideal case of no rotation. At 0.5°, all targets had D95 and V95 values > 95%. For rotational errors of 1.0°, 7% of targets had D95 and V95 values below 95%. Only a small percentage of PTVs had D95 or V95 values < 90%, 1% and 2% respectively. Coverage worsened substantially when the rotational error increased to 2.0°. D95 and V95 values were > 95% for only 63% of the targets; coverage values were < 90% in approximately 20% of the cases. In general, target coverage worsened with increasing rotational error and distance to isocenter.

Fig 1.

D95 (left) and V95 (right) are plotted as a function of PTV distance to isocenter and stratified by rotational error. Ideal values for D95 and V95 are ≥ 100% and 100%, respectively.

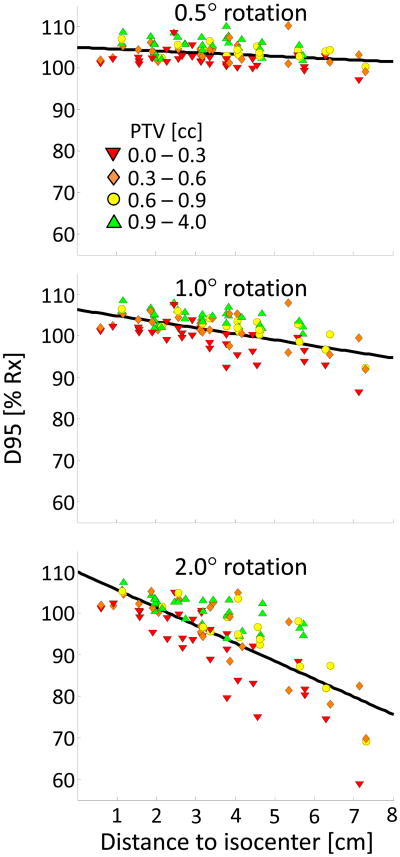
Multivariate GEE linear regression showed that target volume and distance to isocenter are strong predictors of D95; statistical significance was found at all rotations. Parameter estimates, confidence intervals, and p-values are reported in Table 1. A Kolmogorov-type supremum testing procedure showed adequate fit (p > 0.05) for the three linear GEE models at rotations of 0.5°, 1.0° and 2.0°. D95 values are plotted versus distance to isocenter and stratified by volume in Figure 2. The relative effects of distance and volume on coverage vary with rotational error. At 0.5°, D95 increases by twice as much per unit increase in volume [cc] as it decreases per unit increase in distance [cm]. At 1.0°, the rate by which D95 values increase is approximately the same per unit increase in volume or decrease in distance. At 2.0°, a unit change in distance has about twice the effect on D95 values as a unit change in volume. At a nominal distance, D95 values tend to be higher for larger targets and lower for smaller targets, and the difference is more pronounced at larger rotations.

Table 1.

GEE multivariate linear regression model (Eq 1) for predicting D95 as a percentage of the prescription dose. The model is parameterized at rotational errors of 0.5°, 1.0° and 2.0°. Variables are the volume of a PTV [cc] and the distance [cm] from a PTV centroid to the point of rotation. Parameter estimates related to volume (a) and distance (b) are reported with respective 95% confidence intervals and p-values. The constant (c) is also reported at each rotational level.

Rotation [°]	Parameter Estimate		95% CI	p-value
	a	0.84	0.45, 1.24	<0.0001
0.5°	b	-0.43	-0.76,-0.11	0.0088
	c	104.47
	a	1.28	0.81, 1.75	<0.0001
1.0°	b	-1.45	-1.86, -1.05	<0.0001
	c	105.50
	a	2.19	1.40, 2.97	<0.0001
2.0°	b	-4.30	-5.17, -3.44	<0.0001
	c	108.64

D95 GEE Linear Regression Model: D95[%] = a · PTV[cc] + b · Distance [cm] + c

Fig 2.

D95 values are plotted as a function of PTV distance to isocenter and stratified by PTV volume at rotations of 0.5°, 1.0°, and 2.0°. A trend line (Eq 1) is plotted as a guide for 0.6 cc PTVs.

In the multivariate logistic regression model, as shown in Fig. 3, both PTV volume and distance to isocenter are significantly associated with V95 coverage rates ≥ 95% at a rotational error of 1.0° and 2.0° (Table 2). At 0.5°, a model was not estimable because coverage rates exceeded 95% in all cases. In the corresponding ROC analysis, AUC values were 0.82 and 0.87 respectively for the models at 1.0° and 2.0°. As observed with the D95 model, the effects of volume become less important as the rotational error increases.

Fig 3.

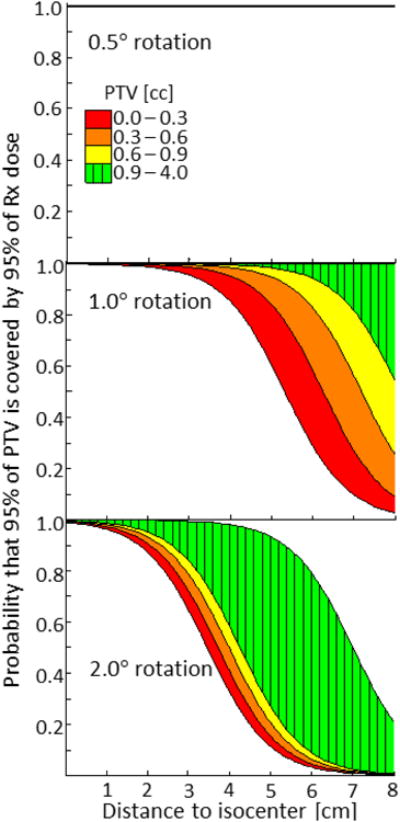
Shows the probability – estimated from GEE logistic regression – that at least 95% of a PTV will be covered by 95% of the prescribed dose. Plots are separated by rotational error and color coded by volume. The top subplot is ideal; at 0.5°, the probability of V95 ≥ 95% extends out to 8 cm from isocenter for all PTVs.

Table 2.

GEE multivariate logistic regression model (Eq 2) for predicting the probability (p) that V95 exceeds 95%. The model is parameterized at rotational errors of 0.5°, 1.0° and 2.0°. Variables are the volume of a PTV [cc] and the distance [cm] from a PTV centroid to the point of rotation. Parameter estimates related to volume (A) and distance (B) are reported with respective odds ratios (OR) and the OR 95% confidence intervals and p-values. The constant (C) is also reported.

Rotation [°]	Parameter Estimate		Odds Ratio	OR 95% CI	p-value
0.5°	Not Estimable: V95 > 95% in all cases
	A	4.14	63.0	2.97, 1337.24	0.0079
1.0°	B	-1.33	0.26	0.12, 0.56	0.0005
	C	7.09
	A	1.18	3.27	1.70, 6.28	0.0004
2.0°	B	-1.36	0.26	0.15, 0.44	<0.0001
	C	4.60

V95 GEE Logistic Regression Model: $log\left(\frac{p}{1-p}\right)=A\cdot \mathit{\text{PTV}}[cc]+B\cdot \mathit{\text{Distance}}[cm]+c$

As an illustrative case, Fig. 4 shows the dosimetric effects of 2.0° rotational errors when targets are on opposite sides of the brain. The minimum dose of a PTV is reduced to half of the prescription dose. Greater than 35% of a PTV is not covered by the prescription dose. Approximately 20% of the GTV is under dosed.

Fig 4.

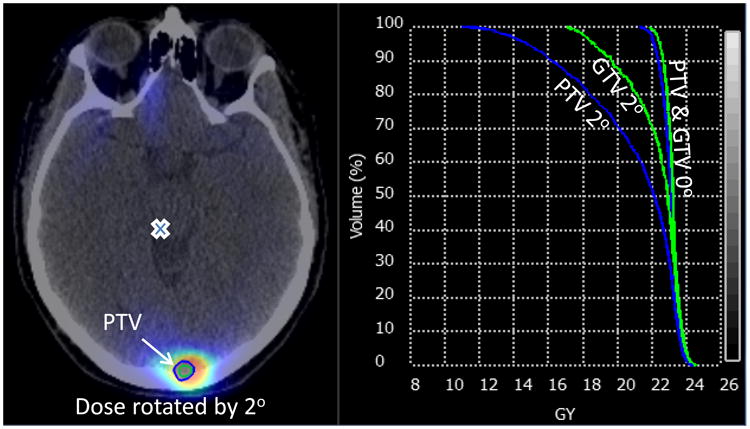
shows a substantial loss in target coverage for a 0.78 cc PTV at 7.3 cm from isocenter when rotated by 2.0°. The other PTV, not shown, is in a different plane. A cross denotes the transaxial position of the isocenter. Dose volume histogram data are reported for the GTV and PTV at 0.0° and 2.0°.

Discussion

Results show that PTV volume and distance to isocenter are statistically significant predictors of target coverage. Larger targets in close proximity are more robust to rotational errors than smaller targets on opposite sides of the brain. The effects of PTV volume and distance on target coverage were quantified using multivariate regression models. These findings may help determine whether an individual patient is a good candidate for single-isocenter VMAT SRS. Patient-specific parameters are easy to obtain from modern treatment planning systems, which have tools for measuring volumes and distances, allowing the decision on the treatment technique to be made early in the planning process. Further, models of target coverage may be used at the treatment machine to estimate the dosimetric consequences of any rotational setup errors.

In this study, the same degree of rotational error was applied about all axes. Though clinical errors are not likely to be uniform about all axes, the corresponding data quantifies how much target coverage can be affected in a worst-case scenario. The rotational levels were selected based on prior studies of rotational setup errors. For clinics equipped with real-time tracking capabilities and robotic couches capable of correcting for three orthogonal rotations, residual rotational errors may be within 0.5° for the majority of patients [3, 8]. In this study, rotations of 0.5° were found to have only a minimal effect on target coverage. However, not all clinics performing SRS have real-time tracking capabilities or the ability to correct for rotations other than the couch yaw. Therefore, it is not safe to assume that rotational errors are kept below 0.5°. At our clinic, we observe initial rotational errors in the range of 1° to 2°. An extreme case reported in a prior study demonstrates a rotational error of 3° in the initial setup [3]. Though our clinic has a robotic couch, other clinics may depend on manual patient repositioning to correct for rotational errors in the initial setup. In another case, over 1° of rotation was observed in confirmation imaging immediately after rotational corrections were applied [6]. Patient rotations observed during treatment can be substantial. Though uncommon, extreme rotational errors have the potential to compromise target coverage in multi-target, single-isocenter SRS. Unlike PTV volume and distance to isocenter, rotational errors are not known a priori. Therefore a conservative approach to ensuring a safe and accurate treatment must account for at least some percentage of the extreme rotational errors that are observed clinically.

The plan isocenter was positioned midway between two PTV centroids in this study. The results, however, suggest that the midway point is not necessarily the optimal isocenter position. To minimize risk of compromised coverage, the plan isocenter should be positioned closer to the smaller PTV. The distance that the isocenter should be offset depends on the PTV volumes, separation, and achievable uncertainty in rotational positioning. While the dosimetric models of this study are formulated to predict target coverage given inputs of target size and distance from isocenter for a particular rotational error, another approach is to set target coverage to an acceptable level and solve for the distance to isocenter given a known target size. The distance then provides a maximum radius from the target centroid where the plan isocenter can be positioned to achieve a set level of target coverage. In the treatment planning system, contours could be generated for each target using a target-specific radius described above in order to visualize potential isocenter locations. In the ideal scenario, a region exists where the contours overlap, suggesting that the patient is a good candidate for multi-target single-isocenter SRS. Alternatively, a large separation between such contours suggests that the patient may not be a good candidate. Though this study exclusively considers patients with two lesions, this approach for determining the isocenter position is applicable to patients with a greater number of lesions. The 3D Venn diagram becomes more complex.

This study characterizes the dosimetric effects of rotational errors on PTV coverage, examining the interactions between PTV volume and the distance to the point of rotation. However, we recognize that additional complex factors may have important dosimetric effects. Both rotational and translational errors are likely to occur in clinical practice, though translational errors are routinely corrected and have the same effect when lesions are treated independently or simultaneously. There is also variability in clinical practice regarding the amount of margin, if any, used for GTV expansion to PTV to account for setup errors. Our study is limited to the dosimetric effects on the PTV. The dosimetric impact of rotational errors on the GTV will vary depending on the amount of margin used for expansion. While not evaluated in this study, the potential of rotational errors to overdose normal tissues is an important clinical concern. For lesions in close proximity to critical structures, e.g., optic nerves, chiasm, or brainstem, setup errors that result in collateral damage to these adjacent structures may be as critical as setup errors that underdose a target. These considerations are areas for future investigation.

In conclusion, multi-target single-isocenter VMAT is a promising approach to SRS that can reduce treatment time. However, the rotational errors observed in patient studies can compromise target coverage, in particular for small targets on opposite sides of the brain. It is therefore crucial for any clinic considering multi-target single-isocenter VMAT SRS to characterize the rotational setup accuracy of their system. Once rotational uncertainty is characterized, multivariate regression models may be used to predict target coverage given patient-specific input parameters of PTV volume and distance to the isocenter. Dose estimates may be used to guide treatment planning or determine if patient setup is sufficiently accurate for treatment.

Summary.

VMAT is a relatively new approach to SRS, which allows multiple targets to be treated simultaneously. However, setup accuracy becomes more critical than when each target is treated independently. This study quantifies the effects of rotational errors on target coverage as a function of target volume and the distance between a target and plan isocenter using multivariate analyses. Corresponding predictive models may be used for patient selection and to create more robust treatment plans.