Fibonacci family of dynamical universality classes

Significance

Universality is a well-established central concept of equilibrium physics. It asserts that, especially near phase transitions, the properties of a physical system do not depend on its details such as the precise form of interactions. Far from equilibrium, such universality has also been observed, but, in contrast to equilibrium, a deeper understanding of its underlying principles is still lacking. We show that the two best-known examples of nonequilibrium universality classes, the diffusive and Kardar−Parisi−Zhang classes, are only part of an infinite discrete family. The members of this family can be identified by their dynamical exponent, which, surprisingly, can be expressed by a Kepler ratio of Fibonacci numbers. This strongly indicates the existence of a simpler underlying mechanism that determines the different classes.

Abstract

Universality is a well-established central concept of equilibrium physics. However, in systems far away from equilibrium, a deeper understanding of its underlying principles is still lacking. Up to now, a few classes have been identified. Besides the diffusive universality class with dynamical exponent $z=2$, another prominent example is the superdiffusive Kardar−Parisi−Zhang (KPZ) class with $z=3/2$. It appears, e.g., in low-dimensional dynamical phenomena far from thermal equilibrium that exhibit some conservation law. Here we show that both classes are only part of an infinite discrete family of nonequilibrium universality classes. Remarkably, their dynamical exponents $z_{\alpha }$ are given by ratios of neighboring Fibonacci numbers, starting with either $z_1=3/2$ (if a KPZ mode exist) or $z_1=2$ (if a diffusive mode is present). If neither a diffusive nor a KPZ mode is present, all dynamical modes have the Golden Mean $z=\left(1+\sqrt{5}\right)/2$ as dynamical exponent. The universal scaling functions of these Fibonacci modes are asymmetric Lévy distributions that are completely fixed by the macroscopic current density relation and compressibility matrix of the system and hence accessible to experimental measurement.

The Golden Mean, $\phi =1/2+\sqrt{5}/2\approx \mathrm{1.61803...}$, also called Divine Proportion, has been an inspiring number for many centuries. It is widespread in nature; i.e., arrangements of petals of the flowers and seeds in the sunflower follow the golden rule (1). Being considered an ideal proportion, the Golden Mean appears in famous architectural ensembles such as the Parthenon in Greece, the Giza Great Pyramids in Egypt, or Notre Dame de Paris in France. Ideal proportions of the human body follow the Golden Rule.

Mathematically, the beauty of the Golden Mean number is expressed in its continued fraction representation: All of the coefficients in the representation are equal to unity,

$$\phi =1+\frac{1}{1}\begin{array}{c}\\ +\hspace{0.17em}\frac{1}{1}\begin{array}{c}\\ +\hspace{0.17em}\frac{1}{1}\begin{array}{c}\\ +\begin{array}{c}\\ \ddots \end{array}\end{array}\end{array}.\end{array}$$ [1]

Systematic truncation of the above continued fraction gives the so-called Kepler ratios, $1/1,2/1,3/2,5/3,8/5,\mathrm{...}$, which approximate the Golden Mean. Subsets of denominators (or numerators) of the Kepler ratios form the celebrated Fibonacci numbers, $F_i=\mathrm{1,1,2,3,5,8},\mathrm{..}$, such that Kepler ratios are ratios of two neighboring Fibonacci numbers. As well as the Golden Mean, Fibonacci ratios and Fibonacci numbers are widespread in nature (1).

The occurrence of the Golden Mean is not only interesting for aesthetic reasons but often indicates the existence of some fundamental underlying structure or symmetry. Here we demonstrate that the Divine Proportion as well as all of the truncations (Kepler ratios) of the continued fraction (Eq. 1) appear as universal numbers, namely, the dynamical exponents, in low-dimensional dynamical phenomena far from thermal equilibrium. The two well-known paradigmatic universality classes, Gaussian diffusion with dynamical exponent $z=2$ (2, 3) and the Kardar−Parisi−Zhang (KPZ) universality class with $z=3/2$ (4), enter the Kepler ratios hierarchy as the first two members of the family.

The universal dynamical exponents in the present context characterize the self-similar space−time fluctuations of locally conserved quantities, characterizing, e.g., mass, momentum, or thermal transport in one-dimensional systems far from thermal equilibrium (5). The theory of nonlinear fluctuating hydrodynamics (NLFH) has recently emerged as a powerful and versatile tool to study space−time fluctuations, and specifically the dynamical structure function that describes the behavior of the slow relaxation modes, and from which the dynamical exponents can be extracted (6).

The KPZ universality class has been shown to explain the dynamical exponent observed in interface growth processes as diverse as the propagation of flame fronts (7, 8), the growth of bacterial colonies (9), or the time evolution of droplet shapes such as coffee stains (10) where the Gaussian theory fails. For a nice introduction into the KPZ class and its relevance, we refer to ref. 11. Recent reviews (12, 13) provide a more detailed account of theoretical and experimental work on the KPZ class. The dynamical structure function originating from the one-dimensional KPZ equation has a nontrivial scaling function obtained exactly by Prähofer and Spohn from the totally asymmetric simple exclusion process (TASEP) and the polynuclear growth model (14, 15) and was beautifully observed in experiments on turbulent liquid crystals (16, 17). The theoretical treatment, both numerical and analytical, of generic model systems with Hamiltonian dynamics (18), anharmonic chains (19, 20), and lattice models for driven diffusive systems (21, 22) have demonstrated an extraordinary robust universality of fluctuations of the conserved slow modes in one-dimensional systems.

Despite this apparent ubiquity, dynamical exponents different from $z=2$ or $z=3/2$ were observed frequently. Usually, it is not clear whether this corresponds to genuinely different dynamical critical behavior or is just a consequence of imperfections in the experimental setting. Moreover, recently, a new universality class with dynamical exponent $z=5/3$ for the heat mode in Hamiltonian dynamics (18) was discovered, followed by the discovery of some more universality classes in anharmonic chains (19, 20) and lattice models for driven diffusive systems (21, 22). What is lacking, even in the conceptually simplest case of the effectively one-dimensional systems that we are considering, is the understanding of the plethora of dynamical nonequilibrium universality classes within a larger framework. Such a framework exists, e.g., for 2D critical phenomena in equilibrium systems where the spatial symmetry of conformal invariance together with internal symmetries give rise to discrete families of universality classes in which all critical exponents are simple rational numbers.

It is the aim of this article to demonstrate that discrete families of universality classes with fractional critical exponents appear also far from thermal equilibrium. This turns out to be a hidden feature of the NLFH equations that we extract using mode coupling theory. It is remarkable that one finds dynamical exponents $z_{\alpha }$, which are ratios of neighboring Fibonacci numbers $\left\{\mathrm{1,1,2,3,5,8},\dots \right\}$ defined recursively as $F_n=F_{n-1}+F_{n-2}$. The first two members of this family are diffusion ($z=2=F_3/F_2$) and KPZ ($z=3/2=F_4/F_3$). The corresponding universal scaling functions are computed and shown to be (in general asymmetric) $z_{\alpha }$-stable Lévy distributions with parameters that can be computed from the macroscopic current density relation and compressibility matrix of the corresponding physical system and which thus can be obtained from experiments without detailed knowledge of the microscopic properties of the system. The theoretical predictions, obtained by mode coupling theory, are confirmed by Monte Carlo simulations of a three-lane asymmetric simple exclusion process, which is a model of driven diffusive transport of three conserved particle species.

Nonlinear Fluctuating Hydrodynamics

We consider a rather general interacting nonequilibrium system of length L described macroscopically by n conserved order parameters ${\rho }_{\lambda }\left(x,t\right)$ with stationary values ${\rho }_{\lambda }$ and associated macroscopic stationary currents $j_{\lambda }\left({\rho }_1,\dots ,{\rho }_n\right)$ and compressibility matrix K with matrix elements $K_{\lambda \mu }=\left(1/L\right)\langle \left(N_{\lambda }-{\rho }_{\lambda }L\right)\left(N_{\mu }-{\rho }_{\mu }L\right)\rangle$ where $N_{\lambda }={\displaystyle {\int }_0^L\text{d}x{\rho }_{\lambda }\left(x,t\right)}$ are the time-independent conserved quantities.

The starting point for investigating density fluctuations $u_{\lambda }\left(x,t\right):={\rho }_{\lambda }\left(x,t\right)-{\rho }_{\lambda }$ in the nonequilibrium steady state are the NLFH equations (5)

$${\partial }_t\overrightarrow{u}=-{\partial }_x\left(J\overrightarrow{u}+\frac{1}{2}\langle u|\overrightarrow{H}|u\rangle -{\partial }_{x}D\overrightarrow{u}+B\overrightarrow{\xi }\right)$$ [2]

where J is the current Jacobian with matrix elements $J_{\lambda \mu }=\partial j_{\lambda }/\partial {\rho }_{\mu }$, $\overrightarrow{H}$ is a column vector whose entries ${\left(\overrightarrow{H}\right)}_{\lambda }=H^{\lambda }$ are the Hessians with matrix elements $H_{\mu \nu }^{\lambda }={\partial }^2{j}_{\lambda }/\left(\partial {\rho }_{\mu }\partial {\rho }_{\nu }\right)$, and the bra-ket notation represents the inner product in component space $\langle u|{\left(\overrightarrow{H}\right)}_{\lambda }|u\rangle ={\overrightarrow{u}}^T{H}^{\lambda }\overrightarrow{u}={\displaystyle {\sum }_{\mu \nu }{u}_{\mu }{u}_{\gamma }{H}_{\mu \nu }^{\lambda }}$ with $\langle u|={\overrightarrow{u}}^T$ and $|u\rangle =\overrightarrow{u}$. The diffusion matrix D is a phenomenological quantity. The noise term $B\overrightarrow{\xi }$ does not appear explicitly below, but plays an indirect role in the mode coupling analysis. The product $JK$ of the Jacobian with the compressibility matrix $K$ is symmetric (23), which guarantees a hyperbolic system of conservation laws (24). We ignore possible logarithmic corrections arising from cubic contributions (25).

This system of coupled noisy Burgers equations is conveniently treated in terms of normal modes $\overrightarrow{\varphi }=R\overrightarrow{u}$, where $RJ{R}^{-1}=\text{diag}\left(v_{\alpha }\right)$ and the transformation matrix R is normalized such that $RK{R}^T=1$. The eigenvalues $v_{\alpha }$ of J are the characteristic velocities of the system. From Eq. 2, one thus arrives at ${\partial }_t{\varphi }_{\alpha }=-{\partial }_x\left(v_{\alpha }{\varphi }_{\alpha }+\langle \varphi |G^{\alpha }|\varphi \rangle -{\partial }_x{\left(\tilde{D}\overrightarrow{\varphi }\right)}_{\alpha }+{\left(\tilde{B}\overrightarrow{\xi }\right)}_{\alpha }\right)$, with $\tilde{D}=RD{R}^{-1}$, $\tilde{B}=RB$, and the mode coupling matrices

$$G^{\alpha }=\frac{1}{2}{\displaystyle \sum _{\beta }{R}_{\alpha \beta }{\left(R^{-1}\right)}^T{H}^{\beta }{R}^{-1}},$$ [3]

whose matrix elements we denote by $G_{\beta \gamma }^{\alpha }$.

Computation of the Dynamical Structure Function

The dynamical structure function describes the stationary fluctuations of the conserved slow modes and is thus a key ingredient for understanding the interplay of noise and nonlinearity and their role for transport far from equilibrium. We focus on the case of strict hyperbolicity where all $v_{\alpha }$ are pairwise different and study the large-scale behavior of the dynamical structure function $S^{\alpha \beta }\left(x,t\right)=\langle {\varphi }_{\alpha }\left(x,t\right){\varphi }_{\beta }\left(\mathrm{0,0}\right)\rangle$. Because all modes have different velocities, only the diagonal elements $S_{\alpha }\left(x,t\right):=S^{\alpha \alpha }\left(x,t\right)$ are nonzero for large times. Mode coupling theory yields (5)

$$\begin{array}{c}{\partial }_t{S}_{\alpha }\left(x,t\right)=\left(-v_{\alpha }{\partial }_x+D_{\alpha }{\partial }_x^2\right)S_{\alpha }\left(x,t\right)\\ +{\displaystyle \underset{0}{\overset{t}{\int }}\text{d}s{\displaystyle \underset{\mathrm{ℝ}}{\int }\text{d}y{S}_{\alpha }\left(x-y,t-s\right){\partial }_y^2{M}_{\alpha \alpha }\left(y,s\right)}}\end{array}$$ [4]

with the diagonal element $D_{\alpha }:={\tilde{D}}_{\alpha \alpha }$ of the phenomenological diffusion matrix for the eigenmodes and the memory kernel $M_{\alpha \alpha }\left(y,s\right)={\displaystyle {\sum }_{\beta ,\gamma }{\left(G_{\beta \gamma }^{\alpha }\right)}^2{S}_{\beta }\left(y,s\right)S_{\gamma }\left(y,s\right)}$. The task therefore is to extract for arbitrary n the large-time and large-distance behavior from this nonlinear integro-differential equation.

Remarkably, these equations can be solved exactly in the long-wavelength limit and for $t\to \infty$ by Fourier and Laplace transformation (see Materials and Methods and SI Text). Using a suitable scaling ansatz for the transformed structure function then allows analysis of the small-p behavior from which the dynamical exponents can be determined. We find that different conditions arise depending on which diagonal elements of the mode coupling matrices vanish.

Fibonacci Family of Dynamical Universality Classes

Fibonacci Case.

First, we consider the case where the self-coupling $G_{\alpha \alpha }^{\alpha }$ is nonzero for one mode only, e.g., $G_{11}^1\ne 0$. For all other modes α > 1, we assume a single nonzero coupling to the previous mode, so $G_{\alpha -1,\alpha -1}^{\alpha }\ne 0$, and $G_{\beta ,\beta }^{\alpha }=0$ for $\beta \ne \alpha -1$. Then, as follows from our analysis (see Materials and Methods), we find the following recursion for the dynamical exponents:

$$z_{\alpha }=1+\frac{1}{z_{\alpha -1}}$$ [5]

with $z_1=3/2$.

The dynamical structure function in momentum space is proportional to the $z_{\alpha }$-stable Lévy distribution with maximal asymmetry ${\sigma }^{\alpha }=\pm 1$; see ref. 26 and Eq. 13 below. The sign of the asymmetry depends on whether the mode $\left(\alpha -1\right)$ has bigger or smaller velocity than the mode α, ${\sigma }^{\alpha }=-\text{sgn}\left(v_{\alpha }-v_{\alpha -1}\right)$. The dynamical exponents (Eq. 5) form a sequence of rational numbers,

$$z_{\alpha }=\frac{F_{\alpha +3}}{F_{\alpha +2}},$$ [6]

which are consecutive ratios of neighboring Fibonacci numbers $F_{\alpha }$, defined by $F_{\alpha }=F_{\alpha -1}+F_{\alpha -2}$ with initial values $F_0=0,F_1=1$, which converge exponentially to the Golden Mean $\phi :=\frac{1}{2}\left(1+\sqrt{5}\right)\approx 1.618$, as first observed by Kepler in 1611 in a treatise on snowflakes. In a model with n conservation laws, one has the Fibonacci modes with dynamical exponents $\left\{3/2,5/3,8/5,\dots ,z_n\right\}$.

Finally, we remark that if mode 1 is diffusive rather than KPZ, then we find the same sequence (Eq. 6) of exponents, except that it starts with $z_1=F_2=2$.

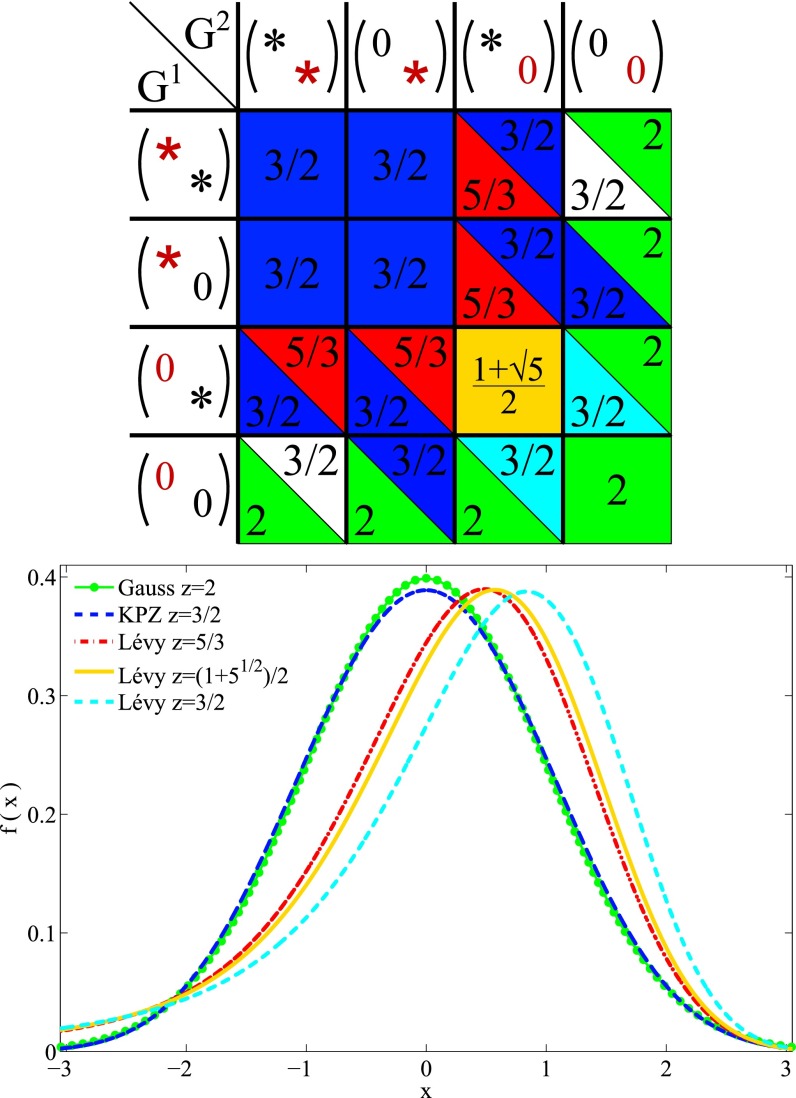
In Fig. 1, we show some representative examples of the scaling functions that are quite different in shape. Furthermore, the relation between the exponents $z_{\alpha }$, determined by Eq. 11 in Materials and Methods, and the mode coupling matrices $G^{\alpha }$ is illustrated for the case $n=2$.

Fig. 1.

The scaling functions (Bottom) and dynamical exponents are related to the structure of the mode coupling matrices $G^{\alpha }$ (Top). The table shows the dynamical exponents $z_{\alpha }$ in the case $n=2$; see Eq. 11. The symbols $\mathrm{\ast }$ and $\mathrm{\star }$ denote nonzero elements. Red symbols correspond to self-coupling; black symbols correspond to couplings to other modes. Matrix elements not indicated can take any value. The colors in the table correspond to the colors of the graphs of the scaling functions.

Golden Mean Case.

As a second representative example, we consider the case where all self-coupling coefficients vanish, $G_{\alpha \alpha }^{\alpha }\equiv 0$ for all α, while each mode has at least one nonzero coupling to another mode, $G_{\beta \beta }^{\alpha }\ne 0$ for some $\beta \ne \alpha$. Then, Eq. 5 reduces to $z_{\alpha }=1+1/z_{\beta }$ for all modes $\alpha ,\beta$. The unique solution of this equation is the Golden Mean $z_{\alpha }=\phi =\left(1+\sqrt{5}\right)/2$ for all α. The scaling functions (see SI Text) are proportional to φ-stable Lévy distributions with parameters fixed by the collective velocities and the mode coupling coefficients. The asymmetry of the fastest right-moving (left-moving) mode is predicted to be $\beta =-1$ ($\beta =1$).

Simulation Results

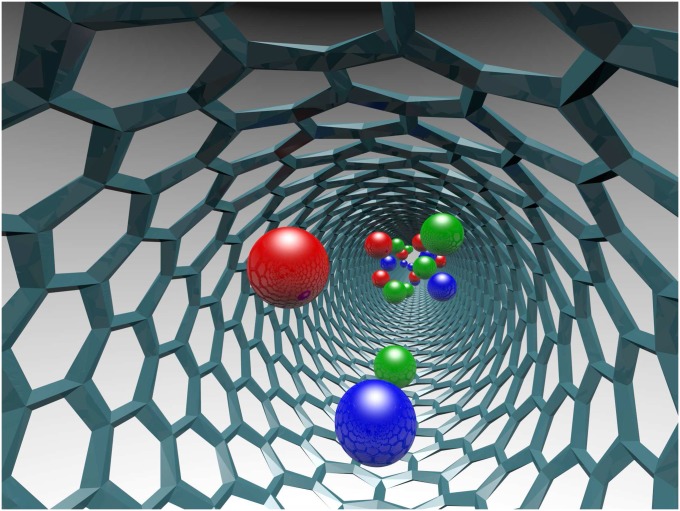
To check the theoretical predictions for the two cases, we simulate mass transport with three conservation laws, i.e., three distinct species of particles. To maintain a far-from-equilibrium situation, a driving force is applied that leads to a constant drift superimposed on undirected diffusive motion. This is a natural setting for transport of charged particles in nanotubes (see Fig. 2 for an illustration), where a direct measurement of the stationary particle currents is experimentally possible (27). However, due to the universal applicability of NLFH, the actual details of the interaction of the particles with their environment and the driving field are irrelevant for the theoretical description of the large-scale dynamics. Hence, for good statistics, we simulate a lattice model for transport that represents a minimal realization of the essential ingredients, namely, a nonlinear current density relation for all three conserved masses.

Fig. 2.

Schematic drawing of three particle species drifting inside a nanotube. Due to the interaction between the particles and with the walls, one expects a nonlinear current density relation.

Our model is the three-species version of the multilane TASEP (28). Particles hop randomly in field direction on three lanes to their neighboring sites on a periodic lattice of $3\times L$ sites with rates that depend on the nearest-neighbor sites. Lane changes are not allowed so that the total number of particles on each lane is conserved. Due to excluded volume interaction, each lattice site can be occupied by at most one particle. Thus, the occupation numbers $n_k^{\left(\lambda \right)}$ of site k on lane λ take only values 0 or 1. The hopping rate $r_k^{\left(\lambda \right)}$ from site k on lane λ to site $k+1$ on the same lane is given by

$$r_k^{\left(\lambda \right)}=b_{\lambda }+\frac{1}{2}{\displaystyle \sum _{\left\{\mu :\mu \ne \lambda \right\}}{\gamma }_{\lambda \mu }\left(n_k^{\left(\mu \right)}+n_{k+1}^{\left(\mu \right)}\right)}$$ [7]

with a species-dependent drift parameter $b_{\lambda }$ and symmetric interaction constants ${\gamma }_{\lambda \mu }={\gamma }_{\mu \lambda }$. Hopping attempts onto occupied sites are rejected. The conserved quantities are the three total numbers of particles $N_{\lambda }$ on each lane with corresponding densities ${\rho }_{\lambda }=N_{\lambda }/L$.

The stationary distribution of our model factorizes (28) and thus allows for the exact computation of the macroscopic current density relations $j_{\lambda }\left({\rho }_1,{\rho }_2,{\rho }_3\right)$ and the compressibility matrix $K\left({\rho }_1,{\rho }_2,{\rho }_3\right)$. Furthermore, because there is no particle exchange between lanes, the compressibility matrix is diagonal, with elements denoted by ${\kappa }_{\lambda }$. One has

$$j_{\lambda }={\rho }_{\lambda }\left(1-{\rho }_{\lambda }\right)\left(b_{\lambda }+{\displaystyle \sum _{\left\{\mu :\mu \ne \lambda \right\}}{\gamma }_{\lambda \mu }{\rho }_{\mu }}\right)$$ [8]

$${\kappa }_{\lambda }={\rho }_{\lambda }\left(1-{\rho }_{\lambda }\right).$$ [9]

The diagonalization matrix R and the mode coupling matrices $G^{\alpha }$ are fully determined by these quantities.

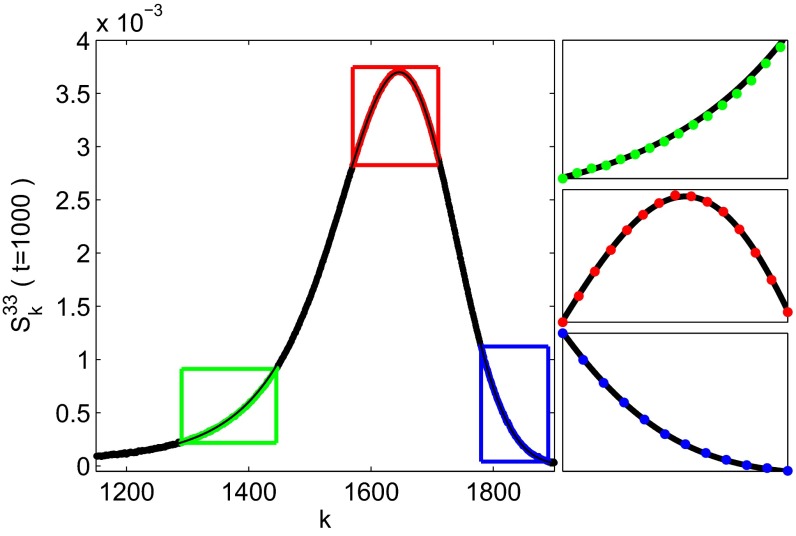
According to mode coupling theory, three different Fibonacci modes with $z_1=3/2,z_2=5/3,z_3=8/5$ occur, e.g., when $G_{11}^1\ne 0$, $G_{11}^2\ne 0$, $G_{22}^3\ne 0$, and $G_{22}^2=G_{33}^2=G_{33}^3=0$. For our simulation, we compute numerically densities, bare hopping rates, and interaction parameters to satisfy these properties as described in Materials and Methods. For this choice, the velocities of the normal modes are $v_1=0.592315$, $v_2=0.0281578$, and $v_3=1.58226$, which ensures a good spatial separation after quite small times. The propagation of the three normal modes (Fig. 3) with the predicted velocities is observed with an error of less than ${10}^{-3}$. Moreover, the numerically obtained dynamical structure function for mode 3 shows a startling agreement with the theoretically predicted Lévy scaling function with $z=8/5$ and maximal asymmetry (see Fig. 4). It takes longer for the other two modes (KPZ mode and Lévy stable $5/3$ mode) to reach their asymptotic form, which we argue is due to the much smaller respective couplings, ${\left(G_{11}^1/G_{22}^3\right)}^2\ll 1$, ${\left(G_{11}^2/G_{22}^3\right)}^2\ll 1$.

Fig. 3.

Space−time propagation of three normal modes in the three-lane model. The modes (from left to right) are the Fibonacci mode with $z=8/5$ (mode 3), the KPZ mode with $z=3/2$ (mode 1), and the Fibonacci mode with $z=5/3$ (mode 2). The physical and simulation parameters are given in Materials and Methods.

Fig. 4.

(Left) Vertical least squares fit of the numerically obtained dynamical structure function for the Fibonacci 8/5 mode (points), at time $t=\mathrm{1,000}$ with an 8/5-stable Lévy distribution, maximal asymmetry $-1$, and theoretical center of mass (line), predicted by the mode coupling theory. The only fit parameter is the scale parameter of the Lévy stable distribution. The simulation results agree very well with the asymptotic theoretical result already for moderate times. (Right) Close-ups of the peak region and tail regions, according to a color code. Every tenth data point is plotted, to improve the visibility of the data. The statistical error ${\mathit{ϵ}}_{99\text{\%}}$ with 99% confidence bound is for every data point smaller than $1.6299\cdot {10}^{-5}$.

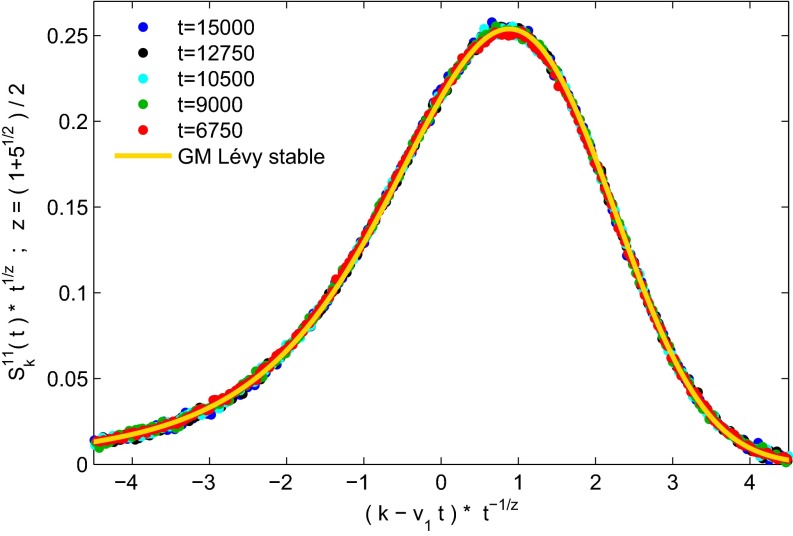
To observe three Golden Mean modes, it is sufficient to require that each mode has zero self-coupling and at least one nonzero coupling to other modes. This can be achieved with the set of parameters given in Materials and Methods, which lead to the velocities $v_1=1.83149$, $v_2=0.762688$, and $v_3=0.326778$ of the normal modes. The propagation of the three normal modes with the predicted velocities is observed, approaching, for large times, a very small relative error of about ${10}^{-4}$. The structure function for the fastest mode 1 converges to its asymptotic shape faster than for the other modes, due to the large coupling coefficient $G_{33}^1$. In Fig. 5, we show a scaling plot of the measured structure function for mode 1 with dynamical exponent $z\equiv \phi =\left(1+\sqrt{5}\right)/2$ together with a fitted to a φ-stable Lévy function (Eq. 13) with maximal asymmetry $\beta =-1$ as predicted by the theory. The data collapse shows a striking agreement between the measured and theoretical scaling function. Alternatively, the dynamical exponent $z_{\alpha }$ can be derived from the maximum of the structure function, which scales as $\text{max}\left(S_1\left(x,t\right)\right)=\text{const}\cdot t^{-1/z}$. We obtain $z\approx 1.63$, which differs from the predicted value $z\equiv \phi =\left(1+\sqrt{5}\right)/2$ by less than $0.8\text{\%}$.

Fig. 5.

Scaling plot of the measured structure function of mode 1 with dynamical exponent $z\equiv \phi =\left(1+\sqrt{5}\right)/2$ for the Golden Mean case, fitted to a φ-stable Lévy distribution with maximal asymmetry $-1$ (see Eq. 13). The scale parameter $E_1$ for the Lévy-stable distribution and the center of mass velocity $v_1$ are obtained by a vertical least square fit. Fitted parameters are $v_{1,\text{fit}}=1.83107\pm 0.00009$ and $E_{1,\text{fit}}=1.1\pm 0.01$. The fitted velocity $v_{1,\text{fit}}$ differs by $0.02\text{\%}$ from the theoretical velocity.

Discussion

Our work demonstrates that nonequilibrium phenomena are much richer than just the diffusive and KPZ universality suggest. We have established that in nonequilibrium phenomena governed by NLFH with n conservation laws, mode coupling theory predicts a family of dynamical universality classes with dynamical exponents given by the sequence of consecutive Kepler ratios (Eq. 6) of Fibonacci numbers. With slightly modified initial conditions on $G_1^{11}$, this result is easily generalized for the case when the first mode $\alpha =1$ is diffusive. Then the sequence of dynamical exponents becomes shifted by one unit with respect to Eq. 6. On the other hand, if all self-couplings vanish, but at least one other diagonal element $G_{\beta \beta }^{\alpha }$ of the mode coupling matrix is non-zero, one has, as a unique solution for all modes α, the fixed point value $z_{\alpha }=z_{\infty }=\phi$, which is the Golden Mean.

For general mode coupling matrices, all critical exponents can be computed (from Eq. 11 in Materials and Methods). The scaling functions of the nondiffusive and non-KPZ modes are asymmetric Lévy distributions whose parameters are completely determined by the macroscopic current density relation and compressibility matrix of the system.

For 1+1 dimensional systems out of equilibrium, this is the first time, to our knowledge, that an infinite family of discrete universality classes is found. Recalling that 1 + 1 dimensional nonequilibrium systems with short-range interactions can be mapped onto 2D equilibrium systems (with the time evolution operator playing the role of the transfer matrix), one is reminded of the discrete families of conformally invariant critical equilibrium systems in two space dimensions (29, 30). We do not know whether there is any mathematical link, but the analogy is suggestive in so far as conformal invariance is a local symmetry of spatially isotropic systems with $z=1$ (which happens to be the lowest-order Kepler ratio) whereas $z>1$ corresponds to strongly anisotropic systems for which local symmetry groups are also known to exist (31).

Because an infinite number of lanes of coupled one-dimensional systems correspond to a 2D system, it is intriguing to observe that the Golden Mean is close to the numerical value $z=1.612-1.618$ of the dynamical exponent of the $2+1$-dimensional KPZ equation (32, 33). The scaling function of the $2+1$-dimensional KPZ equation, however, is not Lévy (34).

To observe and distinguish between the different new classes, highly precise experimental data will be required. For example, in the Fibonacci case, the dynamical exponents converge quickly to the Golden Mean. A feature that might be easier to observe experimentally is the scaling function itself, which, for higher Fibonacci ratios $5/3,8/5,\dots$, usually has a strong asymmetry (see Figs. 1, 4, and 5), whereas KPZ and Gauss scaling functions are symmetric. Growth processes that can be mapped on exclusion processes with several conservation laws might be potentially suitable candidates for an experimental verification; see, e.g., refs. 16 and 17 for an example of a system with one conservation law.

Materials and Methods

Computation of the Dynamical Structure Function.

The mode coupling Eq. 4 can be solved in the scaling limit by applying a Fourier transform (FT) $f\left(x\right)\to \tilde{f}\left(p\right)$ and a Laplace transform (LT) $f\left(t\right)\to \tilde{f}\left(\omega \right)$. For more details, we refer to ref. 22, where the case $n=2$ of two conservation laws has been treated. After making the scaling ansatz

$${\tilde{S}}_{\alpha }\left(p,{\tilde{\omega }}_{\alpha }\right)=p^{-z_{\alpha }}{g}_{\alpha }\left({\zeta }_{\alpha }\right)$$ [10]

for the transformed dynamical structure function where ${\widehat{S}}_{\alpha }\left(p,0\right)=1/\sqrt{2\pi }$ and ${\zeta }_{\alpha }={\tilde{\omega }}_{\alpha }{\left|p\right|}^{-z_{\alpha }}$, we are in a position to analyze the small-p behavior. One has to search for dynamical exponents for which the limit $p\to 0$ is nontrivial, which requires a self-consistent treatment of all modes. We find that different conditions arise depending on which diagonal elements of the mode coupling matrices vanish. To characterize the possible scenarios, we define the set ${\mathbb{I}}_{\alpha }:=\left\{\beta :G_{\beta \beta }^{\alpha }\ne 0\right\}$ of nonzero diagonal mode coupling coefficients. Through power counting one obtains

$$z_{\alpha }=\{\begin{array}{lll}2\hfill & \text{if}\hfill & {\mathbb{I}}_{\alpha }=\mathrm{Ø}\hfill \\ 3/2\hfill & \text{if}\hfill & \alpha \in {\mathbb{I}}_{\alpha }\hfill \\ {\text{min}}_{\beta \in {\mathbb{I}}_{\alpha }}\left[\left(1+\frac{1}{z_{\beta }}\right)\right]\hfill & \text{else}\hfill & \hfill \end{array}$$ [11]

and the domain

$$1<z_{\alpha }\le 2\forall \alpha .$$ [12]

for the possible dynamical exponents.

In the Fibonacci case, the dynamical structure function of mode α in momentum space has the scaling form

$${\widehat{S}}_{\alpha }\left(p,t\right)=\frac{1}{\sqrt{2\pi }}{\text{e}}^{-i{v}_{\alpha }pt-E_{\alpha }{\left|p\right|}^{z_{\alpha }}t\left(1-i{\sigma }_p^{\alpha \beta }\text{tan}\left(\frac{\pi z_{\alpha }}{2}\right)\right)}$$ [13]

with inverse time scales $E_{\alpha }$. The dynamical exponents then satisfy the recursion (Eq. 5). Up to the normalization $1/\sqrt{2\pi }$ the scaling form (Eq. 13) is an α-stable Lévy distribution (26).

Simulation Algorithm.

For the Monte Carlo simulation of the model, we choose a large system size $L\ge 5\cdot {10}^5$, which avoids finite-size effects. At time $t=0$, $N_{\lambda }$ particles are placed on each lane according to the desired initial state. One Monte Carlo time unit consists of $3\cdot L\cdot r\text{*}$ random sequential update steps where $r\text{*}=\text{max}\left\{r_k^{\left(\lambda \right)}\right\}$: In each update step, a bond $\left(k^{\left(\lambda \right)},k^{\left(\lambda \right)}+1\right)$ is chosen randomly with uniform distribution. If $n_k^{\left(\lambda \right)}\left(1-n_{k+1}^{\left(\lambda \right)}\right)=1$, then the particle at site k is moved to $k+1$ with probability $r_k^{\left(\lambda \right)}/r\text{*}$ where $r\text{*}$ is the maximal value that the $r_k^{\left(\lambda \right)}$ can take among all possible particle configurations on the neighboring lanes. If $n_k^{\left(\lambda \right)}\left(1-n_{k+1}^{\left(\lambda \right)}\right)=0$, the particle configuration remains unchanged.

Simulation of the Dynamical Structure Function.

To determine the dynamical structure function, we initialize the system by placing $N_{\lambda }$ particles uniformly on each lane λ. This yields a random initial distribution drawn from the stationary distribution of the process. No relaxation is required.

Then we use translation invariance and compute the space and time average

$${\sigma }_{L,k}^{\lambda \mu }\left(M,\tau ,t\right)=\frac{1}{M}{\displaystyle \sum _{j=1}^M\frac{1}{L}{\displaystyle \sum _{l=1}^L{n}_{l+k}^{\left(\lambda \right)}\left(j\tau +t\right)n_l^{\left(\mu \right)}\left(j\tau \right)-{\rho }_{\lambda }{\rho }_{\mu }}}.$$ [14]

To avoid noisy data of ${\sigma }_{L,k}^{\lambda \mu }$, we take in Eq. 14 the system size L and the time average parameter M sufficiently large. To obtain $S_k^{\lambda \mu }\left(t\right)$, we average over P independently generated and propagated initial configurations of ${\sigma }_{L,k}^{\lambda \mu }$. The error estimates for $S_k^{\lambda \mu }\left(t\right)$ are calculated from the P independent measurements. From $S_k^{\lambda \mu }\left(t\right)$, we compute the structure function of the normal modes by transformation with the diagonalizing matrix R determined by Eqs. 8 and 9.

To obtain model parameters for three different Fibonacci modes with $z_1=3/2,z_2=5/3,z_3=8/5$, we solve the equations given in the text after Eq. 9 numerically with a C program performing direct minimization of the absolute values of the targeted G elements until the given tolerance value (${10}^{-6}$) is reached. The data shown here for the three-mode case have been obtained from simulations with densities ${\rho }_1=0.2,{\rho }_2=0.25,{\rho }_1=0.3$, bare hopping rates $b_1=0.613185$, $b_2=0.425714$, $b_3=0.799831$, and interaction parameters ${\gamma }_{12}=1.36145$, ${\gamma }_{23}=3.69786$, ${\gamma }_{13}=0.143082$ for which the needed relations are satisfied. This choice of parameters yields $G_{11}^1=0.322507$, $G_{11}^2=-0.15$, $G_{22}^3=1.04547$, while the absolute values of $G_{22}^2,G_{33}^2,G_{33}^3$ are smaller than ${10}^{-6}$. Besides these physical parameters, the simulation parameters for the Fibonacci modes (Figs. 3 and 4) are $L=5·{10}^5$, $\tau =250$, $M=\mathrm{1,400}$, $P=98$.

For the Golden Mean case (Fig. 5), the set of parameters is ${\rho }_1=0.2,{\rho }_2={\rho }_3=0.25$, ${\gamma }_{12}=0.0082334758646$, ${\gamma }_{23}=1.68447706968$, ${\gamma }_{13}=3.72140740146$, and $b_1=0.905073261248$, $b_2=0.86$, and $b_3=1.18875738638$. This leads to $G_{22}^1=0.405702$, $G_{33}^1=0.929315$, $G_{11}^2=-0.104141$, $G_{33}^2=-0.208477$, $G_{11}^3=-0.182467$, $G_{22}^3=0.271246$, while the absolute values of $G_{11}^1,G_{22}^2,G_{33}^3$ are smaller than ${10}^{-6}$. The simulation parameters for the Golden Mean case are $L=5·{10}^6$ $\tau =750$, $M=30$ and $P=303$.

SI Text

Remarkably, the mode coupling equations (Eq. 4) can be solved exactly in the scaling limit by FT and LT. To this end, we define the FT as

$$\widehat{f}\left(p\right):=\frac{1}{\sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\text{d}x{\text{e}}^{-ipx}f\left(x\right)}$$ [S1]

and the LT as

$$\tilde{f}\left(\omega \right):={\displaystyle \underset{0}{\overset{\infty }{\int }}\text{d}t{\text{e}}^{-\omega t}f\left(t\right)}.$$ [S2]

With ${\widehat{D}}_{\alpha }\left(p\right)=i{v}_{\alpha }p+D_{\alpha }{p}^2$, we obtain from Eq. 4, in momentum−frequency space,

$${\tilde{S}}_{\alpha }\left(p,\omega \right)=\frac{{\widehat{S}}_{\alpha }\left(p,0\right)}{\omega +{\widehat{D}}_{\alpha }\left(p\right)+{\tilde{C}}_{\alpha \alpha }\left(p,\omega \right)}$$ [S3]

with memory kernel

$${\tilde{C}}_{\alpha \alpha }\left(p,\omega \right)=2{\displaystyle \sum _{\beta ,\gamma }{\left(G_{\beta \gamma }^{\alpha }\right)}^2{p}^2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\text{d}s{\text{e}}^{-\omega s}}{\displaystyle \underset{\mathrm{ℝ}}{\int }\text{d}q{\widehat{S}}_{\beta }\left(q,s\right){\widehat{S}}_{\gamma }\left(p-q,s\right).}$$ [S4]

and ${\widehat{S}}_{\alpha }\left(p,0\right)=1/\sqrt{2\pi }$.

Next, we introduce ${\tilde{\omega }}_{\alpha }:=\omega +i{v}_{\alpha }p$ and make the scaling ansatz

$${\tilde{S}}_{\alpha }\left(p,{\tilde{\omega }}_{\alpha }\right)=p^{-z_{\alpha }}{g}_{\alpha }\left({\zeta }_{\alpha }\right)$$ [S5]

with ${\zeta }_{\alpha }={\tilde{\omega }}_{\alpha }{\left|p\right|}^{-z_{\alpha }}$. Having in mind systems with short-range interactions, we anticipate that all modes spread subballistically, i.e., $z_{\alpha }>1$ for all α. Using strict hyperbolicity, one obtains, after some substitutions of variables,

$$g_{\alpha }\left({\zeta }_{\alpha }\right)=\underset{p\to 0}{\text{lim}}{\left[{\zeta }_{\alpha }+D_{\alpha }{\left|p\right|}^{2-z_{\alpha }}+Q_{\alpha \alpha }{\zeta }_{\alpha }^{2-z_{\alpha }-\frac{1}{z_{\alpha }}}{\left|p\right|}^{3-2z_{\alpha }}+{\displaystyle \sum _{\beta \ne \alpha }{Q}_{\alpha \beta }{\left(-i{v}_p^{\alpha \beta }\right)}^{\frac{1}{z_{\beta }}-1}{\left|p\right|}^{1+\frac{1}{z_{\beta }}-z_{\alpha }}}\right]}^{-1}.$$ [S6]

with $v_p^{\alpha \beta }:=\left|v_{\alpha }-v_{\beta }\right|\text{sgn}\left[p\left(v_{\alpha }-v_{\beta }\right)\right]$ and

$$Q_{\alpha \beta }=2{\left(G_{\beta \beta }^{\alpha }\right)}^2\mathrm{\Gamma }\left(1-\frac{1}{z_{\beta }}\right)\mathrm{\Omega }\left[{\widehat{S}}_{\beta }\right]\ge 0,$$ [S7]

where

$$\mathrm{\Omega }\left[\widehat{f}\right]={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\text{d}p\widehat{f}\left(p\right)\widehat{f}\left(-p\right)}.$$ [S8]

With ${\sigma }_p^{\alpha \beta }=\text{sgn}\left[p\left(v_{\alpha }-v_{\beta }\right)\right]$, one has

$${\left(-i{v}_p^{\alpha \beta }\right)}^{\frac{1}{z_{\beta }}-1}=\text{sin}\left(\frac{\pi }{2z_{\beta }}\right)|v_{\alpha }-v_{\beta }{|}^{\frac{1}{z_{\beta }}-1}\cdot \left[1-i{\sigma }_p^{\alpha \beta }\text{tan}\left(\left(1+\frac{1}{z_{\beta }}\right)\frac{\pi }{2}\right)\right].$$ [S9]

Now we are in a position to analyze the small-p behavior. One has to search for dynamical exponents for which the limit $p\to 0$ is nontrivial, which is determined by the smallest power of p in Eq. S6. This has to be done self-consistently for all modes. We find that different conditions arise depending on which diagonal elements of the mode coupling matrices vanish. To characterize the possible scenarios, we define the set ${\mathbb{I}}_{\alpha }:=\left\{\beta :G_{\beta \beta }^{\alpha }\ne 0\right\}$ of nonzero diagonal mode coupling coefficients. One obtains, from Eq. S6, through power counting the system of equations,

$$z_{\alpha }=\{\begin{array}{lll}2\hfill & \text{if}\hfill & {\mathbb{I}}_{\alpha }=\mathrm{Ø}\hfill \\ 3/2\hfill & \text{if}\hfill & \alpha \in {\mathbb{I}}_{\alpha }\hfill \\ {\text{min}}_{\beta \in {\mathbb{I}}_{\alpha }}\left[\left(1+\frac{1}{z_{\beta }}\right)\right]\hfill & \text{else}\hfill & \hfill \end{array}$$ [S10]

and the domain

$$1<z_{\alpha }\le 2\forall \alpha$$ [S11]

for the possible dynamical exponents.