Mathematical framework for activity-based cancer biomarkers

Significance

The discovery of cancer at an early stage improves treatment outcomes, yet cancer detection thresholds based on measuring the abundance of biomarkers produced by small tumors are biologically limited. Here we develop a mathematical framework to explore the use of activity-based biomarkers for early cancer detection. In contrast to abundance-based biomarkers, activity-based biomarkers rely on the catalytic activity of enzymes to amplify cancer-derived signals and allow detection of small tumors. Using a class of activity-based biomarkers called synthetic biomarkers, we comprehensively explore how detection sensitivities depend on probe design, enzymatic activity, and organ physiology, and how they may be precisely tuned to reveal the presence of small tumors in humans.

Abstract

Advances in nanomedicine are providing sophisticated functions to precisely control the behavior of nanoscale drugs and diagnostics. Strategies that coopt protease activity as molecular triggers are increasingly important in nanoparticle design, yet the pharmacokinetics of these systems are challenging to understand without a quantitative framework to reveal nonintuitive associations. We describe a multicompartment mathematical model to predict strategies for ultrasensitive detection of cancer using synthetic biomarkers, a class of activity-based probes that amplify cancer-derived signals into urine as a noninvasive diagnostic. Using a model formulation made of a PEG core conjugated with protease-cleavable peptides, we explore a vast design space and identify guidelines for increasing sensitivity that depend on critical parameters such as enzyme kinetics, dosage, and probe stability. According to this model, synthetic biomarkers that circulate in stealth but then activate at sites of disease have the theoretical capacity to discriminate tumors as small as 5 mm in diameter—a threshold sensitivity that is otherwise challenging for medical imaging and blood biomarkers to achieve. This model may be adapted to describe the behavior of additional activity-based approaches to allow cross-platform comparisons, and to predict allometric scaling across species.

The clinical management of cancer is increasingly dependent on the discovery of new biomarkers and the development of ultrasensitive technologies to detect them at a stage when therapeutic interventions may be effective (1, 2). However, despite their growing importance, biomarkers lack predictive power to impact patient outcomes during the earliest stages of disease. The challenges are multifaceted: Biomarkers are shed from tumors at rates that vary by four orders in magnitude (3), are significantly diluted in blood, and circulate for short periods. Recent mathematical studies showed that tumors may remain undetectable with blood biomarkers for an entire decade following tumorigenesis, reaching 1–2.5 cm in diameter (4, 5). To increase sensitivity, major research areas include the development of ultrasensitive in vitro diagnostic platforms (6–11), as well as methods to increase biomarker production by solid tumors (12, 13). These approaches are designed to measure the quantity, or abundance, of a disease biomarker.

In contrast to abundance-based methods, activity-based probes are a class of agents that are administered in prodiagnostic form but produce strong diagnostic signals after enzymatic activation (14, 15). These approaches rely on disease-associated enzymes as catalysts to produce a detection signal, of which proteases are particularly potent because the cleavage of peptide bonds is irreversible, and a single protease can cleave many substrates to amplify signals. However, activity-based probes operate within a narrow time window and are activated by off-target tissues. A mathematical model of activity-based probes may aid in examining the critical parameters that determine specificity and sensitivity, and predict the use of activity-based probes in new clinical settings such as predicting disease progression earlier than standards of care (3).

To date, pharmacokinetic models have been developed for abundance-based drugs and diagnostics—such as predicting nanoparticle (NP) targeting to tumor vasculature (11), identifying rate-limiting steps in the distribution of drugs within tumors (16–18), providing guidelines to increase NP penetration (19), and modeling NP disassembly at the glomerulus (20). Here, we establish a mathematical framework for synthetic biomarkers, a class of activity-based probes that amplify disease-derived signals into urine for easy analysis (3, 21–24). We use model formulations based on a size-tunable PEG core conjugated with protease substrates in a mouse model of colorectal cancer (CRC). By accounting for key nanomaterial, biochemical, and physiological parameters, our model predicts urine pharmacokinetics and reveals nonintuitive behavior of activity-based biomarkers.

Results

Multicompartment Model of Synthetic Biomarkers.

Synthetic biomarkers are made of NPs conjugated with protease-cleavable peptides. Following administration, a chain of events unfolds to detect disease: (i) NPs accumulate in diseased tissue, (ii) peptides are cleaved by local proteases, (iii) the cleavage fragments are cleared into urine, and (iv) the urine is analyzed by multiple analytical platforms. In previous studies (3, 21–23), we engineered synthetic biomarkers for use in different diseases and methods of urinalysis. Here we chose to use PEG cores to formally explore the role of scaffold size, fluorogenic substrates to quantify kinetics by fluorescent imaging, and a xenograft model of CRC.

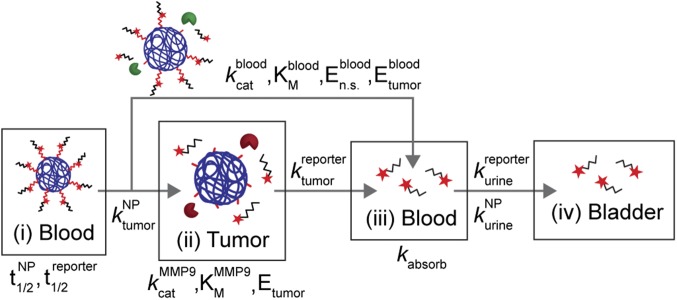
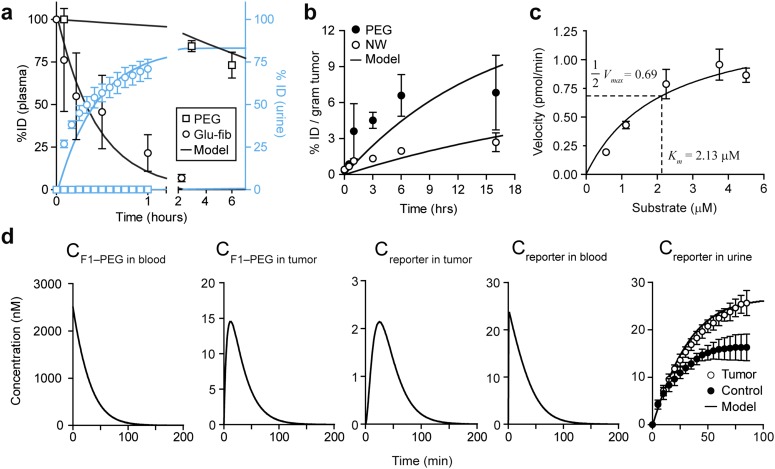
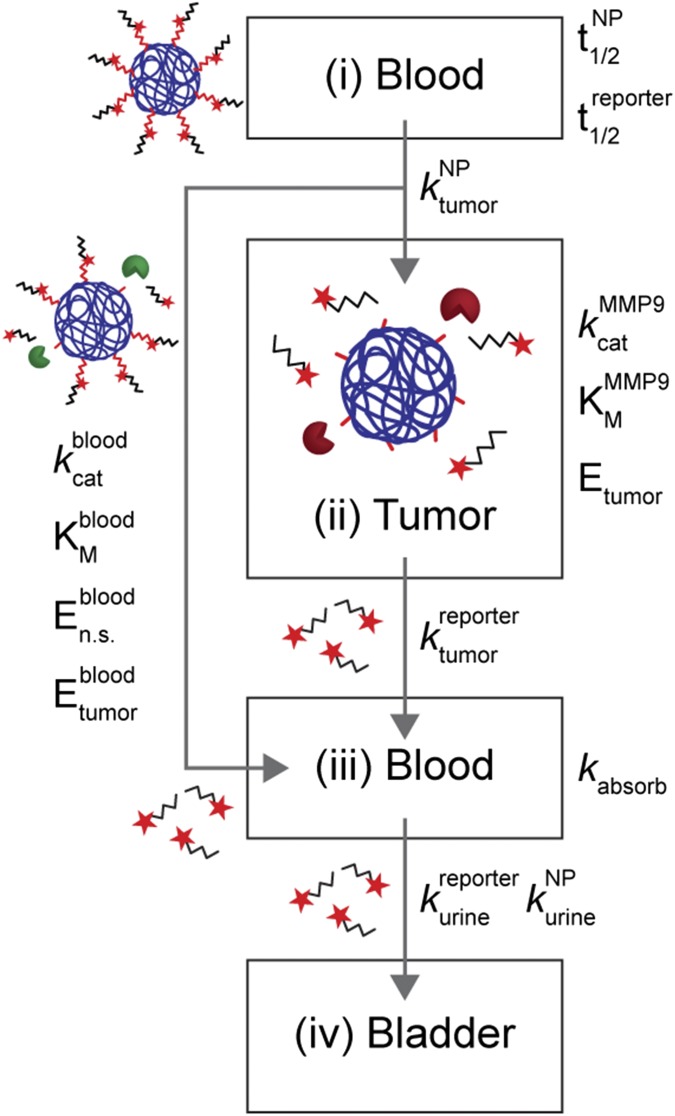
Our multicompartment model (Fig. 1 and SI Text) is made of a blood compartment (compartment i) where synthetic biomarkers circulate with half-life $t_{1/2}$, and passively diffuse into the tumor compartment (compartment ii) by the rate constant $k_{tumor}^{NP}$. In the tumor, peptides are cleaved by tumor proteases [e.g., matrix metalloproteinase 9 (MMP9)] following Michaelis−Menten enzyme kinetics (i.e., $k_{cat}^{MMP9}$, $K_M^{MMP9}$, $E_{MMP9}^{tumor}$), and passively diffuse ($k_{tumor}^{reporter}$) to the blood compartment (compartment iii). These reporters combine with reporters cleaved in the blood by circulating nonspecific proteases ($k_{cat}^{blood}$, $K_M^{blood}$, $E_{n.s.}^{blood}$) and tumor-secreted proteases ($E_{tumor}^{blood}$) before filtering into urine ($k_{urine}$). We assumed negligible nonspecific protease activities within the tumor compartment, and introduced a rate constant, $k_{absorb}$, to account for nonspecific binding (e.g., on blood vessels) and kidney reabsorption of our reporter. In each compartment, our model assumes a homogeneous, well-mixed distribution of NPs or reporters. A deterministic, well-mixed assumption is valid for Michaelis−Menten kinetics when a large number of molecules are involved, which is true for this study involving solution concentrations ranging from micromolar to nanomolar. Model parameters are summarized in Table S1.

Fig. 1.

Multicompartment model for synthetic biomarkers. Synthetic biomarkers sense tumor protease activity to produce detection signals in urine. After i.v. administration, synthetic biomarkers diffuse into the tumor ($k_{tumor}^{NP}$) and are cleaved by tumor-associated proteases (e.g., MMP9) according to Michaelis−Menten kinetics ($k_{cat}^{MMP9}$, $K_M^{MMP9}$). The cleaved reporters then diffuse back into blood, where they combine with reporters produced from nonspecific proteases ($k_{cat}^{blood}$, $K_M^{blood}$, and $E_{n.s.}^{blood}$) and secreted tumor-associated proteases ($E_{tumor}^{blood}$). A fraction of the reporters are reabsorbed by the kidneys ($k_{absorb}$) before clearance into urine ($k_{urine}^{reporter}$). See SI Text for derivation of model equations.

Table S1.

Nanomaterial and physiological parameters used in the model

	Parameter	Description	Unit	Value	Range simulated
NP and reporter clearance rates	N	NP dose	M	2.5 × 10−6	1.3–2 × 10−5
	$k_{MPS}^{NP}$	rate of NP clearance by MPS	min–1	6 × 10−4	—
	$k_{MPS}^{reporter}$	rate of reporter clearance by MPS	min–1	6.4 × 10−3	—
	$k_{urine}^{NP}$	rate at which NP filters into urine	min–1	1.7 x 10−5	—
	$k_{urine}^{reporter}$	rate at which reporters filter into urine	min–1	3.2 × 10−2	—
	$t_{1/2}^{NP}$	plasma half-life of NP scaffold*	hr	18.7	18–300 h
	$t_{1/2}^{reporter}$	plasma half-life of reporter*	min	18.1	—
	$k_{absorb}$	rate of NP and reporter reabsorption	min–1	2.9	—
Tumor permeability	$k_{tumor}^{NP}$	rate of NP diffusion across tumor vessels	min–1	1.4 × 10−4	1.4 × 10−4–1.4
	$k_{tumor}^{reporter}$	rate of reporter diffusion across tumor vessels	min–1	8.9 × 10−2	—
Tumor-specific protease activity	$k_{cat}^{tumor}$	catalytic efficiency of MMP-9 for Q1†	min–1	0.5	1.3 × 10−1–2.0
	$K_M^{tumor}$	Michaelis−Menten constant of MMP-9 for Q1	M	2.1 × 10−6	—
	$E_{tumor}$	concentration of proteases in tumor	M	7.2 × 10−7	1.8 × 10−7–2.9 × 10−6
	$E_{tumor}^{blood}$	concentration of shed proteases in blood	M	7.2 × 10−8	1.8 × 10−8–2.9 × 10−7
Nonspecific protease activity	$k_{cat}^{blood}$	catalytic efficiency for Q1	min–1	6.0 × 10−2	3.8 × 10−3–6.0 × 10−2
	$K_M^{blood}$	Michaelis−Menten constant for Q1	M	1.0 × 10−5	—
	$E_{n.s.}^{blood}$	concentration in blood	M	4.0 × 10−6	2.7 × 10−7–4.0 × 10−6
CEA	R	CEA secretion rate	ng per cells per day	—	1.5 × 10−9–2.6 × 10−5
	$t_{1/2}^{CEA}$	plasma half-life of CEA	h	72	—

^*$t_{1/2}=[1/(k_{MPS}+k_{urine})]\text{ln}\left(2\right)$.

^†Q1 = PLGVRG.

Sensing Protease Activity with Peptide−PEG Synthetic Biomarkers.

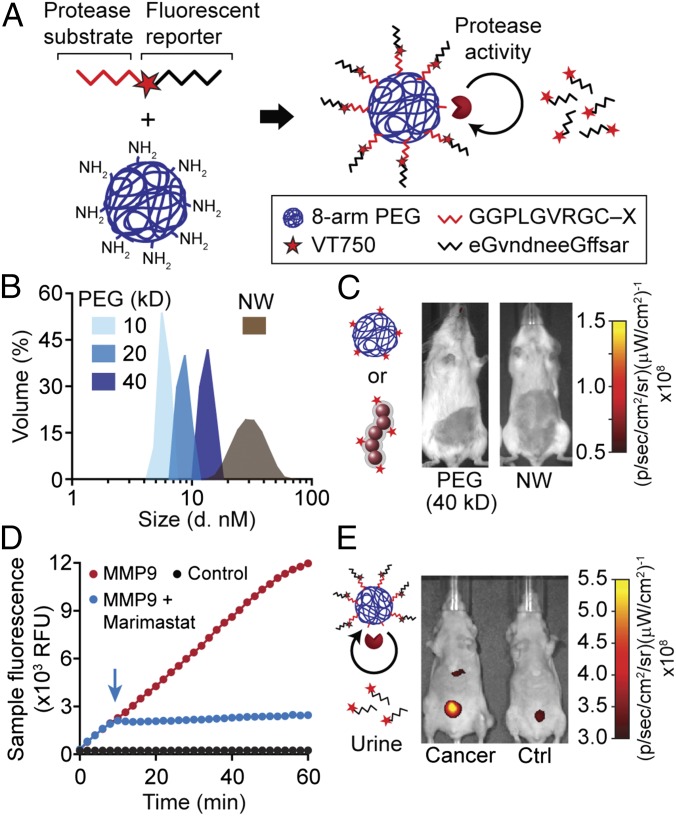
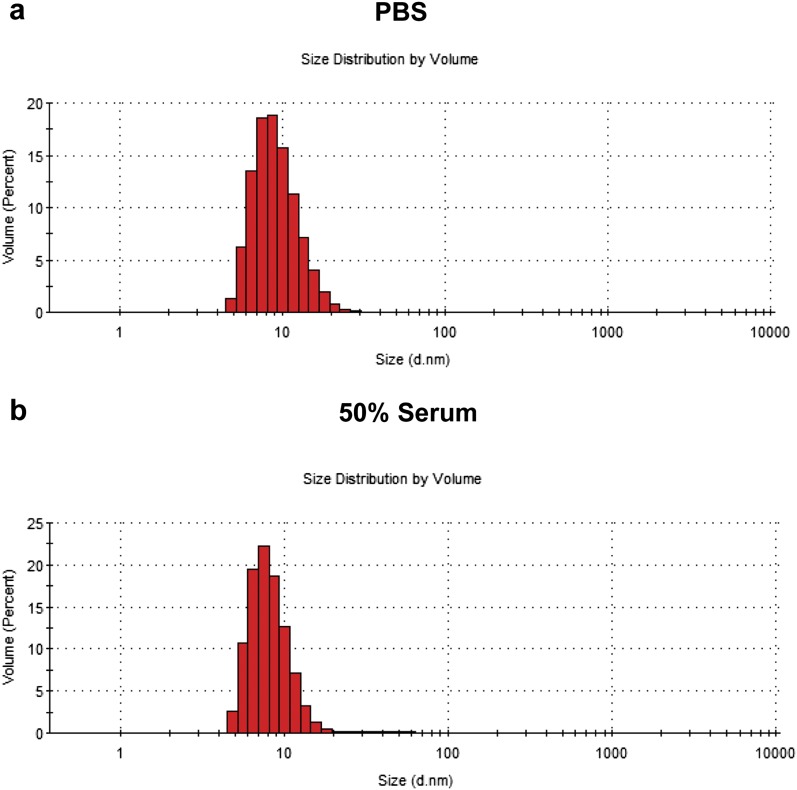
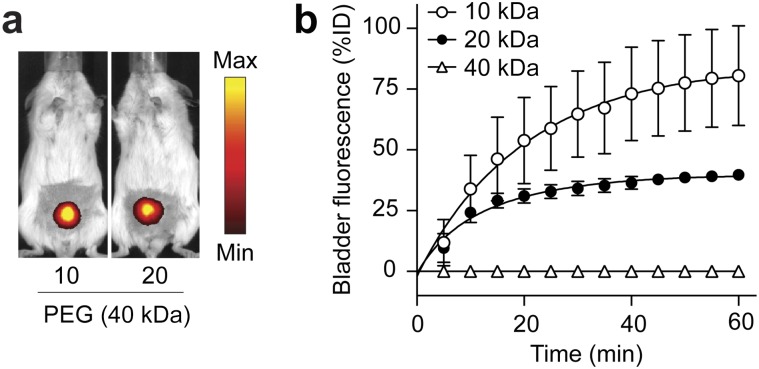
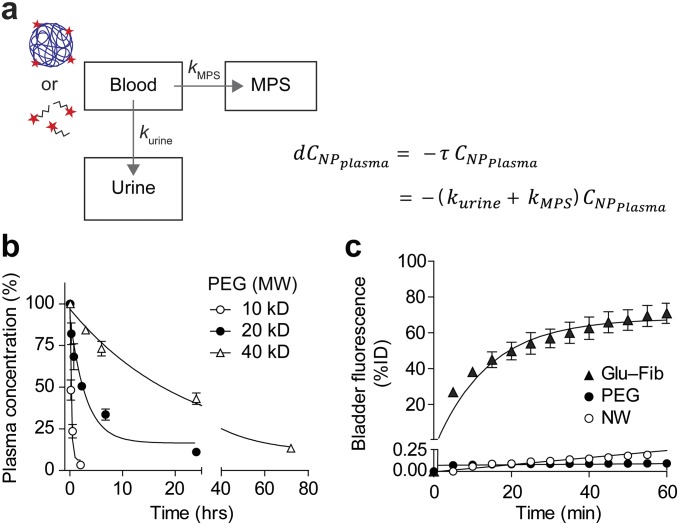
A key feature of synthetic biomarkers is the use of a nanoscale core to increase the hydrodynamic diameter of surface-conjugated peptides beyond the pore size of the glomerulus, which for NPs is ∼5 nm in diameter (25); as a result, peptides conjugated to NPs appear in the urine after a cleavage event. To explore this size dependency in a model system, we analyzed amine-terminated eight-arm branched PEG (10 kDa, 20 kDa, and 40 kDa) by dynamic light scattering (DLS) and observed increases in hydrodynamic diameters from ∼3 nm to 10 nm corresponding to their molecular weights (Fig. 2 A and B) that were similar to measurements made in 50% FBS (Fig. S1). Benchmarked against the size of our previous nanoworm (NW) formulation (∼30 nm), PEG NPs were smaller by severalfold, which increases passive diffusion rates (18). To determine renal clearance efficiencies, we administered fluorescent PEG and NWs and detected urine levels up to ∼80% of injected dose (ID) for 10 kDa PEG and ∼40% ID for 20 kDa PEG within 60 min (Fig. S2). By contrast, 40 kDa PEG and NWs filtered at negligible levels into the urine (∼0.09% ID and ∼0.19% ID, respectively), consistent with the size exclusion limit of the glomerulus (Fig. 2C). Based on these results, we selected 40kD PEG to develop our model.

Fig. 2.

PEG-based synthetic biomarkers detect cancer from urine. (A) Schematic of a PEG core conjugated with tandem peptides made of an MMP-sensitive substrate (red) and a fluorophore-labeled reporter (black). The reporter fragments are released from the PEG scaffold after cleavage by proteases. (B) DLS analysis of PEG (blue) and NWs (brown) with hydrodynamic diameters. (C) Representative images of healthy mice after infusion with fluorescent 40-kDa PEG or NWs showing negligible clearance into the bladder. (D) Kinetics of substrate hydrolysis after incubation of Q1–PEG with MMP9 (red), MMP + Marimastat (blue), or PBS control (black). Arrow indicates time point when Marimastat was added. RFU, relative fluorescence units. (E) Representative fluorescent images of tumor-bearing and healthy mice following administration of F1-PEG showing higher urine fluorescence in tumor-bearing mice.

Fig. S1.

DLS measurements of the diameter of eight-arm PEG. Histogram of the size distribution of 40kD PEG (A) in PBS with an average diameter of 9.5 nm and (B) in 50% FBS with an average of 8.4 nm.

Fig. S2.

Renal filtration kinetics of PEG in living animals. (A) Representative whole animal fluorescent IVIS images of mice dosed with 10 kDa or 20 kDa PEG. (B) Quantification of bladder fluorescence in mice given different molecular weight fractions of PEG (n = 3; error bars, s.d.).

Next, we investigated the use of peptide−PEG NPs to sense protease activity. We selected an MMP substrate PLGVRG (26) and synthesized a fluorogenic derivative, Q1, containing an N-terminal fluorophore (FAM), an internal quencher (CPQ-2), and a C-terminal cysteine residue for thiol-mediated coupling onto 40 kDa PEG (Q1 = 5FAM-GGPLGVRGKK(CPQ-2)-PEG2-C). To test substrate cleavage, we incubated Q1–PEG with MMP9, a gelatinase overexpressed by solid tumors, and detected a rapid increase in sample fluorescence (Fig. 2D). In the presence of the MMP inhibitor Marimastat (Fig. 2D, arrow), we observed an immediate arrest in fluorogenesis, confirming protease-dependent activation of Q1–PEG. To validate the use of PEG-based probes to cancer mice, we synthesized F1 (sequence, eGvndneeGffsarkGGPLGVRGC), a tandem peptide made of our MMP substrate PLGVRG and the protease-resistant d-stereoisomer of glutamate−fibrinopeptide B (Glu–Fib; sequence = eGvndneeGffsar, lowercase = d-isomer) (Fig. 2A). Glu–fib is a biologically inert peptide we used in past studies to promote renal clearance of cleaved peptide fragments (3). In mice bearing LS174T CRC tumors and given F1-PEG, we observed significant increases in bladder fluorescence compared with their healthy counterparts (Fig. 2E)—similar to our previous results using MMP-sensitive NWs (3). Together, our data indicated that synthetic biomarkers with PEG cores can sense protease activity and detect CRC from urine.

Extracting Model Parameters in Vivo.

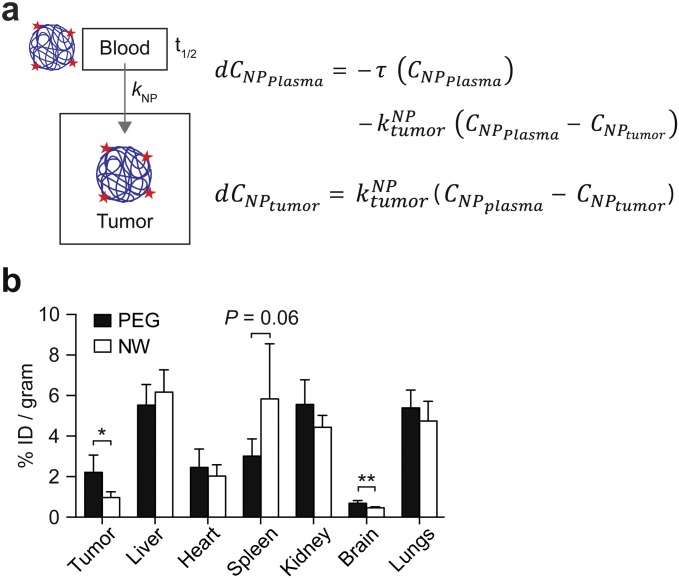
We next sought to identify the values of the parameters for our system of ordinary differential equations (ODEs). To determine circulation times, we assumed that systemic clearance is due to renal filtration and clearance by the mononuclear phagocyte system (MPS). Thus, to identify clearance rate constants ($k_{MPS}^{NP}$, $k_{MPS}^{reporter}$, $k_{urine}^{NP}$, and $k_{urine}^{reporter}$), we administered fluorescent PEG and Glu–fib and fitted their levels in blood and urine to a simplified three-compartment model (n = 3; error bars, s.d.; Figs. S3 and S4). Consistent with their relative size, Glu–fib cleared into the urine at a rate approximately fivefold greater than MPS clearance ($k_{urine}^{reporter}$ vs. $k_{MPS}^{reporter}$), but, by contrast, PEG was characterized by an MPS to renal clearance ($k_{MPS}^{NP}$ vs. $k_{urine}^{NP}$) ratio of ∼35 (Table S1). From these values, we calculated circulation half-lives of ∼18 min and ∼18.7 h for Glu–fib and PEG, respectively. To determine NP transport rate into tumors ($k_{tumor}^{NP}$), we administered fluorescent PEG and NWs into mice and analyzed tumor homogenates along with major organs at 0 h, 0.5 h, 1 h, 3 h, 6 h, and 16 h to determine the levels of localized NPs (n = 3; error bars, s.d.; Figs. S3 and S5). Using a simplified two-compartment model (Fig. 5A), we determined a tumor transport rate constant for PEG that was ∼3.5-fold greater than NWs (Table S1) and consistent with its smaller hydrodynamic diameter.

Fig. S3.

Identifying model parameters in a mouse model of CRC. The constants for the mathematical model were extracted by fitting governing equations to synthetic biomarker kinetics obtained in a mouse model of CRC. (A) Plasma (black) and urine (blue) kinetics following administration of 40 kDa PEG or Glu–fib (n = 3; error bars, s.d.). Solid lines represent model predicted behavior. (B) Kinetics of NP transport into tumors normalized against ID and size of tumors (n = 3; error bars, s.d.). (C) Michaelis−Menten analysis of the catalytic efficiency of human MMP9 for F1-PEG (substrate is PLGVRG; n = 3; error bars, s.d.). K_m, Michaelis−Menten constant. (D) Model and experimental data of the kinetics of NPs and reporters in model compartments (n = 3; error bars, s.d.). Solid lines represent model predicted behavior.

Fig. S4.

Mathematical modeling of circulation time. (A) Schematic of compartments and governing equations. (B) Plasma concentration of fluorescent PEG NPs following i.v. administration (n = 3; error bars, s.d.). (C) Bladder fluorescence of mice following i.v. administration of fluorescent Glu–Fib, PEG, or NWs (n = 3; errors bars, s.d.).

Fig. S5.

Mathematical modeling of tumor accumulation. (A) Schematic of compartments and governing equations. (B) Major organ distribution of fluorescently labeled PEG and NW following i.v. administration (n = 3; error bars, s.d.).

Fig. 5.

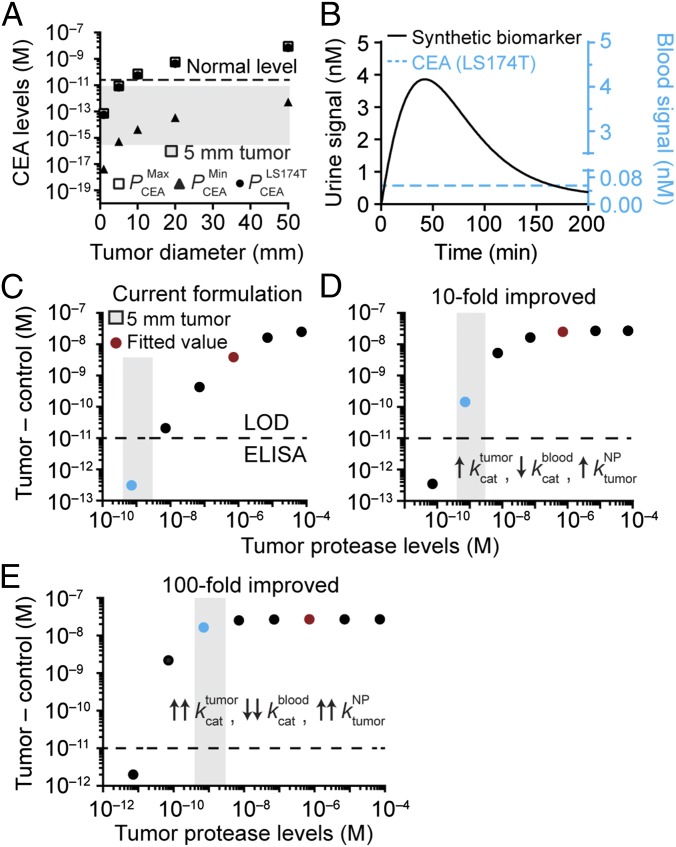
Strategies for ultrasensitive detection of cancer. Model predictions for detecting small tumors in humans. (A) Steady-state levels of CEA as a function of tumor diameter. CEA at levels resulting from tumors smaller than 10 mm in diameter is below the baseline value in healthy patients (5 ng/mL, dashed line). (B) The urine signal after administration of synthetic biomarkers showing amplification kinetics that surpass the steady-state concentration of CEA in blood. (C) Examining the use of synthetic biomarkers to detect tumors 5 mm in diameter, with the limit of detection of ELISA (dashed line), estimated range of protease concentrations (gray box), and detection signals in urine (dots). Urine signal versus protease concentration using synthetic biomarker parameters from study. The theoretical detection signal produced by 5 mm tumors in humans (blue dot) was below the limit of detection. (D) A 10-fold improved formulation of synthetic biomarkers resulted in over a two-decade increase in detection signal above the limit of detection. (E) A 100-fold improvement resulted in a four-decade increase to the maximum signal.

To incorporate the role of tumor proteases, we sought to determine a representative set of Michaelis−Menten constants to describe the rate at which F1-PEG may be cleaved by tumor proteases. For simplification, we focused on MMP9, a gelatinase that is involved in the growth and invasion of solid tumors and secreted by LS174T cells (n = 3; error bars, s.d.; Fig. S6). To determine the cleavage efficiency, we incubated different concentrations of F1-PEG with MMP9 and extracted initial cleavage velocities to calculate $k_{cat}^{MMP9}$ and $K_M^{MMP9}$ (n = 3; error bars, s.d.; Fig. 3C), resulting in a catalytic efficiency kcat/K_M ∼2.0 × 10⁵ M^–1⋅s^–1 that was similar to published values (27, 28). Similarly, we simplified nonspecific protease activities in blood into a single set of representative Michaelis−Menten constants ($k_{cat}^{blood}$, $K_M^{blood}$, $E_{n.s.}^{blood}$) whose values were determined by fitting our system of ODEs against urine kinetics obtained in healthy mice (Table S1). These values allowed us to fit for the concentration of tumor-specific proteases in the tumor and blood compartments ($E_{tumor}$ and $E_{tumor}^{blood}$, respectively) using tumor-bearing animals (n = 3; error bars, s.d.; Fig. S3D). Taken together, our experimentally fitted multicompartment model predicted urine pharmacokinetics that closely aligned with our experimental observations.

Fig. S6.

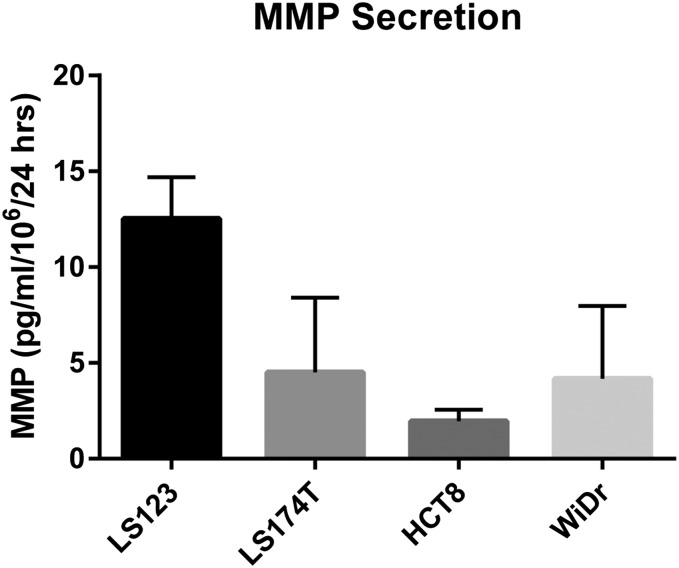
In vitro MMP9 secretion rates by representative CRC cell lines. ELISA quantification of human MMP9 in conditioned media. Rates were normalized by the number of tumor cells over a 24-h incubation period (n = 3; error bars, s.d.).

Fig. 3.

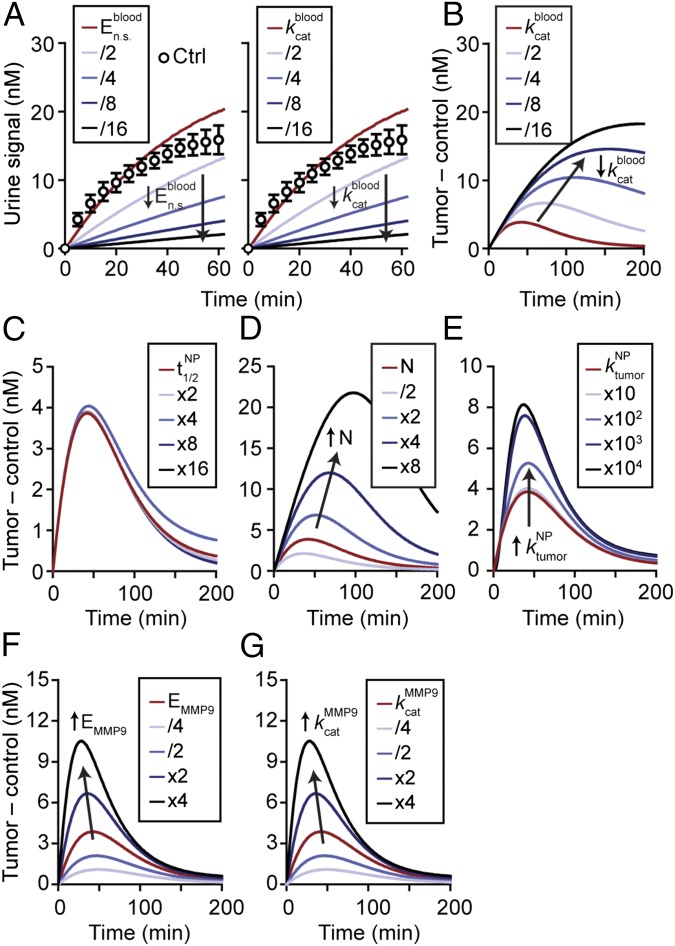
Model-predicted behavior of synthetic biomarkers. Key parameters within the mathematical model were varied to explore how they affect urine signals. (A) Urine signals decrease as background protease activities in blood ($E_{n.s.}^{blood}$, $k_{cat}^{blood}$) are decreased (n = 3; error bars, s.d.). (B) Normalized urine signals (Tumor – control) increased as $k_{cat}^{blood}$ was decreased. Predicted response of the urine signal as circulation time $t_{1/2}$ (C), dose $N$ (D), scaffold transport into tumor $k_{tumor}^{NP}$ (E), concentration of enzymes $E_{MMP9}$ (F), and rate of catalysis $k_{cat}^{MMP9}$ (G) were increased. Except for dose of NPs, all increases in the parameters resulted in increased detection signals. Arrows show direction of trend.

Exploring Synthetic Biomarker Properties in Silico.

We next set out to explore the parameters important for detection sensitivity. In healthy blood, circulating proteases such as the coagulation and complement family may cleave peptide substrates. Consequently, to explore the effect of nonspecific protease activity, we varied $k_{cat}^{blood}$ and $E_{n.s.}^{blood}$ from their starting values and observed that background urine signals were reduced to ∼10% of their original values if either $k_{cat}^{blood}$ or $E_{n.s.}^{blood}$ was reduced by a factor of 16 (n = 3; error bars, s.d.; Fig. 3A). Under these conditions, the difference in urine signal (i.e., tumor – control) increased and broadened, shifting the maximum peak intensity from ∼50–200 min (Fig. 3B). The time point at which our formulation was predicted to reach maximum levels (∼50 min, red line, Fig. 3B) was consistent with our previous studies in which we found maximum disease contrast to occur at 1 h (3, 22).

Synthetic biomarkers are formulated from nanomaterials whose properties can be precisely tuned (29); therefore, we explored how these properties may affect detection sensitivity. We increased the NP half-life ($t_{1/2}^{NP}$, Fig. 3C) from 18 h to 300 h by factors of 2, which had negligible effects, indicating that our formulation was sufficiently long-circulating to sense protease activity. By contrast, signal curves broadened and increased in magnitude when the administered dose of NPs ($N$, Fig. 3D) was increased from 2.5 μM (∼0.5 mg/kg) to 20 μM (∼4 mg/kg)—a range of concentrations for iron oxide nanomaterials that are well-tolerated in humans (30, 31). Intuitively, larger substrate reservoirs are created at higher NP doses, consequently prolonging and extending peak signal intensities. Similarly, increasing NP transport rates into tumors ($k_{tumor}^{NP}$, Fig. 3E) increased signal intensities, reaching a limit at values three to four decades above the starting rate constant (1.4 min^–1). At this point, detection signals are no longer dependent on NP transport but limited by the rate at which tumor proteases cleave the probe. Lastly, we increased the concentration of proteases in the tumor and blood compartments ($E_{MMP9}$, Fig. 3F), which shifted signal curves upward and maximum disease contrast earlier. Varying $k_{cat}^{MMP9}$ resulted in identical results (Fig. 3G) because protease activity is directly proportional to $k_{cat}$ and $E$ in the Michaelis−Menten model. Collectively, our mathematical model allows us to systematically explore the landscape of synthetic biomarker properties and identify critical system parameters that influence detection signals.

Validation of a Model Prediction.

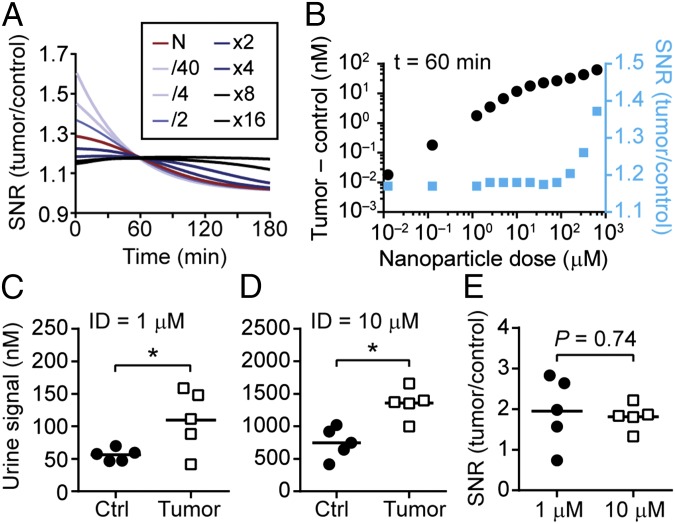
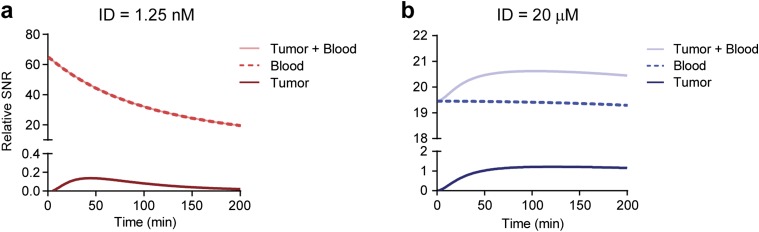
To validate the predictions of our model, we normalized the urine kinetics to examine the signal-to-noise ratio (SNR). At low concentrations of the administered dose, N, the SNR started at a peak and decreased exponentially (light blue, Fig. 4A), and by high N, the SNR kinetic curves appeared constant (black, Fig. 4A). To explain this nonintuitive behavior, we hypothesized that at low concentrations of N, the NPs are quickly degraded in the blood by tumor-secreted and background proteases, leaving a small fraction of the ID to diffuse into the tumor bed. Therefore, the SNR traces at low N are largely reflective of blood activity. By contrast, at high N, an NP reservoir is created in the circulation that saturates probe activation by circulating proteases, and maintains a sufficiently large concentration of unactivated NPs to move down their concentration gradient into the tumors. Because this process depends on passive diffusion, the signal generated from tumor proteases is expected to occur later than blood cleavage; therefore, the combined effect of early activation by blood and delayed activation by tumors results in relatively constant SNR kinetic curves. To test this in silico, we examined the bounds of our model at small N and observed that the signal (tumor + blood) was generated largely by blood but not tumor activation, and rapidly decayed (Fig. S7A). We then tested large N and observed that the detection signal resulted from a constant contribution from blood (i.e., protease activity saturated) and a delayed activation signal from the tumor (Fig. S7B), consistent with our hypothesis.

Fig. 4.

Validation of a nonintuitive model prediction. The model prediction that the SNR is invariant to NP concentrations was validated in a mouse model of CRC. (A) Kinetic curves of the SNR versus the administered dose N. At low N, SNR decays rapidly whereas at higher N, the SNR is held at a relatively steady value. (B) At an hour after NP administration, the SNR (blue) is invariant below an administered dose of 100 μM. The difference in signal between tumor and control urine samples is shown as black dots. Quantified urine signals from two cohorts of mice an hour after infusion with NPs at (C) 1 μM or (D) 10 μM (*P < 0.05, two-tailed paired t test, n = 5 mice). (E) The SNR between the two cohorts of mice was not statistically significant (P = 0.74).

Fig. S7.

Detection signals are due to blood and tumor activation at different times. The relative contributions to the detection signal from blood and tumor activation. (A) At low concentrations of the ID, detection signals are largely derived from blood activation, with negligible contributions from the tumor compartment. (B) Conversely, at high concentration of the ID, the signal from blood is nearly constant due to saturation of activity, revealing the underlying kinetics of tumor activation that reaches a maximum rate 50–75 min after NP administration.

One consequence of this model prediction is that within the range of reasonable NP doses (< 10 μM or ∼10 mg/kg) that would be expected to be well-tolerated in humans, the combined effect of probe activation by the blood and tumor compartments results in an SNR that would be relatively constant within an hour following administration (Fig. 4A and blue dots in Fig. 4B). To validate this prediction, we administered our probe in two cohorts of tumor-bearing mice at doses separated by an order of magnitude (1 μM and 10 μM, n = 5 mice, Fig. 4 C and D). Consistent with our model, the signal of the urine samples collected from tumor animals was significantly higher compared with the control group, and the difference in SNR was not statistically different (Fig. 4E). One implication of this result is that it may be possible to detect disease by administering our probes at “microdose” levels (≤ 100 μg in humans), a regulatory pathway created by the US Food and Drug Administration to compress the time frame and translational path to the clinic (32). This approach would require an ultrasensitive analytical method for urine analysis such as digital ELISA (23). Taken together, these experiments validate the potential of our quantitative framework to predict nonintuitive behavior in living systems.

Strategies for Early Cancer Detection.

Synthetic biomarker-based signals are produced by the catalytic activity of tumor proteases and concentrated into urine; therefore, we hypothesized that this platform may be used to detect early clinical-stage tumors that are otherwise challenging to detect using blood biomarkers. To establish a basis for comparison, we adapted a steady-state ODE model (5) for the blood biomarker carcinoembryonic antigen (CEA), a biomarker for CRC. At steady state, the concentration of CEA depends on its tumor production rate and circulation half-life (SI Text). To estimate the bounds, we assumed an average tumor cell density of 10⁶ cells per cubic millimeter, a CEA retention rate of 90% (5), a half-life of 72 h (33) ($t_{1/2}^{CEA}$), and minimum ($P_{CEA}^{Min}$) and maximum ($P_{CEA}^{Max}$) CEA production rates to be 15 pg and 260 ng per 10⁶ cells per 10 d, respectively, based on our previous analysis of 24 human CRC cell lines (median value = 1.5 ng per 10⁶ cells per 10 d) (3). At steady state, our model predicted that tumors smaller than 10 mm in diameter (e.g., 5 mm, gray box, Fig. 5A) would result in CEA levels beneath the baseline threshold expected in healthy individuals (34) (5 ng/mL, dashed line, Fig. 5A) and therefore, indistinguishable. By contrast, tumors that were 10 mm, 20 mm, and 50 mm in diameter were predicted to be detectable above normal levels of CEA only if the tumors produced the biomarker at a rate within the top 11%, 32%, or 60% of the range bounded by the maximum (square, Fig. 5A) and minimum (triangle, Fig. 5A) production rates, respectively. These results were consistent with previous mathematical studies, which established a detection limit of 1–2 cm for blood biomarkers (5). We next combined both models to analyze 10-mm-sized LS174T tumors, which produce CEA at a rate 100-fold above the median, and our model predicted that our activity-based probe would result in urine signals that would eclipse the steady-state level of CEA in blood (Fig. 5B). This prediction in humans is consistent with our prior study in mice, where we showed that synthetic biomarkers detected LS174T tumors earlier and with significantly higher predictive power compared with CEA analysis (3).

We next applied our model to calculate its potential to detect a theoretical human solid tumor of 5 mm in diameter, by considering the concentration of proteases expected in a tumor of this size. We chose 5-mm tumors as a target sensitivity threshold to represent a detection limit that is below the current thresholds associated with computed tomography (CT) (∼1 cm) (35) or blood biomarkers (∼1–2 cm) (4, 5). To estimate protease production rates, we analyzed conditioned media collected from four human CRC lines and detected MMP9 secretion rates ranging from ∼1.9 pg/10⁶ cells per day to 12.5 pg/10⁶ cells per day by ELISA (Fig. S6). To calculate a range of possible protease concentrations, we assumed an average tumor cell density of ∼10⁶/mm³ and a protease retention rate of 90% (i.e., 10% of proteases secreted by tumor cells are shed into the blood) (5) and arrived at protease levels ranging from ∼0.4 nM to 2.7 nM (gray box, Fig. 5C). We further adjusted the administered NP dose to reflect the higher total blood volume (∼5 L) in humans compared with mice (∼2 mL) to maintain an identical starting concentration.

Using these parameters, we explored how detection signals depend on the concentration of proteases produced by tumors. Our selected PEG formulation (red dot, Fig. 5C) produced detection signals in urine at concentrations (∼7 μM) that are readily detectable by ELISA (21, 22), which has a lower limit of detection of ∼10 pM (dashed line, Fig. 5C). Using 10 pM as the lower detection limit, we decreased protease levels from the empirically fitted value (red) by several decades to reach the range expected for 5-mm tumors (gray box), and observed that our model predicted urine signals to fall below the limit of detection (blue dot) (Fig. 5C). We then tested a 10-fold improved synthetic biomarker formulation by increasing the rates for tumor proteases and penetration by a factor of 10 ($k_{cat}^{tumor}$ and $k_{tumor}^{NP}$, respectively) while simultaneously decreasing nonspecific cleavage in blood ($k_{cat}^{blood}$) (Fig. 5D). With these values, the sensitivity markedly increased, elevating urine signals from 5-mm tumors to levels (Fig. 5D, blue dot) above the limit of detection by ELISA. Lastly, to assess the boundaries of our platform, we tested a 100-fold improved formulation (Fig. 5E) and found that urine signals were bounded by the maximum plateau (Fig. 5E, blue dot). Collectively, these data revealed important design variables for our diagnostic, and identified strategies to formulate ultrasensitive synthetic biomarkers for detecting 5-mm tumors.

Discussion

The development of computational techniques in concert with preclinical testing may provide the abilities to rapidly assess system parameters, identify tunable nanomaterial properties, and predict allometric scaling to humans (11, 16–19). Here, we established a computational framework to describe the pharmacokinetics of activity-based synthetic biomarkers and to quantitatively explore the parameters that are important for sensitive detection of disease.

In this study, we used a xenograft model of cancer to fit our mathematical model. Tumor vessels in both primary tumors and xenografts are poorly formed and fenestrated, and there is abundant evidence demonstrating the effectiveness of passive NP delivery to primary human tumors (36, 37)—results that are consistent with observations that were first borne out in xenograft tumor models. Based on these studies, xenograft tumors may be a reasonable first step for building a quantitative framework. Looking forward, our system of ODEs may be readily adapted for orthotopic or patient-derived xenografts, syngeneic transplant models, or genetically engineered models—because it is built from fundamental principles of mass transport—by identifying the values of the parameters that are specific for these tumors. In addition, our framework may be extended to describe the behavior of activity-based biomarkers such as fluorogenic peptide substrates designed to emit fluorescent signals after cleavage, or chemical substrates that covalently modify target proteases (14, 15). Here the model parameters related to probe pharmacokinetics will be different for each probe, and, within the tumor compartment, additional parameters will need to be incorporated to account for the mechanism by which the probe produces a detection signal. For example, for fluorogenic probes, these include the fluorescent intensity of a quenched and cleaved probe, background fluorescence of the target tissue, and clearance rate of the fluorescent reporter.

The main focus of this model is to address the limit of detection issue; thus we selected MMP9, a protease that is broadly dysregulated in solid cancers. MMPs have been implicated in cancer cell invasion and metastasis for over 35 years (38), and many of the hallmarks of cancer (39) are dependent on MMP activity. An ultrasensitive diagnostic for MMP9 activity may be used in clinical settings when the tumor type is known, such as after primary resection, when the surveillance protocol relies on CT or magnetic resonance imaging (MRI) despite their difficulties detecting metastasis 1–2 cm in diameter (35). MMP9 is expressed to activate VEGF ligands (40) during the angiogenic “switch” that occurs when nascent tumors are 1–2 mm in diameter; therefore, measuring MMP9 activity may allow detection of tumors smaller than the detection threshold of medical imaging. To address specificity in addition to sensitivity, the development of a cancer-type-specific diagnostic would require a multiplexed library of activity-based probes to account for the over 550 proteases expressed by the human genome that are dysregulated with disease or are organ-specific. Previous studies showed that the cleavage signatures of a 10-plex set of activity-based probes detected disease with significantly improved sensitivity and specificity compared with single probes, and identified activity-based signatures for CRC, liver fibrogenesis, and its resolution (3). Expanding our model to include multiple proteases as well as their endogenous inhibitors [e.g., tissue inhibitor of matrix metalloproteinases (TIMPs)] may allow prediction of disease signatures for use in multiplexed formats by mass spectrometry (3).

Methods

Synthetic Biomarker Synthesis.

Amine terminated eight-arm PEG (10 kDa, 20 kDa, and 40 kDa; Jenkem Technologies) was dissolved in PBS and passed through a 0.2-μm filter. DLS measurements were conducted on a Zetasizer (Malvern) in PBS and 50% FBS. A 20-fold molar excess of succinimidyl iodoacetate (SIA; Pierce) was reacted to introduce thiol reactive handles. Excess SIA was removed by FPLC on a Superdex 200 column (AKTA purifier; GE Healthcare). Cysteine-terminated peptides (Q1 = 5FAM-GGPLGVRGKK(CPQ-2)-PEG2-C, CPC Scientific; F1 = eGvndneeGffsarkGGPLGVRGC, lowercase = d-stereoisomer, Tufts University Peptide Core Facility) were then reacted with PEG at a 20:1 molar ratio before excess peptides were removed by FPLC. F1-PEG conjugated was further reacted with NHS-Vivotag750 (Perkin-Elmer) for imaging applications. NWs were synthesized according to previously published protocols and functionalized with peptides as above (41). All peptide−NP formulations were stored in PBS at 4 °C.

In Vitro Protease Assays.

Q1–PEG (3 μM by peptide) was mixed with human MMP-9 (5 μg/mL working concentration; Enzo Life Science) in a 384-well plate at 37 °C in activity buffer (50 mM Tris, 150 mM NaCl, 5 mM CaCl₂, 1 μm ZnCl₂) containing 1% BSA and monitored with a microplate reader (SpectroMax Gemini EM). Marimastat (Tocris Bioscience) was dissolved in DMSO and used at a final concentration of 5 μM. Michaelis−Menten constants were determined by assessing initial cleavage velocities at different substrate concentrations followed by mathematical fit using GraphPad 5.0 (Prism).

In Vivo Imaging.

All animal work was approved by the Committee on Animal Care at Massachusetts Institute of Technology (protocol 0414–022-17). To produce tumor xenografts, LS174T cancer cells (ATCC) were maintained in 10% FBS Eagle's minimum essential medium (EMEM) and inoculated s.c. (5 × 10⁶ cells/flank) in NU/NU mice (Charles River). Tumors were allowed to grow for ∼2 wk before administration of F1-PEG. Urinary kinetics was monitored by whole animal imaging (IVIS, Xenogen). For absolute quantification of urine fluorescence, urine samples were collected and quantified against VT-750 Glu–fib standards on a Licor Odyssey scanner.

Pharmacokinetics.

For organ distribution, VT-750-labeled PEG or NWs were administered i.v. (5 μM, 200 μL PBS) before necropsy. Major organs were placed in five volumes (wt/vol) of homogenization buffer (20 mM Tris, 1% SDS, pH 8.0) and homogenized by gentleMACS Octo dissociator (Mitenyi Biotec). VT-750 fluorescence in the supernatant was quantified against free VT-750 by Licor scanner. For half-life measurements, fluorescent NWs or PEG was administered i.v. (5 μM, 200 μL PBS) and ∼10 μL of blood was collected by retroorbital draws using microhematocrit tubes (VWR). Samples were transferred into 100 μL of PBS containing 5 mM EDTA and spun at 1,000 × g to pellet blood cells. Fluorescent VT-750 levels were quantified against a ladder of free VT-750 by Licor scanner.

Mathematical Modeling.

Our system of ODEs was solved with MatLAB using the differential equation solver ODE15s. The model was fitted to our experimental data by minimizing the square of the difference with a default tolerance of 10⁻²⁰. See SI Text for model equations.

Compartment Model of Activity-Based Biomarker

To construct a mathematical model of the NP’s flow through the body, we simplified the body into four separate compartments, each governed by its unique set of transport equations. The compartments are listed below, with the rationale for their representation as well as methodology and clarification on the various constants used.

A schematic of the model is shown as Scheme S1.

Scheme S1.

Compartment model for activity-based synthetic biomarkers.

Compartment I: Blood.

Following administration, we modeled the concentration of NPs in the blood, $d{C}_{N{P}_{plasma}}$, to take into account three primary actions. The first is clearance of the NPs in the plasma with a half-life of t_1/2, which depends on renal filtration (k_urine) and MPS (k_MPS) clearance rates,

$$d{C}_{N{P}_{plasma}}=\hspace{0.17em}-\tau \ast C_{N{P}_{Plasma}}=-\left(k_{urine}+k_{MPS}\right)\ast C_{N{P}_{Plasma}}$$ [S1]

where C_NP is the concentration of the NP in the plasma and

$$t_{1/2}=\frac{ln\left(2\right)}{\tau }.$$ [S2]

This clearance is represented in the first expression of Eq. S4 below. The second action taken into account is the transport of NPs into the tumor bed by diffusion according to Fick’s Law of Diffusion. Whereas Fick’s Law is usually written

$$d{C}_{N{P}_{plasma}}=\hspace{0.17em}\frac{P\ast S_{tumor}\ast (C_{N{P}_{tumor}}-C_{N{P}_{plasma}})}{V_{plasma}}$$ [S3]

with the parameters P, S_Tumor, and V_tumor representing the permeability constant, surface area, and volume of the tumor, respectively, we combined them into one parameter $k_{tumor}^{NP}$. Lastly, the third action is enzymatic degradation in the blood due to both specific (i.e., tumor-secreted MMP9) and nonspecific protease activity. This was modeled according to Michealis−Menten enzyme kinetics where the constants k_cat and K_M were determined through in vitro experiments and subsequent curve fittings. The commonly accepted Michaelis−Menten derivation uses the quasi-steady-state approximation (QSSA). QSSA is valid if [Eo/(So + K_m)] << 1, which, for our final fitted model (assuming 0–5 nM substrate concentration), results in an error (eta) term ∼0.1–0.3. Collectively, all three actions are represented in the following differential equation:

$$d{C}_{N{P}_{Plasma}}=-\tau \ast \left(C_{N{P}_{Plasma}}\right)-k_{tumor}^{NP}\ast \left(C_{N{P}_{Plasma}}-C_{N{P}_{Tumor}}\right)-\frac{k_{cat}^{MMP9}\ast E_{MMP9}^{blood}\ast C_{N{P}_{plasma}}}{\left(K_M^{MMP9}+C_{N{P}_{plasma}}\right)}-\frac{k_{cat}^{blood}\ast E_{n.s.}^{blood}\ast C_{N{P}_{plasma}}}{\left(K_M^{blood}+C_{N{P}_{plasma}}\right)}.$$ [S4]

Compartment II: Tumor Bed.

We modeled the concentration of our NPs within the tumor by describing the compartment by two equations, one describing $d{C}_{N{P}_{tumor}}$, the diffusion of the NP into the tissue and its subsequent cleaving by tumor-associated proteases, and the second equation describing $d{C}_{R_{tumor}}$, the production of cleaved reporter and its subsequent transport out of the tumor bed.

The first equation governing the concentration of the NP in the tumor is shown below in Eq. S5. It was constructed through a combination of Fick’s Law of Diffusion and the Michealis−Menten equation for enzyme kinetics, the assumption being that the only two dynamic changes to the concentration of the NPs in the tumor are the rate of diffusion from blood and the rate of enzymatic activity on the NP. Thus, the first equation for the diseased tissue is as follows:

$$d{C}_{N{P}_{tumor}}=k_{tumor}^{NP}\ast (C_{N{P}_{plasma}}-C_{N{P}_{tumor}})-\frac{k_{cat}^{MMP9}\ast E_{MMP9}^{tumor}\ast C_{N{P}_{tumor}}}{(K_M^{MMP9}+C_{N{P}_{tumor}})}.$$ [S5]

The second equation in the tumor compartment is the complement to Eq. S5; it focuses on the concentration of reporter cleaved from the NPs by protease activity and its subsequent diffusion into the blood stream. These processes are described as follows:

$$d{C}_{R_{tumor}}=\frac{k_{cat}^{MMP9}\ast E_{MMP9}^{tumor}\ast C_{N{P}_{tumor}}}{(K_M^{MMP9}+C_{N{P}_{tumor}})}-k_{tumor}^{reporter}\ast \left(C_{R_{tumor}}\right).$$ [S6]

Here the Michealis−Menten expression is the same as in Eq. S5 except it is of opposite sign (i.e., to represent production instead of loss), and the second expression governs the diffusion of the reporter out of the tumor bed. This equation omits C_Rplasma in the second expression for simplification because the reporter in the plasma is markedly diluted (by 2 mL of blood in mice, or 5 L in humans) and cleared rapidly (half-life ∼18 min, Table S1).

Compartment III: Blood.

The ODE to model reporter levels in blood is built from four expressions: (i) for the diffusion of the reporter into the blood stream from the tumor, (ii) for reporters cleaved form the NP by nonspecific protease activity in the blood, (iii) for clearance the reporter from blood (i.e., kidney filtration and MPS clearance), and (iv) for reabsorption of reporter (e.g., from renal tubules). The first three expressions are complements to expressions in Eqs. S4−S6 above. The fourth expression models reporter clearance, and the last expression models reporter reabsorption. The ensuing differential is

$$d{C}_{R_{Plasma}}=k_{tumor}^{reporter}\ast \left(C_{R_{tumor}}\right)+\frac{k_{cat}^{MMP9}\ast E_{MMP9}^{blood}\ast C_{N{P}_{plasma}}}{\left(K_M^{MMP9}+C_{N{P}_{plasma}}\right)}+\frac{k_{cat}^{blood}\ast E_{n.s.}^{blood}\ast C_{N{P}_{plasma}}}{\left(K_M^{blood}+C_{N{P}_{plasma}}\right)}-(k_{urine}^{reporter}+k_{MPS}^{reporter})\ast C_{R_{plasma}}-k_{absorb}\ast C_{R_{plasma}}.$$ [S7]

Here, $d{C}_{R_{plasma}}$ represents the rate of change of the concentration of the reporter protein in the plasma, where $C_{R_{plasma}}$ is the concentration of the reporter in the blood stream.

Compartment IV: Bladder.

The bladder compartment is described by a single rate equation on filtration with a first-order rate constant k_r. The resulting equation for the amount of the reporter secreted into the urine is

$$d{C}_{R_{urine}}=k_{urine}^{bladder}\ast C_{R_{plasma}}.$$ [S8]

Compartment Model of Abundance-Based Blood Biomarker.

A schematic of the blood biomarker model for CEA is shown as Scheme S2.

Scheme S2.

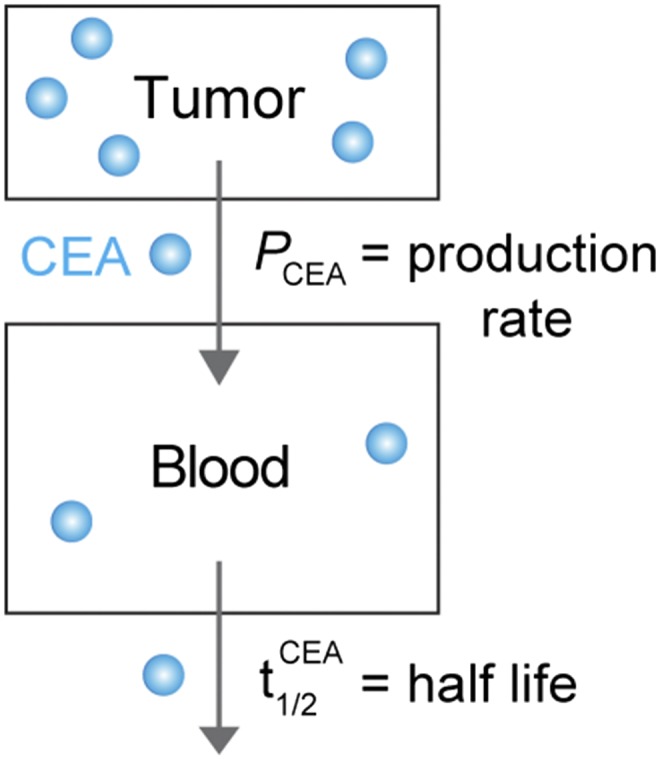
Compartment model for the blood biomarker CEA.

The concentration of CEA in blood is dependent on the tumor secretion rate ($P_{CEA}$) and the half-life of CEA ($t_{1/2}^{CEA}$),

$$\frac{dCEA}{dt}=P_{CEA}-\alpha CEA$$ [S9]

where

$P_{CEA}=\left(D\ast R\ast F\right)/V$; D is tumor cell density, R is CEA production rate, F is retention factor, V is volume of blood, and $\alpha =\hspace{0.17em}\ln \left(2\right)/t_{1/2}^{CEA}$.

At steady state,

$$\frac{dCEA}{dt}=P_{CEA}-\alpha CEA=0\to CE{A}_{s.s.}=\frac{P_{CEA}{t}_{1/2}^{CEA}}{\text{ln}\left(2\right)}.$$ [S10]