Significance
Untargeted metabolomics experiments usually rely on tandem MS (MS/MS) to identify the thousands of compounds in a biological sample. Today, the vast majority of metabolites remain unknown. Recently, several computational approaches were presented for searching molecular structure databases using MS/MS data. Here, we present CSI:FingerID, which combines fragmentation tree computation and machine learning. An in-depth evaluation on two large-scale datasets shows that our method can find 150% more correct identifications than the second-best search method. In comparison with the two runner-up methods, CSI:FingerID reaches 5.4-fold more unique identifications. We also present evaluations indicating that the performance of our method will further improve when more training data become available. CSI:FingerID is publicly available at www.csi-fingerid.org.
Keywords: mass spectrometry, small compound identification, metabolomics, bioinformatics, machine learning
Abstract
Metabolites provide a direct functional signature of cellular state. Untargeted metabolomics experiments usually rely on tandem MS to identify the thousands of compounds in a biological sample. Today, the vast majority of metabolites remain unknown. We present a method for searching molecular structure databases using tandem MS data of small molecules. Our method computes a fragmentation tree that best explains the fragmentation spectrum of an unknown molecule. We use the fragmentation tree to predict the molecular structure fingerprint of the unknown compound using machine learning. This fingerprint is then used to search a molecular structure database such as PubChem. Our method is shown to improve on the competing methods for computational metabolite identification by a considerable margin.
Metabolites, small molecules that are involved in cellular reactions, can provide detailed information about cellular state. Untargeted metabolomic studies may use NMR or MS technologies, but liquid chromatography followed by MS (LC/MS) can detect the highest number of metabolites from minimal amounts of sample (1, 2). Untargeted metabolomics comprehensively compares the mass spectral intensities of metabolite signals (peaks) between two or more samples (3, 4). Advances in MS instrumentation allow us to simultaneously detect thousands of metabolites in a biological sample. Identification of these compounds relies on tandem MS (MS/MS) data, produced by fragmenting the compound and recording the masses of the fragments. Structural elucidation remains a challenging problem, in particular for compounds that cannot be found in any spectral library (1): In total, all available spectral MS/MS libraries of pure chemical standards cover fewer than 20,000 compounds (5). Growth of spectral libraries is limited by the unavailability of pure reference standards for many compounds.
In contrast, molecular structure databases such as PubChem (6) and ChemSpider (7) contain millions of compounds, with PubChem alone having surpassed 50 million entries. Searching in molecular structure databases using MS/MS data is therefore considered a powerful tool for assisting an expert in the elucidation of a compound. This problem is considerably harder than the fundamental analysis step in the shotgun proteomics workflow, namely, searching peptide MS/MS data in a peptide sequence database (8): Unlike proteins and peptides, metabolites show a large structural variability and, consequently, also large variations in MS/MS fragmentation. Computational approaches for interpreting and predicting MS/MS data of small molecules date back to the 1960s (9): Due to the unavailability of molecular structure databases at that time, structure libraries were combinatorially generated and then “searched” using the experimental MS/MS data. “Modern” methods for this question have been developed since mid-2000. Particular progress has been made for restricted metabolite classes such as lipids (5), but as with peptides, results cannot be generalized to other metabolite classes. For the general case, several strategies have been proposed during recent years, including simulation of mass spectra from molecular structure (10, 11), combinatorial fragmentation (12–17), and prediction of molecular fingerprints (18, 19).
Searching in a molecular structure database is clearly limited to those compounds present in the database. Fragmentation trees have been introduced as a means of analyzing MS/MS data without the need of any (structural or spectral) database (20–22). In this paper, the term “fragmentation tree” is exclusively used to refer to the graph-theoretical concept introduced in ref. 20, not “spectral trees” that describe the dependencies of multiple MS measurements; see Vaniya and Fiehn (23) for a review. In more detail, our fragmentation trees are predicted from MS/MS data by an automated computational method such that peaks in the MS/MS spectrum are annotated with molecular formulas of the corresponding fragments, and fragments are connected via assumed losses. Clearly, there exist other approaches with the broad aim of identifying metabolites, such as network-based methods (24–26) and combined approaches (27); see Hufsky et al. (28) for a review of computational methods in MS-based metabolite identification.
It is undisputed that MS/MS data alone are insufficient for full structural elucidation of metabolites. We argue that elucidation of stereochemistry is currently beyond the power of automated search engines, so we try to recover the correct constitution (bond structure) of the query molecule, that is, the identity and connectivity (with bond multiplicities) of the atoms, but no stereochemistry information. Throughout this paper, we refer to the constitution of the molecule as its structure. In practice, orthogonal information is usually available, both analytical (retention time, ion mobility drift time, infrared and UV spectroscopy, and NMR data) and on the experimental setup (extraction procedure and organism) (29, 30). We assume that this information is not presented to the search engines but rather used in a postprocessing step to manually select the best solution from the output list of the engine. This is comparable to the everyday use of search engines for the internet.
Here, we present CSI (Compound Structure Identification):FingerID for searching a molecular structure database using MS/MS data. Our method combines computation and comparison of fragmentation trees with machine learning techniques for the prediction of molecular properties of the unknown compound (19). Our method shows significantly increased identification rates compared with all existing state-of-the-art methods for the problem. CSI:FingerID is available at www.csi-fingerid.org/. Our method can expedite the identification of metabolites in an untargeted workflow for the numerous cases where no reference measurements are available in spectral libraries.
Results
Methods Overview.
Recently, we used fragmentation trees to boost the performance of molecular fingerprint prediction using multiple kernel learning (19). Here, we further combine this method with a kernel encoding chemical elements, a kernel based on recalibrated MS/MS data, five additional kernels based on fragmentation tree similarity, and two pseudokernels based on fragmentation tree alignments (31). We then add PubChem (CACTVS) fingerprints (881 molecular properties) and Klekota–Roth fingerprints (32) (4,860 molecular properties) to the pool of predictable fingerprints. This results in 1,415 molecular properties that can be learned from the data; we will refer to these molecular properties as the fingerprint of a molecular structure. Finally, we use maximum likelihood considerations and Platt probabilities to refine the fingerprint similarity scoring.
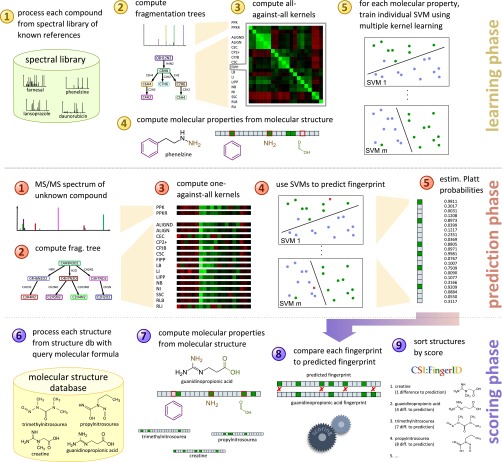
Our method can roughly be divided into three phases (Fig. 1): one phase for training the method on some reference set of known compounds and two phases for identifying unknown compounds. In all cases, MS/MS spectra of each compound are first transformed into a fragmentation tree by the automated method described in refs. 22 and 33, and both the MS/MS spectra and the fragmentation tree of the compound are used as input for the subsequent analysis. In the learning phase, we use a database of reference compounds with known molecular structure. The used machine learning method falls into the class of kernel methods (34), where a kernel denotes a similarity measure for either MS/MS spectra or fragmentation trees. We compute several such similarity measures for each pair of compounds in the reference data and also determine weights to combine all similarity measures into one (multiple kernel learning) (19). In addition, we compute the molecular fingerprint of each reference compound using its known structure. For each molecular property in the fingerprint, we then train a support vector machine (35) (SVM) that, using the kernel similarities, tries to separate compounds into those that exhibit the molecular property and those that do not. Platt probabilities (36) allow for a more fine-grained prediction, replacing the 0/1 predictions of classical SVM by some (posterior) probability for the presence of the molecular property.
Fig. 1.
Workflow of our method CSI:FingerID. During the learning phase, we use MS/MS reference data to train a set of predictors for molecular properties (the fingerprint). In the prediction phase we use MS/MS data of an unknown compound to find a fragmentation tree and to predict the fingerprint of the unknown. In the scoring phase we compare the predicted fingerprint of the unknown to fingerprints of molecular structures in a structure database, searching for a best match. See Materials and Methods for details.
The second part, where we want to find an unknown compound in a database of molecular structures, consists of two phases. In the prediction phase, we are given the MS/MS spectra of an unknown compound. We compute kernel similarities of the unknown compound against all compounds in the reference dataset, based on MS/MS spectra and fragmentation trees. We then use SVMs trained above to predict the (probability of the) presence or absence of each molecular property for the unknown compound. This results in a predicted fingerprint of the unknown compound. In the scoring phase, we compare the predicted fingerprint of the unknown compound against fingerprints of compounds in a molecular structure database such as PubChem. For each candidate molecular structure, its fingerprint is scored against the predicted fingerprint; candidate structures are sorted with respect to this score and reported back to the user. We stress that the unknown compound is usually not part of the training data; in our evaluation below, we make sure that this is never the case, using cross-validation.
Identification Quality.
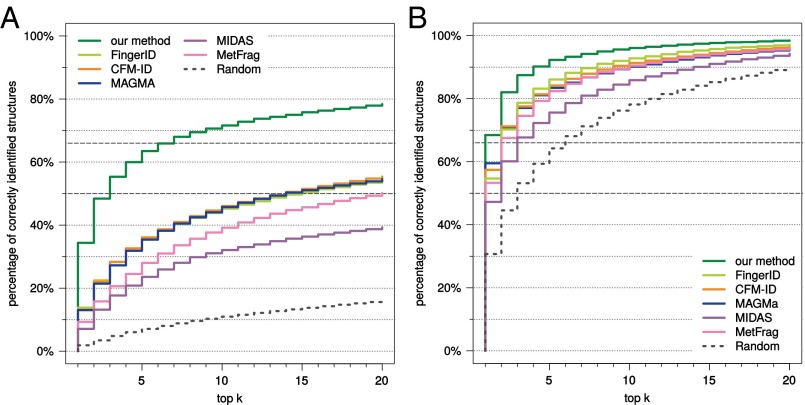
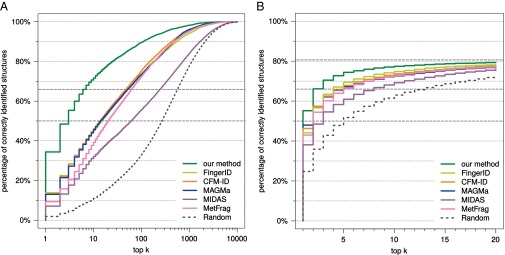
We first evaluate each method using compounds from the combined Agilent and GNPS (Global Natural Products Social) dataset. Our method strongly outperforms all other available tools for searching MS/MS data in a molecular structure database (Fig. 2). Compared with the runner-up, FingerID, the number of correct identifications is 2.5-fold higher (34.4% vs. 13.8%) when searching PubChem. CFM-ID reaches third place with 13.2% identification. We achieve 63.5% correct identifications in the top five output; next come FingerID with 36.1% and CFM-ID with 36.0%. Our method reaches an identification rate of 50% at the fractional rank 2.23, far ahead of CFM-ID (fractional rank 13.5) and MAGMa (13.7). It reaches an identification rate of 66.7% for fractional rank 6.38, again far ahead of CFM-ID (50.0) and MAGMa (51.0). See Fig. S1 for identification rates for all ranks. Searching biocompounds in the biodatabase, we achieve 68.5% correct identifications, compared with 59.5% and 57.4% for the two next-best methods, MAGMa and CFM-ID, respectively (Fig. 2). For 92.3% of the query compounds, the correct answer is contained in the top five for our method, compared with runners-up FingerID (86.1%) and CFM-ID (84.2%). Searching the complete combined dataset in the biodatabase, this corresponds to 55.2% correct identifications for our method (Fig. S1).
Fig. 2.
Methods evaluation: percentage of correctly identified structures found in the top k output of the different methods, for maximum rank . Searching compounds from the combined Agilent and GNPS dataset in PubChem (A) and the biocompounds from the combined dataset in the biodatabase (B). Identification rates 50% and 66.7% marked by dashed lines.
Fig. S1.
Methods evaluation: Percentage of correctly identified structures found in the top k output of the different methods, when searching with compounds from the combined dataset Agilent and GNPS. (A) Searching in PubChem for all maximum ranks. (B) Searching all compounds in the biodatabase. The maximum identification rate that can be reached is 80.58%, marked by a dashed gray line. Identification rates 50% and 66.7% are also marked by dashed gray lines.
The Agilent dataset is proprietary and, hence, cannot be used to evaluate future methods. We therefore repeated our analysis, this time searching with query instances from the two datasets individually (Figs. S2–S4). For the Agilent dataset, we reach 39.3% correct identifications, compared with 19.6% for FingerID and 15.3% for MAGMa. For the GNPS dataset, all methods suffer a slight loss in identification quality, but trends are highly similar to those reported above. For example, identification rates when searching PubChem decrease to 31.8% for our method, 12.1% for CFM-ID, and 11.8% for MAGMa, making the identification rate for our method 2.6-fold higher than for the runner-up. Our method achieves an identification rate of 50% for fractional rank 2.59, with the next-best being MAGMa (fractional rank 15.5) and CFM-ID (17.5). Our method reaches 66.7% identifications for fractional rank 7.62, compared with MetFrag (58.5) and MAGMa (63.1). When searching biocompounds in the biodatabase we reach 64.3% correct identifications, compared with 56.5% for MAGMa; the correct answer is in the top five for 90.2%, with runner-up FingerID (81.1%).
Fig. S2.
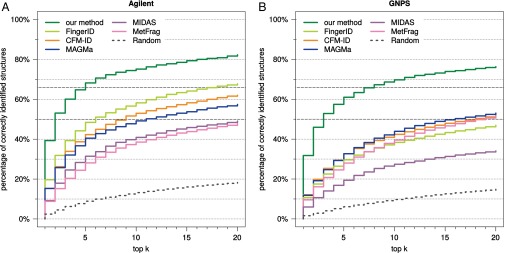
Methods evaluation: Percentage of correctly identified structures found in the top k output of the different methods, for maximum rank . Searching with compounds from Agilent (A) and compounds from GNPS (B) in PubChem. Identification rates 50% and 66.7% are marked by dashed gray lines.
Fig. S4.
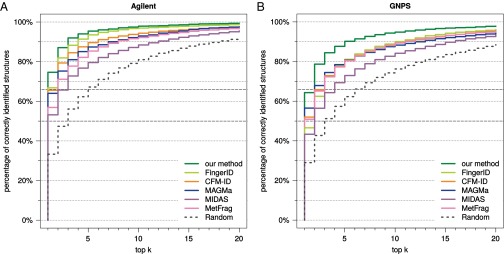
Methods evaluation: Percentage of correctly identified structures found in the top k output of the different methods, for maximum rank . Searching biocompounds from Agilent (A) and biocompounds from GNPS (B) in the biodatabase. Identification rates 50% and 66.7% are marked by dashed gray lines.
Fig. S3.
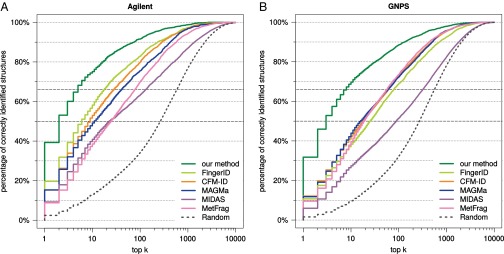
Methods evaluation: Percentage of correctly identified structures found in the top k output of the different methods, for all maximum ranks. Searching with compounds from Agilent (A) and compounds from GNPS (B) in PubChem. Identification rates 50% and 66.7% are marked by dashed gray lines.
We also evaluated against the baseline method of randomly ordering candidates with the correct molecular formula. Random ordering performs well for searching biocompounds in the biodatabase, with 30.7% correct identifications and 64.3% in the top five for the combined dataset. This demonstrates the power of knowing the correct molecular formula for structure elucidation when searching in a restricted structure database.
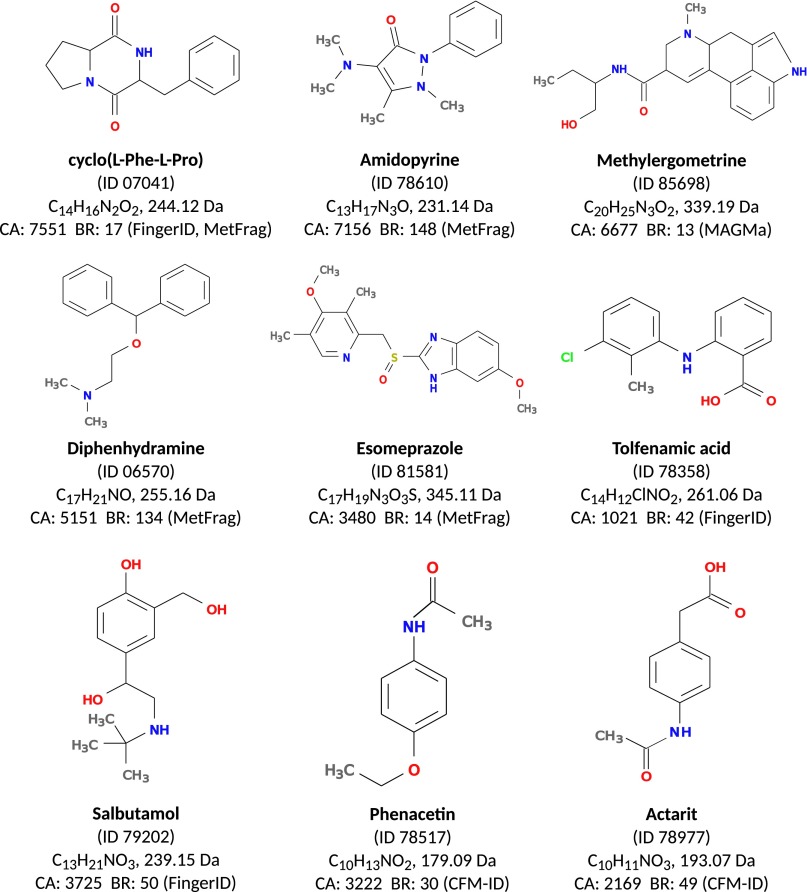
Next, we compare methods for each individual query instance. See Fig. 3 for the overlap in identifications of our method, CFM-ID, and MAGMa; our method reaches 5.4-fold more unique identifications (correctly identified compounds not identified by one of the other two methods) than CFM-ID and MAGMa for the combined dataset. A method outperforms another for some query instance if it places the correct structure on a better rank. On the combined dataset, our method outperforms CFM-ID for 65.6% of the instances, whereas CFM-ID outperforms our method for 23.8% of them. Our method outperforms MAGMa for 66.1% and is outperformed for 24.1% of the instances. For MIDAS, MetFrag, and FingerID, our method outperforms each of these methods for more than 68.9% of the instances and is outperformed for at most 20.6%. In all cases, the significance (sign test P value) is below . See Table S1 for an all-against-all comparison of methods. In Fig. S5 we show nine exemplar compounds that were correctly identified by our method, but not by any other method in this evaluation.
Fig. 3.
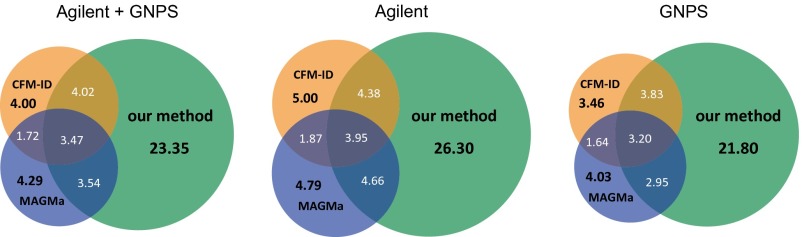
Venn diagram, percentages of correct identifications of our method, CFM-ID, and MAGMa. (Left) Searching compounds from Agilent and GNPS in PubChem. Here, 44.4% of the compounds were identified by at least one of the three methods. (Middle) Searching with compounds from Agilent in PubChem, with 51.0% identified by at least one method. (Right) Searching with compounds from GNPS in PubChem, with 40.9% identified by at least one method.
Table S1.
All-against-all comparison of methods
| Methods | Our method, % | FingerID, % | CFM-ID, % | MAGMa, % | MIDAS, % | MetFrag, % |
| Combined dataset | ||||||
| Our method | n/a | 68.99 | 65.60 | 66.09 | 76.18 | 70.95 |
| FingerID | 16.06 | n/a | 45.59 | 46.88 | 60.90 | 50.50 |
| CFM-ID | 23.83 | 46.68 | n/a | 46.12 | 61.48 | 52.31 |
| MAGMa | 24.10 | 46.61 | 44.82 | n/a | 59.08 | 50.80 |
| MIDAS | 17.34 | 34.43 | 31.72 | 32.89 | n/a | 37.39 |
| MetFrag | 20.58 | 43.35 | 39.98 | 41.10 | 55.86 | n/a |
| Agilent | ||||||
| Our method | n/a | 62.21 | 63.52 | 65.62 | 73.24 | 74.41 |
| FingerID | 17.80 | n/a | 49.48 | 52.92 | 61.81 | 62.76 |
| CFM-ID | 24.84 | 41.39 | n/a | 48.01 | 59.08 | 60.62 |
| MAGMa | 23.12 | 38.11 | 41.34 | n/a | 54.89 | 56.05 |
| MIDAS | 18.23 | 30.83 | 31.30 | 33.65 | n/a | 44.63 |
| MetFrag | 17.86 | 31.02 | 31.43 | 35.35 | 46.84 | n/a |
| GNPS | ||||||
| Our method | n/a | 72.60 | 66.71 | 66.35 | 77.74 | 69.11 |
| FingerID | 15.14 | n/a | 43.52 | 43.68 | 60.41 | 43.99 |
| CFM-ID | 23.29 | 49.49 | n/a | 45.12 | 62.75 | 47.89 |
| MAGMa | 24.62 | 51.12 | 46.66 | n/a | 61.30 | 48.01 |
| MIDAS | 16.87 | 36.35 | 31.95 | 32.49 | n/a | 33.55 |
| MetFrag | 22.02 | 49.90 | 44.52 | 44.15 | 60.65 | n/a |
Percentage of instances where one method (row) outperforms another one (column). Difference to 100% due to tied ranks. Results for the combined Agilent and GNPS dataset ( compounds), the Agilent dataset ( compounds), and the GNPS dataset ( compounds). n/a, not applicable.
Fig. S5.
Nine compounds from GNPS that were correctly identified in the PubChem database by our method, but not by any other method in our evaluation. ID is the GNPS ID of the compound, with prefix CCMSLIB000000. CA is the number of candidate structures in PubChem with the given molecular formula. BR (method) is the best (smallest) rank achieved by any method but CSI:FingerID.
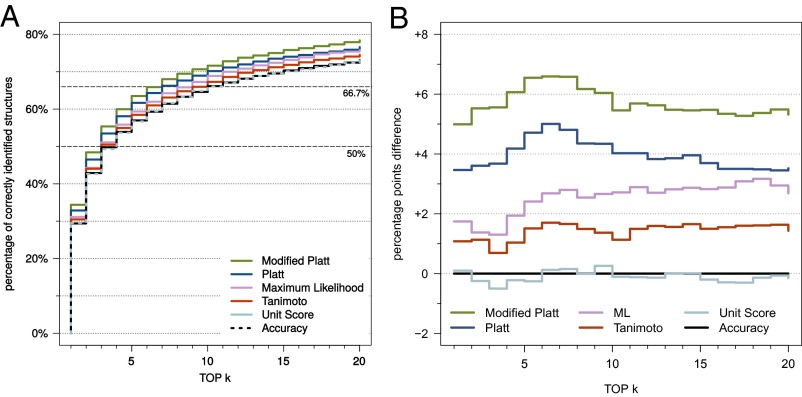
We evaluated several new scoring functions for CSI:FingerID and found three that perform better than the function proposed in refs. 18 and 19 (Fig. 4). Among these, “modified Platt” achieves the best identification rates and was therefore selected as the default scoring function for CSI:FingerID. Compared with the original scoring function based on predictor accuracy (18, 19), we reach 17.0% (4.99 percentage points) more correct identifications.
Fig. 4.
(A) Evaluation of different scoring functions for our method. Searching with compounds from the combined Agilent and GNPS dataset. See Materials and Methods for a description of the different scoring functions. (B) Difference in percentage points to the “accuracy” scoring function from refs. 18 and 19.
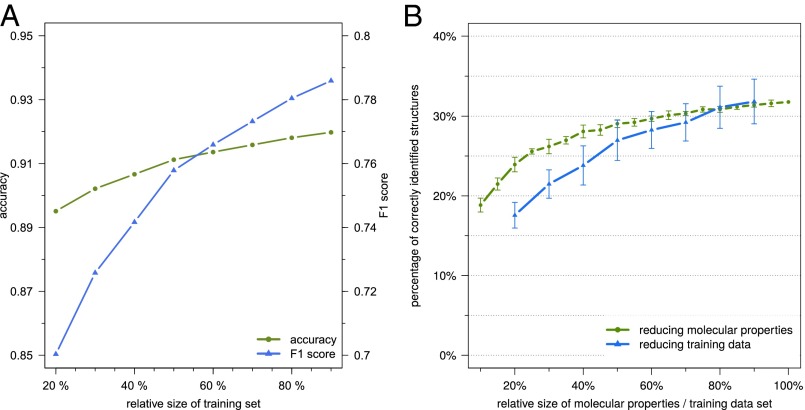
Because our method employs machine learning to predict molecular properties of the query compound, additional data can improve the performance of the predictors. To estimate the scale of this effect, we repeated the learning step for all predictors but this time presented the method with only a fraction of the data for learning. Average accuracy and F1 score of the predictors, as well as their performance for searching PubChem, are shown in Fig. 5. Varying the amount of training data, a monotonic increase is observed in accuracy and F1 score of the molecular property predictions. This growth does not saturate with the amount of data available in our experiments. For the resulting identification rates, we observe an almost linear increase when varying relative training data size between 40% and 90%, whereby 400 additional compounds in the training data result in an increase of roughly one percentage point in the identification rate.
Fig. 5.
Effects of training dataset size and of reducing the available molecular properties. (A) Average accuracy (green) and F1 score (blue) when training predictors on 20–90% of the combined training dataset (6,258 compounds), where 90% corresponds to the original 10-fold cross-validation. Note the different scales. From the 2,765 molecular properties that can be learned from the data, we use only those 712 for which the smaller class in the complete training dataset contains at least 5% of the structures. (B) Percentage of correctly identified structures when only a part of the training data (20–90%, blue) or only a part of the 2,765 molecular properties (10–100%, green) are available for prediction. Searching with compounds from GNPS in PubChem. SD calculated from 10 replicates (molecular property plot) or 10-fold cross-validation (training data plot).
We found that the performance of our method is influenced by more than just the amount of available training data: To a great extent, our method depends on “useful” molecular properties it can predict. Whether or not a particular molecular property is “useful” is determined by a multitude of parameters, such as discriminating power in PubChem (a molecular property that is inherited by the vast majority of compounds in PubChem is of little use in filtering out wrong candidates) or availability of training data for both the presence and absence of the property. To estimate how additional molecular properties can further improve the power of our method in the future, we artificially restricted the properties available for prediction and evaluated the method for the reduced sets of molecular properties (Fig. 5). We find that increasing the available molecular properties causes a monotonic, logarithm-like increase in the identification rate.
Finally, we evaluated all methods on an independent dataset from MassBank (Fig. S6). For this dataset, our method reaches 39.5% correct identifications searching PubChem, compared with 19.0 and 5.77% for the runners-up FingerID and MIDAS. For 267 compounds, we find corresponding structures in the training data; our method correctly identifies more than two-thirds (68.8%) of these compounds. We observe a major drop in identification accuracy for all methods but ours and FingerID on the complete MassBank dataset, and a similar behavior for all methods on the “novel” compounds: Searching for the 358 “novel” compounds in PubChem, our method reaches 17.7% correct identifications, followed by FingerID (8.34%) and MetFrag (5.70%).
Fig. S6.
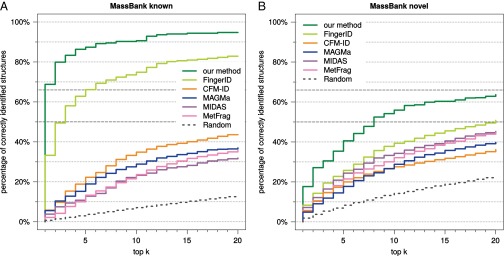
Evaluation on an independent dataset. (A) compounds from MassBank where a corresponding structure is contained in the training dataset. (B) “novel” compounds, with structures that are not present in the training dataset.
Discussion
When searching a molecular structure database using MS/MS data, CSI:FingerID achieves significantly better results than existing state-of-the-art methods. We observe a 2.5-fold increase of correct identifications compared with the runner-up method when searching PubChem and a 6.0- to 7.8-fold fractional rank decrease when trying to recover the correct solution for 50% or 66.7% of the instances, respectively.
It must be understood that finding the correct molecular structure in a molecular structure database as enormous as PubChem, being four orders of magnitude larger than existing MS/MS libraries, is highly challenging and will never be possible without a certain fraction of bogus identifications. We have deliberately left it to the expertise of the user to select the best molecular structure from the suggested candidates. Additional information such as citation frequencies or “number of PubChem substances” (16) can further assist the user in identifying the most promising candidates. We did not use such information in our evaluation to avoid overestimating the method’s power: Spectral libraries mostly contain well-described compounds where pure reference standards are available, and such compounds also receive many citations and have many PubChem substance entries.
For the independent dataset, our method shows good identification performance, but for the 358 “novel” compounds where no corresponding structure is present in the training data, we observe a severe drop in identification rates for all methods. We manually inspected the MS/MS data but detected no peculiarities. Currently, we cannot convincingly explain the drop of identification rates, despite testing numerous possible explanations such as number of candidates of an instance, or structural similarity of candidates to the true solution. The only peculiarity we found is distinctively reduced identification rates for flavonoid compounds in the “Washington” subdataset.
Running times of FingerID are fastest, whereas our approach, MetFrag, and MAGMa are roughly on par; in contrast, those of CFM-ID and MIDAS are two orders of magnitude higher (Table S2). This is not a problem for CFM-ID because spectrum simulation is done only once for each molecular structure during preprocessing, whereas comparison of spectra is very fast, but it can severely hinder the use of MIDAS in practice.
Table S2.
Running time estimation
| Measurement | Our method | CFM-ID | MAGMa | MIDAS | MetFrag | FingerID |
| Average running time per instance | 7 min 39 s | 7 h 30 min | 2 min 16 s | 1 d 9 h | 3 min 31 s | 2 s |
| Estimated time for GNPS dataset | 12 d 12 h | 407 d | 6 d 2 h | 5,389 d | 9 d 11 h | 2 min 18 s |
Programs were run on several different computer platforms. To allow for a fair comparison of running times, we randomly selected 100 query instances from the GNPS dataset (prefix ‟CCMSLIB000000”: 01653, 04381, 04518, 04871, 05595, 05789, 06205, 75306, 75308, 77117, 77152, 77991, 77993, 78067, 78096, 78142, 78259, 78304, 78312, 78359, 78391, 78416, 78452, 78524, 78532, 78554, 78587, 78601, 78699, 78705, 78741, 78761, 78799, 78814, 78872, 78964, 78998, 79053, 79176, 79194, 79362, 79417, 79435, 79503, 79536, 79542, 79611, 79615, 79627, 79640, 79645, 79661, 79743, 79749, 79872, 79906, 79942, 79955, 80085, 80098, 80132, 80156, 80216, 80329, 80348, 80386, 80391, 80438, 80452, 80458, 80476, 80477, 80516, 80557, 80603, 80604, 81549, 81558, 81726, 81747, 84737, 84790, 85057, 85130, 85229, 85243, 85270, 85288, 85335, 85401, 85558, 85891, 85901, 85932, 85950, 86022, 86066, 86107, 86114, and 86165), then ran all methods on the same compute platform (2x Intel XEON 6 Core E5-2630 at 2.30 GHz with 128 GB RAM). Running times are given for a single core. For our method, running times cover computation of the fragmentation tree and the kernel functions, prediction of all molecular properties, and scoring, but not the fingerprint computation for PubChem structures. For FingerID, we found that the original implementation was rather slow, requiring more than 1 h 41 min per instance. To this end, we used the same implementation as for CSI:FingerID, which resulted in the running times reported above. For MIDAS, five instances were not completed after running 6 d each; we count these instances as 6 d when taking the average. For CFM-ID, running times include the simulation of mass spectra, which has to be performed only once during preprocessing; when simulated spectra are available, running CFM-ID boils down to spectra comparison and, hence, is very swift. Running times for the GNPS dataset estimated for processing 3,868 compounds, except for CFM-ID: Here, spectral simulation has to be performed only once for each candidate molecular equation (97 molecular formulas in the randomly selected instances vs. 2,108 molecular formulas in GNPS).
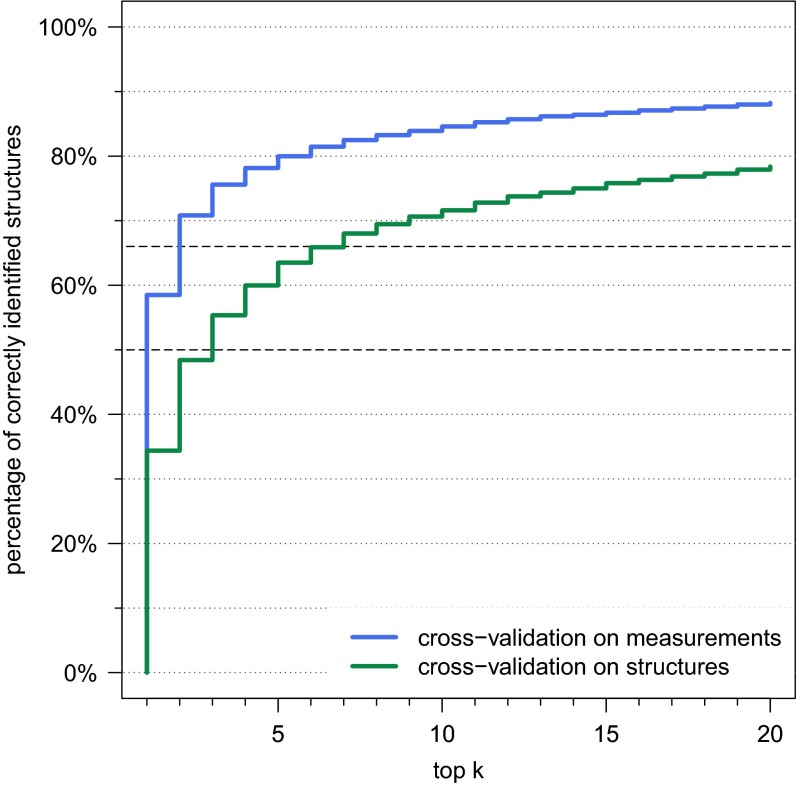
We found that choosing the correct cross-validation setup has a huge impact on our evaluation: If we choose cross-validation batches solely based on the individual measurements of the compounds, ignoring that two batches may contain the same structure, then our identification rate for searching in PubChem increases to a staggering 58.5% (Fig. S7). Manual inspection confirmed that different compounds with identical structure (constitution) often show highly similar MS/MS data.
Fig. S7.
Evaluation of the cross-validation setup for CSI:FingerID: Percentage of correctly identified structures found in the top k output, for maximum rank . Searching compounds from Agilent and GNPS in PubChem. We perform 10-fold cross-validation over the training compounds, ignoring that structures or even compounds may be found in two or more cross-validation batches (blue). For comparison, we plotted results for our method with structure-based cross-validation batches (green), identical to Fig. 2.
Molecular structure databases keep growing at a pace beyond synthesizing capacities. To this end, CSI:FingerID and other methods for searching in molecular structure databases represent a paradigm shift in the metabolomics field. Clearly, CSI:FingerID can and should be combined with other search engines. In particular, it should be accompanied by a search in spectral libraries (37) such as GNPS itself, and alternative methods for structural elucidation (24–26). In cases where the class of the query compound is known, more specialized approaches may be available, such as LipidBlast for lipids (5), or database searching and de novo sequencing for small peptides (38).
Compared with the original FingerID method of 2012 (18), identification rates of our method are 2.5-fold higher. With this and our experiments on limiting training data and molecular properties (Fig. 5), we predict that CSI:FingerID will reach even better identification rates in the near future. Our method can open up new paths beyond searching in structure databases such as PubChem: An obvious next step will be to search in structure databases containing hypothetical compounds (39, 40), potentially allowing us to overcome the limits of molecular structure databases.
Materials and Methods
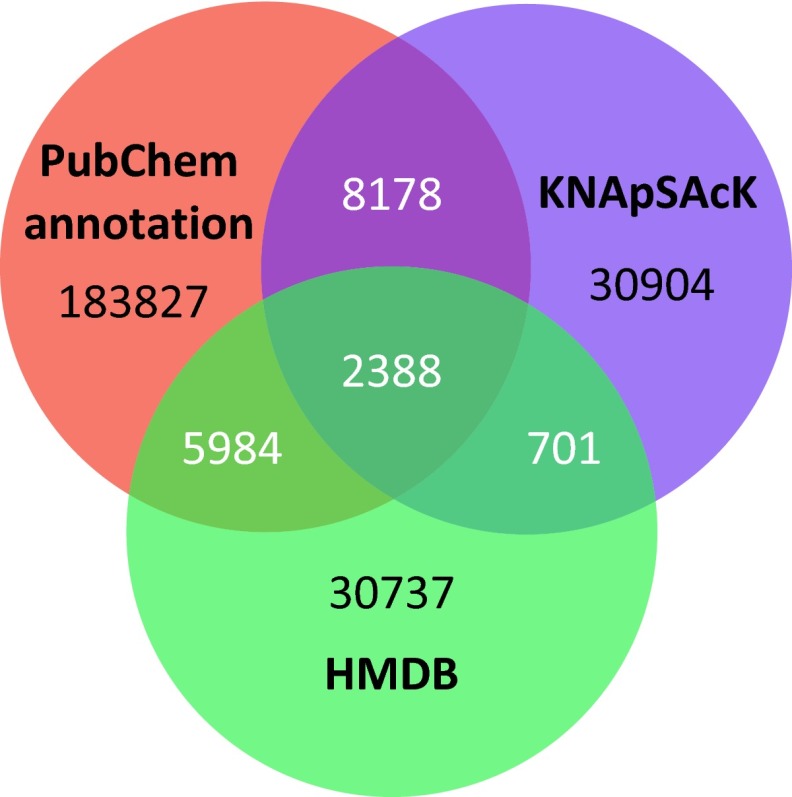
For training the method, we use a set of 4,138 small compounds from the public GNPS Public Spectral Libraries (https://gnps.ucsd.edu/ProteoSAFe/libraries.jsp) and 2,120 compounds from the MassHunter Forensics/Toxicology PCDL library (Agilent Technologies, Inc.). Evaluation is carried out by 10-fold cross-validation, such that no two batches may contain the same structure. We evaluate all methods using 3,868 compounds from GNPS and 2,055 compounds from the Agilent dataset. We present results for the combined Agilent and GNPS dataset, and for the two datasets individually. As an independent dataset, we use MS/MS data of 625 compounds from MassBank (41). We search a version of PubChem (downloaded on September 15, 2014) containing 52,926,405 compounds and 40,805,940 structures, and a filtered version of PubChem (biodatabase; see Table S3 and Fig. S8) containing 268,633 structures of biological interest (about 300,000 compounds); 1,010 compounds from the GNPS dataset and 140 compounds from the Agilent dataset cannot be found in the biodatabase. We refer to the remaining compounds as biocompounds. Searching the biodatabase was performed using both the complete datasets and the subsets of biocompounds.
Table S3.
Composition of the database of structures of biological interest (biodatabase)
| Database | No. of structures | No. of new structures |
| PubChem, with annotations | 200,377 | 200,377 |
| PubChem, with PubMed MESH citation | 62,782 | 36 |
| KNApSAcK | 42,171 | 31,605 |
| HMDB | 39,810 | 30,735 |
| ChEBI | 19,070 | 5,880 |
| Total biodatabase | 268,633 |
For each included subdatabase, we have listed its size at the time of inclusion (July 2014), and the number of structures it contributes to the biodatabase not present in the subdatabases above. For “PubChem, with annotations” only structures with at least one of the annotations “Biomedical Effects and Toxicity,” “Biomolecular Interactions and Pathways,” “Bionecessity,” “Biosystems and Pathways,” “Metabolism/Metabolites,” “Plant Concentrations,” “Depositor Provided PubMed Citations,” “Literature,” or “NLM Curated PubMed Citations” were accepted.
Fig. S8.
Venn diagram for the three largest subdatabases (filtered PubChem, KNApSAcK, and Human Metabolome Database): number of structures for compounds of biological interest (biodatabase).
We assume that we are able to identify up front the molecular formula of the unknown compound. For this, several approaches have been developed that analyze the MS/MS and isotope pattern data of the compound (42); for example, CFM-ID (10) identified the correct molecular formula for more than 90% of 1,491 nonpeptide metabolites using MS/MS data, and SIRIUS (43) was able to find the correct molecular for 10 out of 12 instances of the CASMI (Critical Assessment of Small Molecule Identification) 2013 contest. For all evaluated tools, molecular structure candidates are extracted from PubChem using the known molecular formula of the query.
We evaluate our method against the original FingerID method (18), CFM-ID (10), MAGMa (16), MIDAS (15), and MetFrag (14). FingerID was retrained on the combined training data, to enable a sensible evaluation against its successor presented here. CFM-ID also uses machine learning techniques but was not retrained on the new dataset due to computational limitations, resulting in an overlap (972 structures) between training and evaluation set. Identification rates reported here are slightly better than to those reported in ref. 10 using cross-validation. Average running times per query range from 2 s (FingerID) to more than 1 d (MIDAS) (Table S2). To avoid proliferating running times, MIDAS was stopped after 24 h of computation (more than 10 times the estimated average running time of any other program) for any instance. If the output of a tool did not contain the correct candidate, then all candidates not in the output were added to the end of the output list with identical, minimal score. Similarly, if a tool was unable to process an instance, then all candidates received identical score.
Lists are sorted with respect to scores provided by each tool. Ties in the score of a method are broken randomly, comparable to adding weak random noise to the scores. A given query instance is correctly identified if the correct structure is at the top position of the output list; it is in the top k if its rank in the output list is at most k.
See SI Materials and Methods for details.
SI Materials and Methods
Datasets and Structure Databases.
For training our method, the GNPS dataset of MS/MS spectra was downloaded from https://gnps.ucsd.edu/ProteoSAFe/libraries.jsp in December 2014 (FDA Library Pt 1 and Pt 2, PhytoChemical Library, NIH Clinical Collections 1 and 2, NIH Natural Products Library, Pharmacologically Active Compounds in the NIH Small Molecule Repository, and Faulkner Legacy Library provided by Sirenas MD). We analyzed compounds with mass below 1,010 Da where mass spectra were recorded in positive mode and mass accuracy of the parent peak was 10 ppm or better. We discarded compounds for which the structure could not be resolved and compounds containing deuterium, as well as spectra containing fewer than five peaks with relative intensity above 2%. After filtering, 4,138 compounds remain in the GNPS dataset. For each compound, GNPS provides a single collision-induced dissociation (CID) fragmentation spectrum at varying collision energies, recorded on an Agilent Q-TOF with electrospray ionization (few compounds were measured on a different experimental platform). The Agilent dataset is available under the name “MassHunter Forensics/Toxicology PCDL” (version B.04.01) from Agilent Technologies. The commercial library has been cleaned by idealizing peak masses and removing noise peaks, but Agilent provided us with an uncorrected version of this dataset, which is used here. For this dataset, 2,120 compounds fulfill the above criteria. Fragmentation spectra at collision energies 10, 20, and 40 eV were recorded on an Agilent 6500 series instrument with electrospray ionization. For this dataset, only relative intensities were recorded, so preprocessing was applied to merge spectra recorded at different collision energies (19, 22).
PubChem structures were downloaded from pubchem.ncbi.nlm.nih.gov/ in September 2014. For the biodatabase of compounds of biological interest, we start with all compounds in PubChem that have an appropriate Medical Subject Heading (MeSH; see Table S3), or at least one citation in PubMed (6) (www.ncbi.nlm.nih.gov/pubmed). We then include all compounds that are present in KNApSAcK (44) (kanaya.naist.jp/KNApSAcK/), the Human Metabolome DataBase (45) (HMDB, www.hmdb.ca/), or Chemical Entities of Biological Interest (46) (ChEBI, www.ebi.ac.uk/chebi/), all downloaded in July 2014. See Table S3 for details and Fig. S8 for the overlap of the filtered PubChem, KNApSAcK, and HMDB, which constitute the three largest sources of biomolecules; 1,018 compounds from the GNPS dataset and 143 compounds from the Agilent dataset are not included in any biomolecular structure database. We use IUPAC International Chemical Identifier (InChI) layer 1 to represent structures.
Molecular Fingerprints.
Molecular fingerprints (or “fingerprints” for short) are a method to encode the structure of a molecule. The most common type of a molecular fingerprint is a bit vector where each bit describes the presence or absence of a particular, fixed molecular property, such as the existence of a certain substructure in the molecule. As an example, bit 416 of the PubChem fingerprint (discussed below) encodes for the presence of two carbon atoms connected by a double bond. Given the molecular structure of a compound, we can deterministically transfer this into a molecular fingerprint. Fingerprints have been extensively used in the field of virtual screening (47); in particular, fingerprints can be used to estimate the structural similarity of two molecular structures using the Tanimoto coefficient (Jaccard index).
Different fingerprints have been defined and used in the literature over the last decades, including commercial fingerprints such as the Daylight fingerprints (Daylight Chemical Information Systems, Inc.). We use the following fingerprints, because these can be computed using freely available software:
CDK Substructure fingerprints with 307 molecular properties; see cdk.github.io/cdk/1.5/docs/api/org/openscience/cdk/fingerprint/SubstructureFingerprinter.html.
PubChem (CACTVS) fingerprints with 881 molecular properties; see ftp://ftp.ncbi.nlm.nih.gov/pubchem/specifications/pubchem_fingerprints.pdf.
Klekota–Roth fingerprints with 4,860 molecular properties; see ref. 32.
FP3 fingerprints with 55 molecular properties; see https://github.com/openbabel/openbabel/blob/master/data/patterns.txt. Computed using SMARTS patterns defined in Open Babel 2.3.2 (48).
MACCS fingerprint with 166 molecular properties; see https://github.com/openbabel/openbabel/blob/master/data/MACCS.txt. Computed using SMARTS patterns defined in Open Babel 2.3.2 (48).
All molecular properties are computed using the Chemistry Development Kit (CDK) 1.5.8 (49, 50) (sourceforge.net/projects/cdk/).
In total, we use 6,269 molecular properties; of these, 3,166 are constant within the training set structures. That is, either all structures show a particular molecular property or none do. From the remaining, 338 molecular properties are redundant: For each such property, there exists another property that is present or absent for exactly the same compounds in the training dataset. We remove redundant molecular properties because they do not provide additional information. We are left with 2,765 molecular properties that can be learned from the training data.
Fragmentation Tree Calculation.
We transform the MS/MS data of each compound into a fragmentation tree. Fragmentation trees were formally introduced by Böcker and Rasche in 2008 (20). The term “fragmentation tree” has been used much earlier in the MS literature (51); the important difference is that fragmentation trees in refs. 20 and 21 are computed directly from the data by an automated method, without knowing the molecular structure of the compound, and without the need for a database of spectra or molecular structures. We stress that here fragmentation trees are computed using tandem MS (MS/MS) data, not multiple MS data.
Formally, a fragmentation tree consists of a set of nodes V that are molecular formulas over some alphabet of elements and directed edges (arcs) E connecting these nodes. All edges are directed away from the root of the tree, and every node can be reached from the root via a unique series of edges. In small compound fragmentation, many fragments result from fragmentation cascades, that is, series of subsequent fragmentation events; these cascades are modeled by the tree structure of the fragmentation tree. Nodes of the fragmentation tree are molecular formulas of the unfragmented ion and its fragments; edges correspond to losses. For any fragmentation tree, each molecular formula can appear at most once as a node of the tree. For an edge , is the molecular formula of the corresponding loss; we demand that holds, that is, v is a subformula of u.
Given the molecular formula of the query compound, the optimal fragmentation tree was determined using integer linear programming (33) with the maximum a posteriori scoring scheme described in ref. 22. We set the maximal allowed mass deviation to 10 ppm (relative) and 0.002 Da (absolute). The tree size parameter is dynamically changed per tree such that at least 90% of the intensity is explained: We start with tree size prior . We then sum up the intensity of peaks that are explained by the resulting tree and divide this by the sum of intensity of peaks that have a decomposition as a subformula of the parent molecular formula. If the resulting ratio is smaller than 0.9, we multiply the prior by and restart computations.
Fingerprint Prediction.
Supervised learning is the machine learning task of inferring some predictor function from labeled training data. The learning algorithm analyzes the training data and produces a predictor function, which is then used for mapping new examples that are not part of the training data. To this end, the learning algorithm has to generalize from the training data to novel data with unknown labels in a “reasonable” way. To assess the power of the predictor function or to tune some external parameters, one can use cross-validation where the predictor function is trained on part of the data, then evaluated on the remainder. This shows whether the predictor function is able to generalize from the training data to unknown data.
Our goal is to predict a set of n molecular properties based on the available training data for , where is an MS/MS spectrum, is the corresponding fragmentation tree, and is a vector of n molecular properties for this molecular structure (the desired output). Here, denotes the presence and the absence of a given property. We will learn each molecular property of the fingerprint independently. For classification, we use SVMs, which we will briefly review first. Next, the concept of kernels is explained, followed by the mass spectra kernels and fragmentation tree kernels used in this paper. Finally, the multiple kernel learning approach to combine different kernels is described.
SVMs.
Given a set of training examples, each marked for having the property or not, the SVM training algorithm builds a model that assigns new examples into one of the two categories. We assume that our training data with is of the form (features are d-dimensional real-valued vectors) and (we predict each molecular property individually). The objective of an SVM is to find a hyperplane that separates the positive and negative examples with a large margin. Usually, we cannot find any such hyperplane in : To this end, we use a feature mapping ϕ that maps each into some high-dimensional real-valued space.
However, even after applying the feature mapping ϕ, our data are usually not linearly separable. To this end, we represent the amount of error made by misclassified as . This results in the following optimization problem for training the SVM, known as primal soft-margin SVM:
| [S1] |
| [S2] |
| [S3] |
Parameter C controls the error we allow to make: When C is large, we barely allow any mistakes and the algorithm is struggling to find a to make the error as small as possible. When C is small, the algorithm tries to find a hyperplane with maximum margin, even if some classification mistakes are made. In other words, a small parameter C prevents overfitting but also has the risk of underfitting. In practice, this parameter is usually tuned by cross-validation.
The kernel trick.
SVMs can be applied to nonlinear, high-dimensional and structured data using kernels. Given some input space , a function is a kernel function if for all ,
| [S4] |
where ϕ is a feature mapping and is an inner product in some space . The “trick” is to avoid the computation of , which can be computationally costly, or even impossible in case has infinite dimension. The kernel function allows us to compute the inner product without having to apply ϕ.
Consider the following simple example: Let ϕ map a mass spectrum x to a binary vector that, for each integer mass, encodes whether a peak is present or not. One can easily check that simply counts the number of common peaks between the mass spectra x and . However, it is clear that to compute this number we do not have to apply the mapping ϕ: If the two mass spectra are given as sorted lists, we can compute this number in time linear in the size of the two lists. To this end, shared peak counting is indeed a kernel function.
We apply the kernel function to a set of m examples in an all-against-all manner to compute the kernel matrix (Gram matrix) ,
| [S5] |
Using standard Lagrangian technique (35), the primal soft-margin SVM can be converted to the following optimization problem:
| [S6] |
| [S7] |
| [S8] |
where is a kernel function. This is known as the dual form of the soft margin SVM. For training the SVM, only labels and the kernel matrix are required, whereas the original data may be discarded. As a result, one can just focus on design and choose the kernel functions to best fit the application. For prediction, we are given an unknown example we want to classify. The decision function is the sign of the function
| [S9] |
where and are found as the optimal solutions in the training. We see that only training examples with affect the decision; these examples are called support vectors.
Kernels for mass spectra and fragmentation trees.
We now describe all kernels used as part of CSI:FingerID. We use most of the kernels described in ref. 19 and one kernel from ref. 52; we restate them here to make the paper more self-contained.
The following spectra kernel was introduced in ref. 52 and used as part of the original FingerID (18):
PPK: Probability product kernel. Each peak in the spectrum is modeled as a 2D Gaussian distribution and a spectrum will be a mixture of Gaussians. The kernel between two spectra is the product of probability masses integrated over the 2D space and it can be computed in closed form (18).
The following fragmentation tree kernels were introduced in ref. 19:
NB: Nodes binary. We use an (infinite-dimensional) binary vector to encode the presence of any possible molecular formula as a node (fragment) of the fragmentation tree. The resulting kernel counts the number of common fragments of two trees.
NI: Nodes intensity. We encode intensities of nodes (fragment peaks) in a real-valued vector. The resulting kernel is a weighted variant of NB.
LB: Loss binary. We encode the presence of all losses in a binary vector. The resulting kernel counts the number of common losses of two fragmentation trees.
LI: Loss intensity. A weighted variant of LB that uses the average intensity of the terminal nodes.
RLB: Root loss binary. We encode the presence of all root losses (that is, the total loss from the root to some node) in a binary vector.
RLI: Root loss intensity. A weighted variant of RLB that uses the intensity of the terminal node of a root loss if it is present in a fragmentation tree.
CSC: Common subtree counting kernel. We count the number of common subtrees between two fragmentation trees. If we find subtrees of the two trees with the same structure and the same losses attached to the edges, we regard this as a common subtree. The resulting kernel can be efficiently computed using dynamic programming (19).
In addition to the kernels above, we introduce nine additional kernels. Let be the subtree of T rooted at node u and containing all nodes that are descendants of u. When we explicitly construct feature space, the kernel function is just an inner product of the vectors in the space.
CEC: The chemical element counting kernel computes the dot product of a vector representation of the molecular formula. Elements of the molecular formula are weighted with 0 for hydrogen, 1 for carbon, 100 for nitrogen and oxygen, and 1,000 for all other elements.
- SSC: The substructure counting kernel counts common substructures: We first build a substructure set S containing molecular formulas of all fragments in the training data that occur at least 10 times and have a mass greater than Da. We then construct feature vectors
for all , where if s is a subformula of the molecular formula v. This vector counts for each substructure in S how many fragments in the tree are a superset of this substructure.[S10] CP2+: The common paths of length at least 2 kernel is a modification of the common path kernel from ref. 19 that counts only common paths of length at least two.
- CPJB: The common path joined binary kernel is a modification of the root loss binary kernel, and evaluates losses between all fragments and their descendants:
for all molecular formulas p of losses along a fragmentation path.[S11] ALIGN and ALIGND are fragmentation tree alignment pseudokernels (31), using the Pearson correlation of alignment scores of each query fragmentation tree to all trees in the training data. Alignments for the ALIGN kernel are computed as described in refs. 31 and 53 and do not penalize gaps. The ALIGND kernel uses a slightly different scoring function: each gap in the alignment is penalized with whereas the penalty for mismatches is reduced to for fragments and for losses.
For intensities , the probability product of logarithmized intensity ratios is defined as
| [S12] |
where σ is the SD of logarithmized intensity ratios. Probability products were introduced for the probability product kernel (18). In contrast to the PPK kernel, the PPK-recalibrated (PPKr) kernel is computed on preprocessed spectra: Peaks from different collision energies are merged, and noise peaks that have no explanation for the parent molecular formula within 20 ppm are removed. Furthermore, peaks are recalibrated using fragmentation trees as described in ref. 22. Similar to PPK, PPKr integrates the probability product using the 2D normal distribution of mass and intensity deviations.
We introduce two additional tree kernels that use one-dimensional normal distribution of logarithmized intensity ratios: Let be the intensity of the peak explained by the fragment v in the tree T.
- FIPP: The fragment intensity probability product kernel estimates the probability product of shared fragments in the trees, using a log-normal distribution over the intensities:
[S13] - LIPP: The loss intensity probability product kernel is similar to FIPP but computes the probability product of shared losses:
[S14]
Multiple kernel learning.
Multiple Kernel Learning (MKL) can be used when several sources of information are available for learning, all of which are represented by kernels. Given a set of kernels with corresponding kernel matrices , multiple kernel learning tries to assign weights to the individual kernels such that the resulting combined kernel has improved prediction performance. We apply the multiple kernel learning method ALIGNF of Cortes et al. (54), which was found to be the best-performing MKL method for this application in ref. 19.
The ALIGNF method relies on the concept of kernel-target alignment, the correlation of an input kernel matrix (pairwise similarities of training inputs) to an ideal target kernel matrix (pairwise similarities of training outputs). The kernel-target alignment is given by
| [S15] |
where denotes the Frobenius product of two matrices and denotes the Frobenius norm.
For single-label binary classification, the ideal target kernel is given by , which will give a kernel value of if and a kernel value of otherwise. Here, we have n molecular properties that we wish to jointly align against. Thus, we define the target kernel matrix based on multiple labels by
| [S16] |
which can be interpreted as the sum of n ideal target kernels of individual fingerprints.
For multiple kernel learning the ALIGNF method first centers the kernel matrices (making them zero-mean), by setting
| [S17] |
where is the identity matrix and is a vector with all ones. Then ALIGNF jointly seeks the weights μ that maximize the alignment score defined above between the convex combination of the centered input kernels and the target kernel by solving the following optimization problem:
| [S18] |
where . The learned kernel combination is subsequently used to train a set of SVMs, one for each fingerprint. We use the popular SVM implementation LIBSVM (55).
After the model has been trained, we are given MS/MS data of an unknown compound. To predict the fingerprint, we again compute the similarities between the novel spectrum and all training spectra, as well as the novel fragmentation tree and all training fragmentation trees. This is carried out using the kernel functions described above, resulting in a set of test kernel matrices. We combine these matrices using weights determined by multiple kernel learning in the training phase, and the combined kernel matrix is used by the SVM to make predictions.
Platt Probabilities.
Platt scaling allows us to transform the output of a predictor function into a probability distribution over classes: We ask for a classification that not only gives an answer, but also a degree of certainty about the answer. Formally, we want to estimate the posterior probability that our unknown molecule has a particular property, or not.
Platt (36) proposed using a sigmoid function as an approximation of posterior probabilities:
| [S19] |
where is the decision value and is the predicted label. Given training examples and labels , , we search for parameters that maximize the following likelihood (36):
where
| [S20] |
Here, is the number of examples with positive labels and the number of examples with negative labels. To solve this optimization problem, Lin et al. (56) proposed using a Newton method with backtracking line search. We refer readers to the original papers for more details. We use LIBSVM to estimate Platt probabilities.
Parameter Tuning and Cross-Validation.
Cross-validation is used to estimate how “accurately” a predictor function will perform on the unseen data and can also be used to estimate some external parameters specified by the user. One round of cross-validation involves partitioning a dataset into two complementary subsets, performing the analysis on one subset (the training set), and validating the analysis on the other subset (the testing set). Multiple rounds of cross-validation are performed using different partitions, and results are averaged over the rounds.
An n-fold cross-validation corresponds to partitioning the dataset into n subsets of (almost) identical size. Then, n rounds of cross-validation are performed, where in each round subsets are concatenated to form the training set, and the remaining subset is used as the testing set. For our cross-validation, we ensured that all compounds in the dataset with identical structure are contained in the same subset (batch) of the cross-validation.
The mass and intensity variance parameters of the PPK kernels were selected by a fivefold cross-validation on an independent dataset. The best parameter learned for mass variance is and for intensity variance is . These parameters are kept constant throughout subsequent learning steps. These parameters are used for the PPK and PPKr kernel of CSI:FingerID, and the FingerID method.
Individual SVMs were trained by 10-fold cross-validation on the combined dataset with 6,258 compounds. In our experiments, the parameter C in SVM is learned for each molecular property independently, using 10-fold cross-validation on the training data.
Performance Measures.
For a binary prediction, let TP, FP, TN, and FN denote the number of true positives, false positives, true negatives, and false negatives, respectively. The precision (positive predictive value) is , the sensitivity or recall is , and the specificity is . The F1 score is the harmonic mean of precision and recall, . The accuracy equals .
To avoid numerical instabilities, we add 0.5 pseudocounts to TP, FP, TN, and FN before estimating the above measures for any predictor of a molecular property. Similarly, we apply Laplace smoothing (additive smoothing) to Platt probabilities and replace probability x by for some small α; here, we choose where is the size of the evaluation dataset.
Fingerprint Scores.
A molecular property encodes the presence or absence of a particular substructure in the molecule structure as a binary value. To make our method robust and avoid overfitting to the training data, we discard molecular properties where the trained predictor reaches F1 score below 0.5 in cross-validation. We find that of the total 2,765 molecular properties pass this criterion. Let be the molecular property indices. A fingerprint is a subset . Each molecular structure candidate has an associated fingerprint. Because our fingerprint prediction is imperfect, we compare fingerprints via a scoring function . For finding the best-fitting candidate, we compare the predicted fingerprint to all candidate fingerprints , and sort candidates according to . A straightforward scoring function between the predicted and the database fingerprint is the Tanimoto score (Jaccard index) .
For all other scores, the predicted fingerprint and the candidate fingerprint F are compared via a weighted sum,
| [S21] |
with coefficients for . The accuracy score suggested in refs. 18 and 19 sets and , where is the accuracy of the predictor for molecular property i. The unit score sets and , simply counting the number of common molecular properties. The maximum likelihood score sets , , and , where and are the sensitivity and specificity of the predictor for molecular property i, respectively. This score can be interpreted as a log-likelihood estimate if we assume all predictors to be independent random variables. The Platt score sets and where is the Platt approximation of the posterior probability for molecular property i. This score is a posterior probability estimate of the complete fingerprint. The modified Platt score combines maximum likelihood and Platt score considerations, and sets
| [S22] |
Evaluation.
For evaluation, we discarded some compounds from the two datasets. Namely, we discarded compounds containing metal complexes and other structures not connected by covalent bonds, nonprotonated ions, and compounds that carry other charges. We discarded a total of 270 compounds from the GNPS dataset and 65 compounds from the Agilent dataset, including 27 compounds from Agilent that are absent from PubChem. This leaves us with 3,868 (GNPS) and 2,055 (Agilent) compounds, respectively. The reason for excluding these compounds is that some or all of the tested tools cannot process molecules that do not obey the above criteria: For example, the evaluated version of CFM-ID does not allow processing intrinsically charged molecules.
As an independent dataset, we downloaded MS/MS data measured in positive ion mode from MassBank (www.massbank.jp/). These measured compounds are provided by the Washington State University (268), the University of Connecticut (102), the Oswaldo Cruz Foundation (95), the Leibniz Institute for Plant Biochemistry (39), and the RIKEN Plant Science Center (403). All these compounds were measured on Q-TOF instruments. We discarded compounds exhibiting fewer than five peaks with relative intensity above 2% in the MS/MS data (222 compounds) and 52 compounds carrying a charge or containing nonprotonated ions as well as 8 compounds that are not contained in PubChem, leaving us with 625 compounds in the dataset. For 267 compounds the corresponding structure is contained in our training set, whereas 358 structures are “novel.”
Candidates from PubChem and the biodatabase were filtered by the above-mentioned criteria, that is, we discarded unconnected structures and compounds that carry charges.
FingerID (18) was used as described in the publication and predicts 528 molecular properties. Competitive Fragmentation Modeling ID (CFM-ID) (10) was downloaded from sourceforge.net/projects/cfm-id/ (version 1.5). As suggested in (10) we used the Combined Energy model (CE-CFM). From the 10 cross-validation models provided on the CFM website, we selected the first one. The GNPS dataset was processed using the “medium energy” model. We used the mass accuracy (maximum of 10 ppm and 0.01 Da) and probability threshold (0.001) suggested in ref. 10. MetFrag (14) was downloaded from c-ruttkies.github.io/MetFrag/projects/commandline/ on June 18, 2014 (MetFrag does not provide version numbers). We used a 10-ppm relative mass accuracy, a 0.005-Da absolute mass accuracy, and the Java virtual machine option Djava.util.Arrays.useLegacyMergeSort = true. In contrast to other approaches, MetFrag uses the sum (instead of the maximum) of relative and absolute mass accuracy. MIDAS (15) was downloaded from midas.omicsbio.org (version 1.1). MIDAS does not allow us to choose a relative mass accuracy; we chose an absolute mass accuracy of 0.01 Da. We modified MIDAS to output all candidates, instead of the top five only. In view of exceedingly long running times, we stopped MIDAS for those instances where computation was not completed after 24 h; the resulting instances were counted as random. MAGMa (16) (version 1.0) was provided as a standalone program by Lars Ridder, Wageningen University, Wageningen, The Netherlands, and was run with options -f -b 4 -c 0 -d 0 and mass accuracies of 0.001 Da and 10 ppm.
In our evaluation, we performed a certain amount of parameter optimization for all methods but found that the above choices resulted in maximum identification rates for the combined dataset. We retrained the original FingerID on the same training data as the method proposed here, using cross-validation; this is done to allow a sensible evaluation of the impact of the methodological advances. For CFM-ID, we also evaluated the “low-energy” and “high-energy” model for the GNPS dataset as well as an absolute mass accuracy of 0.002 Da and an intensity baseline of 0.02%. For MAGMa and MetFrag, we merge spectra at different fragmentation energies by choosing mass and intensity of the largest peak within the given mass accuracy. For MetFrag, this resulted in significantly better identification rates than the method proposed in the original MetFrag publication (14). For MetFrag, we also tested absolute mass accuracies of 0.001, 0.002, and 0.01 Da. For MAGMa, we also tested absolute mass accuracies of 0.002, 0.005, and 0.01 Da, and option -b 3.
CFM-ID, MAGMa, MIDAS, and MetFrag cannot process all instances, sometimes crashing and sometimes omitting the correct answer from the output list. Some problems are seemingly caused by atoms that have uncommon valence states, such as chlorine with valence five in 5-chlorylsulfanyl-1-methylindazole (PubChem CID 57613613). Using SMILES from PubChem for CFM-ID and SDF files from PubChem for MAGMa resulted in fewer crashes and was used here. The following numbers are for the combined Agilent and GNPS dataset with 5,923 instances: CFM-ID crashed for 3,429 candidates (less than 0.1% of the candidates) and did not return the correct structure in its output for 19 instances (0.3%). MAGMa crashed for 20 instances (0.3%) and did not return the correct answer in its output for 357 instances (6.0%). For 2,148 instances (36.3%), MIDAS crashed or ran into the time-out of 24 h; for 21 instances (0.4%), it did not return the correct answer in its output list. Finally, MetFrag did not return the correct answer in its output list for 45 instances (0.8%). Without crashes, identification rates of these methods would be slightly increased. For example, assuming MAGMa shows the same performance for the 377 instances as for the successfully processed 5,546, identification rate for the combined dataset would increase by 0.9 percentage points to 13.9%, making MAGMa runner-up after CSI:FingerID but before FingerID (13.8%).
Assume a method assigns the correct structure the same score x as other candidates in the ranked output list, so that all candidate structures from rank i to rank j have identical score x, with i minimal and j maximal. Then, we increase the number of correct identifications for rank k by , for each . This corresponds to uniformly choosing some order among the candidates with identical score. If a method reaches correct identifications in the top k, and correct identifications in the top , we say that the method reaches x correct identifications for fractional rank .
For the all-against-all comparison of methods, we process tied ranks as follows: If method A returns the correct answer on ranks 5–8 (all candidates on these ranks have identical score) and method B returns it on ranks 7–9, we iterate over all 12 possibilities and count this as wins for method A, ties, and wins for method B. For computing sign tests, we multiply percentages from Table S1 by N and round conservatively to the nearest integer (rounding down for larger class, rounding up for smaller class). We use approximation by the normal distribution to compute P values.
Acknowledgments
We thank Agilent Technologies, Inc. for providing uncorrected peak lists of their spectral library and Lars Ridder (Wageningen University) for the MAGMa software. We are particularly grateful to Pieter Dorrestein and Nuno Bandeira (University of California) and the GNPS (Global Natural Products Social) community for making their data publicly accessible. This work was funded in part by Deutsche Forschungsgemeinschaft Grant BO 1910/16 (to K.D. and M.M.) and Academy of Finland Grant 268874/MIDAS (to H.S. and J.R.).
Footnotes
Conflict of interest statement: S.B. holds a patent on comparing fragmentation trees, whose value might be influenced by the manuscript.
This article is a PNAS Direct Submission.
See Commentary on page 12549.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1509788112/-/DCSupplemental.
References
- 1.Patti GJ, Yanes O, Siuzdak G. Innovation: Metabolomics: The apogee of the omics trilogy. Nat Rev Mol Cell Biol. 2012;13(4):263–269. doi: 10.1038/nrm3314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Baker M. Metabolomics: From small molecules to big ideas. Nat Methods. 2011;8(2):117–121. [Google Scholar]
- 3.Rinehart D, et al. Metabolomic data streaming for biology-dependent data acquisition. Nat Biotechnol. 2014;32(6):524–527. doi: 10.1038/nbt.2927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kenar E, et al. Automated label-free quantification of metabolites from liquid chromatography-mass spectrometry data. Mol Cell Proteomics. 2014;13(1):348–359. doi: 10.1074/mcp.M113.031278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kind T, et al. LipidBlast in silico tandem mass spectrometry database for lipid identification. Nat Methods. 2013;10(8):755–758. doi: 10.1038/nmeth.2551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.NCBI Resource Coordinators Database resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2013;41(Database issue):D8–D20. doi: 10.1093/nar/gks1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Williams A, Tkachenko V. The Royal Society of Chemistry and the delivery of chemistry data repositories for the community. J Comput Aided Mol Des. 2014;28(10):1023–1030. doi: 10.1007/s10822-014-9784-5. [DOI] [PubMed] [Google Scholar]
- 8.Altelaar AFM, Munoz J, Heck AJR. Next-generation proteomics: Towards an integrative view of proteome dynamics. Nat Rev Genet. 2013;14(1):35–48. doi: 10.1038/nrg3356. [DOI] [PubMed] [Google Scholar]
- 9.Lindsay R, Buchanan B, Feigenbaum E, Lederberg J. Applications of Artificial Intelligence for Organic Chemistry: The DENDRAL Project. McGraw-Hill; New York: 1980. [Google Scholar]
- 10.Allen F, Greiner R, Wishart D. Competitive fragmentation modeling of ESI-MS/MS spectra for putative metabolite identification. Metabolomics. 2015;11(1):98–110. [Google Scholar]
- 11.Allen F, Pon A, Wilson M, Greiner R, Wishart D. CFM-ID: A web server for annotation, spectrum prediction and metabolite identification from tandem mass spectra. Nucleic Acids Res. 2014;42(Web Server issue):W94-9. doi: 10.1093/nar/gku436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hill AW, Mortishire-Smith RJ. Automated assignment of high-resolution collisionally activated dissociation mass spectra using a systematic bond disconnection approach. Rapid Commun Mass Spectrom. 2005;19(21):3111–3118. [Google Scholar]
- 13.Heinonen M, et al. FiD: A software for ab initio structural identification of product ions from tandem mass spectrometric data. Rapid Commun Mass Spectrom. 2008;22(19):3043–3052. doi: 10.1002/rcm.3701. [DOI] [PubMed] [Google Scholar]
- 14.Wolf S, Schmidt S, Müller-Hannemann M, Neumann S. In silico fragmentation for computer assisted identification of metabolite mass spectra. BMC Bioinformatics. 2010;11:148. doi: 10.1186/1471-2105-11-148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang Y, Kora G, Bowen BP, Pan C. MIDAS: A database-searching algorithm for metabolite identification in metabolomics. Anal Chem. 2014;86(19):9496–9503. doi: 10.1021/ac5014783. [DOI] [PubMed] [Google Scholar]
- 16.Ridder L, et al. Automatic chemical structure annotation of an LC-MS(n) based metabolic profile from green tea. Anal Chem. 2013;85(12):6033–6040. doi: 10.1021/ac400861a. [DOI] [PubMed] [Google Scholar]
- 17.Ridder L, et al. Substructure-based annotation of high-resolution multistage MS(n) spectral trees. Rapid Commun Mass Spectrom. 2012;26(20):2461–2471. doi: 10.1002/rcm.6364. [DOI] [PubMed] [Google Scholar]
- 18.Heinonen M, Shen H, Zamboni N, Rousu J. Metabolite identification and molecular fingerprint prediction through machine learning. Bioinformatics. 2012;28(18):2333–2341. doi: 10.1093/bioinformatics/bts437. [DOI] [PubMed] [Google Scholar]
- 19.Shen H, Dührkop K, Böcker S, Rousu J. 2014. Metabolite identification through multiple kernel learning on fragmentation trees. Bioinformatics 30(12): i157–i164.
- 20.Böcker S, Rasche F. Towards de novo identification of metabolites by analyzing tandem mass spectra. Bioinformatics. 2008;24(16):i49–i55. doi: 10.1093/bioinformatics/btn270. [DOI] [PubMed] [Google Scholar]
- 21.Rasche F, Svatoš A, Maddula RK, Böttcher C, Böcker S. Computing fragmentation trees from tandem mass spectrometry data. Anal Chem. 2011;83(4):1243–1251. doi: 10.1021/ac101825k. [DOI] [PubMed] [Google Scholar]
- 22.Dührkop K, Böcker S. 2015. Fragmentation trees reloaded. Research in Computational Molecular Biology, Lecture Notes in Computer Science (Springer, Berlin), Vol 9029, pp 65–79.
- 23.Vaniya A, Fiehn O. Using fragmentation trees and mass spectral trees for identifying unknown compounds in metabolomics. Trends Analyt Chem. 2015;69:52–61. doi: 10.1016/j.trac.2015.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Watrous J, et al. Mass spectral molecular networking of living microbial colonies. Proc Natl Acad Sci USA. 2012;109(26):E1743–E1752. doi: 10.1073/pnas.1203689109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nguyen DD, et al. MS/MS networking guided analysis of molecule and gene cluster families. Proc Natl Acad Sci USA. 2013;110(28):E2611–E2620. doi: 10.1073/pnas.1303471110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Morreel K, et al. Systematic structural characterization of metabolites in Arabidopsis via candidate substrate-product pair networks. Plant Cell. 2014;26(3):929–945. doi: 10.1105/tpc.113.122242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gerlich M, Neumann S. MetFusion: Integration of compound identification strategies. J Mass Spectrom. 2013;48(3):291–298. doi: 10.1002/jms.3123. [DOI] [PubMed] [Google Scholar]
- 28.Hufsky F, Scheubert K, Böcker S. Computational mass spectrometry for small molecule fragmentation. Trends Analyt Chem. 2014;53:41–48. doi: 10.1186/1758-2946-5-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sumner LW, et al. Proposed minimum reporting standards for chemical analysis Chemical Analysis Working Group (CAWG) Metabolomics Standards Initiative (MSI) Metabolomics. 2007;3(3):211–221. doi: 10.1007/s11306-007-0082-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dunn WB, et al. Mass appeal: Metabolite identification in mass spectrometry-focused untargeted metabolomics. Metabolomics. 2013;9(1):44–66. [Google Scholar]
- 31.Rasche F, et al. Identifying the unknowns by aligning fragmentation trees. Anal Chem. 2012;84(7):3417–3426. doi: 10.1021/ac300304u. [DOI] [PubMed] [Google Scholar]
- 32.Klekota J, Roth FP. Chemical substructures that enrich for biological activity. Bioinformatics. 2008;24(21):2518–2525. doi: 10.1093/bioinformatics/btn479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rauf I, Rasche F, Nicolas F, Böcker S. Finding maximum colorful subtrees in practice. J Comput Biol. 2013;20(4):311–321. doi: 10.1089/cmb.2012.0083. [DOI] [PubMed] [Google Scholar]
- 34.Shawe-Taylor J, Cristianini N. Kernel Methods for Pattern Analysis. Cambridge Univ Press; New York: 2004. [Google Scholar]
- 35.Scholkopf B, Smola AJ. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press; Cambridge, MA: 2001. [Google Scholar]
- 36.Platt JC. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. In: Smola AJ, Schölkopf B, editors. Advances in Large Margin Classifiers. MIT Press; Cambridge, MA: 1999. Chap 5. [Google Scholar]
- 37.Stein S. Mass spectral reference libraries: An ever-expanding resource for chemical identification. Anal Chem. 2012;84(17):7274–7282. doi: 10.1021/ac301205z. [DOI] [PubMed] [Google Scholar]
- 38.Bandeira N, Pham V, Pevzner P, Arnott D, Lill JR. Automated de novo protein sequencing of monoclonal antibodies. Nat Biotechnol. 2008;26(12):1336–1338. doi: 10.1038/nbt1208-1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ridder L, et al. In silico prediction and automatic LC-MS(n) annotation of green tea metabolites in urine. Anal Chem. 2014;86(10):4767–4774. doi: 10.1021/ac403875b. [DOI] [PubMed] [Google Scholar]
- 40.Menikarachchi LC, Hill DW, Hamdalla MA, Mandoiu II, Grant DF. In silico enzymatic synthesis of a 400,000 compound biochemical database for nontargeted metabolomics. J Chem Inf Model. 2013;53(9):2483–2492. doi: 10.1021/ci400368v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Horai H, et al. MassBank: a public repository for sharing mass spectral data for life sciences. J Mass Spectrom. 2010;45(7):703–714. doi: 10.1002/jms.1777. [DOI] [PubMed] [Google Scholar]
- 42.Scheubert K, Hufsky F, Böcker S. Computational mass spectrometry for small molecules. J Cheminform. 2013;5(1):12. doi: 10.1186/1758-2946-5-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dührkop K, Hufsky F, Böcker S. Molecular formula identification using isotope pattern analysis and calculation of fragmentation trees. Mass Spectrom (Tokyo) 2014;3:S0037. doi: 10.5702/massspectrometry.S0037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shinbo Y, et al. 2006. KNApSAcK: A comprehensive species-metabolite relationship database. Plant Metabolomics, Biotechnology in Agriculture and Forestry, eds Saito K, Dixon RA, Willmitzer L (Springer, Berlin), Vol 57, pp 165–181.
- 45.Wishart DS, et al. HMDB 3.0--The Human Metabolome Database in 2013. Nucleic Acids Res. 2013;41(Database issue):D801–D807. doi: 10.1093/nar/gks1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hastings J, et al. The ChEBI reference database and ontology for biologically relevant chemistry: Enhancements for 2013. Nucleic Acids Res. 2013;41(Database issue):D456–D463. doi: 10.1093/nar/gks1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Willett P. Similarity-based virtual screening using 2D fingerprints. Drug Discov Today. 2006;11(23-24):1046–1053. doi: 10.1016/j.drudis.2006.10.005. [DOI] [PubMed] [Google Scholar]
- 48.O’Boyle NM, et al. Open Babel: An open chemical toolbox. J Cheminform. 2011;3:33. doi: 10.1186/1758-2946-3-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.May JW, Steinbeck C. Efficient ring perception for the Chemistry Development Kit. J Cheminform. 2014;6(1):3. doi: 10.1186/1758-2946-6-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Steinbeck C, et al. The Chemistry Development Kit (CDK): An open-source Java library for chemo- and bioinformatics. J Chem Inf Comput Sci. 2003;43(2):493–500. doi: 10.1021/ci025584y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rebentrost F, Ben-Shaul A. On the fragmentation of benzene by multiphotoionization. J Chem Phys. 1981;74(6):3255–3264. [Google Scholar]
- 52.Jebara T, Kondor R, Howard A. Probability product kernels. J Mach Learn Res. 2004;5:819–844. [Google Scholar]
- 53.Hufsky F, Dührkop K, Rasche F, Chimani M, Böcker S. Fast alignment of fragmentation trees. Bioinformatics. 2012;28:i265–i273. doi: 10.1093/bioinformatics/bts207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cortes C, Mohri M, Rostamizadeh A. Algorithms for learning kernels based on centered alignment. J Mach Learn Res. 2012;13:795–828. [Google Scholar]
- 55.Chang C-C, Lin C-J. LIBSVM: A library for support vector machines. ACM Trans Intell Syst Technol. 2011;2(3):27-1–27-27. [Google Scholar]
- 56.Lin H-T, Lin C-J, Weng RC. A note on Platt’s probabilistic outputs for Support Vector Machines. Mach Learn. 2007;68:267–276. [Google Scholar]