Discriminating direct and indirect connectivities in biological networks

Significance

We used a combination of computational and theoretical approaches coupled to synthetic biology experimentation in mammalian cells to study direct and indirect connectivities in biological networks. After subjecting benchmark circuits to a range of perturbations, we recovered the edge weights using nonparametric single-cell data resampling coupled with modular response analysis. We discovered that inferred weights of specific network edges undergo divergent shifts under differential perturbations, and that the particular behavior is topology dependent. Incorporating this insight in the analysis of high-throughput experiments may provide a sought-after solution to a longstanding reverse engineering problem.

Abstract

Reverse engineering of biological pathways involves an iterative process between experiments, data processing, and theoretical analysis. Despite concurrent advances in quality and quantity of data as well as computing resources and algorithms, difficulties in deciphering direct and indirect network connections are prevalent. Here, we adopt the notions of abstraction, emulation, benchmarking, and validation in the context of discovering features specific to this family of connectivities. After subjecting benchmark synthetic circuits to perturbations, we inferred the network connections using a combination of nonparametric single-cell data resampling and modular response analysis. Intriguingly, we discovered that recovered weights of specific network edges undergo divergent shifts under differential perturbations, and that the particular behavior is markedly different between topologies. Our results point to a conceptual advance for reverse engineering beyond weight inference. Investigating topological changes under differential perturbations may address the longstanding problem of discriminating direct and indirect connectivities in biological networks.

A focal point of systems biology is the reverse engineering of gene regulatory networks (1–5). The methods have shifted from intuitive inference of local connectivities to comprehensive analysis of large networks, involving heterogeneous data sets from high-throughput experiments and complex theoretical tools (6–10). Despite significant advances, a fundamental reverse engineering bottleneck is the ability to discriminate between direct and indirect connections. In a simple case, assuming three nodes in a cascade formulation, where an input node is activating an intermediary node which in turn is activating an output node, a reverse engineering algorithm may infer an activating edge from the input node to the output, even though there is no direct biological interaction.

Unfortunately, the limitation in correctly distinguishing the effects stemming from indirect connectivities is pervasive (11–13) and justifies the urgent need for new and reliable methods to eliminate spurious edges. Importantly, remedies to address this problem should not further muddle the interpretation by removing true network edges (14). A number of theoretical approaches have been proposed to overcome this hurdle (4, 15–18), but the ability to experimentally verify the conclusions drawn by reverse engineering tools remains paramount.

The majority of efforts to address the verification issue adopt in silico benchmark suites that are based on biological pathway approximations (19). Although these models do include a number of commonly observed topologies and have provided significant insights, they do not fully capture the complexity of the biological realm and the associated heterogeneity and intrinsic variability. On the other hand, engineered synthetic gene circuits are orthogonal to the endogenous pathways yet operate within the natural cellular context using the available resources. Thus, synthetic networks are a versatile platform for investigating specific connectivities and topological properties and can ultimately guide us to deriving fundamental insights about biological systems and pathways (20–23).

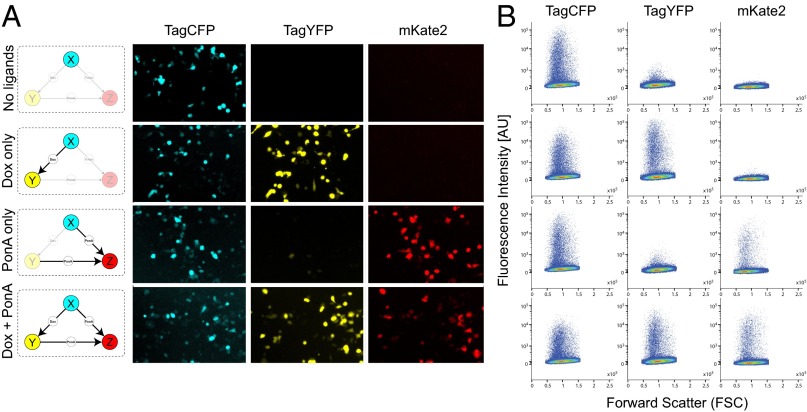
We previously proposed a strategy based upon using a synthetic gene network in human cells as a benchmark for reverse engineering validation and refinement (24). Here, we built three-node synthetic gene regulatory networks that incorporate direct and indirect connectivities and used them as benchmarks in human kidney cells. The first network is the type I coherent feed-forward loop (25, 26), where the origin node (X) activates the target node (Z) directly but also through an intermediate node (Y), with OR logic at the output (Fig. 1A). The second network is a cascade motif, where the origin node (X) regulates the target node (Z) indirectly via an intermediary node (Y) (Fig. 1B). More specifically, the node-to-node interactions are achieved through inducible transcriptional regulation. The origin (X) and intermediary nodes (Y) contain bidirectional promoter elements that drive the production of a fluorescent reporter protein and a transactivator unit, and the target node (Z) contains a unidirectional promoter for the production of a fluorescent reporter protein only. Each node produces a fluorescent reporter, which allows monitoring its state.

Fig. 1.

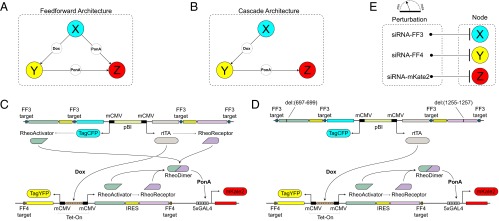
The benchmark synthetic regulatory networks. (A) The first motif is a coherent feed-forward loop where node X regulates node Z in both a direct and an indirect manner. (B) The second motif is a cascade, where node X activates node Z only by activating node Y. (C and D) Detailed information about the synthetic gene networks. The activity of the three nodes X, Y, and Z can be quantified by the output fluorescent proteins TagCFP, TagYFP and mKate2, respectively. The constitutive bidirectional promoter of node X also transcribes rtTA for node Y induction and the RheoSwitch dimers for node Z induction. For the cascade motif, the translation of RheoSwitch dimer protein is prevented by nonsense mutation. In the presence of doxycycline, the constitutively transcribed rtTA induces transcription of RheoSwitch in node Y. When ponasterone A binds to the RheoSwitch dimer, the entire complex serves as a transactivator for the yeast Gal4 domain. Transcription at Gal4 domain results in production of mKate2 to indicate node Z activity. (E) Perturbation of each node in the system is performed siRNA. Nodes X and Y are perturbed by synthetic siRNAs (FF3 and FF4, respectively) with the targets located in the 3′ UTR of their corresponding targets. Node Z is perturbed by a custom siRNA that directly targets mKate2. IRES, internal ribosome entry site.

We commenced the experiments confirming the baseline behavior of the synthetic networks under boundary and control conditions. Subsequently, we systematically perturbed each network node using short interfering RNAs (siRNAs) (27); then, we collected and processed the flow cytometry measurements. Using these data, we performed network reconstruction via nonparametric single-cell data resampling followed by modular response analysis (4, 28). The reconstruction results reproduced the benchmark network topologies. Importantly, we identified divergent shifts in predicted interaction strengths under differential perturbations, a feature that can be critical toward discriminating between direct and indirect connectivities.

Results

Design and Assembly of the Benchmark Synthetic Regulatory Networks.

The first of the two networks is the type I coherent feed-forward loop (Fig. 1C). The plasmid for node X consists of a constitutively active bidirectional promoter flanked by the reporter fluorescent protein TagCFP and reverse tetracycline-controlled transactivator (rtTA) on either side. The regulatory unit rtTA serves as the transactivator of the tetracycline-inducible expression system (Tet-On) upon forming a homodimer and binding with the ligand doxycycline (Dox). Activation of the downstream target node Y, which consists of tetracycline response element (TRE) enhancer flanked by cytomegalovirus (CMV) promoters on either side, requires binding of active rtTA–Dox complex to the TRE enhancer. Thus, the activation of node Y by node X depends on doxycycline. The activation of node Y results in production of its fluorescent reporter TagYFP and a heterodimeric transactivator composed of the RheoActivator and RheoReceptor domains. The RheoActivator domain consists of a ligand binding domain fused with the viral transactivator VP16, whereas the RheoReceptor domain is a hybrid of insect hormone ecdysone receptor (EcR) fused to yeast GAL4 DNA binding domain for target binding specificity to GAL4 response element. After dimerization of RheoActivator and RheoReceptor, an EcR agonist such as ponasterone A induces conformational change to the RheoReceptor such that the heterodimer bound to GAL4 response element initiates transcription. In our synthetic network, RheoSwitch dimer activates node Z by initiating transcription of its reporter fluorescent protein mKate2. To achieve direct activation of node Z by node X, the node X produces the RheoSwitch proteins in addition to TagCFP and rtTA.

The second of the two networks is a cascade motif (Fig. 1D), where node X controls node Z exclusively through the activation of intermediate node Y. To implement this architecture, we modified the coherent feed-forward architecture by inserting a single base pair in both of the node X RheoSwitch genes to induce a nonsense frame-shift mutation. As the RheoSwitch heterodimer genes together constitute ∼30% of total plasmid size we selected introducing a mutation instead of complete excision to avoid possible discrepancies in transfection and transcription efficiencies due to differences in plasmid and cassette size.

During the design stage we opted for a simple yet effective means of perturbing the individual nodes via RNA interference (Fig. 1E). We use a set of siRNA with previously confirmed function (29) for X and Y and a custom siRNA for Z. More specifically, the siRNA-based suppression of node X is achieved through addition of an FF3 target into 3′ untranslated region (UTR) of each transcript produced by the constitutive bidirectional promoter. Similar to X, ubiquitous siRNA-based suppression of Y is made possible by inserting an FF4 target into the 3′ UTR of each transcript produced by the bidirectional TRE enhancer/CMV promoter. Node Z contains a single transcript (reporter protein mKate2), and its activity is modulated by a custom siRNA that directly targets the mKate2 transcript.

Validation of the Synthetic Gene Network Behavior.

With the exception of node X which relies on a constitutive promoter, the activity of the synthetic networks depends on the presence of the appropriate ligand. In the cascade motif, Y requires doxycycline (Dox), and Z requires an EcR agonist such as Genostat or ponasterone A (PonA). In the type I coherent feed-forward loop, the requirement for activation of Y remains the same, whereas Z can be activated by the combination of Dox and PonA or PonA alone. To confirm these baseline conditions, the circuits were transfected in human embryonic kidney cell line (HEK293), the ligands were introduced at saturating concentrations, and measurements were performed using microscopy and flow cytometry ∼48 h after transfection.

The microscopy measurements of the fluorescent outputs of both benchmark networks show that the inducible transactivators for both architectures function as desired with minimal leakage, thus confirming the designed circuit topologies. In the feed-forward loop, node X activity is represented by the constitutively produced fluorescent protein TagCFP and is observed regardless of the ligand conditions (Fig. 2A). The addition of doxycycline, which enables X-to-Y interaction by activating the synthetic transactivator rtTA, results in production of the TagYFP fluorescent protein (Fig. 2A). The activation of node Z is mediated by the active form of RheoSwitch dimer, which is produced by both nodes X and Y. Due to the constitutive activity of node X, PonA is sufficient to activate node Z in the feed-forward loop (Fig. 2A). These observations are confirmed by flow cytometry-based population measurements, which show TagCFP population in all scenarios and a distinct TagYFP population when Dox is present, and mKate2 when PonA is present (Fig. 2B). The same control experiments using the cascade network plasmid show an identical response to the ligand combinations except for the node Z activity (Fig. 3A). In the cascade motif, sequential activation of node X and node Y are necessary for node Z activation. Thus, mKate2 is only observed when Dox and PonA are present (Fig. 3A). Again, we confirm these observations with flow cytometry (Fig. 3B).

Fig. 2.

Validation of the coherent feed-forward architecture. To validate the circuit behavior we tested all combinations of the two small molecules. The result analyzed by fluorescence microscopy (A) and flow cytometry (B).

Fig. 3.

Validation of the cascade architecture. To validate the circuit behavior we tested all combinations of the two small molecules. The result analyzed by fluorescence microscopy (A) and flow cytometry (B).

Subsequently, to probe the parameter space and general behavior of the circuits under perturbations we created mathematical models of our benchmark circuits (SI Appendix, SimBiology Model, Figs. S1 and S2). The kinetic parameters were selected from literature (21, 30). We performed sensitivity analysis of the output node Z protein concentration against the mRNA species of nodes X and Y (thereby emulating RNAi perturbation). We observe that, in the feed-forward loop, where node X activates node Z in a direct manner as well as an indirect manner, the cumulative sensitivity of the Z node protein to mRNA species of node X was always higher than that of node Y (SI Appendix, Fig. S3). Conversely, in the cascade, where node X only activates node Z indirectly through node Y, the production of node Z protein was more sensitive to the node Y mRNA. Based on the simulation results, we hypothesized that the topological differences of the examined architectures may yield divergent responses to different degrees of perturbation. This hypothesis points to an intriguing scenario where the properties and outcome of signal propagation after custom perturbation experiments can be exploited toward distinguishing direct from indirect connectivities.

Modular Response Analysis.

An intrinsic difficulty in capturing direct interactions in a biological network is that any perturbation to a particular node may rapidly propagate throughout the network, thus causing global changes which cannot be easily distinguished from direct effects. Rooted in metabolic control analysis, Modular Response Analysis (MRA) uses steady state data obtained from node-wise perturbation to express the network in terms of pair-wise interaction sensitivities. To perform MRA (SI Appendix, Modular Response Analysis Method), we first calculate the global response coefficients (GRC) from experimentally measured responses to perturbations using Δln(x_i), where x_i represents in our case the quasi steady-state measurement of fluorescent reporter obtained via flow cytometry. Once the functional modules (i.e., perturbation targets) of the target network have been selected, the experimental procedure consists of the following steps: (i) measure the steady-state x_i corresponding to the unperturbed set of inputs p_i, (ii) perform a perturbation to each p_i individually and measure the new steady-state x_i’, (iii) calculate the global response coefficients using the steady-state data, and (iv) convert global response coefficients to local response coefficients by inversion of the global response matrix.

In higher eukaryotes, perturbation can be achieved through the down-regulation of mRNA, and hence protein levels, using RNA interference (RNAi). This approach has shown to be successful in mapping the positive and negative feedback effects in the Raf/Mek/Erk MAPK network of rat adrenal pheochromocytoma (PC-12) cells (31). Using a variant of the MRA algorithm (32), the authors uncovered connectivity differences depending on whether the cells were stimulated by epidermal growth factor (EGF) or, alternatively, by neuronal growth factor (NGF).

We commenced the experimental reverse engineering process by performing a systematic perturbation of each benchmark architecture node. We first tested the efficacy of siRNA and calibrated the perturbation dosage against the feed-forward loop architecture plasmid (SI Appendix, Figs. S4–S6; quantitative RT-PCR results in SI Appendix, Fig. S7). As our goal was to find a range of siRNA concentrations that result in moderate yet distinct levels of suppression, we set our maximum siRNA concentration at the manufacturer-recommended dose of 5 pmol and tested five additional concentrations in decreasing magnitudes. To ensure consistency, we cotransfected each siRNA with the network plasmid and measured the circuit activity after 48 h via flow cytometry. Across all three nodes, each of the siRNA was most effective at suppressing the node for which it was designed to disrupt; at least 60% suppression was achieved with the highest siRNA concentration. We then selected the pair of siRNA concentrations that yield the largest difference in the activity of their respective target node, as measured by mean fluorescence level. Specifically, as illustrated in SI Appendix, Fig. S8A, we selected 1 pmol as “high” perturbation and 0.1 pmol as “low.”

After selecting the perturbation magnitude, we performed a node-wise perturbation of the feed-forward circuit using the siRNAs that target each node supplemented with scrambled siRNA to control for the total mass. As before, we used saturating concentrations of the small molecule inducers and applied the predefined set of perturbations based on our calibration results. The three fluorescent reporter protein profiles indicate a response consistent with the benchmark network topologies, confirming the siRNA operation (SI Appendix, Fig. S8B). Down-regulation in the fluorescence reporter expression is observed in two cases. Directly by perturbing the actual node or indirectly by perturbing the upstream node responsible for its activation. For node X, a decrease in TagCFP is observed only after direct perturbation; for node Y, a decrease in TagYFP is observed after perturbation of nodes X and Y; and for node Z, a decrease in mKate2 is observed after perturbation of nodes X, Y, and Z (SI Appendix, Fig. S8B).

We then proceeded with the recovery of the network topology using population data (SI Appendix, Reverse Engineering of the Benchmark Topologies Using Population Data). For each set of perturbation responses, the global response coefficients were calculated based on the weighted mean fluorescence of gated populations. The pairwise sensitivity coefficients were then obtained via calculating the local response coefficient (LRC) (SI Appendix, Figs. S8 C and F and S9). To determine the significance of the recovered LRC, we performed error propagation using Monte Carlo simulations (31) rendering most of the predicted regulatory connections insignificant (SI Appendix, Monte Carlo Simulation and Fig. S10). Notably, the reverse engineering recovered a direct inhibitory connection between nodes X and Z for both perturbation magnitudes (SI Appendix, Fig. S8F), which may be attributed to mild retroactivity effects (33).

Reverse Engineering of the Benchmark Topologies Using Resampled Single-Cell Data.

To increase our confidence in predictions we developed a technique based upon bootstrapping, an alternative to the sample statistics obtained from an aggregate population (i.e., mean and SD). Bootstrapping is a nonparametric resampling method (34) designed to estimate the confidence interval of a given statistic, and is particularly useful when the observed population distribution cannot be characterized by typical distributional assumptions such as normality (e.g., typical flow cytometry data). To obtain a bootstrapped mean we: (i) resample with replacement the dataset to the same number of times as the original population, (ii) calculate the desired statistic from each sample, (iii) repeat the process several times to form the probability distribution of the subsampled mean (SI Appendix, Fig. S11). For our analysis, we repeated the entire process 2,000 times to form the representative probability distribution of a fluorescent reporter expression.

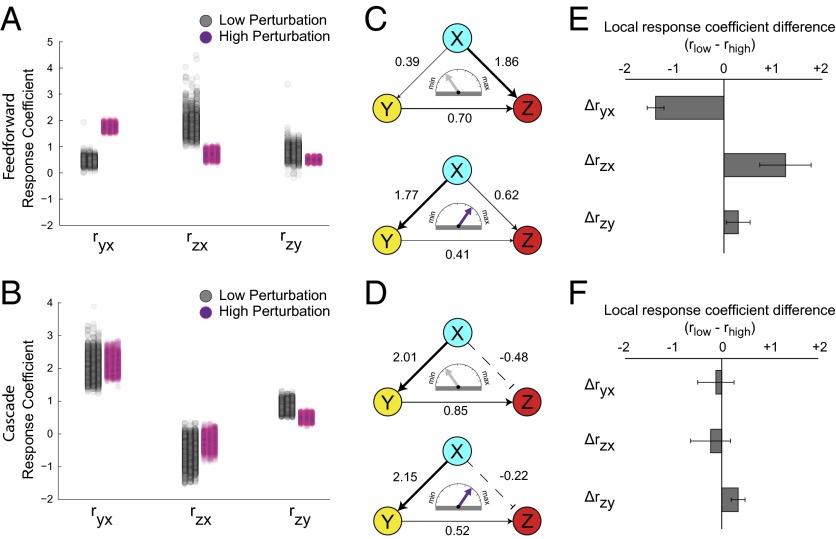
Subsequently, we produced a unique panel for each of the three fluorescent reporters after perturbations to three different nodes, for a total of nine distinct panels for the feed-forward circuit (Fig. 4 A–C) and nine for the cascade (Fig. 4 D–F). Each frequency plot consists of four different probability distributions, from resampled means of fluorescent reporter before (empty) and after the two perturbations (filled with gray for low and purple for high). For every set of subsampled means that make up the probability distributions, we treated them as a unique instance of the perturbation response and fed these values to MRA to calculate the local response coefficients. The results, along with the 95% confidence interval of the distribution, are plotted as a 1D scatter plot and shown in Fig. 5 A and B. In this case, we were able to successfully recover all relevant regulatory connections of feed-forward loop (Fig. 5C) and cascade (Fig. 5D) networks with increased confidence. All of the reconstructed edges are included in SI Appendix, Fig. S12.

Fig. 4.

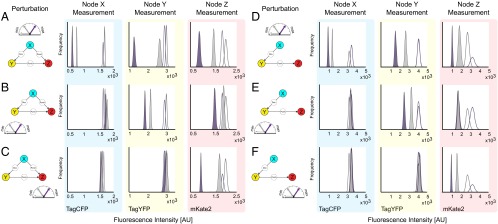
Resampling the single-cell flow cytometry data after node-wise perturbations. Forty-eight h after siRNA perturbation, the expression level of the fluorescence reporters that represent nodes X, Y, and Z (TagCFP, TagYFP and mKate2, respectively) are measured using flow cytometry. To calculate the mean fluorescence of each population and the associated uncertainty, bootstrap resampling was performed. The resulting probability distributions of the resampled mean before perturbation (empty) and after perturbation (color-filled) are shown for the feed-forward loop (A–C), and the cascade (D–F). The colors of the peaks indicate the relative strength of the suppression applied (gray is used to indicate the low and purple the high perturbation). (A) The graphical representation of the X-node perturbation and the corresponding nodal responses using the feed-forward architecture. Probability distributions are composed of bootstrapped mean of the fluorescence reporters TagCFP, TagYFP and mKate2 (left to right) following perturbations to node X at two different siRNA concentrations. Color of the peak indicates the relative degree of suppression. (B and C) The graphical representation of the Y- and Z-node perturbations and the corresponding nodal responses using the feed-forward architecture. (D–F) Results from the same process using the cascade architecture.

Fig. 5.

Reverse engineering of the benchmark topologies using resampled single-cell data. (A and B) The complete reconstruction of the network with modular response analysis performed after two perturbations. For every set of subsampled means that make up the probability distributions, the MRA results along with the 95% confidence interval of the distribution are plotted as a 1D scatter plot. (C and D) The graphical representation of the reconstructed synthetic networks. (E and F) To probe the effect of response coefficient change due to perturbation magnitude shift we calculated the difference between coefficients of equivalent edges (C and D). The error bars were obtained using a propagation of error among the pair of local response coefficient distributions used to calculate this difference.

Using our prior knowledge of our network, we confirmed that the inferred connectivities are consistent with the network topology. Moreover, the inferred interaction strengths and distributions produced by the reverse engineering algorithm reveal features of the network that are not readily apparent and are in agreement with our in silico sensitivity analysis. Specifically, to probe the effect of response coefficient change due to perturbation magnitude shift we calculated the difference between coefficients of equivalent edges (Fig. 5 E and F).

For the feed-forward architecture we identified “perturbation-sensitive edges.” In other words, we discovered edges that undergo distinctively large shift in interaction strengths under differential perturbations. In particular, we observe that for the feed-forward architecture, increasing the perturbation magnitude dramatically alters the inferred interactions arising from node X. Importantly, there is a noticeable reversal in the strengths of activation between node X to nodes Y and Z, whereas the interaction from node Y to node Z remain largely unchanged (Fig. 5C). Specifically, after a low perturbation, the recovered topology shows a prominent direct activation of node Z by node X, whereas the topology recovered after high perturbation shows a prominent activation of node Y by node X. We postulate that the low perturbation is buffered as it propagates through the intermediate node Y, therefore the direct connection between X and Z appears to be more important. Aligned with this observation, node Z is less sensitive to disruption of node Y in the context of the feed-forward loop (Fig. 5B).

Compared with the feed-forward circuit, we found that the reverse engineering of the cascade is robust to perturbation strengths. In fact, the recovered topology from two perturbation magnitudes are almost indistinguishable except for small decrease in the Y-to-Z interaction strength (Fig. 5F), despite the fact that the fluorescence reporter profiles clearly reflect the differences in perturbation magnitude (Fig. 4 D–F). In contrast with the feed-forward circuit, there is only one possible path of activation in the cascade motif thereby the presumed buffering effect is not critical.

To further explore the effect of differential perturbation on the reverse engineering results, we performed an additional experiment using three perturbation magnitudes (SI Appendix, Fig. S13). In this instance, we refer to the perturbation magnitudes as “low,” “medium,” and “high.” We again observe the diverging trend of response coefficient values between the two architectures. In the feed-forward loop, each step-wise increase in perturbation magnitude affects the two edges originating from node X in contrasting manner, highlighting the activation from node X to node Y while reducing the weight of activation from node X to node Z (SI Appendix, Fig. S13 A and C). The recovered topologies of the cascade motif undergo little to no change over same perturbation magnitude intervals (SI Appendix, Fig. S13 B and D). Finally, to qualitatively probe our observations we developed a phenomenological model of the architectures (SI Appendix, Phenomenological Model). Using this model we analytically calculated the local response coefficients under low and high perturbations and we indeed confirmed the divergent shifts in interaction strengths.

Discussion

Direct and indirect interactions are pervasive in all networks. The inability to disentangle these interactions hampers reverse engineering progress. Recent advancements in high-throughput approaches, combined with algorithm and methodological advances through a host of community-wide efforts (12, 14, 19, 35) have examined these aspects. In fact, attempts to fundamentally address the issue by recognizing and filtering out the effects of indirect interactions at a global scale have begun to surface (11). Meanwhile, parallel developments in synthetic biology (23) have endowed researchers with new tools that allow precise emulation of naturally occurring topologies (21, 22). Networks orthogonal to the cellular milieu can serve as a biomolecular topological “ground truth” (20, 24). Data gathered from benchmark synthetic circuits can complement and inform algorithms, and offer a unique opportunity to correlate topological properties to system identification.

The number of possible networks for a given set of nodes is large and it grows exponentially with the number of nodes, making impractical their exhaustive construction. Fortunately, recent research has uncovered that certain topologies appear more frequently than others. Those topologies were dubbed “network motifs (25, 36). The network topology does not specify the nature of the nodes, and indeed the expectation is that the network behavior will be invariant to the changes in the molecular nature of the nodes and the exact mechanism of the interactions between the nodes.

Here we constructed two synthetic networks that incorporate direct and indirect connectivities. We successfully engineered the benchmark architectures to be inducible with negligible leakage and amenable to simple perturbations to facilitate the reverse engineering analysis. After applying systematic perturbations and a combination of nonparametric single-cell data resampling and modular response analysis, we discovered response patterns that are markedly different between the two topologies.

Using the proposed methodology, individual nodes of a network can be perturbed from their steady-state using transcriptional or posttranscriptional inhibitors [e.g., TALEs/CRISPR (37, 38) or siRNAs]. The pre- and postperturbation steady states can be measured at the mRNA or protein levels, and fed into MRA to predict divergent LRC and accordingly the network structure. Beyond small-scale networks, although motifs are composed of relatively few elements, they are often embedded as “modules” (39–41) in large networks that exhibit complex behavior. The term “modular” in MRA indicates that the same theoretical tools, in principle, scale up to cover large networks that are connected through a small number of “communicating intermediaries” (4, 28).

To conclude, unraveling the complexity of biological networks is central to understanding biology. Our results point to a transformative opportunity in reverse engineering of biological networks. Taking into account inferred topological changes under differential perturbations may provide a solution to the longstanding problem of discriminating between direct and indirect connections.

Methods

Mammalian Cell Culture and Transfections.

HEK293 cell line was maintained at 37°C, 100% humidity and 5% (vol/vol) CO₂. Circuit plasmid transfection was performed with jetPRIME (Polyplus) in 12-well plates at a plating density of 200,000 cells. Transfection was performed 24 h after seeding, and each well received 10 ng of plasmid containing node X and 25 ng of plasmid containing nodes Y and Z, with 500 ng of cotransfection junk DNA and varying amounts of siRNA. Detailed information is provided in SI Appendix, SI Methods.

Fluorescence Microscopy.

Approximately 48 h after transfection of network plasmid, fluorescence images of live cells were captured using an Olympus IX81 microscope. For ambient temperature control, the entire apparatus was housed in a Precision Control environmental chamber. The images were captured using a Hamamatsu ORCA 03 digital camera. Detailed information is provided in SI Appendix, SI Methods.

Flow Cytometry.

All FACS experiments were performed 48 h after transfection with BD LSRFortessa. Data acquisition was performed using FACS Diva software and subsequent analysis with FlowJo (Treestar). The threshold fluorescence unit for selecting fluorescence-positive population was determined based on untransfected HEK293 cells (SI Appendix, Fig. S14). There was no compensation performed (SI Appendix, Fig. S15). Detailed information is provided in SI Appendix, SI Methods.

Modular Response Analysis.

To obtain the pair-wise sensitivities between each node, we performed modular response analysis. In MRA, the local intermodular interactions, described by the local response matrix r_ij, are calculated from the global response matrix R_ij, which contains the observed change in the steady-state measurement of each node (x_i) due to the experimental perturbation (p_j). Because precise measurement of parameter perturbation size (p_j) is not possible in an experimental setting, the global response matrix is approximated by the fractional change of the steady states R_ij ∼ ∆ln(x_j). After obtaining R_ij from experimental data, we calculate the local response matrix r_ij by solving r_ij = −[dg(R_ipj^-1)] ^-1·R_ipj^-1. Detailed information is provided in SI Appendix, Modular Response Analysis Method.

Resampling.

To estimate the 95% confidence interval of the obtained local response matrix, bootstrap resampling of the original flow cytometry population is performed. The steps for bootstrap resampling are as follows: From the original flow cytometry population, resample with replacement the same number of cells as the original population. Using the resampled population, compute the desired population statistic (mean), and then calculate the local response matrix using MRA. The bootstrapping and MRA process is repeated 2,000 times to create a distribution of local responses. The 95% confidence interval, which corresponds to values from 2.5th to 97.5th percentile of the calculated values, is used to estimate the error. The process is shown in SI Appendix, Fig. S11.