Long-term reliability of the Athabasca River (Alberta, Canada) as the water source for oil sands mining

Significance

We show that current and projected surface water allocations from the Athabasca River, Alberta, Canada, for the exploitation of the Alberta oil sands are based upon an untenable assumption of the representativeness of the short instrumental gauge record. Our trend analysis of the instrumental data shows declining regional flows. Our tree-ring reconstruction shows periods of severe and prolonged low flows not captured by the instrumental record.

Abstract

Exploitation of the Alberta oil sands, the world’s third-largest crude oil reserve, requires fresh water from the Athabasca River, an allocation of 4.4% of the mean annual flow. This allocation takes into account seasonal fluctuations but not long-term climatic variability and change. This paper examines the decadal-scale variability in river discharge in the Athabasca River Basin (ARB) with (i) a generalized least-squares (GLS) regression analysis of the trend and variability in gauged flow and (ii) a 900-y tree-ring reconstruction of the water-year flow of the Athabasca River at Athabasca, Alberta. The GLS analysis removes confounding transient trends related to the Pacific Decadal Oscillation (PDO) and Pacific North American mode (PNA). It shows long-term declining flows throughout the ARB. The tree-ring record reveals a larger range of flows and severity of hydrologic deficits than those captured by the instrumental records that are the basis for surface water allocation. It includes periods of sustained low flow of multiple decades in duration, suggesting the influence of the PDO and PNA teleconnections. These results together demonstrate that low-frequency variability must be considered in ARB water allocation, which has not been the case. We show that the current and projected surface water allocations from the Athabasca River for the exploitation of the Alberta oil sands are based on an untenable assumption of the representativeness of the short instrumental record.

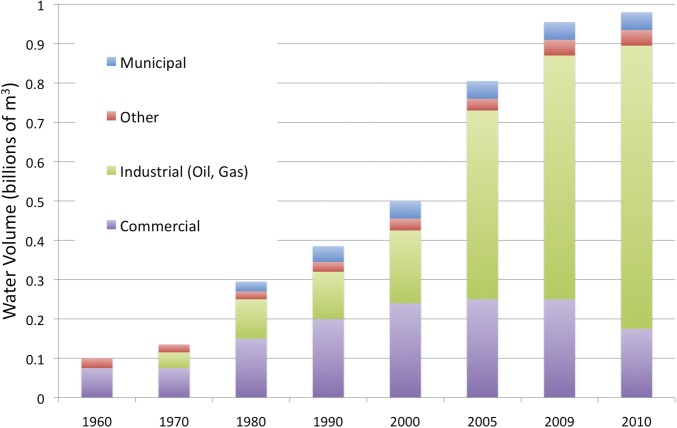
Over the past several decades, the province of Alberta has had Canada’s fastest growing economy, driven largely by the production of fossil fuels. Climatic change, periodic drought, and expanding human activities impact the province’s water resources, creating the potential for an impending water crisis (1). The Athabasca River (Fig. 1) is the only major river in Alberta with completely unregulated flows. It is the source of surface water for the exploitation of the Alberta oil sands, the world’s third-largest proven crude oil reserve at roughly 168 billion barrels. The oil and gas industry accounted for 74.5% of total surface water allocations in the Athabasca River Basin (ARB) in 2010 (Fig. 2) (2). An almost doubling of ARB water allocations since 2000, or 13 times the provincial average, is attributable to expanding oil sands production, which began in 1967 (Fig. 2).

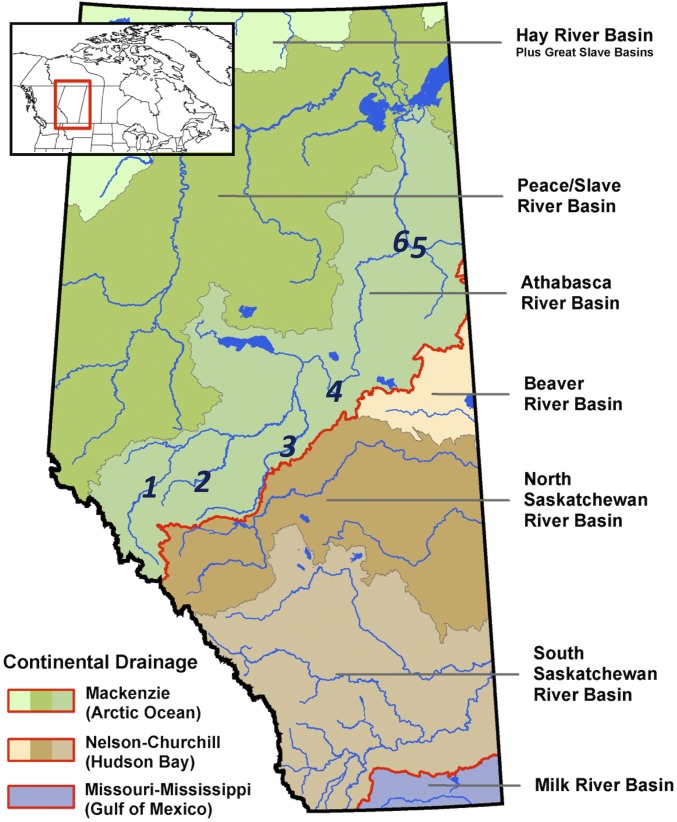
Fig. 1.

Alberta’s seven major drainage basins. The numbers refer to hydrometric gauges identified in Table 1. The Alberta oil sands development is in the vicinity of Fort McMurray (6). Reproduced with permission from the Government of Alberta.

Fig. 2.

Licensed water allocations by sector and decades to 2000 and selected subsequent years in the Athabasca River Basin, 1900–2010. Reproduced with permission from the Government of Alberta.

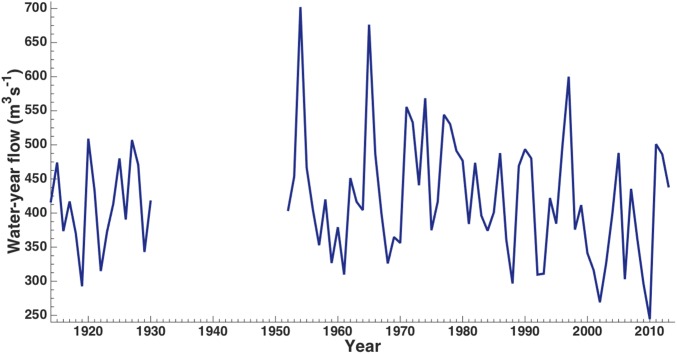
According to the Canadian Association of Petroleum Producers, in 2012, surface mining of the oil sands and in situ extraction (drilling) required 3.1 and 0.4 barrels of fresh water, respectively, to produce a barrel of crude oil (3). This amounted to 187 million cubic meters of fresh water use in 2012, or the equivalent of the residential water use of 1.7 million Canadians (4). Within the next decade, cumulative water use for oil sands production is projected to peak at about 505 million cubic meters per year or a rate of 16 m³⋅s⁻¹ (5). The current (2010 data) total water allocation represents only 4.4% of the mean annual Athabasca River flow (2) (Fig. 3); however, allocation and use as a proportion of average water levels does not account for the large variability in flow between seasons and years (interannual coefficient of variation = 22%). During 1952–2013, the Athabasca River gauge at Athabasca recorded mean seasonal flows of 100 m³⋅s⁻¹ in winter (December−February) and 911 m³⋅s⁻¹ in summer (June−August), with extreme monthly flows of 48 m³⋅s⁻¹ in December 2000 and 2,280 m³⋅s⁻¹ in June 1954. The mean, maximum, and minimum annual flows were 422 m³⋅s⁻¹, 702 m³⋅s⁻¹, and 245 m³⋅s⁻¹, respectively (Water Survey of Canada, wateroffice.ec.gc.ca/search/search_e.html?sType=h2oArc).

Fig. 3.

Mean annual flow of the Athabasca River at Athabasca (gauge 07BE001, Water Survey of Canada) for the water year (October 1 to September 30, 1913–2013).

Assessing the sustainability of ARB surface water availability is difficult because most regional streamflow gauges have been operational for a few years to a few decades, with long intervals of missing values, including during the 1930s and 1940s when drought was prevalent throughout the North American western interior. Various critics (e.g., ref. 4) emphasize the intraannual variability and express concern about water withdrawals in the low-flow winter season. Less attention has been given to flow variability at interannual to decadal scales associated with climate oscillations such as the Pacific Decadal Oscillation (PDO) and Pacific North American mode (PNA), which are known to have significant impacts on runoff from the Rocky Mountains, including in the ARB (6–9), and the potential consequences of a long period of predominantly low flow. We investigate the response of ARB flows to the low-frequency components of the PDO and PNA. This paper is the first, to our knowledge, to explicitly model the variability linked to the PDO and PNA, when testing for trends in discharge, thereby removing the tendencies associated with these climatic oscillations, which can confound trend detection in the relatively short instrumental records (6, 7). However, the available instrumental hydrologic records provide a limited sample of these low-frequency fluctuations; exploring longer records of this variability is critical. Therefore, we also reconstructed the Athabasca River annual flow from the growth rings in moisture-sensitive conifers at a network of sites in the upper reaches of the ARB and in an adjacent watershed (Fig. S1). We compare 900 y of inferred proxy flows to the streamflow variability recorded in recent decades, identifying extended periods of paleo low flow that exceeded the worst-case scenario in the instrumental records. We consider (i) the extent to which gauged flows (e.g., Fig. 3), which are the basis for surface water allocation, fail to capture the full range of hydroclimatic variability and extremes evident in a longer proxy record and (ii) the temporal evolution of low-frequency Athabasca River variability, related to the PDO and PNA, with its consequences for ARB surface water availability.

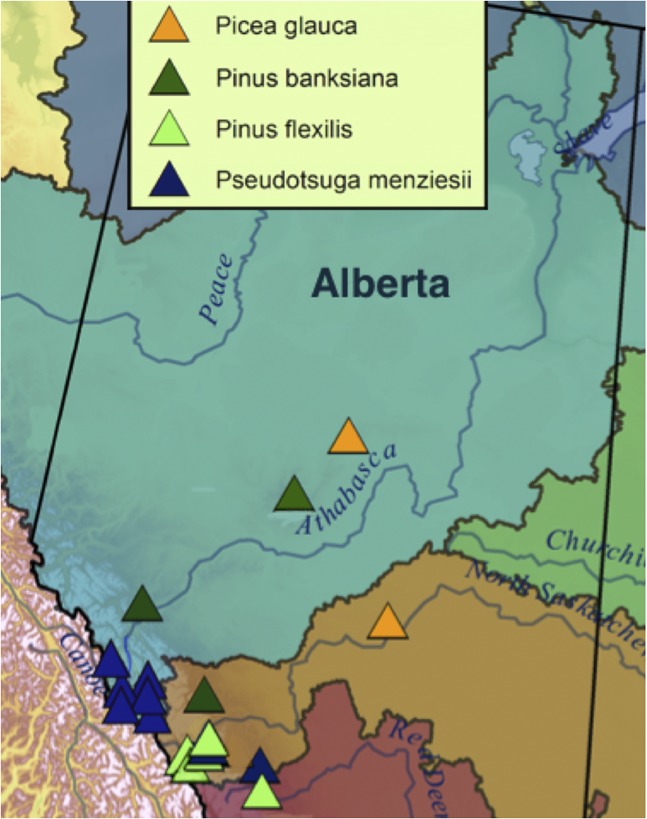
Fig. S1.

The tree-ring sampling sites within and near the Athabasca River Basin in north-central Alberta. The colored triangles represent four coniferous tree species.

Results

We examined the nine longest and most complete ARB instrumental streamflow records for significant trends, while explicitly modeling and removing the possible effects of the PDO, the PNA, and the El Niño−Southern Oscillation (ENSO) using generalized least-squares regression (GLS) (Fig. 1, Table 1, and Tables S1 and S2). Low‐frequency variability (i.e., data slightly smoothed by a 5-y binomial filter) was analyzed given the associated severe socioeconomic and ecological impacts of prolonged low flows. We found declining flows throughout the ARB: in the upper reaches (Athabasca River at Hinton and McLeod River), the middle reaches (Athabasca River at Athabasca), and the lower reaches (Clearwater River, Athabasca River at Fort McMurray, and the McMurray−Athabasca segment). The PDO or PNA are significant predictors of annual river flow variability for all nine records, whereas the trend and ENSO (the SOI term) enter in most, but not all, regression models.

Table 1.

The results of GLS trend analysis of the annual flow (water year) of the Athabasca River and its tributaries recorded at nine gauges and segments

Gauge no.	Gauge	Record period	Predictors*	Change, %/y	Rood et al. (9)	Peters et al. (8)
1	Athabasca R. at Hinton	1915–1939,1955–2011	trend, PDO, SOIN1, SOIP1	−0.21	decreasing	decreasing
2	McLeod R. above Embarras R.	1955–2012	trend, PNA, PDON1	−0.29	no trend	NA
3	Pembina R. near Entwistle	1955–2011	PNA, PDO, PNAP1, PDOP1	−0.04	no trend	NA
4	Athabasca R. at Athabasca (water year)	1952–2013	trend, PDO, SOIN1, PDOP2, SOIP2	−0.42	NA	no trend
4	Athabasca R. at Athabasca (only May−October available)	1913–1930, 1938–2013	PNA, SOIN1, SOIP1	−0.05	no trend	no trend
	Athabasca−Hinton segment†	1915–1930, 1955–2011	PNA, SOIP1, PNAP2	−0.03	NA	NA
5	Clearwater R. at Draper	1958–2012	trend, SOI, PNAN1, SOIN1, PDOP1	−0.64	no trend	NA
6	Athabasca R. at Fort McMurray	1958–2012	trend, PNA, PDOP2, SOIP2	−0.56	decreasing	decreasing
	Fort McMurray−Athabasca segment‡	1958–2012	trend, PNA, SOIN2, PDOP2	−0.97	NA	decreasing

Significant trends at the 0.05 level are in bold. Gauges are ordered according to reach. See Fig. 1 for gauge location according to gauge number; NA, not applicable because record was not analyzed.

^*Subscripts for predictors: P1, climate leads streamflow by 1 y; P2, climate leads streamflow by 2 y; N1, climate lags streamflow by 1 y.

^†The difference between the measured water-year flows at Athabasca and Hinton.

^‡The difference between the measured water-year flows at Fort McMurray and Athabasca.

Table S1.

The nine longest and most continuous Athabasca River basin gauge records from the Water Survey of Canada (WSC) analyzed in this study

Flow record name	WSC code	Drainage area, km2	Latitude, N	Longitude, W	Mean annual discharge, m3⋅s−1
Athabasca R. at Hinton*	07AD002	9,765	53°25'27”	117°34'9”	177
McLeod R. above Embarras R.	07AF002	2,562	53°28'12”	116°37'53”	19
Pembina R. near Entwistle	07BB002	4,402	53°36'15”	115°0'17”	20
Athabasca R. at Athabasca (water year)	07BE001	74,602	54°43'19”	113°17'16”	422
Athabasca R. at Athabasca (May−October)	07BE001	74,602	54°43'19”	113°17'16”	685
Athabasca−Hinton segment†	NA	64,838	NA	NA	238
Clearwater R. at Draper	07CD001	30,792	56°41'7”	111°15'19”	119
Athabasca R. at Fort McMurray	07DA001	132,585	56°46'49”	111°24'7”	618
Fort McMurray−Athabasca segment‡	NA	57,983	NA	NA	201

The records span at least 55 continuous years, i.e., at least one PDO cycle approximately, which is needed for the analysis; NA, not applicable.

^*Joined to the adjacent Athabasca R. at Entrance record (07AD001).

^†The Athabasca−Hinton segment is the difference between the measured water-year flows at Athabasca and Hinton.

^‡The Fort McMurray−Athabasca segment is the difference between the measured water-year flows at Fort McMurray and Athabasca.

Table S2.

Identification of the optimum set of trend explanatory variables and residual models for Athabasca River basin streamflow

Flow record name	Low-pass variance,* %	AICc	GLS equation†	Residual model	R2inno	R2reg	RP‡ (p level)
Athabasca R. at Hinton	50.3	526.3	Q = −0.2 – 10.7 trend – 5.1 PDO – 2.8 SOIN1 – 2.5 SOIP1	ARMA (0,3)	0.68	0.52	24.12 (9 × 10−7)
McLeod R. above Embarras R.	33.1	267.6	Q = 0.2 – 0.9 trend – 0.7 PNA + 0.5 PDON1	ARMA (3,2)	0.46	0.11	10.28 (0.001)
Pembina R. near Entwistle	34.4	307.9	Q = −0.1 – 2.1 PNA + 0.7 PDO – 0.3 PNAP1 + 1.2 PDOP1	ARMA (2,3)	0.42	0.10	0.12 (0.73)
Athabasca R. at Athabasca (water year)	46.1	609.9	Q = 4.5 – 29.9 trend – 15.7 PDO – 16.0 SOIN1 + 18.9 PDOP2 + 7.5 SOIP2	ARMA (1,5)	0.76	0.15	8.82 (0.003)
Athabasca R. at Athabasca (May−October)	36.5	1012.8	Q = 1.6 – 32.4 PNA – 8.7 SOIN1 – 14.7 SOIP1	ARMA (2,1)	0.32	0.07	0.76 (0.38)
Athabasca−Hinton segment	48.6	664.7	Q = −1.1 – 9.9 PNA −10.4 SOIP1 – 7.4 PNAP2	ARMA (0,1)	0.52	0.06	0.04 (0.84)
Clearwater R. at Draper	56.1	419.0	Q = 1.0 – 11.3 trend + 4.9 SOI + 8.6 PNAN1 + 6.2 SOIN1 – 4.4 PDOP1	ARMA (1,2)	0.75	0.50	8.64 (0.003)
Athabasca R. at Fort McMurray	56.7	560.4	Q = 1.5 – 51.2 trend – 23.4 PNA – 16.7 PDOP2 – 10.5 SOIP2	ARMA (2,1)	0.73	0.37	8.00 (0.005)
Fort McMurray−Athabasca segment	58.3	464.3	Q = 1.1 – 29.1 trend – 4.2 PNA + 3.2 SOIN2 + 4.5 PDOP2	ARMA (2,0)	0.78	0.38	10.38 (0.001)

See refs. 6 and 41 for further details concerning the methods. ARMA, autoregressive moving-average model.

^*Low-pass variance in low-frequency filtered streamflow data as a percentage of the total variability.

^†We used winter (November−March average) PDO, winter (December−February average) PNA, and previous year’s June−November average Southern Ocean Oscillation (SOI) [following Redmond and Koch (42), who showed that the ENSO teleconnection operates with a lag in this region]. Subscripts for 0, ±1, +2 y lags: P1, climate leads streamflow by 1 y; P2, climate leads streamflow by 2 y; N1, climate lags streamflow by 1 y. Q denotes water-year zero-centered river flow and the predictors are normalized.

^‡RP is the Neyman−Pearson statistic (results significant at the 5% level in bold).

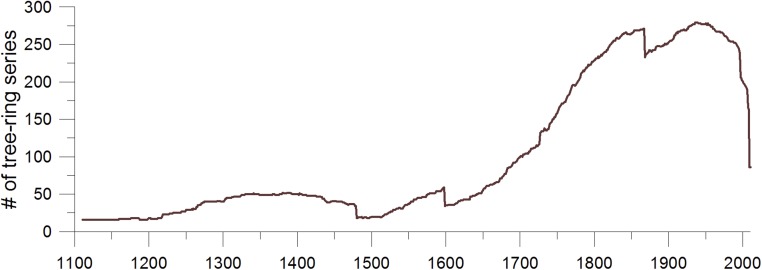
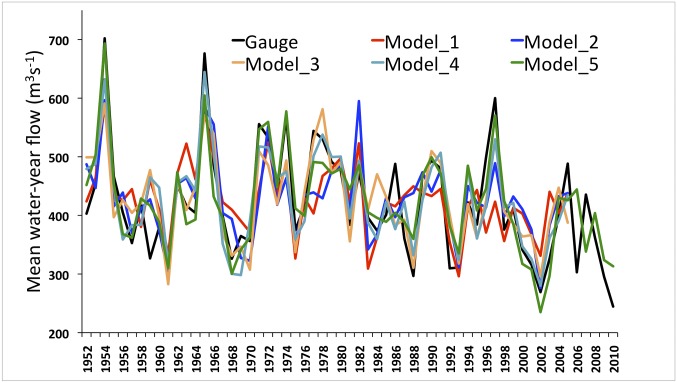
We produced a tree-ring reconstruction of the water-year flow of the Athabasca River at Athabasca for AD 1111–2010. Table 2, Tables S3 and S4, and Fig. S2 give the statistical details for the five tree-ring models that comprise the nested reconstruction. The significant F statistics, positive reduction of error (RE), and similar values of standard error (SE) and root-mean-square error of validation (RMSE_v) indicate robust models with considerable predictive power. Values of R²_adj range from 47% to 80%, with the exception of model 1, which extends back to AD 1111 based on data from three sites. Nonetheless, model 1 is statistically significant. For the five nested models, Fig. 4 shows the water-year reconstructions versus the gauged flow at Athabasca for the common period 1952–2010. For model 5, based on abundant tree-ring data since 1868, the two curves are nearly indistinguishable. As the models encompass more time, and thus tree-ring data from fewer sites, the corresponding modeled flow deviates from the recorded flow. The largest deviations result from the underestimation of high annual recorded flows. However, the tree-ring models consistently capture low flows. Water deficits, rather than excess water, are the major supply issue in the ARB.

Table 2.

The statistics of the five nested tree-ring models comprising the Athabasca River at Athabasca reconstruction for AD 1111–2010

Model no.	Yr1	R2	R2adj	RE	RMSEv	SE	P
5	1868	0.83	0.80	0.73	47.3	41.5	**
4	1725	0.74	0.68	0.62	56.3	52.5	**
3	1599	0.65	0.60	0.50	64.4	58.5	**
2	1482	0.54	0.47	0.34	78.9	66.8	**
1	1111	0.43	0.36	0.23	80.0	73.7	*

The regression model equations are given in Table S4. Yr1, first year of reconstruction; P, P value of F statistic: ** < 0.0001, * < 0.001.

Table S3.

The 16 tree-ring chronology site coordinates and statistics

Code	Name	Species*	Lat, °N	Long, °W	First year†	Last year	No.‡	r§	ms¶	ac#
dea	Douglas Fir Ecological Area	Psme	52.19	116.44	1471	2007	50	0.802	0.389	0.367
dmh	Deadman Hole	Psme	52.87	118.07	1699	2012	35	0.797	0.420	0.181
grn	Gray Nun	Pigl	53.62	113.65	1868	2011	40	0.636	0.305	0.503
jola	Johnson Lake	Psme	51.96	115.49	1446	2011	46	0.730	0.304	0.549
mgc	Maligne Canyon	Psme	52.92	118.00	1758	2012	19	0.705	0.229	0.396
plk	Patricia Lake	Psme	52.88	118.08	1725	2013	45	0.780	0.302	0.398
sfr	Siffleur Ridge	Pifl	52.04	116.39	1018	2012	62	0.776	0.383	0.544
skc	Saskatchewan Crossing	Pifl	51.97	116.72	1109	2007	60	0.667	0.286	0.336
swh	Swan Hills	Piba	54.80	115.60	1733	2004	22	0.572	0.201	0.575
ttb	Trail TwoB	Psme	52.92	118.09	1534	2013	148	0.774	0.376	0.276
two	Two O'Clock Creek	Psme	52.06	116.43	1496	2013	38	0.787	0.428	0.449
vrl	Virl Lake	Psme	52.87	118.25	1660	2013	49	0.789	0.265	0.442
wab	Wabasca	Piba	56.05	113.77	1815	2006	28	0.572	0.227	0.531
wbs	Wabasso Lake	Psme	52.80	117.96	1599	2013	29	0.825	0.422	0.362
wpp	Whirlpool Point	Pifl	52.00	116.45	1062	2013	32	0.751	0.463	0.270
wrc	Whiterabbit Creek	Psme	52.07	116.38	1555	2008	38	0.836	0.414	0.283

^*Psme, Pseudotsuga menziesii (Douglas fir); Pifl, Pinus flexilis (limber pine); Pigl, Picea glauca (white spruce); Piba, Pinus banksiana (jack pine).

^†The year when the chronology’s EPS becomes greater than 0.85.

^‡The number of samples (ring-width time series) in the chronology.

^§The correlation among the ring-width series at the site.

^¶The mean sensitivity: a measure of the interannual ring-width variability.

^#The first-order autocorrelation over the common period 1868–2004.

Table S4.

The five, nested tree-ring multiple linear regression equations for the Athabasca River at Athabasca water-year reconstruction, based upon the 16 tree-ring chronologies described in Table S3, including their codes

Regression equation no.	Date	Equation
1	since AD 1111	Qwy = 64.40 skc_ew + 106.99 wpp + 100.18 sfr-1 − 154.55 skc-2 − 575.07 wpp+2 + 633.38 wpp_ew+2 + 260.13
2	since AD 1482	Qwy = 162.46 skc_ew + 126.65 dea-1 − 170.85 skc-2 − 115.45 jola_lw+2 + 110.13 two+2 − 728.77 wpp+2 + 752.31 wpp_ew+2 + 286.05
3	since AD 1599	Qwy = 162.20 wbs_lw + 125.09 wpp_ew − 77.76 wrc_ew + 197.27 ttb+1, − 98.19 wbs_ew+1 − 80.28 dea+2 + 174.55 skc+2 + 27.92
4	since AD 1725	Qwy = 121.57 wbs_lw + 69.45 wpp_ew + 67.40 two-1 − 226.46 plk_ew-2 − 120.50 skc-2 + 124.10 vrlew-2 + 79.87 wbs_ew-2 + 70.51 dea_lw+1 − 112.33 dea_lw+2 + 188.38 skc+2 + 159.46
5*	since AD 1868	Qwy = −22.95 dmh_lw + 220.77 grnu_lw + 192.1529 mgc_lw + 209.38 skc - 93.5862 plk-1 − 230.72 skc-1 + 243.35 two_ew-1 − 94.83 wab_lw-1 + 152.83 dea_lw+1 − 6.62 plk_lw+1 − 111.85

Q_wy, water-year discharge; ew, early wood; lw, late wood; ±1, ±2, leads or lags of plus 1 or 2 y.

^*Model 5 also was run using only predictor chronologies extending up to 2010 and beyond, to estimate water-year flow for the years 2007–2010.

Fig. S2.

Tree-ring series sample depth in the Athabasca River at Athabasca water-year flow reconstruction. Sample depth is 16–18 series throughout the 1100s and at least 20 series throughout the 1400–1500s.

Fig. 4.

Observed versus modeled flow of the Athabasca River at Athabasca over the calibration period (1952−2010) for the five tree-ring models described in Table 2 and Table S4.

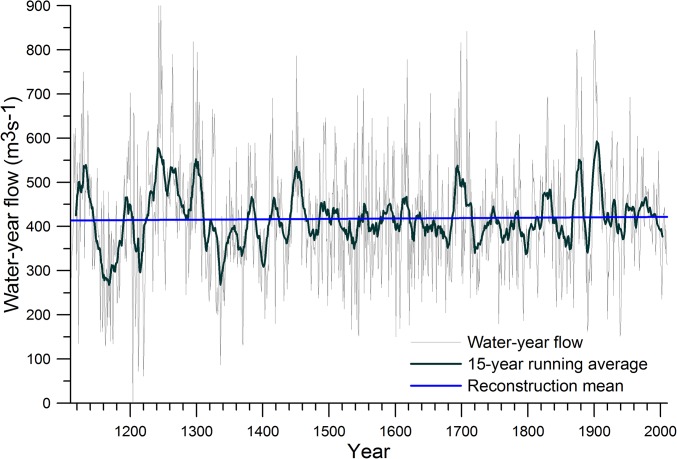
The full Athabasca River reconstruction spanning AD 1111–2010 is plotted in Fig. 5. It indicates that AD 1937–1949 was the longest interval of low flow since the installation of hydrometric gauges on the Athabasca River, although the instrumental data are missing during this period (Fig. 3). Considering only the past several centuries, this modern drought of record is exceeded in severity and duration by periods of sustained low flow in AD 1790–1806 and AD 1888–1896. To depict the relative severity of these paleodroughts, we identify analogous years in the hydrometric record according to annual discharge anomaly (percent) (Table 3). Thus, for example, the drought of AD 1888–1896 can be portrayed as the low flow years of the 2000s plus 1960 and 2 y for which there is no modern analog; discharges in these years were much lower than the minimum recorded annual flow. The drought of AD 1790–1806 also includes a year that has no modern analog, but the most notable property of this drought is its duration: 17 consecutive years of below-average water levels. These two paleodroughts are highlighted because they are relatively recent; however, neither one is a worst-case scenario. Droughts of greater intensity and/or duration occurred in preceding centuries, including the megadroughts of AD 1143–1198 and AD 1311–1409. The reconstructed flows before AD 1482 are based on model 1, with the least explained variance, lowest RE, and highest SE (Table 2). Thus, we have the least confidence here; the large range of reconstructed flows may be an artifact of the lower sample depth. However, the sequence of wet and dry years is valid, and the prolonged periods of low flow indicate the persistence of long dry spells.

Fig. 5.

The full AD 1111–2010 tree-ring reconstruction of the water-year (October−September) flow (cubic meters per second) of the Athabasca River at Athabasca. Also plotted is the mean annual flow for the entire record (418 m³⋅s⁻¹) and a 15-y running mean.

Table 3.

Two severe sustained paleodroughts in the ARB in recent centuries and analogous years from the instrumental hydrometric record

Year	%Δ*	Modern analog†
1790	−12.3	1969
1791	−11.9	1984
1792	−18.3	2000
1793	−55.4	NMA
1794	−31.2	2009
1795	−7.8	1995
1796	−12.2	1969
1797	−16	1957
1798	−3.4	1956
1799	−21.4	1959
1800	−19.7	2000
1801	−13.2	1969
1802	−13.5	2008
1803	−27.2	2006
1804	−26.4	1992
1805	−7	1995
1806	−3.9	1952
1888	−40	2010
1889	−9.9	1960
1890	−61.2	NMA
1891	−55.3	NMA
1892	−27.6	2006
1893	−34.8	2002
1894	−19.1	2000
1895	−22.4	2003
1896	−36.2	2002

^*Negative departure of inferred water-year flow from the reconstruction mean (418 m³⋅s⁻¹).

^†Comparable modern (1952−2010) anomaly relative to mean water-year flow of 419 m³⋅s⁻¹; NMA, no modern analog.

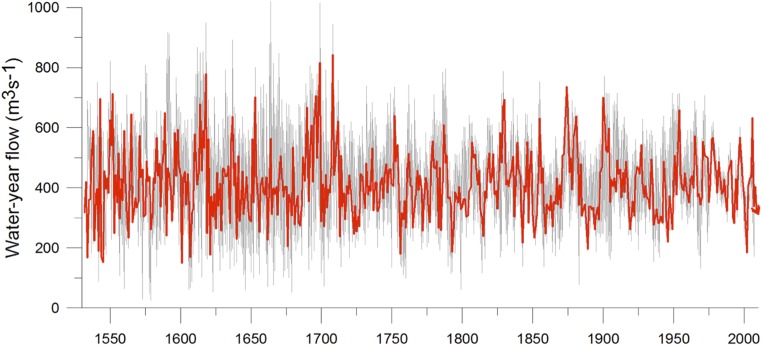
Fig. 5 is a single best streamflow reconstruction based on the limited number of tree-ring chronologies selected by the regression algorithm from the large pool of potential predictors: 43 ring-width chronologies, (early-wood width and annual increments at 16 sites, plus late-wood width at 11 sites), which were lagged by ±2 y, giving a total of 215 predictors. We also generated, based on the methods in Sauchyn et al. (10), 200 streamflow reconstructions for the period with the greatest sample depth (AD 1534–2010, Fig. S2) and with validation R²_adj values ranging from 0.53 to 0.7. This ensemble illustrates the degree of time-varying uncertainty in the tree-ring reconstruction (Fig. S3). The paleodroughts highlighted above (i.e., AD 1790–1806, AD 1888–1896) remain evident in the ensemble reconstruction.

Fig. S3.

An ensemble of 200 tree-ring reconstructions of the water-year flow of the Athabasca River at Athabasca for AD 1599–2010. The red curve represents the best single reconstruction presented in the paper.

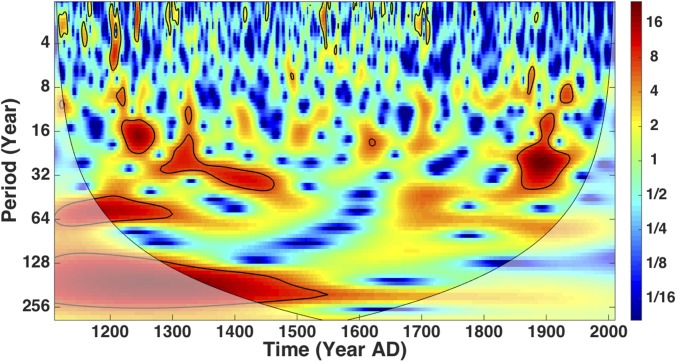
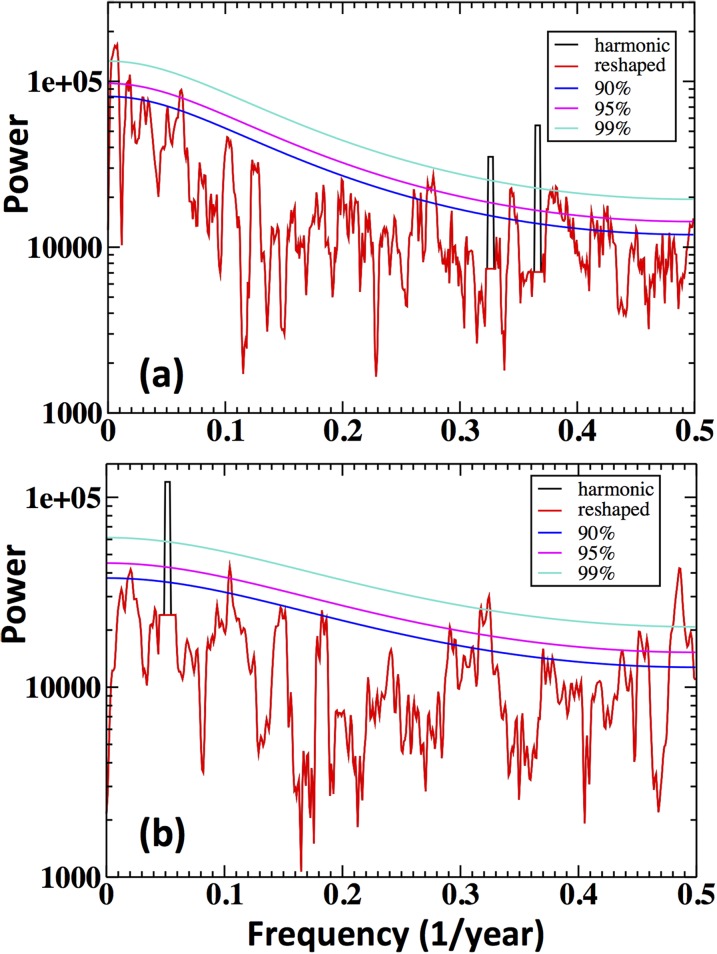
A wavelets evolutionary spectrum of the full reconstruction (AD 1111–2010) shows that the modes of variability have not been consistent over the past millennium, but rather differed among the putative Medieval Climate Anomaly (MCA; ∼AD 1111–1550) (11), the putative Little Ice Age (LIA; ∼AD 1551–1850) (11), and the modern period (AD 1851–2010) (Fig. 6). During the MCA, there are low-frequency modes of variability in the 16- to 20-, ∼32-, ∼55-, and ∼220-y bands. During the LIA, there is significant low-frequency variability in the 16- to 20-y band only. Variability in the higher-frequency 2- to 5-y band, representative of ENSO, is present throughout. Significant power at the ∼32-y band reappears during the modern period. These patterns are confirmed using a multitaper method (MTM) with its superior spectral estimation (12) (Fig. S4). MTM analysis confirms the presence of significant peaks (95% level) in the 2- to 5-, 16- to 20-, 54-, and 220-y frequency bands during the MCA (Fig. S4A). It also confirms the absence of the lower-frequency variability during the LIA, which instead has significant variability only at the 2- to 5-, 10-, and 20-y frequencies (Fig. S4B).

Fig. 6.

Wavelet evolutionary spectrum of the Athabasca River tree-ring reconstruction for AD 1111–2010. Significant (P < 0.05) power exists at the frequencies and time intervals depicted in red and enclosed by a black line.

Fig. S4.

MTM spectral analysis of the Athabasca River at Athabasca tree-ring reconstruction for (A) the Medieval Climate Anomaly (AD 1111–1550) and (B) the Little Ice Age (AD 1551–1850). Significant (P < 0.05) power exists at the frequencies where the spectra project above the magenta line. Analysis was performed with the software described in refs. 12 and 40. “Harmonic” (black) denotes the clear distinct periodic components associated with a coherent phase spectrum; “reshaped” (red) denotes the remaining narrowband quasi-periodic components of the spectra.

Discussion

Our GLS analysis of the instrumental data reveals generally declining flows throughout the ARB (Table 1), confirming concerns of Schindler and Donahue (1) and Peters et al. (8). Other recent studies of historical streamflow trends in the ARB have produced inconsistent results, reflecting the use of various gauge records of varying lengths and, to a lesser extent, different statistical methods; although most used variants of the low-powered Mann–Kendall (MK) nonparametric trend test. Results from Bawden et al. (13) show strong decreasing trends in annual, warm season (March to October) and summer flows over most of the ARB. They used 19 hydrometric records, most of them short (<50 y). Similarly, Rasouli et al. (14) analyzed trends only since 1960, discovering marked declines in the streamflow input to Lake Athabasca. In contrast, Rood et al. (9) and Peters et al. (8), like us, examined streamflow data back to 1913, spanning major data gaps or interpolating shorter ones. Rood et al. (9), using parametric linear regression, found declining trends in summer and in the upper reaches, but found no significant trends in the middle and lower reaches using the centennial length records (Table 1). Peters et al. (8), using the MK test, found declines at Hinton and Fort McMurray, and in the Fort McMurray−Athabasca segment, but not at Athabasca (Table 1). Both Rood et al. (9) and Peters et al. (8) emphasized the teleconnections between the regional hydroclimatic regime and North Pacific climate oscillations (6, 7). They referred to the associated pentadecadal hydrologic variability as the rationale for using only the longest ARB records. However, unlike our study, previous researchers have not modeled and removed the confounding transient trends of the low-frequency components of the PDO and PNA before performing the trend test. Our GLS analysis also correctly handles residual autocorrelation and thus allows a high-powered parametric test. With a higher ratio of trend signal to noise, from the explicit modeling of hydrologic variability related to the climate oscillations, our approach has an improved chance of trend detection. The use of more-tractable hydrometric data, filtered with a 5-y binomial smoother, is not a major limitation, as negative trends in these filtered data represent sustained periods of declining flows with potentially serious consequences. Ecosystems and communities in the ARB can cope with a single severe low-flow year or two, but a prolonged period of lower flows is much more challenging.

The collection and analysis of tree rings from dry sites in the montane forest of western Alberta (e.g., refs. 10 and 15–19) has shown that the rate of tree growth at these sites is limited by the availability of soil moisture. However, there has been no previous attempt to produce a long streamflow reconstruction for the ARB using a network of tree-ring chronologies from the headwaters of the Athabasca River basin. Most of the previous research into the paleohydrology of the ARB has been conducted near the mouth of the Athabasca River at the Peace−Athabasca Delta. There have been two tree-ring reconstructions of the past levels of Lake Athabasca (20, 21); both were relatively short (<200 y). A major study of the paleolimnology of the Peace−Athabasca Delta by Wolfe et al. (22–24) provides important context for the interpretation of recent hydrological changes, although at coarser resolution than that enabled by annual tree rings. Rasouli et al. (14) interpreted trends in recorded streamflow in the context of the Wolfe et al. (23, 24) millennial-length lake level time series, concluding that Lake Athabasca levels could drop by 2–3 m by the end of the 21st century.

Our 900-y reconstruction of water-year flow revealed that the long-term variability of the Athabasca River is considerably greater than recorded by the gauge near the community of Athabasca (Figs. 3 and 5). There are reconstructed pregauge periods of consistent low flows that far exceed the duration of the worst recorded hydrologic droughts. A prolonged interval of low flow occurs in the tree-ring reconstruction from AD 1936–1949, during the period of missing data in the gauged flow of the Athabasca River. This low-flow period is seen throughout southern Alberta in various instrumental records. This modern drought, and more severe hydrologic droughts from the paleorecord, such as in AD 1790–1806 and AD 1888–1896, should be considered in the allocation and use of ARB surface water. The paleodroughts include years when discharges were so low that there is no modern analog in the gauge records. Further evidence of extremely low flows in the AD 1790s comes from Hudson Bay Company journals from Fort Edmonton on the North Saskatchewan River (25). “Amazing” is used to describe the warmness of the winter and shallowness of the water. In the spring of 1796, low river flows caused damage to light canoes and prevented the transport of furs, timber, and supplies. Reports of extensive grass and forest fire, and diminished populations of bison and beaver, are further indications of unusually dry conditions. The adjacent Athabasca and North Saskatchewan Rivers have a similar hydroclimate and emanate from the same ice field. Thus, the ARB paleohydrology presented here shares many characteristics with an initial reconstruction of the flow of the North Saskatchewan River (26) and a subsequent reconstruction (16) using more recent tree-ring data and from more sites. Geographically extensive hydroclimatic events include centennial-length low-flow periods during the megadroughts of AD 1143–1198 and AD 1311–1409, which are well documented in proxy records from other regions of western North America (27).

Our reconstruction provides context that the short instrumental record lacks (Figs. 3 and 5). Never during the last 62 y has the average annual flow of the Athabasca River at Athabasca been less than 200 m³⋅s⁻¹. Our 900-y reconstruction shows 36 occurrences of flow below 200 m³⋅s⁻¹. Within the instrumental period of 1952–2013, winter (DJF) flow was, on average, 23% of water-year flow. If we assume this ratio roughly holds over a longer time period, then a year with an annual flow of less than 200 m³⋅s⁻¹, would have had a winter flow of less than 46 m³⋅s⁻¹. The Government of Alberta (5) estimates that oil sands water use will reach 16 m³⋅s⁻¹ in the next decade. This water is withdrawn from the Athabasca River in the Fort McMurray region, not at Athabasca. Flow at Athabasca is 68% of that downstream at Fort McMurray (1958−2012 average). If a low flow year of less than 200 m³⋅s⁻¹ occurs at Athabasca, this is roughly equivalent to 68 m³⋅s⁻¹ in winter at Fort McMurray. In this case, water permanently withdrawn for oil sands extraction is an appreciable amount, particularly if these low flows repeatedly occur for a decade or more, as our reconstruction shows can be the case.

Our spectral analysis demonstrates the low-frequency variability in ARB flows linked to teleconnections with large-scale climate oscillations (Fig. 6 and Fig. S4). The GLS trend analysis of instrumental data confirms that the PDO and the PNA, with their similar low-frequency components (28), have a significant impact on historical ARB flows (8). In the 900-y proxy flow record, the MCA spectrum contains the modes of variability typical of the PDO and the associated North Pacific Index. These frequencies (i.e., pentadecadal and bidecadal) are also seen in spectra of modern instrumental records along with the ENSO band at 2–5 y (29, 30). The LIA spectrum is very different, without a strong pentadecadal band. This suggests that the low-frequency variability of the PDO and PNA has varied between the MCA, LIA, and modern periods, or that the teleconnections between these climate oscillations and ARB hydroclimate naturally varies. Either possibility would imply nonstationarity in a major driver of ARB hydroclimate over the past millennium, as speculated by some researchers (e.g., ref. 31).

Conclusions

Water resource engineering, and decisions about water allocation, supply, and storage, have relied on the assumption of stationarity—that hydroclimatic regimes fluctuate within a consistent range of variability captured by relatively short instrumental records (32). This assumption is undermined by research on the hydroclimate of the past millennium (e.g., refs. 33–35), including our 900-y tree-ring reconstruction of the Athabasca River, which encompasses periods of sustained low flow spanning multiple decades, unlike any hydrologic drought recorded instrumentally. When these prolonged droughts reoccur, it will be in a much warmer climate, presenting significant challenges for ARB surface water management (36). Our GLS trend analysis, with its superior trend detection ability, shows declining flows in much of the ARB, consistent with regional climate warming and the loss of glacier ice and snowpack at high elevations in the Rocky Mountains (33). Our study provides evidence of multidecadal variability of ARB discharges, at the low frequency of the large-scale climate oscillations (i.e., the PDO and PNA). At the very least, risk assessment in the oil sands industry should consider the repeated decadal droughts that are a common feature of the regional hydroclimate but have not occurred since the industry was established. The industry, and government agencies that regulate the use of surface water, may also want to consider the implications of a future period of sustained low flow in a warmer climate. The long-term trends and variability in river flow examined in this paper extend beyond the ARB, and thus the lessons for water resource management are transferrable to watersheds across Canada’s western interior.

Methods

We used the nine longest gauge records and segments from the ARB (i.e., of at least 55 y in length, approximately one full PDO cycle) for a GLS multiple linear regression trend analysis, modeling the low-frequency variability associated with the PDO and PNA and also the higher-frequency variability driven by ENSO, using the South Oscillation Index (SOI) (see Table S2 for more details) (6). We spliced some records from sequential gauges following Rood et al. (9), but performed only minor gap filling. These nine gauge records were the predictands in the GLS regression models (Table 1). The predictors were the winter (November−March average) PDO, winter (December−February average) PNA and (previous year’s June−November average) SOI indices, and a monotonic trend. Because streamflow is lagged and smoothed relative to precipitation by surface and subsurface hydrology, and these large‐scale climatic phenomena act at interannual time scales, the stream records were lagged from the climate indices by 0 y, ±1 y, and +2 y, and a 5-y binomial smoother was applied to the hydrologic and climatic data. The statistical model used in this study is Q_t = µ + λT_t + β₁x_1,t + … + βkX_k,t + ε_t, t = 1,…, L, where {Q_t} is mean daily streamflow; index t runs over L years; µ is the mean streamflow over these years; T_t is a linear trend with coefficient λ; {x_i,t, t = 1,…,L} is the i^th explanatory variable; k is the number of explanatory variables; β_i is the ith explanatory variable’s coefficient; and {ε_t} is the residual time series, which is an ARMA(p, q) process. An optimum minimal subset of significant predictors and an optimum minimal ARMA(p,q) residual model were chosen using the corrected Akaike Information Criterion (AICc) statistic applied to all predictor subsets of size ≤6, and for all p + q ≤ 6. The nonzero significance of the trend coefficient λ was tested by the Neyman−Pearson statistic (RP) using the null model of the optimum set of explanatory variables (minus the trend variable if included in the optimum set) versus the alternative model of the optimum set of explanatory variables together with the linear trend (if not already added).

The Athabasca River at Athabasca gauge provides the longest continuous hydrometric record from 1952 to 2013, although there are earlier data for 1913–1930 (Fig. 3). Water-year (October 1 to September 30) flow over 1952–2013 was used for the calibration and validation of the tree-ring models. The tree-ring data are from 16 sites within and near the Athabasca River Basin in north-central Alberta, where, during 2007–2013, increment cores and cross sections were collected in old-growth coniferous forest. Mapped in Fig. S1 and listed in Table S3 are the tree-ring sites in the Athabasca River’s upper reaches and in the adjacent North Saskatchewan River basin headwaters. Nearly all of the tree-ring width data were generated using the WinDendro tree-ring image analysis system. For most sites, we also measured the early- and late-wood widths. Cross-dating of the tree-ring series was verified with COFECHA (37). We standardized the tree-ring series using ARSTAN (38), removing the nonclimatic growth trends in the tree-ring series through conservative detrending based on the use of a negative exponential curve or a cubic smoothing spline (a low-pass digital filter with a 50% frequency response cutoff). The standardized ring-width series of various lengths were averaged for each site, using a mean value function minimizing the effects of outliers (39). Table S3 gives statistical data for the 16 standard index chronologies. The number of time series per site varies from 19 to 148. Significant interseries correlation, as high as 0.836, and high mean sensitivity, mostly greater than 0.3, indicate a strong common response to interannual hydroclimatic variability. At all sites, first-order autocorrelation over the common period (1868−2004) exceeds the 95% significance level of 0.134, matching the similar significant persistence in stream flow (0.265). Table S5 shows the many significant (P < 0.05) correlations of the ring-width index data with streamflow and annual and seasonal precipitation measured at Jasper, Alberta, from 1971 to 2011, demonstrating that these tree-ring chronologies are suitable for reconstructing Athabasca River flow. These correlations are across all seasons, reflecting the role of snowmelt water and spring rain in recharging soil moisture and the role of summer rain in sustaining it.

Table S5.

Significant (P < 0.05, denoted by asterisks) correlations of ring-width index time series with water-year (WY) streamflow and annual (ANN) and seasonal precipitation measured at Jasper, Alberta, from 1971 to 2011

Site	Stream flow					Precipitation
	WY	DJF	MAM	JJA	SON	ANN	DJF	MAM	JJA	SON
dea	*		*	*				*	*
dmh	*			*	*	*	*	*	*
grn	*						*
jola	*	*	*					*
mgc	*	*						*
plk	*	*		*	*			*	*
sfr	*					*	*
skc	*			*	*		*
swh			*		*
ttb	*	*				*		*	*
two	*	*		*				*
vrl	*			*	*			*
wab	*	*	*						*
wbs	*			*	*	*		*	*
wpp	*						*	*
wrc	*		*			*		*	*

Jasper is the climate station nearest to most of the chronologies, which are located in the Athabasca River’s headwaters. 1971–2011 is the longest continuous common period in the instrumental climate and hydrologic records. DJF, December−February; MAM, March−May; JJA, June−August; SON, September−November.

The tree-ring reconstruction of water-year flow followed standard methods, using stepwise multiple linear regression with forward selection. The pool of potential predictors consisted of the standard index chronologies from the 16 sites. There were one to three ring-width index chronologies per site, depending on the availability of measurements of early and late wood. Lagging the predictor chronologies, by up to 2 y behind and ahead of the streamflow data, accounts for an offset between climatic conditions in a given year and the response of tree growth versus water levels. The regression models were validated using the leave-one-out method. The optimal number of predictors per model ranged from 7 to 10, according to various criteria: R²_adj, RMSEv, RE, and SE.