Accurate molecular structures and infrared spectra of trans-2,3-dideuterooxirane, methyloxirane and trans-2,3-dimethyloxirane

Abstract

Oxirane derivatives are the most used benchmarks for chiroptical spectroscopies in view of their small size and relative rigidity. The molecular structure, vibrational harmonic and anharmonic frequencies, and infrared intensities of the ground electronic states are analyzed in this paper. Equilibrium structure and harmonic force fields have been evaluated by means of high-level quantum-chemical calculations at the coupled-cluster level including single and double excitations together with a perturbative treatment of triples (CCSD(T)). Extrapolation to the complete basis-set limit as well as core-correlation effects have also been taken into account. Anharmonic contributions have been computed at the CCSD(T)/cc-pVTZ level for trans-2,3-dideuterooxirane. These data can serve as references to evaluate the accuracy of less expensive computational approaches rooted in the density functional theory (DFT). The latter have been used within hybrid CC/DFT approaches, which have been applied to simulate fully anharmonic infrared (IR) spectra. Finally, the best theoretical estimates of the equilibrium structures and vibrational wavenumbers are compared to the most accurate experimental data and show in all cases very good agreement, i.e., within 0.001 Å, 0.1 degrees and 10 cm⁻¹ and 0.5 km mol⁻¹, for bond lengths, angles, wavenumbers and IR intensities, respectively.

I. INTRODUCTION

Substituted oxiranes have become the de facto standards to benchmark theoretical and experimental methodologies intended for chiroptical spectroscopies^1,2. In particular, trans-2,3-dideuterooxirane (D₂Ox), methyloxirane (MeOx), and trans-2,3-dimethyloxirane (Me₂Ox) have been extensively investigated with both density functional theory (DFT) and post-Hartree-Fock approaches by comparing the computed optical rotation, electronic and vibrational circular dichroism (ECD and VCD, respectively) spectra with their experimental counterparts, recorded in the gas phase and/or in solution^3–27. Although satisfactory results have been obtained with different approaches, thorough studies proceeding from accurate equilibrium structures to anharmonic force fields and further to electric and magnetic moments, excited electronic states and environmental effects are still lacking. Accurate molecular structures and vibrational spectra are the mandatory starting points to an accurate treatment of chiroptical spectroscopies. In fact, the positions of the VCD bands are the same as those of their infrared (IR) counterparts and the VCD intensities depend, in addition to the magnetic moments, on the electric moments involved in the IR intensities. At the same time, optical activity is ruled by molecular structure and vibrational effects. Furthermore, we point out that the vibrational corrections to rotational constants, chiral and non-chiral molecular properties, and thermodynamical functions are in all cases obtained from the same anharmonic force field employed in the IR spectra determination. Finally, vibronic contributions to ECD spectra originate from ground- and excited-state vibrational frequencies (see Ref.²⁸ for an extensive review on different effects underlying the overall spectral phenomena). On these grounds, we decided to undertake a comprehensive study of the substituted oxiranes mentioned above aiming at providing accurate structures and vibrational contributions as a first step toward the determination of reliable chiroptical properties.

Accurate structural determinations are still a challenge for both experiment and theory. The best choice to report structural information is the equilibrium structure since it is well defined (minimum of the Born-Oppenheimer (BO) potential energy surface), it excludes vibrational effects in a rigorous manner and, within the BO approximation, it is independent of the considered isotopic species. In view of the difficulties in dealing with vibrational effects, the so-called semi-experimental equilibrium structure $\left({\mathrm{r}}_e^{\mathit{SE}}\right)$²⁹ probably provides the most reliable route toward the accurate determination of equilibrium geometries^30–33. This requires the determination of experimental ground-state rotational constants (B₀) for different isotopic species, their correction for vibrational effects by means of anharmonic force-field computations, and then a least-square fit of the geometrical parameters to the resulting semi-experimental equilibrium rotational constants $\left(B_e^{\mathit{SE}}\right)$. Unfortunately, this approach is limited by the availability of rotational constants for different isotopic species, which are often not sufficient for determining all geometrical parameters, thus requiring debatable constraints for some of them^{30,32,34–36}. In the present context, sufficient information is available to obtain the semi-experimental equilibrium structure of oxirane^37–39 (which is the same of trans-2,3-dideuterooxirane within the BO approximation) and methyloxirane⁴⁰, but this is not the case for dimethyloxirane. Under such circumstances, one has to resort to pure theoretical geometries. Several studies have shown that, in the absence of a strong multireference character, the coupled-cluster (CC) singles and doubles approximation augmented by a perturbative treatment of triple excitations, CCSD(T)⁴¹, in conjunction with extrapolation to the complete basis-set limit and a proper account of core correlation is able to provide accurate structures, rivaling their best experimental counterparts (see, for example, Refs.^30,42–45). Despite the high computational cost of such an approach, the latest developments in hardware and software permit its use for medium-sized systems^46–48. Recently, we have shown that the dimensions of systems amenable to such accurate analysis can be further extended by performing basis-set extrapolation and inclusion of core correlation by means of second-order Møller-Plesset perturbation theory (MP2)⁴⁹ in place of the much more expensive (and poorly scaling) coupled-cluster ansatz^36,42. This cheaper approach will be further validated in the present work by comparison with full coupled-cluster and semi-experimental results for the two smaller substituted oxiranes.

The situation is more involved for IR spectra when the sought accuracy implies going beyond the harmonic approximation for frequencies and, especially, for intensities⁵⁰. From a methodological point of view, second-order vibrational perturbation theory (VPT2)^51,52 based on Cartesian normal modes still represents, in our opinion, the best compromise between accuracy and efficiency, at least for semi-rigid molecules of medium-to-large size^53–61. Several studies have shown that electron correlation and basis-set extension are of paramount importance for the harmonic contributions, whereas anharmonic corrections can be reliably obtained at lower computational levels^62–70. This led to the introduction of hybrid schemes^62,69,71,72, which are based on the close correspondence between the normal modes obtained at the two different levels of theory and on the hypothesis that the largest part of the differences in calculated observables lies in the harmonic part. While this strategy can be considered well tested for vibrational energies^{42,50,62,69–73}, the corresponding approach for IR intensities has seen limited applications till now, also due to the fact that it has become only recently available in general-purpose computational codes^59,74. However, our first results are promising also in this direction. As a result, hybrid CC/DFT schemes turn out to combine accuracy and computational efficiency^42,50,75. In this context, hybrid density functionals (especially B3LYP) provide particularly good results when coupled with polarized double-ζ basis sets augmented by diffuse functions^50,69,70. Accuracy can be further improved by using the so-called double hybrid functionals (especially B2PLYP), but at the price of increased basis-set requirements (at least of augmented doubly polarized triple-ζ quality) and computational cost^50,76. In the present study, the small size of the dideuterated oxirane allows us to further investigate the accuracy reachable with hybrid CC/DFT schemes with respect to accurate anharmonic force fields derived from best-estimated harmonic force fields with cubic and semi-diagonal quartic force constants computed at the CCSD(T) level.

This manuscript is organized as follows: after an extensive description of the computational protocol used in this work, the equilibrium structures obtained with different computational models are compared to our best theoretical estimates and, where available, to the semi-experimental structures. Subsequently, the accuracy of the harmonic vibrational wavenumbers and IR intensities is discussed, and followed by the analysis of the corresponding anharmonic contributions. Finally, the fully anharmonic IR spectra are simulated and the accuracy of different methods and hybrid approaches is assessed by comparison with the available experimental data and our best theoretical estimates.

II. COMPUTATIONAL DETAILS

The MP2⁴⁹ and CCSD(T)⁴¹ methods were employed in molecular structure and force-field calculations, as described below. Correlation-consistent basis sets, (aug)-cc-p(C)VnZ (n=T,Q,5)^77–79, were used in conjunction with the aforementioned methods. MP2 and CCSD(T) calculations were carried out with the quantum-chemical package CFour⁸⁰.

Density Functional Theory was employed to compute equilibrium geometries, quadratic, cubic and semi-diagonal quartic force fields together with up to the third derivatives of the dipole moment, needed for the computation of fully anharmonic IR spectra. In view of its efficiency in computational spectroscopy studies of relatively large molecular systems,^69,76,81,82 including IR and Raman intensities^42,48,50,75, the standard functional B3LYP⁸³ was chosen in conjunction with a polarized basis set of double-ζ quality supplemented by diffuse functions, SNSD^50,84. Moreover, functional CAM-B3LYP⁸⁵, which has shown a good performance for the computations of chiroptical properties^82,86, has been considered. For both B3LYP and CAM-B3LYP, the basis set convergence has been assessed by comparison with the results obtained with basis set aug-cc-pVTZ. Finally, the double-hybrid functional B2PLYP^87,88 was considered in conjunction with basis set aug-cc-pVTZ because of its well-proved accuracy^50,76. Computations at the B2PLYP level are significantly more expensive than those performed with B3LYP or CAM-B3LYP because of both the inclusion of a second-order perturbation treatment of the electron correlation and larger basis set requirements. On the other hand, they remain very cost-effective alternatives with respect to CCSD(T)^50,76,89,90. All DFT computations were performed employing a locally modified version of the suite of programs for quantum chemistry GAUSSIAN⁹¹.

A. Molecular Structure

Two different composite approaches were employed in view of accurately determining equilibrium structures. Within these composite schemes, the contributions that are considered to be the most important are evaluated separately at the highest possible level and then, by resorting to the additivity approximation, combined in order to obtain the best theoretical estimates.

The first approach considered is the so-called “gradient scheme”. It is a rigorous approach based on the additivity at an energy-gradient level,^43,44 and the included contributions are: the Hartree-Fock self-consistent-field (HF-SCF) energy extrapolated to the complete basis-set (CBS) limit, the valence correlation energy at the CCSD(T) level extrapolated to the CBS limit as well, and the core-correlation correction. The energy gradient used in the geometry optimization is therefore given by

$$\frac{{\mathit{dE}}_{\mathrm{CBS}+\mathrm{CV}}}{\mathit{dx}}=\frac{{\mathit{dE}}^{\infty }(\mathrm{HF}-\mathrm{SCF})}{\mathit{dx}}+\frac{d\Delta E^{\infty }\left(\mathrm{CCSD}\right(\mathrm{T}\left)\right)}{\mathit{dx}}+\frac{d\Delta E\left(\mathrm{CV}\right)}{\mathit{dx}},$$ (1)

where dE^∞(HF-SCF)/dx and dΔE^∞(CCSD(T))/dx are the energy gradients corresponding to the exp(−Cn) extrapolation scheme for HF-SCF⁹² and to the n⁻³ extrapolation formula for the CCSD(T) correlation contribution,⁹³ respectively. In the expression given above, n=T, Q and 5 were chosen for the HF-SCF extrapolation, while n=T and Q were used for CCSD(T) for all molecules, except oxirane for which n=Q and 5 were also considered. Core-correlation effects were included by adding the corresponding correction, dΔE(CV)/dx, with the core-correlation energy correction, ΔE(CV), being obtained as the difference between the all-electron and frozen-core CCSD(T) energies using core-valence basis sets (either cc-pCVTZ or cc-pCVQZ). The resulting structure, which is usually referred to as “CCSD(T)/CBS+CV”, will be simply denoted as “bestCC”.

The second composite approach employed is a cheaper computational scheme recently introduced to obtain accurate equilibrium structures of large molecules^42,94, which relies on the additivity approximation applied directly to geometrical parameters. This scheme mainly involves geometry optimizations at the MP2⁴⁹ level. Within this approach, the CBS limit is evaluated by assuming that the convergence behavior of the structural parameters mimics that of the energy. On a purely empirical (but well tested, see Ref.⁹⁵) basis, the consolidated n⁻³ extrapolation form⁹³ was applied to the case n=T and Q:

$$r\left(\mathrm{CBS}\right)=\frac{n^{3}r\left(n\right)-{(n-1)}^{3}r(n-1)}{n^3-{(n-1)}^3},$$ (2)

where n=4, and thus r(n) and r(n − 1) denote the MP2/cc-pVQZ and MP2/cc-pVTZ optimized parameters, respectively. The effects due to the CV correlation were included by means of the corresponding correction, Δr(CV), derived by analogy with the energy-gradient corrections, but at the MP2 level (with the cc-pCVTZ basis set). The effect of diffuse functions (Δr(aug)) was considered through geometry optimizations at the MP2/aug-cc-pVTZ level within the frozen-core approximation, in order to complement the extrapolation described above (see Refs.^42,94). Higher-order correlation energy contributions to molecular structure (Δr(T)) were derived from the comparison of the geometries optimized at the MP2 and CCSD(T) levels, both with the cc-pVTZ basis set. On the whole, our best-estimated equilibrium structure was thus determined as

$$r\left(\mathrm{best}\right)=r\left(\mathrm{CBS}\right)+\Delta r\left(\mathrm{CV}\right)+\Delta r\left(\mathrm{aug}\right)+\Delta r\left(\mathrm{T}\right).$$ (3)

This structure will be denoted as “best estimate” or, in equations and tables, more simply as “best”.

B. Harmonic force fields

Similarly to molecular structure determination, two different composite schemes were employed to derive best-estimated harmonic force fields. The first approach relies only on CCSD(T) calculations and follows the first composite scheme introduced in the previous section, while the second (“cheap”) one is based on the additivity scheme summarized in Eq. (3). While the former could be applied only to the study of oxirane, the second approach was used for all three investigated molecules. The procedure introduced in Ref.⁹⁶ was employed to perform the extrapolation to the CBS limit of the harmonic wavenumbers, ω, at both the MP2 and CCSD(T) levels (ω(CBS(T, Q))). The extrapolated harmonic wavenumbers were then corrected for the effects of core correlation (Δω(CV)) and diffuse functions (Δω(aug)), obtained at either the CCSD(T) or the MP2 level. For the second approach, the so-called “cheap scheme”, higher-order electron-correlation energy contributions (Δω((T))) were also considered. The best-estimated harmonic wavenumbers obtained by means of the two composite schemes, ω(bestCC) and ω(best), respectively, were thus obtained by applying the additivity approximation and putting together the contributions considered as follows:

$$\omega \left(\text{bestCC}\right)=\omega \left(\text{CCSD(T)/CBS(T,Q)}\right)+\Delta \omega \left(\text{CCSD(T)/CV}\right)+\Delta \omega \left(\text{CCSD(T)/aug}\right)$$ (4)

and

$$\omega \left(\text{best}\right)=\omega \left(\text{CBS(T,Q)}\right)+\Delta \omega \left(\text{CV}\right)+\Delta \omega \left(\text{aug}\right)+\Delta \omega \left(\right(\mathrm{T}\left)\right).$$ (5)

All harmonic force fields were obtained using the analytic second derivatives^80,97.

A composite scheme was also used to determine the best estimates for IR intensities, I(best), within the harmonic approximation. Even if extrapolation schemes have not been formulated yet for such a property, on an empirical basis, the approaches introduced above for wavenumbers were applied:

$$I\left(\text{bestCC}\right)=I\left(\text{CCSD(T)/CBS(T,Q)}\right)+\Delta I\left(\text{CCSD(T)/CV}\right)+\Delta I\left(\text{CCSD(T)/aug}\right)$$ (6)

for the scheme exclusively based on CCSD(T) calculations and

$$I\left(\text{best}\right)=I\left(\text{CBS(T,Q}\right))+\Delta I(\text{CV})+\Delta I(\text{aug})+\Delta I(\left(\mathrm{T}\right)),$$ (7)

for the “cheap scheme”.

C. Anharmonic force fields

For trans-2,3-dideuterooxirane, thanks to its limited molecular size, the anharmonic (full cubic and semi-diagonal quartic) force field was calculated at the CCSD(T)/cc-pVTZ level, within the frozen-core approximation. As implemented in CFour, the harmonic force fields were obtained using analytic second derivatives as described above, whereas the corresponding cubic and semi-diagonal quartic force fields were determined in a normal-coordinate representation via numerical differentiation of the analytically evaluated force constants^98–101.

The DFT cubic and semi-diagonal quartic force fields and up to the third derivatives of the electric dipole moment, were determined by numerical differentiations of analytic force constants matrix and first derivatives of the electric dipole at displaced geometries along the normal modes (with a 0.01 Å step), with the equilibrium structure optimized using tight convergence criteria (maximum forces and displacements smaller than 1.5 × 10⁻⁵ Hartree/Bohr and 6 × 10⁻⁵ Å, respectively). To get accurate results, all computations were carried out with an ultrafine integration grid (99 radial shells and 590 angular points per shell) for the numerical integrations to obtain the two-electron integrals and their derivatives.

The hybrid force fields were obtained in a normal-coordinate representation by replacing in the full anharmonic force fields (computed mainly at the DFT level) the harmonic wavenumbers calculated at a higher lever of theory (mainly the best theoretical estimates). When the normal modes are very similar, which is the present case, DFT cubic and quartic force constants can be used without any transformation. These hybrid force fields were then employed in anharmonic computations within the VPT2 approach^51,52. This procedure also allows us to identify resonances based on the most accurate results.

Vibrational wavenumbers were obtained within the generalized VPT2 model (GVPT2), where nearly-resonant contributions are removed from the perturbative treatment (leading to the deperturbed model, DVPT2) and treated variationally in a second step^55,58. Such an approach relies on semi-empirical thresholds for Fermi and Darling-Denninson resonances. In the present work, the criteria proposed by Martin et al.¹⁰² for Fermi resonances have been chosen as they provide accurate results for fundamental⁵⁰ and non-fundamental⁷⁵ transitions. IR intensities with full account of both mechanical and electrical anharmonicities were computed at the DVPT2 level^74,90, along with the criteria proposed by some of us for 1-1 resonances⁷⁴. In addition to the simulation of fully anharmonic IR spectra, VPT2 computations also provide vibrational corrections to rotational constants.

VPT2 computations were mostly performed employing the GAUSSIAN suite of programs for quantum chemistry (G09 Rev: D.01)⁹¹.

III. RESULTS AND DISCUSSION

A. Equilibrium structures

As mentioned in the computational details section, the equilibrium structures of dideuterooxirane, methyloxirane and dimethyloxirane have been investigated by means of different composite schemes. This allows us to further check the reliability of the “cheap” scheme already introduced and tested, for instance, for uracil³⁶, glycine⁴² and thiouracil⁹⁴. An additional test opportunity is offered by the availability of semi-experimental equilibrium geometries, which are known to have an accuracy of 0.001 Å for bond distances^30–33. For oxirane, the equilibrium structure was investigated in detail by Demaison et al.³⁹, who derived the semi-experimental equilibrium geometry. For methyloxirane, such determination has been carried out in the present work based on the experimental data from Ref.⁴⁰.

The results for D₂Ox, MeOx, and Me₂Ox, collected in Tables I, II, and III, respectively, show that there is a very good agreement between the structural parameters obtained by means of the so-called “cheap” scheme and those derived with the gradient scheme. The only relevant deviation is observed for the C-O distances for all molecules: they turn out to be overestimated with the “cheap” scheme by about 0.004 Å. This is a consequence of rather large corrections due to the inclusion of diffuse functions in the basis set; in fact, the latter result to be one order of magnitude larger for the C-O distances. For oxirane, we furthermore note that the two equilibrium structures obtained by means of the gradient scheme using different sets of basis (see the “Computational details” section) are in very good agreement, with differences smaller than 0.001 Å for the bond lengths and 0.1 degrees for the angles. This confirms that the triple- and quadruple-zeta basis sets are suitable for the extrapolation to the CBS limit and that a triple-ζ quality set is able to provide reliable core-correlation corrections. Moving to the comparison of our computed geometries with the semi-experimental ones, we point out a very good agreement as well, i.e., bond distances agree within 0.001 Å and angles within 0.1 degrees. The overall conclusion is that the present study further confirms the reliability of the so-called “cheap” scheme. For all molecules, the various contributions are collected in the Supplementary Material¹⁰³.

TABLE I.

Equilibrium structure of trans-2,3-dideuterooxirane. Distances are in Å, angles in degrees.

Parameters	B3LYP/ SNSD	B3LYP/ AVTZ	CAM-B3LYP/ SNSD	CAM-B3LYP/ AVTZ	B2PLYP/ AVTZ	MP2/ AVTZ	best “cheap”a	bestCC (TZ,QZ)/(CT)b	bestCC (QZ,5Z)/(CQ)c	semi-exp red
Bonds
C-O	1.4320	1.4296	1.4225	1.4198	1.4330	1.4359	1.4303	1.4259	1.4263	1.42726(2)
C-C	1.4670	1.4632	1.4623	1.4581	1.4619	1.4625	1.4602	1.4601	1.4606	1.46082(2)
C-H/D	1.0890	1.0844	1.0878	1.0834	1.0824	1.0819	1.0816	1.0819	1.0817	1.08209(2)
MAE-re(SE)e	0.0059	0.0024	0.0040	0.0038	0.0024	0.0035	0.0014	0.0008	0.0005
∣MAX∣-re(SE)e	0.0069	0.0024	0.0057	0.0075	0.0057	0.0087	0.0031	0.0013	0.0009
MAE-bestCC f	0.0065	0.0029	0.0039	0.0036	0.0029	0.0039	0.0015	0.0004
∣MAX∣bestCC f	0.0073	0.0033	0.0061	0.0066	0.0067	0.0096	0.0040	0.0005
Angles
DCH	115.75	115.65	115.81	115.73	115.94	116.42	116.33	116.16	116.21	116.189(3)
θ	158.06	157.98	157.97	157.88	158.13	158.12	158.45	157.98	158.05	157.951(8)

^aBest-estimated equilibrium structure obtained by means of the “cheap” scheme (Eq. (3)).

^bBest-estimated “bestCC” equilibrium structure (Eq. (1)) using the cc-pVTZ and cc-pVQZ basis sets for the CBS extrapolation and the cc-pCVTZ set for the core-correlation correction.

^cBest-estimated “bestCC” equilibrium structure (Eq. (1)) using the cc-pVQZ and cc-pV5Z basis sets for the CBS extrapolation and the cc-pCVQZ set for the core-correlation correction.

^dSemi-experimental equilibrium structure: Ref.³⁹.

^eMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the semi-experimental equilibrium structure.

^fMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (bestCC (QZ,5Z)/(CQ)) parameters.

TABLE II.

Equilibrium structure of methyloxirane. Distances are in Å, angles in degrees.

Parameters	B3LYP/ SNSD	B3LYP/ AVTZ	CAM-B3LYP/ SNSD	CAM-B3LYP/ AVTZ	B2PLYP/ AVTZ	MP2/ AVTZ	best “cheap”a	bestCC (TZ,QZ)/(CT)b	semi-exp rec
Bonds
O1-C2	1.4371	1.4344	1.4262	1.4235	1.4372	1.4392	1.4331	1.4289	1.4305
O1-C3	1.4354	1.4326	1.4257	1.4299	1.4366	1.4404	1.4341	1.4299	1.4323
C2-C3	1.4684	1.4644	1.4628	1.4587	1.4627	1.4630	1.4605	1.4600	1.4601
C2-C7	1.5057	1.5017	1.5005	1.4966	1.4997	1.4972	1.4968	1.4969	1.4985
C2-H6	1.0919	1.0872	1.0906	1.0861	1.0854	1.0853	1.0851	1.0852	1.0847
C3-H4	1.0898	1.0853	1.0887	1.0843	1.0834	1.0833	1.0831	1.0837	1.0827
C3-H5	1.0893	1.0849	1.0881	1.0837	1.0828	1.0824	1.0822	1.0826	1.0824
C7-H8	1.0942	1.0849	1.0931	1.0886	1.0884	1.0886	1.0886	1.0881	1.0871
C7-H9	1.0964	1.0918	1.0949	1.0903	1.0904	1.0903	1.0902	1.0900	1.0897
C7-H10	1.0956	1.0912	1.0942	1.0898	1.0896	1.0895	1.0893	1.0890	1.0882
MAE-re(SE)d	0.0068	0.0027	0.0050	0.0028	0.0020	0.0026	0.0011	0.0009
∣MAX∣-re(SE)d	0.0084	0.0043	0.0066	0.0093	0.0067	0.0087	0.0026	0.0024
MAE-bestCCe	0.0070	0.0031	0.0044	0.0018	0.0022	0.0026	0.0011
∣MAX∣bestCCe	0.0088	0.0055	0.0055	0.0070	0.0083	0.0105	0.0042

Angles
C2-O1-C3	61.49	61.43	61.72	61.66	61.19	61.07	61.12	61.44	61.33
C3-C2-C7	122.54	122.63	122.28	122.33	122.27	121.66	121.88	121.73	121.68
C3-C2-H6	116.99	116.98	117.09	117.09	117.06	117.10	117.15	117.22	117.31
C2-C3-H4	119.26	119.28	119.14	119.14	119.09	118.71	118.88	118.84	118.96
C2-C3-H5	120.10	120.14	120.10	120.15	120.12	120.02	120.14	120.07	119.89
C2-C7-H8	110.75	110.80	110.53	110.56	110.52	110.07	110.24	110.17	110.29
C2-C7-H9	110.75	110.43	110.53	110.51	110.43	110.48	110.39	110.48	110.43
C2-C7-H10	110.61	110.59	110.59	110.56	110.53	110.48	110.39	110.54	110.31
H4-C3-C2-O1	103.24	103.33	103.29	103.39	103.18	103.09	102.88	103.21	103.04
H5-C3-C2-O1	−103.03	−103.09	−103.02	−103.08	−102.88	−102.66	−102.53	−102.84	−102.66
H6-C2-C3-O1	101.92	101.97	102.01	102.09	101.90	101.93	101.79	102.04	101.91
H8-C7-C2-C3	25.02	25.15	25.19	25.25	25.02	25.12	23.89	24.84	25.35
H9-C7-C2-C3	−95.44	−95.31	−95.25	−95.18	−95.39	−95.23	−96.46	−95.47	−95.20
H10-C7-C2-C3	145.12	145.29	145.14	145.24	145.05	144.94	143.84	144.73	145.04
MAE-re(SE)d	0.30	0.29	0.23	0.25	0.19	0.12	0.38	0.18
∣MAX∣-re(SE)d	0.87	0.95	0.60	0.65	0.59	0.26	1.45	0.51
MAE-bestCCe	0.24	0.28	0.21	0.24	0.17	0.15	0.34
∣MAX∣bestCCe	0.82	0.90	0.55	0.60	0.54	0.37	0.99

^aBest-estimated equilibrium structure obtained by means of the “cheap” scheme (Eq. (3)).

^bBest-estimated “bestCC” equilibrium structure (Eq. (1)) using the cc-pVTZ and cc-pVQZ basis sets for the CBS extrapolation and cc-pCVTZ for the core-correlation correction.

^cSemi-experimental equilibrium structure: this work.

^dMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the semi-experimental equilibrium structure.

^eMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (bestCC) parameters.

TABLE III.

Equilibrium structure of dimethyloxirane.^a Distances are in Å, angles in degrees.

Parameters	B3LYP/ SNSD	B3LYP/ AVTZ	CAM-B3LYP/ SNSD	CAM-B3LYP/ AVTZ	B2PLYP/ AVTZ	MP2/ AVTZ	best “cheap”b	bestCC (TZ,QZ)/(CT)c
Bonds
O1-C2	1.4402	1.4374	1.4295	1.4268	1.4410	1.4438	1.4369	1.4329
C2-C3	1.4696	1.4658	1.4635	1.4596	1.4638	1.4637	1.4616	1.4611
C2-C7	1.5060	1.5021	1.5007	1.4968	1.4998	1.4972	1.4970	1.4970
C2-H6	1.0927	1.0881	1.0915	1.0870	1.0864	1.0866	1.0866	1.0864
C5-H11	1.0941	1.0896	1.0930	1.0885	1.0883	1.0886	1.0886	1.0884
C5-H12	1.0965	1.0920	1.0950	1.0905	1.0906	1.0905	1.0904	1.0902
C5-H13	1.0958	1.0913	1.0943	1.0899	1.0898	1.0897	1.0895	1.0893
MAEd	0.0071	0.0030	0.0041	0.0013	0.0021	0.0021	0.0007
∣MAX∣d	0.0090	0.0051	0.0051	0.0061	0.0080	0.0109	0.0039

Angles
C2-O1-C3	61.36	61.31	61.58	61.53	61.05	60.91	61.14	61.31
C3-C2-C7	123.13	123.22	122.92	122.97	122.91	122.40	122.55	122.44
C3-C2-H6	116.69	116.67	116.71	116.7	116.67	116.55	116.68	116.71
C2-C7-H8	110.82	110.87	110.60	110.64	110.58	110.13	110.27	110.23
C2-C7-H9	110.52	110.50	110.60	110.57	110.48	110.52	110.43	110.51
C2-C7-H10	110.58	110.55	110.55	110.53	110.50	110.45	110.38	110.52
H4-C3-C2-O1	102.03	102.1	102.14	102.23	102.03	102.06	101.91	102.18
H8-C7-C2-C3	24.33	24.51	24.45	24.56	24.38	24.34	23.50	24.17
H9-C7-C2-C3	−96.24	−96.06	−96.1	−95.97	−96.13	−96.10	−96.94	−96.23
H10-C7-C2-C3	144.34	144.57	144.31	144.48	144.34	144.11	143.37	144.01
MAEd	0.21	0.27	0.20	0.24	0.19	0.13	0.28
∣MAX∣d	0.69	0.78	0.47	0.53	0.47	0.39	0.71

^aBy symmetry, we have the following relationships: O1-C2 = O1-C3; C2-C7 = C3-C5; C2-H6 = C3-H4; C5-H11 = C7-H8; C5-H12 = C7-H9; C5-H13 = C7-H10; C3-C2-C7 = C2-C3-C5; C3-C2-H6 = C2-C3-H4; H4-C3-C2-O1 = H6-C2-C3-O1.

^bBest-estimated equilibrium structure obtained by means of the “cheap” scheme (Eq. (3)).

^cBest-estimated “bestCC” equilibrium structure (Eq. (1)) using the cc-pVTZ and cc-pVQZ basis sets for the CBS extrapolation and cc-pCVTZ for the core-correlation correction.

^dMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (bestCC) parameters.

Regarding the comparison of DFT structures with our best-estimated ones, as already noted for instance in Ref.⁴², the B3LYP/SNSD level provides distances overestimated by about 0.007 Å, with the accuracy that improves once employing the aug-cc-pVTZ basis set (the averaged error thus reducing to about 0.003 Å). The CAM-B3LYP model shows a better agreement with the best theoretical estimates, bond lengths being overestimated by about 0.004 Å with the SNSD basis set and by only 0.002-0.0035 Å at the CAM-B3LYP/aug-cc-pVTZ level. An overall improvement is observed once we move to the B2PLYP/aug-cc-pVTZ level, with the overestimation reduced to 0.001-0.003 Å. Once again, the largest deviations are noted for the C-O distances. For bond angles, the largest discrepancies and mean absolute deviations do not exceed 1 and 0.3 degrees, respectively. Finally, we note that MP2/aug-cc-pVTZ structures are less accurate than their B2PLYP/aug-cc-pVTZ counterparts and show the largest maximum errors (for the C-O bond exceeding 0.01 Å) among the considered computational models.

B. Harmonic force fields

The harmonic wavenumbers of the dideuterated oxirane are reported in Table IV, together with (for all the three molecules considered) the analysis of the accuracy of the different levels of theory, as derived from the comparison with the best theoretical estimates. The results of this analysis are drawn in terms of the mean absolute error (MAE) and maximum absolute deviation (∣MAX∣). Harmonic wavenumbers of MeOx and Me₂Ox, and the various contributions to the best-estimated harmonic wavenumbers of D₂Ox are gathered in the Supplementary Material¹⁰³. For all molecules, we note that the differences between the MP2/cc-pVQZ and CBS values are small, either positive or negative, ranging from −3.7 cm⁻¹ to +3.5 cm⁻¹, with a mean value of −0.06 cm⁻¹. Core-correlation effects are slightly larger, with positive corrections ranging from ~1 to ~6 cm⁻¹ and a mean value of 3.5 cm⁻¹. On the contrary, the contributions due to the inclusion of diffuse functions in the basis set are mostly negative with a mean value of −3.3 cm⁻¹ (from −12.6 to 4.8 cm⁻¹). The largest terms are the higher-order correlation energy contributions, Δω((T)), with corrections mostly negative that can be as large as −50 cm⁻¹.

TABLE IV.

Harmonic vibrational wavenumbers (in cm⁻¹) of trans-2,3-dideuterooxirane. Mean and maximum absolute deviations for methyloxirane and dimethyloxirane are also reported.

Mode	Symmetry	B3LYP/ SNSD	B3LYP/ aug-cc-pVTZ	CAM/ SNSD	B2PLYP/ aug-cc-pVTZ	MP2/ aug-cc-pVTZ	CCSD(T)/ cc-pVTZ	CCSD(T)/ cc-pVQZ	besta cheap	bestCC b	Assignment
trans-2,3-dideuterooxirane
1	A	3134.0	3130.7	3163.1	3167.2	3204.0	3159.3	3163.0	3170.2	3170.0	CH sym stretch
2	A	2309.1	2306.5	2331.8	2333.6	2360.7	2328.4	2330.8	2335.7	2335.6	CD sym stretch
3	A	1426.9	1427.1	1449.9	1434.7	1436.0	1437.5	1434.3	1426.6	1427.2	CHD sym scissor
4	A	1258.2	1258.1	1277.6	1261.9	1264.2	1259.1	1259.3	1254.2	1256.0	ring breathing
5	A	1130.8	1136.0	1147.7	1142.0	1139.2	1142.5	1141.8	1137.3	1138.1	CH sym twisting
6	A	974.2	976.1	994.9	976.7	974.9	982.0	981.8	972.4	976.5	CHD wagging
7	A	895.0	896.2	910.8	899.0	904.0	903.5	903.4	896.6	899.1	ring CC stretching
8	A	759.4	761.8	768.8	767.7	770.9	765.6	767.1	768.0	768.9	CD sym twisting
9	B	3139.8	3136.3	3167.7	3172.5	3208.8	3164.0	3167.7	3175.0	3174.8	CH asym stretch
10	B	2297.4	2295.4	2318.2	2321.5	2347.3	2315.4	2318.0	2323.1	2322.9	CD asym stretch
11	B	1359.9	1364.2	1367.9	1372.7	1371.8	1371.0	1367.0	1360.0	1359.3	CHD asym scissor
12	B	1121.8	1129.6	1136.4	1134.8	1129.9	1125.7	1128.1	1132.8	1133.0	CH asym twisting
13	B	925.9	930.7	940.0	932.3	927.8	930.0	930.2	927.6	928.5	CD asym twisting
14	B	838.7	837.1	880.9	832.0	840.5	844.4	845.1	832.7	839.7	CO asym stretching
15	B	662.5	665.3	669.0	668.5	668.6	662.8	663.6	665.0	665.0	CHD rocking
MAEc		11.1	10.8	11.7	3.8	11.0	6.3	4.7	1.3
∣MAX∣c		36.0	39.3	41.1	13.3	34.0	11.7	7.7	7.0
MAEd		11.2	11.1	12.9	4.0	11.8	7.4	5.8
∣MAX∣d		36.2	39.5	48.2	12.6	33.8	11.8	12.4
methyloxirane		B3LYP/SNSD		CAM/SNSD	B2PLYP/aug-cc-pVTZ	MP2/aug-cc-pVTZ	CCSD(T)/cc-pVTZ	CCSD(T)/aug-cc-pVTZ
MAEd		12.2	-.-	9.5	3.9	12.4	4.1	3.4
∣MAX∣d		34.7	-.-	28.0	11.6	40.1	12.2	13.0
dimethyloxirane
MAEd		12.2	-.-	8.4	4.0	11.9	3.4	.
∣MAX∣d		27.4	-.-	34.4	11.7	41.0	7.6	.

^aBest-estimated (best) harmonic wavenumbers obtained by means of the “cheap” scheme according to Eq. (5).

^bBest-estimated (bestCC) harmonic wavenumbers obtained at the CCSD(T) level according to Eq. (4).

^cMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (bestCC) harmonic wavenumbers.

^dMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (“cheap”) harmonic wavenumbers.

The MAE and MAX values given in Table IV allow us to draw general conclusions about the accuracy of the levels of theory used in the present work. We note that functionals B3LYP and CAM-B3LYP provide accurate harmonic wavenumbers with MAEs for all molecules of about 12 cm⁻¹, already converged when employing basis set SNSD. The B2PLYP/aug-cc-pVTZ results are of the same quality as, or even better than (see D₂Ox) CCSD(T) in conjunction with the cc-pVTZ basis set, but at a strongly reduced computational cost. Similar accuracy is not obtained at the MP2/aug-cc-pVTZ level which yields results comparable to B3LYP or CAM-B3LYP, but at a significantly higher computational cost.

For trans-2,3-dideuterooxirane, as described in the “Computational details” section, the best-estimated harmonic wavenumbers were also obtained by means of a composite scheme entirely relying on CCSD(T) calculations (Eq. (4)). In Table IV, the corresponding results, denoted as bestCC, are compared with those determined with the so-called “cheap” scheme (Eq. (5)). A very good agreement is observed, with the differences being 1-2 wavenumbers (for five modes they are even smaller than 1 cm⁻¹), thus pointing out the accuracy and reliability of the “cheap” scheme. The largest difference is about 7 cm⁻¹, which means in relative terms a discrepancy of about 8%, and it is observed for the ring deformation mode ν₁₄, involving the asymmetric stretch of the C-O bonds. Therefore, it can be related to the difference already observed between the two composite schemes at the structural level. The different contributions to the best estimates obtained at the MP2 level are compared to the corresponding ones evaluated at the CCSD(T) level in the Supplementary Material¹⁰³. It is evident that, with only very few exceptions, the two levels of theory provide very similar contributions, with differences usually being on the order of a few tenths of wavenumber. Slightly larger errors are observed for modes ν₄, ν₅, ν₆ and ν₇ regarding contributions due to the basis set enlargement, but both approaches still agree within 1 cm⁻¹, as discussed above. Larger deviations are only observed for ν₁₄ for both basis-set and higher order correlation contributions, thus leading to an overall difference of about 7 cm⁻¹. In summary, the results for D₂Ox allow us to point out that the so-called “cheap” scheme is able to provide results of the same quality as those obtained with composite approaches involving only CCSD(T) calculations.

As mentioned in the methodology section, the harmonic IR intensities at different levels were combined in order to derive best-estimated values, according to the composite scheme described in Eq. (7). As for the wavenumbers, a composite approach entirely based on CCSD(T) computations was also employed for trans-2,3-dideuterooxirane (Eq. (6)). The different contributions to the best estimates obtained at the MP2 level are compared to their CCSD(T) counterparts in the Supplementary Material¹⁰³, showing that alike for wavenumbers the “cheap” scheme leads to results of the same quality as those obtained with the composite approach involving only CCSD(T) calculations (also for ν₁₄). For all molecules, the IR intensities computed with DFT and CC approaches are compared to the best estimates in Table V, along with the results for D₂Ox, while the results for MeOx and Me₂Ox are found in the Supplementary Material¹⁰³. Conclusions analogous to those deduced for the harmonic wavenumbers can be drawn based on the MAE and MAX values. The B3LYP/SNSD results turn out to be very accurate, similar to those obtainable at the CCSD(T) level and already converged with respect to the basis-set extension. The accuracy slightly improves when moving to CAM-B3LYP/SNSD, in particular as far as the maximum discrepancies (i.e., for the CH asymmetric stretches) are concerned, which become smaller than 10 km mol⁻¹. Moving to the computationally more expensive hybrid functional B2PLYP, the noted improvement is limited; i.e., the deviations with respect to the best-estimated values decrease from 2-3 km mol⁻¹ to 1-2 km mol⁻¹. Concerning MP2, no particular improvement with respect to B3LYP/SNS is noted, despite the increased computational cost. As already noted for the wavenumbers, the “cheap” scheme provides results very similar to those from the full CCSD(T) approach, with a MAE of only 0.4 km mol⁻¹ and a maximum absolute deviation of 1.6 km mol⁻¹. In summary, all DFT methods yield accurate IR intensities, while no relevant improvements are offered by performing computations at the MP2/aug-cc-pVTZ level. As already noted for the harmonic wavenumbers, the comparison of the different contributions to the “cheap” and CCSD(T) composite schemes shows that the two sets well agree with each another, thus supporting the idea beyond the “cheap” scheme, i.e., that the different effects/corrections can be reliably evaluated at the less expensive MP2 level without losing the accuracy that characterizes the CCSD(T) method.

TABLE V.

Harmonic IR intensities (in km mol⁻¹) of trans-2,3-dideuterooxirane. Mean and maximum absolute deviations for methyloxirane and dimethyloxirane are also reported.

Mode	Symmetry	B3LYP/ SNSD	B3LYP/ aug-cc-pVTZ	CAM/ SNSD	B2PLYP/ aug-cc-pVTZ	MP2/ aug-cc-pVTZ	CCSD(T)/ cc-pVTZ	CCSD(T)/ cc-pVQZ	besta cheap	bestCC b	Assignment
trans-2,3-dideuterooxirane
1	A	7.96	7.64	7.09	7.26	6.20	5.70	5.98	7.08	6.99	CH sym stretch
2	A	6.93	6.50	6.42	6.13	5.33	4.87	5.12	6.02	5.93	CD sym stretch
3	A	6.00	5.16	7.34	4.12	3.46	3.88	3.92	3.96	3.92	CHD sym scissor
4	A	9.38	9.33	9.78	7.70	6.40	6.68	6.99	7.50	7.68	ring breathing
5	A	0.08	0.08	0.00	0.21	0.51	0.03	0.05	0.33	0.11	CH sym twisting
6	A	19.00	18.21	27.25	15.99	17.18	17.83	19.20	19.91	21.55	CHD wagging
7	A	28.65	28.25	23.79	30.02	28.39	21.74	23.18	30.83	28.32	ring CC stretching
8	A	21.41	22.25	20.46	22.35	19.90	18.12	18.93	21.61	21.20	CD sym twisting
9	B	39.72	38.91	32.05	33.63	23.22	37.91	33.19	23.12	22.13	CH asym stretch
10	B	25.01	24.53	20.74	21.50	15.36	23.59	21.08	15.49	15.07	CD asym stretch
11	B	0.23	0.24	0.45	0.21	0.22	0.34	0.24	0.27	0.04	CHD asym scissor
12	B	1.42	1.51	1.72	1.50	1.57	1.60	1.59	1.38	1.66	CH asym twisting
13	B	2.78	2.90	3.39	2.80	2.60	3.09	2.94	2.41	2.60	CD asym twisting
14	B	10.67	10.31	10.37	9.24	7.81	7.85	8.24	8.24	8.18	CO asym stretching
15	B	0.11	0.15	0.16	0.17	0.22	0.01	0.06	0.31	0.24	CHD rocking
MAEc		2.6	2.5	2.4	1.9	0.8	2.8	2.0	0.5
∣MAX∣c		17.6	16.8	9.9	11.5	4.4	15.8	11.1	2.5
MAEd		2.6	2.5	2.7	1.6	0.8	2.9	2.0
∣MAX∣d		16.6	15.8	8.9	10.5	2.7	14.8	10.1
methyloxirane		B3LYP/SNSD		CAM/SNSD	B2PLYP/aug-cc-pVTZ	MP2/aug-cc-pVTZ	CCSD(T)/cc-pVTZ	CCSD(T)/aug-cc-pVTZ
MAEd		2.2	-.-	1.2	1.1	1.2	1.6	0.9
∣MAX∣d		11.7	-.-	4.2	5.5	8.3	8.6	3.9
dimethyloxirane
MAEd		1.8	-.-	1.9	1.0	1.8	1.4	.
∣MAX∣d		11.7	-.-	9.4	4.7	19.6	10.7	.

^aBest-estimated (best) harmonic IR intensities obtained by means of the “cheap” scheme according to Eq. (7).

^bBest-estimated (bestCC) harmonic IR intensities obtained at the CCSD(T) level according to Eq. (6).

^cMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (bestCC) harmonic IR intensities.

^dMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best-estimated (“cheap”) harmonic IR intensities.

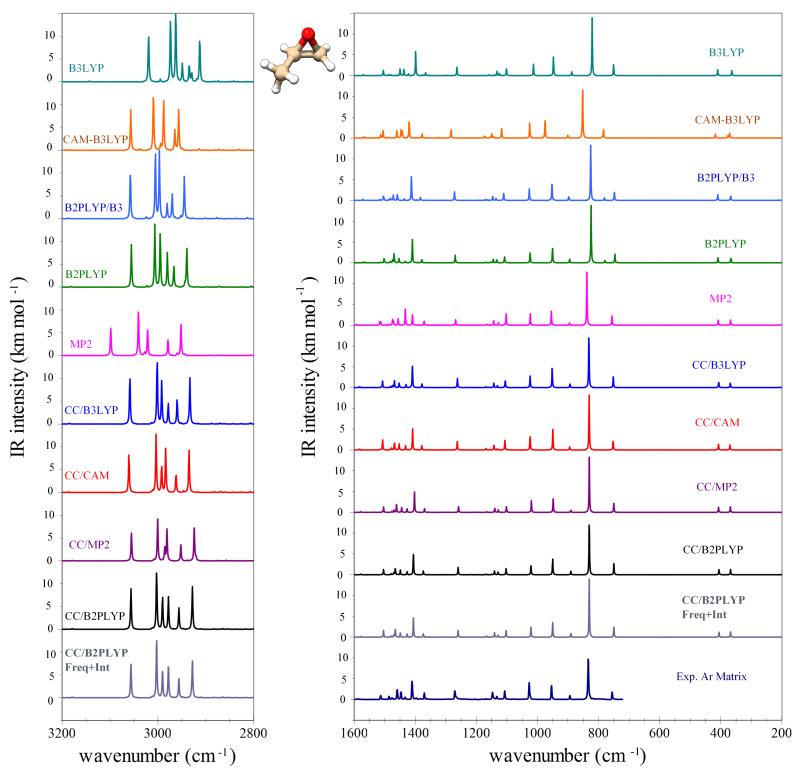
C. IR spectra

For an accurate comparison with experimental data, it is necessary to go beyond the double-harmonic approximation, which involves the inclusion of mechanical anharmonic effects on vibrational energies, i.e., anharmonic shifts, as well as electric anharmonic effects on intensities, thus allowing for the consideration of overtones and combination bands⁷⁴, which have null intensities at the harmonic level. As an example, the simulation of fully anharmonic spectra gives the possibility to distinguish between low-intensity features related to non-fundamental transitions of the most abundant conformer and the fundamental transitions of the less abundant ones⁴². This strategy is particularly effective if complementary vibrational spectroscopies, e.g., IR and Raman^50,104, are combined, together with VCD and Vibrational Raman Optical Activity (VROA) for chiral molecules^104,105.

Let us first consider the accuracy of anharmonic contributions to the vibrational wavenumbers and IR intensities for the fundamental transitions of trans-2,3-dideuterooxirane, which are reported in Tables VI and VII, respectively. Since all computations were performed with hybrid models using the same harmonic part (i.e., the best-estimated harmonic wavenumbers), the differences are only related to the anharmonic part of the force field. For both vibrational wavenumbers and IR intensities, anharmonic corrections computed at the CCSD(T)/cc-pVTZ level are taken as reference. For wavenumbers, rather accurate anharmonic corrections can be computed at the DFT level, with MAE of 4-6 cm⁻¹ and maximum deviations smaller than 15 cm⁻¹ for fundamental transitions when functionals B3LYP and CAM-B3LYP are used in conjunction with basis set SNSD. If all transitions up to two quanta are considered, the mean discrepancy is still about 10 cm⁻¹, and maximum errors do not exceed 40 cm⁻¹. The accuracy can be improved by inclusion of correlation effects at either B2PLYP or MP2 levels; in both cases this leads to an excellent agreement with the CCSD(T) results: MAE of about 2.5 cm⁻¹ and 5 cm⁻¹ and maximum deviations of 6-7 cm⁻¹ and 15 cm⁻¹ are observed for fundamentals and all transitions, respectively. Concerning the intensities, it is interesting to note that essentially all methods perform very well; in particular, the largest absolute errors, on average about 0.5 km mol⁻¹, are associated to fundamental transitions, while overtones and combination bands present mean absolute errors of 0.1 km mol⁻¹, which are therefore largely sufficient to describe correctly these less-intense transitions.

TABLE VI.

Anharmonic corrections to the vibrational wavenumbers (in cm⁻¹) of trans-2,3-dideuterooxirane within a hybrid scheme using the best-estimated (bestCC) harmonic wavenumbers defined in Eq. (4).

Mode	Symmetry	B3LYP/ SNSD	B3LYP/ aug-cc-pVTZ	CAM-B3LYP/ SNSD	B2PLYP/ aug-cc-pVTZ	MP2/ aug-cc-pVTZ	CCSD(T)/ cc-pVTZ	Assignment
1	A	−134.1	−132.1	−136.6	−138.6	−139.9	−143.1	CH sym stretch
2	A	−78.6	−77.8	−82.3	−81.9	−83.9	−84.3	CD sym stretch
3	A	−35.2	−34.8	−36.7	−37.7	−39.9	−39.2	CHD sym scissor
4	A	−24.7	−25.0	−25.4	−27.0	−27.0	−28.2	ring breathing
5	A	−26.3	−26.0	−28.9	−29.3	−29.0	−30.6	CH sym twisting
6	A	−18.8	−18.8	−21.5	−19.6	−19.8	−21.0	CHD wagging
7	A	−17.4	−17.5	−16.5	−19.7	−18.0	−19.6	ring CC stretching
8	A	−12.5	−12.4	−13.4	−14.2	−13.7	−15.6	CD sym twisting
9	B	−135.4	−133.3	−137.6	−139.8	−141.0	−146.8	CH asym stretch
10	B	−77.9	−77.2	−79.4	−81.2	−82.0	−85.5	CD asym stretch
11	B	−28.5	−28.3	−28.6	−30.6	−31.7	−36.0	CHD asym scissor
12	B	−22.2	−22.8	−23.8	−25.4	−23.9	−29.0	CH asym twisting
13	B	−14.2	−14.7	−16.1	−16.0	−15.0	−20.2	CD asym twisting
14	B	−25.3	−24.5	−26.5	−26.3	−25.8	−26.1	CO asym stretching
15	B	−7.1	−7.3	−7.9	−9.0	−8.7	−11.4	CHD rocking
MAE Funda		5.2	5.6	3.8	2.7	2.6
∣MAX∣ Funda		11.4	13.5	9.1	7.0	5.8
MAE Allb		10.2	11.1	7.5	5.3	5.0
∣MAX∣ Allb		28.5	35.5	20.6	14.4	14.6

^aMean absolute error (MAE) and maximum absolute deviations (∣MAX∣), with respect to the hybrid force field with the anharmonic part at the CCSD(T)/cc-pVTZ level, computed for fundamental transitions.

^bMean absolute error (MAE) and maximum absolute deviations (∣MAX∣), with respect to the hybrid force field with the anharmonic part at the CCSD(T)/cc-pVTZ level, computed for fundamental transitions, overtones and combinational bands.

TABLE VII.

Anharmonic corrections to the IR intensities (in km mol⁻¹) of trans-2,3-dideuteriooxirane within a hybrid scheme using the best-estimated (bestCC) harmonic wavenumbers defined in Eq. (4)

Mode	Symmetry	B3LYP/ SNSD	B3LYP/ aug-cc-pVTZ	CAM-B3LYP/ SNSD	B2PLYP/ aug-cc-pVTZ	MP2/ aug-cc-pVTZ	CCSD(T)/ cc-pVTZ	Assignment
1	A	0.70	0.70	0.76	0.67	0.70	– a	CH sym stretch
2	A	−0.47	−0.42	−0.45	−0.37	−0.18	– a	CD sym stretch
3	A	−1.24	−1.07	−1.46	−1.00	−0.90	−0.90	CHD sym scissor
4	A	0.52	0.57	0.40	0.45	0.41	0.12	ring breathing
5	A	0.23	0.23	0.05	0.41	0.66	0.21	CH sym twisting
6	A	−4.60	−4.47	−4.99	−4.63	−4.80	−4.22	CHD wagging
7	A	2.86	2.64	3.79	2.67	2.58	2.56	ring CC stretching
8	A	0.19	0.15	0.03	−0.09	0.20	−0.45	CD sym twisting
9	B	8.95	8.79	7.60	7.73	5.66	4.33	CH asym stretch
10	B	−2.17	−2.31	−2.46	−1.93	−1.22	−2.00	CD asym stretch
11	B	−0.03	−0.03	−0.02	−0.02	0.01	−0.07	CHD asym scissor
12	B	−0.11	−0.13	−0.13	−0.15	−0.13	−0.21	CH asym twisting
13	B	−0.09	−0.12	−0.16	−0.13	−0.08	−0.21	CD asym twisting
14	B	0.91	0.90	0.96	0.67	0.55	0.34	CO asym stretching
15	B	−0.05	−0.06	−0.06	−0.06	−0.07	−0.01	CHD rocking
MAE Fundb		0.6	0.6	0.6	0.4	0.4
∣MAX Fund∣b		4.6	4.5	3.3	3.4	1.3
MAE Allc		0.1	0.1	0.1	0.1	0.1
∣MAX All∣c		4.6	4.5	3.3	3.4	1.3

^aBands involved in Fermi resonances, for which CCSD(T)/cc-pVTZ computations with the CFour code report unreliable anharmonic corrections, were excluded from the analysis.

^bMean absolute error (MAE) and maximum absolute deviations (∣MAX∣), with respect to the hybrid force field with the anharmonic part at the CCSD(T)/cc-pVTZ level, computed for IR intensities of fundamental bands.

^cMean absolute error (MAE) and maximum absolute deviations (∣MAX∣), with respect to the hybrid force field with the anharmonic part at the CCSD(T)/cc-pVTZ level, computed for IR intensities of fundamental bands, overtones and combinational bands.

The overall accuracy of the anharmonic wavenumbers computed at different levels of theory is further assessed by the comparison with experiment and the best theoretical estimates for trans-2,3-dideuterooxirane, methyloxirane and trans-2,3-dimethyloxirane (Tables VIII, IX and X, respectively), while for IR intensities, the experimental values are not adequate for the validation of the theoretical results. In fact, the values reported for D₂Ox⁹ were derived from integrated intensities of solution-phase sample for all bands except ν₃, for which the experimental value was estimated from the relative intensities in the gas-phase spectrum. We thus limit our comparison with experiment to wavenumbers. The DFT computations with functionals B3LYP and CAM-B3LYP already perform fairly well, with MAEs of 10-12 cm⁻¹ and maximum discrepancies of about 30-40 cm⁻¹. It is interesting to note that, while for B3LYP the largest deviations are observed for high-frequency vibrations, the opposite is true for CAM-B3LYP, thus suggesting a sort of recipe to select the most suitable functional to improve the accuracy, if a specific spectral range is under investigation. At variance, an overall improvement in the accuracy can be obtained with ab initio methods and hybrid models with the harmonic part computed at least at the B2PLYP/aug-cc-pVTZ level. As expected, the most accurate results (MAE = 5-8 cm⁻¹ and maximum discrepancies < 20 cm⁻¹) are obtained when best-estimated harmonic wavenumbers are considered. In that respect, as already noted in the previous section, essentially equivalent results are obtained by means of a composite scheme entirely relying on CCSD(T) calculations (Eq. 4) and in the frame of the so-called “cheap” scheme (Eq. 5). With respect to the anharmonic part, all methods provide mean absolute errors within 2 cm⁻¹, with the most accurate results obtained in conjunction with the B2PLYP and MP2 anharmonic corrections that lead to a reduction of the maximum discrepancies within 14-17 cm⁻¹. It is noteworthy that among the various anharmonic computations performed, the full MP2/aug-cc-pVTZ results yield the largest errors, which in turn should be mainly attributed to the harmonic part. On the contrary, B2PLYP/aug-cc-pVTZ computations perform very well at a comparable computational cost, and can be also recommended as an alternative to the best-estimated harmonic wavenumbers within hybrid schemes. Indeed, B2PLYP/B3LYP values show significant improvements over B3LYP (MAE reduced to 6 cm⁻¹), with an accuracy similar to that of full B2PLYP computations.

TABLE VIII.

Anharmonic fundamental vibrational wavenumbers (in cm⁻¹) of trans-2,3-dideuteriooxirane computed with hybrid schemes and the best-estimated anharmonic IR intensities (in km mol ⁻¹).

Mode	Symmetry	B3LYPa	CAM-B3LYPa	B2PLYPb/		MP2b	best cheapc/			bestCCd/					Exp.e	Best IRf	Assignment
				B3LYP	B2PLYP		B3LYP	B2PLYP	CCg	B3LYP	CAM	B2PLYP	MP2	CCf
1	A	2995	3027	3034	3029	3068	3036	3031	3027	3036	3033	3031	3030	3027	3015	6.32	CH sym stretch
2	A	2235	2261	2259	2256	2285	2255	2252	2250	2257	2253	2254	2252	2251	2254	6.30	CD sym stretch
3	A	1391	1415	1399	1397	1397	1391	1389	1387	1392	1390	1389	1387	1388	1397	4.93	CHD sym scissor
4	A	1233	1254	1237	1235	1238	1229	1227	1226	1231	1231	1229	1229	1228	1235	7.23	ring breathing
5	A	1104	1120	1116	1113	1111	1111	1108	1107	1112	1109	1109	1109	1108	1112	0.30	CH sym twisting
6	A	955	975	958	957	955	953	953	951	958	955	957	957	955	961	26.18	CHD wagging
7	A	877	895	882	879	886	879	877	877	882	883	879	881	879	885	25.65	Ring deformation
8	A	747	756	755	753	757	755	754	752	756	755	755	755	753	754	21.29	CD sym twisting
9	B	2999	3031	3039	3035	3073	3041	3036	3029	3039	3037	3035	3034	3028	3028	14.39	CH asym stretch
10	B	2220	2244	2245	2241	2266	2244	2241	2237	2245	2243	2242	2241	2237	2240	17.01	CD asym stretch
11	B	1331	1340	1344	1342	1341	1332	1329	1324	1331	1331	1329	1328	1323	1339	0.07	CHD asym scissor
12	B	1099	1113	1113	1109	1107	1111	1107	1104	1111	1109	1108	1109	1104	1106	1.81	CH asym twisting
13	B	911	924	918	916	913	913	912	907	914	912	913	914	908	914	2.73	CD asym twisting
14	B	813	858	806	805	815	807	806	807	814	813	813	814	814	817	7.51	Ring deformation
15	B	655	661	661	660	660	658	656	654	658	657	656	656	654	673	0.30	CHD rocking
MAEh		10.9	11.2	6.2	4.6	12.6	7.0	7.1	7.8	6.0	5.9	5.8	5.8	6.4
∣MAX∣h		28.6	40.6	18.6	14.1	53.4	20.7	17.0	19.4	20.9	18.4	16.9	16.6	19.3
MAEi		8.9	14.4	8.2	5.8	14.3	5.0	3.1	1.6	5.2	3.8	2.7	2.6
∣MAX∣i		32.0	43.9	21.0	18.9	45.3	12.7	8.2	7.1	11.4	9.1	7.0	5.8

^aComputed with the SNSD basis set.

^bComputed with the aug-cc-pVTZ basis set.

^cBest-estimated (best) harmonic wavenumbers obtained by means of the “cheap” scheme according to Eq. (5).

^dBest-estimated (bestCC) harmonic wavenumbers obtained at the CCSD(T) level according to Eq. (4).

^eExperimental gas-phase data from Ref.⁹

^fBest-estimated anharmonic IR intensities computed at the bestCC/B2PLYP level.

^gAnharmonic corrections computed at the CCSD(T)/cc-pVTZ level.

^hMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to experiment.

ⁱMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best theoretical estimates (bestCC//CCSD(T)/VTZ).

TABLE IX.

Anharmonic fundamental vibrational wavenumbers (in cm⁻¹) of methyloxirane computed with hybrid schemes and the best-estimated anharmonic IR intensities (in km mol ⁻¹).

Mode	B3LYPa	CAMa	B2PLYPb/		MP2b	best cheapc/				Exp.d	Best IRe	Assignment
			B3LYP	B2PLYP		B3LYP	CAM	B2PLYP	MP2
1	3019	3057	3058	3055	3098	3058	3060	3056	3055	3051	24.51	CH2 asym stretch
2	2974	3009	3005	3006	3041	3002	3004	3003	3000	3001	40.62	CH stretch
3	2963	2988	2997	2995	3021	2992	2984	2990	2981	2995	18.66	CH3 asym stretch
4	2949	2994	2981	2980	3028	2978	2992	2978	2986	2974	22.75	CH3 asym stretch
5	2913	2957	2945	2940	2952	2933	2935	2928	2924		25.55	CH2 sym stretch
6	2935	2965	2970	2967	2979	2960	2962	2956	2952	2942	13.73	CH3 sym stretch
7	1505	1505	1504	1502	1516	1507	1507	1504	1504	1514	5.11	CH2 scisor
8	1450	1460	1472	1470	1472	1468	1468	1466	1462	1459	6.02	CH3 asym def
9	1437	1447	1459	1453	1456	1453	1453	1449	1445	1447	3.40	CH3 asym def
10	1399	1420	1413	1410	1409	1409	1409	1406	1403	1411	14.55	CHx bending
11	1366	1378	1383	1379	1371	1378	1379	1374	1370	1371	2.67	CH3 umbrella
12	1264	1283	1272	1269	1268	1262	1263	1260	1258	1271	5.15	ring breathing
13	1158	1172	1171	1170	1168	1169	1169	1168	1167	1170	0.88	CH2 rocking
14	1133	1150	1147	1145	1143	1143	1142	1141	1140	1147	3.45	CH bending
15	1125	1144	1136	1133	1128	1131	1131	1129	1128	1133	1.52	CH2 wagging
16	1102	1117	1111	1108	1105	1106	1107	1103	1102	1108	5.14	CH2 twist
17	1013	1026	1027	1024	1024	1024	1024	1021	1020	1027	7.81	CH2,CH3 rocking
18	948	975	952	951	955	952	950	950	949	954	11.50	ring deformation
19	888	901	898	895	895	894	895	891	891	894	2.71	CH2, CH3 rocking
20	821	852	826	825	838	832	831	831	830	834	44.18	ring CC stretching
21	751	784	748	746	756	752	752	750	750	756	7.76	CO asym stretching
22	410	417	410	409	408	407	407	406	407	409	3.97	CH3 bend
23	364	371	368	367	368	369	370	368	369	375	4.06	CH3 bend
24	193	195	208	200	206	208	200	198	191	200	0.35	CH3 torsion
MAEf	12.0	9.6	6.2	5.1	11.7	4.8	5.7	5.2	6.1
∣MAX∣f	32.4	28.2	28.1	24.6	53.3	17.8	20.2	14.2	13.9
MAEg	11.1	11.2	6.1	4.1	12.0	2.7	3.5		2.6
∣MAX∣g	36.8	34.1	16.9	11.7	49.6	9.1	14.1		9.3

^aComputed with the SNSD basis set.

^bComputed with the aug-cc-pVTZ basis set.

^cBest-estimated (best) harmonic wavenumbers obtained by means of the “cheap” scheme according to Eq. (5).

^dExperimental results. The 2900-3100 cm⁻¹ wavenumbers range: high-resolution jet-cooled IR spectrum from Ref.¹⁰⁶. The 200-1600 cm⁻¹ wavenumbers range: low-temperature matrix data from Refs.^3,27.

^eBest-estimated anharmonic IR intensities computed at the best cheap/B2PLYP level.

^fMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to experiment.

^gMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best theoretical estimates (best cheap/B2PLYP).

TABLE X.

Anharmonic fundamental vibrational wavenumbers (in cm⁻¹) of trans-2,3-dimethyloxirane computed with hybrid schemes and the best estimated anharmonic IR intensities (in km mol ⁻¹).

Mode	Symmetry	B3LYPa	CAMa	B2PLYPb/		best cheapc/			Best IRd	Assignmente
				B3LYP	B2PLYP	B3LYP	CAM	B2PLYP
1	A	2968	3003	2998	2994	2993	2996	2989	3.92	CH3 ∥ bend
2	A	2944	2983	2976	2974	2975	2978	2973	29.65	CH3 ⊥ bend
3	A	2914	2957	2946	2943	2944	2934	2936	2.97	asym C-CH3 str
4	A	2930	2958	2962	2959	2958	2960	2951	3.28	CH3 rocking
5	A	1482	1496	1492	1490	1494	1493	1492	6.79	∥CH
6	A	1441	1454	1465	1461	1462	1462	1454	12.53	CH3 asym def
7	A	1424	1441	1436	1433	1438	1441	1434	0.76	CH3 sym stretch
8	A	1375	1384	1392	1388	1386	1386	1383	0.19	CH3 asym stretch +CH str
9	A	1249	1268	1259	1258	1253	1253	1253	1.25	CH3 torsion
10	A	1156	1175	1164	1165	1161	1167	1171	0.57	CH3 ⊥ bend
11	A	1108	1126	1121	1121	1118	1118	1118	6.39	ring CC stretching
12	A	1015	1031	1027	1030	1024	1022	1027	13.44	⊥ CH + CH3 rock
13	A	886	909	888	887	890	889	889	17.37	∥CH + ring bretching
14	A	801	820	811	809	813	812	811	19.56	CH3 umbrella sym
15	A	458	463	459	460	459	458	459	0.01	Ring breathing
16	A	245	249	250	248	250	249	249	2.14	CH sym stretch
17	A	173	174	189	185	188	178	183	0.32	CH3 asym stretch +CH str
18	B	2971	3006	3001	2994	2996	2998	2989	54.01	CH3 torsion
19	B	2944	2983	2976	2973	2974	2977	2971	4.72	CO asym stretching
20	B	2953	2991	2987	2967	2980	2982	2960	25.02	CH3 rocking + ⊥ CH
21	B	2933	2954	2967	2966	2963	2962	2959	30.46	⊥ CH + CH3 rock
22	B	1451	1459	1470	1467	1468	1468	1465	8.86	CH3 umbrella asym
23	B	1434	1443	1456	1453	1453	1451	1449	5.75	CH3 asym def
24	B	1376	1390	1392	1389	1391	1390	1388	14.43	CH asym stretch
25	B	1333	1344	1346	1345	1334	1334	1334	8.69	CH3 asym stretch +CH str
26	B	1146	1163	1158	1176	1154	1154	1171	1.33	CH3 ∥ bend
27	B	1095	1114	1111	1109	1115	1115	1113	10.08	ring def + C-CH3 str
28	B	1004	1025	1012	1008	1015	1021	1012	10.75	CH3 rocking
29	B	951	960	965	966	959	959	960	1.87	⊥ CH
30	B	730	766	727	727	731	730	731	11.52	CH3 asym def
31	B	472	480	469	472	468	468	468	5.50	CH3 asym def
32	B	281	283	282	283	281	281	282	0.46	CH3 sym stretch
33	B	191	193	208	203	209	200	204	0.27	CH3 asym stretch
MAEf		12.3	9.3	5.8	3.9	4.0	4.3
∣MAX∣f		28.8	34.7	27.8	11.5	20.5	22.5

^aComputed with the SNSD basis set.

^bComputed with the aug-cc-pVTZ basis set.

^cBest-estimated (best) harmonic wavenumbers obtained by means of the “cheap” scheme according to Eq. (5).

^dBest estimated anharmonic IR intensities computed at the best cheap/B2PLYP level.

^eNotation adopted from Ref.¹¹; ⊥: perpendicular and ∥= parallel to the C₂C₃C_5/7 plane (Figure 1), respectively.

^fMean absolute error (MAE) and maximum absolute deviations (∣MAX∣) with respect to the best theoretical estimate (best cheap/B2PLYP).

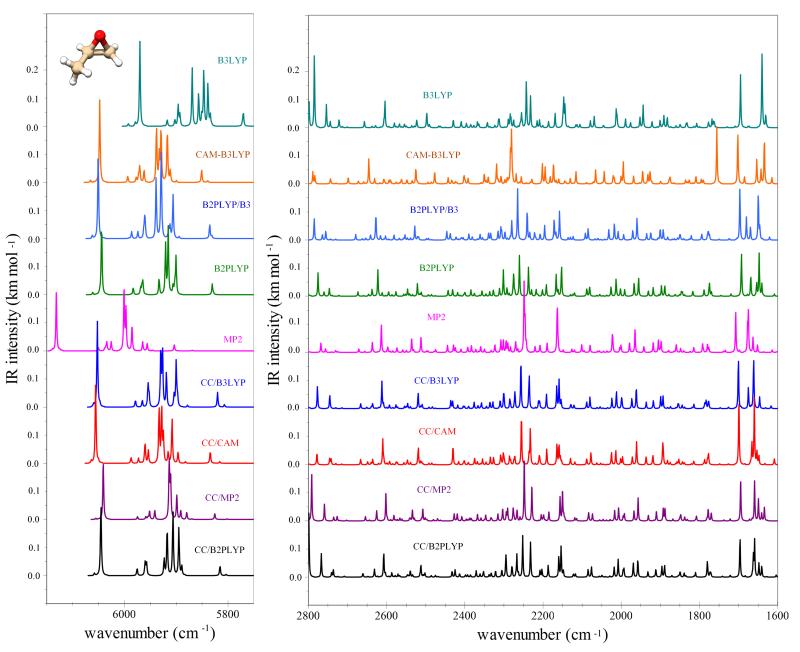
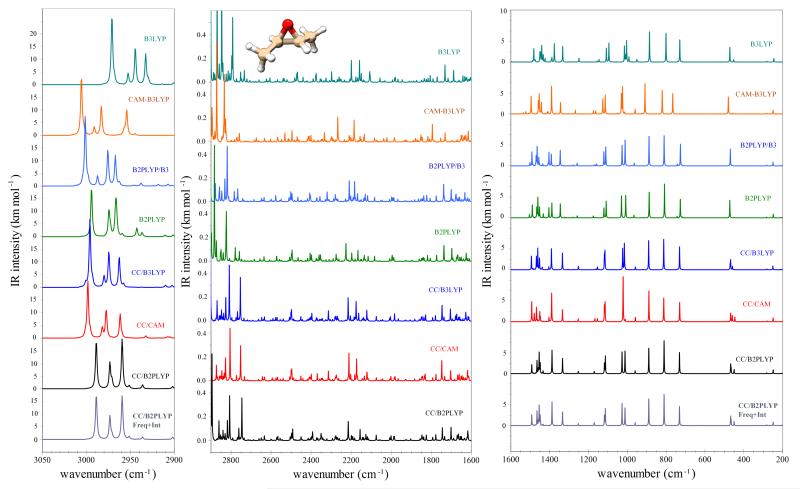
Moving to the issue of simulating IR spectra, in most cases reliable relative intensities along with accurate band positions are sufficient to obtain a correct spectral line-shape/intensity pattern, which in turn is required for the analysis of experimental results. For this reason, we focus on the convergence of simulated IR spectra of methyloxirane and trans-2,3-dimethyloxirane with respect to different methods and hybrid models. These are presented in Figures 2 and 3 for the former, and in Figure 4 for the latter. First of all, we note that the two spectra simulated with vibrational wavenumbers computed at the CC/B2PLYP level are very similar, irrespective of the correction for IR intensities at the harmonic level with best estimates (CC/B2PLYP Freq+Int) or not (CC/B2PLYP). The good accuracy of CC/B2PLYP results is confirmed, whenever feasible, by the comparison with experimental spectra, i.e., for methyloxirane in the 700-1600 cm⁻¹ spectral range²⁷. For this reason, all other spectra are reported by applying the hybrid scheme only for the wavenumbers, with the same level of theory used for harmonic and anharmonic contributions to the IR intensities. At first glance, we observe that in the 200-2800 cm⁻¹ range a similar intensity pattern is obtained in most cases, even in the regions related to overtones and combination bands (1600-2800 cm⁻¹). The largest discrepancies are observed for CAM-B3LYP and MP2, while all hybrid schemes based on the best-estimated harmonic wavenumbers lead to similar spectra. Concerning the C-H stretching vibrations and their overtones, we note more significant differences, with the fully anharmonic MP2 force field leading to a different energy pattern and B3LYP giving spectral features shifted to lower wavenumbers. At variance, all hybrid models with the harmonic part computed at least at the B2PLYP level reproduce well the results obtained with the best-estimated harmonic force field. In conclusion, we can point out that the B2PLYP/B3LYP model provides fairly good estimates of IR spectra up to 6000 cm⁻¹, while for less expensive computations, B3LYP or CAM-B3LYP can be considered for the 200-2800 cm⁻¹ and 2800-3600 cm⁻¹ spectral ranges, respectively. Improved accuracy can be obtained by means of hybrid CC/DFT schemes with the harmonic part based on composite schemes and anharmonic corrections at the B2PLYP level.

FIG. 2.

Anharmonic IR spectra of methyloxirane in the 2800-3200 cm⁻¹ and 200–1600 cm⁻¹ ranges (related to the fundamental bands) computed with hybrid schemes. Spectra line-shapes were convoluted with Lorentzian distribution functions with a HWHM of 1 cm⁻¹. Experimental spectrum measured in argon matrix at 10 K from Ref.²⁷.

FIG. 3.

Anharmonic IR spectra of methyloxirane in the 5750–6150 cm⁻¹ and 1600–2800 cm⁻¹ ranges (related to the overtones and combination bands) computed with hybrid schemes. Spectra line-shapes were convoluted with Lorentzian distribution functions with a HWHM of 1 cm⁻¹.

FIG. 4.

Anharmonic IR spectra of trans-2,3-dimethyloxirane in the 200–1600 cm⁻¹, 1600–2900 cm⁻¹ and 2900–3050 cm⁻¹ ranges computed with hybrid schemes. Spectra line-shapes were convoluted with Lorentzian distribution functions with a HWHM of 1 cm⁻¹.

IV. CONCLUDING REMARKS

In this paper we investigate the equilibrium structures and infrared spectra of prototypical chiral oxiranes by mean of accurate quantum-chemical methods within composite approaches and, for IR spectra the CC/DFT hybrid schemes, thus providing benchmarks for computational approaches applicable also to medium-sized systems. The reported results show that equilibrium geometries accurate to 0.001 Å for bond lengths and 0.1 degrees for angles are obtainable together with vibrational wavenumbers and IR intensities accurate to 10 cm⁻¹ and 0.5 km mol⁻¹, respectively. This systematic analysis paves the route toward reliable studies of larger molecular systems possibly taking into account also solvent effects. Moreover, the validation of a reliable computational protocol for the unequivocal determination of band positions and IR intensities in vibrational spectra of chiral prototypes, like substituted oxiranes, can represent, in our opinion, a robust background toward the development and validation of effective computational strategies for more demanding spectroscopies like VCD, which require not only the values, but also the relative orientations of the derivatives of electric and magnetic moments with respect to normal modes.

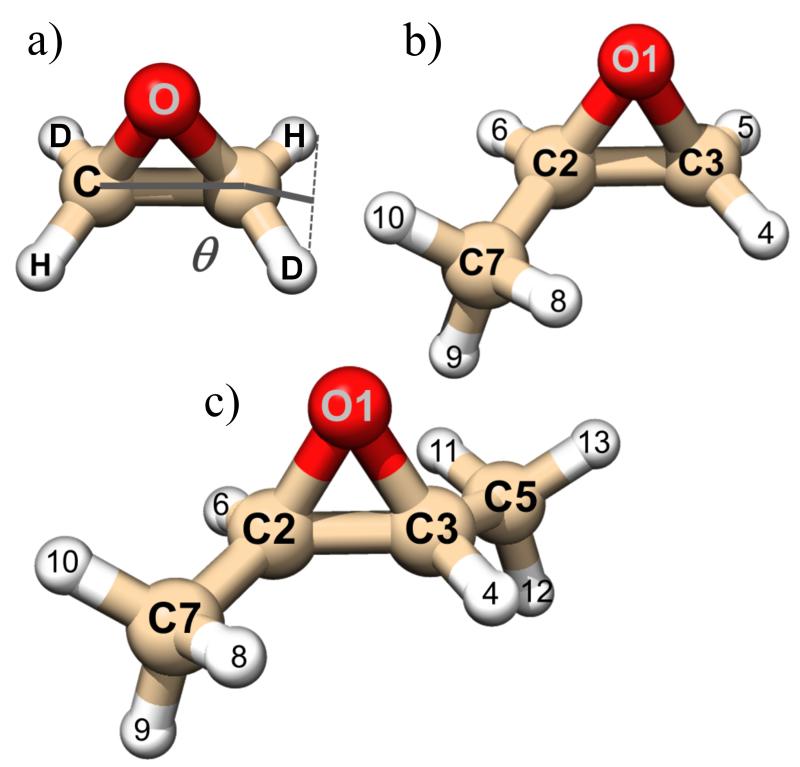
FIG. 1.

Molecular structure of trans-2,3-dideuteriooxirane (a), methyloxirane (b), and trans-2,3-dimethyloxirane (c). The atom labeling is given.