Inference for High-dimensional Differential Correlation Matrices

Abstract

Motivated by differential co-expression analysis in genomics, we consider in this paper estimation and testing of high-dimensional differential correlation matrices. An adaptive thresholding procedure is introduced and theoretical guarantees are given. Minimax rate of convergence is established and the proposed estimator is shown to be adaptively rate-optimal over collections of paired correlation matrices with approximately sparse differences. Simulation results show that the procedure significantly outperforms two other natural methods that are based on separate estimation of the individual correlation matrices. The procedure is also illustrated through an analysis of a breast cancer dataset, which provides evidence at the gene co-expression level that several genes, of which a subset has been previously verified, are associated with the breast cancer. Hypothesis testing on the differential correlation matrices is also considered. A test, which is particularly well suited for testing against sparse alternatives, is introduced. In addition, other related problems, including estimation of a single sparse correlation matrix, estimation of the differential covariance matrices, and estimation of the differential cross-correlation matrices, are also discussed.

1 Introduction

Statistical inference on the correlation structure has a wide array of applications, ranging from gene co-expression network analysis (Carter et al., 2004; Lee et al., 2004; Zhang et al., 2008; Dubois et al., 2010; Fuller et al., 2007) to brain intelligence analysis (Shaw et al., 2006). For example, understanding the correlations between the genes is critical for the construction of the gene co-expression network. See Kostka and Spang (2004), Lai et al. (2004), and Fuller et al. (2007). Driven by these and other applications in genomics, signal processing, empirical finance, and many other fields, making sound inference on the high-dimensional correlation structure is becoming a crucial problem.

In addition to the correlation structure of a single population, the difference between the correlation matrices of two populations is of significant interest. Differential gene expression analysis is widely used in genomics to identify disease-associated genes for complex diseases. Conventional methods mainly focus on the comparisons of the mean expression levels between the disease and control groups. In some cases, clinical disease characteristics such as survival or tumor stage do not have significant associations with gene expression, but there may be significant effects on gene co-expression related to the clinical outcome (Shedden and Taylor (2005); Hudson et al. (2009); Bandyopadhyay et al. (2010)). Recent studies have shown that changes in the correlation networks from different stages of disease or from case and control groups are also of importance in identifying dysfunctional gene expressions in disease. See, for example, de la Fuente (2010). This differential co-expression network analysis has become an important complement to the original differential expression analysis as differential correlations among the genes may reflect the rewiring of genetic networks between two different conditions (See Shedden and Taylor (2005); Bandyopadhyay et al. (2010); de la Fuente (2010); Ideker and Krogan (2012); Fukushima (2013)).

Motivated by these applications, we consider in this paper optimal estimation of the differential correlation matrix. Specifically, suppose we observe two independent sets of p-dimensional i.i.d. random samples ${\mathbf{X}}^{(t)}=\{{\mathbf{X}}_1^{(t)},\dots ,{\mathbf{X}}_{n_t}^{(t)}\}$ with mean μ_t, covariance matrix Σ_t, and correlation matrix R_t, where t = 1 and 2. The goal is to estimate the differential correlation matrix D = R₁ − R₂. A particular focus of the paper is on estimating an approximately sparse differential correlation matrix in the high dimensional setting where the dimension is much larger than the sample sizes, i.e., p ≫ max(n₁, n₂). The estimation accuracy is evaluated under both the spectral norm loss and the Frobenius norm loss.

A naive approach to estimating the differential correlation matrix D = R₁ − R₂ is to first estimate the covariance matrices Σ₁ and Σ₂ separately and then normalize to obtain estimators R̂₁ and R̂₂ of the individual correlation matrices R₁ and R₂, and finally take the difference D̂ = R̂₁ − R̂₂ as the estimator of the differential correlation matrix D. A simple estimate of a correlation matrix is the sample correlation matrix. However, in the high-dimensional setting, the sample correlation matrix is a poor estimate. Significant advances have been made in the last few years on optimal estimation of a high-dimensional covariance matrix. Regularization methods such as banding, tapering, and thresholding have been proposed. In particular, Cai et al. (2010) established the optimal rate of convergence and Cai and Yuan (2012) developed an adaptive estimator of bandable covariance matrices. For sparse covariance matrices where each row and each column has relatively few nonzero entries, Bickel and Levina (2008) introduced a thresholding estimator and obtained rates of convergence; Cai and Liu (2011) proposed an adaptive thresholding procedure and Cai and Zhou (2012) established the minimax rates of convergence for estimating sparse covariance matrices.

Structural assumptions on the individual correlation matrices R₁ and R₂ are crucial for the good performance of the difference estimator. These assumptions, however, may not hold in practice. For example, gene transcriptional networks often contain the so-called hub nodes where the corresponding gene expressions are correlated with many other gene expressions. See, for example, (Barabási and Oltvai, 2004; Barabási et al., 2011). In such settings, some of the rows and columns of R₁ and R₂ have many nonzero entries which mean that R₁ and R₂ are not sparse. In genomic applications, the correlation matrices are rarely bandable as the genes are not ordered in any particular way.

In this paper, we propose a direct estimation method for the differential correlation matrix D = R₁ − R₂ without first estimating R₁ and R₂ individually. This direct estimation method assumes that D is approximately sparse, but otherwise does not impose any structural assumptions on the individual correlation matrices R₁ and R₂. An adaptive thresholding procedure is introduced and analyzed. The estimator can still perform well even when the individual correlation matrices cannot be estimated consistently. For example, direct estimation can recover the differential correlation network accurately even in the presence of hub nodes in R₁ and R₂ as long as the differential correlation network is approximately sparse. The key is that sparsity is assumed for D and not for R₁ or R₂.

Theoretical performance guarantees are provided for direct estimator of the differential correlation matrix. Minimax rates of convergence are established for the collections of paired correlation matrices with approximately sparse differences. The proposed estimator is shown to be adaptively rate-optimal. In comparison to adaptive estimation of a single sparse covariance matrix considered in Cai and Liu (2011), both the procedure and the technical analysis of our method are different and more involved. Technically speaking, correlation matrix estimators are harder to analyze than those of covariance matrices and the two-sample setting in our problem further increases the difficulty.

Numerical performance of the proposed estimator is investigated through simulations. The results indicate significant advantage of estimating the differential correlation matrix directly. The estimator outperforms two other natural alternatives that are based on separate estimation of R₁ and R₂. To further illustrate the merit of the method, we apply the procedure to the analysis of a breast cancer dataset from the study by van de Vijver et al. (2002) and investigate the differential co-expressions among genes in different tumor stages of breast cancer. The adaptive thresholding procedure is applied to analyze the difference in the correlation alternation in different grades of tumor. The study provides evidence at the gene co-expression level that several genes, of which a subset has been previously verified, are associated with the breast cancer.

In addition to optimal estimation of the differential correlation matrix, we also consider hypothesis testing of the differential correlation matrices, H₀ : R₁−R₂ = 0 versus H₁ : R₁−R₂ ≠ 0. We propose a test which is particularly well suited for testing again sparse alternatives. The same ideas and techniques can also be used to treat other related problems. We also consider estimation of a single sparse correlation matrix from one random sample, estimation of the differential covariance matrices as well as estimation of the differential cross-correlation matrices.

The rest of the paper is organized as follows. Section 2 presents in detail the adaptive thresholding procedure for estimating the differential correlation matrix. The theoretical properties of the proposed estimator are analyzed in Section 3. In Section 4, simulation studies are carried out to investigate the numerical performance of the thresholding estimator and Section 5 illustrates the procedure through an analysis of a breast cancer dataset. Hypothesis testing on the differential correlation matrices is discussed in Section 6.1, and other related problems are considered in the rest of Section 6. All the proofs are given in the Appendix.

2 Estimation of Differential Correlation Matrix

We consider in this section estimation of the differential correlation matrix and introduce a data-driven adaptive thresholding estimator. The theoretical and numerical properties of the estimator are investigated in Sections 3 and 4 respectively.

Let ${\mathbf{X}}^{(t)}={(X_1^{(t)},\dots ,X_p^{(t)})}^{\top }$ be a p-variate random vector with mean μ_t, covariance matrix Σ_t = (σ_ijt)_1≤i,j≤p, and correlation matrix R_t = (r_ijt)_1≤i,j≤p, for t = 1 and 2. Suppose we observe two i.i.d. random samples, { ${\mathbf{X}}_1^{(1)},\dots ,{\mathbf{X}}_{n_1}^{(1)}$} from X⁽¹⁾ and { ${\mathbf{X}}_1^{(2)},\dots ,{\mathbf{X}}_{n_2}^{(2)}$} from X⁽²⁾, and the two samples are independent. The goal is to estimate the differential correlation matrix D = R₁ − R₂ under the assumption that D is approximately sparse.

Given the two random samples, the sample covariance matrices and sample correlation matrices are defined as, for t = 1 and 2,

$${\widehat{\mathbf{\sum }}}_t={({\widehat{\sigma }}_{\mathit{ijt}})}_{1\le i,j\le p}=\frac{1}{n_t}\sum _{k=1}^{n_t}({\mathbf{X}}_k^{(t)}-{\overline{\mathbf{X}}}^{(t)}){({\mathbf{X}}_k^{(t)}-{\overline{\mathbf{X}}}^{(t)})}^{\top },$$ (1)

$${\widehat{\mathbf{R}}}_t={({\widehat{r}}_{\mathit{ijt}})}_{1\le i,j\le p}=\text{diag}{({\widehat{\mathbf{\sum }}}_t)}^{-1/2}·{\widehat{\mathbf{\sum }}}_t·\text{diag}{({\widehat{\mathbf{\sum }}}_t)}^{-1/2},$$ (2)

where ${\overline{\mathbf{X}}}^{(t)}=\frac{1}{n_t}{\sum }_{k=1}^{n_t}{\mathbf{X}}_k^{(t)}$ and diag(Σ̂_t) is the diagonal matrix with the same diagonal as Σ̂_t. We propose a thresholding estimator of the differential correlation matrix D by individually thresholding the entries of the difference of the two sample correlation matrices R̂₁ − R̂₂ with the threshold adaptive to the noise level of each entry. A key to the construction of the procedure is the estimation of the noise levels of the individual entries of R̂₁ − R̂₂, as these entries are random variables themselves.

We first provide some intuition before formally introducing the estimate of the noise levels of the individual entries of R̂₁ − R̂₂. Note that $E\left((X_i^{(t)}-{\mu }_{it})(X_j^{(t)}-{\mu }_{jt})\right)={\sigma }_{\mathit{ijt}}$ and ${\mu }_{it}\approx {\overline{X}}_i^{(t)}=\frac{1}{n_t}{\sum }_{k=1}^{n_t}{X}_{ik}$. Define

$${\theta }_{\mathit{ijt}}=var\left((X_i^{(t)}-{\mu }_{it})(X_j^{(t)}-{\mu }_{jt})\right),1\le i,j\le p,t=1,2.$$ (3)

Then one can intuitively write

$${\widehat{\sigma }}_{\mathit{ijt}}=\frac{1}{n_t}\sum _{k=1}^{n_t}(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})\approx {\sigma }_{\mathit{ijt}}+{\left(\frac{{\theta }_{\mathit{ijt}}}{n_t}\right)}^{1/2}{z}_{\mathit{ijt}},$$ (4)

where z_ijt is approximately normal with mean 0 and variance 1. Hence, θ_ijt/n_t measures the uncertainty of the sample covariance σ̂_ijt. Based on the first order Taylor expansion of the 3-variate function $\frac{x}{{(y^z)}^{1/2}}$ for x ∈ ℝ, and y, z > 0,

$$\frac{\widehat{x}}{{(\widehat{y}\widehat{z})}^{1/2}}=\frac{x}{{(yz)}^{1/2}}+\frac{\widehat{x}-x}{{(yz)}^{1/2}}-\frac{x}{{(yz)}^{1/2}}\left(\frac{\widehat{y}-y}{2y}+\frac{\widehat{z}-z}{2z}\right)+o(\widehat{x}-x)+o(\widehat{y}-y)+o(\widehat{z}-z),$$ (5)

the entries r̂_ijt of the sample correlation matrix R̂_t = (r̂_ijt) can be approximated by

$$\begin{array}{l}{\widehat{r}}_{\mathit{ijt}}=\frac{{\widehat{\sigma }}_{\mathit{ijt}}}{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}\approx \frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}+{\left(\frac{{\theta }_{\mathit{ijt}}}{n_t{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}\right)}^{1/2}{z}_{\mathit{ijt}}-\frac{{\sigma }_{\mathit{ijt}}}{2{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\left({\left(\frac{{\theta }_{\mathit{iit}}}{n_t{\sigma }_{\mathit{iit}}^2}\right)}^{1/2}{z}_{\mathit{iit}}+{\left(\frac{{\theta }_{\mathit{jjt}}}{n_t{\sigma }_{\mathit{jjt}}^2}\right)}^{1/2}{z}_{\mathit{jjt}}\right)\\ =r_{\mathit{ijt}}+{\left(\frac{{\xi }_{\mathit{ijt}}}{n_t}\right)}^{1/2}{z}_{\mathit{ijt}}-\frac{r_{\mathit{ijt}}}{2}\left({\left(\frac{{\xi }_{\mathit{iit}}}{n_t}\right)}^{1/2}{z}_{\mathit{iit}}+{\left(\frac{{\xi }_{\mathit{jjt}}}{n_t}\right)}^{1/2}{z}_{\mathit{jjt}}\right),\end{array}$$ (6)

where we denote

$${\xi }_{\mathit{ijt}}=\frac{{\theta }_{\mathit{ijt}}}{{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}},1\le i,j\le p,t=1,2.$$

It then follows from (6) that

$$\begin{array}{l}{\widehat{r}}_{ij1}-{\widehat{r}}_{ij2}\approx r_{ij1}-r_{ij2}+{\left(\frac{{\xi }_{ij1}}{n_1}\right)}^{1/2}{z}_{ij1}-\frac{r_{ij1}}{2}\left({\left(\frac{{\xi }_{ii1}}{n_1}\right)}^{1/2}{z}_{ii1}+{\left(\frac{{\xi }_{jj1}}{n_1}\right)}^{1/2}{z}_{jj1}\right)\\ -\left({\left(\frac{{\xi }_{ij2}}{n_2}\right)}^{1/2}{z}_{ij2}-\frac{r_{ij2}}{2}\left({\left(\frac{{\xi }_{ii2}}{n_2}\right)}^{1/2}{z}_{ii2}+{\left(\frac{{\xi }_{jj2}}{n_2}\right)}^{1/2}{z}_{jj2}\right)\right),1\le i,j\le p,\end{array}$$ (7)

where the random variables z_ij1 and z_ij2 are approximately normal with mean 0 and variance 1, but not necessarily independent for 1 ≤ i, j ≤ p.

Equation (7) suggests that estimation of r_ij1 − r_ij2 is similar to the sparse covariance matrix estimation considered in Cai and Liu (2011), where it is proposed to adaptively threshold entries according to their individual noise levels. However, the setting here is more complicated as r̂_ij1 − r̂_ij2 is not an unbiased estimate of r_ij1 − r_ij2 and the noise levels are harder to estimate. These make the technical analysis more involved. The noise levels are unknown here but can be estimated based on the observed data. Specifically, we estimate θ_ijt and ξ_ijt by the following data-driven quantities,

$${\widehat{\theta }}_{\mathit{ijt}}=\frac{1}{n_t}\sum _{k=1}^{n_t}{\left((X_{ik}^{(t)}-{\overline{X}}_i^{(t)})(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})-{\widehat{\sigma }}_{\mathit{ijt}}\right)}^2,$$ (8)

$${\widehat{\xi }}_{\mathit{ijt}}=\frac{{\widehat{\theta }}_{\mathit{ijt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}=\frac{1}{n_t{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\sum _{k=1}^{n_t}{\left((X_{ik}^{(t)}-{\overline{X}}_i^{(t)})(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})-{\widehat{\sigma }}_{\mathit{ijt}}\right)}^2.$$ (9)

We are now ready to introduce the adaptive thresholding estimator of R₁ − R₂ using data-driven threshold levels. Let s_λ(z) be a thresholding function satisfying the following conditions:

• (C1)|s_λ(z)| ≤ c|y| for all z, y satisfying |z − y| ≤ λ for some c > 0;
• (C2)s_λ(z) = 0 for |z| ≤ λ;
• (C3)|s_λ(z) − z| ≤ λ, for all z ∈ ℝ.

Note that the commonly used soft thresholding function s_λ(z) = sgn(z)(z−λ)₊ and the adaptive lasso rule s_λ = z(1 − |λ/z|^η)₊ with η ≥ 1 satisfy these three conditions. See Rothman et al. (2009) and Cai and Liu (2011). Although the hard thresholding function s_λ(z) = z · 1_{|z|≥λ} does not satisfy Condition (C1), the technical arguments given in this paper still work with very minor changes.

We propose to estimate the sparse differential correlation matrix D by the entrywise thresholding estimator ${\widehat{\mathbf{D}}}^{\ast }=({\widehat{d}}_{ij}^{\ast })\in {ℝ}^{p\times p}$ defined as

$${\widehat{d}}_{ij}^{\ast }=s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2}),1\le i,j\le p,$$

where s_λ(z) is a thresholding function satisfying (C1)–(C3) and the threshold level λ_ij is given by λ_ij = λ_ij1 + λ_ij2 with

$${\lambda }_{\mathit{ijt}}=\tau {\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{ijt}}^{1/2}+\frac{\mid {\widehat{r}}_{\mathit{ijt}}\mid }{2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\right),1\le i,j\le p,t=1,2.$$ (10)

Here ξ̂_ijt are given by (9) and the thresholding constant τ can be chosen empirically through cross-validation. See Section 4.1 for more discussions on the empirical choice of τ.

3 Theoretical Properties

We now analyze the theoretical properties of the data-driven thresholding estimator D̂^* proposed in the last section. We will establish the minimax rate of convergence for estimating the differential correlation matrix D over certain classes of paired correlation matrices (R₁, R₂) with approximately sparse difference D = R₁ − R₂ under the spectral norm loss. The results show that D̂^* is rate-optimal under mild conditions.

3.1 Rate Optimality of the Thresholding Estimator

We consider the following class of paired correlation matrices in ℝ^p×p with approximately sparse difference

$${\mathcal{G}}_q(s_0(p))=\left\{({\mathbf{R}}_1,{\mathbf{R}}_2):{\mathbf{R}}_1,{\mathbf{R}}_2\succcurlyeq 0;\text{diag}({\mathbf{R}}_1)=\text{diag}({\mathbf{R}}_2)=1;\underset{i}{max}\sum _j{\mid r_{ij1}-r_{ij2}\mid }^q\le s_0(p)\right\}$$ (11)

for some 0 ≤ q < 1. Here R₁, R₂ ⪰ 0 and diag(R₁) = diag(R₂) = 1 mean that R₁ and R₂ are symmetric, semi-positive definite, and with all diagonal entries 1. For (R₁, R₂) ∈ 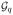(s₀(p)), their difference R₁ − R₂ is approximately sparse in the sense that each row vector of R₁ − R₂ lies in the ℓ_q ball with radius s₀(p) and 0 ≤ q < 1. When q = 0, this constraint becomes the commonly used exact sparsity condition.

Let

$$Y_i^{(t)}=(X_i^{(t)}-{\mu }_{it})/{(var(X_i^{(t)}))}^{1/2},i=1,\dots ,p,t=1,2.$$

We assume that for each i, Y_i is sub-Gaussian distributed, i.e. there exist constants K, η > 0 such that for all 1 ≤ i ≤ p and t = 1, 2,

$$E{e}^{u{(Y_i^{(t)})}^2}\le K,\text{for}\mid u\mid \le \eta .$$ (12)

In addition, we assume for some constant ν₀ > 0

$$\underset{1\le i,j\le p;t=1,2}{min}var(Y_i^{(t)}{Y}_j^{(t)})\ge {\nu }_0.$$ (13)

The following theorem provides an upper bound for the risk of the thresholding estimator D̂^* under the spectral norm loss.

Theorem 3.1 (Upper bound)

Suppose log p = o(min(n₁, n₂)^1/3) and (12) and (13) hold. Suppose the thresholding function s_λ(z) satisfy Conditions (C1)–(C3). Then the thresholding estimator D̂^* defined in (2) and (10) with τ > 4 satisfies

$$\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^2\le C(s_0^2(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$ (14)

$$\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^2\le C(s_0^2(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$ (15)

$$\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^2\le Cp(s_0(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q/2}$$ (16)

for some constant C > 0 that does not depend on n₁, n₂ or p.

Remark 3.1

Condition (13) holds naturally when X^(t) are jointly Gaussian. To see this point, we suppose ρ_ijt is the correlation between $Y_i^{(t)}$ and $Y_j^{(t)}$. Then one can write $Y_j^{(t)}={\rho }_{\mathit{ijt}}{Y}_i^{(t)}+\sqrt{1-{\rho }_{\mathit{ijt}}^2}W$, where $Y_i^{(t)}$, W are independently standard Gaussian. It is easy to calculate that $\text{Var}(Y_i^{(t)}{Y}_j^{(t)})=1+{\rho }_{\mathit{ijt}}^2\ge 1$, which implies (13) holds for ν₀ = 1. Condition (13) is used in Lemma 6.1 to show that θ̂_ijt is a good estimate of θ_ijt and |σ̂_ijt − σ_ijt| can be controlled by C(θ̂_ijt log p/n_t)^1/2 with high probability.

Theorem 3.1 gives the rate of convergence for the thresholding estimator D̂^*. The following result provides the lower bound for the minimax risk of estimating the differential correlation matrix D = R₁ − R₂ with (R₁, R₂) ∈ 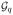(s₀(p)).

Theorem 3.2 (Lower Bound)

Suppose log p = o(min(n₁, n₂)) and s₀(p) ≤ M min(n₁, n₂)^(1−q)/2 × (log p)^−(3−q)/2 for some constant M > 0. Then minimax risk for estimating D = R₁ − R₂ satisfies

$$\underset{\widehat{\mathbf{D}}}{inf}\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{D}}-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^2\ge {cs}_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q},$$ (17)

$$\underset{\widehat{\mathbf{D}}}{inf}\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{D}}-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^2\ge {cs}_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q},$$ (18)

$$\underset{\widehat{\mathbf{D}}}{inf}\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{D}}-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^2\ge c{s}_0(p)p{\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q/2},$$ (19)

for some constant c > 0.

Theorems 3.1 and 3.2 together yield the minimax rate of convergence

$$s_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$

for estimating D = R₁ − R₂ with (R₁, R₂) ∈ 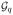(s₀(p)) under the spectral norm loss, and show that the thresholding estimator D̂^* defined in (2) and (10) is adaptively rate-optimal.

Remark 3.2

The technical analysis here for the different of two correlation matrices is more complicated in comparison to the problem of estimating a sparse covariance matrix considered in Cai and Liu (2011). It can be seen in (7), i.e. the “signal + noise” expression of r̂_ij1 − r̂_ij2, the difference of the sample correlation matrices has six “noise terms”. It is necessary to deal with all these six terms in the theoretical analysis of Theorem 3.1.

4 Numerical Studies

We investigate in this section the numerical performance of the adaptive thresholding estimator of the differential correlation matrix through simulations. The method is applied to the analysis of a breast cancer dataset in the next section.

In the previous sections, we proposed the entrywise thresholding method for estimating R₁ − R₂ and then studied the theoretical properties of D̂^* with a fixed τ > 4. However, the theoretical choice of τ may not be optimal in finite sample performance, as we can see in the following example. Let R₁ and R₂ be 200 × 200-dimensional matrices such that R_1,ij = (−1)^|i−j|×max(1−|i−j|/10, 0)×(1_{i=j}+f_if_j1_{i≠j}) and R_2,ij = max(1−|i−j|/10, 0)×(1_{i=j}+f_if_j1_{i≠j}). Here 1_{·} is the indicator function, f₁, ···, f₂₀₀ are i.i.d. random variables that are uniformly distributed on [0, 1]. In this setting, both R₁ and R₂ are sparse, but their difference is even more sparse. We set Σ_t = R_t and generate 200 independent samples from X⁽¹⁾ ~ N(0, Σ₁) and 200 independent samples from X⁽²⁾ ~ N(0, Σ₂). For various values of τ ∈ [0, 5], we implement the proposed method with hard thresholding and repeat the experiments for 100 times. The average loss in spectral, ℓ₁ and Frobenious norms are shown in Figure 1. Obviously in this example, τ > 4 is not the best choice.

Figure 1.

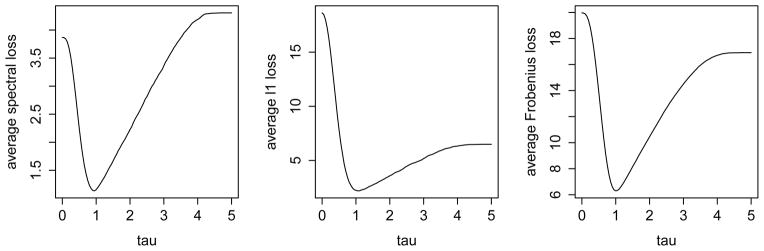
Average (Spectral, ℓ₁, Frobenious) norm losses for τ ∈ [0, 5]. p = 100, n₁ = n₂ = 50.

Empirically, we find that the numerical performance of the estimator can often be improved by using a data-driven choice of τ based on cross-validation. We thus begin by introducing the following K-fold cross-validation method for the empirical selection of τ.

4.1 Empirical Choice of τ

For an integer K ≥ 2, we first divide both samples ${\mathbf{X}}^{(1)}=\{{\mathbf{X}}_1^{(1)},{\mathbf{X}}_2^{(1)},\dots ,{\mathbf{X}}_{n_1}^{(1)}\}$ and ${\mathbf{X}}^{(2)}=\{{\mathbf{X}}_1^{(2)},{\mathbf{X}}_2^{(2)},\dots ,{\mathbf{X}}_{n_2}^{(2)}\}$ randomly into two groups for H times as ${\mathbf{X}}_{I_1^h}^{(1)},{\mathbf{X}}_{T_1^h}^{(1)},{\mathbf{X}}_{I_2^h}^{(2)}$ and ${\mathbf{X}}_{T_2^h}^{(2)}$. Here h = 1, …, H represents the h-th division. For t = 1 and 2, the size of the first group ${\mathbf{X}}_{I_t^h}^{(t)}$ is approximately (K − 1)/K · n_t and the size of the second group ${\mathbf{X}}_{T_t^h}^{(t)}$ is approximately n_t/K. We then calculate the corresponding sample correlation matrices as ${\widehat{\mathbf{R}}}_{I_1^h}^{(1)},{\widehat{\mathbf{R}}}_{T_1^h}^{(1)},{\widehat{\mathbf{R}}}_{I_2^h}^{(2)}$ and ${\widehat{\mathbf{R}}}_{T_2^h}^{(2)}$ for all four sub-samples. Partition the interval [0, 5] into an equi-spaced grid {0, $\frac{1}{N},\dots ,\frac{5N}{N}$}. For each value of τ ∈ {0, $\frac{1}{N},\dots ,\frac{5N}{N}$}, we obtain the thresholding estimator ${\widehat{\mathbf{D}}}_{I^h}^{\ast }$ defined in (2) and (10) with the thresholding constant τ based on the subsamples ${\mathbf{X}}_{I_1^h}^{(1)}$ and ${\mathbf{X}}_{I_2^h}^{(2)}$. Denote the average loss for each τ for the second sub-samples ${\mathbf{X}}_{T_1^h}^{(1)}$ and ${\mathbf{X}}_{T_2^h}^{(2)}$ as

$$L(\tau )=\frac{1}{H}\sum _{h=1}^H{\Vert {\widehat{\mathbf{D}}}_{I^h}^{\ast }-({\widehat{\mathbf{R}}}_{T_1^h}^{(1)}-{\widehat{\mathbf{R}}}_{T_2^h}^{(2)})\Vert }_F^2.$$

We select

$$\widehat{\tau }=\underset{\tau \in \{0,\frac{1}{N},\dots ,\frac{5N}{N}\}}{\text{argmin}}L(\tau )$$

as our empirical choice of the thresholding constant τ, and calculate the final estimator D̂^*(τ̂) with the thresholding constant τ̂ based on the whole samples X⁽¹⁾ and X⁽²⁾.

4.2 Estimation of Differential Correlation Matrix

The adaptive thresholding estimator is easy to implement. We consider the following two models under which the differential correlation matrix is sparse.

1. Model 1 (Random Sparse Difference) R₁ and R₂ are p-dimensional symmetric positive definite matrices such that ${\mathbf{R}}_1=\text{diag}({\mathbf{B}}_1,{\mathbf{I}}_{\frac{p}{2}\times \frac{p}{2}})$ is a fixed matrix, where ${\mathbf{B}}_1\in {ℝ}^{\frac{p}{2}\times \frac{p}{2}}$ with B_1,ij = 1 if i = j and B_1,ij = 0·2 if i ≠ j, ${\mathbf{I}}_{\frac{p}{2}\times \frac{p}{2}}$ is the $\frac{p}{2}\times \frac{p}{2}$ identity matrix, and R₂ is randomly generated as ${\mathbf{R}}_2=\text{diag}({\mathbf{B}}_1+\lambda {\mathbf{D}}_0,{\mathbf{I}}_{\frac{p}{2}\times \frac{p}{2}})$, where ${\mathbf{D}}_0\in {ℝ}^{\frac{p}{2}\times \frac{p}{2}}$ with

   $${\mathbf{D}}_{ij,0}=\{\begin{array}{cc}1,& \text{with}\text{probability}0·05\\ 0,& \text{with}\text{probability}0·9\\ -1,& \text{with}\text{probability}0·05\end{array}$$

   and λ is a constant that ensures the positive definiteness of R₂.

2. Model 2 (Banded Difference) In this setting, p-dimensional matrices R₁ and R₂ satisfy R_1,ij =0·2×1_{i=j}+0·8×(−1)^|i−j| × max(1 − |i − j|/10, 0) and R_2,ij = R_1,ij+0·2×1_{i≠j} × max(1 − |i − j|/3, 0). Here 1_{·} is the indicator function.

In each of the two settings, we set Σ_t = diag(|ω_t|^1/2)R_tdiag(|ω_t|^1/2) for both t = 1, 2, where ω₁, ω₂ ∈ ℝ^p are two i.i.d. samples from N(0, I_p). These operations make the covariance matrices Σ₁ and Σ₂ have different values along the diagonals.

We generate i.i.d. samples from X⁽¹⁾ ~ N(0, Σ₁) and X⁽²⁾ ~ N(0, Σ₂) for various values of p, n₁, and n₂ and then apply the proposed algorithm with 5-fold cross-validation for the selection of the thresholding constant τ. For each setting, both the hard thresholding and adaptive-Lasso thresholding (Rothman et al. (2009)),

$$s_{\lambda }(z)=z·max(1-{\mid \lambda /z\mid }^{\eta },0)\text{with}\eta =4,$$ (20)

are used. For comparison, we also implement three natural estimators of D.

1. The covariance matrices Σ₁ and Σ₂ are estimated individually by the adaptive thresholding method proposed in Cai and Liu (2011) with 5-fold cross-validation and then ${\widehat{\mathbf{\sum }}}_1^{\ast }$ and ${\widehat{\mathbf{\sum }}}_2^{\ast }$ are normalized to yield estimators of R₁ and R₂,

   $${\widehat{\mathbf{R}}}_1^{\ast }=\text{diag}{({\widehat{\mathbf{\sum }}}_1^{\ast })}^{-1/2}{\widehat{\mathbf{\sum }}}_1^{\ast }\text{diag}{({\widehat{\mathbf{\sum }}}_1^{\ast })}^{-1/2},{\widehat{\mathbf{R}}}_2^{\ast }=\text{diag}{({\widehat{\mathbf{\sum }}}_2^{\ast })}^{-1/2}{\widehat{\mathbf{\sum }}}_2^{\ast }\text{diag}{({\widehat{\mathbf{\sum }}}_2^{\ast })}^{-1/2},$$

   and finally D = R₁ − R₂ is estimated by the difference ${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$.

2. The correlation matrices ${\widehat{\mathbf{R}}}_1^{•}$ and ${\widehat{\mathbf{R}}}_2^{•}$ are estimated separately using the method proposed in Section 6.2 and then take the difference.

3. D is estimated directly the difference of the sample correlation matrices R̂₁ − R̂₂.

The numerical results are summarized in Tables 1 and 4.2 for the two models respectively. In each case, we compare the performance of the three estimators D^*, ${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$ and R̂₁ − R̂₂ under the spectral norm, matrix ℓ₁ norm, and Frobenius norm losses. For both models, it is easy to see that the direct thresholding estimator D^* significantly outperforms ${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$ and R̂₁ − R̂₂. Under Model 1, the individual correlation matrices R₁ and R₂ are “dense” in the sense that half of the rows and columns contain many non zeros entries, but their difference D is sparse. In this case, R₁ and R₂ cannot be estimated consistently and the two difference estimators ${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$ and R̂₁ − R̂₂ based on the individual estimators of R₁ and R₂ perform very poorly, while the direct estimator D^* performs very well. Moreover, the numerical performance of the thresholding estimators does not depend on the specific thresholding rules in a significant way. Different thresholding rules including hard thresholding and adaptive Lasso behave similarly.

Table 1.

Comparison of D̂^* with ${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$ and R̂₁ − R̂₂ under Model 1.

p	n1	n2	Hard			Adaptive Lasso			Sample
			D̂*	${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$	${\widehat{\mathbf{R}}}_1^{•}-{\widehat{\mathbf{R}}}_2^{•}$	D̂*	${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$	${\widehat{\mathbf{R}}}_1^{•}-{\widehat{\mathbf{R}}}_2^{•}$	R̂1 − R̂2
Spectral Norm
100	50	50	0·50(0·41)	1·75(1·37)	6·94(1·07)	0·33(0·31)	1·51(1·75)	6·17(0·98)	7·28(0·93)
100	100	100	0·34(0·21)	3·79(3·17)	4·74(0·55)	0·28(0·23)	3·53(2·71)	4·49(0·71)	5·02(0·65)
100	200	200	0·29(0·19)	4·22(2·14)	3·23(0·47)	0·24(0·13)	4·52(1·86)	3·14(0·54)	3·55(0·47)
100	500	500	0·24(0·10)	1·72(0·35)	2·07(0·32)	0·22(0·08)	1·82(0·35)	1·87(0·26)	2·23(0·25)
500	50	50	0·56(0·77)	3·02(2·76)	31·88(4·04)	0·40(0·65)	3·47(4·63)	29·15(4·26)	34·66(3·84)
500	100	100	0·41(0·48)	8·09(11·02)	23·38(4·52)	0·34(0·39)	12·99(13·26)	21·82(3·23)	24·19(2·77)
500	200	200	0·32(0·40)	22·22(13·06)	15·67(3·30)	0·26(0·34)	21·31(9·29)	14·61(2·24)	16·50(1·97)
500	500	500	0·20(0·19)	7·80(1·37)	7·80(1·29)	0·18(0·14)	8·21(1·69)	8·70(1·39)	10·46(1·31)
Matrix ℓ1 Norm
100	50	50	0·89(0·68)	3·63(2·97)	18·91(1·55)	0·78(0·80)	3·14(3·20)	16·88(1·42)	21·33(1·61)
100	100	100	0·64(0·25)	7·34(4·85)	13·42(1·08)	0·70(0·87)	7·03(4·14)	12·72(1·18)	14·97(1·14)
100	200	200	0·64(0·34)	9·63(1·85)	9·22(0·75)	0·61(0·37)	9·37(1·77)	8·67(0·87)	10·60(0·81)
100	500	500	0·58(0·22)	4·54(0·56)	5·92(0·54)	0·56(0·21)	4·85(0·61)	5·33(0·45)	6·69(0·44)
500	50	50	1·69(3·09)	7·85(8·14)	97·28(6·64)	1·37(2·87)	9·49(11·93)	87·02(7·31)	112·40(8·97)
500	100	100	1·06(1·28)	20·12(19·50)	64·98(5·93)	1·17(1·47)	27·95(22·75)	65·60(5·07)	79·66(5·37)
500	200	200	0·97(1·48)	51·64(10·13)	46·74(5·01)	0·95(1·24)	47·87(8·50)	45·54(3·70)	55·77(3·70)
500	500	500	0·68(0·54)	23·19(2·86)	23·47(2·56)	0·69(0·52)	24·67(2·92)	27·21(2·09)	35·32(2·04)
Frobenious Norm
100	50	50	1·40(1·32)	4·34(2·51)	19·01(0·37)	1·06(1·04)	3·26(2·61)	16·60(0·42)	19·87(0·38)
100	100	100	0·96(0·59)	7·14(3·67)	13·38(0·23)	0·94(0·81)	6·23(3·31)	12·10(0·27)	14·05(0·25)
100	200	200	0·89(0·57)	9·09(1·03)	9·30(0·20)	0·84(0·50)	8·15(1·07)	8·42(0·25)	9·94(0·18)
100	500	500	0·85(0·32)	4·37(0·27)	5·92(0·11)	0·82(0·30)	4·43(0·25)	5·26(0·11)	6·39(0·10)
500	50	50	3·33(5·63)	11·18(7·71)	95·05(0·91)	2·27(3·92)	9·57(9·31)	83·40(1·24)	99·97(0·93)
500	100	100	2·18(2·98)	20·17(14·55)	61·37(2·09)	2·10(2·47)	22·54(16·69)	60·58(0·85)	70·40(0·67)
500	200	200	1·77(2·39)	45·06(5·89)	42·11(1·67)	1·63(1·96)	39·52(5·14)	41·88(0·73)	49·53(0·49)
500	500	500	1·27(1·09)	20·17(0·99)	21·74(0·65)	1·22(0·84)	20·48(0·91)	25·47(0·41)	31·34(0·33)

5 Analysis of A Breast Cancer Dataset

Identifying gene expression networks can be helpful for conducting more effective treatment based to the condition of patients. de la Fuente (2010) demonstrated that the gene expression networks can vary in different disease states and the differential correlations in gene expression (i.e. co-expression) are useful in disease studies.

In this section, we consider the dataset “70pathwaygenes-by-grade” from the study by van de Vijver et al. (2002) and investigate the differential co-expressions among genes in different tumor stages of breast cancer. In this dataset, there are 295 records of patients with 1624 gene expressions, which are categorized into three groups based on the histological grades of tumor (“Good”, “Intermediate” and “Poor”) with 74, 101 and 119 records, respectively. We denote these three groups of samples as X⁽¹⁾, X⁽²⁾ and X⁽³⁾. In order to analyze the difference in the correlation alternation in different grades of tumor, we apply our adaptive thresholding method with cross-validation to estimate the differential correlation matrices among those gene expressions from different stages.

The number of gene pairs with significant difference in correlation are listed in Table 3. The results show that the correlation structures between the “Good” and “Intermediate” groups are similar and there is some significant changes between the “Good” and “Poor” group.

Table 3.

The number of gene pairs that have significant differential correlation betweens two groups of different tumor grades

	Good v.s. Intermediate	Intermediate v.s. Poor	Good v.s. Poor
# of selected pairs	0	2	152

More interestingly, by combining the “Good” and “Intermediate” sub-samples and comparing with the “Poor” group, we find significant differences between their correlation structure. There are 4526 pairs of genes that have significantly different correlations between the “Good + Intermediate” and “Poor” groups. For each given gene, we count the number of the genes whose correlation with this gene is significantly different between these two groups, and rank all the genes by the counts. That is, we rank the genes by the size of the support of D̂^* in each row. The top ten genes are listed in Table 4.

Table 4.

The top ten genes that appear for most times in the selected pairs in “Good + Intermediate” v.s. “Poor”

Gene	number of pairs
growth differentiation factor 5 (GDF5)	67
transcription factor 7-like 1 (TCF7L1)	64
3′-phosphoadenosine 5′-phosphosulfate synthase 1 (PAPSS1)	51
secreted frizzled-related protein 1(SFRP1)	43
gamma-aminobutyric acid A receptor, pi (GABRP)	41
mannosidase, alpha, class 2B, member 2 (MAN2B2)	37
desmocollin 2 (DSC2)	36
transforming growth factor, beta 3 (TGFB3)	35
CRADD	35
ELOVL fatty acid elongase 5(ELOVL5)	32

Among these ten genes, six of them, GDF5, TCF7L1, PAPSS1, SFRP1, GABRP, TGFB1, have been previously studied and verified in the literature that are associated with the breast cancer (See Margheri et al. (2012), Shy et al. (2013), Xu et al. (2012), Klopocki et al. (2004), Zafrakas et al. (2006), and Ghellal et al. (2000), respectively). Take for example GDF5 and TCF7L1, the overproduction of Transforming growth factor beta-1 (TGFβ), a multifunctional cytokine, is an important characteristic of late tumor progression. Based on the study by Margheri et al. (2012), TGFβ produced by breast cancer cells brings about in endothelial cells expression of GDF5. The findings in (Shy et al. (2013)) suggested the important role played by TCF7L1 in breast cancer. Although these biological studies mainly focus on the the behavior of the single gene expression, our study provides evidence in the gene co-expression level that these gene expressions are related with the breast cancer.

We should point out that the two well-known genes related to the breast cancer, BRCA1 and BRCA2, were not detected by our method. This is mainly due to the fact that our method focus on the differential gene co-expressions, not the changes in the gene expression levels.

6 Other Related Problems

We have so far focused on optimal estimation of the differential correlation matrix. In addition to optimal estimation, hypothesis testing of the differential correlation matrix is also an important problem. In this section we consider testing the hypotheses H₀ : R₁ − R₂ = 0 versus H₁ : R₁ − R₂ ≠ 0 and propose a test which is particularly well suited for testing again sparse alternatives.

Similar ideas and techniques can also be used to treat several other related problems, including estimation of a single sparse correlation matrix from one random sample, estimation of the differential covariance matrices, and estimation of the differential cross-correlation matrices. We also briefly discuss these problems in this section.

6.1 Testing Differential Correlation Matrices

Suppose we are given two sets of independent and identical distributed samples ${\mathbf{X}}^{(t)}=\{{\mathbf{X}}_1^{(t)},\dots ,{\mathbf{X}}_{n_t}^{(t)}\}$ with the mean μ_t, covariance matrix Σ_t and correlation matrix R_t, where t = 1 and 2, and wish to test the hypotheses

$$H_0:{\mathbf{R}}_1-{\mathbf{R}}_2=0\text{v.s.}{H}_1:{\mathbf{R}}_1-{\mathbf{R}}_2\ne 0.$$ (21)

This testing problem is similar to, but also different from, testing the equality of two high-dimensional covariance matrices, which has been considered in several recent papers. See, for example, Schott (2007), Srivastava and Yanagihara (2010), Li et al. (2012), and Cai et al. (2013). Here we are particularly interested in testing against sparse alternatives and follow similar ideas as those in Cai et al. (2013).

To construct the test statistic, we need more precise understanding of the sample correlation coefficients r̂_ijt. It follows from (5) that

$$\begin{array}{l}{\widehat{r}}_{\mathit{ijt}}=\frac{{\widehat{\sigma }}_{\mathit{ijt}}}{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}\approx \frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}+\frac{{\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}-\frac{{\sigma }_{\mathit{ijt}}}{2{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\left(\frac{{\widehat{\sigma }}_{\mathit{iit}}-{\sigma }_{\mathit{iit}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{iit}})}^{1/2}}+\frac{{\widehat{\sigma }}_{\mathit{jjt}}-{\sigma }_{\mathit{jjt}}}{{({\sigma }_{\mathit{jjt}}{\sigma }_{\mathit{jjt}})}^{1/2}}\right)\\ =r_{\mathit{ijt}}+\frac{1}{n_t}\sum _{k=1}^{n_t}\left[\frac{(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})-{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}-\frac{r_{\mathit{ijt}}}{2}\left(\frac{{(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})}^2-{\sigma }_{\mathit{iit}}}{{\sigma }_{\mathit{iit}}}+\frac{{(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})}^2-{\sigma }_{\mathit{jjt}}}{{\sigma }_{\mathit{jjt}}}\right)\right]\end{array}$$

Since ${\overline{X}}_i^{(t)}\approx {\mu }_{it},{\overline{X}}_j^{(t)}\approx {\mu }_{jt},E\left(X_{ik}^{(t)}-{\overline{X}}_i^{(t)}\right)\left(X_{jk}^{(t)}-{\overline{X}}_j^{(t)}\right)\approx {\sigma }_{\mathit{ijt}}$, we introduce

$${\eta }_{\mathit{ijt}}=var\left[\frac{(X_i^{(t)}-{\mu }_{it})(X_j^{(t)}-{\mu }_{jt})}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}-\frac{r_{\mathit{ijt}}}{2}\left(\frac{{(X_i^{(t)}-{\mu }_{it})}^2}{{\sigma }_{\mathit{iit}}}+\frac{{(X_j^{(t)}-{\mu }_{jt})}^2}{{\sigma }_{\mathit{jjt}}}\right)\right].$$

Then asymptotically as n, p → ∞,

$${\widehat{r}}_{\mathit{ijt}}-r_{\mathit{ijt}}\approx {\left(\frac{n_{\mathit{ijt}}}{n_t}\right)}^{1/2}{z}_{\mathit{ijt}},\text{where}{z}_{\mathit{ijt}}~N(0,1).$$

The true value of η_ijt is unknown but can be estimated by

$$\begin{array}{l}{\widehat{\eta }}_{\mathit{ijt}}=\frac{1}{n_t}\sum _{k=1}^{n_t}{\left\{\frac{(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})(X_{jk}-{\overline{X}}_j^{(t)})-{\widehat{\sigma }}_{\mathit{ijt}}}{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}-\frac{{\widehat{r}}_{\mathit{ijt}}}{2}\left(\frac{{(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})}^2-{\widehat{\sigma }}_{\mathit{iit}}}{{\widehat{\sigma }}_{\mathit{iit}}}+\frac{{(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})}^2-{\widehat{\sigma }}_{\mathit{jjt}}}{{\widehat{\sigma }}_{\mathit{jjt}}}\right)\right\}}^2\\ =\frac{1}{n_t}\sum _{k=1}^{n_t}{\left\{\frac{(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})(X_{jk}-{\overline{X}}_j^{(t)})}{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}-\frac{{\widehat{r}}_{\mathit{ijt}}}{2}\left(\frac{{(X_{ik}^{(t)}-{\overline{X}}_i^{(t)})}^2}{{\widehat{\sigma }}_{\mathit{iit}}}+\frac{{(X_{jk}^{(t)}-{\overline{X}}_j^{(t)})}^2}{{\widehat{\sigma }}_{\mathit{jjt}}}\right)\right\}}^2.\end{array}$$

We define the test statistic by

$$T_n=\underset{1\le i\le j\le p}{max}{T}_{ij}$$

where

$$T_{ij}=\frac{{({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})}^2}{{\widehat{\eta }}_{ij1}/n_1+{\widehat{\eta }}_{ij2}/n_2},1\le i,j\le p.$$

Under regularity conditions (similar to (C1)–(C3) in Cai et al. (2013)), the asymptotic distribution of T_n can be shown to be the type I extreme value distribution. More precisely,

$$P(T_n-4logp+loglog\mathit{p}\le t)\to exp\left(-{(8\pi )}^{-1/2}exp(-t/2)\right)$$ (22)

for any given t ∈ ℝ.

The asymptotic null distribution (22) can then be used to construct a test for testing the hypothesis H₀ : R₁ − R₂ = 0. For a given significance level 0 < α < 1, define the test Ψ_α by

$${\mathrm{\Psi }}_{\alpha }=I(M_n\ge 4logp-loglog\mathit{p}+{\tau }_{\alpha })$$ (23)

where τ_α = −log(8π) − 2 log log(1 − α)⁻¹ is the 1 − α quantile of the type I extreme value distribution with the cumulative distribution function exp(−(8π)^−1/2 exp(−x/2)). The hypothesis H₀ : R₁ − R₂ = 0 is rejected whenever Ψ_α = 1. As the test proposed in Cai et al. (2013) for testing the equality of two covariance matrices, the test Ψ_α defined in (23) can also be shown to be particularly well suited for testing H₀ : R₁ − R₂ = 0 against sparse alternatives.

6.2 Optimal Estimation of a Sparse Correlation Matrix

The ideas and technical tools can also be used for estimation of a single correlation matrix from one random sample, which is a simpler problem. Suppose we observe an independent and identical distributed sample X = (X₁, …, X_n) from a p-dimensional distribution with mean μ ∈ ℝ^p, covariance matrix Σ, and correlation matrix R ∈ ℝ^p×p. When R is approximately sparse, it can be naturally estimated by a thresholding estimator R̂ as follows. Let ${\overline{X}}_i=\frac{1}{n}{\sum }_{k=1}^n{X}_{ik}$. Define the sample covariance matrix Σ̂ = (σ̂_ij)_1≤i,j≤p and the sample correlation matrix R̂ = (r̂_ij)_1≤i,j≤p respectively by

$${\widehat{\sigma }}_{ij}=\frac{1}{n}\sum _{k=1}^n(X_{ik}-{\overline{X}}_i)(X_{jk}-{\overline{X}}_j)\text{and}{\widehat{r}}_{ij}=\frac{{\widehat{\sigma }}_{ij}}{{({\widehat{\sigma }}_{ii}{\widehat{\sigma }}_{jj})}^{1/2}}.$$

Same as in (8) and (9), we define

$${\widehat{\theta }}_{ij}=\frac{1}{n}\sum _{k=1}^n{((X_{ik}-{\overline{X}}_i)(X_{jk}-{\overline{X}}_j)-{\widehat{\sigma }}_{ij})}^2,$$ (24)

$${\widehat{\xi }}_{ij}=\frac{{\widehat{\theta }}_{ij}}{{\widehat{\sigma }}_{ii}{\widehat{\sigma }}_{jj}}=\frac{1}{n{\widehat{\sigma }}_{ii}{\widehat{\sigma }}_{jj}}\sum _{k=1}^n{((X_{ik}-{\overline{X}}_i)(X_{jk}-{\overline{X}}_j)-{\widehat{\sigma }}_{ij})}^2,$$ (25)

$${\lambda }_{ij}=\tau {\left(\frac{logp}{n}\right)}^{1/2}\left({\widehat{\xi }}_{ij}^{1/2}+\frac{\mid {\widehat{r}}_{ij}\mid }{2}\left({\widehat{\xi }}_{ii}^{1/2}+{\widehat{\xi }}_{jj}^{1/2}\right)\right),$$ (26)

where τ is the thresholding constant that can be chosen empirically through cross-validation. The correlation matrix R is then estimated by ${\widehat{\mathbf{R}}}^{\ast }={({\widehat{r}}_{ij}^{\ast })}_{1\le i,j\le p}$ with

$${\widehat{r}}_{ij}^{\ast }=s_{{\lambda }_{ij}}({\widehat{r}}_{ij}).$$

We consider the following class of approximately sparse correlation matrices

$${\mathcal{G}}_q^1(s_0(p))=\left\{\mathbf{R}=(r_{ij}):\mathbf{R}\succ 0;\text{diag}(\mathbf{R})=1;\underset{j}{max}\sum _{i=1,i\ne j}^p{\mid r_{ij}\mid }^q\le s_0(p)\right\},0\le q<1.$$

The following theoretical results for R̂^* can be established using a similar analysis.

Proposition 6.1

Suppose log p = o(n^1/3) and X satisfies (12), (13). For τ > 6, there exists some constant C does not depend on n or p such that

$$\underset{\mathbf{R}\in {\mathcal{G}}_q^1(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }^2\le C(s_0^2(p)+1){\left(\frac{logp}{n}\right)}^{1-q}$$ (27)

$$\underset{\mathbf{R}\in {\mathcal{G}}_q^1(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_{{\ell }_1}^2\le C(s_0^2(p)+1){\left(\frac{logp}{n}\right)}^{1-q}$$ (28)

$$\underset{\mathbf{R}\in {\mathcal{G}}_q^1(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_F^2\le Cp(s_0(p)+1){\left(\frac{logp}{n}\right)}^{1-q/2}.$$ (29)

Moreover, when log p = o(n), s₀(p) ≤ Mn^(1−q)/2(log p)^−(3−q)/2 for some constant M > 0, the rate in (27) is optimal as we also have the lower bound

$$\underset{\widehat{\mathbf{R}}}{inf}\underset{\mathbf{R}\in {\mathcal{G}}_q^1(s_0(p))}{sup}E{\Vert \widehat{\mathbf{R}}-\mathbf{R}\Vert }^2\ge {cs}_0^2(p){\left(\frac{logp}{n}\right)}^{1-q}$$ (30)

$$\underset{\widehat{\mathbf{R}}}{inf}\underset{\mathbf{R}\in {\mathcal{G}}_q^1(s_0(p))}{sup}E{\Vert \widehat{\mathbf{R}}-\mathbf{R}\Vert }_{{\ell }_1}^2\ge {cs}_0^2(p){\left(\frac{logp}{n}\right)}^{1-q}$$ (31)

$$\underset{\widehat{\mathbf{R}}}{inf}\underset{\mathbf{R}\in {\mathcal{G}}_q^1(s_0(p))}{sup}E{\Vert \widehat{\mathbf{R}}-\mathbf{R}\Vert }_F^2\ge {\mathit{cps}}_0(p){\left(\frac{logp}{n}\right)}^{1-q/2}.$$ (32)

Remark 6.1

Cai and Liu (2011) proposed an adaptive thresholding estimator Σ̂^* of a sparse covariance matrix Σ. This estimator leads naturally to an estimator R̃ = (r̃_ij) of a sparse correlation matrix R by normalizing ${\widehat{\mathbf{\sum }}}^{\ast }=({\widehat{\sigma }}_{ij}^{\ast })$ via ${\stackrel{\sim }{r}}_{ij}={\widehat{\sigma }}_{ij}^{\ast }{({\sigma }_{ii}^{\ast }{\sigma }_{jj}^{\ast })}^{-1/2}$. The correlation matrix estimator R̃ has similar properties as the estimator introduced above. For example, R̃ and R̂^* achieve the same rate of convergence.

6.3 Optimal Estimation of Sparse Differential Covariance Matrices

Our analysis can also be used for estimation of sparse differential covariance matrices, Δ = Σ₁ − Σ₂. Define θ_ijt as in (3) and its estimate θ̂_ijt as in (8). Similar to the estimation of the differential correlation matrix D = R₁ − R₂, we estimate Δ = Σ₁ − Σ₂ by adaptive entrywise thresholding. Specifically, we define the thresholding estimator ${\widehat{\mathbf{\Delta }}}^{\ast }=({\widehat{\delta }}_{ij}^{\ast })\in {ℝ}^{p\times p}$ by

$${\widehat{\delta }}_{ij}^{\ast }=s_{{\gamma }_{ij}}({\widehat{\sigma }}_{ij1}-{\widehat{\sigma }}_{ij2}),1\le i,j\le p$$ (33)

where γ_ij is the thresholding level given by

$${\gamma }_{ij}=\tau \left({\left(\frac{logp}{n_1}{\widehat{\theta }}_{ij1}\right)}^{1/2}+{\left(\frac{logp}{n_2}{\widehat{\theta }}_{ij2}\right)}^{1/2}\right).$$ (34)

Same as in the last section, here s_λ(z) belongs to the class of thresholding functions satisfying Conditions (C1)–(C3) and the thresholding constant τ can be taken chosen empirically by cross-validation.

We consider the following class of paired covariance matrices with approximately sparse differences, for 0 ≤ q < 1,

$${\mathcal{F}}_q(s_0(p))\triangleq \left\{({\mathbf{\sum }}_1,{\mathbf{\sum }}_2):{\mathbf{\sum }}_1,{\mathbf{\sum }}_2\succcurlyeq 0,\underset{1\le i\le p,t=1,2}{max}{\sigma }_{\mathit{iit}}\le B,\underset{i}{max}\sum _{j=1}^p{\mid {\sigma }_{ij1}-{\sigma }_{ij2}\mid }^q\le s_0(p)\right\}.$$ (35)

Under the same conditions as those in Theorems 3.1 and 3.2, a similar analysis can be used to derive the minimax upper and lower bounds. It can be shown that the estimator Δ̂^* given in (33) with τ > 4 satisfies

$$\underset{({\mathbf{\sum }}_1,{\mathbf{\sum }}_2)\in {\mathcal{F}}_q(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{\Delta }}}^{\ast }-({\mathbf{\sum }}_1-{\mathbf{\sum }}_2)\Vert }^2\le C(s_0^2(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$ (36)

for some constant C > 0. Furthermore, the following minimax lower bound holds,

$$\underset{\widehat{\mathbf{\Delta }}}{inf}\underset{({\mathbf{\sum }}_1,{\mathbf{\sum }}_2)\in {\mathcal{F}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{\Delta }}-({\mathbf{\sum }}_1-{\mathbf{\sum }}_2)\Vert }^2\ge {cs}_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$ (37)

for some constant c > 0. Equations (36) and (37) together show that the thresholding estimator Δ̂^* defined in (33) and (34) is rate-optimal.

6.4 Estimate Differential Cross-Correlation Matrices

In many applications such as phenome-wide association studies (PheWAS) which aims to study the relationship between a set of genomic markers X and a range of phenotypes Y, the main focus is on the cross-correlations between the components of X and those of Y. That is, the object of interest is a submatrix of the correlation matrix of the random vector $\left(\begin{array}{c}\mathbf{X}\\ \mathbf{Y}\end{array}\right)$. More specifically, let X = (X₁, …, X_p1)′ be a p₁-dimensional random vector and Y = (Y₁, …, Y_p2)′ be a p₂-dimensional random vector. In the PheWAS setting, X may be all phenotypic disease conditions of interest and Y is a vector of genomic markers.

Suppose we have two independent and identical distributed samples of the (X, Y) pairs, one for the case group and one for the control group,

$$\left(\begin{array}{c}{X}_k^{(1)}\\ Y_k^{(1)}\end{array}\right)=\left(\begin{array}{c}{X}_{1k}^{(1)}\\ ⋮\\ X_{p_{1}k}^{(1)}\\ Y_{1k}\\ ⋮\\ Y_{p_{2}k}^{(1)}\end{array}\right),k=1,\dots ,n_1;\left(\begin{array}{c}{X}_k^{(2)}\\ Y_k^{(2)}\end{array}\right)=\left(\begin{array}{c}{X}_{1k}^{(2)}\\ ⋮\\ X_{p_{1}k}^{(2)}\\ Y_{1k}\\ ⋮\\ Y_{p_{2}k}^{(2)}\end{array}\right),k=1,\dots ,n_2$$

Here for $t=1,2,{(X_k^{(t)T},Y_k^{(t)T})}^T$, k = 1, …, n₁ are independent and identical distributed samples generated from some distribution with mean μ_t, covariance matrix Σ_t and correlation matrix R_t given by

$${\mu }_t=\left(\begin{array}{c}{\mu }_{Xt}\\ {\mu }_{Yt}\end{array}\right),{\mathbf{\sum }}_t=\left[\begin{array}{cc}{\mathbf{\sum }}_{\mathit{XXt}}& {\mathbf{\sum }}_{\mathit{XYt}}\\ {\mathbf{\sum }}_{\mathit{YXt}}& {\mathbf{\sum }}_{\mathit{YYt}}\end{array}\right],{\mathbf{R}}_t=\left[\begin{array}{cc}{\mathbf{R}}_{\mathit{XXt}}& {\mathbf{R}}_{\mathit{XYt}}\\ {\mathbf{R}}_{\mathit{YXt}}& {\mathbf{R}}_{\mathit{YYt}}\end{array}\right]$$

In applications such as PheWAS, it is of special interest to estimate the differential cross-correlation matrix of X and Y, i.e. D_XY = R_XY1 − R_XY2 ∈ ℝ^p₁×p₂. Again, we introduce the following set of paired correlation matrices with sparse cross-correlations,

$${\mathcal{G}}_q(s_0(p_1,p_2))=\{({\mathbf{R}}_1,{\mathbf{R}}_2):{\mathbf{R}}_1,{\mathbf{R}}_2\succcurlyeq 0,\text{diag}({\mathbf{R}}_1)=\text{diag}({\mathbf{R}}_2)=1;\underset{1\le i\le p_1}{max}\sum _{j=1}^{p_2}{\mid {(r_{XY})}_{ij1}-{(r_{XY})}_{ij2}\mid }^q\le s_0(p_1,p_2)\},0\le q<1.$$

The thresholding procedure proposed in Section 2 can be applied to estimate D_XY,

$${({\widehat{d}}_{XY}^{\ast })}_{ij}=s_{{\lambda }_{ij}}({({\widehat{r}}_{XY})}_{ij1}-{({\widehat{r}}_{XY})}_{ij2}),1\le i\le p_1,1\le j\le p_2$$ (38)

where R̂_XY is sample cross-correlation matrix of X and Y; λ_ij is given by (10). Similar to Theorem 3.1, the following theoretical results hold for the estimator ${\widehat{\mathbf{D}}}_{XY}^{\ast }=({\widehat{d}}_{XY}^{\ast })$.

Proposition 6.2

Suppose p = p₁ + p₂, log(p) = o(min(n₁, n₂)^1/3) and (12) and (13) hold. Suppose the thresholding function s_λ(z) satisfies Conditions (C1)–(C3). Then D̂^* defined in (38) with the thresholding constant τ > 4 satisfies

$$\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p_1,p_2))}{sup}E{\Vert {\widehat{\mathbf{D}}}_{XY}^{\ast }-({\mathbf{R}}_{XY1}-{\mathbf{R}}_{XY2})\Vert }^2\le C(s_0^2(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$ (39)

$$\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p_1,p_2))}{sup}E{\Vert {\widehat{\mathbf{D}}}_{XY}^{\ast }-{({\mathbf{R}}_{XY1}-{\mathbf{R}}_{XY2})}^{\top }\Vert }_{{\ell }_1}^2\le C(s_0^2(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}$$ (40)

$$\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p_1,p_2))}{sup}E{\Vert {\widehat{\mathbf{D}}}_{XY}^{\ast }-({\mathbf{R}}_{XY1}-{\mathbf{R}}_{XY2})\Vert }_F^2\le Cp(s_0(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q/2}$$ (41)

for some constant C > 0 that does not depend on n₁, n₂ or p.

The proof of Proposition 6.2 is similar to that of Theorem 3.1 by analyzing the block D̂_XY − (R_XY1 − R_XY2) instead of the whole matrix D* − (R₁ − R₂). We omit the detailed proof here.

Table 2.

Comparison of D̂^* with ${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$ and R̂₁ − R̂₂ under Model 2.

p	n1	n2	Hard			Adaptive Lasso			Sample
			D̂*	${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$	${\widehat{\mathbf{R}}}_1^{•}-{\widehat{\mathbf{R}}}_2^{•}$	D̂*	${\widehat{\mathbf{R}}}_1^{\ast }-{\widehat{\mathbf{R}}}_2^{\ast }$	${\widehat{\mathbf{R}}}_1^{•}-{\widehat{\mathbf{R}}}_2^{•}$	R̂1 − R̂2
Spectral Norm
100	50	50	0·98(1·00)	4·61(1·49)	7·25(0·87)	0·71(0·70)	4·47(1·44)	6·05(0·74)	8·29(0·98)
100	100	100	0·70(0·51)	2·88(0·81)	5·01(0·57)	0·62(0·47)	2·93(0·87)	4·25(0·52)	5·83(0·59)
100	200	200	0·60(0·35)	1·93(0·55)	3·53(0·42)	0·48(0·24)	1·98(0·57)	2·98(0·37)	4·07(0·47)
100	500	500	0·47(0·14)	1·23(0·27)	2·32(0·23)	0·46(0·17)	1·30(0·36)	1·98(0·21)	2·66(0·27)
500	50	50	0·97(0·99)	5·03(1·00)	20·61(1·07)	0·80(0·75)	4·55(0·96)	16·91(0·90)	24·96(1·16)
500	100	100	0·79(0·62)	3·17(0·49)	13·64(0·59)	0·59(0·41)	3·14(0·63)	11·13(0·53)	16·39(0·71)
500	200	200	0·60(0·36)	2·13(0·30)	9·12(0·42)	0·51(0·31)	2·11(0·35)	7·44(0·37)	10·94(0·50)
500	500	500	0·51(0·20)	1·34(0·16)	5·63(0·23)	0·49(0·20)	1·35(0·22)	4·65(0·21)	6·78(0·29)
Matrix ℓ1 Norm
100	50	50	1·84(2·66)	10·61(3·48)	19·11(1·55)	1·26(1·86)	9·88(3·14)	16·18(1·55)	21·92(1·61)
100	100	100	1·18(1·44)	6·73(2·24)	13·62(1·08)	1·10(1·26)	6·73(2·12)	11·73(1·20)	15·87(1·11)
100	200	200	0·98(0·98)	4·53(1·47)	9·79(0·85)	0·71(0·71)	4·68(1·46)	8·39(0·89)	11·37(0·97)
100	500	500	0·67(0·48)	2·95(0·89)	6·44(0·56)	0·65(0·59)	3·08(1·03)	5·58(0·47)	7·47(0·53)
500	50	50	1·79(2·65)	11·03(2·80)	79·71(2·64)	1·64(2·26)	10·38(3·02)	64·46(2·73)	97·88(2·55)
500	100	100	1·45(1·75)	7·66(1·79)	56·52(2·16)	1·02(1·35)	7·73(2·40)	45·65(1·86)	69·42(1·76)
500	200	200	1·02(1·18)	4·97(1·09)	39·86(1·39)	0·83(1·14)	5·03(1·27)	31·90(1·15)	49·11(1·33)
500	500	500	0·81(0·70)	3·15(0·72)	25·34(0·77)	0·82(0·77)	3·27(1·00)	20·39(0·77)	31·36(0·79)
Frobenious Norm
100	50	50	3·36(2·53)	13·82(1·83)	18·46(0·81)	2·66(1·47)	12·13(2·00)	15·87(0·79)	19·92(0·94)
100	100	100	2·67(1·19)	9·46(1·28)	13·26(0·55)	2·54(1·10)	8·77(1·18)	11·51(0·54)	14·32(0·58)
100	200	200	2·43(0·69)	6·94(0·72)	9·75(0·39)	2·26(0·51)	6·68(0·76)	8·59(0·37)	10·49(0·43)
100	500	500	2·24(0·34)	5·29(0·36)	6·96(0·19)	2·25(0·46)	5·28(0·44)	6·33(0·17)	7·39(0·19)
500	50	50	6·77(4·86)	34·24(3·33)	91·09(0·85)	6·18(3·86)	27·39(3·39)	75·97(0·83)	100·71(0·92)
500	100	500	6·19(2·98)	22·76(1·92)	64·37(0·56)	5·30(1·79)	20·12(2·21)	53·72(0·56)	71·23(0·58)
500	200	200	5·32(1·49)	16·34(1·18)	45·79(0·44)	5·10(1·36)	15·01(1·15)	38·36(0·42)	50·61(0·43)
500	500	500	5·00(0·62)	12·14(0·59)	29·77(0·27)	4·99(0·69)	11·76(0·70)	25·27(0·24)	32·80(0·25)

Appendix: Proofs

We prove the main theorems in the Appendix. Throughout the Appendix, we denote by C a constant which does not depend on p, n₁ and n₂, and may vary from place to place.

Proof of Theorem 3.1

To prove this theorem, we consider the following three events separately,

$$A_1=\left\{\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{\left({\widehat{\theta }}_{\mathit{ijt}}logp/n_t\right)}^{1/2}}\le \frac{\tau }{4}+3,\text{and}\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\theta }}_{\mathit{ijt}}-{\theta }_{\mathit{ijt}}\mid }{{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}\le \epsilon \right\}$$ (42)

$$A_2=\left\{\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{\left({\widehat{\theta }}_{\mathit{ijt}}logp/n_t\right)}^{1/2}}>\frac{\tau }{4}+3,\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\theta }}_{\mathit{ijt}}-{\theta }_{\mathit{ijt}}\mid }{{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}\le \epsilon ,\text{and}\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\le min(0.5,C_1{C}_3)\right\}$$ (43)

$$A_3={(A_1\cup A_2)}^c.$$ (44)

Here ε is the fixed constant which satisfies 0 < ε < ν₀/2 where ν₀ is introduce in (13); C₁ and C₃ are constants which do not depends on p, n₁, n₂ and shall be specified later in Lemma 6.1.

1. First we would like to show that under the event A₁,

$${\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^2\le {Cs}_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q},$$ (45)

$${\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^2\le {Cs}_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q},$$ (46)

$${\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^2\le {\mathit{Cps}}_0(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q/2}.$$ (47)

In fact,

$${EY}_i^{(t)4}\le \frac{2Eexp(\eta Y_i^{(t)2})}{{\eta }^2}\le \frac{2K}{{\eta }^2}$$

for all 1 ≤ i ≤ p, so

$$\begin{array}{l}{\theta }_{\mathit{ijt}}=\text{Var}(X_i^{(t)}-{\mu }_i)(X_j^{(t)}-{\mu }_j)\le E{(X_i^{(t)}-{\mu }_i)}^2{(X_j^{(t)}-{\mu }_j)}^2\\ \le {\left(E{(X_i^{(t)}-{\mu }_i)}^{4}E{(X_j^{(t)}-{\mu }_j)}^4\right)}^{1/2}={\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}{\left({EY}_i^{(t)4}{EY}_j^{(t)4}\right)}^{1/2}\le C{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}},\\ \hfill {\theta }_{\mathit{ijt}}=\text{Var}(Y_i{Y}_j)·{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}\stackrel{(13)}{\ge }{\nu }_0{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}.\hfill \end{array}$$ (48)

So by the definition of A₁, we have

$${\widehat{\theta }}_{\mathit{ijt}}\le {\theta }_{\mathit{ijt}}+\mid {\widehat{\theta }}_{\mathit{ijt}}-{\theta }_{\mathit{ijt}}\mid \le C{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}},\text{for}\text{all}i,j,t,$$ (49)

$${\widehat{\theta }}_{\mathit{ijt}}\ge {\theta }_{\mathit{ijt}}-\mid {\widehat{\theta }}_{\mathit{ijt}}-{\theta }_{\mathit{ijt}}\mid \ge {\nu }_0{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}-\epsilon {\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}\ge \frac{{\nu }_0}{2}{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}.$$ (50)

Hence,

$$\left|\frac{{\widehat{\sigma }}_{\mathit{iit}}}{{\sigma }_{\mathit{iit}}}-1\right|\le \frac{\mid {\widehat{\sigma }}_{\mathit{iit}}-{\sigma }_{\mathit{iit}}\mid }{{\sigma }_{\mathit{iit}}}\stackrel{(42)}{\le }\frac{\tau /4+3}{{\sigma }_{\mathit{iit}}}{\left(logp\frac{{\widehat{\theta }}_{\mathit{iit}}}{n_t}\right)}^{1/2}\stackrel{(49)}{\le }C{\left(\frac{logp}{n_t}\right)}^{1/2}$$ (51)

$$\left|\frac{{\sigma }_{\mathit{iit}}}{{\widehat{\sigma }}_{\mathit{iit}}}-1\right|\le \frac{\mid {\widehat{\sigma }}_{\mathit{iit}}-{\sigma }_{\mathit{iit}}\mid }{{\widehat{\sigma }}_{\mathit{iit}}}\stackrel{(42)}{\le }(\tau /4+3){\left(\frac{logp}{n_t}\right)}^{1/2}\frac{{\widehat{\theta }}_{\mathit{iit}}^{1/2}}{{\widehat{\sigma }}_{\mathit{iit}}}$$ (52)

Suppose x = σ_iit/σ̂_iit, y = σ_jjt/σ̂_jjt. By (51) and ${\left(\frac{logp}{n_t}\right)}^{1/2}\to 0$, we have $max\{\mid x-1\mid ,\mid y-1\mid \}\le C{\left(\frac{logp}{n_t}\right)}^{1/2}$ when n_t is large enough. Thus for large n_t, we obtain

$$\begin{array}{l}\left|{\left(\frac{{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\right)}^{1/2}-1\right|=\left|{(xy)}^{1/2}-1\right|=\frac{\mid xy-1\mid }{{(xy)}^{1/2}+1}\le \frac{\mid x-1\mid +x\mid y-1\mid }{2-max(\mid x-1\mid ,\mid y-1\mid )}\\ \le \frac{max(1,x)}{2-max(\mid x-1\mid ,\mid y-1\mid )}(\mid x-1\mid +\mid y-1\mid )\\ \le \left(\frac{1}{2}+O\left({\left(\frac{logp}{n_t}\right)}^{1/2}\right)\right)(\mid x-1\mid +\mid y-1\mid ).\end{array}$$ (53)

It then follows from the assumption $logp=o(n_t^{1/3})$ that for large n_t,

$${\widehat{\xi }}_{\mathit{ijt}}=\frac{{\widehat{\theta }}_{\mathit{ijt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\stackrel{(49)}{\le }\frac{C{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\stackrel{(51)}{\le }C$$ (54)

and

$$\begin{array}{l}\mid {\widehat{r}}_{\mathit{ijt}}-r_{\mathit{ijt}}\mid =\left|\frac{{\widehat{\sigma }}_{\mathit{ijt}}}{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}-\frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\right|\le \frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}+\frac{\mid {\sigma }_{\mathit{ijt}}\mid }{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\left|{\left(\frac{{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\right)}^{1/2}-1\right|\\ \stackrel{(42)(53)}{\le }\left(\frac{\tau }{4}+3\right){\left(\frac{logp}{n_t}\frac{{\widehat{\theta }}_{\mathit{ijt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\right)}^{1/2}+\mid r_{\mathit{ijt}}\mid \left(\frac{1}{2}+O\left({\left(\frac{logp}{n_t}\right)}^{1/2}\right)\right)\left(\left|\frac{{\sigma }_{\mathit{iit}}}{{\widehat{\sigma }}_{\mathit{iit}}}-1\right|+\left|\frac{{\sigma }_{\mathit{jjt}}}{{\widehat{\sigma }}_{\mathit{jjt}}}-1\right|\right)\\ \stackrel{(52)}{\le }\left(\frac{\tau }{4}+3\right){\left(\frac{logp}{n_t}\right)}^{1/2}\left({\left(\frac{{\widehat{\theta }}_{\mathit{ijt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\right)}^{1/2}+\mid r_{\mathit{ijt}}\mid \left(\frac{1}{2}+O\left({\left(\frac{logp}{n_t}\right)}^{1/2}\right)\right)\left(\frac{{\widehat{\theta }}_{\mathit{iit}}^{1/2}}{{\widehat{\sigma }}_{\mathit{iit}}}+\frac{{\widehat{\theta }}_{\mathit{jjt}}^{1/2}}{{\widehat{\sigma }}_{\mathit{jjt}}}\right)\right)\\ \le \left(\frac{\tau }{2}+2\right){\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{ijt}}^{1/2}+\frac{\mid r_{\mathit{ijt}}\mid }{2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\right)\\ \le \left(\frac{\tau }{2}+2\right){\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{ijt}}^{1/2}+\frac{\mid {\widehat{r}}_{\mathit{ijt}}\mid }{2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\right)+\mid {\widehat{r}}_{\mathit{ijt}}-r_{\mathit{ijt}}\mid \left(\frac{\tau }{4}+1\right){\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\\ \stackrel{(54)}{\le }\left(\frac{\tau }{2}+2\right){\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{ijt}}^{1/2}+\frac{\mid {\widehat{r}}_{\mathit{ijt}}\mid }{2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\right)+C{\left(\frac{logp}{n_t}\right)}^{1/2}\mid {\widehat{r}}_{\mathit{ijt}}-r_{\mathit{ijt}}\mid .\end{array}$$

We shall note the difference between $\frac{\mid r_{\mathit{ijt}}\mid }{2}$ and $\frac{\mid {\widehat{r}}_{\mathit{ijt}}\mid }{2}$ above. Next, we rearrange the inequality above and write it into an inequality for |r̂_ijt − r_ijt|,

$$\begin{array}{l}\mid {\widehat{r}}_{\mathit{ijt}}-r_{\mathit{ijt}}\mid \le \frac{(\frac{\tau }{2}+2){\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{ijt}}^{1/2}+\frac{\mid {\widehat{r}}_{\mathit{ijt}}\mid }{2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\right)}{1-C{\left(\frac{logp}{n_t}\right)}^{1/2}}\\ \le \tau {\left(\frac{logp}{n_t}\right)}^{1/2}\left({\widehat{\xi }}_{\mathit{ijt}}^{1/2}+\frac{\mid {\widehat{r}}_{\mathit{ijt}}\mid }{2}\left({\widehat{\xi }}_{\mathit{iit}}^{1/2}+{\widehat{\xi }}_{\mathit{jjt}}^{1/2}\right)\right)\stackrel{(10)}{=}{\lambda }_{\mathit{ijt}}.\end{array}$$ (55)

(55) implies

$$\mid ({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \le {\lambda }_{ij1}+{\lambda }_{ij2}={\lambda }_{ij}\text{holds}\text{for}\text{all}1\le i,j\le p$$ (56)

Next, by (56) and (C1) and (C3) of s_λ(z),

$$\begin{array}{l}\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \le \mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})\mid +\mid (r_{ij1}-r_{ij2})\mid \\ \le (1+c)\mid r_{ij1}-r_{ij2}\mid ,\end{array}$$ (57)

$$\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \le \mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})\mid +\mid ({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \le 2{\lambda }_{ij},$$ (58)

which implies

$$\mid s_{r_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \le {(2{\lambda }_{ij})}^{1-q}{(1+c)}^q{\mid r_{ij1}-r_{ij2}\mid }^q,$$ (59)

$${\mid s_{r_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid }^2\le {(2{\lambda }_{ij})}^{2-q}{(1+c)}^q{\mid r_{ij1}-r_{ij2}\mid }^q,$$ (60)

where 0 ≤ q < 1. Hence,

$$\begin{array}{l}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}=\underset{i}{max}\sum _{j=1}^p\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \\ \stackrel{(59)}{\le }\underset{i}{max}{2}^{1-q}{(1+c)}^q\sum _{j=1}^p{\lambda }_{ij}^{1-q}{\mid r_{ij1}-r_{ij2}\mid }^q\\ \stackrel{(10)}{\le }\underset{i}{max}{2}^{1-q}{(1+c)}^q\sum _{j=1}^p\{{\tau }^{1-q}{(logp)}^{(1-q)/2}\times {\left(\frac{{\widehat{\xi }}_{ij1}^{1/2}+\mid {\widehat{r}}_{ij1}\mid ({\widehat{\xi }}_{ii1}^{1/2}+{\widehat{\xi }}_{jj1}^{1/2})/2}{n_1^{1/2}}+\frac{{\widehat{\xi }}_{ij2}^{1/2}+\mid {\widehat{r}}_{ij2}\mid ({\widehat{\xi }}_{ii2}^{1/2}+{\widehat{\xi }}_{jj2}^{1/2})/2}{n_2^{1/2}}\right)}^{1-q}{\mid r_{ij1}-r_{ij2}\mid }^q\}\\ \stackrel{(54)}{\le }\underset{i}{max}C\sum _{j=1}^p\left\{{(logp)}^{(1-q)/2}{\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}^{(1-q)/2}{\mid r_{ij1}-r_{ij2}\mid }^q\right\}\\ \le C{s}_0(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{(1-q)/2}.\end{array}$$

which yields to (46). (45) also holds due to the fact that ||A||₂ ≤ ||A||_L1 for any symmetric matrix A. Similarly,

$$\begin{array}{l}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^2=\sum _{i=1}^p\sum _{j=1}^p{\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid }^2\\ \stackrel{(60)}{\le }{2}^{2-q}{(1+c)}^q\sum _{i=1}^p\sum _{j=1}^p{\lambda }_{ij}^{2-q}{\mid r_{ij1}-r_{ij2}\mid }^q\\ \stackrel{(10)}{\le }{2}^{2-q}{(1+c)}^q\sum _{i=1}^p\sum _{j=1}^p\{{\tau }^{2-q}{(logp)}^{(2-q)/2}\times {\left(\frac{{\widehat{\xi }}_{ij1}^{1/2}+\mid {\widehat{r}}_{ij1}\mid ({\widehat{\xi }}_{ii1}^{1/2}+{\widehat{\xi }}_{jj1}^{1/2})/2}{n_1^{1/2}}+\frac{{\widehat{\xi }}_{ij2}^{1/2}+\mid {\widehat{r}}_{ij2}\mid ({\widehat{\xi }}_{ii2}^{1/2}+{\widehat{\xi }}_{jj2}^{1/2})/2}{n_2^{1/2}}\right)}^{2-q}{\mid r_{ij1}-r_{ij2}\mid }^q\}\\ \stackrel{(54)}{\le }Cp\underset{i}{max}\sum _{j=1}^p\left\{{(logp)}^{(2-q/2)}{\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}^{(2-q)/2}{\mid r_{ij1}-r_{ij2}\mid }^q\right\}\\ \le {\mathit{Cps}}_0(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q/2}.\end{array}$$

which implies (47).

2. For A₂, we wish to prove,

$${\int }_{A_2}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^{2}dP\le C(p^{-\tau /4+1}logp)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)$$ (61)

$${\int }_{A_2}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^{2}dP\le C(p^{-\tau /4+1}logp)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)$$ (62)

$${\int }_{A_2}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^{2}dP\le C(p^{-\tau /4+1}logp)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)$$ (63)

In order to prove these probability bounds, we introduce the following lemma, which revealed the relationship between θ̂_ijt, θ_ijt and σ̂_ijt, σ_ijt.

Lemma 6.1

For any τ > 0,

$$\text{pr}\left(\underset{i,j,t}{max}\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid >(\tau /4+3){\left({\widehat{\theta }}_{\mathit{ijt}}logp/n_t\right)}^{1/2}\right)\le C{(logp)}^{-1/2}{p}^{-\tau /4-1};$$ (64)

There exist constants C₁, C₂, C₃ which do not depend on p, n₁, n₂ such that

$$\text{pr}\left(\underset{i,j}{max}\frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}>C_{1}x\right)\le C_2{p}^2(exp(-n_t{x}^2)),\mathit{for}\mathit{all}0<x\le C_3,t=1,2;$$ (65)

For any ε > 0 and M > 0,

$$\text{pr}\left(\underset{i,j,t}{max}\mid {\widehat{\theta }}_{\mathit{ijt}}-{\theta }_{\mathit{ijt}}\mid /({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})>\epsilon \right)\le C{p}^{-M}(1/n_1+1/n_2)$$ (66)

The proof of Lemma 6.1 is given later. Note that (64) immediately leads to

$$\text{pr}(A_2)\le C{(logp)}^{-1/2}{p}^{-\tau /4-1}.$$ (67)

By the definition of A₂ (43), we still have (49). Besides, by the definition of A₂, $\frac{\mid {\widehat{\sigma }}_{\mathit{iit}}-{\sigma }_{\mathit{iit}}\mid }{{\sigma }_{\mathit{iit}}}\le 0.5$, which leads to σ̂_iit ≥ 0.5σ_iit. Thus,

$${\widehat{\xi }}_{\mathit{ijt}}=\frac{{\widehat{\theta }}_{\mathit{ijt}}}{{\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}}}\le \frac{C{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}{(0.5{\sigma }_{\mathit{iit}})(0.5{\sigma }_{\mathit{jjt}})}=4C.$$ (68)

For convenience, we denote the random variable

$$T=\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}.$$ (69)

Under A₂, we have T ≤ 0.5. Then for all 1 ≤ i, j ≤ p, t = 1, 2,

$$\begin{array}{l}{\widehat{r}}_{\mathit{ijt}}-r_{\mathit{ijt}}=\frac{{\widehat{\sigma }}_{\mathit{ijt}}}{{({\widehat{\sigma }}_{\mathit{iit}}{\widehat{\sigma }}_{\mathit{jjt}})}^{1/2}}-\frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\\ =\frac{\frac{{\widehat{\sigma }}_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}}{{({\widehat{\sigma }}_{\mathit{iit}}/{\sigma }_{\mathit{iit}})}^{1/2}\times {({\widehat{\sigma }}_{\mathit{jjt}}/{\sigma }_{\mathit{jjt}})}^{1/2}}-\frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\\ \le \frac{\frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}+T}{{({\sigma }_{\mathit{iit}}/{\sigma }_{\mathit{iit}}-T)}^{1/2}\times {({\sigma }_{\mathit{jjt}}/{\sigma }_{\mathit{jjt}}-T)}^{1/2}}-\frac{{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}\\ =\frac{r_{\mathit{ijt}}+T}{1-T}-r_{\mathit{ijt}}\\ \le (1+2T)(r_{\mathit{ijt}}+T)-r_{\mathit{ijt}}\\ \le 4T.\end{array}$$

Similarly calculation also leads to r̂_ijt − r_ijt ≥ −4T. Then, by (C3) of s_λij (z),

$$\begin{array}{l}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^2=\underset{i}{max}{\left(\sum _{j=1}^p\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \right)}^2\\ \le \underset{i}{max}{\left(\sum _{j=1}^p(\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})\mid +\mid ({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid )\right)}^2\\ \le \underset{i}{max}{\left(\sum _{j=1}^p({\lambda }_{ij}+8T)\right)}^2\stackrel{(10)(68)}{\le }C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}+T^2\right).\end{array}$$ (70)

In addition, due to ||·||_ℓ1 ≥ ||·||, we also have ${\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^2\le C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}+T^2\right)$. Similarly,

$$\begin{array}{l}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^2=\sum _{i=1}^p\sum _{j=1}^p{\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid }^2\\ \le 2\sum _{i=1}^p\sum _{j=1}^p(\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-{({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})}^2\mid +{\mid ({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid }^2)\\ \le C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}+T^2\right)\end{array}$$ (71)

Therefore,

$$\begin{array}{l}{\int }_{A_2}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^{2}dP\stackrel{(70)}{\le }{\int }_{A_2}C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}+T^2\right)dP\\ \le C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)\text{pr}(A_2)+C{p}^2{\int }_0^{min(0.5,C_1{C}_3)}2x\text{pr}(\{T\ge x\}\cap A_2)dx\\ \le C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)\text{pr}(A_2)+C{p}^2{\int }_0^{C_1{(\mathit{M}logp(1/n_1+1/n_2))}^{1/2}}2x\text{pr}(A_2)dx+{\int }_{C_1{(\mathit{M}logp(1/n_1+1/n_2))}^{1/2}}^{min(0.5,C_1{C}_3)}2x\text{pr}(T\ge x)dx\\ \stackrel{(65)}{\le }C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)\text{pr}(A_2)+C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)\text{pr}(A_2)+{\int }_{C_1{(\mathit{M}logp(1/n_1+1/n_2))}^{1/2}}^{+\infty }2{xC}_2(exp(-n_1{(x/C_1)}^2)+exp(-n_2{(x/C_1)}^2))dx\\ \le C{p}^2\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)\text{pr}(A_2)\\ +C\left(\frac{1}{n_1}exp(-n_1{(x/C_1)}^2)+\frac{1}{n_2}exp(-n_2{(x/C_1)}^2)\right){|}_{+\infty }^{C_1{(\mathit{M}logp(1/n_1+1/n_2))}^{1/2}}\\ \stackrel{(67)}{\le }C{p}^{-\tau /4+1}\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)+C{p}^{-M}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\end{array}$$ (72)

Similarly, we have

$$\begin{array}{l}{\int }_{A_2}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^{2}dP\le C{p}^{-\tau /4+1}\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)+C{p}^{-M}\left(\frac{1}{n_1}+\frac{1}{n_2}\right),\\ {\int }_{A_2}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^{2}dP\le C{p}^{-\tau /4+1}\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)+C{p}^{-M}\left(\frac{1}{n_1}+\frac{1}{n_2}\right),\end{array}$$

which finishes the proof of (61), (62) and (63) when we choose M > τ /4 − 1.

3. For A₃, (66) and log p = o(n^1/3) leads to

$$\begin{array}{l}\text{pr}(A_3)\le \text{pr}\left(\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\theta }}_{\mathit{ijt}}-{\theta }_{\mathit{ijt}}\mid }{{\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}}}>\epsilon \right)+\text{pr}\left(\underset{\mathit{ijt}}{max}\frac{\mid {\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}\mid }{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}>min(0.5,C_1{C}_3)\right)\\ \le C{p}^{-M}(1/n_1+1/n_2)+C_2{p}^2\left(exp(-n_{1}min{(\frac{1}{2C_1},C_3)}^2)+exp(-n_{2}min{(\frac{1}{2C_1},C_3)}^2)\right)\\ =C{p}^{-M}(1/n_1+1/n_2)\end{array}$$ (73)

Besides, since r_ijt, r̂_ijt are the population and sample correlations, |r_ijt| ≤ 1, |r̂_ijt| ≤ 1. By (C1) of thresholding s_λ(z), we have |s_λ(x) − x| ≤ c|x| for all x ∈ ℝ. Thus,

$$\begin{array}{l}\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \le \mid r_{ij1}\mid +\mid r_{ij2}\mid +\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})\mid \\ \le 2+c\mid {\widehat{r}}_{ij1}-{\widehat{r}}_{ij2}\mid \le 2+2c\end{array}$$

which yields

$${\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^2=\underset{i}{max}{\left(\sum _{j=1}^p\mid s_{{\lambda }_{ij}}({\widehat{r}}_{ij1}-{\widehat{r}}_{ij2})-(r_{ij1}-r_{ij2})\mid \right)}^2\le {(2+2c)}^2{p}^2$$ (74)

Similarly, ||D̂^* − (R₁ − R₂)||² ≤ (2 + 2c)²p², ${\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^2\le {(2+2c)}^2{p}^2$. Therefore,

$${\int }_{A_3}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^{2}dP\stackrel{(73)}{\le }C{p}^{-M+2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)$$ (75)

$${\int }_{A_3}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_{{\ell }_1}^{2}dP\stackrel{(73)}{\le }C{p}^{-M+2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)$$ (76)

$${\int }_{A_3}{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }_F^{2}dP\stackrel{(73)}{\le }C{p}^{-M+2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)$$ (77)

Finally, we combine the situations of A₁, A₂ and A₃. When τ > 4 and M > 2, we have

$$\begin{array}{c}E{\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^2=\left({\int }_{A_1}+{\int }_{A_2}+{\int }_{A_3}\right){\Vert {\widehat{\mathbf{D}}}^{\ast }-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^{2}dP\\ \stackrel{(45)(61)(75)}{\le }C(s_0^2(p)+1){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}\end{array}$$ (78)

which has proved (14). (15) and (16) can be proved similarly by (46), (62), (76) and (47), (63), (77).

Proof of Lemma 6.1

(64) is directly from (25) in Cai and Liu (2011). For (66), the proof is essentially the same as the proof of (26) in Cai and Liu (2011) as long as we use x = ((M + 2) log p + log n)^1/2 in stead of x = ((M + 2) log p)^1/2 in their proof. Now we mainly focus on the proof of (65). Without loss of generality, we can translate X and assume that μ₁ = μ₂ = 0. Note that we have the following formulation,

$$\frac{{\widehat{\sigma }}_{\mathit{ijt}}-{\sigma }_{\mathit{ijt}}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}=\frac{1}{n_t}\sum _{k=1}^{n_t}\frac{(X_{ik}^{(t)}{X}_{jk}^{(t)}-{\sigma }_{\mathit{ijt}})}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}-\frac{{\overline{X}}_i^{(t)}{\overline{X}}_j^{(t)}}{{({\sigma }_{\mathit{iit}}{\sigma }_{\mathit{jjt}})}^{1/2}}=\left(\frac{1}{n_t}\sum _{k=1}^{n_t}(Y_{ik}^{(t)}{Y}_{jk}^{(t)}-r_{\mathit{ijt}})-{\overline{Y}}_i^{(t)}{\overline{Y}}_j^{(t)}\right)$$ (79)

Since

$$\begin{array}{l}E{(Y_i^{(t)}{Y}_j^{(t)}-r_{\mathit{ijt}})}^2{e}^{\frac{\eta }{2}\mid Y_i^{(t)}{Y}_j^{(t)}-r_{\mathit{ijt}}\mid }\le \frac{4}{{\eta }^2}E{e}^{\eta \mid Y_i^{(t)}{Y}_j^{(t)}-r_{\mathit{ijt}}\mid }\le \frac{4}{{\eta }^2}E{e}^{\eta (Y_i^{(t)}{Y}_j^{(t)}-r_{\mathit{ijt}})}+\frac{4}{{\eta }^2}E{e}^{-\eta (Y_i^{(t)}{Y}_j^{(t)}-r_{\mathit{ijt}})}\\ \le \frac{8}{{\eta }^2}\left(E{e}^{\mid \eta \mid Y_i^{(t)2}}+E{e}^{\mid \eta \mid Y_j^{(t)2}}\right)e^{\mid \eta r_{\mathit{ijt}}\mid }\le C_4\end{array}$$

where C₄ is a constant which does not depend on n₁, n₂, p. Thus, we set ${\overline{B}}_n^2=n_t{C}_1$; based on lemma 1 in Cai and Liu (2011), we have

$$\text{pr}\left(\left|\frac{1}{n_t}\sum _{k=1}^{n_t}(Y_{ik}^{(t)}{Y}_{jk}^{(t)}-r_{\mathit{ijt}})\right|\ge C_{\eta /2}{C}_4^{1/2}x\right)\le exp(-n_t{x}^2).$$ (80)

for all $0<x\le C_1^{1/2}$, where C_η/2 = η/2 + 2/η. Next for ${\overline{Y}}_i^{(t)}$, we similarly apply Lemma 1 in Cai and Liu (2011) and get

$$\text{pr}\left(\mid {\overline{Y}}_i^{(t)}\mid \ge C_{5}x\right)\le exp(-n_t{x}^2)$$ (81)

for all $0<x\le C_5^{1/2}$. Combining (80) and (81),

$$\text{pr}\left(\underset{ij}{max}\left|\frac{1}{n_t}\sum _{k=1}^{n_t}(Y_{ik}^{(t)}{Y}_{jk}^{(t)}-r_{\mathit{ijt}})\right|\le C_{\eta /2}{C}_4^{1/2}x\text{and}\underset{i,t}{max}\mid {\overline{Y}}_i^{(t)}\mid \le C_{5}x\right)\le 1-2p^{2}exp(-n_t{x}^2)$$ (82)

for all $0<x\le min\left(C_1^{1/2},C_5^{1/2}\right)$. Finally, (79) and (82) yield (65).

Proof of Theorem 3.2

Without loss of generality, we assume n₁ ≤ n₂. For (R₁, R₂) ∈ 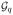(s₀(p)), set Σ₂ = R₂ = I_p×p and we have already known this information. The estimation of sparse difference immediately becomes the estimation of the sparse correlation matrix R₁. Then the lower bound result for estimating single sparse covariance matrix can be used to prove this theorem.

We follow the idea of Cai and Zhou (2012) and define the set of diagonal-1 covariance matrices as

$${\mathcal{F}}_q(s_0(p))=\left\{\mathbf{\sum }:\mathbf{\sum }\succcurlyeq 0,\text{diag}(\mathbf{\sum })=1,\underset{i}{max}\sum _{j=1}^p{\mid {\sigma }_{ij}\mid }^q\le s_0(p)\right\}.$$

We have {(R₁, I) : R₁ ∈ 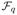(s₀(p))} ⊆ 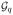(s₀(p)). Besides, the proof of Theorem 2 in Cai and Zhou (2012) shows that

$$\underset{\widehat{\mathbf{\sum }}}{inf}\underset{\mathbf{\sum }\in {\mathcal{F}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{\sum }}-\mathbf{\sum }\Vert }^2\ge C{s}_0(p){\left(\frac{logp}{n}\right)}^{1-q}$$ (83)

Since the correlation matrix equals to covariance matrix (i.e. R = Σ) when diag(Σ) = 1, then

$$\begin{array}{l}\underset{\widehat{\mathbf{D}}}{inf}\underset{({\mathbf{R}}_1,{\mathbf{R}}_2)\in {\mathcal{G}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{D}}-({\mathbf{R}}_1-{\mathbf{R}}_2)\Vert }^2\ge \underset{\widehat{\mathbf{D}}}{inf}\underset{({\mathbf{R}}_1,\mathbf{I}):{\mathbf{R}}_1\in {\mathcal{F}}_q(s_0(p))}{sup}E{\Vert \widehat{\mathbf{D}}-({\mathbf{R}}_1-\mathbf{I})\Vert }^2\\ \ge \underset{{\widehat{\mathbf{R}}}_1}{inf}\underset{{\mathbf{R}}_1\in {\mathcal{F}}_q(s_0(p))}{sup}E{\Vert {\widehat{\mathbf{R}}}_1-{\mathbf{R}}_1\Vert }^2\\ \ge \underset{\widehat{\mathbf{\sum }}}{inf}\underset{{\mathbf{\sum }}_1\in {\mathcal{F}}_q(s_0(p)),\text{diag}({\mathbf{\sum }}_1)=1}{sup}E\Vert {\widehat{\mathbf{\sum }}}_1-{\mathbf{\sum }}_1\Vert \\ \ge {Cs}_0^2(p){\left(\frac{logp}{n_1}\right)}^{1-q}\ge \frac{C}{2}{s}_0^2(p){\left(\frac{logp}{n_1}+\frac{logp}{n_2}\right)}^{1-q}\end{array}$$ (84)

which implies (17). By ||·||_ℓ1 ≥ ||·|| for symmetric matrices, (18) also follow immediately.

Similarly, (19) follows from Theorem 4 of Cai and Zhou (2012).

Proof of Proposition 6.1

The proof of Proposition 6.1 is similar to Theorem 3.1. For the upper bound, again, we split the whole events into three,

$$A_1=\{\underset{ij}{max}\frac{\mid {\widehat{\sigma }}_{ij}-{\sigma }_{ij}\mid }{{\left(logp{\widehat{\theta }}_{ij}/n\right)}^{1/2}}\le \tau /4+3,\text{and}\underset{ij}{max}\frac{\mid {\widehat{\theta }}_{ij}-{\theta }_{ij}\mid }{{\sigma }_{ii}{\sigma }_{jj}}\le \epsilon \},$$ (85)

$$A_2=\left\{\underset{ij}{max}\frac{\mid {\widehat{\sigma }}_{ij}-{\sigma }_{ij}\mid }{{\left(logp{\widehat{\theta }}_{ij}/n\right)}^{1/2}}>\tau /4+3,\underset{ij}{max}\frac{\mid {\widehat{\theta }}_{ij}-{\theta }_{ij}\mid }{{\sigma }_{ii}{\sigma }_{jj}}\le \epsilon \text{and}\underset{ij}{max}\frac{\mid {\widehat{\sigma }}_{ij}-{\sigma }_{ij}\mid }{{({\sigma }_{ii}{\sigma }_{jj})}^{1/2}}\le min(0.5,C_1{C}_3)\right\}$$ (86)

$$A_3={(A_1\cup A_2)}^c.$$ (87)

Here ε is the fixed constant which satisfies 0 < ε < ν₀/2 where ν₀ was introduced in (13); C₁, C₃ are constants specified in Lemma 6.1. Similarly to the proof of Theorem 3.1, we can prove the following statements.

1. Under A₁,

   $$\begin{array}{l}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }^2\le {Cs}_0^2(p){\left(\frac{logp}{n}\right)}^{1-q},\\ {\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_{{\ell }_1}^2\le {Cs}_0^2(p){\left(\frac{logp}{n}\right)}^{1-q},\\ {\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_F^2\le C{s}_0(p){\left(\frac{logp}{n}\right)}^{1-q/2}.\end{array}$$
2. For A₂,

   $$\begin{array}{l}{\int }_{A_2}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }^{2}dP\le C(p^{-\tau /4+1}logp)\frac{1}{n}\\ {\int }_{A_2}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_{{\ell }_1}^{2}dP\le C(p^{-\tau /4+1}logp)\frac{1}{n}\\ {\int }_{A_2}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_F^{2}dP\le C(p^{-\tau /4+1}logp)\frac{1}{n}\end{array}$$
3. For A₃,

   $$\begin{array}{l}{\int }_{A_3}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }^{2}dP\le C\frac{p^{-M+2}}{n}\\ {\int }_{A_3}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_{{\ell }_1}^{2}dP\le C\frac{p^{-M+2}}{n}\\ {\int }_{A_3}{\Vert {\widehat{\mathbf{R}}}^{\ast }-\mathbf{R}\Vert }_F^{2}dP\le C\frac{p^{-M+2}}{n}\end{array}$$

The rest of proof, including the lower bound results, are omitted here as they are essentially the same as Theorem 3.1.