An integrated experimental and quantum-chemical investigation on the vibrational spectra of chlorofluoromethane

Abstract

The vibrational analysis of the gas-phase infrared spectra of chlorofluoromethane (CH₂ClF, HCFC-31) was carried out in the range 200 – 6200 cm⁻¹. The assignment of the absorption features in terms of fundamental, overtone, combination and hot bands was performed on the medium-resolution (up to 0.2 cm⁻¹) Fourier transform infrared (FTIR) spectra. From the absorption cross section spectra accurate values of the integrated band intensities were derived and the Global Warming Potential (GWP) of this compound was estimated, thus obtaining values of 323, 83 and 42 on a 20-, 100- and 500- year horizon, respectively. The set of spectroscopic parameters here presented provides the basic data to model the atmospheric behavior of this greenhouse gas. In addition, the obtained vibrational properties were used to benchmark the predictions of state-of-the-art quantum-chemical computational strategies. Extrapolated complete basis set (CBS) limit values for the equilibrium geometry and harmonic force field were obtained at the coupled-cluster singles and doubles level of theory augmented by a perturbative treatment of triple excitations, CCSD(T), in conjunction with a hierarchical series of correlation-consistent basis sets (cc-pVnZ, with n = T, Q and 5), taking also into account the core-valence (CV) correlation effects and the corrections due to diffuse (aug) functions. To obtain the cubic and quartic semi-diagonal force constants, calculations employing second-order Møller-Plesset perturbation (MP2) theory, the double-hybrid DFT functional (B2PLYP) as well as CCSD(T) were performed. For all anharmonic force fields the performances of two different perturbative approaches in computing the vibrational energy levels (i.e., the generalized second order vibrational treatment, GVPT2, and the recently proposed hybrid degeneracy corrected model, HDCPT2) were evaluated and the obtained results allowed us to validate the spectroscopic predictions yielded by the HDCPT2 approach. The predictions of the deperturbed second-order perturbation approach, DVPT2, applied to the computation of infrared intensities beyond the double-harmonic approximation were compared to the accurate experimental values here determined. Anharmonic DFT and MP2 corrections to CCSD(T) intensities led to a very good agreement with the absorption cross section measurements over the whole spectral range here analysed.

I. INTRODUCTION

The growing concerns on the adverse environmental effects of halogenated hydrocarbons have motivated the numerous experimental and computational investigations carried out in the last decades aiming at their characterization. Once these compounds have been released into the atmosphere, their reactions toward OH and O radicals determine the atmospheric lifetime; in the stratosphere their photolysis by means of sunlight provides the free halogen atoms which are the main species responsible for the destruction of the Earth’s protective ozone layer. Besides, these molecules are usually characterized by strong infrared absorptions falling in the atmospheric window (spectral region between ca. 8 and 12 μm wavelength), thus strongly contributing to the greenhouse effect. It is nowadays widely accepted by the majority of the scientific community¹ that among the factors driving the global climate change, the release in the atmosphere of greenhouse gases and ozone depleting compounds plays a very important role. The Montreal and Kyoto protocols list them (grouped separately as halons, hydrofluorocarbons (HFCs), hydrochlorofluorocarbons (HCFCs), chlorofluorocarbons (CFCs), and perfluorocarbons) and strictly rule their uses and scheduled phase out. On these bases, the thermochemistry and the kinetic behaviour of the atmospheric reaction of these compounds have been the subject of many computational works² which have been carried out to obtain useful parameters for the chemistry-climate models³ and also to support the analysis of the discrepancies which may be found between the data available in different databases (for example the CODATA⁴ and ATcT⁵). Accurate spectroscopic investigations are needed in order to provide the necessary experimental parameters required by the atmospheric applications (such as probing and quantitatively monitoring the temporal trends) focused on these molecules; in the last decade many studies on haloalkanes and haloalkenes, carried out in both the microwave⁶ and the infrared⁷ region, have led to the determinations of a large number of accurate constants useful to model their environmental impacts. Concerning the infrared region, measurements carried out at medium resolution on the gas-phase spectra of these compounds, besides leading to the analysis of the absorption features and the corresponding assignments, are also performed to obtain the accurate determination of the absorption cross section spectra. These experimental intensities are mandatory data for a reliable assessment⁸ of the radiative forcing and global warming potential (GWP) of these compounds; it is estimated⁹ that the radiative forcing related to anthropogenic sources equals to +1.6 W m⁻² .

Chlorofluoromethane (CH₂ClF, HCFC-31) belongs to the HCFC’s group of compounds, which have been proposed as replacement gases for CFC’s since, due to the attack by hydroxyl radicals,^10,11 they generally have a shorter atmospheric lifetime (for CH₂ClF, it is equal to 1.3 years¹²). Its first low resolution infrared spectra have been recorded in the 1950s by Plyler et al.^13,14 and then by Porto;¹⁵ later, the assignment of the fundamentals has been validated by means of normal coordinate computations.^16,17 Concerning the microwave region, the first investigation dates back to the work of Muller,¹⁸ followed several years later by the analysis of Nandi and Chatterji.¹⁹ More recently, due to its potential role as greenhouse gas and ozone depleting compound (its Ozone Depletion Potential, ODP, is reported²⁰ to be 0.02), chlorofluoromethane has been the subject of many experimental works. Rotational constants for the ground and V₆ = 1 states have been determined²¹ for different chlorine isotopologues; later, the rotational spectra of the V₅ = 1 and V₆ = 2 vibrational states have been recorded and analysed.²² About the infrared region, several high resolution analyses have been performed^{23 – 27} in the region of the atmospheric window and accurate spectroscopic parameters have been obtained. In addition, its anharmonic force field has been investigated²⁸ at the Hartree-Fock (HF) self consistent field²⁹ (HF-SCF) and second-order Møller-Plesset³⁰ (MP2) theory levels by employing medium-sized basis sets (DZP and TZ2P).

Anyway, a detailed investigation of the infrared spectra and of the corresponding absorption cross sections of CH₂ClF up to the overtone region is still lacking; in the present paper we therefore present the results obtained by combining experimental investigation on the vibrational spectra up to 6200 cm⁻¹ with the information obtained from state-of-the-art quantum-chemical approaches. The gas-phase infrared spectra were thoroughly explored and analysed, and assignment in terms of fundamental, overtone and combination bands was carried out. After having obtained the absorption cross section spectrum, by means of a multi-spectrum least-squares analysis, accurate values of integrated band intensities were determined for all the most relevant absorptions falling in the range 500 – 6200 cm⁻¹, thus allowing us to derive the GWP values of CH₂ClF over different timescales (to our knowledge, these are the first published ones for this greenhouse gas).

The reliable and complete experimental characterization of the vibrational properties was combined with theoretical investigations based on vibrational second-order perturbation theory³¹ (VPT2) for the calculation of spectra beyond the double-harmonic approximation. Such an approach is plagued by the well-known problem of resonances (e.g. the so-called Fermi resonances). Such singularities are usually identified and removed from the perturbative treatment using ad hoc thresholds (DVPT2 model). Next a variational treatment (GVPT2 model) is employed to recover the discarded terms. On the other hand, the recently proposed hybrid degeneracy-corrected second-order perturbation theory³² (HDCPT2 approach), being free of the direct evaluation of the resonant terms,^33,34 provides a reliable – although approximated– black-box alternative for the determination of spectroscopic and thermochemical properties. The two approaches, namely GVPT2 and HDCPT2, have been compared in order to evaluate the reliability of the HDCPT2 method for the molecule under study. In addition, the infrared intensities beyond the double-harmonic approximation were computed within the VPT2 framework, evaluating transition electric dipole moments with proper account of both mechanical and electric anharmonic effects.^35,36 The necessary derivatives of the potential energy surface (PES) and of the dipole moments have been computed using different computational methods, ranging from the coupled-cluster (CCSD(T))³⁷ to MP2 and DFT models. Finally, structural and spectroscopic parameters were determined by means of composite approaches,^{38 – 40} and hybrid schemes (vide infra). The accurate absorption cross sections here reported allow us to investigate the reliability of the predictions about the dipole moment surface obtained by following the VPT2 formulation of transition properties and the corresponding implementation recently published.⁴¹ The performances of the different levels of theory with respect to the experimental data are reported and discussed, taking into account also the corresponding computational cost with respect to the observed accuracy.

II. EXPERIMENTAL SECTION

Concerning the vibrational analysis, the gas-phase absorption spectra of CH₂ClF were recorded at room temperature in the 200 – 6200 cm⁻¹ region by means of two different Fourier transform infrared (FTIR) spectrometers. In the lower wavenumber region (200 – 400 cm⁻¹) the spectra were acquired at a resolution of 1.0 cm⁻¹ using the Nicolet Magna 750 FTIR (Thermo Scientific, USA), coupled to a cell having an optical path-length of 150.0 (± 0.5) mm and equipped with KRS-5 windows. In the 400 – 6200 cm⁻¹ spectral range the Bruker Vertex 70 FTIR instrument (Bruker Optics, Karlsruhe, Germany), coupled to 134.0 (± 0.5) mm optical path-length, double walled, stainless steel cell fitted with KBr windows, was employed at a resolution of 0.2, 0.5 and 1.0 cm⁻¹. The signal-to-noise ratio (SNR) was maximized in the two different spectral ranges by acquiring up to 600 scans in the former and up to 128 scans in the latter region. For the spectra to be used in the vibrational analysis step, the pressure of the sample (CH₂ClF) was varied in the 0.1 – 60 kPa range.

To obtain the absorption cross section data, the measurements were carried out in the spectral range 500 – 6200 cm⁻¹; the temperature inside the stainless steel cell was kept constant at 298.0 K (±0.5 K) and the spectra were acquired at a resolution of 0.2 cm⁻¹ employing boxcar apodisation function. To improve the SNR, up to 256 interferograms were added and the instrumental sensitivity over the whole spectral range was optimized by employing two different detectors according to the region: deuterated L-alanine doped triglycene sulphate, DTLaTGS, (400 – 4000 cm⁻¹) and InGaAs (4000 – 6200 cm⁻¹). The pressure of CH₂ClF was varied in the 0.1 – 70 kPa range; to minimize the effects of finite resolution⁴² and the corresponding instrumental distortion, following the experimental procedure already established in previous studies,⁴³ the sample was mixed with N₂ (purchased by SIAD, Italy, with a purity > 99%) to a total pressure of 101 kPa (we estimate the N₂-pressure broadening parameter for CH₂ClF to be in the range 0.1 – 0.3 cm⁻¹ atm⁻¹). Accurate determination of the pressure was performed by means of different capacitance vacuum gauges; namely, the Alcatel ARD 1001, 1002, and 1003 models with a full scale range of 1013, 101, and 10 mbars, respectively (each with a quoted manufacturer’s full scale accuracy of 0.15%). To achieve the complete equilibrium inside the cell, a 15 min delay was adopted between the filling and the recording of the corresponding spectrum. Before and after each spectrum acquisition, the cell was evacuated to about 10⁻⁴ Pa by means of a diffusion pump backed by a double stage rotary pump, and the corresponding background spectra were acquired.

The CH₂ClF sample was purchased by PCR, Inc, with a stated purity of 98%, and used without any further purification.

III. COMPUTATIONAL METHODOLOGIES AND DETAILS

A. Coupled-cluster calculations of equilibrium geometries and harmonic force field

The equilibrium structure of CH₂ClF was determined by performing quantum-chemical calculations at the CCSD(T) level of theory. The effects due to basis-set incompleteness and core-valence electronic correlation were taken into account by means of a composite scheme, which is based on the additivity approximation and the inclusion of the various contributions computed separately at the highest possible level. Geometry optimizations were performed within the frozen-core (fc) approximation by employing correlation-consistent basis sets:⁴⁴ more precisely, the cc-pVnZ (n = T, Q and 5) and aug-cc-pVQZ sets. Core-correlation effects (CV) were accounted for by means of calculations carried out using the correlation-consistent cc-pCVTZ basis set.⁴⁴ To derive the complete basis set limit (CBS) for each structural parameter r, the geometrical convergence was assumed to follow the same behavior as the correlation energy contribution. As proposed by Helgaker et al.,⁴⁵ the following n⁻³ formula was applied with n = Q and 5:

$$\Delta r^{\mathit{corr}}\left(n\right)=\Delta r^{\mathit{corr}}\left(\mathrm{CBS}\right)+\mathrm{A}{n}^{-3}.$$ (1)

The extrapolated correlation contributions, Δr^corr (CBS), were then added to the corresponding HF-SCF geometrical parameters extrapolated to the CBS limit:

$$r\left(\mathrm{CBS}\right)=r^{\mathit{SCF}}\left(\mathrm{CBS}\right)+\Delta r^{\mathit{corr}}\left(\mathrm{CBS}\right).$$ (2)

The HF-SCF CBS limit, r^SCF (CBS), was obtained by means of an exponential extrapolation formula,⁴⁶

$$r^{\mathit{SCF}}\left(n\right)=r^{\mathit{SCF}}\left(\mathrm{CBS}\right)+{\mathit{Be}}^{-\mathit{Cn}}$$ (3)

with n = Q, 5 and 6. To evaluate CV effects on molecular structure, Δr(CV), the following difference was evaluated:

$$\Delta r\left(C\mathrm{V}\right)=r(\mathrm{cc}-\mathrm{pCVTZ},\text{all})-r(\mathrm{cc}-\mathrm{pCVTZ},\mathrm{fc})$$ (4)

where r(cc-pCVTZ,all) and r(cc-pCVTZ,fc) denote the geometry optimized at the CCSD(T)/cc-pCVTZ level correlating all and only valence electrons, respectively. The effect due to the diffuse functions, Δr(aug), was determined in an analogous manner by the following expression:

$$\Delta r\left(\mathrm{aug}\right)=r(\mathrm{aug}-\mathrm{cc}-\mathrm{pVQZ},\mathrm{fc})-r(\mathrm{cc}-\mathrm{pVQZ},\mathrm{fc})$$ (5)

where r(aug-cc-pVQZ,fc) and r(cc-pVQZ,fc) correspond to the optimized geometries obtained at the CCSD(T)/aug-cc-pVQZ and CCSD(T)/cc-pVQZ level of theory, respectively. All these terms were then added to determine the best-estimated equilibrium structure, r(best):

$$r\left(\text{best}\right)=r\left(\mathrm{CBS}\right)+\Delta r\left(\mathrm{CV}\right)+\Delta r\left(\mathrm{aug}\right).$$ (6)

The reliability of this empirical procedure based on the additivity assumption at a geometrical level is already well established (see for example, Refs. 47, 48) and its validation was performed by comparing the corresponding results to those obtained by means of a theoretically well justified approach.^39,40 The last comment concerns on the inclusion of the effect of diffuse functions in the basis set. While there is no theoretical justification for the inclusion of such an effect once the extrapolation to the CBS limit is performed, the latter correction is introduced to ensure on an empirical basis the correct description of electronegative atoms. In passing, we note that the equilibrium rotational constants are straightforwardly derived from the corresponding equilibrium structures.⁴⁹

Analogously, harmonic force fields were computed at the CCSD(T) level of theory with the same basis sets used for geometry optimizations. By means of the composite scheme described above best-estimated harmonic frequencies, ω(best), and quartic centrifugal-distortion terms, D(best), were evaluated. Within the harmonic approximation, best-estimated values for the infrared intensities, I(best), of each normal mode were evaluated by adding to the result at the CCSD(T)/cc-pV5Z level, I(V5Z), the core-correlation correction, ΔI(CV), and that due to the effect of the diffuse functions, ΔI(aug), according to:⁴⁸

$$I\left(\text{best}\right)=I\left(\mathrm{V}5\mathrm{Z}\right)+\Delta I\left(\mathrm{CV}\right)+\Delta I\left(\mathrm{aug}\right)$$ (7)

where the ΔI(CV) = I(cc-pCVTZ,all) – I(cc-pCVTZ,fc) and ΔI(aug) = I(aug-cc-pVQZ,fc) – I(cc-pVQZ,fc) corrections are defined in a similar way as for geometrical parameters.

B. Anharmonic Force Field and Vibrational Spectra

Anharmonic computations of the vibrational spectra beyond the double-harmonic approximation were carried out within the framework of vibrational second-order perturbation theory,³¹ VPT2, using both the standard GVPT2 and recently proposed HDCPT2 models, thus allowing us to compare the corresponding performances. GVPT2 is a common approach to avoid the singularities that arise in the expressions of the anharmonicity constants x_ij when a resonance occurs, which consists of two subsequent steps. The first one is the deperturbed model, DVPT2, which removes from the VPT2 equations the divergent terms that otherwise would bias the final values, thus leading to the corresponding deperturbed anharmonicity constants. Then, in the second step, the resonances are treated variationally by properly setting up an effective vibrational Hamiltonian matrix, in which the diagonal entries are given by the band positions computed with the deperturbed anharmonicity constants and the off-diagonal ones are the interaction terms that account for the considered resonance. The subsequent diagonalization of this matrix provides both the predicted wavenumbers and the corresponding eigenvectors. Within GVPT2, the resonant terms have been identified based on the difference in frequency and the magnitude of the possibly resonant terms, using the Martin’s test.⁵⁰ For details concerning the HDCPT2 model, the interested reader is referred to Ref. 32, here we only mention that HDCPT2 combines an alternative approach, called degeneracy-corrected PT2 (DCPT2), where all potentially resonant terms are rewritten in a non-resonant way,⁵¹ with standard VPT2, in a way to avoid problems related to degeneracies and near-degeneracies as well as to the validity of assumptions used to derive DCPT2 terms, thus leading to a general and black-box procedure to compute anharmonic frequencies.

In all cases, the anharmonic cubic and semi-diagonal quartic force constants were determined by means of numerical differentiation of the analytical second derivatives of the energy. These terms were evaluated employing different levels of theory (B2PLYP,⁵² MP2 and CCSD(T)) in conjunction with appropriately chosen correlation-consistent basis sets. At the CCSD(T) level, the results of the calculations carried out using the cc-pVQZ basis set were combined with those computed using the cc-pCVTZ and aug-cc-pVTZ basis sets to derive the best-estimated values for the sextic centrifugal-distortion constants according the following expression:

$$H\left(\text{best}\right)=H(\mathrm{cc}-\mathrm{pVQZ})+\Delta H\left(\mathrm{aug}\right)+\Delta H\left(\mathrm{CV}\right)$$ (8)

where H(best) refers to the best estimate obtained for a generic constant, H(cc-pVQZ) is the corresponding value computed at the CCSD(T)/cc-pVQZ level, ΔH(aug) = H(aug-cc-pVTZ, fc) – H(cc-pVTZ,fc) and ΔH(CV) = H(cc-pCVTZ,all) – H(cc-pCVTZ,fc) are the corrections due to the effects of diffuse functions in the basis set and to core correlation, respectively. Sextic centrifugal-distortion constants were evaluated in the Watson A reduction (I^r representation),⁵³ as recently implemented⁵⁴ in CFOUR.⁵⁵ The best-estimated values of the equilibrium rotational constants together with the vibration-rotation interaction constants computed at the CCSD(T)/cc-pCVTZ level were employed to determine the best-estimated ground-state rotational constants:

$$B_0^i=B_e^i-\sum _{r=1}^{3N-6}{\alpha }_r^i$$ (9)

where $B_0^i$ and $B_e^i$ denote to the ground and equilibrium rotational constant, respectively, along the i (= a, b or c) principal axis of inertia, while ${\alpha }_r^i$ is the corresponding vibration-rotation interaction constant, with the sum running over all r normal modes.

The anharmonic force constants were computed also at the more computationally affordable B2PLYP and MP2 levels in conjunction with the aug-cc-pVTZ basis set. The quality of the force constants provided by these methods have been checked against the corresponding ones calculated at the CCSD(T) level with the same basis set. By combining the best-estimated harmonic frequencies, ω(best), with the anharmonic terms, three different hybrid force fields were obtained. The first one, labelled HYB-1, has the cubic and quartic semi-diagonal force constants obtained at the B2PLYP/aug-cc-pVTZ level, while the other two, HYB-2 and HYB-3, have those provided by MP2/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ calculations, respectively. These three models were used to evaluate anharmonic frequencies to be compared with the experimental ones. In addition, to test the performances of the HDCPT2 approach in predicting reliable spectroscopic data, the three hybrid force fields defined above were used, thus leading to the sets of results labeled as HDHYB-1, HDHYB-2 and HDHYB-3, respectively, and compared with the measured fundamental frequencies and the GVPT2 calculated ones.

Finally, to compute infrared intensities beyond the harmonic approximation, the best-estimated intensity for each i-th fundamental mode, I_i (best), obtained according to equation (7), was corrected by the corresponding anharmonic shift, ΔI_i, thus leading to the anharmonicity corrected infrared intensity, $I_i^{\mathit{Anh}}$, according to the following⁵⁶ expression:

$$I_i^{\mathit{Anh}}=I_i\left(\text{best}\right)+\Delta I_i.$$ (10)

In the present work, the DVPT2 anharmonic corrections to intensities were considered at the B2PLYP and MP2 levels of theory employing the aug-cc-pVTZ basis set (again within the frozen core approximation). In DVPT2 computations of fundamental transitions, in addition to Fermi resonances also the 1-1 resonances have been considered and identified on the basis of the criteria described in Ref. 32.

All the CCSD(T) computations were performed by means of the CFOUR program package, while the MP2 and B2PLYP calculations as well as VPT2 (GVPT2/DVPT2 and HDCPT2) treatments were carried out by employing Gaussian09.⁵⁷ Tables collecting harmonic intensities predicted with different basis sets, observed band types, sextic centrifugal-distortion terms, vibration-rotation interaction constants and Coriolis zeta parameters are available in the supplementary material.⁵⁸

IV. RESULTS AND DISCUSSION

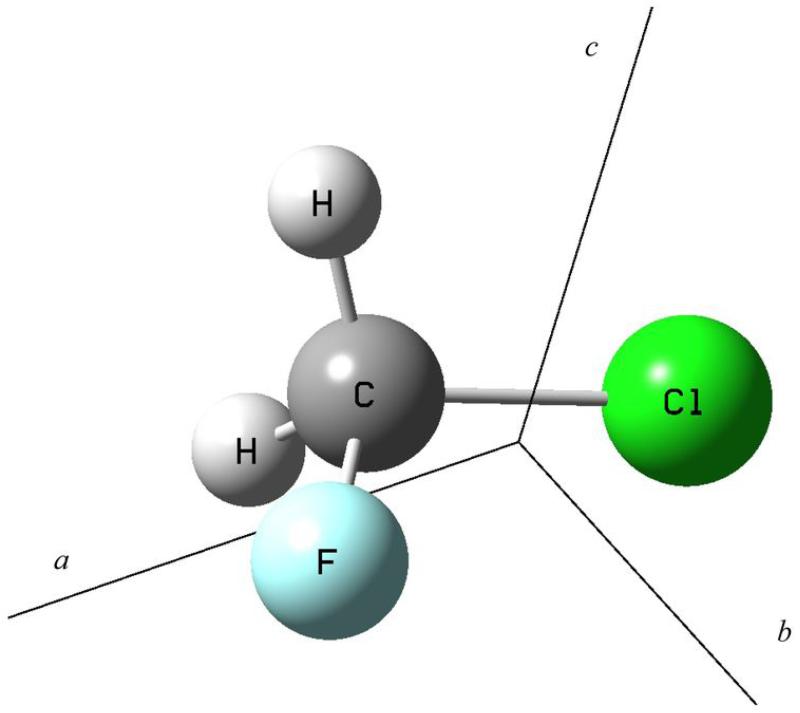
Chlorofluoromethane is a near prolate (κ = −0.97) asymmetric rotor which belongs to the C_s symmetry point group. Its nine normal modes are grouped, according to their symmetry, into six (ν₁ - ν₆) of A′ symmetry species (which give rise to a/b hybrid bands) and three (ν₇ - ν₉) of A″ symmetry species (which produce c-type band contours). Figure 1 reports the CH₂ClF molecule with the three principal axes of inertia.

Figure 1.

Molecular structure of CH₂ClF and its principal axis of inertia.

A. Equilibrium geometry and normal mode frequency determinations

As described in Sec. III, the optimized geometries and the harmonic force fields were determined at the CCSD(T) level using different correlation-consistent basis sets, up to cc-pV5Z, to determine the corresponding best-estimated values. Concerning the structural parameters, Table 1 reports those obtained by increasing the basis-set dimension and also taking into account the effects of core-valence electron correlation and diffuse functions in the basis set. As it can be seen, the results obtained with the quintuple-ζ quality basis set are almost converged with respect to the CBS values, the differences being not larger than 0.0025 Å and 0.1 degrees for bond lengths and angles, respectively. Corrections due to core correlation are rather small, the bond lengths shortening by less than 0.003 Å, and the effects on bond angles ranging from 0.005 (H-C-F) to −0.065 degrees (H-C-H). With the inclusion of the diffuse functions, the bond lengths change by a small amount (generally not greater than 0.002 Å), while the angles show larger corrections (a decrease up to 0.13 degrees for F-C-Cl). On the whole, the differences between the best-estimated and CBS values are in the range −0.004 – 0.0007 Å and −0.11 – 0.13 degrees for bond lengths and angles, respectively. Concerning the accuracy of the best-estimated structural parameters here presented, in view of the smooth convergence to the CBS limit, the extent of the core-valence electron correlation and diffuse functions effects and on the basis of previous studies,^48,59 we can estimate it to be about 0.001 – 0.002 Å and 0.2-0.5 degrees for bond distances and angles, respectively. A way for confirming such an error estimate is to compare our best-estimated results to experiment. In the literature the only experimental geometry available is the so-called substitution structure (r_s),²¹ which unfortunately is known to be affected by large uncertainties and to be not reliable especially when light atoms (like hydrogens) and nuclei for which isotopic substitution is not feasible are involved. In fact, from Table 1 we note that the C-H distance is badly determined and the C-F bond length seems to be too long. A way out is offered by the evaluation of the semi-experimental equilibrium structure. According to the procedure explained for instance in Ref. 38 (see also references therein), using the experimental ground-state rotational constants for different isotopic species (from Ref. 21) and the corresponding computed vibrational corrections, a highly accurate equilibrium structure can be derived by a least-squares fit procedure involving the semi-experimental equilibrium moments of inertia (the reader is referred to Ref. 38 for a detailed explanation of the methodology). This structure is reported in Table 1 and, according to the thorough study of Pawlowsky et al.,⁶⁰ it has an accuracy of at least 0.001 Å for bond distances and 0.1 degrees for angles. It is noted that its comparison with our computed equilibrium geometries confirms the error estimate given above.

TABLE I.

Equilibrium structure of CH₂CIF as computed at the CCSD(T) level of theory employing different basis sets. Distances in Å and angles in degrees. The experimental data available from literature are also reported.

Basis set	C-H	C-F	C-Cl	<H-C-Cl	<H-C-F	<H-C-H	<F-C-Cl
CCSD(T)/cc-pVQZ	1.08556	1.35927	1.77285	107.809	109.247	112.535	110.166
CCSD(T)/cc-pV5Z	1.08551	1.36040	1.76860	107.956	109.119	112.580	110.085
CCSD(T)/CBSa	1.08544	1.36124	1.76606	108.053	109.028	112.658	109.998
CCSD(T)/CBS + Δr(CV)b	1.08430	1.35966	1.76287	108.071	109.033	112.593	110.019
Best estimate: CCSD(T)/CBS + Δr(CV) + Δr(aug)c	1.08468	1.36197	1.76224	108.179	108.926	112.721	109.885
Semi-exp. red	1.083984(17)	1.359385(15)	1.764123(13)	107.9446(18)		112.5632(26)	110.0180(18)
Exp. rse	1.09(1)	1.370(1)	1.7621(2)	109.4(3.0)		110.4(5.0)	110.1(0.5)

^aCBS extrapolation using the cc-pVQZ and cc-pV5Z basis set (see text).

^bCore-valence electron correlation effects, Δr(CV), evaluated as described in the text, employing the cc-pCVTZ basis set added to the CBS limit.

^cEffects of diffuse functions, Δr(aug), evaluated as described in the text, employing the aug-cc-pVQZ basis set added to the CBS + CV structure.

^dThis work. Semi-experimental equilibrium structure, see text. Vibrational corrections at the (all)-CCSD(T)/cc-pcVTZ level are used. Standard deviations of the fit in units of the last significant digits are given in parentheses.

^eSubstitution structure, r_s, from Ref. 21: as reported in the original work, errors in parentheses are given as twice the estimated ones.

Moving to the spectroscopic parameters, inspection of the computed rotational constants collected in Table II shows that the values obtained with the cc-pV5Z basis set differ from the corresponding CBS results in the range of −51 – 14 MHz (i.e. less than 0.3 %); the core correlation corrections are up to 120 MHz for A (but on the order of 16 MHz for B and C), while inclusion of the diffuse functions led to differences of about the same order of magnitude but opposite in sign for A (−158 MHz). Looking at the quartic centrifugal-distortion terms listed in the same Table, a similar smooth convergence towards the CBS limit can be observed by analysing the trend cc-pVQZ – cc-pV5Z. Inclusion of CV and diffuse functions effects led to corrections not greater than 0.2-0.3 %, the only exception being δ_J where the aug-cc-pVQZ basis set resulted in difference around 0.5 %. The comparison between the experimental (ground-state) rotational constants and their quantum-chemical counterpart, obtained by adding vibrational corrections (at the (all)-CCSD(T)/cc-pCVTZ level) to the best-estimated equilibrium rotational constants, allows us to point out a good accuracy: the discrepancies for B and C are smaller than 10 MHz (well within 0.2%), while for the A constant the difference is around 150 MHz (0.4 %). It is worthwhile noting that a better agreement is observed if the CBS+CV equilibrium rotational constants are considered. This is also reflected in a better agreement of the CBS+CV structure with the semi-experimental equilibrium geometry than the best-estimated one. This suggests that the inclusion of the effects of the diffusion functions in the basis set partially overlaps the corrections introduced by the extrapolation to the CBS limit. It is therefore suggested to consider with great care the use of such correction when the extrapolation to the CBS limit is performed using large basis sets, as in the present case.

TABLE II.

Rotational (equilibrium and vibrational ground-state) and quartic centrifugal-distortion constants of CH₂³⁵ClF as computed at the CCSD(T) level of theory. The experimental data are also given. All the values are reported in MHz except for δ_J which is expressed in kHz. ^a

	cc-pVQZ	cc-pV5Z	CBS b	CBS + CV c	CBS + CV + aug d	Expt. e
Ae	42206.19	42167.75	42116.35	42235.76	42077.46
Be	5698.06	5717.90	5731.71	5748.70	5753.16
Ce	5189.68	5205.63	5216.42	5231.81	5233.45
A0				41820.87 e	41662.57 e	41811.2198(98)
B0				5720.02 e	5724.48 e	5715.97941(42)
C0				5198.55 e	5200.19 e	5194.89167(14)
Δ J	0.00360	0.00363	0.00365	0.00365	0.00367	0.00369558(21)
Δ JK	−0.03512	−0.03528	−0.03546	−0.03554	−0.03554	−0.0351952(37)
Δ K	0.56369	0.56364	0.56387	0.56564	0.56330	0.563360(32)
δ J	0.50239	0.50887	0.51414	0.51516	0.51984	0.523618(18)
δ K	0.01302	0.01309	0.01313	0.01316	0.01320	0.0138912(43)

^aThe values refer to Watson’s A-reduced Hamiltonian in the I^r representation.

^bCBS extrapolation carried out using the cc-pVQZ and cc-pV5Z basis sets (see text).

^cCV effects evaluated by employing the cc-pCVTZ basis set (see text) added to the CBS limit.

^dThe effects of diffuse functions were evaluated by using the aug-cc-pVQZ basis set (see text) and added to the CBS + CV results.

^eFrom Ref. 21: standard deviations in units of the last significant digits are given in parentheses.

^fVibrational corrections at the (all)-CCSD(T)/cc-pCVTZ level.

Upon inspection of the results listed in Table II, for quartic centrifugal-distortion constants, a trend similar to that observed for rotational constants is noted. Our best-estimated values compare very well with the experimental data (well within 0.1%), and the reached agreement denotes^38,59 the great accuracy of the present investigation; the only exception is δ_K which is about 0.7 kHz smaller than its experimental counterpart, but still agrees well (within 5%) with experiment.

As concerns the theoretical harmonic wavenumbers, Table III collects all results obtained in the present study. The CCSD(T)/cc-pV5Z harmonic frequencies can be considered well converged with respect to the CBS values, with discrepancies below 2 cm⁻¹ for all modes but ω₄ (C-F stretching mode of A′ symmetry), for which the cc-pV5Z and CBS frequencies differ by about 4 cm⁻¹. The CV corrections are always positive and smaller than 5 cm⁻¹. The inclusion of diffuse functions leads to negative corrections smaller than 3 cm⁻¹, except for the ω₃, ω₄ and ω₈ modes, the largest effect (≈ 9 cm⁻¹) being on ω₄. According to the literature,⁶¹ in view of the smooth convergence to the CBS limit, of the contributions included (core correlation and diffuse functions) and of the negligible role usually played by other contributions (relativistic and non-adiabatic effects) we expect that the overall accuracy reached in the present investigation is of the order of a few wavenumbers.

TABLE III.

Wavenumber values (cm⁻¹) of CH₂³⁵ClF computed at the CCSD(T) level of theory employing different basis sets.

	cc-pCVTZ (fc)	cc-pCVTZ (all)	cc-pVQZ (fc)	aug-cc-pVQZ (fc)	cc-pV5Z (fc)	CBSa	CBS + CV b	CBS + CV + aug c
ω 1	3102.5	3107.7	3106.1	3103.9	3107.2	3108.2	3113.3	3111.1
ω 2	1520.4	1522.5	1516.8	1515.3	1514.4	1512.2	1514.2	1512.8
ω 3	1387.7	1390.1	1386.4	1380.0	1382.1	1380.3	1382.7	1379.3
ω 4	1113.1	1115.5	1103.9	1095.1	1098.5	1094.0	1096.3	1087.5
ω 5	770.3	773.0	774.4	774.2	777.3	778.7	781.4	781.2
ω 6	387.7	389.0	387.8	387.0	388.1	387.9	389.2	388.3
ω 7	3178.4	3183.3	3183.8	3182.3	3185.0	3186.7	3191.7	3190.1
ω 8	1270.9	1273.8	1269.1	1263.0	1268.2	1267.3	1270.2	1264.1
ω 9	1016.4	1018.2	1018.7	1016.4	1020.8	1022.8	1024.7	1022.4

^aCBS limit obtained as explained in the text .

^bCV effects evaluated by employing the cc-pCVTZ basis set (see text) added to the CBS limit.

^cThe effects of diffuse function were evaluated by employing the aug-cc-pVQZ basis set (see text) and added to the CBS + CV values.

The CCSD(T) harmonic intensities obtained with different basis sets together with the corresponding final best-estimated values (equation (7)) are reported in Table S.I in the supplementary material:⁵⁸ their analysis allow us to investigate the effects of the basis set, core correlation and inclusion of diffuse functions. Inspection of these results points out that for the largest intensities moving from cc-pVQZ to cc-pV5Z leads to differences smaller than 5%, whereas some low intensity transition shows larger changes. The overall trend thus suggests a rather good convergence of the results at the CCSD(T)/cc-pV5Z level. The corrections introduced by taking into account core-valence effects are small, generally within a few percent, thus confirming the trends reported in recent studies.^40,62 In line with the findings given in literature,⁶³ the effects due to the inclusion of diffuse functions are larger, within 2% for the most intense transitions and 10% for the medium intensity ones. Larger relative discrepancies are observed for some low-intensity transitions, with the most significant correction found in the case of ω₂, where the diffuse function correction computed at the aug-cc-pVQZ basis set led to a variation of intensity by 0.08 km/mol, which is equal to the value itself computed with the cc-pV5Z basis set; in any case the precision for such low-intensity transitions remains satisfactory. These findings confirm that reliable (i.e. converged) computations of band intensities (related to the dipole moment derivatives) can be strongly affected by basis-set and electron-correlation effects, thus requiring the use of an appropriate high level of theory, which can become prohibitively expensive for larger molecules.

B. Vibrational analysis of FTIR spectra up to 6200 cm⁻¹

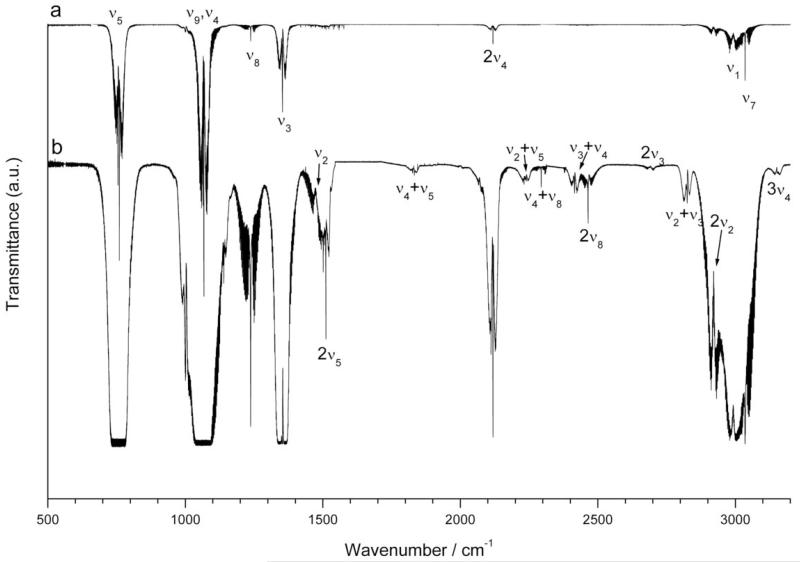
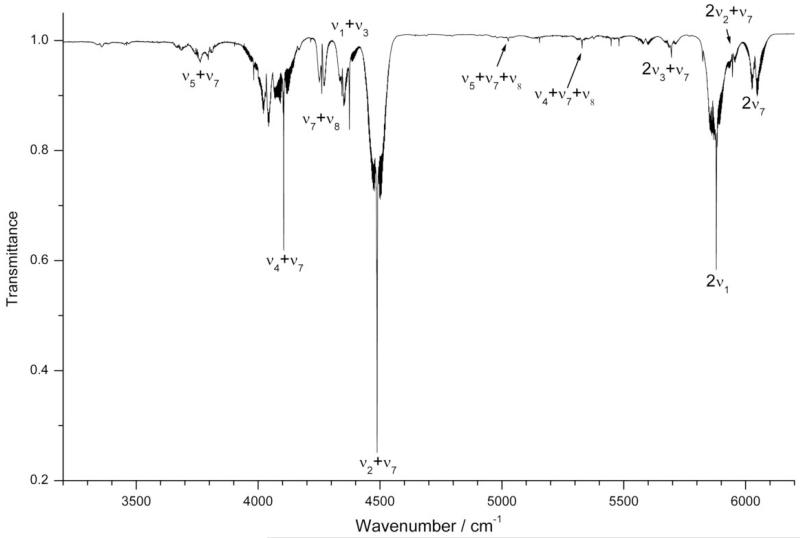
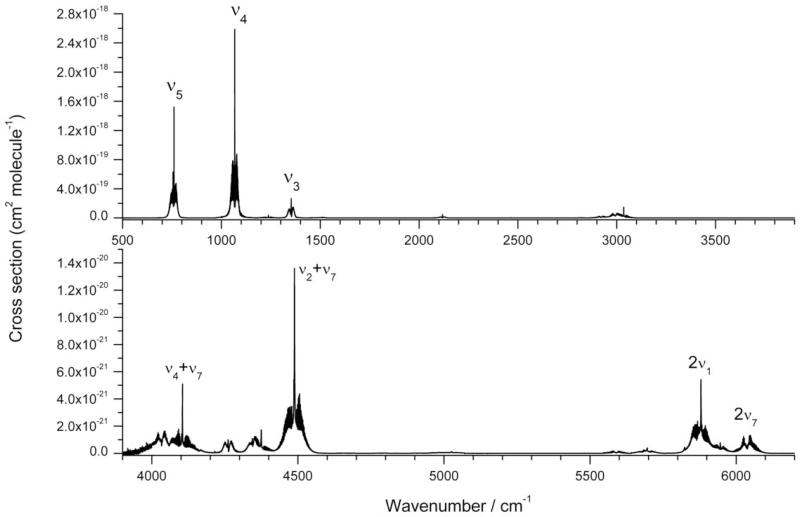
Figures 2 and 3 report the survey spectrum of CH₂ClF in the 320 – 440 cm⁻¹ and 500 – 3200 cm⁻¹ spectral ranges, respectively, mainly characterized by the absorptions of all the fundamentals. The analysis of the spectra recorded at low pressure allowed us to identify and assign the main absorptions. As it can be seen, the strongest features are localized in the 750 – 1360 cm⁻¹ (therefore occurring in the 13 – 7.3 μm atmospheric window); they are related to vibrational modes of A′ symmetry involving the halogen atoms. The C-³⁵Cl stretching originates the ν₅ band at 759.9 cm⁻¹, and the C-F stretching gives rise to the ν₄ fundamental at 1067.8 cm⁻¹, the latter being the most intense one (with a quantum-chemical best estimated harmonic intensity of 165.57 km/mol). Moving to higher wavenumbers, the spectra show the features corresponding to some vibrations involving the CH₂ group; the ν₃ band (located at 1353.3 cm⁻¹), approximately described as wagging, has an intensity greater than ν₈ (1236.8 cm⁻¹) which is related to a twisting mode (their quantum-chemical harmonic intensities are 29.16 and 2.47 km/mol, respectively). Concerning the other fundamentals, two are found in the 2900 – 3050 cm⁻¹ region: they are the ν₁ (at 2992.57 cm⁻¹) and ν₇ (at 3035.38 cm⁻¹) bands, associated to the symmetric (A′ symmetry) and asymmetric (A″) CH₂ stretching modes, respectively. The former shows a predominant b-type band contour, while the latter is characterized by a c-type one. The ν₂ fundamental, associated to the CH₂ deformation, is located at 1473.6 cm⁻¹: given its very low intensity (the quantum-chemical harmonic value for this band is 0.15 km/mol) it is barely visible at low pressure and becomes clearly visible only increasing the sample concentration. The low pressure spectra show also additional features which were assigned to the first overtone of ν₄ (at 2118.6 cm⁻¹) and ν₂ (at 2920.4 cm⁻¹), the latter being involved in a Fermi type I resonance with the nearby V₁ = 1 vibrational state. The identification and assignment of the other bands were carried out by analyzing the spectra recorded at higher pressure and at different resolution in order to maximize the SNR. In the 3200 – 6200 cm⁻¹ region the strongest feature belongs to the ν₂ + ν₇ combination located at 4488.2 cm⁻¹, as clearly seen in Figure 4; on the low frequency side there are the absorptions coming from many other combination bands, like the ν₁ + ν₃ (at 4343.8 cm⁻¹), ν₇ + ν₈ (at 4261.1 cm⁻¹) and ν₄ + ν₇ (centered at 4102.82 cm⁻¹). Moving to higher wavenumbers, the weak signals due to three quanta combination bands become identifiable by increasing the sample pressure; for example, in Figure 4 the features related to ν₄ + ν₇ + ν₈ (at 5329.1 cm⁻¹) and 2ν₃ + ν₇ (at 5695.6 cm⁻¹) are labeled. Finally, the region from 5850 up to 6100 cm⁻¹ is characterized by absorptions corresponding to the first overtones of ν₁ and ν₇, centered at 5879.25 and 6038.09 cm⁻¹, respectively, and by the feature occurring at 5946.43 cm⁻¹ which, on the basis of ab initio predicted band positions, could be tentatively assigned as 2ν₂ + ν₇.

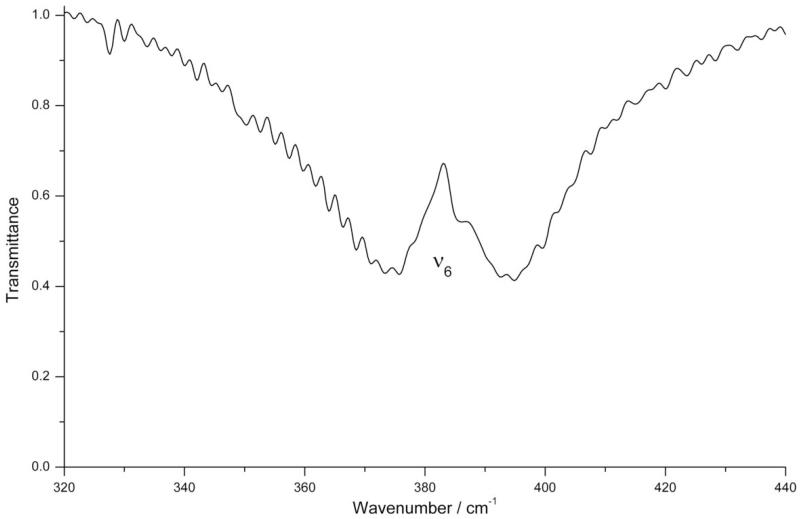
Figure 2.

Survey spectra (320 – 440 cm⁻¹) of CH₂ClF (resolution = 1.0 cm⁻¹, path length = 150 mm, room temperature, pressure = 52 kPa).

Figure 3.

Survey spectra (500 – 3200 cm⁻¹) of CH₂ClF (resolution = 0.2 cm⁻¹, path length = 134 mm, room temperature). Traces (a) and (b) refer to the spectrum recorded with a sample pressure of 41.2 Pa and 23 kPa, respectively. Trace (b) displaced for clarity. Some relevant bands are labeled.

Figure 4.

Survey spectra of CH₂ClF in the range 3200 – 6200 cm⁻¹ (resolution = 0.5 cm⁻¹, sample pressure = 35 kPa, path length = 134 mm, room temperature). Some relevant bands are labeled.

Besides the fundamentals, absorption features coming from overtones, combination and hot bands up to three quanta of vibrational excitation were positively assigned in terms of vibrational quantum numbers and the overall vibrational analysis led to the assignment of 54 bands in the spectral range from 200 to 6200 cm⁻¹ which are collected in Table IV (Table S.II in the supplementary material⁵⁸ lists the experimentally observed band contours).

TABLE IV.

Summary of the assigned bands (cm⁻¹) from the gas-phase infrared spectra of CH₂ClF.

Band	Wavenumber a	Band	Wavenumber a
ν 6	383.5(3)	3ν4	3152.3(5)
ν5 + ν6 − ν6	751.2(3)	ν3 +2ν4	3460.2(3)
ν 5	759.9(1)/755.1(1) b	ν7 + ν5	3795.7(3)
2ν6	768.0	ν1 + ν9	3982.1(3)
ν 9	1000.8(1)	ν7 + ν9	4033.7(3)
ν 4	1067.7(.1)	ν4 + ν7 + ν6 − ν6	4102.2(3)
ν5 + ν6	1139.6(3)	ν4 + ν7	4102.82(3) c
ν 8	1237.3(3)	ν1 + ν8	4215.5(3)
ν 3	1353.1(1)	ν7 + ν8	4261.1(3)
ν 2	1473.6(1)	ν1 + ν3	4343.8(3)
2ν5	1510.9(3)/1501.3(3) b	ν3 + ν7	4374.4(3)
ν4 + ν5	1826.52(3)	ν2+ ν7 + ν6 − ν6	4486.3(3)
ν2 + ν6	1857.1(3)	ν2+ ν7	4488.2(3)
2ν9	2001.6(1)	ν6 + ν7 + ν8	4645.9(3)/4642.3(3) b
ν3 + ν5	2111.5(3)	ν5 + ν7 + ν9	4788.4(3)/4782.8(3) b
2ν4	2118.6(3)	ν5 + ν7 + ν8	5025.8(5)
ν2 + ν5	2226.3(3)	ν7 + 2ν9	5026.8(5)
ν8 + ν9	2240.0(3)	2ν4 + ν7	5154.8(5)
ν4 + ν8	2294.0(3)	ν4 + ν7 + ν8	5329.1(3)
ν3 + ν4	2415.3(3)	ν3 + ν7 + ν9	5377.35(5)
2ν8	2462.47(12) c	ν3 + ν4 + ν7	5448.2(3)
2ν3	2691.6(3)	ν7 + 2ν8	5480.5(3)
ν2 + ν3 + ν6 − ν6	2823.0(5)	ν3 + ν7 + ν8	5589.66(2) c
ν2 + ν3	2824.9(3)	2ν3 + ν7	5695.6(3)
2ν2	2920.4(3) c	2ν1	5879.25(4) c
ν 1	2992.57(13) c	2ν2 + ν7	5946.43(13) c
ν 7	3035.38(4) c	2ν7	6038.09(12) c

^aThe experimental error in parentheses is on the last significant digit.

^b35/37Cl isotopologues.

^cObtained by employing polynomial equation, see text.

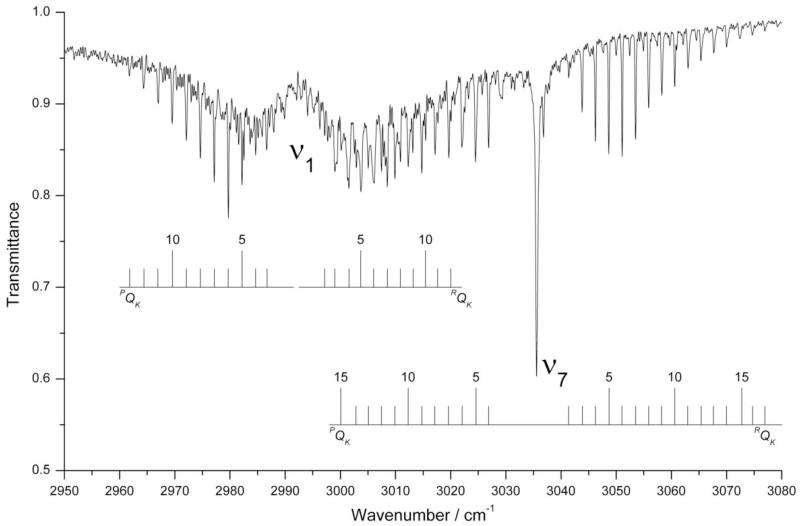
Since the CH₂ClF rotational constants are relatively large, some absorptions show a partially resolved rotational structure when recorded at the highest resolution (0.2 and 0.5 cm⁻¹): as an example, Figure 5 reports the region around 3000 cm⁻¹ characterized by the ^P,RQ_K clusters of ν₁ and ν₇. The analysis of these structures were carried out within the symmetric-top approximation and by employing the following polynomial equation:

$${\tilde{\nu }}^{P,R}={\tilde{\nu }}_0+(A^{\prime }-{\overline{B}}^{\prime })\mp 2(A^{\prime }-{\overline{B}}^{\prime })K+\left[\right(A^{\prime }-{\overline{B}}^{\prime })-(A^{″}-{\overline{B}}^{″}\left)\right]K^2\pm 4{D_K}^{\prime }{K}^3$$ (11)

where in the double signs the upper and lower refer to the P- and R-branches, respectively, ${\tilde{\nu }}_0$ is the band origin and $\overline{B}=\frac{1}{2}(B+C)$. This procedure has been carried out to derive accurate band origin values for 2ν₈, 2ν₂, ν₁, ν₇, ν₄ + ν₇, ν₃ + ν₇ + ν₈, 2ν₁, 2ν₂ + ν₇ and 2ν₇.

Figure 5.

Details of the partially resolved rotational structures of the ν₁ (A′) and ν₇ (A″) fundamentals in the 2950 – 3080 cm⁻¹ spectral region (resolution = 0.2 cm⁻¹, sample pressure = 926 Pa, path length = 134 mm, room temperature).

C. Comparison of theory and experiment: band position accuracy and dipole moment surface quality

As previously described, different anharmonic force fields were defined by combining the best-estimated values obtained for the harmonic wavenumbers (see Section III.B) with the anharmonic force constants computed at the B2PLYP, MP2 and CCSD(T) levels by employing the aug-cc-pVTZ basis set, thus leading to the models labeled as HYB-1, HYB-2 and HYB-3, respectively. All these force fields have also been used in view of establishing the performance of the HDCPT2 theoretical framework by comparing its predictions with the corresponding GVPT2 results. Table V collects the hybrid fundamental frequencies computed by the GVPT2 (GHYB-1, GHYB-2 and GHYB-3) and HDCPT2 (HDHYB-1, HDHYB-2 and HDHYB-3) approaches; the comparison with the corresponding experimental data is also reported. We point out that all the results have been obtained by hybrid approaches, thus the differences between the methods are fully due to the cubic and semi-diagonal quartic force constants and, within the same anharmonic force field, to the theoretical model applied to compute frequencies (GVPT2 or HDCPT2). Concerning the GVPT2 framework, we note that the employed threshold criteria⁵⁰ have led to the identification of two type-1 Fermi resonances (2ω_r ≈ ω_s), for all the three hybrid models; the first one involves the V₁ = 1 and V₂ = 2 vibrational states (related to the CH₂ asymmetric stretching and bending modes of A′ symmetry), while the second one occurs between V₅ = 1 and V₆ = 2 vibrational states (related to the CCl stretching and CFCl bending modes of A′ symmetry).

TABLE V.

Comparison between the GVPT2 and the HDCPT2 wavenumber values (cm⁻¹) of CH₂³⁵ClF, benchmarked against the experimental data.

Symmetry Species	Mode	Obs.	GHYB-1 a	GHYB-2 b	GHYB-3 c	HDHYB-1 a	HDHYB-2 b	HDHYB-3 c
A′	ν 1	2992.57	3009.2	3004.2	2996.1	2992.5	2989.1	2984.1
	ν 2	1473.6	1472.7	1469.7	1465.1	1468.3	1465.4	1461.5
	ν 3	1353.1	1350.0	1348.0	1348.2	1349.0	1346.9	1347.3
	ν 4	1067.7	1061.5	1060.0	1061.7	1061.5	1060.0	1061.7
	ν 5	759.9	764.6	763.4	763.5	770.4	768.1	769.0
	ν 6	383.5	384.2	383.9	383.9	383.5	383.2	383.2
A″	ν 7	3035.38	3047.0	3044.7	3037.7	3045.7	3043.4	3036.6
	ν 8	1237.3	1235.8	1234.9	1230.3	1235.6	1234.7	1230.1
	ν 9	1000.8	1007.2	1005.1	1001.1	1007.0	1004.8	1000.9
Statistics d		MSE	−3.2	−1.1	1.8	−1.1	0.9	3.3
		MAE	5.8	5.4	4.1	4.9	5.4	5.6
		Min.	−16.6	−11.6	−3.6	−10.5	−8.2	−9.1
		Max.	6.2	7.7	8.5	6.2	8.2	12.1
		RMSE	7.6	6.3	4.9	6.2	6.1	6.9

^aCCSD(T)/CBS + CV + aug harmonic frequencies augmented by the B2PLYP/aug-cc-pVTZ cubic and quartic semi-diagonal force constants (f.c.).

^bCCSD(T)/CBS + CV + aug harmonic frequencies augmented by the MP2/aug-cc-pVTZ cubic and quartic semi-diagonal force constants (f.c.).

^cCCSD(T)/CBS + CV + aug harmonic frequencies augmented by the CCSD(T)/aug-cc-pVTZ cubic and quartic semi-diagonal force constants (f.c.).

^dThe statistics reported (in cm⁻¹) refer to errors computed as observed – calculated frequency values for each hybrid model. MSE and MAE stand for mean signed error and mean absolute error, respectively. Min. and Max. refer to the minimum and maximum value of error, respectively; RMSE stands for root mean square error.

The fundamental frequency of mode 1 (ν₁), computed with the GHYB-3 approach is in remarkable agreement (within 3.5 cm⁻¹) with the experimental value, while the GHYB-1 and GHYB-2 approaches overestimate it by more than 10 cm⁻¹, with the values following the trend GHYB-1 > GHYB-2 > GHYB-3. With the DVPT2 approach, ν₁ follows the same trend, with the values being 2977 cm⁻¹, 2974 cm⁻¹ and 2970 cm⁻¹ at the B2PLYP, MP2 and CCSD(T) levels, respectively. These findings are in line with the high computational requirements for a proper description of the anharmonic PES in the region of the CH stretching vibrations. These results can be explained in terms of differences between the force constants computed by different methods. In particular, the values of the quartic force constants obtained with the different levels of theory considered are quite similar except for K₂₂₂₂ (28 cm⁻¹ and 4 cm⁻¹ at the B2PLYP and CCSD(T) levels, respectively). In any case the quartic force constants have a small effect on the overall error, so that the differences between the GHYB-3 and GHYB-1 frequencies are mainly due to the terms involving the cubic force constants. Differences larger than 10 cm⁻¹ between the B2PLYP and the CCSD(T) cubic force constants have been found for K₅₄₄, K₉₃₇, K₃₃₃, K₈₂₇, K₉₉₁ and K₂₂₁. Among these constants, K₂₂₁ is probably the most important, since it couples mode 1 with its counterpart of the resonant dyad (mode 2), and, when the GVPT2 approach is applied, it is involved in the off diagonal terms – i.e., the coupling between ν₁ and 2ν₂ – of the matrix which is diagonalized. At the B2PLYP and CCSD(T) levels the K₂₂₁ values are 184 and 172 cm⁻¹, respectively. This could explain the difference of 13 cm⁻¹ between the GHYB-1 and GHYB-3 fundamental frequencies for the mode 1. Within the HDCPT2 approach, the resonant terms are approximated, so that the coupling between the resonant modes is somewhat screened. This could be the reason why the difference between the HDHYB-1 and HDHYB-3 frequencies of mode 1 is reduced to about 8 cm⁻¹, Similar arguments can be used to discuss the dyad of resonant frequencies ν₅/2ν₆ and the MP2 results.

To sum up, considering only the fundamentals, GHYB-3 reaches an extremely good accuracy, as pointed out by its mean absolute error (MAE) of 4.1 cm⁻¹ and root mean square error (RMSE) of 4.9 cm⁻¹; within this model, the cubic force constants K₅₆₆ and K₂₂₁, ruling the magnitudes of the Fermi resonances occurring in the ν₅/2ν₆ and ν₁/2ν₂ dyads, are 15.3 and 171.6 cm⁻¹, respectively. Anyway, the other two models, GHYB-1 and GHYB-2, led to results which should be considered more than satisfactory (MAEs of 5.8 and 5.4 cm⁻¹, respectively), especially in view of the much reduced computational cost. On the other hand, moving to the HDCPT2 framework, the three force fields considered (HDHYB-1, HDHYB-2 and HDHYB-3) gave similar errors (MAE around 5 cm⁻¹, RMSE less than 7 cm⁻¹). These results could be considered as a further validation of the reliability of the HDCPT2 approach (which is free from the problems related to degeneracies and the corresponding somewhat arbitrary definitions of the criteria for assessing the resonances) in accurate anharmonic computations. Furthermore, it is noteworthy that the fundamentals obtained by HDCPT2, besides their application in spectroscopic studies, can be used for computing the vibrational partition function and other thermodynamical properties beyond the harmonic approximation, in an easy black-box manner.³²

Concerning the whole set of assigned transitions, Table VI reports the main statistics for the three hybrid force fields here analyzed within the GVPT2 framework: as it can be seen, there are no large differences among them when the overall spectral range (200 – 6200 cm⁻¹) is considered. They all gave close results, thus performing equally well in predicting reliable anharmonic frequencies for overtone and combination bands up to three quanta, as confirmed by the very good MAE values (about 9.0 cm⁻¹). All the three models predicted anharmonicity constants in an overall good agreement with the experimentally measured ones: as an example, Table VII reports the results obtained by GHYB-2 (which can be routinely used for much larger systems) together with those retrieved from the vibrational assignments. For the anharmonicity constants related to the vibrational levels involved in Fermi resonances, in addition to the DVPT2 deperturbed data we reported also the corresponding perturbed values; these are the biased results yielded by standard VPT2 equations without removing the divergent terms related to anharmonic interactions.

TABLE VI.

Main statistics ^a of different hybrid models within the VPT2 framework.

		GHYB-1b	GHYB-2c	GHYB-3d
Combination bands (up to two quanta)	MAE	9.5	8.7	11.2
	RMSE	10.9	10.1	13.2
Overtones (up to two quanta)	MAE	8.3	7.8	8.5
	RMSE	9.8	9.3	11.0
Overall (up to three quanta)	MAE	9.7	8.6	9.5
	RMSE	11.6	10.3	12.0

^aThe statistics reported (in cm⁻¹) refer to errors computed as observed – calculated frequency values for each hybrid model. MAE stands for mean absolute error, RMSE stands for root mean square error.

^bCCSD(T)/CBS + CV + aug harmonic frequencies augmented by the B2PLYP/aug-cc-pVTZ cubic and quartic semi-diagonal force constants.

^cCCSD(T)/CBS + CV + aug harmonic frequencies augmented by the MP2/aug-cc-pVTZ cubic and quartic semi-diagonal force constants.

^dCCSD(T)/CBS + CV + aug harmonic frequencies augmented by the CCSD(T)/aug-cc-pVTZ cubic and quartic semi-diagonal force constants.

TABLE VII.

Computed (GHYB-2) and experimental anharmonicity constants x_ij (cm⁻¹) of CH₂³⁵ClF.^a

i \ j	1	2	3	4	5	6	7	8	9
1	−29.31 [−52.95± 0.13]	−31.43* (16.79)	4.69 [−1.9 ± 0.4]	2.33	0.30	0.71	−119.97	−8.87 [−14.4 ± 0.4]	−4.82 [−11.3 ± 0.3]
2		−1.77* (−13.82) [−13.4 ± 0.2]	−1.49 [−1.8 ± 0.3]	−5.17	−1.44 [−7.2 ± 0.4]	−1.15 [0.0 ± 0.4]	−20.56 [−20.8 ± 0.3]	−5.75	−12.08
3			−7.70 [−7.3 ± 0.2]	−5.5 [−5.5 ± 0.3]	−3.60 [−1.5 ± 0.4]	−0.93	−11.47 [−14.1 ± 0.3]	−11.84 [−10.2 ± 0.4]	−1.65 [4.9 ± 0.5]
4				−8.60 [−8.4 ± 0.2]	0.44 [−1.1 ± 0.4]	−3.72	3.33 [2.0 ± 0.3]	−10.62 [−11.0 ± 0.4]	−1.67
5					−4.19 [−4.4 ± 0.3]	−2.77* (2.86) [−3.8 ± 0.5]	1.64 [0.4 ± 0.4]	−3.32	−3.81
6						−0.12* (−1.52) [0.5 ± 0.3]	1.22 [0.7 ± 0.4]	−0.53 [0.6 ± 0.7]	−1.22
7							−33.94 [−16.34 ± 0.07	−6.09 ] [−11.6 ± 0.4]	−3.11 [−2.5 ± 0.3]
8								−3.21 [−6.1 ± 0.3]	1.43 [1.9 ± 0.3]
9									−1.92 [0.00 ± 0.07]

^aThe asterisk denotes ab initio deperturbed constants (taken from the GHYB-2 model); the corresponding perturbed values (i.e. those biased by the contributions of nearly singular terms related to resonances, see text) are given in parentheses. Experimental values are reported within square brackets.

From the cubic and quartic force constants together with the data coming from the quadratic force fields, the full set of sextic centrifugal-distortion constants was computed; Table S.III in the supplementary material⁵⁸ reports the corresponding results together with the available experimental data. As it can be seen, there is an overall satisfactory agreement between the computed and measured values. Since large discrepancies (about 50% of the experimental values) are observed for Φ_JK, ϕ_JK, and ϕ_K, a more detailed discussion is deserved. The first comment concerns their experimental uncertainty; it is in fact noted that these constants are not very well determined with errors ranging from 7% to 23% (21% to 69%, if one considers 3σ), while the remaining constants show uncertainties of the order of 1%. More interesting is to note that our computed values agree well with those derived from empirically scaled MP2 force fields, as reported in Ref. 28. The conclusion that can be drawn is that the experimental values for Φ_JK, ϕ_JK, and ϕ_K might be as not reliable as expected and an experimental re-investigation is warranted. The limited reliability might be ascribed to either the missing account of higher-order centrifugal-distortion constants or the presence of interactions. We furthermore note that, according to Ref. 21, these three centrifugal-distortion constants are highly correlated in the fit; therefore, a possible solution might be to constrain at least one of these to its computed value in the fitting procedure.

In addition to the thorough vibrational assignments of its gas-phase infrared spectra, the present study on CH₂ClF also involved the accurate measurements of integrated band intensities performed on the corresponding absorption cross section spectrum. These data, besides being mandatory for a reliable assessment of the potential impact of this compound on the Earth’s radiative budget, make it possible to assess the quality of the computed anharmonic dipole moment surface. The determination of the absorption cross section spectrum was performed on the basis of the different spectra obtained at increasing radiator pressures and in presence of N₂ as inert buffer gas. The analysis of this series of absorption spectra was performed by least square fitting the point-by-point measured absorbance value $A\left(\tilde{\nu }\right)$ at each wavenumber, $\tilde{\nu }$, versus the corresponding gas concentration (mol cm⁻³), assuming the validity of Beer’s law. The regression algorithm yields the slope $\sigma \left(\tilde{\nu }\right)$ that is the absorbance cross section per molecule (cm² molecule⁻¹) of the sample retrieved at each wavenumber according to:⁶⁴

$$\sigma \left(\tilde{\nu }\right)=\frac{A\left(\tilde{\nu }\right)\ln \left(10\right)}{N_{A}cl}$$ (12)

where N_A is Avogadro’s constant, l is the optical path length (cm) and c is the sample concentration (mol cm⁻³). This procedure, first suggested by Chu et al.,⁶⁵ yields to a greatly enhancement of the SNR. Following this method, the upper limit in the range of sample pressures is not dictated by the necessity of keeping the stronger features on scale to avoid saturation issues in the measured absorbance values; it is therefore possible to obtain accurate measurements even of the weak signals. In addition, the fitting algorithm provides the point-by-point statistical uncertainty in the absorption cross section spectrum. In the current analysis the statistical errors were generally not greater than 3% for the most intense features. Figure 6 displays the absorption cross section spectrum of CH₂ClF in the 500 – 6200 cm⁻¹ range: it is seen that the most intense bands, ν₅ and ν₄, fall in the atmospheric window region 750 – 1200 cm⁻¹ (13.3 – 8.3 μm) thus being the main causes for the greenhouse potential of this molecule. As previously described, the anharmonic corrections to the CCSD(T) harmonic intensities were determined by performing calculations at the B2PLYP and MP2 levels of theory employing the aug-cc-pVTZ basis set, thus leading to the HYB-1 and HYB-2 models, respectively. Table VIII lists the corresponding data obtained for all the fundamentals. By inspecting them, it is evident that the two models provide similar corrections. The differences between the HYB-1 and HYB-2 predictions are generally lower than 0.5 km/mol, the only exceptions being the ν₅ and ν₇ bands, for which discrepancies of 1.2 and 1.0 km/mol are observed, respectively. To compare the ab initio values with the experimental data for each absorption feature, the experimental integrated cross section G_int (cm molecule⁻¹) was retrieved by integrating the absorbance cross section $\sigma \left(\tilde{\nu }\right)$ over an integration limit corresponding to wavenumbers of negligible absorption. By following the procedure outlined elsewhere,⁶⁶ the experimental uncertainty was estimated to be generally better than 5% and 10% for the strongest and weakest signals, respectively. Table IX presents the obtained integrated absorption cross sections and the corresponding integration limits; for comparison purposes the HYB-1 and HYB-2 values are also reported. The theoretical estimation of the integrated cross sections was done by integration of a theoretical stick spectrum (i.e., the lineshapes have been obtained by convoluting each transition with a Dirac delta function). The comparison between the results obtained with such a procedure and the experimental ones is straightforward as long as we assume that the experimental cross sections vanish at the boundaries of the integration intervals (i.e., the area associated to a specific transition is completely included within the integration limits). An overall satisfactory agreement between experiment and theory is noted; in the region 700 – 3115 cm⁻¹, which is mainly characterized by absorptions due to fundamentals, the discrepancies are about 9%, with the computed intensities being larger than the experimental integrated cross sections. Considering the whole spectral range here employed for the integration (700 – 6100 cm⁻¹), the MAE of the HYB-1 and HYB-2 models is 1.93 and 1.95 km/mol, respectively (about 0.7% with respect to an overall experimental integrated intensity of 285.5 km/mol). On these bases, we can conclude that the two hybrid models, based on two different levels of theory, perform equally well in calculating the anharmonic intensities. It is also worthwhile noting that, similarly to what observed in a recent study on a set of halogenated molecules,⁶⁷ a very good agreement has been obtained also in those spectra intervals that are fully related to non-fundamental transitions, further confirming the reliability of the whole procedure used to simulate IR spectra. These results are particularly encouraging in view of the extent of the discrepancies recently reported for the overtone transitions computed at the CCSD(T)/cc-pVTZ level for the ethyl radical.⁶⁸

Figure 6.

Absorption cross section spectra of CH₂ClF (resolution = 0.2 cm⁻¹, T = 298 K) in the region 500 – 3900 cm⁻¹ and 3900 – 6200 cm⁻¹. The most relevant absorptions are labeled.

TABLE VIII.

Computed anharmonic intensities of fundamentals (in km/mol).

Symmetry Species	Mode	CCSD(T) best-estimated	B2PLYP/aug-cc-pVTZ	MP2/ aug-cc-pVTZ	HYB-1 a	HYB-2 b
		I (harm)	I(anharm)	I(anharm)	I(anharm)	I(anharm)
A′	ν 1	17.06	21.55	19.72	20.04	19.40
	ν 2	0.15	0.28	0.21	0.23	0.23
	ν 3	29.16	26.68	27.03	25.64	25.24
	ν 4	165.57	165.41	159.67	161.05	160.73
	ν 5	84.54	101.16	90.91	87.58	86.35
	ν 6	1.50	1.06	1.32	1.42	1.41
A″	ν 7	3.01	6.60	4.84	5.48	4.89
	ν 8	2.47	2.35	2.29	2.43	2.42
	ν 9	0.38	0.42	0.46	0.41	0.40

^aCCSD(T) best-estimated harmonic intensities augmented by anharmonic shifts computed at the B2PLYP/aug-cc-pVTZ level (see text).

^bCCSD(T) best-estimated harmonic intensities augmented by anharmonic shifts computed at the MP2/aug-cc-pVTZ level (see text).

TABLE IX.

Integrated cross sections (cm² molecule⁻¹ cm⁻¹) of CH₂ClF in the range 700 – 6100 cm⁻¹.

Integration limits (cm−1)	Main bands	Integrated absorption cross sections
		Experimental a (×1018 cm2 molecule−1 cm−1)	Experimental a (km / mol)	HYB-1b (km / mol)	HYB-2b (km / mol)
700-800	ν 5	13.05(13)	78.6(1.4)	86.61	86.38
950-1175	ν9, ν4	23.8(4)	144(2)	162.37	162.13
1175-1290	ν 8	0.396(7)	2.40(4)	2.43	2.42
1290-1410	ν 3	4.22(2)	25.41(12)	25.65	25.25
1430-1550	ν2, 2ν5	0.26(2)	1.51(12)	1.01	1.20
2050-2170	2ν4, ν3 + ν5	0.488(8)	2.94(5)	2.91	3.02
2380-2530	ν3 + ν4, 2ν8	0.097(13)	0.22(8)	0.55	0.58
2780-2850	ν2 + ν3	0.060(6)	0.36(3)	0.30	0.30
2850-3115	2ν2, ν1, ν7	4.37(3)	26.3(2)	25.68	24.43
3950-4200	ν1 + ν9, ν7 + ν9, ν4 + ν7	0.15(4)	0.9(2)	0.96	0.99
4220-4300	ν7 + ν8	0.028(3)	0.17(2)	0.13	0.17
4310-4420	ν1 + ν3, ν3 + ν7	0.053(4)	0.32(2)	0.39	0.35
4420-4570	ν2 + ν7	0.210(5)	1.26(3)	1.31	1.34
5800-5990	2ν1, 2ν2 + ν7	0.134(9)	0.81(6)	1.00	0.80
5990-6100	2ν7	0.041(6)	0.25(4)	0.65	0.48

^aStandard deviations in units of the last significant digits are given in parentheses.

^bSum of the intensities computed for fundamental, overtone and combination bands comprised in the integration limits. HYB-1 refers to the model with CCSD(T) best-estimated harmonic intensities augmented by anharmonic shifts computed at the B2PLYP/aug-cc-pVTZ level, HYB-2 refers to the model with CCSD(T) best-estimated harmonic intensities augmented by anharmonic shifts computed at the MP2/aug-cc-pVTZ level.

Finally, the Global Warming Potential of CH₂ClF was determined for different timescales following the narrowband model proposed by Pinnock et al.⁶⁹ As a first step, an instantaneous radiative forcing (RF) value of 7.96 × 10⁻² W m⁻² ppbv⁻¹ was obtained for CH₂ClF using the absorption cross section spectrum measured in this study as well as the cloudy-sky radiative forcing data available in literature.⁶⁹ Then, the GWP was determined taking CO₂ as reference compound and employing the RF value previously determined; the time-dependent decay of CH₂ClF atmospheric concentration was modeled using its atmospheric lifetime. In this way we obtained a value of 323, 83 and 42 on a 20-, 100- and 500-year horizon, respectively. Concerning the RF value, the narrowband approach here employed is believed⁶⁹ to yield an uncertainty generally around ±15% with respect to line-by-line calculation. Errors on the GWP can be evaluated by taking into account the uncertainties in the radiative forcing and the lifetime values, and assuming no correlation between them (even if the short atmospheric lifetime of CH₂ClF can limit to some extent the validity of this assumption): on these bases we estimated the overall uncertainty of our proposed GWP values to be around ±30%.

V. CONCLUSIONS

In the present work the gas-phase infrared spectrum of CH₂ClF was subjected to a detailed vibrational study up to 6200 cm⁻¹ performed by coupling accurate data coming from medium-resolution infrared spectra with state-of-the-art quantum-chemical calculations at different levels of theory. The analysis of FTIR spectra led to the accurate determination of the band positions for fundamental, overtone and combination bands up to three quanta. The vibrational investigation was combined with measurements of the absorption cross section spectra carried out over the 500 – 6200 cm⁻¹ spectral region; from these data, the integrated band intensities for the most relevant absorption features were obtained with a great accuracy. The retrieved results were then employed to determine the radiative forcing and the global warming potential of CH₂ClF. The whole set of experimental data allowed benchmarking the performances of recently proposed models for computing spectroscopic properties beyond the harmonic approximation. Concerning the HDCPT2 approach, all hybrid force fields here considered provided results in very close agreement with both the corresponding GVPT2 results and the measured fundamental band positions. These findings definitely confirm the validity of the HDCPT2 method for providing accurate spectroscopic data, thus allowing the evaluation of all thermodynamic properties related to fundamental band positions (i.e. vibrational partition functions, constant volume specific heat capacities, enthalpies and free energies) without relying on the definition of threshold criteria for defining resonant terms. The accurate values of integrated band intensities here determined permitted us to accurately test the quality of the dipole moment surface computed taking into account also the anharmonic corrections to the calculated harmonic infrared intensities. The good agreement of the quantum-chemical results here reported with the experimental data confirms the applicability of the present implementation to spectroscopic studies of more complex molecular systems, also in the region of overtone and combination bands.