Structural Priming as Implicit Learning: Cumulative Priming Effects and Individual Differences

Abstract

We explored the claim that structural priming is a case of implicit learning within the language production system. The experiment began with a baseline phase, in which we assessed participants’ rates of production for double object and prepositional object constructions. Then participants were biased toward the production of either the double object or prepositional object construction. Finally, we again assessed participants’ rates of production for the target constructions. Consistent with claims that structural priming is a case of implicit learning, we found that biasing participants toward the prepositional object construction produced stronger cumulative priming effects than did biasing participants toward the double object construction. We also found that individual differences in implicit learning were marginally correlated with overall rates of production for the double object construction. Participants who scored better on the learning task tended to produce fewer double object constructions.

Structural priming refers to the tendency for individuals to repeat syntactic structures across utterances (Bock, 1986). For example, a person who just produced a double object construction (DO; e.g., Meghan gave Michael a toy) is more likely to produce another DO when describing a transfer situation (e.g., John sent Tim the files) than to produce a prepositional object (PO) construction describing the same event (e.g., John sent the files to Tim). Structural priming has been widely studied, because the presence (or absence) of priming between prime and target sentences is revealing about linguistic representations. As one illustration, researchers have used structural priming to explore the relationship between verbs and syntactic constructions (e.g., Bernolet & Hartsuiker, 2010; Coyle & Kaschak, 2008; Kaschak & Borreggine, 2008).

Structural priming is used to explore linguistic representations, but it can be studied as a phenomenon unto itself to understand the mechanisms through which the language system adapts its behavior (e.g., Bock & Griffin, 2000). Structural priming has been explained as transient spreading of activation (e.g., Pickering & Branigan, 1998), implicit learning (e.g., Chang, Dell, & Bock, 2006), or a combination of both mechanisms (e.g., Reitter, Keller, & Moore, 2011). There is evidence for both mechanisms. Transient increases in priming arising when lexical items are repeated across sentences suggest an activation-type mechanism (e.g., Hartsuiker, Bernolet, Schoonbaert, Speybroeck, & Vanderelst, 2008), and long-lasting priming (e.g., Kaschak, Kutta, & Schatschneider, 2011) indicates a role for implicit learning.

Our study explored two aspects of the claim that long-range structural priming effects are examples of implicit learning. First, we examined the inverse frequency effect, or the finding that lower-frequency constructions produce stronger priming than do higher-frequency constructions (see, e.g., Ferreira, 2003; Hartsuiker & Westenberg, 2000; Jaeger & Snider, 2008; Scheepers, 2003). The inverse frequency effect arises from long-range accumulations of production experience, and it is predicted by implicit learning accounts of structural priming (e.g., Chang et al., 2006). Despite these predictions, few demonstrations of inverse frequency effects have been reported. Reitter et al. (2011) examined the inverse frequency effect in the context of cumulative structural priming (i.e., structural priming accumulating over many tokens of one construction; e.g., Kaschak, Loney, & Borreggine, 2006). Using an ACT–R-based model of language production, they simulated cumulative priming for DO and PO constructions over a range of 1–25 prime sentences. Reitter et al. assessed how much structural priming increases as the number of prime constructions produced prior to a target sentence increases. Their simulation generated an intriguing result: robust cumulative priming for the lower-frequency PO construction (priming increased as the number of primes produced increased), but weaker, nonsignificant priming for the higher-frequency DO construction.

Reitter et al.’s (2011) simulation suggests an interaction between the long-range frequency of constructions and the extent to which priming accumulates over shorter ranges of experience. If this prediction were confirmed empirically, it would put constraints on the mechanisms that can explain structural priming. Although inverse frequency effects have been reported in the literature (e.g., Scheepers, 2003), including cases in which priming has accumulated over several sentences (e.g., Hartsuiker & Westenberg, 2000; Kaschak, 2007), the previous studies were not designed so that structure-based differences in cumulative priming could be observed. The relevant studies either had multiple constructions produced throughout the experiment (thus, not producing the sort of cumulative priming simulated by Reitter et al., 2011; e.g., Hartsuiker & Westenberg, 2000) or required cross-experiment comparisons to examine the strength of cumulative priming. Thus, additional work is needed to assess Reitter et al.’s prediction.

Our study employed a modification of Kaschak’s (2007) cumulative priming paradigm to test whether Reitter et al.’s (2011) simulation result could be observed using written language production. Participants completed a series of target stems that allowed for the production of either a DO or a PO construction (e.g., Meghan gave …). This provided baseline information about the use of DO and PO constructions. Bock and Griffin (2000) suggested that American English speakers have a 2:1 bias toward the DO construction, so something close to these relative frequencies should be observed here. Next, cumulative priming was instantiated by presenting prime stems that disposed participants toward producing either a DO (Meghan gave Michael …) or a PO (Meghan gave the toy …) construction. Participants saw either 100% DO primes or 100% PO primes. Finally, we measured cumulative priming by presenting another set of target stems. Reitter et al.’s model predicts that DO-biased participants will show less change in production behavior between the first and last phases of the study than will PO-biased participants.

Our second goal was to test the structural-priming-as-implicit learning view, by assessing how individual differences in implicit learning relate to cumulative structural priming. It had long been thought that there were no important individual differences in implicit learning (e.g., Reber, 1993), but subsequent work has shown that such differences do exist (e.g., Kaufman et al., 2010). Moreover, individual differences in implicit learning appear to be related to language comprehension skill (e.g., Conway, Bauernschmidt, Huang, & Pisoni, 2010; Misyak & Christiansen, in press). If cumulative structural priming is a case of implicit learning, the magnitude of the observed cumulative priming effects should be positively correlated with participants’ implicit learning ability. Based on Reitter et al. (2011), this relationship may be particularly strong for participants biased toward the PO construction (as the DO construction may produce weak cumulative priming).

METHOD

Participants

A group of 113 undergraduate psychology students participated for partial course credit. As in previous work (e.g., Kaschak, 2007), we ensured the integrity of the cumulative priming manipulation by eliminating data from participants who did not complete at least 80% of the prime stems as intended (e.g., participants biased toward the DO construction must complete >80% of the prime stems as DOs). All participants met this requirement, producing the intended construction 97% of the time. Furthermore, because we were interested in changes in rates of DO and PO production across time, we excluded participants who did not produce DO or PO constructions on 50% (i.e., 3 out of 6) of the target trials in both the pre- and post-bias phases of the experiment. Eleven of the participants were excluded based on this criterion.

Materials

A total of 12 target stems were constructed (e.g., Meghan gave …). These could be completed as either DO or PO constructions. Target stems were arranged into a fixed order, and then split into two sets of 6 (A and B). Half of the participants saw Set A in the pre-bias phase and Set B in the post-bias phase, and the other half saw the sets in the opposite order. Fourteen pairs of prime stems were constructed. One pair member elicited the DO construction (Meghan gave Michael …), and the other elicited the PO construction (Meghan gave the toy …). We constructed 104 filler stems that could not easily be completed as DO or PO constructions. Fillers were presented throughout the experiment, with four fillers separating each prime or target stem.

Our measure of individual differences in implicit learning was the Simon task described by Conway et al. (2010). Following the Milton Bradley game, the computer screen showed four colored squares (red, green, blue, yellow). On each trial, the squares lit up in sequence (e.g., red–green–red–yellow). Participants used labeled keys on the keyboard to reproduce the sequence. Sequences were scored as correct if participants reproduced the entire sequence correctly. The initial game trials trained participants on the probabilistic rules used to generate the sequences. Afterward, participants saw sequences that followed the rules and other sequences that did not. Sequence length ranged from four to eight responses. Our task employed the same rules, training, and test sequences as had been employed by Conway et al. For sequences produced correctly in the test phase, participants received one point for each response in the sequence (e.g., an eight-response sequence was worth 8 points). The measure of implicit learning (IL score) was generated by subtracting the number of points earned on rule-violating items from the number of points earned on rule-following trials. IL scores ranged from −8 (the participant performed better on non-rule-following items than on rule-following items) to 74 (M = 31.5, SD = 15.1).

Procedure

Participants were randomly assigned to the DO or PO Bias condition, with half of the participants in each condition. Participants were told that they would see a series of sentence stems on the computer screen, and that they should complete each as a grammatical sentence. The experiment began with the pre-bias phase, in which participants completed six target stems. Next came the Bias phase, in which participants saw 14 prime stems that elicited either the DO or PO construction; participants were biased 100% toward one construction. Then, the participants completed 6 more target stems (post-bias phase). Finally, participants performed the Simon task.

Scoring

Prime and target stem completions were scored “DO,” “PO,” or “other,” as described in Kaschak (2007).

Design and analysis

Trials scored as “other” (PO bias = 13%, DO bias = 16%) were excluded from the analysis, creating a binary dependent variable (DO responses coded “1,” PO responses coded “0”). A mixed logit analysis was conducted to predict the log odds of producing a DO target completion. This analysis was done with the lme4 package (Bates, Maechler, & Bolker, 2011) in R (R Development Core Team, 2011). All predictors in all analyses were centered. For every model reported here, collinearity was assessed using the collin.fnc() procedure in R. All obtained kappa values were < 2.64. Thus, collinearity was not a concern. Models included participants and items as crossed random factors. The intercepts could vary across participants and items. We employed a model comparison approach to determine the best-fitting model for our data. We first ran a model including Bias condition (DO bias = 1, PO bias = 0), Time (pre-bias = 0, post-bias = 1), and the Bias × Time interaction without random slopes, and then the same model with the full complement of random slopes. Because the random slopes marginally improved the model fit (p = .07), we tested whether each individual random slope improved model fit. Subsequent to this, we assessed whether the addition of IL score as a variable and its associated interactions improved model fit. The best-fitting model included Bias condition, Time, and the Bias × Time interaction, with random slopes for participants on the Time variable.

RESULTS

The best-fitting mixed logit model predicting the log odds of producing a DO target completion is presented in Table 1. The Time × Bias condition interaction was significant (p < .001). In a mixed logit model analyzing only DO-biased participants, the effect of Time was not significant (p = .30): Participants produced similar rates of DO responses in the pre- and post-bias phases (see Table 1). The effect of Time was significant (p < .001) in a model assessing PO-biased participants. These participants showed cumulative priming, producing fewer DOs in the post-bias than in the pre-bias phase. Adding IL score to the model in Table 1 showed that IL score was a marginally significant predictor (B = −.02, p = .06) and that it marginally improved model fit [χ²(1) = 3.52, p = .07]. As IL scores increased, the likelihood of producing a DO completion decreased. Interactions involving IL score did not improve the model fit.

Table 1.

Mixed logit analysis with raw and estimated means

Predictor	Coefficient	SE	Z	p Value
Mixed Logit Model
Intercept	0.42	0.38	1.09	.28
Timea	−0.35	0.19	−1.86	.06
Bias condition	0.58	0.37	1.56	.12
Time × Bias	1.51	0.38	4.01	<.001
DO-Only Analysis
Intercept	0.69	0.38	1.83	.07
Timea	0.24	0.23	1.04	.30
PO-Only Analysis
Intercept	0.08	0.47	<1	.86
Timea	−1.16	0.30	−3.88	<.001
Raw and Estimated Mean Proportions of DO Target Completions
	Raw Means		Estimated Means
Bias Condition	DO	PO	DO	PO
Pre-bias	.61	.63	.62	.66
Post-bias	.63	.45	.71	.40

Coefficients express log odds.

^aRandom slopes for participants

We observed an inverse frequency effect: The lower-frequency PO construction produced stronger cumulative priming than did the higher-frequency DO construction. However, our results did not directly test Reitter et al.’s (2011) claim about changes in cumulative priming based on the Current run of DO and PO constructions (more consecutive POs = stronger priming; less change in priming based on the number of consecutive DOs). To assess this hypothesis, we analyzed responses from the post-bias phase, coding for Bias condition and IL score, plus the Current run of consecutive DO or PO constructions (ignoring trials with “other” responses) produced prior to each target stem. The latter measure approximates Reitter et al.’s cumulative priming manipulation. Participants could produce DO or PO constructions at any time (even in the Bias phase), and thus the run of consecutive DOs or POs varied across trials. The Current run was coded as a positive number when the preceding trial(s) had used the construction toward which the participant was biased (called the bias construction). These runs could vary from 1 (trial n–1 had featured the bias construction, but trial n–2 had not) to 25 (on the final post-bias phase trial, all 25 prior prime and target stem completions had employed the bias construction). The Current run was coded as a negative number when the preceding trial(s) had featured the construction opposite the one toward which the participant was biased. These runs could vary from −1 (trial n–1 had featured the non-bias construction, but trial n–2 had featured the bias construction) to −25 (on the final post-bias phase trial, all preceding trials had been completed as the non-bias construction), though the presence of prime stems in the Bias phase made it unlikely that negative runs would exceed 5 non-bias constructions. Current run measures were similar across Bias conditions (DO bias: range = −5 to 25, M = 8.49, SD = 8.9; PO bias: range = −5 to 22, M = 8.06, SD = 8.9).

The best-fitting model for this analysis is presented in Table 2. As before, the inclusion of IL score did not significantly improve the model fit (p = .06). The critical result was a significant Bias condition × Current run interaction (p < .001). We explored the interaction by performing separate mixed logit analyses on the DO and PO Bias conditions. Beyond the “Current run” variable, we coded for the Cumulative probability of producing a DO construction across the experiment (i.e., up to a given trial, what proportion of prime and target stems were completed as a DO?; see Jaeger & Snider, 2008). Cumulative probability is a proportion, where higher values are expected to predict higher rates of DO production. (To yield more interpretable coefficients, we converted this proportion to a percentage for the analysis. Both predictors were centered within each Bias condition prior to analysis.) We included Cumulative probability in this model to determine whether effects of the Current run would be observed after accounting for participants’ overall likelihood of producing the DO construction.

Table 2.

Follow-up mixed logit analysis

Predictor		Coefficient	SE	Z	p Value
Mixed Logit Model
	Intercept	0.17	0.31	<1	.59
	Bias condition	1.13	0.30	3.81	<.001
	Current Run	−0.017	0.016	−1.09	.27
	Bias × Current Run	0.19	0.03	6.33	<.001
DO-Only Analysis
	Intercept	0.75	0.30	2.50	.01
	Cumulative priming	0.05	0.018	2.80	<.01
	Current Run	0.04	0.03	1.46	.14
PO-Only Analysis
	Intercept	−0.42	0.37	−1.13	.26
	Cumulative priming	0.083	0.025	3.26	.001
	Current Run	−0.09	0.028	−3.22	.001

Raw and Estimated Mean Proportions of DO Target Completions (per Run Length Bin)
	Raw Means			Estimated Means
	−5 to −1	1–15	16–25	−5 to −1	1–15	16–25
DO bias	.36	.63	.87	.49	.68	.82
PO bias	.65	.45	.19	.67	.40	.18

Coefficients express log odds. For the purposes of generating raw and estimated means, we split the “Current run” variable into three bins, with one bin representing runs of the opposite construction (i.e., negative numbers), and the remaining two bins splitting the positive runs. The numbers of observations per bin were as follows: DO bias, −5 to −1 = 70, 1–15 = 106, 16–25 = 76; PO bias, −5 to −1 = 97, 1–15 = 97, 16–25 = 78. The numbers of observations vary across bins because (a) we needed to keep all observations with the same run length in the same bin, and (b) we wanted to have the same bin parameters for both conditions. To generate the estimated means, we used run values corresponding to the mean run length within each bin. The mean run lengths within each bin were slightly different for the DO and PO Bias conditions, so we rounded to the nearest whole number between the two condition means, and then converted this value to its corresponding “centered” value (because the variables in the regression were centered). Thus, we employed run values of −10, 0, and 10 to generate the estimated means.

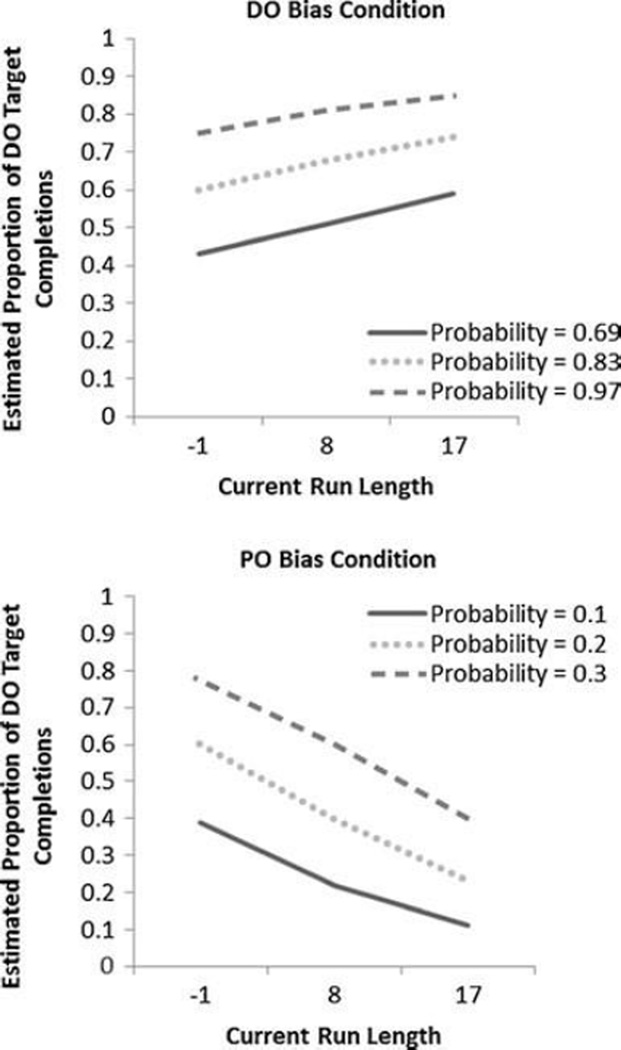
In the DO condition, Cumulative probability predicted the likelihood of producing a DO, but Current run did not (see Table 2; Fig. 1, top). This finding supports our main analysis—experiencing longer runs of the DO construction does not significantly affect the likelihood of producing a DO completion. The PO condition showed a different pattern: both Cumulative probability and Current run predicted the likelihood of a DO completion (Table 2; Fig. 1, bottom). Higher Cumulative probabilities led to higher odds of producing a DO response, and longer runs of the PO construction led to lower odds of producing a DO response. One concern about our conclusions regarding the “Current run” variable is that these results might be constrained by the patterns in our main analysis: Current run cannot show an effect when there is no cumulative priming on an experiment-wide level (DO condition), but it can show an effect when there is cumulative priming (PO condition). Our data argue against this concern. The range, average length, and variance in runs were similar across conditions, as were the proportions of bias constructions produced (63% DOs in the DO condition, 55% POs in the PO condition). Based on the similarities seen across conditions, if the global patterns of performance were driving the effect of the Current run, we would expect a similar runs effect across conditions. This was not the case.

Fig. 1.

Estimated proportions of DO target completions as a function of Current run and Cumulative probability for the DO (top) and PO (bottom) Bias conditions. Predicted values are derived from the regression models at the bottom of Table 2. The variables of interest were centered in the analyses, but we have converted the scales back to raw run length and raw Cumulative probability for the figure. The probability and run lengths selected represent the mean of each variable within each Bias condition, plus the values 1 SD above and 1 SD below the mean (rounded to whole numbers). “Probability” refers to the probability of producing a DO. In the DO condition, negative run lengths refer to runs of PO constructions, and positive run lengths refer to runs of DO constructions. In the PO condition, negative run lengths refer to runs of DO constructions, and positive run lengths refer to runs of PO constructions

DISCUSSION

We explored the view that cumulative structural priming reflects implicit learning in the language production system. Our data confirm one element of this claim: As predicted by Reitter et al. (2011), the main analysis showed cumulative priming for the (lower-frequency) PO construction, and weaker priming for the (higher-frequency) DO construction (i.e., an inverse frequency effect). Subsequent analysis supported this result, since PO-biased participants showed an effect of the Current run, but DO-biased participants did not.

We have two additional comments on our data. First, the rate of DO completions in the pre- and post-bias phases of the DO Bias condition (.61 and .63) are similar to the post-bias phase rates ofDO production in our other studies using written production (Kaschak, 2007: Exp. 1 = .64, Exp. 2 = .66; Kaschak et al., 2011 = .66). Rates of DO production across these post-bias phases, viewed in light of our pre-bias data, suggest a reinterpretation of our earlier results, namely that the previous cumulative priming effects were largely driven by the PO Bias condition. DO bias effects were probably small. Second, rates of DO production in these studies (and in natural language use) suggest that DO production was not at ceiling. The lack of a Current run effect for this construction was therefore striking, since there was ample room for DO production to increase. Although it is striking, the weakness of the Current run effect for the DO Bias condition is predicted by at least one model (Reitter et al., 2011). The result is also consistent with the spirit of other implicit learning accounts of structural priming. Whether the “Current run” variable ultimately has no effect on DO production, or merely a weak one (note that data in the DO Bias condition hint at a weak effect of runs), it is clear that inverse frequency effects occur for alternations that do not have stark frequency differences between members. Models such as Reitter et al.’s appear to provide mechanisms for understanding such effects. However, in their present form, the mechanisms posited, and the modeling assumptions that were made, might not be optimally sensitive to some types of local regularities. For example, it is noteworthy that the strength of the cumulative priming generated by Reitter et al.’s model is weaker than that observed here and in other studies (a point raised in their article).

Our results are consistent with studies showing that language comprehenders (see, e.g., Farmer, Fine, & Jaeger, 2011; Kaschak, 2006; Kaschak & Glenberg, 2004; Wells, Christiansen, Race, Acheson, & MacDonald, 2009) and producers (e.g., Jaeger & Snider, 2008; Kaschak, 2007) rapidly adapt to the probabilistic use of syntactic structures within their linguistic environment The present data provide an important qualification to demonstrations of flexibility in language use. Specifically, the difference in the effects of the Current run in the DO and PO Bias conditions suggests that not all experiences with language on a given time scale count equally in modifying language processing (cf. Jaeger & Snider, 2008; Kraljic, Brennan, & Samuel, 2008). It will be important to determine whether our findings hold for other structural alternations. If so, interactions between long-range frequency and shorter-range cumulative priming will place constraints on the mechanisms posited to explain structural priming and other adaptations in language processing.

A second aim of our study was to determine whether the magnitude of cumulative priming is predicted by individual differences in implicit learning. We expected that (a) stronger implicit learning performance would predict stronger cumulative priming, and (b) this relationship would be stronger in the PO Bias condition. These predictions were not confirmed. Although one interpretation of these findings is that implicit learning does not drive cumulative structural priming, this interpretation might be premature. Correlations between implicit learning measures are often low (e.g., Gebauer & Mackintosh, 2007; Misyak & Christiansen, in press), raising the possibility that different implicit learning measures might correlate with cumulative priming. Furthermore, there are distinctions between implicit learning based models of language processing that instantiate learning through either procedural (e.g., Chang et al., 2006) or declarative (e.g., Reitter et al., 2011) memory. If different learning mechanisms underlie Simon task performance and language production, it might explain our null result.

A final possibility that may be worth exploring is that individual differences in implicit learning relate to a more nuanced sensitivity to statistical structure in language than we have assessed. We examined how global frequencies of use for the DO and PO constructions interact with local frequencies of use within the experiment in shaping language production. We did not examine finer-grained levels of statistical structure, such as that found on the word level (e.g., verb biases; Bernolet & Hartsuiker, 2010), and individual variation in implicit learning may have a stronger effect on that level. Indeed, Conway et al.’s (2010) finding that Simon task performance relates to language processing emerged from study of a task in which word-level expectancies were central to performance. The relationship between implicit learning tasks and language-processing tasks may not be straightforward and may depend on the degree to which the learning demands of the two tasks overlap.