Coupling and electrical control of structural, orbital and magnetic orders in perovskites

Abstract

Perovskite oxides are already widely used in industry and have huge potential for novel device applications thanks to the rich physical behaviour displayed in these materials. The key to the functional electronic properties exhibited by perovskites is often the so-called Jahn-Teller distortion. For applications, an electrical control of the Jahn-Teller distortions, which is so far out of reach, would therefore be highly desirable. Based on universal symmetry arguments, we determine new lattice mode couplings that can provide exactly this paradigm, and exemplify the effect from first-principles calculations. The proposed mechanism is completely general, however for illustrative purposes, we demonstrate the concept on vanadium based perovskites where we reveal an unprecedented orbital ordering and Jahn-Teller induced ferroelectricity. Thanks to the intimate coupling between Jahn-Teller distortions and electronic degrees of freedom, the electric field control of Jahn-Teller distortions is of general relevance and may find broad interest in various functional devices.

Widespread interest in transition metal perovskite-like oxides over the last several decades can be ascribed to two key discoveries: high-temperature superconductivity in the cuprates and colossal magnetoresistance in the manganites¹,². Physical behavior exhibited by perovskites is by no means limited to these two phenomena, but also includes ferroelectricity and (anti)ferromagnetism or both simultaneously and coupled in magnetoelectric multiferroics, metal-insulator transitions and thermoelectricity, to name a few. The wide range of functional properties is usually thanks to an interplay between the structural (lattice), electronic (orbital and charge) and magnetic (spin) degrees of freedom allowed within the transition metal oxides³,⁴,⁵,⁶. This playground for novel materials physics is not only of fundamental academic interest, but oxide perovskites have already entered industry and have huge potential for novel device applications⁷,⁸.

The possibility of tuning the magnetic properties of a material with an applied electric field has received particular attention for low energy consumption spintronic devices⁷,⁹. In this regard, a promising route to achieve ferroelectricity in magnets is via the so-called the hybrid improper ferroelectricity¹⁰,¹¹,¹². Here, non-polar modes such as antiferrodistortive (AFD) motions, which are ubiquitous in perovskites, eventually combined with antipolar motions, simultaneously drives the polarization and can couple to the magnetic orders¹³,¹⁴,¹⁵,¹⁶,¹⁷. However, those motions are rather weakly linked to the electronic properties and hence the magnetoelectric coupling is likely not the most efficient. It would be advantageous to replace the AFD or anti-polar motions by another lattice distortion which couples directly to the electronic properties. Such a motion common in perovskites is the Jahn-Teller distortion (JT), and recently, a hybrid improper ferroelectricity mechanism involving such a distortion was reported in metal-organic frameworks¹⁸,¹⁹, yielding promising magnetoelectric multiferroic properties.

In an attempt to generalize and extend the concept to any perovskite, we reveal from a universal symmetry analysis that a hybrid improper polarization may arise solely from Jahn-Teller distortions. This mechanism is intrinsic to the perovskite structure and demonstrated here on the vanadate perovskites which exhibit a complex structural ground state including different Jahn-Teller distortions. Using first-principles calculations, we reveal in AA’V₂O₆ superlattices an unprecedented orbital ordering and purely Jahn-Teller induced ferroelectricity. We demonstrate that this enables an electric field control of both JT distortions and magnetism. Since JT distortions are intimately connected to electronic degrees of freedom²⁰, such as magnetism, orbital orderings and metal-insulator phase transitions to name a few, the proposed mechanism may find broader interest for novel functional devices outside the field of magnetoelectrics.

Bulk A³⁺V³⁺O₃

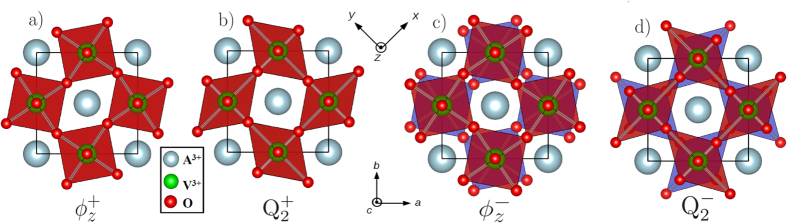
Whilst the V⁴⁺ perovskites (e.g. SrVO₃²¹) have been studied mainly for their interesting metallic properties, the V³⁺ perovskites are Mott insulators. A³⁺V³⁺O₃ compounds have attracted much attention since the fifties when they were first synthesized²². During this time, many studies began to determine their magnetic, electronic and structural properties²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³²,³³,³⁴,³⁵,³⁶,³⁷,³⁸,³⁹. A central theme at the core of these properties in vanadates is the so-called Jahn-Teller (JT) distortion. The famous Jahn-Teller theorem claims that a material with degenerate electronic states will be unstable towards undergoing a structural distortion lowering its symmetry to remove the electronic degeneracy. In other words, the Jahn-Teller effect is an electronic instability that can cause a structural and metal-insulator phase transition. For instance, in the cubic perovskite symmetry, the crystal field effect splits the d electron levels into a lower lying degenerate three-fold t_2g and a higher lying degenerate two-fold e_g state. Hence in 3d² systems such as the rare-earth vanadates, a Jahn-Teller distortion is required to split the t_2g levels in order to form a Mott insulating state. We note here the distinction between the Jahn-Teller effect and what we call the Jahn-Teller distortion in this study. Here we define the Jahn-Teller distortion by the symmetry of the atomic distortion as shown in Fig. 1b,d. Whilst a distortion of this symmetry will by definition remove the d electronic degeneracy, the origin of such a distortion does not necessarily need to appear from the Jahn-Teller effect. An important result of this study is that the Jahn-Teller distortion can instead be induced by structural anharmonic couplings, being therefore not only restricted to Jahn-Teller active systems⁴⁰.

Figure 1.

Comparison of JT and AFD motions around the z axis; (a) in-phase 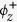AFD motion ( 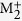mode); (b) in-phase 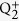Jahn-Teller motion ( 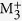mode); (c) anti-phase 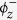motion ( 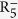mode); (d) anti-phase 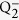motion ( 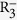mode). Octahedras for the plane in z = 0 are plotted in red and in blue for the plane in z = c/2. The AFD motions can also appear around the y and z axes (not shown), whereas the Jahn-Teller motions only manifest around the z axis in the vanadates.

In the vanadates, two different JT distortions are observed²⁴,²⁵,²⁶,³³, with each one consisting to two V-O bond length contractions and two elongations, often labelled as a Q₂ distortion⁴¹. The corresponding distortions are displayed in Fig. 1 where they are compared to the antiferrodistortive (AFD) motions. The AFD motions can be viewed as oxygen octahedra rotations around an axis going through the B cations, while the Jahn-Teller distortions in the present case correspond to oxygen rotations around an axis going through the A cations. Both JT and AFD motions can be either in-phase (Fig. 1.a+b) or anti-phase (Fig. 1.c+d) between consecutive layers and therefore appear at the M or R points of the Brillouin zone respectively. Consequently, we label the Jahn-Teller distortions as 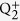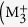mode) and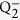 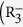mode). While AFD motions do not distort the BO₆ octahedra, JT motions lift the degeneracy of the d levels through octahedra deformations. According to such distortions, the V³⁺ 3d² occupation consists of either a d_xy and d_xz 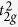or a d_xy and d_yz 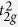state in an ideal picture. Nearest-neighbor vanadium sites within the (xy)-plane develop opposite distortions and hence alternative d_xy and d_xz / d_xy and d_yz occupations as shown in the top panel of Fig. 2. Along the axis, the octahedra deformations and hence orbital ordering are either in phase (C-type orbital order) or anti-phase (G-type orbital order) for the 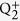or 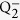Jahn-Teller distortion respectively (see Fig. 2 bottom panel). Crucially, the orbital ordering determines the magnetic ordering through superexchange interactions⁴²,⁴³,⁴⁴. Strongly overlapping and parallel orbitals between neighboring sites favors antiferromagnetic superexchange interactions. With this in mind, the 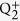motion favors a purely antiferromagnetic solution called G-AFM whilst the 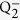motion favors (xy)-plane antiferromagnetic alignment and ferromagnetic out-of-plane alignment called C-AFM. In other words, a C-type orbital ordering (C-o.o.) is linked to a G-type antiferomagnetic ordering (G-AFM), while a G-type orbital ordering (G-o.o.) is linked to a C-type antiferromagnetic ordering (C-AFM). Experiments indeed observe both G-AFM and C-AFM magnetic phases in the vanadates, with each magnetic ordering favoring a certain structural symmetry²⁵,²⁶,³³.

Figure 2. Schematic picture of the idealized orbital orderings between the d_xz (blue) and d_yz (red) orbitals.

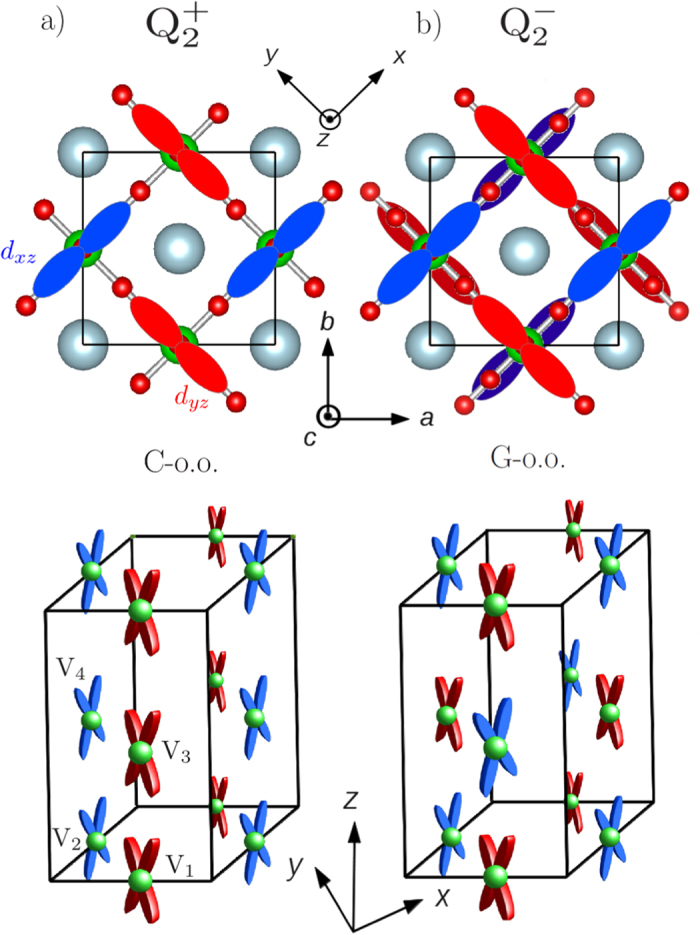
The d_xy orbital is not shown for clarity. (a) Top view of the orbital-ordering induced by a 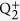distortion (top). Consecutive planes exhibit identical orbital orderings labelled as a C-type orbital-ordering (C-o.o.) (middle). This results in a G-AFM ordering. (b) Orbital-ordering induced by a 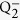distortion (top). Consecutive planes exhibit out-of phase orbital orderings labelled as a G-type orbital-ordering (G-o.o.) (middle). This results in a C-AFM ordering.

At room temperature, all rare-earth A³⁺V³⁺O₃ vanadates crystallize in a Pbnm structure²⁴,²⁵,²⁶,³³. With decreasing temperature, they undergo an orbital ordering phase transition to a G-type orbital ordered (G-o.o.) phase between 200 K and 150 K (depending on the A-cation size). This transition is accompanied by a symmetry lowering from Pbnm to P2₁/b. A magnetic phase transition from a paramagnetic to an C-AFM antiferromagnetic state occurs within this phase at a slightly lower temperature between 150 K and 100 K. Finally, for the smallest A cations (A = Yb-Dy, Y), another orbital ordering phase transition to a purely C-type (C-o.o.) arises and is accompanied by a structural phase transition from P2₁/b back to Pbnm, and a magnetic phase transition from C-AFM to G-AFM. For medium A cations (A = Tb-Nd), a coexistence of P2₁/b (G-oo) and Pbnm (C-oo) phases is reported²⁶,⁴⁵. No further transitions are found for larger A cations (A = Pr, Ce and La).

To better understand the distorted structures of vanadates, we perform a symmetry mode analysis⁴⁶,⁴⁷ of the allowed distortions with respect to a hypothetical cubic phase on three different compounds, covering a wide range of A-cation sizes: YVO₃, PrVO₃ and LaVO₃. The analysis is performed on experimental structural data, and the amplitudes of distortions are summarized in Table 1.

Table 1. Amplitudes of distortions (in Å) on experimental structures of vanadates at different temperatures.

Mode (Irreps)	YVO3			PrVO3		LaVO3
	Pbnm	P21/b	Pbnm	Pbnm	P21/b	Pbnm	P21/b
	295 K51	100 K36	5 K51	295 K26	5 K26	298 K52	10 K23
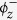
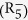
+	—	1.72	—	—	1.34	—	1.16
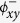
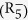
	1.71	—	1.73	1.34	—	1.17	—
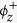
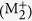
	1.22	1.24	1.22	0.94	0.96	0.68	0.75
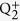
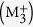
	0.05	0.06	0.14	0.02	0.02	0.08	0.01
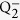
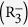
	—	0.10	—	—	0.18	—	0.08
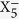
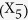
	0.86	0.87	0.87	0.53	0.64	0.37	0.39
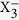
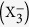
	—	0.01	—	—	0.06	—	0.00

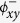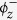In the P2₁/b symmetry, both and AFD motions belong to the same irreducible representation 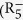mode) even if the 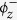amplitude is likely very small. The reference structure was chosen as a cubic structure whose lattice vector corresponds to the pseudo cubic lattice vector associated to the room temperature Pbnm phase.

In the Pbnm phase (a⁻ a⁻ c⁺ in Glazer’s notations⁴⁸), all three vanadates develop two unique antiferrodistortive (AFD) motions 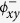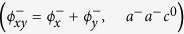and 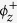(a⁰ a⁰ c⁺). Table 1 shows that the magnitudes of these AFD motions strengthen with decreasing A-cation size as expected via simple steric arguments⁴⁹. Within this Pbnm tilt pattern, the 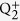lattice motion is already compatible and does not require any symmetry lowering to appear³⁸. This latter observation is in agreement with the sizeable 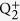lattice distortion extracted from our analysis on room temperature structures, despite the fact that no orbital-ordering has yet been reported for this temperature range²⁵,²⁶. The Pbnm phase then appears to always be a pure 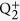phase. Additionally, an anti-polar 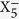mode whose motion is in the (xy)-plane is allowed in the Pbnm symmetry (see supplementary materials).

Going to the P2₁/b symmetry, a subgroup of Pbnm, the aforementioned AFD motions are still present, but the 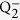distortion is now allowed and would lead to a G-o.o. phase. However, the P2₁/b phase is never an exclusive 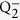phase but always coexists with the 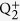distortion, even for the larger A cations (A = Pr, La). A mixed C-o.o. and G-o.o. should then manifest for all P2₁/b structures, independent of orthorhombic/monoclinic phase coexistence. Additionally, another anti-polar 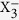mode, whose motion is now along the z direction, arises in this new phase (see supplementary materials).

In order to understand the origin and coupling between these distortions, we can perform a free energy 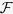expansion (see methods) around a hypothetical cubic 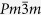phase with respect to the different distortions. Among all the possible terms in the Pbnm phase, two trilinear couplings are identified:

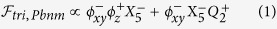Within the Pbnm symmetry, when 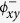and 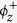are non zero in magnitude, the free energy of the system is automatically lowered by the appearance of 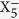due to the first trilinear term of Eq. 1. Similarly, through the appearence of 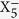, the free energy is again lowered by forcing the appearance of the 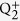motion thanks to the second trilinear coupling. This explains the presence of the 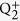distortion in the Pbnm phase of vanadates, even at room temperature. This demonstrates that, in addition to its possible appearance as an electronic instability, it may also appear as a structural anharmonic improper mode within the Pbnm phase (whose strength depends on the coupling constant) even in non Jahn-Teller active materials⁴⁰,⁵⁰. Going to the P2₁/b phase, two additional trilinear couplings are identified:

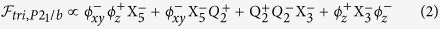The orbital-ordering phase transition to a G-o.o. phase experimentally observed between 150 K and 200 K for all vanadates²⁵,²⁶ manifests itself through the appearance of a 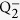distortion. Consequently, through the third trilinear coupling of Eq. (2), both JT distortions produce the additional anti polar 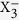motion. This is in agreement with the experimental data of Table 1. Finally, an extra 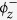(a⁰ a⁰ c⁻) AFD motion arises in the P2₁/b phase through the last trilinear coupling, yielding a rare a⁻ a⁻ c^± tilt pattern with both in-phase and out-of phase AFD motion around the axis. This tilt pattern has previously been predicted to appear within this space group³⁸.

Therefore, within this P2₁/b phase, both Jahn-Teller distortions coexist, but likely with different origins. The 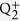mode is “pinned” into the system through an improper anharmonic coupling with the robust AFD motions while the 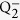mode may appear through the traditional Jahn-Teller electronic instability. It is interesting to note that this coexistence is allowed due to the improper appearance of 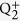, despite there likely being a competition between both JTs. This competition would be understood as an electronic origin to favor one type of orbital ordering over the other, producing a biquadratic coupling with a positive coefficient in the free energy expansion. In the light of there being an abundance of 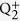with respect to 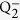phases across the perovskites, we then propose whether it is this improper appearance of 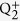via the robust AFD motions that helps favor this phase universally. The vanadates would then be a special case where the 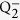instability is robust enough to appear despite this competition. This universal symmetry analysis and free energy expansion rationalizes the origin of the coexisting orbital ordered phase in the P2₁/b symmetry as observed in vanadates both experimentally and theoretically²⁵,²⁶,³⁷,³⁸.

The coexistence of both Jahn-Teller motions in the vanadates, will also clearly affect the orbital ordering and consequently the magnetic ordering. One might expect a complex canted magnetic ordering to occur, resembling partly C-AFM and partly G-AFM, as indicated experimentally from neutron scattering on several vanadates. While a pure G-type AFM ordering is observed in the Pbnm phase of YVO₃ with magnetic moments lying along the axis, a non-collinear spin arrangement is observed in the P2₁/b phase²⁹,³⁰,⁵¹,⁵³. Indeed, the spin arrangement corresponds to a C-AFM ordering with magnetic moments located in the (ab)-plane plus a weaker G-AFM ordering with magnetic moments along the axis. This observation is totally in line with the coexistence of both Jahn-Teller distortions in the P2₁/b phase. Indeed, while the Pbnm phase can only stabilize a C-o.o./G-AFM ordering, the P2₁/b phase has a dominant G-o.o./C-AFM character coexisting with a smaller C-o.o. and consequently a weak G-AFM ordering may appear with magnetic moments along the axis⁵³. Interestingly, even at the collinear level, our first-principles calculations on the three aforementioned bulk vanadates already indicate this complex magnetic ordering in the P2₁/b phase. Within the YVO₃ Pbnm G-AFM C-o.o. ground state, all magnetic sites hold roughly the same magnetic moment (1.811 ± 0.002 μ_B) indicating a purely C-o.o./G-AFM ordering as observed experimentally. Going to the P2₁/b G-o.o./C-AFM phase of both PrVO₃ and LaVO₃, two magnetic sublattices are observed. Indeed, two different magnitudes for the magnetic moments are found in consecutive (xy)-VO₂ layers (1.833 ± 0.001 and 1.826 ± 0.001 for PrVO₃ and 1.822 ± 0.002 μ_B and 1.813 ± 0.001 μ_B for LaVO₃) which can be seen as a dominant G-o.o. plus a smaller C-o.o. on the top of the latter one, and consequently a dominant C-AFM plus a weaker G-AFM.

(AVO₃)₁/(A’VO₃)₁ layered structures

Magneto-electric multiferroics are widely studied due to their intriguing coupling between ferroelectricity and magnetism (electric field control of magnetism and conversely), and are proposed as promising candidates for lower energy consumption spintronic devices⁷,⁹. However, materials combining both ferroelectric and (anti)-ferromagnetic order parameters are elusive in nature and the identification of new single phase multiferroics remains a challenge for modern day research⁵⁴.

Hybrid improper ferroelectricity, in which a polar distortion is driven by two non-polar motions, emerged recently as a possible new mechanism to induce ferroelectricity in otherwise non-ferroelectric compounds¹⁰,¹¹,¹²,¹³. When considering magnetic compounds, the trilinear coupling between polar and non-polar lattice distortions achieved in such systems appeared moreover as a promising pathway to achieve enhanced magneto-electric coupling¹³,¹⁴,¹⁸,¹⁹,⁵⁵. Rondinelli and Fennie clarified¹² the emergence of rotationally driven ferroelectricity in ABO₃/A’BO₃ superlattices, providing concrete rules for the design of new hybrid improper ferroelectrics.

Following the same spirit, we consider (AVO₃)₁/(A’VO₃)₁ structures with planes of different A cations layered along the [001] direction. This structure can either appear naturally as in the double perovskites, or through single layer precision epitaxial deposition techniques. The free energy expansion around a P₄/mmm layered reference structure (equivalent to 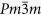in bulk) then becomes:

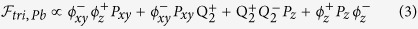The first observation is that the symmetry breaking due to the A cation layering turns the X antipolar modes to polar modes, i.e. in-plane (110) P_xy and out-of-plane (001) P_z¹⁰,¹²,⁵⁴,⁵⁶,⁵⁷. The first and fourth trilinear couplings of Eq. 3 correspond to the rotationally driven hybrid improper ferroelectricity mechanism¹⁰,¹¹,¹². The second trilinear term links the in-plane polarization to both an antiferrodistortive (AFD) and Jahn-Teller (JT) distortion, already observed in reference ¹⁸. However, we identify in Eq. 3 a new trilinear term 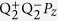coupling the out-of-plane polarization P_z to both JT distortions. Since JT distortions are intimately connected to orbital-orderings and particular magnetic states as discussed in the previous section, we can expect to have a direct and strong coupling between polarization and magnetism from this term.

In the present work, we have performed first-principles calculations in order to show that (AVO₃)₁/(A’VO₃)₁ layered structures are indeed ferroelectric and develop both in plane and out-of-plane polarizations. On the one hand, P_xy appears as a slave to the rotations and is indirectly linked to magnetism through the modification of the superexchange path as in the usual rotationally driven ferroelectrics¹³. On the other hand, P_z appears thanks to an electronic instability manifested as a particular orbital and magnetic ordering. Finally, we demonstrate that an electric control of the magnetic state is indeed possible, providing a novel paradigm for the elusive magnetoelectric multiferroics.

In order to test the above hypothesis, we considered two different superlattices: (PrVO₃)₁/(LaVO₃)₁ (PLVO) and (YVO₃)₁/(LaVO₃)₁ (YLVO). First principles geometry relaxations (see method section) of the superlattices converged to two metastable states: a C-AFM ordering is found in a Pb structure (equivalent to the P2₁/b in bulk) while a G-AFM ordering is found in a Pb2₁m symmetry (equivalent to Pbnm in bulk). We find that PLVO adopts a Pb C-AFM ground state while YLVO adopts a Pb2₁m G-AFM ground state. The symmetry adapted modes and computed polarizations of all metastable phases are presented in the supplementary material. As predicted, the Pb2₁m ground state of YLVO only exhibits a P_xy polarization, whose magnitude is 7.89 μC.cm⁻². However, the Pb ground state of PLVO develops both P_xy and P_z polarizations of 2.94 and 0.34 μC.cm⁻² respectively. The P_z contribution indicates a Jahn-Teller induced ferroelectricity (third term of Eq. 3). Below we explore the origin of P_xy and P_z in more detail.

Bulk vanadates exhibit a Pbnm phase at room temperature and hence both superlattices should first go to the equivalent Pb2₁m intermediate phase. We therefore begin by providing insight on the driving force yielding the various distortions within this phase. For this purpose, we condense different amplitudes of distortions (see methods) within the metastable Pb2₁m state of the PLVO superlattice starting from an ideal P₄/mmm structure (for each potential, see supporting information). Four main distortions are then present in this Pb2₁m phase: 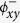, , 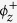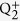and P_xy. As expected, the two antiferrodistortive motions are strongly unstable (approximately 1 eV of energy gains for each) and are the primary order parameters of this Pb2₁m symmetry. P_xy and 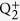present single wells which are the signature of an improper anharmonic appearance⁵⁵. Therefore, the P_xy polarization appears through a hybrid improper mechanism driven by the two rotations through the first term of Eq. 3. Furthermore, as predicted in the first section, this analysis suggests that the 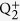appears with a structural hybrid improper mechanism rather than an electronic instability in this compound.

Having considered the intermediate Pb2₁m phase, we next turn our attention to the phase transition of PLVO to its Pb ground state. Curiously, a phonon calculation on the intermediate Pb2₁m phase did not identify any unstable modes, indicating that no lattice motions can be responsible for the phase transition. Clearly, the system has to switch from G-AFM to C-AFM and therefore in an attempt to understand this phase transition we performed the following two sets of calculations. The atomic positions were fixed to the intermediate Pb2₁m structure and the energy was computed i) with imposed and ii) with no imposed, Pb2₁m symmetry for the electronic wavefunction, both within the two possible magnetic states. While for the G-AFM calculations, no energy difference is observed between calculations with and without symmetry, the C-AFM calculation with no symmetry leads to a lower energy (around 4.5 meV) than the one with imposed symmetry. The only difference between the two calculations is that the electronic structure is allowed to distort and consequently breaks the symmetry. We discover that, even with the atoms fixed in centrosymmetric positions along the z axis, the electronic instability creates an out-of-plane polarization P_z of 0.04 μC.cm⁻².

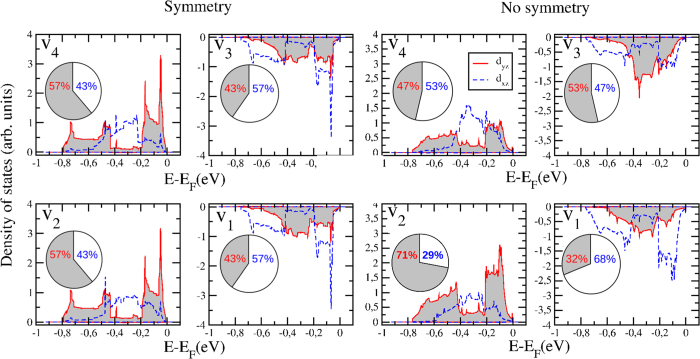
In order to understand the nature of this electronic instability, we plot the projected density of states on vanadiums in Fig. 3. Starting from the projected density of states with Pb2₁m symmetry, consecutive atoms along the z direction (V₁ and V₃, V₂ and V₄ on Fig. 2) exhibit identical density of states. Consequently, the orbital ordering appears to be of C-type. When allowing the electronic structure to distort, several changes appear in the orbital occupations. Consecutive atoms along the z direction now prefer to occupy either more of the d_xz or the d_yz orbital, which results in a mixed G-type (G-o.o.) plus C-type orbital ordering (C-o.o.). The G-o.o. that appears, despite the absence of the 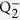motion, is allowed via the Kugel-Khomskii mechanism⁴⁴. This mixed orbital ordering produces an asymmetry between the VO₂ planes, as indicated by the two magnitudes of magnetic moments in each layer (1.816 ± 0.001 μ_B and 1.819 ± 0.001 μ_B). The mixed orbital ordering also appears in the bulk vanadates, such as the G-o.o. + C-o.o. ground state of LaVO₃ or PrVO₃ (previously thought to be just G-o.o. from experiments)²⁵,²⁶. However, here it is not enough to break the inversion symmetry along the z axis yielding no out-of-plane polarization. The second necessary ingredient is the symmetry breaking due to the A and A’ ordering along the [001] direction in the superlattices. The combination of both effects (in the AO and VO₂ planes) is required to break inversion symmetry along the z axis and to produce the out-of-plane polarization. The result is an orbital ordering induced ferroelectricity in vanadate superlattices.

Figure 3. Projected density of states on the d_yz (grey filled red curve) and d_xz (unfilled blue dashed curve) orbitals of vanadium by imposing the Pb2₁m atomic positions and computing the energy with Pb2₁m symmetry (left) for the electronic wavefunction and by removing the symmetry (right) for the electronic wavefunction.

d_xy is not displayed for clarity. V₁ (V₃) and V₂ (V₄) are located within the same (001) plane as defined in Fig. 2. The percentage of total d_yz (red) and d_xz (blue) character on each vanadium is shown as a pie chart to illustrate the change from C-o.o to C + G-o.o. once the symmetry constraint for the wavefunction is lifted.

Interestingly, the direction of the orbital ordering induced ferroelectric polarization is found to be arbitrary, and both + 0.04 and −0.04 μC.cm⁻² are observed. Each state displays a reversal of the magnitude of the magnetic moment of the two VO₂ planes. Starting from these two possibilities, we performed the geometry relaxation and it ended with the previously identified Pb ground states, with both possibilities (up and down) for the out-of-plane polarization. We note that the difference in magnetic moment between both VO₂ planes is more pronounced (1.820 ± 0.001 μ_B and 1.828 ± 0.001 μ_B) after the geometry relaxation. Three new lattice distortions develop to reach the Pb phase: P_z, 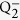and .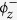

To understand the nature of their appearance, we plot in Fig. 4 each potential as a function of the distortion amplitude. All potentials present single wells, more or less shifted through an improper coupling with the electronic instability. This confirms that the electronic instability is the primary order parameter driving the phase transition. Moreover, the 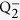motion presents an energy gain of one to two orders of magnitude larger than those of the 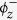motion, indicating that the 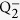couples more strongly with the electronic instability, which might be expected. Consequently, once the electronic instability condenses, the 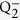lattice distortion is forced into the system which consequently produces the lattice part of the polarization through the structural hybrid improper coupling. This Jahn-Teller induced ferroelectricity amplifies by one order of magnitude the electronic out-of-plane polarization. The sign of the three lattice distortions is again imposed by the initial sign (up or down) of the electronic polarization. Consequently, the reversal of P_z through an application of an external electric field would require the reversal of both 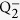, 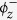and the magnitude of the magnetic moment of both VO₂ planes. The saddle point at the midway of this reversal (all three modes equal zero, i.e. the Pb2₁m phase) is of the order of 10 meV higher in energy, which represents a reasonable estimate of the ferroelectric switching barrier. Compared to the rotationally driven ferroelectricity P_xy, whose energy barrier is of the order of 0.1 to 1 eV¹²,¹⁴,¹⁵, this Jahn-Teller induced ferroelectricity is therefore very likely to be switchable. The large difference between the two energy barriers is due to two different energy landscapes involving i) the robust AFD motions inducing P_xy and ii) the relatively soft distortions inducing P_z.

Figure 4. Energy gains (in meV) by condensing various amplitudes of the individual 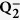, 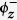and P_z distortions.

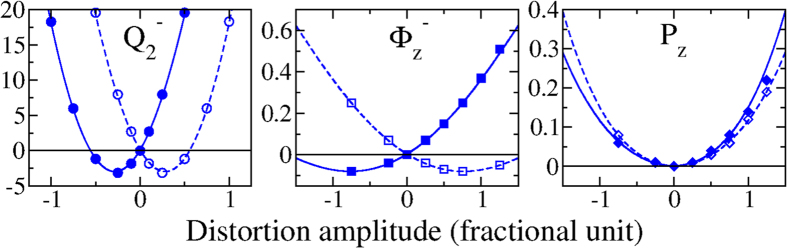
Potentials are plotted for a ‘↑’ (open blue symbols) and a ‘↓’ (filled blue symbols) initial electronic polarization.

Finally we discuss a novel route to create the technologically desired electrical control of magnetization. Starting from a Pb2₁m phase with an G-AFM magnetic ordering, the application of an external electric field along z will induce P_z in the system through the dielectric effect. As a result, the distortion is automatically induced through the  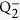 P_z trilinear term. This electric field induced 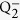distortion is a general result for any (ABO₃)₁/(A’BO₃)₁ superlattice consisting of two Pbnm perovskites. Since 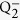distortions are intimately connected to the G-o.o. and the C-AFM magnetic ordering, for a finite value of 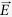, the system may switch from the initial G-AFM phase to the C-AFM phase. In reality, the C-AFM phase should exhibit a net weak magnetization from a non collinear magnetic structure as observed in several bulk vanadates of P2₁/b symmetry²⁸,³⁰,⁵³. Therefore, the application of an electric field may not only switch between AFM orderings, but also produce a net magnetic moment in the material. However, for illustrative purposes, even at the collinear level in our calculations, we can look at the relative stability between the two magnetic states under an external electric field in the YLVO superlattice, which presents the desired Pb2₁m ground state (8 meV lower than the Pb phase).

Figure 5 (top panel) plots the internal energy U(D) of the Pb and Pb2₁m phases as a function of the amplitude of the electric displacement field D applied along the z axis. In such a graph, the switching E-field at which the the Pb phase with the G-o.o./C-AFM ordering becomes more stable than the Pb2₁m phase with the C-o.o./G-AFM ordering, is given by the slope of the common tangent between the two curves and is evaluated to be around 6.54 MV.cm⁻¹. This corresponds to a voltage of 0.50 V for one bilayer 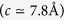. This critical electric field could be further decreased by reducing the energy difference between the two phases at zero field. This can be achieved by changing the A cations or applying biaxial epitaxial strain (see supplementary material).

Figure 5. (top) Internal energy U(D) (in meV) as a function of the electric displacement field D along the z axis for the different phases of YLVO superlattices.

The black dashed line is the common tangent of the two potentials defining the value of the switching electric field. Two polar states are possible for the Pb phase starting from an initial up or down P_z polarization. (bottom) Amplitude of 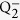distortion as a function of the electric field along the z direction in the Pb2₁m-G-AFM phase (red filled squares) and in the Pb-C-AFM phases with initial up (blue open circles) and down (blue filled circles) polarisation in zero field.

As illustrated in Fig. 5, what we demonstrate more generally in the present study is an electric field control of the JT distortions, mediated by their coupling with the polar mode. Since this mechanism arises from universal symmetry relations, we can expect this effect to also appear in other perovskite superlattices, such as nickelates, fluorites or manganites to name a few. This effect may find applications outside the field of magnetoelectrics such as for tunable band gaps and metal-insulator transitions, since the JT distortion affects the electronic structure in general.

Conclusions

In conclusion, we have identified novel lattice mode couplings in the vanadates, helping to clarify the origin of the unusual coexisting Jahn-Teller phase, and indeed the role of Jahn-Teller distortions in perovskites in general. These findings have enabled the prediction of a novel paradigm for the elusive magnetoelectric multiferroics, based on a Jahn-Teller/orbital ordering induced ferroelectricity. Due to the intimate connection between Jahn-Tellers and orbital ordering with magnetism, this unprecedented type of improper ferroelectric facilitates an electric field control of both orbital-ordering and magnetization. The rationale is completely general, and a challenge for applications will be to identify new materials with a magnetic and co-existing Jahn-Teller phase at room temperature. The demonstration of an electric field control of Jahn-Teller distortions may find more general applications for novel functional devices, outside the field of multiferroics. We hope these discoveries will help motivate future studies that will further unlock the potential of vanadate perovskites, and other Jahn-Teller systems, such as fluorites, nickelates and manganites.

Methods

The basic mechanism we propose here is solely based on symmetry arguments. Symmetry mode analysis of experimental data were performed using amplimodes⁴⁶,⁴⁷. The free energy expansion of Eq. (1 is performed using the invariants software from the isotropy code⁵⁸. The results from these symmetry considerations are not dependent on the technical parameters of the first-principles calculations. The latter are only there to illustrate on a concrete basis and quantify the effect. First principles density functional theory calculations were performed using the VASP package⁵⁹,⁶⁰. We used a 6 × 6 × 4 Monkhorst-Pack k-point mesh to model the Pbnm (P2₁/b) phase and a plane wave cut off of 500 eV. Optimized Projector Augmented wave (PAW) potentials for PBEsol exchange-correlation functional were used in the calculations. The polarization was computed using the Berry phase approach as implemented in VASP. The study was performed within the LDA + U framework⁶¹,⁶². The LDA + U framework has already been shown to be sufficient to reproduce the ground state of vanadates³⁷,⁶³. The U parameter was first fitted on bulk compounds in order to correctly reproduce the ground state of the bulk vanadates. A value of U = 3.5 eV was obtained (see Table 2 and Table 3 in the supporting information). Phonon calculations were performed using the density functional perturbation theory. We used a collinear approach to model the magnetic structures. Structural relaxations were performed until the maximum forces were below 5 μeV.Å⁻¹ and the energy difference between conjugate gradient steps was less than 10⁻⁹ eV. The superlattices were relaxed starting from four different initial guesses: two magnetic orderings (C-AFM and G-AFM) and two space groups (Pb2₁m and Pb, subgroups of Pbnm and P2₁/b respectively for the layered structures). Lattice distortion potentials were plotted as a function of the fractional amplitude of each mode separately appearing in the ground state. In order to determine the electric field required to switch from the Pb2₁m to the Pb phase, the internal energy at fixed D was estimated for each phase as follows. First, the polar atomic distortion pattern ξ associated to the linear response of the system to an electric field E along z was determined from the knowledge of the phonon frequencies and oscillator strengths. Second, the Kohn-Sham energy well U_KS(ξ) in terms of the amplitude of ξ was computed, yielding a model U_KS(P⁰) restricted to the subspace spanned by ξ using P⁰ = Z^*ξ/Ω where Z^* is the Born effective charge associated to ξ, Ω the unit cell volume. Third, U(D) was deduced as⁶⁴:

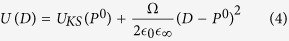where 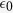is the permittivity of vacuum and 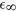, the optical dielectric constant.

Additional Information

How to cite this article: Varignon, J. et al. Coupling and electrical control of structural, orbital and magnetic orders in perovskites. Sci. Rep. 5, 15364; doi: 10.1038/srep15364 (2015).