Abstract
Plastic scintillation detectors (PSDs) work well for radiation dosimetry. However, they show some temperature dependence, and a priori knowledge of the temperature surrounding the PSD is required to correct for this dependence. We present a novel approach to correct PSD response values for temperature changes instantaneously and without the need for prior knowledge of the temperature value. In addition to rendering the detector temperature-independent, this approach allows for actual temperature measurement using solely the PSD apparatus. With a temperature-controlled water tank, the temperature was varied from room temperature to more than 40°C and the PSD was used to measure the dose delivered from a cobalt-60 photon beam unit to within an average of 0.72% from the expected value. The temperature was measured during each acquisition with the PSD and a thermocouple and values were within 1°C of each other. The depth-dose curve of a 6-MV photon beam was also measured under warm non-stable conditions and this curve agreed to within an average of −0.98% from the curve obtained at room temperature. The feasibility of rendering PSDs temperature-independent was demonstrated with our approach, which also enabled simultaneous measurement of both dose and temperature. This novel approach improves both the robustness and versatility of PSDs.
1. Introduction
In the past two decades, plastic scintillation detectors (PSDs) have been shown to be a valuable option for radiation dosimetry before and during radiation treatment delivery (Beddar et al., 1992b, Beddar et al., 1992c, Beddar et al., 2004, Archambault et al., 2010, Suchowerska et al., 2011, Beaulieu et al., 2013). Small size, fast response, water equivalence, linear response to dose, and independence to dose rate and energy are among the advantageous characteristics of PSDs that distinguish them from other detectors. One challenge for PSDs is the presence of radiation-induced stem effect light, often referred to as Cerenkov light (typically the majority component of the stem effect), but many highly effective approaches to account for the stem effect have been validated over the years (Beddar et al., 1992a, De Boer et al., 1993, Clift et al., 2000, Fontbonne et al., 2002, Beddar et al., 2004, Archambault et al., 2005, Frelin et al., 2005, Archambault et al., 2006, Lambert et al., 2008, Archambault et al., 2010, Therriault-Proulx et al., 2011, Guillot et al., 2011). Work has also been done on improving the light collection efficiency (Beddar et al., 2003). Various groups have also reported that some PSDs exhibit temperature dependence (Beddar, 2012, Buranurak et al., 2013, Wootton and Beddar, 2013, Carrasco et al., 2015). Variations of 0.1% to 0.5%/°C were reported depending on the type of scintillator used. This becomes particularly important when the PSD is calibrated at a temperature far from intended use conditions, as could be the case for a detector used in vivo (Wootton et al., 2014). One solution to this problem is to calibrate the PSD at the intended use temperature. Another solution is to apply a linear correction factor to the PSD’s response value that is based on the intended use of the PSD (Buranurak et al., 2013). However, to be highly accurate, both solutions require the temperature to be known and stable. An ideal detector would account for instantaneous variations in temperature.
Here, we describe and demonstrate the feasibility of an approach to correct PSD response values for real-time temperature changes instantaneously and without prior knowledge of the temperature value. The proposed approach takes advantage of the fact that both the intensity and the shape of the scintillator emission spectrum are affected by temperature changes. The feasibility of using this approach to perform accurate dosimetry in external beam radiation therapy under fluctuating temperature conditions is shown. The approach also allows direct measurement of temperature with a PSD. Although this approach is limited to temperature adjustment in this paper, the approach could also potentially be used for any condition leading to similar changes in the emission spectrum of PSDs. The approach described in this paper should therefore lead to an improvement in the versatility and robustness of PSDs as radiation dose measurement probes.
2. Materials and methods
2.1. Mathematical formalism
2.1.1. Measuring the dose
A widely used method to correct for the stem effect is to obtain measurements simultaneously in two spectral windows (Fontbonne et al., 2002, Archambault et al., 2006, Guillot et al., 2011). As reported by Guillot et al. (2011), the radiation dose can be calculated from the following equation:
| (1) |
where M1,i and M2,i represent measurements in different spectral bands for a given irradiation condition (i). The calibration constants (a and b) are obtained under known calibration conditions. This method is referred as the multispectral approach throughout this text.
Another approach, reported by Archambault et al. (2012) and Therriault-Proulx et al. (2012), allowed for the development of multi-point PSDs (Archambault et al., 2012, Therriault-Proulx et al., 2012). In this hyperspectral approach, acquisition of the entire light spectrum allows calculation of the contribution (x) of each light-emitting component of the array of spectra R to a measured spectrum (m). Basically, each measured spectrum is linearly fitted by the different spectra constituting R. The following equations detail this approach for the case of a single-point PSD:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where m is the measured spectrum, R is an array containing the scintillation and stem effect spectra from the different light-emitting components, and x is a vector containing the weights of the different components under a given measurement condition. The dose is obtained from a ratio of the scintillation contribution under a measurement and the calibration condition multiplied by the calibration dose (DCalib; see equation 6).
However, these approaches are based on the assumption that the scintillation intensity varies linearly with dose and dose only. These approaches also assume that the shapes of the spectra stay the same. As mentioned above, it has been shown that this is not always the case and that some influencing factors (e.g., temperature) can lead to changes in both intensity and shape of the scintillation spectrum. This therefore complicates the use of the multispectral and hyperspectral approaches in the forms described above. To overcome this problem, we propose to model the change in spectral shape and amplitude by separating the scintillation spectrum into two sub-components: one that depends on the influencing factor and one that is independent of it (i.e., the reference spectrum). For a given influencing condition, the scintillation spectrum would then be expressed as:
| (7) |
The dose using the hyperspectral approach is still determined using equations 5 and 6, but the scintillation spectrum is now split into two spectra in R and two contribution factors in x, as represented in the following equations:
| (8) |
| (9) |
As was shown previously, the stem effect is actually a combination of the Cerenkov effect and fluorescence, and the contribution of each can change independently (Therriault-Proulx et al., 2013). Therefore, we accounted for these two components separately. Equations 8 and 9 therefore become:
| (10) |
| (11) |
In the approach described here, the influencing factor being the change in temperature, the spectrum ΔScint(λ) was obtained by subtracting the spectra obtained under similar irradiation conditions, but at different temperatures. Therefore, any change in temperature from the condition under which Scint(λ) was obtained is reflected in the value of xΔScint. The value of xScint is now independent from the change in temperature and depends only on dose. The dose can therefore be obtained using equation 6.
2.1.2. Measuring the temperature
In addition to determining the dose value, our approach was also used to determine the temperature value. An approach similar to that shown in equation 6 was used, but this time using the xΔScint factor. However, the proportionality of the ΔScint(λ) spectrum to dose must be accounted for when calculating the value of the temperature. The values for xΔScint therefore have to be normalized by the dose values, or more simply xScint.
Therefore, the change in temperature is obtained by:
| (12) |
where ΔTCalib=TCalib2−TCalib1.
The temperature under a given condition is therefore obtained from:
| (13) |
2.2. Materials
2.2.1. PSD
A PSD was constructed in our laboratory. The PSD consisted of a 3-mm long, green-emitting scintillating fiber (BCF-60; Saint-Gobain Crystals, Hiram, OH, USA), which was chosen for its high temperature dependence compared with other studied scintillating fibers. The scintillating fiber was 1 mm in diameter and coupled with index-matching epoxy to a plastic optical fiber (Eska GH-4001; Mitsubishi Rayon Co., Ltd, Tokyo, Japan). An opaque polyethylene jacket was used to prevent the admission of external light. Black epoxy was used to fill the jacket distal to the scintillating fiber, thus forming an opaque cap within the jacket, also for the purpose of light tightness. The optical fiber was 18 m long to allow the photodetection equipment to remain outside of the radiation vaults. An SMA connector was attached to the proximal end of the optical fiber to interface the detector with a spectrograph (Shamrock; Andor Technology, Belfast, UK) that dispersed the light over a wide-chip charge-coupled device camera (iDus; Andor Technology). The spectra were acquired using Solis Software (Andor Technology) and processed using a MatLab script developed in-house.
2.2.2. Temperature-controlled phantom
A 30 cm × 30 cm × 30 cm acrylic tank filled with water was used. The water in the tank was maintained at a user-specified temperature with a heating system constructed in our laboratory, shown in Figure 1. This system consisted of an intake hose powered by a DC pump, a high-density heating element and K-type thermocouple connected to a proportional-integral-derivative (PID) controller, and an output hose. Both hoses were made of flexible plastic so they could easily be placed in the tank. Between the pump and output hose, water traveled through PVC pipes. PVC caps were used to position the high-density heating element and thermocouple within the PVC pipes and ensure that they were in contact with the water. The PID controller determined whether the high-density heating element was on or off through a solid-state relay. This system allowed the water to be heated and maintained at specific temperatures. The heating element was placed upstream of the thermocouple so that it would read the temperature of water coming from the tank. This setup offers no mechanism for cooling other than natural convection from the ambient air; therefore, the experiments were performed starting at the lowest temperature of interest and gradually working upwards.
Figure 1.
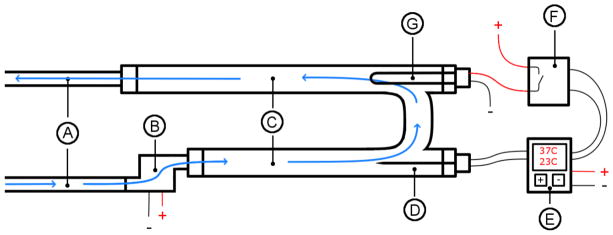
Setup for controlling the temperature in the water tank. A: Input and output hoses. B: Pump. C: PVC pipes. D: Thermocouple. E: Proportional-integral-derivative temperature controller. F: Solid-state relay. G: Electrical heating element.
2.3. Experimental protocol
2.3.1. Calibration
For accurate dosimetry using the hyperspectral approach described previously, it is important to accurately determine the shape of the spectrum of each component accounted for in the composition of the total light output spectrum (i.e., each spectrum constituting R). For our approach, the scintillation, Cerenkov, and fluorescence spectra, as well as the temperature-induced difference in the scintillation spectrum were obtained separately. We varied the emission from one of the spectral components while fixing the others to obtain what is referred to here as the pure spectra. Multiple measurements of each spectrum (resulting in a stack of spectra) were obtained to decrease the associated uncertainty. A sliding median was computed over the acquired wavelengths and the signal was then binned as a function of wavelength in groups of 5. This was done for each individual acquired spectrum, and a median was then calculated over the stack of spectra (i.e., taking the median intensity value over the stack at each wavelength separately).
The pure scintillation spectrum was obtained using a kV irradiator operated at 125 kVp. This energy was below the threshold for Cerenkov production and the fluorescence was minimized by collimating the photon beam on the scintillating element using lead to shield the optical fiber. The acquisition was performed at room temperature. The same radiation modality was used to acquire the pure fluorescence spectrum. In this case, the optical fiber was coiled in the radiation field while the scintillating element was kept outside of the field and shielded by a lead block to avoid the production of any scintillation light.
The pure Cerenkov spectrum was obtained by subjecting the PSD to the same conditions (same dose, same temperature) in two separate sets of measurements using the cobalt-60 irradiator, but with an extra 40 cm of optical fiber coiled in the field for the second set of measurements, as recommended in a previous study by Guillot et al. (2011). A specially designed solid water slab (Standard Imaging, Madison, WI, USA) was used to ensure that the scintillator position was identical for each measurement.
The pure temperature difference spectrum was obtained by immersing the PSD in a beaker filled with water at around 10°C and irradiating it with a cobalt-60 external photon beam. The beaker was insulated with low-density polystyrene to minimize temperature variation. The water was then heated to a warmer temperature (50°C) using a hot plate. A magnetic stirrer was used to ensure homogeneous water temperature. The PSD was then once again irradiated using the cobalt-60 unit and the resulting spectrum was obtained from the difference between the spectra obtained at 50°C and 10°C.
With the shape of the different spectra composing R now well defined, the remaining step for the calibration was to determine the factor relating the amplitude of the spectra to the associated physical value for both dose and temperature. Using the temperature-controlled phantom, we obtained measurements for a defined expected dose (DCalib) at a given temperature (TCalib1 = 20.75°C) under the photon beam from the cobalt-60 unit. The water was then heated to a different temperature (TCalib2 = 38.9°C) and the same dose delivery was repeated. The factors xScint,Calib1, xScint,Calib2, xΔScint,Calib1, and xΔScint,Calib1 were obtained from these 2 measurements and therefore allowed us to determine the dose under any given condition using equation 6 and the temperature using equation 13.
2.3.2. In-phantom measurements
Using the cobalt-60 unit (Theratron), we performed sets of five 10-second irradiations at temperatures differing by increments of about 2°C, ranging from 20.75°C to 40.6°C. Temperature in the water tank was measured using a thermistor.
The dose for each irradiation was calculated using the multispectral approach and the hyperspectral approach with and without the temperature correction. Values were compared with the expected values and the measurement error under each condition was calculated:
| (14) |
The output factors from irradiation of 5 × 5 cm2, 10 × 10 cm2, and 15 × 15 cm2 field sizes were also measured at 0.5-cm and 10-cm depths of maximum dose.
The temperature self-correction approach was also validated using a 6-MV photon beam from a TrueBeam linear accelerator (Varian TrueBeam, Palo Alto, CA, USA). With the PSD inside a motorized water tank, a depth-dose curve was obtained from 1.5 cm to 12 cm at room temperature and under varying temperature conditions. The temperature variation was achieved by heating the water tank to 40°C and then letting it cool down naturally while performing the different measurements. Ten-second acquisitions were performed while irradiating at 600 MU/minute with the linear accelerator. Measured doses were compared with the expected values as measured during the annual calibration of the machine.
Finally, because the proposed approach dispersed the optical signal and more spectra were used to fit the measurements, we wanted to verify that the precision of the PSD and its ability to perform real-time dosimetry were not compromised. The self-correcting hyperspectral approach was therefore compared with the multispectral approach for different acquisition times. With the PSD at depth of maximum dose and at approximately 40°C, the precision of the dose measurement was evaluated for acquisition times ranging from 0.021 seconds to 5 seconds. The measured doses were normalized to the value obtained for the average of 5-second acquisitions.
3. Results
The spectra of the different light-emitting components were normalized to the area under the curve and are shown in Figure 2. As explained above, the light emitted by the scintillator was separated into a temperature-independent scintillation component and a component representing the change in spectrum with temperature. The temperature-dependent spectrum was negative because the light emission was shown to decrease with increasing temperatures.
Figure 2.
Emission spectra of the different light-emitting components. The total scintillation was separated in a temperature-independent spectrum (shown in black) at an arbitrary fixed temperature, and the change in spectrum due to temperature is shown in red.
The error on measured dose over a wide range of temperatures was compared among the multispectral, hyperspectral, and hyperspectral self-correcting approaches. Figure 3 shows the measurement error for each approach as a function of temperature when the PSD was calibrated at room temperature. The performance of the multispectral and hyperspectral approaches was similar, with error increasing by about 0.75%/°C in the negative direction. The novel approach (i.e., the hyperspectral self-correcting approach) minimized the temperature dependence of the PSD, with an average error of 0.72% and standard deviation of 0.63% over the entire temperature range, and a maximum deviation of (1.6±0.9)%. The output factors for different field sizes and depths measured under warm conditions are presented in Table 1. These factors agree well with the actual output factors.
Figure 3.
Average error on measured dose (±standard deviation) as a function of temperature for the different dosimetry approaches.
Table 1.
Average (Avg) and standard deviation (Std) of the measured error on the output factor determined for 7 repeated measurements at different field sizes and depths under warm conditions. Output factors were normalized to the value of the 10 × 10 cm2 field size at 0.5-cm depth.
| Field size | ||||||
|---|---|---|---|---|---|---|
| 5 × 5 cm2 | 10 × 10 cm2 | 15 × 15 cm2 | ||||
| Depth | Avg | Std | Avg | Std | Avg | Std |
| 0.5 cm | 0.09% | 0.49% | 0% | 0.65% | −1.17% | 0.85% |
| 10 cm | 1.23% | 0.31% | −0.21% | 0.29% | −1.88% | 0.34% |
The measurement of dose as a function of depth for the 6-MV photon beam from a TrueBeam linear accelerator is shown in Figure 4. Measurements at room temperature were in good agreement with the expected values, with an average error of 0.06% and standard deviation 0.17%. The depth dose curve obtained under warm conditions showed an average error of −0.92% and standard deviation of 0.50%. The bottom panel of Figure 4 shows the relative difference between the two sets of measured doses, and the average difference was −0.98% (standard deviation = 0.42%).
Figure 4.
Depth-dose curve from a 6-MV linear accelerator photon beam measured at room temperature and under warm conditions as recorded by the plastic scintillation detector, compared with the expected values (top panel). Dose values (mean ± standard uncertainty) were normalized to the value measured at room temperature at depth of maximum dose. The relative differences between doses measured under warm conditions and room temperature are presented in the bottom panel.
Table 2 shows the average measured error and standard deviation (std) as a function of the integration time. The measurements were in good agreement with the expected values for all integration times, but the standard deviation was higher for faster acquisitions.
Table 2.
Average error and standard deviation(std) of the detector for different acquisition times. Values were normalized to the values obtained for 5-second acquisitions.
| Acquisition time, seconds | No. of measurements | Average error (± std)
|
|
|---|---|---|---|
| Hyperspectral | Multispectral | ||
| 0.021 | 59 | 0.85 ± 5.23 | −0.19 ± 5.64 |
| 0.1 | 29 | 0.41 ± 1.60 | −0.20 ± 0.58 |
| 0.5 | 9 | −0.38 ± 0.66 | −0.39 ± 0.53 |
| 1 | 9 | −0.38 ± 0.70 | −0.38 ± 0.54 |
| 3 | 9 | −0.13 ± 0.38 | −0.18 ± 0.53 |
| 5 | 9 | 0.00 ± 0.24 | 0.00 ± 0.54 |
Finally, as shown in Figure 5, the temperature-dependent contribution factor (xTemp) varied linearly with the temperature when normalized by the dose-only dependent factor (xscint). Related temperature differences between the measured data and the fit were all within 1°C, with an average value of 0.0°C (std= 0.3°C).
Figure 5.
Variation in temperature measured using the plastic scintillation detector compared with the expected values (top panel). Average and standard deviation of the calculated values are shown. Calibration of the plastic scintillation detector for temperature measurement was performed using the contribution factors measured at 20.75°C and 38.9°C. The differences between measured and expected values (ΔT) are shown in the bottom panel.
4. Discussion
4.1. Proof of feasibility
Here, we have demonstrated the feasibility of a spectral-based correction mechanism to adjust for temperature variations when using a PSD. As shown in Figure 3, under variable temperature conditions, this approach outperformed the multispectral and naïve hyperspectral approaches, which were similar to one another. This is relevant when a PSD is calibrated at room temperature and used at any other unknown or fluctuating temperature. When a PSD is used at a known and stable temperature, the three approaches would show similar performances. Because the multispectral and hyperspectral approaches show a linear relationship with temperature, a correction factor could be calculated from measurements at a minimum of two different temperatures as part of the calibration process, as recommended by Buranurak et al. (2013). The technical difficulty of obtaining such measurements is similar to that of the self-correcting approach. However, the correction factor method additionally requires the temperature at the point of measurement to be known accurately and could not account for unexpected temperature fluctuations.
The proposed approach was also shown to be accurate when measuring the output factors for different field sizes under cobalt-60 irradiation at temperatures significantly above room temperature (see Table 1). In Figure 4, the capability of the novel approach to provide accurate dose measurements at varying temperatures warmer than room temperature was demonstrated for 6-MV photon beam radiation. The relative differences between the values obtained at warm temperatures and those obtained at room temperature were in agreement with the PSD’s error under cobalt-60 irradiation (see Figure 3). It is also interesting to note that as the temperature was cooling down (and therefore getting closer to the calibration temperature), the relative difference between the two conditions decreased. The relative difference was less than 2% for all measurement conditions, demonstrating the added versatility and robustness of the PSD with the self-correcting approach.
The results presented in Table 2 suggest that a PSD system could be effectively used with the temperature-independent hyperspectral approach for real-time dosimetry. These results addressed the concern that dispersing the optical signal to obtain spectral information and using more spectra to fit a measurement could result in light losses severe enough to require longer acquisitions to achieve an acceptable signal-to-noise ratio. As shown in Table 2, the hyperspectral and multispectral approaches performed similarly in this respect down to a 0.5-second acquisition time. The multispectral approach proved slightly more accurate and precise for a 0.1-second acquisition time (average error and standard deviation of 0.41% and 1.60% for the hyperspectral approach compared with −0.20% and 0.58% for the multispectral approach). However, optimizing the selection of the weighting factors and binning intervals could improve the temporal performance of the hyperspectral approach in a manner similar to that previously demonstrated for the multispectral approach (Guillot et al., 2011).
4.2. In vivo dosimetry applications
The effect of temperature on real-time in vivo dosimetry is a known problem. Whether MOSFETs, diodes, or scintillation detectors are used, the temperature change between the calibration and use conditions must be accounted for (Soubra et al., 1994, Saini and Zhu, 2002, Cheung et al., 2004, Mijnheer et al., 2013, Tanderup et al., 2013). Knowing the temperature in real-time to adjust the temperature correction factor accordingly would require the addition of a temperature probe in the vicinity of the detector, which would make the detector more challenging to develop or more cumbersome to use. This is why a general estimate of the temperature is used, but this is subject to uncertainty and fluctuations, as outlined above.
To illustrate this challenge, we consider in vivo measurements obtained within the body. A detector might be inserted within a catheter already placed as part of the treatment (in brachytherapy for example), but it is unlikely that a temperature probe can be placed in the same catheter. Another catheter could be used, but this would preclude the possibility of measuring temperature fluctuations in the immediate vicinity of the detector and would give only a general idea of the local temperature. As a second illustration, we consider skin dose measurements, which are currently the most widely practiced form of in vivo dosimetry (Fiorino et al., 2000, Bloemen-van Gurp et al., 2003, Appleyard et al., 2005). Determining the absolute temperature and fluctuations is problematic. Because the detector is placed at the skin surface, it is at a temperature somewhere between that of the skin and the ambient air. Placing a temperature probe next to the detector does not guarantee that the probe and the detector would be at the same temperature because they are composed of different materials. Furthermore, there may be a temperature gradient between the two positions. Also, because the detector is subject to convection from the ambient air and conduction from the skin surface, the temperature may vary at the point of measurement during the treatment delivery. The proposed approach accounts for all of these variables without the need for further consideration by automatically correcting for signal fluctuations due to temperature. The proposed approach also allows a simpler system to be used because a temperature probe is not needed, and therefore limits the introduction of materials that are not water equivalent and potentially perturbing the dose delivery.
4.3. Simultaneous measurement of dose and temperature
In addition to making PSDs temperature-independent, the proposed approach enables PSDs to measure temperature during irradiation. All measured temperatures shown in Figure 5 were within 1°C of the water temperature value measured with the thermistor. The possibility of simultaneously measuring dose and temperature is advantageous in ways that extend beyond the scope of this paper and could possibly lead to new avenues of research. One potential application would be to use the detector for in vivo dose and temperature measurement during regional hyperthermia radiation therapy. This is a procedure during which part of the body is heated to enhance the effectiveness of radiation therapy, because cancer cells are relatively less tolerant to heat than healthy cells (Field and Bleehen, 1979, Overgaard, 1980, Kim et al., 1982, Overgaard, 1989, Overgaard et al., 1995, Vernon et al., 1996, Matsuda et al., 1997, Falk and Issels, 2001, Chicheł et al., 2007). This has been an ongoing field of research for the past couple of decades and could benefit from new measurement tools.
4.4. Generalization of the approach
Finally, it is important to emphasize that even though our approach accounts only for temperature dependence, the approach could be generalized to other influencing factors affecting the scintillation emission spectrum in a similar manner. This would further improve the versatility and robustness of scintillation detectors because they would then be independent of those factors and simultaneously capable of measuring the physical value of the factor, all with a detector made solely of water-equivalent materials.
4.5. Conclusion
We have demonstrated the feasibility of a spectral approach to render a PSD temperature-independent while maintaining the ability of the PSD to perform real-time measurements. Additionally, the proposed approach enables PSDs to serve simultaneously as dose detectors and temperature probes. There are many possible applications for such a detector, including internal and external in vivo dosimetry as well as a temperature measurement tool during hyperthermal radiation therapy.
Acknowledgments
F. Therriault-Proulx was supported in part by the Odyssey Program at The University of Texas MD Anderson Cancer Center, and the Natural Sciences and Engineering Research Council (NSERC). This project and SB were supported in part by a NIH/NCI award # CA182450 from the National Cancer Institute.
Footnotes
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
References
- Appleyard R, Ball K, Hughes FE, Kilby W, Nicholls R, Rabett V, Sage J, Smith M, Thomson E. Systematic in vivo dosimetry for quality assurance using diodes 2: Assessing radiotherapy techniques and developing an appropriate action protocol. Journal of Radiotherapy in Practice. 2005;4:143–154. [Google Scholar]
- Archambault L, Arsenault J, Gingras L, Sam Beddar A, Roy R, Beaulieu L. Plastic scintillation dosimetry: Optimal selection of scintillating fibers and scintillators. Med Phys. 2005;32:2271–2278. doi: 10.1118/1.1943807. [DOI] [PubMed] [Google Scholar]
- Archambault L, Beddar AS, Gingras L, Roy R, Beaulieu L. Measurement accuracy and cerenkov removal for high performance, high spatial resolution scintillation dosimetry. Med Phys. 2006;33:128–35. doi: 10.1118/1.2138010. [DOI] [PubMed] [Google Scholar]
- Archambault L, Briere TM, Pönisch F, Beaulieu L, Kuban DA, Lee A, Beddar S. Toward a Real-Time In Vivo Dosimetry System Using Plastic Scintillation Detectors. International Journal of Radiation Oncology*Biology*Physics. 2010;78:280–287. doi: 10.1016/j.ijrobp.2009.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archambault L, Therriault-Proulx F, Beddar S, Beaulieu L. A mathematical formalism for hyperspectral, multi-point, plastic scintillation detectors. Phys Med Biol. 2012;57:7133–7145. doi: 10.1088/0031-9155/57/21/7133. [DOI] [PubMed] [Google Scholar]
- Beaulieu L, Goulet M, Archambault L, Beddar S. Current status of scintillation dosimetry for megavoltage beams. Journal of Physics: Conference Series. 2013;444:012013. [Google Scholar]
- Beddar AS, Law S, Suchowerska N, Mackie TR. Plastic scintillation dosimetry: optimization of light collection efficiency. Phys Med Biol. 2003;48:1141–52. doi: 10.1088/0031-9155/48/9/305. [DOI] [PubMed] [Google Scholar]
- Beddar AS, Mackie TR, Attix FH. Cerenkov light generated in optical fibres and other light pipes irradiated by electron beams. Phys Med Biol. 1992a;37:925. [Google Scholar]
- Beddar AS, Mackie TR, Attix FH. Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: I. Physical characteristics and theoretical considerations. Phys Med Biol. 1992b;37:1883. doi: 10.1088/0031-9155/37/10/006. [DOI] [PubMed] [Google Scholar]
- Beddar AS, Mackie TR, Attix FH. Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: II. Properties and measurements. Phys Med Biol. 1992c;37:1901. doi: 10.1088/0031-9155/37/10/007. [DOI] [PubMed] [Google Scholar]
- Beddar AS, Suchowerska N, Law SH. Plastic scintillation dosimetry for radiation therapy: minimizing capture of Cerenkov radiation noise. Phys Med Biol. 2004;49:783–90. doi: 10.1088/0031-9155/49/5/009. [DOI] [PubMed] [Google Scholar]
- Beddar S. On possible temperature dependence of plastic scintillator response. Med Phys. 2012;39:6522. doi: 10.1118/1.4748508. [DOI] [PubMed] [Google Scholar]
- Bloemen-Van Gurp E, Du Bois W, Visser P, Bruinvis IN, Jalink D, Hermans J, Lambin P. Clinical dosimetry with MOSFET dosimeters to determine the dose along the field junction in a split beam technique. Radiotherapy and Oncology. 2003;67:351–357. doi: 10.1016/s0167-8140(03)00035-5. [DOI] [PubMed] [Google Scholar]
- Buranurak S, Andersen CE, Beierholm AR, Lindvold LR. Temperature variations as a source of uncertainty in medical fiber-coupled organic plastic scintillator dosimetry. Radiation Measurements. 2013;56:307–311. [Google Scholar]
- Carrasco P, Jornet N, Jordi O, Lizondo M, Latorre-Musoll A, Eudaldo T, Ruiz A, Ribas M. Characterization of the Exradin W1 scintillator for use in radiotherapy. Med Phys. 2015;42:297–304. doi: 10.1118/1.4903757. [DOI] [PubMed] [Google Scholar]
- Cheung T, Butson MJ, Yu PKN. Effects of temperature variation on MOSFET dosimetry. Phys Med Biol. 2004;49:N191. doi: 10.1088/0031-9155/49/13/n02. [DOI] [PubMed] [Google Scholar]
- Chicheł A, Skowronek J, Kubaszewska M, Kanikowski M. Hyperthermia – description of a method and a review of clinical applications. Reports of Practical Oncology & Radiotherapy. 2007;12:267–275. [Google Scholar]
- Clift MA, Sutton RA, Webb DV. Dealing with Cerenkov radiation generated in organic scintillator dosimeters by bremsstrahlung beams. Phys Med Biol. 2000;45:1165–82. doi: 10.1088/0031-9155/45/5/307. [DOI] [PubMed] [Google Scholar]
- De Boer F, Beddar AS, Rawlinsott JA. Optical filtering and spectral measurements of radiation-induced light in plastic scintillation dosimetry. Phys Med Biol. 1993;38:945–958. [Google Scholar]
- Falk MH, Issels RD. Hyperthermia in oncology. International Journal of Hyperthermia. 2001;17:1–18. doi: 10.1080/02656730150201552. [DOI] [PubMed] [Google Scholar]
- Field SB, Bleehen NM. Hyperthermia in the treatment of cancer. Cancer Treatment Reviews. 1979;6:63–94. doi: 10.1016/s0305-7372(79)80043-2. [DOI] [PubMed] [Google Scholar]
- Fiorino C, Corletto D, Mangili P, Broggi S, Bonini A, Cattaneo GM, Parisi R, Rosso A, Signorotto P, Villa E, Calandrino R. Quality assurance by systematic in vivo dosimetry: results on a large cohort of patients. Radiotherapy and Oncology. 2000;56:85–95. doi: 10.1016/s0167-8140(00)00195-x. [DOI] [PubMed] [Google Scholar]
- Fontbonne JM, Iltis G, Ban G, Battala I, Vernhes JC, Tillier J, Bellaize N, Lebrun C, Taiman B, Mercier K, Motin JC. Scintillating fiber dosimeter for radiation therapy accelerator. IEEE Trans Nucl Sci. 2002;49:2223–2227. [Google Scholar]
- Frelin A-M, Fontbonne J-M, Ban G, Colin J, Labalme M, Batalla A, Isambert A, Vela A, Leroux T. Spectral discrimination of Čerenkov radiation in scintillating dosimeters. Med Phys. 2005;32:3000–3006. doi: 10.1118/1.2008487. [DOI] [PubMed] [Google Scholar]
- Guillot M, Gingras L, Archambault L, Beddar S, Beaulieu L. Spectral method for the correction of the Cerenkov light effect in plastic scintillation detectors: a comparison study of calibration procedures and validation in Cerenkov light-dominated situations. Med Phys. 2011;38:2140–50. doi: 10.1118/1.3562896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JH, Hahn EW, Ahmed SA. Combination hyperthermia and radiation therapy for malignant melanoma. Cancer. 1982;50:478–482. doi: 10.1002/1097-0142(19820801)50:3<478::aid-cncr2820500316>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Lambert J, Yin Y, Mckenzie DR, Law S, Suchowerska N. Cerenkov-free scintillation dosimetry in external beam radiotherapy with an air core light guide. Phys Med Biol. 2008;53:3071–80. doi: 10.1088/0031-9155/53/11/021. [DOI] [PubMed] [Google Scholar]
- Matsuda H, Kuwano H, Ohno S, Maehara Y, Sugimachi K. Effectiveness of hyperthermia and radiation treatments for patients with esophageal cancer predicted by the succinate dehydrogenase inhibition test. Int Surg. 1997;82:91–3. [PubMed] [Google Scholar]
- Mijnheer B, Beddar S, Izewska J, Reft C. In vivo dosimetry in external beam radiotherapy. Med Phys. 2013;40:070903. doi: 10.1118/1.4811216. [DOI] [PubMed] [Google Scholar]
- Overgaard J. Simultaneous and sequential hyperthermia and radiation treatment of an experimental tumor and its surrounding normal tissue in vivo. International Journal of Radiation Oncology*Biology*Physics. 1980;6:1507–1517. doi: 10.1016/0360-3016(80)90008-5. [DOI] [PubMed] [Google Scholar]
- Overgaard J. The current and potential role of hyperthermia in radiotherapy. International Journal of Radiation Oncology*Biology*Physics. 1989;16:535–549. doi: 10.1016/0360-3016(89)90470-7. [DOI] [PubMed] [Google Scholar]
- Overgaard J, Bentzen SM, Gonzalez Gonzalez D, Hulshof MCCM, Arcangeli G, Dahl O, Mella O. Randomised trial of hyperthermia as adjuvant to radiotherapy for recurrent or metastatic malignant melanoma. The Lancet. 1995;345:540–543. doi: 10.1016/s0140-6736(95)90463-8. [DOI] [PubMed] [Google Scholar]
- Saini AS, Zhu TC. Temperature dependence of commercially available diode detectors. Med Phys. 2002;29:622–630. doi: 10.1118/1.1461842. [DOI] [PubMed] [Google Scholar]
- Soubra M, Cygler J, Mackay G. Evaluation of a dual bias dual metal oxide-silicon semiconductor field effect transistor detector as radiation dosimeter. Med Phys. 1994;21:567–572. doi: 10.1118/1.597314. [DOI] [PubMed] [Google Scholar]
- Suchowerska N, Jackson M, Lambert J, Yin YB, Hruby G, Mckenzie DR. Clinical trials of a urethral dose measurement system in brachytherapy using scintillation detectors. Int J Radiat Oncol Biol Phys. 2011;79:609–15. doi: 10.1016/j.ijrobp.2010.03.030. [DOI] [PubMed] [Google Scholar]
- Tanderup K, Beddar S, Andersen CE, Kertzscher G, Cygler JE. In vivo dosimetry in brachytherapy. Med Phys. 2013;40:070902. doi: 10.1118/1.4810943. [DOI] [PubMed] [Google Scholar]
- Therriault-Proulx F, Archambault L, Beaulieu L, Beddar S. Development of a novel multi-point plastic scintillation detector with a single optical transmission line for radiation dose measurement. Phys Med Biol. 2012;57:7147–7160. doi: 10.1088/0031-9155/57/21/7147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Therriault-Proulx F, Beaulieu L, Archambault L, Beddar S. On the nature of the light produced within PMMA optical light guides in scintillation fiber-optic dosimetry. Phys Med Biol. 2013;58:2073–2084. doi: 10.1088/0031-9155/58/7/2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Therriault-Proulx F, Beddar S, Briere TM, Archambault L, Beaulieu L. Technical note: removing the stem effect when performing Ir-192 HDR brachytherapy in vivo dosimetry using plastic scintillation detectors: a relevant and necessary step. Med Phys. 2011;38:2176–9. doi: 10.1118/1.3562902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vernon CC, Hand JW, Field SB, Machin D, Whaley JB, Zee JVD, Van Putten WLJ, Van Rhoon GC, Van Dijk JDP, González DG, Liu F-F, Goodman P, Sherar M Princess Margaret Hospital/Ontario Cancer I. Radiotherapy with or without hyperthermia in the treatment of superficial localized breast cancer: Results from five randomized controlled trials. International Journal of Radiation Oncology*Biology*Physics. 1996;35:731–744. doi: 10.1016/0360-3016(96)00154-x. [DOI] [PubMed] [Google Scholar]
- Wootton L, Beddar S. Temperature dependence of BCF plastic scintillation detectors. Phys Med Biol. 2013;58:2955. doi: 10.1088/0031-9155/58/9/2955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wootton L, Kudchadker R, Lee A, Beddar S. Real-time in vivo rectal wall dosimetry using plastic scintillation detectors for patients with prostate cancer. Phys Med Biol. 2014;59:647–660. doi: 10.1088/0031-9155/59/3/647. [DOI] [PMC free article] [PubMed] [Google Scholar]