Physiologically Based Pharmacokinetic (PBPK) Modeling and Simulation Approaches: A Systematic Review of Published Models, Applications, and Model Verification

Abstract

Modeling and simulation of drug disposition has emerged as an important tool in drug development, clinical study design and regulatory review, and the number of physiologically based pharmacokinetic (PBPK) modeling related publications and regulatory submissions have risen dramatically in recent years. However, the extent of use of PBPK modeling by researchers, and the public availability of models has not been systematically evaluated. This review evaluates PBPK-related publications to 1) identify the common applications of PBPK modeling; 2) determine ways in which models are developed; 3) establish how model quality is assessed; and 4) provide a list of publically available PBPK models for sensitive P450 and transporter substrates as well as selective inhibitors and inducers. PubMed searches were conducted using the terms “PBPK” and “physiologically based pharmacokinetic model” to collect published models. Only papers on PBPK modeling of pharmaceutical agents in humans published in English between 2008 and May 2015 were reviewed. A total of 366 PBPK-related articles met the search criteria, with the number of articles published per year rising steadily. Published models were most commonly used for drug-drug interaction predictions (28%), followed by interindividual variability and general clinical pharmacokinetic predictions (23%), formulation or absorption modeling (12%), and predicting age-related changes in pharmacokinetics and disposition (10%). In total, 106 models of sensitive substrates, inhibitors, and inducers were identified. An in-depth analysis of the model development and verification revealed a lack of consistency in model development and quality assessment practices, demonstrating a need for development of best-practice guidelines.

Introduction

Prediction of disposition characteristics of new drug candidates can identify pharmacokinetic (PK) liabilities such as poor bioavailability, high clearance, potential for drug-drug interactions (DDIs), or the need for dose adjustments in special populations (Obach et al., 1997; Jones et al., 2009; Zhao et al., 2011; Chen et al., 2012; Di et al., 2013; Shardlow et al., 2013). Such predictions can help decision making in relation to development progression, dose selection, and clinical study strategies (Obach et al., 1997; Jones et al., 2009, 2015; Rowland et al., 2011; Zhao et al., 2011; Chen et al., 2012; Di et al., 2013; Shardlow et al., 2013). Various allometric scaling, in vitro-to-in vivo extrapolation (IVIVE), and in silico methods have been developed over the years to enable predictions of human pharmacokinetics prior to first in human dosing. More than 30 different methods exist to predict human volume of distribution (Di et al., 2013), including interspecies scaling (Lombardo et al., 2013a) and in silico methods. Generally, in vivo animal data, log P values, plasma protein binding, and blood-to-plasma ratios are used to predict the human steady-state volume of distribution and tissue-to-plasma partitioning (Poulin and Theil, 2000, 2002; Poulin et al., 2001; Berezhkovskiy, 2004; Rodgers et al., 2005; Rodgers and Rowland, 2006). While interspecies scaling allows predictions of the human volume of distribution, its utility in the prediction of human clearance is limited due to species differences in the expression and substrate specificity of drug metabolizing enzymes and transporters (Obach et al., 1997; Di et al., 2013). Instead, IVIVE tools have been developed to predict hepatic bioavailability and whole organ clearances using in vitro intrinsic clearance, protein binding and permeability data and in vivo blood flows (Houston, 1994; Iwatsubo et al., 1997; Obach et al., 1997; Lombardo et al., 2013b; Cho et al., 2014). While further efforts are needed to improve IVIVE, particularly for transporters and non-P450 enzymes, IVIVE has become an important tool in the process of predicting human exposures and effective dosages.

Quantitative methods to predict pharmacokinetics range in complexity from static mechanistic predictions of specific PK parameters to dynamic physiologically based PK (PBPK) models used to predict plasma concentration-time curves. Static mechanistic methods typically use one or two in vitro parameters to predict specific human PK parameters, and can therefore be easily adopted in screening programs to prioritize and triage compounds based on undesirable pharmacokinetics. Static prediction methods have been used extensively to predict human metabolic (Gillette, 1971; Rowland et al., 1973; Iwatsubo et al., 1997; Obach et al., 1997) and transporter-mediated clearance (Liu and Pang, 2005; Barton et al., 2013; Varma et al., 2013) and drug-drug interactions (Mayhew et al., 2000; Wang et al., 2004; Obach et al., 2007; Fahmi et al., 2008). However, while static models are very useful for predictions of overall drug exposures in humans or the overall magnitude of DDIs, they rely on steady-state assumptions and hence cannot predict the overall shape of the plasma concentration-time curve, time-varying changes in enzyme or transporter inhibition, or the distribution kinetics of new drugs. In contrast, PBPK models provide simulated concentration versus time profiles of a drug and its metabolite(s) in plasma or an organ of interest and simultaneously allow for estimation of maximum plasma concentrations, absorption kinetics, distribution kinetics, and drug elimination. While the simultaneous modeling of drug disposition processes provides multiple advantages (Rostami-Hodjegan and Tucker, 2007; Almond et al., 2009; Fahmi et al., 2009; Jamei et al., 2009a; Rowland et al., 2011; Huang and Rowland, 2012; Di et al., 2013; Shardlow et al., 2013; Galetin, 2014; Tsamandouras et al., 2015; Varma et al., 2015b), it also makes PBPK modeling labor intensive and requires considerably more parameter estimates and more detailed physiologic and drug-specific data than static predictions. The simulated concentration-time profiles can aid in selection of optimal sampling times or dosing strategies in different study populations, including vulnerable subjects (Rowland et al., 2011). They can also aid in design of DDI studies in which the timing of the dosing of the perpetrator drug and the victim drug is critical (Zhao et al., 2009; Shardlow et al., 2013), or in situations where perpetrator concentrations fluctuate over the sampling and dosing interval (Almond et al., 2009; Fahmi et al., 2009; Pang and Durk, 2010; Di et al., 2013). Additionally, the simulated concentrations can be linked to pharmacodynamic endpoints to allow for PK/PD (pharmacokinetic-pharmacodynamic) simulations. Furthermore, because PBPK models account for sequential metabolism and permeability limited processes, they may provide advantages for predicting bioavailability when compared with static models (Fan et al., 2010; Chow and Pang, 2013). This can have important implications for first in human dose selection, particularly for drugs with active or toxic metabolites. In some cases, PBPK models incorporate interindividual variability, thus allowing for the prospective simulation of the population variability in the pharmacokinetics of a given drug. Population variability is not typically accounted for in static models but can provide insight into variability in exposure and drug response in a given population (Rostami-Hodjegan and Tucker, 2007; Jamei et al., 2009a; Cubitt et al., 2011; Brown et al., 2012). Finally, the separation of drug-specific and physiologic parameters within the model can allow a more mechanistic understanding of the sources of interindividual variability than can be provided by population and compartmental modeling techniques (Rostami-Hodjegan and Tucker, 2007; Vinks, 2013; Tsamandouras et al., 2015). However, detailed understanding of physiologic variables in the population of interest is required but not always available, which can hinder the use of PBPK modeling in special populations.

In recent years, the number of publications (Rowland et al., 2011; Rostami-Hodjegan et al., 2012) and regulatory submissions (Zhao et al., 2011; Huang et al., 2013; Sinha et al., 2014) referencing or including PBPK modeling has increased substantially. The development of user-friendly software tools such as Simcyp, GastroPlus, and PK-Sim have made modeling more accessible to those without extensive modeling and/or programming experience (Zhao et al., 2011; Chen et al., 2012; Huang et al., 2013). However, it is possible that many users are not completely familiar with, or aware of, the assumptions made and equations used during model building and implementation. As such, the increased implementation of PBPK modeling has led to a need for comprehensive software and modeling-focused education as well as the need to confirm the sound knowledge of users in ADME principles and fundamental physiology (Jones et al., 2015). A recommendation for the presence of a modeling expert for advice and to review models has also been made to ensure appropriate decision making and interpretation of the modeling (Jones et al., 2015). Advancements in computer science and physiologically based mathematical models have led to the expansion of the potential applications of PBPK modeling. For example, more complex absorption models such as advanced dissolution, absorption, and metabolism (ADAM) models (Jamei et al., 2009b) and advanced compartmental absorption and transit (ACAT) models (Agoram et al., 2001) have been developed that enable the use of PBPK modeling for the simulation of food effects (Shono et al., 2009; Turner et al., 2012; Heimbach et al., 2013; Xia et al., 2013b; Patel et al., 2014; Zhang et al., 2014), the impact of drug properties on absorption kinetics (Kambayashi et al., 2013; Parrott et al., 2014), and intestinal interactions (Fenneteau et al., 2010). The development of sophisticated models that allow for the simulation of multiple inhibitors or inducers, relevant metabolites, and multiple mechanisms of interaction have permitted the prediction of complex DDIs involving enzymes, transporters, and multiple interaction mechanisms (Zhang et al., 2009; Rekić et al., 2011; Varma et al., 2012, 2013; Dhuria et al., 2013; Gertz et al., 2013, 2014; Guo et al., 2013; Kudo et al., 2013; Siccardi et al., 2013; Wang et al., 2013a; Sager et al., 2014; Chen et al., 2015; Shi et al., 2015). Furthermore, the mechanistic understanding of ADME changes that occur in different age groups or disease states has improved, and consequently PBPK modeling has been used to simulate drug disposition in special populations including hepatic (Johnson et al., 2014) and renal impairment populations (Li et al., 2012; Zhao et al., 2012a; Lu et al., 2014; Sayama et al., 2014), children (Leong et al., 2012), and pregnant women (Andrew et al., 2008; Gaohua et al., 2012; Horton et al., 2012; Ke et al., 2012, 2013, 2014; Lu et al., 2012).

In the past 10 years, PBPK modeling has become increasingly accepted by regulatory agencies as a means of informing clinical study strategy, and it has become a useful tool in drug development (Leong et al., 2012; Zhao et al., 2012b; Huang et al., 2013; Sinha et al., 2014). PBPK approaches have been included in regulatory guidance on hepatic impairment [Committee for Medicinal Products for Human Use (CHMP), 2005], pediatrics [Center for Drug Evaluation and Research (CDER), 2014], DDIs (CDER, 2012; CHMP, 2012; Ministry of Health, Labor and Welfare Research Group, 2014), and pharmacogenetics (CHMP, 2011; CDER, 2013) as a means to guide clinical study design and labeling decisions. Hence, in addition to being used to inform internal development decisions (Jones et al., 2009, 2015; Chen et al., 2012; Shardlow et al., 2013), PBPK modeling is increasingly being used in investigating new drugs and new drug applications (Huang et al., 2013; CHMP, 2014; Sinha et al., 2014). The U.S. Food and Drug Administration (FDA) Office of Clinical Pharmacology has been tracking the use of PBPK modeling in regulatory submissions since 2008 (Huang et al., 2013; Pan et al., 2014). Based on 2013 submissions, the models included in regulatory filings were most commonly used for DDI (60%), pediatric (21%), and absorption (6%) predictions (Pan et al., 2014). PBPK models have been used during the review process to inform dose selection and optimal design for clinical studies (Leong et al., 2012), and in some cases to directly inform labeling (Zhao et al., 2012b). For example, cabazitaxel is predicted to cause in vivo CYP3A4 inhibition based on the ratio between its concentration and inhibition constant, ([I]/K_i ratio). However, modeling and simulation suggested minimal risk for DDI in vivo. As a result, the label states that “a post-marketing requirement for the effect of cabazitaxel on the pharmacokinetics of a sensitive CYP3A4 substrate is therefore not necessary” (Huang and Rowland, 2012; Huang et al., 2013; CDER, 2010). Additional examples of PBPK-informed labeling between 2008 and 2014 are included in recent reviews (Zhao et al., 2012b; Huang et al., 2013; Sinha et al., 2014; Jones et al., 2015).

Despite the increasing use of PBPK modeling, there are many challenges that limit the utility of PBPK modeling and simulation. In general, IVIVE using PBPK models requires considerably more experimental and in silico data than static models. Due to the large number of parameters required for PBPK modeling and the limited availability of in vivo data to verify individual parameters, model predictions can be confounded by lack of confidence in individual parameters. For example, for drugs that have not been administered intravenously to humans, distribution and absorption parameters cannot be validated or verified experimentally, which introduces uncertainty into model parameters and output. The application of PBPK modeling to predict the pharmacokinetics in disease populations is hindered by lack of in vivo data in patient populations, poor understanding of the physiologic changes that occur in certain populations, and limited knowledge of tissue-specific changes in enzyme and transporter expression (Edginton and Joshi, 2011; Sjöstedt et al., 2014; Jones et al., 2015). Furthermore, absolute abundances of transporters and non-P450 enzymes in the liver and other tissues are not well established, resulting in poor IVIVE of the kinetics of non-P450 substrates and permeability limited drugs (Edginton and Joshi, 2011; Jones et al., 2012, 2015; Varma et al., 2012; Harwood et al., 2013). Additionally, a lack of selective substrates and inhibitors for some non-P450 enzymes and transporters has prevented model validation against in vivo data (Jones et al., 2015). While efforts are being made to characterize tissue-specific transporter expression, current models of the disposition of transporter substrates rely on the incorporation of empirical scaling factors (Varma et al., 2015b). Although scaling factors have allowed for predictions of the kinetics of a number of uptake transporter substrates (Varma et al., 2012, 2014, 2015a; Kudo et al., 2013; Gertz et al., 2014; Jamei et al., 2014), it is not possible to experimentally verify whether unbound tissue exposures are adequately predicted (Chu et al., 2013; Jones et al., 2015; Varma et al., 2015b). This could have important implications for IVIVE of efflux clearance, metabolism-transporter interplay, and predictions of pharmacological effects. The utility of PBPK modeling in the prediction of therapeutic protein disposition is still relatively limited, as was recently discussed (Jones et al., 2015). While a number of PBPK models have been used to accurately predict the kinetics of monoclonal antibodies (Baxter et al., 1995; Ferl et al., 2005; Shah and Betts, 2012; Cao and Jusko, 2014; Elmeliegy et al., 2014; Li et al., 2014a; Chetty et al., 2015; Zhao et al., 2015), model structures are inconsistent (Chetty et al., 2012; Jones et al., 2015). Limited data on target expression and changes in disease populations result in the risk for overparameterization with PBPK models, and thus there is an effort to move toward reduced PBPK models for therapeutic proteins (Elmeliegy et al., 2014; Li et al., 2014a; Chetty et al., 2015; Diao and Meibohm, 2015).

Another current challenge in the PBPK modeling field is determining how to assess model quality. To date, neither the FDA nor the European Medicines Agency (EMA) have issued a formal guidance regarding model quality assessment during regulatory review. However, the FDA has acknowledged the use of the best-practice methods proposed by the World Health Organization International Program for Chemical Safety (International Programme on Chemical Harmonization Project, 2010; Zhao et al., 2012b). These practices include ensuring the physiologic plausibility of the input parameters, demonstrating the ability of the model to predict the pharmacokinetics in an independent data set, and confirming that sensitivity and uncertainty analysis support model quality. The recommendation to establish guidelines for reporting and qualification of PBPK models was made at the Ministerial Industry Strategy Group (2014) New Technologies Forum on Physiologically Based Modeling and Simulation, and the EMA released a concept paper on the reporting and quality assessment of PBPK models with the goal of publishing a draft guidance in 2015 (CHMP, 2014). However, while some basic guidelines for assessing model quality prior to regulatory review are accepted or in development, no standards exist for how model quality should be evaluated in peer-reviewed publications. Additionally, no formal analysis of the literature has previously been performed to evaluate what quality assessment methods, if any, are typically used in peer-reviewed publications.

Despite the growth of the PBPK modeling field and the well-established use of PBPK models in regulatory submissions, the overall public availability of PBPK models is unclear and the breath of use of PBPK modeling by the research community has not been systematically evaluated. The PBPK models used in regulatory submissions are not publicly available to the outside research community, which prevents the broad use of models that have been accepted by regulatory agencies. Furthermore, the applications of the models in regulatory submissions may be driven primarily by the needs of drug developers and may not reflect how PBPK modeling is used in the larger research community. Identifying and compiling a list of the publicly available models could be beneficial to future research efforts since published models could be used either unchanged or as a starting point in future modeling efforts. Furthermore, determining the common applications of the published PBPK models will provide insight into current modeling interests as well as highlight under-represented applications. This review evaluates recent PBPK publications and identifies the common applications of PBPK modeling, how models are typically developed, and ways in which model quality is assessed, and provides a list of publicly available PBPK models, with a focus on enzyme probes, marker substrates and important perpetrators of DDIs.

Literature Search Strategy

PubMed searches were conducted using the search terms “PBPK” and “physiologically based pharmacokinetic model” within the abstract or title of the manuscript. Papers were selected for review if they were published in English between 2008 and May 20, 2015, and focused on PBPK modeling of pharmaceutical agents in humans. The number of papers referenced is likely an under-representation of the overall body of literature on PBPK modeling due to the strict search criteria and the search terms used. Publications were categorized as a review, commentary, letter to the editor, or an original data paper containing one or more PBPK models. Papers that focused on the development of new modeling software or a modeling strategy were classified as prediction method papers. Original data papers were further categorized by the primary application of the models.

Models for FDA and EMA recommended probe substrates, inhibitors, and inducers (CDER, 2012; CHMP, 2012) were identified within the original data papers. Complete lists of the compounds recognized by the regulatory agencies are shown in Supplemental Tables 1 and 2. Models for these compounds were included in our analysis if 1) they were original published models; 2) enough information was provided to allow for replication of the model in an appropriate software program; and 3) the simulation results were compared with observed in vivo data. A number of models were excluded because they were default library files in a simulation software package, the model input parameters were not reported, or the simulation results were not compared with in vivo data. Compound models were categorized as substrates, inhibitors, and/or inducers based on their classification in the FDA or EMA DDI guidance (CDER, 2012; CHMP, 2012) if the model was built with the clearance pathways or interaction parameters that permitted it to be used for the specified purpose. Models for FDA substrates, inhibitors, and inducers that lacked the appropriate clearance pathways or inhibition/induction parameters to allow them to be used according to their FDA or EMA classification were placed into a category of their own. For each FDA and EMA recommended substrate, inhibitor, or inducer that met the search criteria, information regarding the simulated formulation, genotype, and software used was extracted. Furthermore, the source of the clearance input parameter (in vitro or in vivo), the type of independent quality assessment data set used, and the a priori model acceptance criteria were collected. Finally, the type of model (full or minimal PBPK) was determined. PBPK models were considered to be minimal if the model included no more than five compartments, including the gastrointestinal tract, blood, and liver, and up to two additional compartments. More complex models were considered to be full PBPK.

PBPK Modeling Articles by Year and Application

A total of 366 PBPK-related articles meeting our search criteria were published since 2008. While it is unlikely that the literature search identified all of the papers presenting PBPK modeling in the literature, the search likely provides adequate and representative coverage of the existing models and practices. The number of articles published per year rose steadily with time from nine articles in 2008 to 94 articles published in 2014 (Fig. 1A). Of the papers identified, 74% were original data papers that included one or more PBPK models, while 26% were reviews, commentaries, letters to the editor, or prediction methods papers. The original data papers were analyzed to identify the common applications of PBPK models. The distribution of the model applications is shown in Fig. 1B. The published PBPK models were most commonly used for DDI predictions (28%). The majority of the DDI prediction models were used to simulate P450-mediated DDIs (81%), while the remainder of the models focused on transport DDIs (10%) or a combination of P450 and transporter-mediated interactions (10%). Additionally, models were commonly used to predict interindividual variability and general clinical pharmacokinetics (23%), absorption kinetics (12%), and age-related changes in pharmacokinetics (10%). This distribution of model applications is distinctly different from what has been reported for regulatory submissions to the FDA. The models included in FDA regulatory filings were primarily used for DDI predictions (60%), followed by pediatrics (21%) and absorption (6%) predictions (Pan et al., 2014). Based on this analysis the use of PBPK modeling to evaluate interindividual variability and overall drug disposition characteristics is far more common in the broader research community than in regulatory review. This difference reflects the fact that both the FDA guidance on pediatrics (CDER, 2014) and DDIs (CDER, 2012) includes PBPK modeling as a potentially useful tool for guiding clinical study design; however, PBPK modeling is currently not included in FDA guidance on bioequivalence or first in human studies.

Fig. 1.

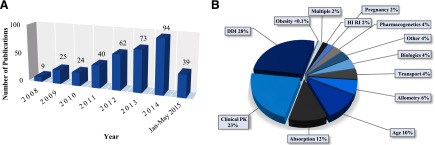
Summary of the PBPK literature analyzed. The number of articles per year that contain one or more PBPK models of pharmaceutical agents in humans is shown in (A). The distribution of the PBPK model applications in the original data papers is shown in (B).

Published Models of FDA and EMA Recommended Substrates, Inhibitors, and Inducers

Each of the 271 original data papers identified included at least one PBPK model of a pharmaceutical agent. The majority of the papers included models of approved drugs, and only 21 papers (8%) used PBPK modeling to simulate the pharmacokinetics of drugs in development. The published PBPK models included default models from software libraries as well as original models. Of the published original models, the models for the FDA and EMA recommended sensitive substrates, inhibitors, and inducers were further evaluated. While these models only represent a fraction of the published PBPK models, these compounds represent a group of drugs for which PBPK models are particularly useful since the models can be used in DDI predictions or to validate altered expression levels or activity of transporters and enzymes in new physiologic models. Fifty-six papers were found that included models for FDA and EMA listed sensitive substrates, inhibitors, and inducers. In these papers, 107 original models representing 61 different compounds were identified. These models were analyzed to gain insight into how peer-reviewed models are commonly developed and how authors assess overall model quality. For each model, information about model development was collected, including the software used, the complexity of the model (full or minimal PBPK), the source of the clearance input value, and the type of dosing simulated. Additionally, information regarding model quality and quality assessment was recorded, including whether the simulated population matched the observed population, if an independent dataset was used to verify model quality, and the type of criteria authors used to determine if a model performance was acceptable. The compounds modeled, the model development methods, and the quality assessment criteria are provided in Tables 1–6, along with references to the original publications.

Table 1.

Summary of PBPK models published for P450 Sensitive Substrates

Main Clearance Enzyme	Compound	Application	Minimal or Full PBPK	Oral or IV	Clearancea	Simulated genotype specified?	Population matched?b	Verificationc	Acceptance Criteriad	Software	Citation
CYP1A2	Caffeine	Allometry	Full	Oral	SF	No	N.S	A,D	1	PK Sim	(Thiel et al., 2014)
CYP2B6	Efavirenz	DDI	Minimal	Oral	In vitro	Yes	N.S	A, E	1	Simcyp	(Siccardi et al., 2013)
	Efavirenz	DDI	Full	Oral	In vitro	Yes	Sex	D,E	1	Simcyp	(Rekic et al., 2011)
	Efavirenz	Absorption	Full	Oral	In vitro	No	N.S	B	5	Matlab	(Rajoli et al., 2014)
CYP2C8	Repaglinide	Diabetes	Full	Oral	In vitro	No	N.S.	B,D	3	WinNonlin	(Li et al., 2014b)
	Repaglinide	RI	Full	Oral	BC	Yes	N.S.	D	1	Simcyp	(Zhao et al., 2012a)
	Repaglinide	DDI	Minimal	Oral	PE	No	N.S	B, E	1	Napp	(Kudo et al., 2013)
	Repaglinide	DDI	Full	Oral	BC	No	N.S	C,E	1	Simcyp	(Varma et al., 2013)
CYP2C19	Clobazam	Pediatrics	Full	Oral	In vitro	No	N.S.	B,D,E	1	Matlab	(Ogungbenro and Aarons, 2015)
	Omeprazole	Clinical PK	Minimal	Both	BC	Yes	N.S.	B,E	1	Simcyp	(Wu et al., 2014)
CYP2D6	Metoprolol	Pregnancy	Full	Oral	In vitro, SF	Yes	Sex, PGX	D, E	2	Simcyp, Matlab	(Ke et al., 2013b)
	Dextromethorphan	Pregnancy	Full	Oral	PE	No	Sex, PGX	D, E	2	Simcyp, Matlab	(Ke et al., 2013b)
	Dextromethorphan	Allometry	Full	Oral	SF	No	N.S	A,D	1	PK Sim	(Thiel et al., 2014)
CYP3A4	Alfentanil	DDI	Full	Oral	BC	No	N.S.	C, E	5	Gastroplus	(Baneyx et al., 2014)
	Alfentanil	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Buspirone	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Indinavir	Pregnancy	Full	Both	In vitro, SA	No	Sex	C, D, E	2	Simcyp, Matlab	(Ke et al., 2012)
	Maraviroc	DDI	Minimal	Oral	In vitro	No	N.S.	A,E	1	Simcyp	(Hyland et al., 2008)
	Midazolam	Pregnancy	Full	Oral	In vitro	No	Sex	A, D	2	Simcyp, Matlab	(Ke et al., 2012)
	Midazolam	DDI	Full	Oral	BC	No	N.S	C, D	5	Gastroplus	(Baneyx et al., 2014)
	Midazolam	DDI	Full	Oral	PE	No	N.S	A	4	Berkeley Madonna	(Brantley et al., 2014)
	Midazolam	Pregnancy	Full	Oral	In vivo	No	Sex	B,D	3	Gastroplus	(Xia et al., 2013b)
	Midazolam	DDI	Minimal	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Wang et al., 2013a)
	Midazolam	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Midazolam	Allometry	Full	Oral	SF	No	N.S	A, D	1	PK Sim	(Thiel et al., 2014)
	Quetiapine	Pediatrics	Both	Oral	BC	No	Age, Sex	D, E	1	Simcyp	(Johnson et al., 2014)
	Sildenafil	RI	Full	Oral	BC	Yes	N.S.	D	2	Simcyp	(Zhao et al., 2012a)
	Simvastain	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Simvastatin	DDI	Minimal	Oral	In vitro	No	N.S.	A, E	5	WinNonlin	(Wang et al., 2013a)
	Triazolam	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Triazolam	DDI	Full	Oral	BC	No	N.S.	C, E	5	Gastroplus	(Baneyx et al., 2014)

^aBC = back-calculated from in vivo data, PE = parameter estimate, SA = sensitivity analysis, SF = scaling factor from mice.

^bPGX = genotype, N.S. = not specified.

^cData sets used in model verification included: (A) Single dose PK, (B) alternative dosing regimen, (C) alternative formulation, (D) alternative population, (E) DDI.

^dAcceptance criteria fell into 5 categories: (1) Not specified, (2) Ratio of PK parameter(s) must be within 30% of observed ratio, (3) Ratio of PK parameter(s) must be within 2 fold of observed ratio, (4) PK parameters must be within 30% of observed parameters, (5) PK parameters must be within 2 fold of observed parameters.

Table 6.

Summary of the PBPK models published for compounds that are FDA probe substrates, inhibitors, or inducers but the models were developed for a different purpose than the FDA category.

Compound	Application	Type	Oral or IV	Simulated genotype specified?	Clearancea	Verificationb	Population matched?c	Acceptance Criteriad	Software	Citation
Alprazolam	DDI	Full	Oral	No	In vitro	E	N.S.	5	Winnonlin	(Guo et al., 2013)
Clopidogrel	DDI	Minimal	Oral	Yes	In vitro	B, E	Sex	1	Simcyp	(Tornio et al., 2014)
Clopidogrel	Genetics	Full	Oral	Yes	In vitro	B, D, E	N.S.	1	Simcyp	(Djebli et al., 2015)
Lansoprazole	Absorption	Minimal	Oral	No	In vivo	C	N.S.	1	Gastroplus	(Wu et al., 2013)
Metformin	Other (diabetes)	Full	Oral	No	in vivo	D	N.S.	3	Winnonlin	(Li et al., 2015)
Metformin	Pregnancy	Full	Oral	No	In vivo	D	Sex	5	Gastroplus	(Xia et al., 2013a)
Methadone	Pregnancy	Full	Oral	No	BC	B, D	Sex	4	Simcyp, Matlab	(Ke et al., 2013a)
Nisoldipine	Other (diabetes)	Full	Oral	No	In vivo	D	N.S.	3	Winnonlin	(Li et al., 2015)
Oseltamivir	Pediatrics	Full	Both	No	In vitro, SF	C, D, E	N.S.	1	Gastroplus	(Parrott et al., 2011)
Oseltamivir	Clinical PK	Full	Oral	Yes	In vitro	D	N.S.	1	PK-Sim	(Hu et al., 2014)
Oseltamivir	RI	Full	Oral	No	In vivo	B	N.S.	1	Simcyp	(Hsu et al., 2014)
Phenobarbital	DDI	Full	Oral	No	In vivo	B,E	N.S	5	WinNonlin	(Guo et al., 2013)
Pravastatin	Clinical PK	Full	IV	No	In vitro, SF	C	N.S.	1	Berkeley Madonna	(Jones et al., 2012)
Propranolol	Formulation	Full	Oral	No	In vivo	B, C	N.S.	1	Gastroplus	(Wang et al., 2013b)
Rosuvastatin	Clinical PK	Full	IV	No	In vitro, SF	C	N.S.	1	Berkeley Madonna	(Jones et al., 2012)
Sertraline	DDI	Minimal	Oral	Yes	In vitro	E	N.S.	1	Simcyp	(Siccardi et al., 2013)
Theophylline	DDI	Minimal	Oral	No	In vivo	B,E	Age, Sex, PGX	3	Simcyp	(Xu et al., 2009)
Valsartan	Clinical PK	Full	IV	No	In vitro, SF	C	N.S.	1	Berkeley Madonna	(Jones et al., 2012)
Verapamil	DDI	Full	Oral	No	In vitro	E	N.S.	3	Winnonlin	(Guo et al., 2013)
Voriconazole	Pediatrics	Full	Both	No	In vitro, SF	C, D	N.S.	1	Simcyp	(Zane and Thakker, 2014)
Voriconazole	DDI	Minimal	Oral	Yes	In vitro	E	Sex, PGX	1	Simcyp	(Damle et al., 2011)

^aBC = back calculated from in vivo data, SF = scaling factor.

^bData sets used in model verification included: (A) Single dose PK, (B) alternative dosing regimen, (C) alternative formulation, (D) alternative population, (E) DDI.

^cPGX = genotype, N.S. = not specified.

^dAcceptance criteria fell into 5 categories: (1) Not specified, (2) Ratio of PK parameter(s) must be within 30% of observed ratio, (3) Ratio of PK parameter(s) must be within 2 fold of observed ratio, (4) PK parameters must be within 30% of observed parameters, (5) PK parameters must be within 2 fold of observed parameters.

Table 2.

Summary of PBPK models published for narrow therapeutic index substrates

Main Clearance Enzyme	Compound	Application	Model Type	IV or Oral	Clearancea	Simulated genotype specified?	Population matched?b	Verificationc	Acceptance Criteriad	Software	Citation
CYP1A2	Theophylline	Pregnancy	Full	Oral	BC	No	Sex	B, D	2	Simcyp, Matlab	(Ke et al., 2013b)
	Theophylline	DDI	Minimal	Both	In vitro	No	N.S.	B, E	1	Matlab	(Pan et al., 2011)
CYP2C9	Phenytoin	Clinical PK	Minimal	Oral	In vitro	Yes	Age, Sex, PGX	B	1	Simcyp	(Polasek et al., 2009)
	Warfarin	DDI	Full	Oral	PE	No	Age, Sex, PGX	A	4	Berkeley Madonna	(Brantley et al., 2014)
CYP3A4	Cyclosporine	Pediatrics	Full	IV	In vivo, SF	No	Age	C	1	AdaptII	(Gérard et al., 2010)
	Cyclosporine	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Cyclosporine	DDI	Full	Both	PE	No	N.S.	C, E	5	Matlab	(Gertz et al., 2013)
	Cyclosporine	Allometry	Full	Oral	SF	No	N.S	A, D	1	PK Sim	(Thiel et al., 2014)
	Quinidine	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Sirolimus	Clinical PK	Full	Oral	In vitro, PE	No	Age, Sex	B, D, E	1	Simcyp	(Emoto et al., 2013)
	Tacrolimus	DDI	Full	Oral	In vitro	No	N.S.	E	5	WinNonlin	(Guo et al., 2013)
	Tacrolimus	Clinical PK	Minimal	Oral	BC	Yes	Age, Sex, PGX	D, E	1	PKquest	(Gérard et al., 2014)

^aBC = back-calculated from in vivo data, PE = parameter estimate, SF = scaling factor.

^bPGX = genotype, N.S. = not specified.

^cData sets used in model verification included: (A) Single dose PK, (B) alternative dosing regimen, (C) alternative formulation, (D) alternative population, (E) DDI.

^dAcceptance criteria fell into 5 categories: (1) Not specified, (2) Ratio of PK parameter(s) must be within 30% of observed ratio, (3) Ratio of PK parameter(s) must be within 2 fold of observed ratio, (4) PK parameters must be within 30% of observed parameters, (5) PK parameters must be within 2 fold of observed parameters.

Table 3.

PBPK models and model details for recognized P450 inhibitors

Enzyme Inhibited	Compound	Application	Minimal or Full PBPK	Oral or IV	Clearancea	Additional Inhibition Parameters	Simulated genotype specified?	Population matched?b	Verificationc	Acceptance Criteriad	Software	Citation
Strong Inhibitors
CYP2C8	Gemfibrozil	DDI	Minimal	Oral	PE	CYP3A4	No	N.S.	A, B, E	1	Napp	(Kudo et al., 2013)
CYP2D6	Paroxetine	Pregnancy	Full	Oral	In vitro	CYP3A4	Yes	Sex, PGX	D, E	2	Simcyp, Matlab	(Ke et al., 2013b)
	Fluoxetine	DDI	Minimal	Oral	In vitro	CYP1A2	Yes	N.S.	E	1	Simcyp	(Siccardi et al., 2013)
						CYP2C9
						CYP2C19
CYP3A4	Clarithromycin	DDI	Minimal	Oral	In vivo	—	Yes	Age, Sex, PGX	A, B, E	3	Simcyp	(Wang, 2010)
	Clarithromycin	DDI	Minimal	Oral	In vivo	—	No	Age, Sex, PGX	B, E	3	Simcyp	(Xu et al., 2009)
	Itraconazole	DDI	Minimal	Oral	PE	—	No	N.S.	A, B, E	1	Napp	(Kudo et al., 2013)
	Ritonavir	DDI	Minimal	Oral	In vitro	CYP2C9	Yes	N.S.	A, E	1	Simcyp	(Siccardi et al., 2013)
						CYP2D6
	Ritonavir	Clinical PK	Minimal	Oral	In vitro	CYP3A5	Yes	N.S.	D	1	Simcyp	(Kaspera et al., 2014)
						CYP2D6
						CYP2J2
	Telithromycin	RI	Full	Oral	BC	P-gp	Yes	N.S.	D, E	1	Simcyp	(Zhao et al., 2012a)
	Telithromycin	DDI	Full	Oral	BC	P-gp	No	N.S.	A, B, E	1	Simcyp	(Vieira et al., 2012)
						CYP3A5
Moderate Inhibitors
CYP2C9	Amiodarone	DDI	Full	Both	BC	CYP2D6	No	N.S.	A, E	1	Simcyp	(Chen et al., 2015)
						CYP3A4
CYP2C19	Omeprazole	Clinical PK	Minimal	Both	BC	—	Yes	PGX	B, D, E	1	Simcyp	(Wu et al., 2014)
CYP3A4	Diltiazem	DDI	Minimal	Oral	In vivo	—	No	Age, Sex, PGX	B, E	3	Simcyp	(Xu et al., 2009)
	Diltiazem	DDI	Minimal	Oral	In vitro	—	No	N.S.	A, B, E	1	WinNonlin	(Zhang et al., 2009)
	Diltiazem	DDI	Minimal	Oral	In vivo	CYP2D6	No	Age, Sex	B	1	Simcyp	(Friedman et al., 2011)
	Erythromycin	DDI	Minimal	Oral	In vivo	CYP2C8	No	Age, Sex, PGX	B, E	3	Simcyp	(Xu et al., 2009)
	Verapamil	DDI	Minimal	Oral	In vitro	CYP2C8	No	N.S.	A, B, C, E	5	WinNonlin	(Wang et al., 2013a)
						OATP1B1
	Verapamil	DDI	Full	Oral	BC	—	No	Age, Sex	A, E	1	Simcyp	(Neuhoff et al., 2013a)
	Verapamil	DDI	Minimal	Oral	In vivo	—	No	Age, Sex, PGX	B, E	3	Simcyp	(Xu et al., 2009)
Weak Inhibitors
CYP2C8	Trimethoprim	DDI	Minimal	Oral	In vivo	—	Yes	N.S.	B, E	1	Simcyp	(Yeo et al., 2013)

^aPE = parameter estimation from in vivo data, BC = back-calculated from in vivo data.

^bPGX = genotype, N.S. = not specified.

^cData sets used in model verification included: (A) Single dose PK, (B) alternative dosing regimen, (C) alternative formulation, (D) alternative population, (E) DDI.

^dAcceptance criteria fell into 5 categories: (1) Not specified, (2) Ratio of PK parameter(s) must be within 30% of observed ratio, (3) Ratio of PK parameter(s) must be within 2 fold of observed ratio, (4) PK parameters must be within 30% of observed parameters, (5) PK parameters must be within 2 fold of observed parameters.

Table 4.

PBPK models published for P450 inducers

Enzyme Induced	Compound	Application	Minimal or Full	IV or Oral	Clearancea	Simulated genotype specified?	Population matched?b	Verificationc	Acceptance Criteriad	Software	Citation
CYP2B6 and CYP3A4	Efavirenz	DDI	Minimal	Oral	In vitro	Yes	N.S	A, E	1	Simcyp	(Siccardi et al., 2013)
	Efavirenz	Absorption	Full	Oral	In vitro	No	N.S.	B	5	Matlab	(Rajoli et al., 2014)
	Efavirenz	DDI	Full	Oral	In vitro	Yes	Sex	D, E	1	Simcyp	(Rekic et al., 2011)
CYP3A4	Carbamazepine	DDI	Full	Oral	In vitro	No	N.S.	B, E	5	WinNonlin	(Guo et al., 2013)
	Etravirine	Absorption	Full	Oral	In vitro	No	N.S.	B	5	Matlab	(Rajoli et al., 2014)
	Rifampin	DDI	Full	Oral	BC	No	N.S.	E	5	Gastroplus	(Baneyx et al., 2014)
	Rifampin	DDI	Full	Oral	In vivo	No	N.S.	B, E	5	WinNonlin	(Guo et al., 2013)
	Rifampin	DDI	Full	Oral	BC	No	Age, sex, PGX	A	1	Simcyp	(Neuhoff et al., 2013b)

^aBC = back calculated from in vivo data.

^bPGX = genotype, N.S. = not specified.

^cData sets used in model verification included: (A) Single dose PK, (B) alternative dosing regimen, (C) alternative formulation, (D) alternative population, (E) DDI.

^dAcceptance criteria fell into 5 categories: (1) Not specified, (2) Ratio of PK parameter(s) must be within 30% of observed ratio, (3) Ratio of PK parameter(s) must be within 2 fold of observed ratio, (4) PK parameters must be within 30% of observed parameters, (5) PK parameters must be within 2 fold of observed parameters.

Table 5.

Summary of the PBPK models published for transporter substrates, inhibitors and inducers

Compound Modeled (Relevant Transporter)	Application	Minimal or Full	Oral or IV	Clearancea	Simulated genotype specified?	Population matched?b	Verificationc	Acceptance Criteriad	Software	Citation
Inducers
Rifampin (P-gP)	Transport	Minimal	Oral	BC	No	A,S	A, E	1	Simcyp	(Neuhoff et al., 2013b)
Inhibitors
Cyclosporine ( OATP1B1)	Transport	Full	Oral	In vivo	Yes	N.S.	A, E	1	Simcyp	(Varma et al., 2012)
Cyclosporine (OATP1B1, OATP1B3 BCRP)	Transport	Full	Oral	BC	No	Age, sex, PGX	B	1	Simcyp	(Jamei et al., 2014)
Cyclosporine (OATP1B1, OATP1B3 BCRP)	DDI	Full	Both	PE	No	N.S.	C, E	5	Matlab	(Gertz et al., 2013)
Gemfibrozil ( OATP1B1)	DDI	Minimal	Oral	PE	No	N.S.	A, B, E	1	Napp	(Kudo et al., 2013)
Gemfibrozil (OATP1B1)	Transport	Full	Oral	BC	Yes	N.S.	E	1	Simcyp	(Varma et al., 2015a)* updated Varma et al 2012
Probenecid (OAT1, OAT3)	DDI	Full	Both	BC	No	N.S.	C	1	Simcyp	(Hsu et al., 2014)
Verapamil (P-gp)	DDI	Full	Oral	BC	No	Age, sex	A, E	1	Simcyp	(Neuhoff et al., 2013b)
Substrates
Atorvastatin (OATP1B1)	Absorption	Full	Oral	In vitro	No	Age, sex	D	1	Simcyp	(Darwich et al., 2013)
Bosentan (OATP1B1)	Transport	Full	IV	In vitro, SF	No	N.S.	None	1	Berkeley Madonna	(Jones et al., 2012)
Dabigatran (P-gp)	DDI	Full	Both	In vitro	No	N.S.	A, B, E	1	PK Sim	(Zhao and Hu, 2014)
Digoxin (P-gp)	Transport	Full	Both	BC	No	Age, sex	A, B	4	Simcyp	(Neuhoff et al., 2013b)
Fluvastatin (OATP1B1)	Transport	Full	IV	In vitro, SF	No	N.S.	None	1	Berkeley Madonna	(Jones et al., 2012)
Glyburide (OATP1B1)	DDI	Full	Both	In vitro	Yes	PDX	B, C, E	1	Simcyp	(Varma et al., 2014)
Glyburide (OATP1B1)	Pregnancy	Full	Oral	BC	No	sex	B, D, E	2	Simcyp, Matlab	(Ke et al., 2013a)
Pravastatin (OATP1B1, OAT3)	Clinical PK	Full	Both	In vitro, SF	No	N.S.	C	1	Matlab, PK Sim	(Meyer et al., 2012)
Pravastatin (OATP1B1)	Transport	Full	Both	In vitro, SF	No	N.S.	A, B, E	1	Simcyp	(Varma et al., 2012)
Repaglinide (OATP1B1)	Transport	Full	IV	In vitro, SF	No	N.S.	None	1	Berkeley Madonna	(Jones et al., 2012)
Repaglinide (OATP1B1)	RI	Full	Oral	BC	Yes	N.S.	D	1	Simcyp	(Zhao et al., 2012a)
Repaglinide (OATP1B1)	DDI	Minimal	Oral	In vivo	No	N.S.	E	1	Napp	(Kudo et al., 2013)
Repaglinide (OATP1B1)	DDI	Full	Both	BC	No	N.S.	C, E	1	Simcyp	(Varma et al., 2013)
Rosuvastatin (BCRP OATP1B1, OATP1B3)	Transport	Full	Oral	BC, PE, SA	No	Age, sex	B, E	1	Simcyp	(Jamei et al., 2014)
Rosuvastatin (OATP1B1, OATP1B3)	Transport	Full	Both	In vitro, SF	No	N.S.	C	1	ASCLX	(Bosgra et al., 2014)
Telmisartan (OATP1B3)	Transport	Full	Both	In vitro, SF	No	N.S.	C	1	Matlab	(Li et al., 2014c)

^aBC = back calculated from in vivo data, PE = parameter estimation, SA= sensitivity analysis, SF = scaling factor.

^bPGX = genotype, N.S. = not specified.

^cData sets used in model verification included: (A) Single dose PK, (B) alternative dosing regimen, (C) alternative formulation, (D) alternative population, (E) DDI.

^dAcceptance criteria fell into 5 categories: (1) Not specified, (2) Ratio of PK parameter(s) must be within 30% of observed ratio, (3) Ratio of PK parameter(s) must be within 2 fold of observed ratio, (4) PK parameters must be within 30% of observed parameters, (5) PK parameters must be within 2 fold of observed parameters.

How Were the Models Developed?

PBPK models can vary in complexity from full PBPK models, where all of the distribution organs and tissues are represented as separate perfused compartments, to more simplified, minimal PBPK models in which tissues with similar kinetics are lumped (Nestorov et al., 1998; Leahy, 2003; Parrott et al., 2005; Bois et al., 2010; Pilari and Huisinga, 2010; Cao and Jusko, 2012; Tsamandouras et al., 2015). The majority of the models for the FDA and EMA substrates, inhibitors, and inducers listed in Tables 1–6 were full PBPK models (72%) as opposed to minimal PBPK models (27%). Full PBPK models will typically fit the experimental data better than minimal models due to the larger number of parameters used, which increases the degrees of freedom. However, confidence in any individual parameter is decreased when moving from a minimal to a full PBPK model. Minimal PBPK models can be used to reduce model complexity while still allowing for mechanistic simulations in only the compartments of interest (Nestorov et al., 1998; Pilari and Huisinga, 2010; Cao and Jusko, 2012; Tsamandouras et al., 2015). One advantage of full PBPK modeling is the ability to simulate the exposure of a drug or its metabolites in specific tissues that are not accessible to clinical sampling. This can be particularly important if the pharmacological or toxicological effects are driven by the concentrations in that tissue (Tsamandouras et al., 2015). However, none of the models listed in Tables 1–6 and only 13 of the 271 original data papers used simulated tissue concentrations to address pharmacology and toxicology questions (Table 7). Instead, full PBPK models were generally used to enable the systematic prediction of distribution kinetics in order to simulate plasma concentration-time profiles. All of the models that were used to simulate kinetics in special populations in which distribution kinetics can be highly altered, such as pediatrics and pregnancy, incorporated full PBPK models. Full PBPK modeling was also used in all but two of the models for transporter substrates and inhibitors due to the need to capture permeability rate–limited processes.

Table 7.

List of compounds for which Full PBPK models were used to address pharmacological and toxicological questions

Compound	Model purpose	A priori criteria?	Model Quality Assessment	Conclusions	Citation
Acetaminophen	Assessing various calibration strategies for linking PBPK models to toxicodynamic models of hepatotoxicity	No	Qualitative discussion of the agreement between simulated and observed Cmax, and metabolite ratios	Predicted liver toxicity in agreement with observed	(Péry et al., 2013)
Cyclosporine	Simulation of receptor occupancy in accute graft-versus-host organs and kidneys after intermittent or continuous infusion	No	Mann-Whitney test to compare means, chi-square test to compare proportions, bias and precision, number of simulations within 2-fold of the observed, weighted residuals	A greater therapeutic index was predicted following continuous infusion	(Gérard et al., 2010)
Cyclosporine	Establish a connection between the likelihood and severity of graft-versus-host disease and cyclosporine exposures in circulation, graft-versus-host target organs and lymphoid tissues	No	Student's t-test to compare means, chi-square test to compare proportions, Akaike information criterion for model selection	Blood cyclosporine levels can be used as an indicator of therapeutic efficacy	(Gérard et al., 2011)
Efalizumab	Develop a PD linked PBPK model to predict efficacy of efalizumab	Yes	Observed data within the predicted 5th and 95th centile	The model predicted the efficacy of efalizumab in treatment of psoriasis	(Chetty et al., 2015)
Formamide	Evaluate the relationship between dose and hepatic exposure	No	—	40mg/day dose was proposed bases on a safety index	(Yan et al., 2012)
Levofloxacin	Exploratory study to predict the extent of tissue exposure of levofloxacin in humans as a basis for future PK/PD work.	Yes	Fold error in PK parameters less than 2	Levofloxacin penetrated well into tissues, including the liver kidneys and spleen	(Zhu et al., 2015a)
Moxifloxacin	Simulate tissue concentrations versus time in patients with intra-abdominal infections	Yes	Fold error in PK parameters less than 2	Concentrations in intra-abdominal tissues were predicted to be higher than the minimum inhibitory concentration for common pathogens	(Zhu et al., 2015b)
Moxifoxacin	Evaluate the effect of macrophages on tissue concentrations of moxifloxacin to enhance understanding of the effects of disease on PK/PD	No	Simulated concentration versus time profiles were evaluated for bias and precision	Macrophage concentrations are predicted to effect tissue concentration of moxifloxacin	(Edginton et al., 2009)
Nicotine	Develop a PBPK model to describe nicotine exposure and receptor binding in the brain	No	Qualitative discussion of the agreement of the predicted and observed data	PK/PD modeling allowed for prediction of nicotine receptor occupancy in the brain	(Teeguarden et al., 2013)
“S1”	Predicting brain extracellular fluid concentrations as a starting point for PK-PD modeling	No	—	Unclear whether the PBPK model would accurately predict PD	(Ball et al., 2014)
Temozolomide	PD linked PBPK model for simulating the brain concentration of temozolomide and the levels DNA brain adducts	No	—	Predictions were in close agreement with observed data and parameter estimates had low coefficients of variation	(Ballesta et al., 2014)
Zidovudine	Model intra-cellular concentrations of zidovudine in peripheral blood mononuclear cells and establish efficacy and toxicity following various dosing regimens	No	PK features are well represented by the predictions	100mg 4 times daily is predicted to be the safest and most efficacious dosing scheme	(von Kleist and Huisinga, 2009)
Theoretical Compounds	Proof of concept study to evaluate mechanisms for differences in unbound plasma and tissue concentrations	No		This approach can be used to predict free tissue concentrations of various classes of drugs	(Poulin, 2015)

PBPK models are comprised of system- and drug-specific parameters. System-specific parameters include blood flow, organ volumes, enzyme and transporter expression, and plasma protein concentrations (Jamei et al., 2009a; Rowland et al., 2011; Galetin, 2014). Drug-specific parameters include intrinsic clearances, volume of distribution, solubility and physicochemical parameters, tissue partitioning, plasma protein binding affinity, and membrane permeability. As a result, drug-dependent parameters are independent of the system parameters, allowing for mechanistic extrapolation of human pharmacokinetics from in vitro and in silico data in a bottom-up approach (Jamei et al., 2009a; Rowland et al., 2011; Rostami-Hodjegan et al., 2012; Galetin, 2014; Tsamandouras et al., 2015). While bottom-up approaches are generally considered to be more mechanistic, in many cases sufficient in vitro data and characterization of all drug elimination pathways are not available to allow bottom-up predictions, or existing in vitro data do not predict in vivo disposition well enough. Similarly, in many cases, the knowledge of the biologic system is too limited to allow for bottom-up predictions of disposition kinetics in the population of interest. The bottom-up approach is usually not the method of choice in situations where PBPK models are built to specifically evaluate the disposition characteristics of a drug that has been administered to humans or to a special population. In these situations, the model is built to fit the data rather than for predictive IVIVE purposes and a combination of top-down and bottom-up approaches is often used. Several reviews have provided excellent discussions of the utility and setbacks of these combination or middle-out approaches to model development (Jamei et al., 2009a; Li et al., 2014b; Tsamandouras et al., 2015). In general, when using middle-out approaches, in vitro intrinsic clearances are back-calculated from in vivo clearance by assigning the fractions of the in vivo clearance associated with each clearance pathway, or scaling factors are assigned to the in vitro or in vivo clearance value(s) to accurately predict the observed data. Parameter estimation methods and sensitivity analysis can also be used in instances where in vitro data are unavailable and in vivo f_m values are not known.

For the models shown in Tables 1–6, in vitro clearance values (bottom-up approach) were used for clearance parameters in 35% of the cases. The most common alternative to IVIVE was back-calculating in vitro intrinsic clearance data from in vivo clearance (21%). Because this approach incorporates the fractional contribution of individual enzymes into the model, models developed using this technique can potentially be used to simulate pharmacokinetics in situations where enzyme expression levels or activity are altered. However, the reliability of the back-calculations to capture the true intrinsic clearances requires knowledge of the fractional contribution of each enzyme to in vivo clearance and an understanding of the true systemic clearance and bioavailability, which may not be available. In 18% of the models, in vivo clearance was used as an input parameter. While this can be a reliable way to ensure that the total body clearance is captured, no specific elimination pathways are accounted for, and thus the model is not useful for predicting the effects of an inhibitor or inducer or the consequences of changes in enzyme or transporter expression levels. In 17% of the models, a scaling factor was applied to the in vitro or in vivo clearance value(s) to accurately predict the observed data. Scaling factors were particularly common for transporter substrates, likely due to the current limitations in IVIVE of transporter-mediated clearance (Harwood et al., 2013; Li et al., 2014b). Finally, parameter estimation methods and sensitivity analysis were performed to determine the in vitro clearance values required to capture the true in vivo clearance for 9% of the models. While these approaches can permit extrapolation to observed in vivo clearance, caution should be exercised when estimating input parameters. In cases where in vitro parameter values and their variability are well understood, low prediction success could indicate that the model is lacking a critical PK process (Jones et al., 2015; Tsamandouras et al., 2015).

What Makes a Good Model and How Is Model Quality Assessed?

Best practices for model assessment have been proposed by the World Health Organization (International Programme on Chemical Harmonization Project, 2010) and have been discussed in the context of regulatory review (Caldwell et al., 2012; Zhao et al., 2012b; CHMP, 2014; Ministerial Industry Strategy Group, 2014). However, no requirements or guidelines exist regarding how to determine the quality of a PBPK model in general research applications and prior to publication. In regulatory guidance the criteria for assessing model validity are often presented in the context of whether the model meets the performance requirements for its specific purpose. However, in the research literature the specific goal or purpose for the model is often not specified, and PBPK modeling is frequently used to explain observed clinical findings or to support a particular mechanistic hypothesis rather than to predict drug disposition in a specific population or clinical situation. To establish the scope of current practices in the PBPK models that have been published for various purposes and applications, an evaluation of the current state of model development and quality assessment was conducted. The compound models listed in Tables 1–6 were assessed 1) to identify the criteria that were typically used to determine if a model was adequate and 2) to determine if models were tested against multiple in vivo data sets.

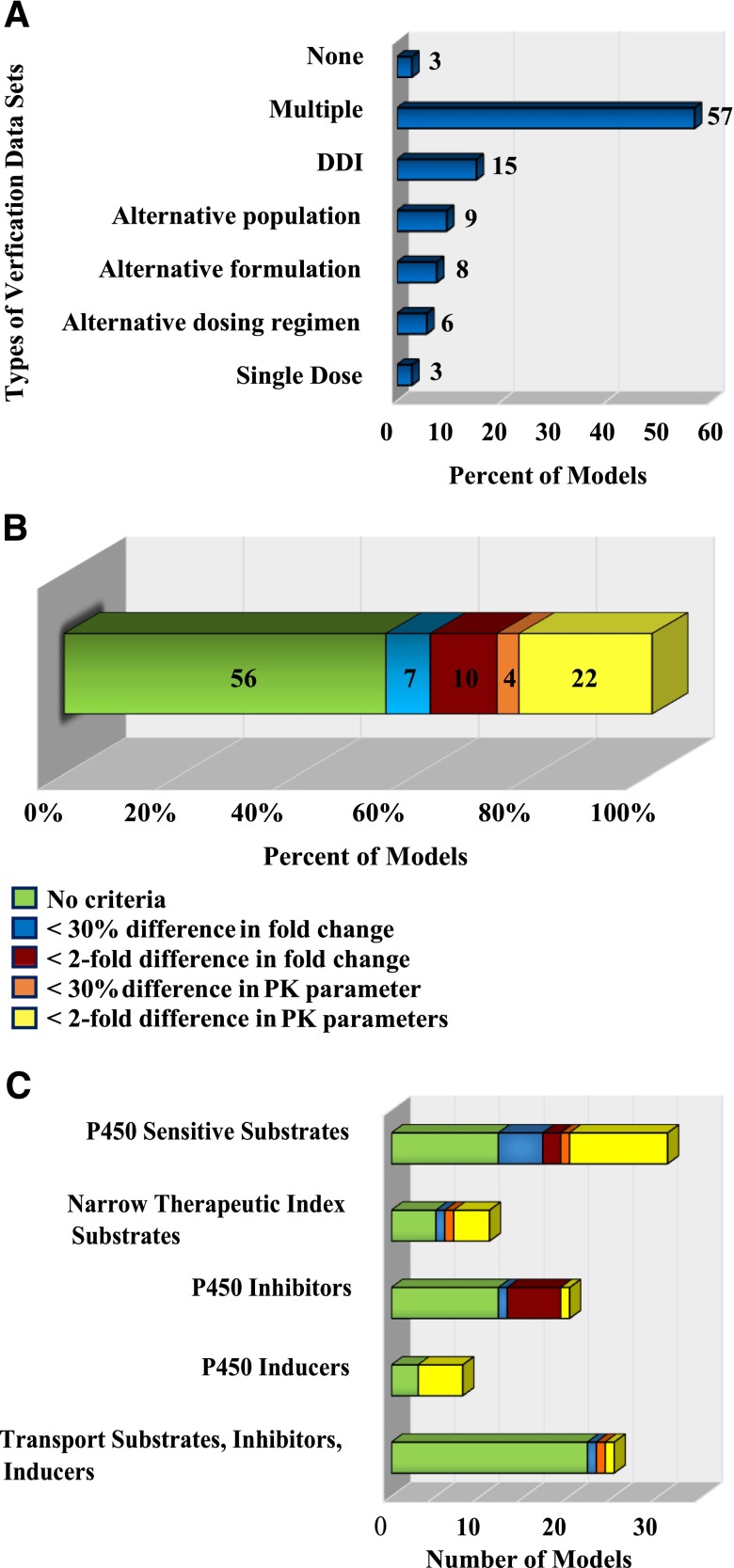
It is considered good practice to assess the quality of a model against in vivo data that were not used in the model development process and in situations where one of the parameters is altered, such as in a DDI or an alternative genotype population (International Programme on Chemical Harmonization Project, 2010; McLanahan et al., 2012; Zhao et al., 2012b; Sinha et al., 2014; Jones et al., 2015). Our analysis revealed that the PK simulations of 97% of the models were compared with pharmacokinetics in independent study populations. When an independent data set was used to test a model, the data set typically described the pharmacokinetics after a single dose or DDI, or for an alternative population, formulation, or dosing regimen. The distribution of the types of in vivo data sets used to assess the quality of the models is shown in Fig. 2A. Most of the models were assessed using multiple types of data sets (57%), DDI data (15%), or PK data from alternative populations (9%). Only 3% of the models were not compared with an independent data set. However, despite the fact that most models were assessed against data that were not used in model development, the simulated populations were rarely matched with the population demographics of the clinical study subjects, or the population demographics used in the simulations were not reported (Tables 1–6). The simulated age, gender, and genotypes were reported to match the observed population for only 32% of the models. Additionally, the simulated genotypes were only specified for 21% of the models. It is possible that the demographics of the clinical study and the simulated population were matched in many of the papers but were not reported. However, reporting the strategy for how the simulated populations were made to reflect the observed would provide greater confidence for the reader that the simulated population was reasonably representative of the true observed population. The population-specific parameters used in PBPK models (such as enzyme and transporter abundance, organ volume, blood flow, plasma protein binding, and glomerular filtration rate) are dependent on the population demographics (such as age, gender, genotype, and disease state). Similarly, the interindividual variability in the physiologic parameters is dependent on the population demographics. Thus, ensuring that the demographics of the simulated population match those of the observed population may improve the accuracy of both the mean PK parameters (Steere et al., 2015) and the predicted population variability. More careful reporting of the simulated and observed study populations would also be critically important when model performance is assessed. As has been highlighted in the literature (Abduljalil et al., 2014), PBPK simulations are often compared to clinical studies with small study populations, and the true inter- and intraindividual variability of the observed PK parameters of the compound of interest are not known. This can lead to a situation in which one clinical study does not accurately predict the PK parameters observed in another study with the same compound (Abduljalil et al., 2014). In such situations, a PBPK model cannot simultaneously meet the common acceptance criteria for both studies. However, the simulated population variability was rarely compared with the observed variability in the literature evaluated, and we found no papers in our analysis in which a priori model acceptance criteria were driven by knowledge of the variability in the PK parameters of the drug of interest in the target population. However, the 90% confidence interval is generally shown in simulated plasma concentration-time curves (Jones et al., 2015), and several studies used the simulated 90% confidence interval of the plasma concentration curves as a criterion for model acceptance (Sager et al., 2014; Bui et al., 2015; Chetty et al., 2015).

Fig. 2.

Summary of the verification criteria and alternative datasets used for the PBPK models in the literature evaluated. The types of in vivo datasets used to verify the quality of the models are shown in (A). The distribution of the acceptance criteria used in PBPK models of FDA probe substrates and inhibitors is shown in (B). The distribution of the model acceptance criteria used specifically for each compound class is shown in (C).

Determination of model performance was inconsistent and largely subjective in a majority of the papers. In 56% of the published models in Tables 1–6, the authors did not specify a priori a criterion by which they would decide if their model was successful or not (Fig. 2B). A recent publication from the International Consortium for Innovation & Quality in Pharmaceutical Development (IQ) IQ PBPK working group suggests that criteria should be predefined regarding whether a model fits the purpose (Jones et al., 2015). However, there is no consensus on what criteria should be applied for different modeling purposes. The IQ working group suggested that for drugs with a broad therapeutic window, common 2-fold criteria for the model would be acceptable, but for drugs with a narrow therapeutic index more stringent criteria would be appropriate (Jones et al., 2015). On the other hand, for PBPK models used for risk assessment the IQ proposed that acceptance criteria should reflect the effect of accuracy on dose selection. However, these recommendations are not consistent with the methods used to evaluate model performance in the literature. Overall, in the papers (Tables 1–6) in which the acceptance criteria were specified a priori, four standard choices were employed for model acceptance. For 22% of the models, the authors specified that predicted ADME characteristics [i.e., the area under the plasma concentration-time curve (AUC), the steady state average or the maximum concentration in plasma (C_ss,avg, and C_max)] in a given population must be within 2-fold of the observed value in order for the model to be considered acceptable. In 7% of the cases, predicted mean PK parameters were required to be within 25%–30% of the observed mean. In addition, for 10% of the models, the predicted fold change in the AUC or C_max between different simulated populations or study conditions had to be within 2-fold of the observed fold change in order for the model to be acceptable. Finally, for 4% of the models, the authors specified that the predicted fold change in the AUC and C_max needed to be within 30% of the observed fold change. When the acceptance criteria were analyzed according to the types of applications, a more striking discrepancy with the proposed guidance was observed (Fig. 2C). For models built for narrow therapeutic index drugs only 17% (two papers) used a 30% difference as the standard for model acceptance; 50% (six papers) of the papers had no criteria; and 33% (four papers) considered a 2-fold difference to be an acceptable criterion for these drugs. Similarly, for P450-sensitive substrates, which are expected to clinically report less than 2-fold changes in clearance, only 3% (one paper) used <30% difference in fold change as an acceptance criterion for the PBPK models, and 42% (13 papers) considered less than 2-fold difference between predicted and observed values or in fold changes acceptable. Only 16% of the papers (five papers) used the <30% difference observed and predicted values as acceptance criteria for P450-sensitive substrates. For P450 inducers, there were no models that required a <30% difference in PK parameters, and for transporter substrates, inhibitors, and inducers nearly all papers (84%) had no specified acceptance criteria. Taken together, these data suggest that there is a lack of consistency in model quality assessment, which does not reflect the different purposes for which the models are developed. The data also suggest that there is a need for more rigorous evaluation of model quality assessment during peer review. The issue of the lack of strict peer-review requirements for published models has been discussed previously in the literature (McLanahan et al., 2012) but it has not been formally addressed by the larger research community.

Based on the analysis of the PBPK models used to simulate drug absorption, more stringent criteria of model assessment were used in this field, likely adapted from bioequivalence standards. For some absorption models, model performance was determine to be high if error was <25%, medium if error was 25%–50%, low if error was 50%–100%, and inaccurate if error was greater than 2-fold (Sjögren et al., 2013). Importantly, many of the absorption models systematically evaluated model performance in terms of the plasma concentration-time curves rather than specific PK parameters using a similarity factor (f₁ or f₂) to calculate the percent difference between the simulated and measured plasma concentrations at each measured time point (Shono et al., 2009; Wagner et al., 2012; Fei et al., 2013; Kambayashi et al., 2013; Wang et al., 2013a). In addition, many absorption models were evaluated using statistical criteria such as linear regression between observed and predicted parameters or concentrations and method of residuals (Shono et al., 2009; Turner et al., 2012; Kambayashi et al., 2013). In some studies evaluating PBPK models of biologics (Kletting et al., 2010; Cao et al., 2013) model performances and discrimination between different models was achieved using statistical criteria that account for the added degrees of freedom in the model. The Akaike information criterion and correlation analyses were used to specifically differentiate between developed PBPK models and to identify the model that best fit the observed data (Kletting et al., 2010; Cao et al., 2013). Adaptation of some of these methods and criteria into PBPK modeling in other research areas may provide good standardization of model acceptance criteria.

Conclusions

PBPK modeling is increasingly being used in peer-reviewed publications to provide mechanistic predictions of pharmacokinetics and disposition in diverse populations and dosing regimens. Since 2008, 106 models of sensitive substrates, inhibitors, and inducers have been published, with applications ranging from DDIs to pregnancy. However, there is a relative lack of consistency in how models are developed and how model quality is assessed. Published models use bottom-up, top-down, and middle-out approaches to estimate clearance input values, and they vary in complexity. While model performance was found to be tested against model-independent data sets 97% of the time, model acceptance criteria and the extent to which the simulated populations reflect the observed population were not always specified. Thorough and consistent reporting of model development techniques and quality assessment could increase reader confidence and result in more widespread acceptance of published models. Thus, the development of best-practice guidelines for peer-review submissions might be beneficial. Table 8 includes suggestions for the information that should be included in peer-reviewed publications containing PBPK models. These suggestions are consistent with best-practice guidelines for regulatory review (International Programme on Chemical Harmonization Project, 2010; Zhao et al., 2012b; CHMP, 2014; Ministerial Industry Strategy Group, 2014) but also acknowledge that guidelines for peer-reviewed models may not require the same degree of reporting detail as has been proposed for regulatory submissions.

TABLE 8.

List of relevant details to report for publication of PBPK models.

Modeling workflow	Suggested information
Objectives	What is the purpose of the model?
Model acceptance criteria	What criteria are being used to determine if a model is fit-for-purpose?
	What is the clinical relevance of these criteria?
	What independent data sets are used for model testing?
Model development	Was the model built using a PBPK software package? If not, information regarding the model structure, the source of parameters, and their physiologic context should be reported.
	What input parameters were used? For recommended parameters to include, see Zhao et al., 2012b
	What parameters, if any, were estimated when using parameter estimation or sensitivity analysis?
	Are the estimated parameters physiologically plausible?
	Are the parameters within the range of previously reported values (if applicable)?
	Population demographics (Do the simulated and observed populations and study sizes match?)
Model outcomes	Comparison of the predicted and observed PK
	Do the predictions meet the predetermined model specification criteria?
Model performance	Was sensitivity analysis performed to assess whether model output parameters are sensitive to specific input parameters? (Yes/No)
	What are the verified applications of the model?
	What is the level of uncertainty in the model components?

Abbreviations

AUC

Area under plasma concentration time curve

CDER

Center for Drug Evaluation and Research

CHMP

Committee for Medicinal Products for Human Use

DDI

drug-drug interaction

EMA

European Medicines Agency

FDA

Food and Drug Administration

IVIVE

in vitro-to-in vivo extrapolation

IQ

innovation and quality in pharmaceutical development

PBPK

physiologically based pharmacokinetic

PD

Pharmacodynamics

PK

pharmacokinetic

Authorship Contributions

Participated in research design: Sager, Yu, Ragueneau-Majlessi, Isoherranen.

Performed data analysis: Sager.

Wrote or contributed to the writing of this manuscript: Sager, Yu, Ragueneau-Majlessi, Isoherranen.