How body torque and Strouhal number change with swimming speed and developmental stage in larval zebrafish

Abstract

Small undulatory swimmers such as larval zebrafish experience both inertial and viscous forces, the relative importance of which is indicated by the Reynolds number (Re). Re is proportional to swimming speed (v_swim) and body length; faster swimming reduces the relative effect of viscous forces. Compared with adults, larval fish experience relatively high (mainly viscous) drag during cyclic swimming. To enhance thrust to an equally high level, they must employ a high product of tail-beat frequency and (peak-to-peak) amplitude fA_tail, resulting in a relatively high fA_tail/v_swim ratio (Strouhal number, St), and implying relatively high lateral momentum shedding and low propulsive efficiency. Using kinematic and inverse-dynamics analyses, we studied cyclic swimming of larval zebrafish aged 2–5 days post-fertilization (dpf). Larvae at 4–5 dpf reach higher f (95 Hz) and A_tail (2.4 mm) than at 2 dpf (80 Hz, 1.8 mm), increasing swimming speed and Re, indicating increasing muscle powers. As Re increases (60 → 1400), St (2.5 → 0.72) decreases nonlinearly towards values of large swimmers (0.2–0.6), indicating increased propulsive efficiency with v_swim and age. Swimming at high St is associated with high-amplitude body torques and rotations. Low propulsive efficiencies and large yawing amplitudes are unavoidable physical constraints for small undulatory swimmers.

1. Introduction

Being small has costs and benefits for swimmers and flyers. On the one hand, small swimmers and flyers experience relatively strong viscous forces resulting in high drag, reduced stride length ℓ_stride (distance travelled per cycle) and propulsive efficiency [1–5]. On the other hand, they have relatively high muscle strength and low body inertia, affording small flyers and swimmers excellent manoeuvrability—they achieve high rotational accelerations [6–8]. Small swimmers often move in the intermediate flow regime, where both viscous and inertial forces play an important role. The ratio of inertial to viscous forces is expressed by the Reynolds number:

1.1

with ρ_water the density of water, ℓ_body the body length of the fish, v_swim the swimming speed (defined here as the speed of the centre of mass (CoM)) and μ the dynamic viscosity of water. Symbols and definitions are listed in the electronic supplementary material, table S1.

Fish larvae, compelled to generate high thrust with their posterior body to overcome the high drag on the anterior body [9], must use high tail-beat frequencies and amplitudes to generate the required high rate of change of momentum of the fluid. Fast, large-amplitude tail beats can cause large lateral forces on the body and large torques around the CoM, in turn causing large yaw accelerations. Large yaw can increase drag, which then requires more thrust to overcome. The large body deformations should also cause significant fluctuations in the fish's moment of inertia. Furthermore, we expect fluctuations in swimming speed and kinetic energy due to the time-varying nature of thrust production with a flapping propeller that causes large fluctuations in instantaneous force, both in direction and in amplitude. So far, these consequences have not been explored systematically and their relation with swimming speed and Re is unclear. Here, we quantify these aspects in zebrafish larvae using a combined kinematic and inverse-dynamics approach and show how body kinematics and dynamics vary with Re.

Large body undulations affect also the fluid-dynamic efficiency of swimming and cost of transport. Computational studies of larval swimmers have shown that increasing body-wave amplitude steadily increases energy cost per unit distance while propulsive efficiency plateaus at a value just above 0.3 at tail-beat frequency f = 57 Hz [9], suggesting that fish larvae use body-wave amplitudes that maximize fluid-dynamic efficiency at acceptable costs of transport. Nevertheless, swimmers in the viscous and intermediate flow regime (Re < 300) often achieve only low propulsive efficiency [3,2]. Propulsive efficiency in fluids strongly depends on vortex shedding dynamics, which correlates with the Strouhal number:

1.2

where 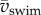is the mean swimming speed during cyclic swimming, A_tail is the peak-to-peak amplitude of the tail tip. Several studies suggest [10–13] that swimmers in the inertial flow regime swim close to the St that maximizes efficiency (St = 0.25–0.35 for carangiform swimmers and 0.4–0.5 for anguilliform swimmers [2,14–16]). By contrast, small organisms swimming in the viscous and intermediate flow regimes experience relatively higher drag forces, which reduces relative stride length (ℓ_stride/ℓ_body) and increases St, indicating a high-energy wake with a relatively large component of lateral momentum and thus low efficiency [2,7,17]. Adult fish increase 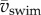in proportion to f while keeping A_tail nearly constant, implying that St and propulsive efficiency remain nearly constant [17–19]. In cyclic swimming, St must increase with decreasing Re if a swimmer is to balance thrust and drag over the tail-beat cycle [2]. Fish larvae are particularly interesting because they swim in the critical Re range that corresponds to the transition from high to low St [2,20]. As body size and swimming speed increase, Re increases, and so should efficiency.

By changing v_swim, larvae change Re and thus the relative influence of inertial and viscous forces. Using 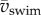to compute Re (electronic supplementary material, equation (S3.3)), it follows that St relates to Re as

1.3

where 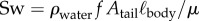is the dimensionless swimming number (introduced by Gazolla et al. [21]). To explore how St varies with Re, and hence what larval fish can do to increase hydrodynamic efficiency, we determined f and A_tail for a range of (nearly) cyclic swimming speeds spanning more than one order of magnitude.

Changes in Re and St are confounded by larval development. We expect developmental stage to profoundly affect swimming performance, because body shape and size as well as sensory, neural and muscular properties change rapidly in the first days of larval development. The changes in muscle size, structure and physiology are expected to provide a higher power output, enabling an increase in f or A_tail, or a combination of both.

We aim to quantify the body kinematics and dynamics of larval zebrafish aged 2–5 dpf (days post-fertilization), including body torques and Strouhal number, and their relation with developmental age and swimming speed, which indirectly yields performance requirements for swimming muscles. Our data also provide validation criteria for computational swimming models.

2. Material and methods

2.1. Animals

Zebrafish larvae (Danio rerio Hamilton 1822) were reared in the laboratory from wild-type stock at a water temperature of 28°C and a 12 L : 12 D cycle. We used larvae at age 2, 3, 4 and 5 dpf. Larvae were fed Paramecium twice a day at age 5 dpf.

2.2. Kinematic analysis and force on centre of mass

We used custom software developed in Matlab R2013a (Mathworks, MA, USA) for our analysis. To collect kinematic data of cyclically swimming larvae, we used three video set-ups recording at 1000–2000 frames s⁻¹ (see the electronic supplementary material, §2 for details). We recorded spontaneous and elicited swimming sequences (by approaching individual larvae with a horse hair) and selected 8–11 sequences per age group. We manually digitized 18–25 points on the fish's midline of every video frame, then smoothed and interpolated the midlines to obtain 51 equidistant points (see the electronic supplementary material, §3.1 for details). We defined two Cartesian coordinate systems, an earth-bound frame of reference, XYZ, and a ‘fish-bound frame’ X_movY_movZ_mov with the origin located at the fish's CoM and axes parallel to XYZ. We selected sequences with a small Z-component, and assumed that fish moved parallel to the XY-plane. To ensure that we include only (near-)cyclic swimming events (a prerequisite for computing Strouhal numbers), we identified 38 close-to-cyclic swimming events by calculating auto-correlation functions of the body wave (expressed as 51 segment angles) for all tail beats of a given event and selected video sequences comprising at least three consecutive tail beats above the normalized auto-correlation threshold of 0.975 and at least two extrema in the body angle (α_body).

To determine the body shape of larvae (details in the electronic supplementary material, §3.1), we digitized the outline of the fin fold, body, eye and yolksac in dorsal and lateral views of larvae aged 2–5 dpf (five per age group) at 51 equidistant points from snout to tail tip. We selected the larva whose values were closest to the per age average, to represent the body shape of its age group.

We estimated body volume by modelling the fish as a series of 51 segments by fitting ellipses to the head, eyes, fin fold, trunk (excluding fins) and yolk sac (for details, see the electronic supplementary material, §3.1 and figure S1). We assumed a uniform mass density (ρ_fish = 1000 kg m⁻³) over the entire body. For each segment, we computed volume V_i, mass m_i, and position vector r_i of the local CoM by numerical integration. The average ℓ_body for stages 2–5 dpf were 3.39, 3.81, 4.37 and 4.36 mm (N = 5 larvae per age group). Body mass m_body was computed as the sum of the segmental masses, resulting in 239, 289, 414 and 373 µg for stages 2–5 dpf. These values for ℓ_body and m_body were used for all subsequent computations.

We then calculated the instantaneous position, velocity, acceleration and force acting on the CoM from the instantaneous positions of the body segments (see electronic supplementary material, §3.1 for details).

2.3. Instantaneous moment of inertia, body angle, angular velocity and torque

For each body segment i, we computed the moment of inertia J_i about the segmental vertical centre line and the moment of inertia with respect to the CoM J_CoM,i about the vertical Z_mov-axis in the fish frame of reference (electronic supplementary material, §3.3 equations (S3.6) and (S3.7)) to ultimately derive the instantaneous moment of inertia of the body J_body with respect to the CoM location (electronic supplementary material, equation (S3.8)). We computed the instantaneous body angle α_body, angular velocity ω_body and angular acceleration 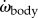(electronic supplementary material, §3.3.). We computed the inertial body torque about the CoM, τ_body, as the summation of the contributions of all body segments to the inertial torque about the CoM (electronic supplementary material, §3.3: equation (S3.15)).

To explore the spatio-temporal contributions of external fluid forces along the body to the net torque on the body, we computed skin friction-based 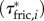, dynamic pressure-based 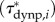and acceleration reaction-based 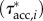torques per unit length along the fish, which include, respectively, the effects of forces associated with the local velocity components parallel and perpendicular to the body, and the acceleration of an added mass perpendicular to the body, as well as the relevant surface per unit length and position vector from the CoM to the location of interest along the body. The net estimated contributions of the three torque distributions to the external body torque (τ_fric, τ_dynp, τ_acc) were obtained by integration along the fish and compared with the fluctuations in τ_body. Computational details are provided in the electronic supplementary material, §3.3.

2.4. Kinetic energy and power

We computed the total kinetic energy of the body E_kin,body, as well as the kinetic energy associated with translation of the CoM, E_tr,CoM, and the kinetic energy due to rotation of the body segments about the CoM, E_rot,body. The latter is a close approximation of the internal kinetic energy of the body. We computed also the total power due to kinetic energy changes of the body, P_kin,body, the power associated with translation of the CoM, P_tr,CoM and the power associated with rotation of the body about the CoM, P_rot,body. Specific energies and powers were computed by dividing the respective values by body mass (designated as E* and P*). Details on energy computations are provided in the electronic supplementary material, §3.4.

2.5. Dimensionless quantities and trend analyses

We defined dimensionless swimming speed along the path of the CoM as

2.1

To compute f for (near-)cyclic swimming events, we first determined a series of positive and negative extremes in α_body with the ‘findpeaks' function of Matlab's Signal Processing toolbox (v. 2013a). Frequency was computed as

2.2

where n is the number of extrema in α_body, and t₁ and t_n the time, respectively, at the first and last extreme in α_body. Dimensionless tail amplitude was computed as

2.3

Dimensionless body torque was defined as

2.4

where 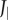is the value of J_body for the straight fish. Details about the computation of Re and St are provided in the electronic supplementary material, §3.2.

We fitted curves to the datasets used for trend analyses (figures 6–9) using an optimization procedure with Matlab's ‘fminsearch’ function. Fitted variables were scaled by their mean value, then we computed for each set of optimized coefficients the perpendicular distance from each data point to the curve (i.e. total least-squares approach for either a line, a parabola, a power curve or a power curve plus a constant). We used the sum of squared distances as the objective function for the optimization and estimated 95% confidence intervals for the coefficients of each curve fit with a Monte Carlo approach (see the electronic supplementary material, §3.5 for details). We computed the ratio of the root of the sum of squared distances for each nonlinear curve fit and the corresponding linear curve fit. Standard linear regression curve fits were applied for the log transformed data of Sw and Re for a comparison with previous work [21].

Figure 6.

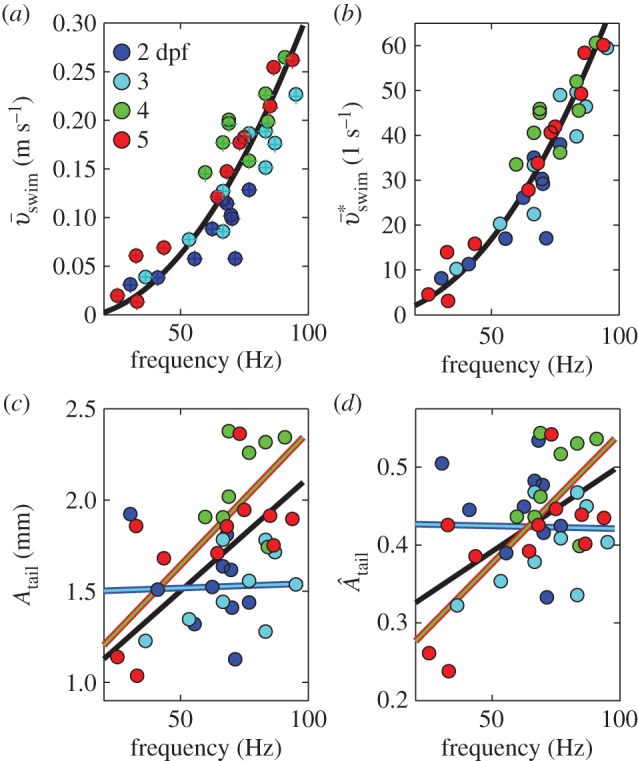
Swimming kinematics during (near-)cyclic swimming for 9–11 swimming events per age group (2–5 dpf). (a) Mean swimming speed 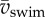along the path of the CoM (○) and along a straight line approximation of the path of motion (+) against cycle frequency f. Both speeds differ little, indicating small sideslip. 2, 3 dpf larvae reach lower speeds for a given f than 4, 5 dpf larvae. (b) Specific swimming speed (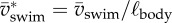) against f (same dataset as (a)). (c) Peak-to-peak tail-beat amplitude A_tail against f. Data in (c) and (d) were fitted by total least squares. In (c), the black curve shows the fit for the total dataset. The combined datasets for 2 and 3 dpf (blue-cyan line) and 4 and 5 dpf (red-green line) were fitted also separately. The 4–5 dpf age group tended to use higher A_tail than the 2–3 dpf group for f > 50 Hz, and they vary A_tail more over the frequency range. Panel (d) shows same data as (c) for dimensionless tail-beat amplitude (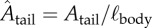). Parameter values for each curve fit are given in electronic supplementary material, table S2.

Figure 9.

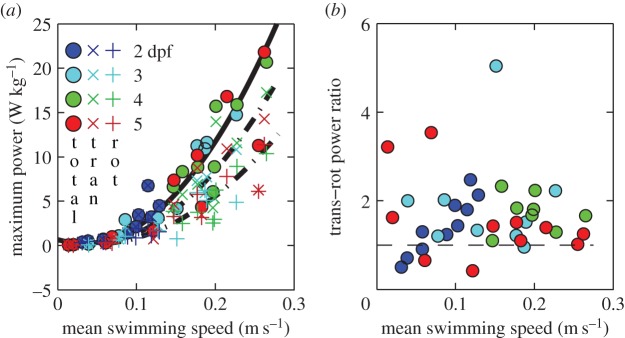
Maximum specific power computed as rate of change of kinetic energy of the body per body mass during (near-)cyclic swimming for same dataset as figure 6. (a) Total (○), translational (×) and rotational (+) power over mean swimming speed. Second-order polynomial curve fits for maximum total (continuous curve), and translational, and rotational (dashed curves) powers are shown. (b) Ratio of maximum translational to rotational power. The horizontal dashed line indicates a ratio of 1. Parameter values of the curve fits in (a) are given in electronic supplementary material, table S4.

3. Results and discussion

3.1. Body morphology

During larval development, mass is redistributed within the body as the yolk sac is absorbed and the body grows allometrically (e.g. [22,23]; electronic supplementary material, figure S3). Yet, the shift in mass distribution does not affect the location of the CoM along the straight fish (expressed as fraction of total length). At 2 dpf, the CoM is at 0.287 ℓ_body from the snout tip, at age 5 dpf at 0.286 ℓ_body.

3.2. Larval fish swim with small centre of mass sideslip and large body angle fluctuations

Fish larvae typically swim with wide body undulations [7] (see figure 1a,b for an example with 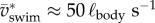, f ≈ 83 Hz). Snout tip (figure 1a: green curve) and tail tip (figure 1a: red curve) oscillate substantially. While the large-amplitude body undulations do not result in large sideslip (lateral movements of the CoM, figure 1a: black curve; lateral component of net force with respect to 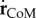, figure 1d: dotted curve), they do cause the CoM to move outside the body (twice per cycle) (figure 1b). CoM speed (v_swim) fluctuates strongly (figure 1c), a result of the oscillating net force on the body (figure 1d). The forward speed of the fish fluctuates over the tail-beat cycle in tune to the fore–aft force component (figure 1c,d).

Figure 1.

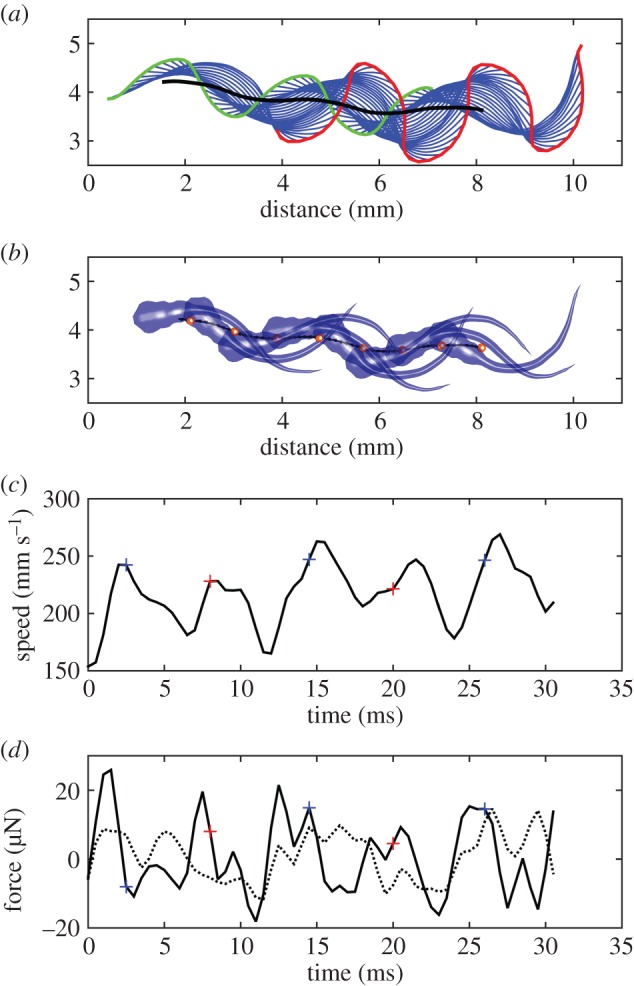
A 5 dpf fish larva swimming at approximately 50 ℓ_body s^–1. (a) Sequence of body midlines at 0.5 ms intervals (blue); path of snout tip (green), tail tip (red) and CoM (black). (b) Body shape at 3 ms intervals. CoM (red sphere) periodically falls outside the body. (c) Translational speed of CoM and (d) force on CoM in the direction of (continuous curve) and perpendicular to (dotted curve) the instantaneous velocity vector. The blue and red ‘+’ signs in panel (c) and (d) correspond to the minima and maxima in α_body (figure 2a). The time between two ‘+’ signs of the same colour represents a full tail-beat cycle.

Body yaw is smaller than head yaw—the peak-to-peak amplitude of the body angle α_body is half that of the head angle α_head (figure 2a, for event in figure 1). Changes in α_body are also delayed with respect to α_head. Thus, α_head is not a valid approximation for α_body in undulatory swimming fish larvae. Both ω_body and 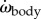reach high amplitudes, respectively ≈10° ms⁻¹ and ≈5° ms⁻² for the example event (figure 2b,c); 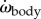generally shows a double peak per tail beat.

Figure 2.

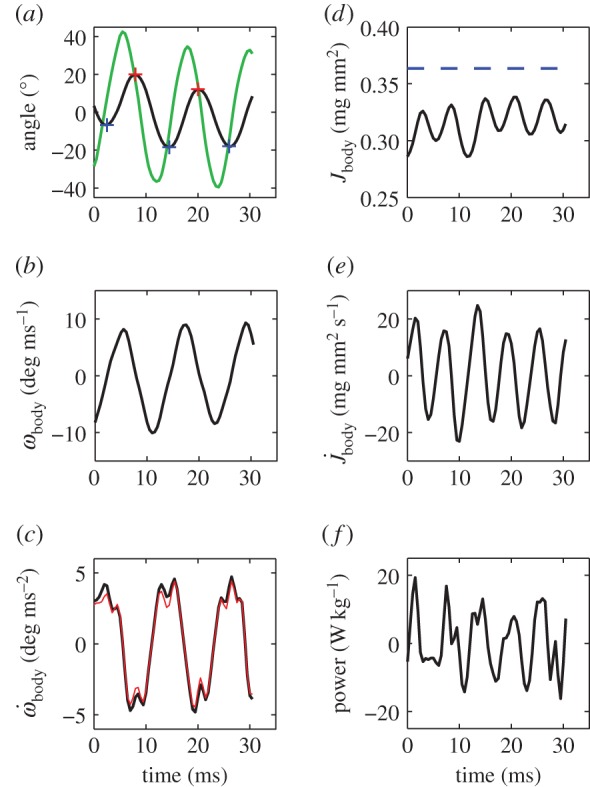
Body angle, moment of inertia and power for episode in figure 1. (a) Instantaneous body angle α_body (black; blue and red ‘+’ signs: minima and maxima) and head angle α_head (green); (b) body angular velocity ω_body; (c) body angular acceleration 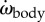(black: by differentiation of ω_body; red: according to electronic supplementary material, equation (S3.18)); (d) moment of inertia about the CoM J_body; dashed blue line shows 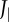(i.e. J_body for the straight fish), (e) rate of change of the moment of inertia 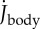; (f) total specific body power 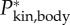based on the rate of change of kinetic energy.

The undulatory body movements cause the body moment of inertia J_body and its rate 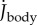to fluctuate (figure 2d,e). They also cause J_body to be smaller than 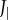of the straight fish. Furthermore, specific power fluctuates due to changes in kinetic energy (up to 20 W kg⁻¹ in figure 2f).

3.3. Body dynamics during cyclic swimming: insights from torque

Body torque around the CoM (τ_body) fluctuates strongly (figure 3a), causing large changes in 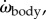ω_body and α_body (figure 2a–c). Torque τ_body oscillates in a non-sinusoidal manner with usually a double peak per tail beat (four peaks per tail-beat cycle; figure 3a), consistent with the double peak in 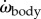. Body torque is just ahead of the fluctuations in angle-of-attack of the tail with respect to the local velocity vector (β_tail), which is also double peaked and deviates considerably from a sine wave (figure 3b) due to the large-amplitude motion. These observations indicate that the force associated with tail velocity may contribute significantly to τ_body.

Figure 3.

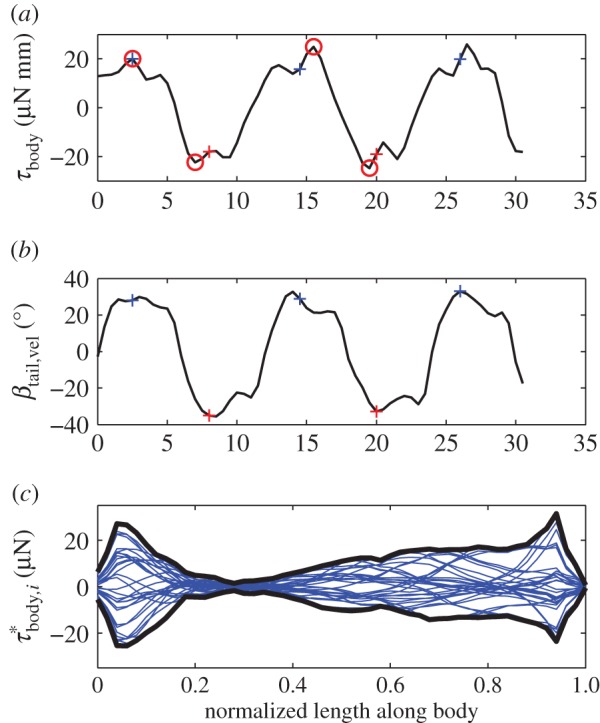
Body torque and angle-of-attack of the tail at 0.96 ℓ_body for the episode in figure 1. (a) Instantaneous inertial body torque τ_body (circles: selected extrema). (b) Angle-of-attack of the tail with respect to the velocity vector of the tail (β_tail). The blue and red ‘+’ signs in panel (a) and (b) correspond to the minima and maxima in α_body (figure 2a). The time between two ‘+’ signs of the same colour represents a full tail-beat cycle. (c) Distribution of the contribution to τ_body by the 51 body segments expressed as torque per unit length 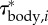. Each blue curve represents the torque distribution at a particular instant (at 1 ms intervals). The heavy black curves show the envelope. The narrowest location along of the ‘neck’ of the envelope corresponds to the location of the straight-body CoM.

We will now consider how the segmental contribution to the inertial torque about the CoM varies in time and along the body (derived by an inverse-dynamics analysis; electronic supplementary material, §3.3; note that this is not a distribution of the segmental inertial torque with respect to the segmental CoM). The amplitude of the inertial torque about the CoM per unit length 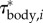is largest at the head and tail, as indicated by the amplitude envelope over a tail-beat cycle (figure 3c). Although the tail has less mass per unit length than the head, it contributes similar to inertial torque of the body, because the tail is further away from the CoM and moves at higher accelerations. The location of the ‘neck’ at about 0.28 ℓ_body of the envelope corresponds to the caudo-rostral location of the CoM in the straight fish. Inertial torque behaves as a travelling wave along the flexible posterior two-thirds of the body and as a standing wave along the stiff head (figure 4a).

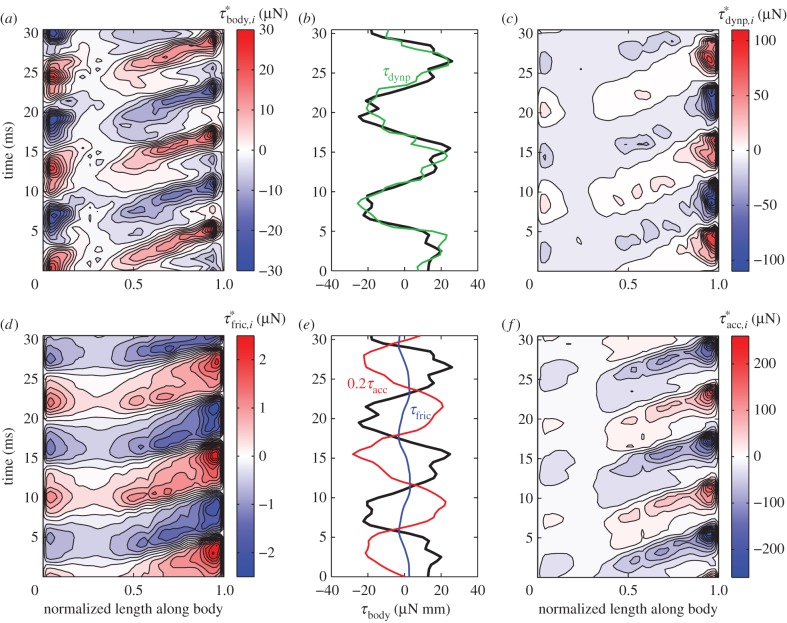
Figure 4.

Estimated torques. (a) Contour plot of inertial torque per unit length with respect to the CoM against normalized position along the body (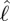) and time. (b) Inertial body torque τ_body against time (black); torque on the body due to dynamic pressure, τ_dynp (green). (c) Contour plot of torque on the body per unit length due to dynamic pressure against 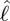and time. (d) Contour plot of torque on the body per unit length due to shear-force distribution against 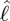and time. (e) Inertial body torque τ_body against time (black); torque on the body torque due to shear-force distribution, τ_fric (blue) and acceleration reaction forces (τ_acc) × 0.2 (red). (f) Contour plot of torque per unit length on the body due to acceleration reaction forces against 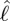and time.

To explore how external forces on the body contribute to the external torque on the body, we estimated 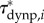(figure 4c), 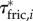(figure 4d) and 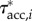(figure 4f) for the swimming event of figure 1. Our simplified approach to calculate external torque contributions is useful for our analysis but causes the sum of τ_dynp, τ_fric and τ_acc to not equal the inertial body torque τ_body. Torque τ_dynp (figure 4b: green curve) is of similar magnitude and phase as τ_body (figure 4e: black curve). By far the highest 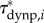amplitudes are found in the tail region (figure 4c). By contrast, τ_fric contributes little and is shifted forward in phase with respect to τ_body (figure 4e: blue and black curve, respectively), indicating that skin friction has a relatively small effect on body torque. Peak values of 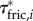are found in the tail region where high velocities occur (figure 4d). Finally, the estimated contribution of τ_acc (figure 4e: red curve; a fivefold scale reduction was applied to preserve the visible dynamic range of the other curves) is about five times as large in peak amplitude as τ_body and almost in counter-phase. From this grossly simplified analysis, we conclude that τ_dynp performs remarkably well as an indicator of the external torque on the body, while τ_fric is relatively small. The estimate of τ_acc deviates significantly in amplitude and phase and should be avoided as an indicator of the external torque on the body. A future computational fluid-dynamics solution may show how pressure and shear-stress distributions on the body contribute to the external torque on the body.

3.4. Kinetic energy fluctuations

While cyclic swimming entails no changes in body dynamics between successive cycles, instantaneous values oscillate considerably in fish larvae. Kinetic energy comprises two main contributions: translational kinetic energy of the CoM (E_tr,CoM) and rotational energy around the CoM (E_rot,body). Translational kinetic energy varies in proportion to 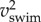. Rotational kinetic energy never drops to zero because the body undulates continuously (figure 5). Kinetic energy fluctuates by a factor of 3 during slow swimming (figure 5b, ), and less than twofold during fast swimming (figure 5a, 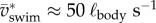), caused by fluctuations of the net force on the body (F_CoM) [9]. Figure 5 shows that instantaneous and mean E_tr,CoM are higher than the corresponding values for E_rot,body at a relatively high swimming speed (figure 5a), whereas the low-speed example (figure 5b) shows the reverse, which suggests a lower efficiency at the lower speed. Most of the in-phase reductions of both kinetic energy components over the swimming cycle will be dissipative (without useful conversion into elastic energy). Both translational kinetic energy and rotational kinetic energy fluctuate in phase (figure 5), mainly due to the varying amplitude and direction of the fluid force on the posterior body that causes oscillations in both F_CoM and τ_body.

Figure 5.

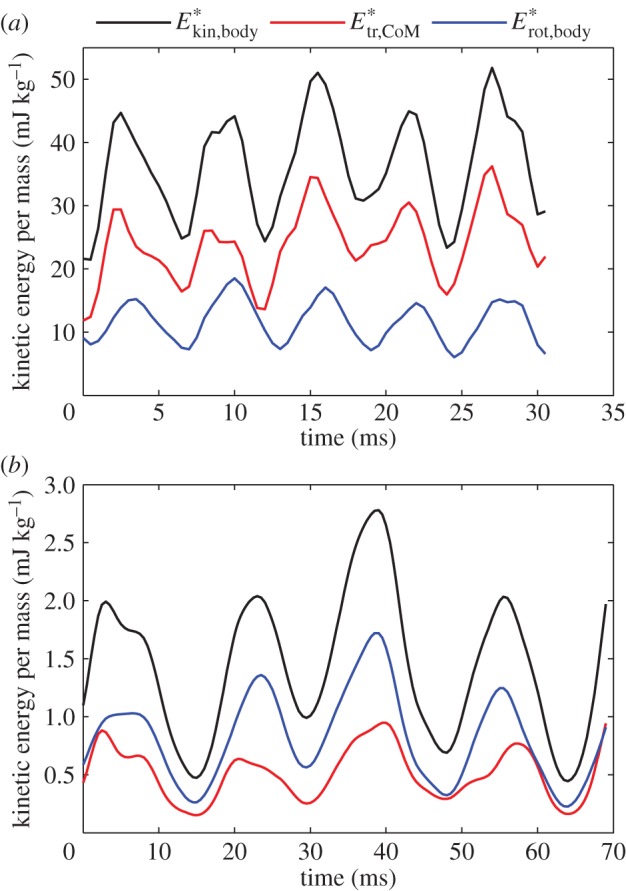
Specific kinetic energy for (a) a near-cyclic swimming event at approximately 50 ℓ_body s^–1 (age 5 dpf) (same as figure 1) and (b) approximately 8 ℓ_body s^–1 (age 3 dpf). Total kinetic energy of the body (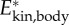; black), kinetic energy due to speed of the CoM (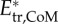; red), and sum of kinetic energy due to rotation of the segmental masses around CoM and rotation of the segments about their central vertical axis (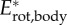; blue). .

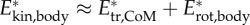3.5. Changes in swimming speed and tail-beat amplitude with frequency

To reach higher speeds, fish tend to increase tail-beat frequency f rather than body-wave amplitude [7,20]. However, the relationship between f and mean swimming speed 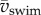is not a simple proportionality in larval zebrafish (figure 6a) during (near-)cyclic swimming. We previously found a decreasing slope with speed [7], based on a small dataset biased towards younger stages. Based on a much larger dataset, this study found that younger larvae swim slower than older larvae at f > 50 Hz (figure 6a). Stage 2 dpf reached frequencies of close to 80 Hz with 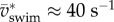(figure 6b). Stages 3–5 dpf top off at about 95 Hz and 60 s⁻¹. The largest improvement in maximum swimming speed occurs between stage 2 and 3 dpf.

Swimming speed depends also on tail-beat amplitude. When looking at the trend of A_tail with f within age groups, there is only a weak trend in early larvae (figure 6c,d blue line: data for 2 and 3 dpf combined). By contrast, A_tail increases markedly with frequency in older larvae (figure 6c,d red-green line: data for 4 and 5 dpf combined). Older larvae use higher amplitudes as f > 50 Hz. Correspondingly, for f > 50 Hz swimming speed tends to be higher in older larvae for the same tail-beat frequency (figure 6a). While younger larvae mainly increase frequency, older larvae increase both frequency and amplitude to swim faster. Increasing both frequency and amplitude requires more muscle power, suggesting that 4–5 dpf larvae have more powerful muscles than younger larvae. Non-dimensionalizing A_tail reduces the differences in how much amplitude changes with frequency (figure 6d), showing the importance of size in between-stage differences.

Plots of 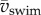against fA_tail and 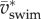against 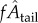show the expected upward trend (electronic supplementary material, figure S4), yet the scatter is largest at the highest swimming velocities (caused by a relatively large range of tail-beat amplitudes of the 4–5 dpf larvae and small deviations from an ideal cyclic swimming pattern).

3.6. Body torque and yawing angle

Higher swimming speeds imply higher drag and require more thrust, resulting in higher amplitudes of body torques and yaw, because local forces on the body are generally not in line with the CoM (figure 7a). This trend remains even after removing size effects (figure 7b). With swimming speed proportional to Re, torque increases with increasing Re (figure 7c,d). Higher torques at higher speeds result in higher body yaw (despite the decreasing cycle time with increasing 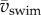)—the peak-to-peak amplitude of α_body increases with swimming speed (figure 7e,f), reaching almost 40°. Head yaw (fluctuation in α_head) is twice as large as body yaw (fluctuation in α_body; mean ± s.d. of peak-to-peak ratio of α_head over α_body is 2.11 ± 0.49), indicating that head yaw is not a valid proxy of body yaw. Maximum τ_body increases fivefold from stage 2 to 4 dpf (figure 7a,c). Maximum torque more than doubles from stage 2 to 3 dpf. Non-dimensionalizing torque reduces these increases (although it increases scatter), showing the important effect of size on torque (figure 7b,d).

Figure 7.

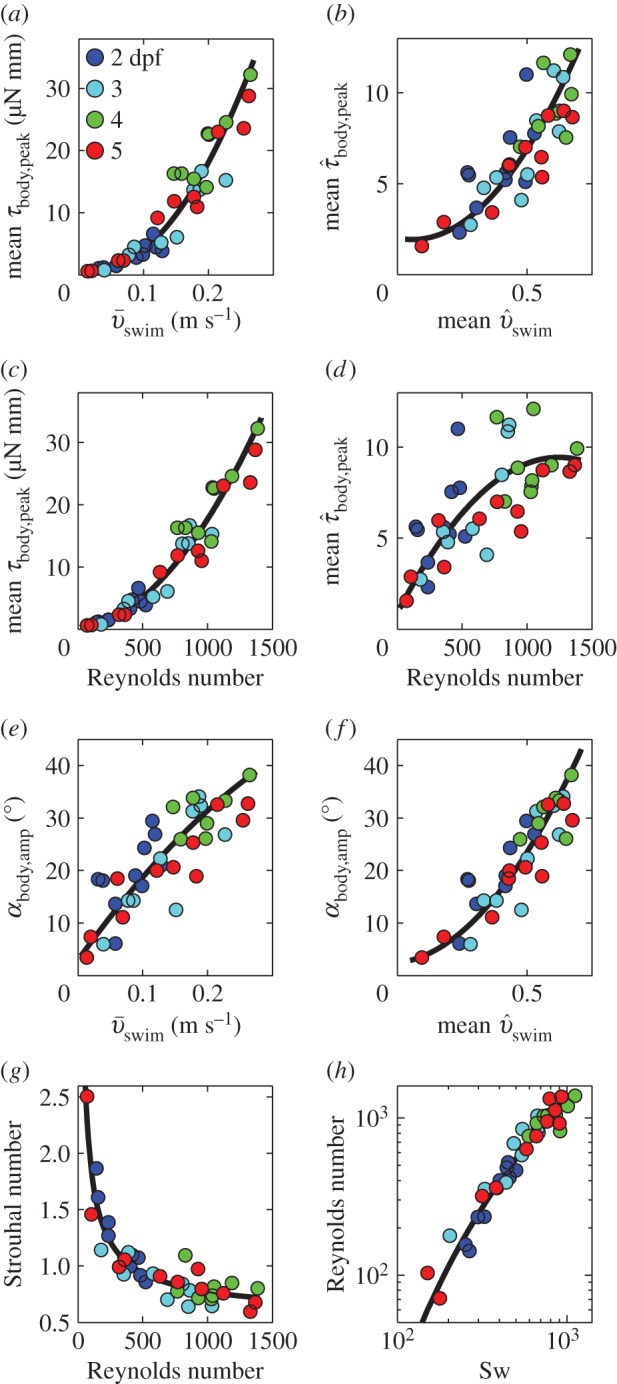
Dynamics of (near-)cyclic swimming for same dataset as figure 6. (a) Amplitude of torque peaks (mean per event, colour code: age 2–5 dpf) over mean swimming speed (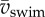). (b) As (a), but non-dimensionalized. (c) Amplitude of torque peaks against Reynolds number (Re). (d) As (c) but non-dimensionalized. (e) Peak-to-peak amplitude of body angle (mean per event) against 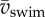. (f) Idem, but against dimensionless swimming speed. Second-order polynomial curve fits are shown for (a)–(f). (g) St against Re, with a fit of a (negative) power function plus a constant. (h) Re against swimming number Sw (logarithmic scales). The curve fit follows from the fit of St against Re, by using St = Sw/Re. Parameter values for each curve fit are given in electronic supplementary material, table S3.

3.7. Effects of Reynolds number on Strouhal number and swimming number

The same increase in the product of tail-beat frequency and amplitude causes a larger increase in swimming speed at high than at low swimming speeds (electronic supplementary material, figure S4a). This larger increase in speed for a given increase in fA_tail causes St to drop with increasing Re, which is proportional to 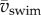. The lowest swimming speeds result in Strouhal numbers of up to 2.5; St drops to 0.72 as larvae reach top swimming speeds of nearly 0.30 m s⁻¹ or 60 ℓ_body s⁻¹ (figure 7g). The decrease in St is largely explained by the increase in Re: St decreases from 2.5 to 0.72 (with ≈0.72/2.5 = 0.29) at a similar rate as the ratio of the product of tail-beat frequency and amplitude to Re—the product fA_tail increases by a factor of ≈8 as Re increases by a factor of ≈23 (8/23 ≈ 0.30). More precisely, the St relates to Re as 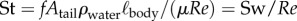. The St–Re data of larval fish are described well by a (negative) power function plus a constant (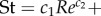 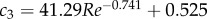; figure 7g, black curve). The youngest larvae of 2 dpf do not reach the high Re—low St combinations exploited by the older larvae. With St = Sw/Re, our curve fit can be rewritten as 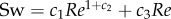, which deviates from a simple power function. When plotted on a double logarithmic scale (figure 7h) this fit is still curved, the slope decreases with increasing Re.

Our experimental data do not conform with the theoretical prediction of Gazolla et al. [21], which states that 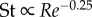and 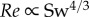(giving a straight line in a double log Re–Sw plot) based on small-amplitude body undulations and Blasius resistive theory for the laminar swimming regime. The predicted exponent of −0.25 lies outside the 95% confidence interval [−1.250, −0.389] of the experimentally obtained exponent of −0.741. A large deviation is to be expected because neither assumption is substantiated by the actual swimming motions of larval fish. To further compare the predicted exponent with our data, we also made linear regressions for 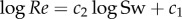. For the full Sw–Re range in the dataset, we obtained values for c₂ of 1.464 and 1.572 for, respectively, Re and Sw as the dependent variable. Both values are well above 4/3. Restricting the maximum in Re to 800 (used as upper limit for numerical simulations of the laminar regime in Gazolla), we found corresponding values of 1.614 and 1.710, deviating even more from 4/3. The higher value of the exponent for the lower Re range is in agreement with the curved shape of the double log Sw–Re fit (figure 7h).

3.8. Kinetic energy and power

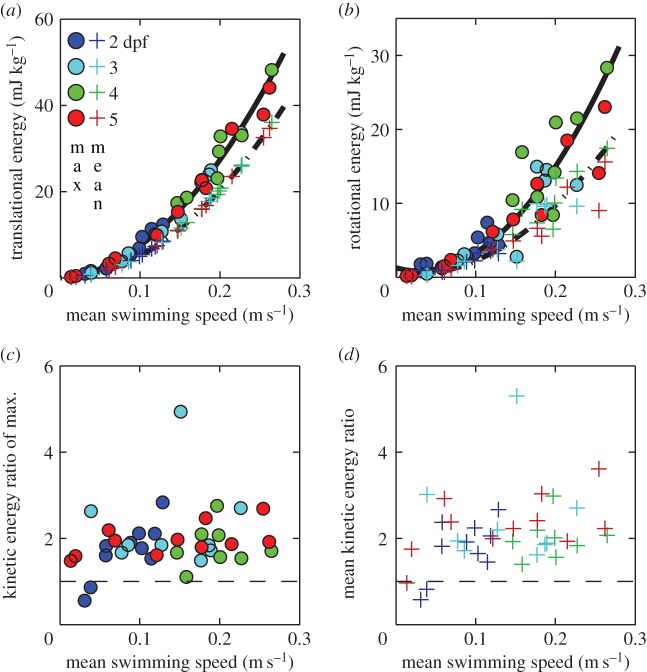
Translational and rotational kinetic energy increase nonlinearly with swimming speed (figure 8a,b). The contribution of translational versus rotational kinetic energy changes with age and swimming speed (figures 5 and 8a,b). Maximum mass-specific 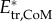and 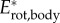more than triple between age 2 and 4 dpf. Translational energy outweighs rotational energy in most recorded swimming events (figure 8c,d) except a few young larvae (age 2 dpf) at low 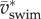(<15 ℓ_body s^–1) and high St, when the tail produces a relatively high lateral force component. In general, rotational kinetic energy is a substantial component of the total kinetic energy of the body in larval swimmers.

Figure 8.

Specific kinetic energy due to translation E*_tr,CoM and rotation E*_rot,body during (near-)cyclic swimming for the same dataset as figure 6. (a,b) Maximum (○) and mean (+) values against mean swimming speed 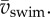Second-order polynomial curve fits for maxima (continuous curve) and mean (dashed curve) are shown in (a,b). (c,d) Ratio of the maxima (c) and the means (d) of E_tr,CoM and E_rot,body over . The horizontal dashed line indicates a ratio of 1. Parameter values for each curve fit in (a) and (b) are given in electronic supplementary material, table S4.

Maximum specific power due to fluctuations in kinetic energy of the body increases nonlinearly with 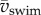(figure 9a). The two main contributors to power are translational and rotational power (figure 9b). Rotational power exceeds translational power rarely and only at low 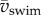(figure 9b). Specific power triples within 3 days of development—peak 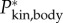at the highest observed 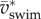in 5 versus 2 dpf larva is 22 versus 7 W kg⁻¹. These values are much lower than the total power required for swimming, neglecting energy dissipated in the body and power spent on external fluid flow. Assuming that this body kinematics-based motion power is 25% of muscle power, and that 50% of the body is locomotion musculature, and 50% of these contribute at any one time, zebrafish larvae require muscle peak power outputs of 112–352 W kg⁻¹ muscle at the respective maximum performance at 2 and 4–5 dpf with contraction frequencies of 80–95 Hz. Given the high maximum tail-beat frequencies, these projected muscle powers match or exceed the currently known maxima for aerobic fast, super-fast and asynchronous muscles (tree frog: 200 W kg⁻¹ (peak), 54 W kg⁻¹ (average in work loop) at 44 Hz at 25°C [24]; toadfish: 14 W kg⁻¹ (average in workloop) at 22 Hz at 15°C [25]; beetle: 200 W kg⁻¹ (peak), 127 W kg⁻¹ (average in workloop) at 94 Hz at 35°C [26]), but are less than maximum power in anaerobic quail muscles (1121 W kg⁻¹ (peak), 390 W kg⁻¹ (average during shortening phase in workloop) at 23 Hz at 40°C [27]).

4. General discussion

4.1. Body dynamics of undulatory swimming in larval fish: improving swimming skills within a narrow time window

Using a distributed-mass inverse-dynamics approach, we shed new light on the swimming mechanics of larval fish. Across the observed range of swimming speeds, large body undulations do not cause large sideslip of the CoM, but considerable body yaw. We expect that adult fish, which use narrower, lower frequency body waves, will show considerably lower relative fluctuations in body yaw, torque and moment of inertia.

Comparing within larval stages, swimming performance greatly improves between 2 and 5 dpf. Over this age range, larval fish increasingly favour intermittent over cyclic swimming [7]. Yet burst periods are sufficiently long and cyclic to analyse trends that elucidate the physics of swimming in the intermediate Reynolds regime and the development of swimming in larval fish. From 2 to 3 dpf, the larvae increase maximum tail-beat frequency f_max from 80 to 95 Hz. The 4 dpf larvae used similar f_max as 3 dpf larvae, but generated higher maximum tail-beat amplitudes for frequencies above 50 Hz. The higher tail-beat frequencies and amplitudes lead to higher swimming speeds and indicate that maximum power output of the swimming musculature increases rapidly after hatching. Improving swimming speed reduces the predation risk of larval fish [28] and enhances their ability to catch prey when they start feeding at 5 dpf. Several other performance criteria require future attention, such as fast-start performance and manoeuvres in three-dimensional space.

4.2. Coping with high-friction forces: trading efficiency for thrust

Vortex shedding mechanics (as expressed by St) changes with flow regime (as expressed by Re) in a nonlinear way [16,19,29]. The inverse relationship between St and Re is mapped out by larval fish (figure 7g). Slow larvae swim at higher St (St ≈ 2.5 at Re = 60) than fast larvae (St ≈ 0.72 at Re = 1400). Thus, across the examined larval size range (body length 3–4.5 mm), increasing swimming speed by one order of magnitude from 25 to 250 mm s⁻¹ causes a drastic, nonlinear drop in St. The Strouhal number remains roughly constant across the typical speed range of adult fish and cetaceans (St = 0.2–0.4 for Re = 10³–10⁵) [13,16,19,30]. When adult fish increase tail-beat frequency, their swimming speed increases proportionally without increasing tail-beat amplitude, so St drops little with increasing speed [31]. The Strouhal number reflects differences in vortex shedding mechanics caused by body shape. Swimmers with high aspect-ratio tail fins use lower St values [16,30] than anguilliform swimmers [16,31]. Overall, undulatory swimmers operate close to optimal St values, yet optimal Strouhal numbers vary with body shape and swimming speed.

Undulatory swimmers use high Strouhal numbers in high-friction environments. High Strouhal numbers occur not just at small body sizes, but generally in systems with high body drag, such as adult lungfish moving through highly viscous watery solutions [32]; sandfish and nematodes moving through granular media [33–36]; and alligators (data in [21]). When facing higher frictional forces, undulatory swimmers swim at lower stride lengths—tail-beat frequency f and amplitude A_tail must increase to achieve the same displacement (computational: [2,14,15,37], experimental: [19,32,38,39]). Theoretical studies [10,16] show that maximal efficiency decreases and St increases with decreasing Re. When viscous or other frictional forces become large relative to inertial forces, undulatory swimmers must sacrifice efficiency for higher thrust.

The Strouhal number decreases steeply as undulatory swimmers transition from the viscous to the inertial flow regime (figure 7g,h), consistent with the inverse relationship between St and Re. As seen in larval fish, swimming at lower Re requires generating relatively higher propulsive forces by increasing f and A_tail (figure 7h). Both increase the torque around the CoM and hence decrease the ratio of translational to rotational kinetic energy. Undulatory swimmers have no known mechanisms to store rotational kinetic energy. Hence, a lower ratio of translational to rotational kinetic energy implies a lower propulsive efficiency, as indicated by a high St value. As Re drops, a given increase in f or A_tail causes less of an increase in swimming speed and St increases. By swimming faster, larval fish crank up their Re, which might enable them to increase propulsive efficiency at the expense of higher power expenditure. High swimming speeds require very high tail-beat frequencies, which demand super-fast muscles, which are known to have low efficiencies [40], which counteracts the gain in fluid-dynamic efficiency. In larval zebrafish of 4–5 dpf, this limitation tops off f_max at about 100 Hz and Re at about 1400. The general trend of a decreasing St with Re in the intermediate regime has been predicted by CFD studies (e.g. [2,20,21]).

4.3. Scaling of the swimming number Sw

We obtained a more complex relationship between Re and the swimming number Sw than suggested by Gazolla et al. [21]. They explored the relation between Re (range 200–20 000) and Sw with CFD simulations. They suggested that the nonlinear Sw–Re relationship can be described by first approximation by two power functions. While the theoretical prediction matches both the CFD and the experimental data on large swimmers, the match is less convincing in the laminar flow regime, where the power exponents predicted using Blasius theory (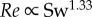) and CFD (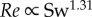) are considerably lower than the experimentally observed exponent (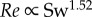, power function fit to zebrafish data over 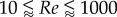) and depend critically on the exact value of transitional Re—Gazolla et al. obtain a good fit between Blasius prediction (exponent 1.33), CFD data (exponent 1.31) and experimental data (exponent 1.33) partly by placing the transition from the laminar to the turbulent flow regime at different Re and Sw (CFD: Re 800, Sw 2000; experimental data: Re 3000, Sw 10 000).

The large discrepancy between experimental data on the one hand and theoretical Blasius prediction on the other hand stem from the complex fluid-dynamic effects caused by large-amplitude tail motion. Any high anterior drag must be balanced by high thrust, which the swimmer generates by increasing tail-beat amplitude and frequency, which in turn increase anterior drag by positive feedback on τ_body and hence amplitudes of α_head and α_body. The nature of this feedback depends on Re and body shape. The Blasius prediction of Gazolla et al. is not able to capture this complex feedback, leading them to underestimate drag and hence St.

4.4. Swimming performance varies with size and speed

Small organisms (ℓ_body < 10 mm) operating in the intermediate flow regime (10¹ < Re < 10³) reach not only much higher tail-beat frequencies, but also higher ℓ_body-specific swimming speeds than large undulatory swimmers (ℓ_body > 10 mm). Despite experiencing relatively higher viscous fluid forces and despite a lower swimming efficiency, zebrafish larvae can reach extreme forward speeds of up to 60 ℓ_body s⁻¹, because they can generate relatively high propulsive forces at tail-beat frequencies of up to 95 Hz. By contrast, large undulatory swimmers have considerably lower tail-beat frequencies and ℓ_body-specific swimming speeds. And adult fish retain those low values when placed in more viscous flow regimes. Lungfish maintain swimming speeds of 0.15–0.25 ℓ_body s⁻¹ and tail-beat frequencies of 1–2 Hz over a 1000-fold increase in viscosity [32]. Sandfish ‘swimming’ in sand use similar tail-beat frequencies (1–4 Hz) [33]. Compared with small undulatory swimmers, which are adapted to the intermediate flow regime, large undulatory swimmers have muscles optimized to operate at low cycle frequencies in order to swim at low Strouhal numbers. Large swimmers cannot adjust to increased friction forces by increasing tail-beat frequency by orders of magnitude, because their axial muscles have a low maximum cycling frequency.

Across body sizes, distance/ℓ_body covered per tail beat in the viscous flow regime is low compared with undulatory swimmers in the inertial flow regime: lungfish and sandfish reach 0.1–0.2 ℓ_body/tail-beat cycle [32,33], zebrafish larvae 0.2–0.6 [4,7], tadpoles 0.3–0.6 [41], insect larvae 0.3 [42]. By contrast, adult fish in the inertial flow regime swim at 0.4 (anguilliform swimmers; [43,44]) to 0.9 ℓ_body/tail-beat cycle (carangiform swimmers; [45–47]) during routine swimming. In summary, during undulatory swimming in systems with high viscous or friction forces, St is high and efficiency is low.

Ethics

The experiments were approved by the Wageningen University Animal Experiments Committee.

Data accessibility

Data available from the Dryad Digital Repository: http://doi.org/10.5061/dryad.r503m.

Authors' contributions

U.K.M. manually digitized the video data. J.L.v.L. and C.J.V. wrote the Matlab codes used to process and analyse data. J.L.v.L. and U.K.M. wrote most of the paper. All authors participated in experimental design, execution of the experiments, development of concepts, and critical revisions and gave their approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by the Earth and Life Sciences Foundation (ALW814.02.006 to J.L.v.L. and U.K.M.; ALW824.15.001 to J.L.v.L. and C.J.V.) and National Science Foundation (DBI-0821820, BIO-IOS-1440576 to U.K.M.).