Influence of physico-chemical, mechanical and morphological fingerpad properties on the frictional distinction of sticky/slippery surfaces

Abstract

This study investigates how the fingerpad hydrolipid film, shape, roughness and rigidity influence the friction when it rubs surfaces situated in the slippery psychophysical dimension. The studied counterparts comprised two ‘real’ (physical) surfaces and two ‘virtual’ surfaces. The latter were simulated with a tactile stimulator named STIMTAC. Thirteen women and 13 men rubbed their right forefingers against the different surfaces as their arms were displaced by a DC motor providing constant velocity and sliding distance. Tangential and normal forces were measured with a specific tribometer. The fingerpad hydrolipid film was characterized by Fourier transform infrared spectroscopy. The shape and roughness of fingers were extrapolated from replicas. Indentation measurements were carried out to determine fingerpad effective elastic modulus. A clear difference was observed between women and men in terms of friction behaviour. The concept of tactile frictional contrast (TFC) which was introduced quantifies an individual's propensity to distinguish two surfaces frictionally. The lipids/water ratio and water amount on the finger skin significantly influenced the TFC. A correlation was observed between the TFC and fingerpad roughness, i.e. the height of the fingerpad ridges. This is essentially owing to gender differences. A significant difference between men's and women's finger topography was also noted, because our results suggested that men have rougher fingers than women. The friction measurements did not correlate with the fingerpad curvature nor with the epidermal ridges' spatial period.

1. Introduction

Human tactile perception has been the subject of many studies over past years and has aroused interest from various fields of application such as remote surgery, virtual reality, product designing, tactile deficiencies detection and rehabilitation, e-shopping, smart surfaces, etc. Simultaneously, the recent and dazzling development of touch interfaces for interactive and mobile devices has led to the exciting challenge of developing tactile stimulators. These devices aim at giving the illusion of rubbing various textures when scanning an active and programmable single surface with one's finger [1]. Although tactile stimulators are still in their infancy, some prototypes have been developed in recent years both as useful tools for comprehension improvement of tactile perception as well as for surface and texture simulation. Based on the considered apparatus, the stimulation can be applied either by means of mechanical stretching of the skin [2], setting up of an air-bearing between the finger and a plate (squeeze effect) [1], or generation of electrostatic forces [3]. While different principles and technologies are used, all stimulators operate with the same main objective: modulating friction forces between the fingerpad and a counterpart. Therefore, one can define these stimulators as friction force modifiers that consequently induce tactile perception modulation. Indeed, tactile perception originates in the mechanical activation of sensorial receptors located beneath the skin surface, in the dermis [4–6]. When exploring surfaces with the finger, the induced dynamical friction forces are thus transmitted towards these receptors, producing signals transferred to the central nervous system by means of a mechano-electrical transduction process. Consequently, the finger/surface friction behaviour has a critical influence on tactile perception. This statement, which is assessed by psycho-perceptual studies [7–10], justifies the operating concept of tactile stimulators. Moreover, it underlines the necessity of a better understanding of the fingerpad's friction behaviour on commonly touched ‘real’ surfaces in order to improve stimulators' efficiency.

A usual criterion for quantifying friction during sliding is the coefficient of friction (COF), i.e. the ratio of the tangential force versus the normal load. From a tribological perspective, the factors influencing the friction between a surface and the finger could be classified according to three categories: counterpart features (material properties, roughness, texture, etc.), sliding conditions (speed, motion, normal load, environment, etc.) and finger properties (mechanical behaviour, skin surface chemistry, roughness of fingerprint ridges, etc.). These factors and their influences on the COF between a surface and the finger (or another body region) are discussed below.

The influence of the rubbing surface features on the COF has been extensively studied [11]. First, materials in contact have a strong influence. The COF between the skin and the smooth surface of a homogeneous material can be classified in the following decreasing order: soft polymers such as rubber, hard polymers (except polytetrafluoroethylene, PTFE) [12], metals and PTFE [13]. The rubbing against glass induces a lower or a higher friction coefficient than hard polymers [14] and metals, depending on the moisture amount in the skin/glass interface. Second, the extensively studied effect of the counterbody's roughness on friction has shown different behaviours. The friction regime can be dominated by adhesion on smooth surfaces or by deformation of the fingerpad on rougher surfaces. Consequently, the COF decreases with increasing roughness, because R_a (the arithmetic average of asperity height absolute values) is smaller than 11.5 µm [13,15]. This effect has been explained by the decrease of the tangential force owing to adhesion [16]. But, for higher R_a, the COF rises when roughness increases owing to the increase of skin deformation [17]. Moreover, for well-defined regular surfaces produced by laser texturing with a similar R_a, the COF slightly depends on texture parameters such as asperity radius and spacing [18].

As regards sliding conditions, although rotary set-ups are sometimes used [19], linear-alternate motion of the finger is carried out in most experiments. In this case, the COF is dependent on the finger angle relative to the scanning surface [20] owing to the variations of the contact area. Moreover, the evolution of the COF between finger skin and various materials decreases with an increase of the normal load. The COF commonly follows a linear relationship with W ^n–1, where W is the normal load and n a coefficient ranging from 0.66 to 1 [21]. Nevertheless, the relationship between W and the COF is considered linear in certain cases [14]. When rubbing on smooth counterfaces, some studies point out an increase of the COF for low sliding speed (up to 10 mm s⁻¹) and a decrease for higher velocities [22]. These changes have been linked to the dynamic of occlusion mechanism (moisture accumulation) under the fingerpad [23]. Finally, as some studies have highlighted, the climate (dry, damp, etc.) has a strong effect on COF values [23,24].

Fingerpad properties are related to its complex structure and composition. The outer layer of the epidermis, namely the stratum corneum (SC), is composed of numerous stacked corneocytes (flattened protein-enriched cells) which are embedded in a lipid matrix [25]. Although most of the body regions show SC thickness ranging from 10 to 30 µm [25,26], the fingerpad's SC thickness reaches several hundred micrometres by considering epidermal ridges [23]. The SC's elastic modulus has been extensively measured on various regions of the body [27–29]. Nevertheless, in vivo measurement of the fingerpad elastic modulus was performed, to the best knowledge of the authors, in only one study [30], which reported values ranging from 0.9 to 4 MPa. Another of the finger's crucial surface properties is its physicochemistry. A brief overview of the chemistry of the skin surface could be depicted as a mixture of lipids and water covering the SC [31]. But the origins of these two main components are even more complex: sebum, free fatty acids and water owing to the desquamation process, environmental moisture, adsorbed lipids, water diffusion through the SC, etc. [25,32]. A more accurate denomination of skin physicochemistry than sweat should involve the notion of cutaneous hydrolipid film (CHF). The water amount in the CHF has a strong effect on the skin's mechanical behaviour [27,33], because the plasticizing action of water decreases the SC elastic modulus [34]. The relationships between fingerpad physicochemistry and the COF have rarely been studied [19]. Nevertheless, numerous studies have related the friction of other body regions on various counterbodies to the CHF. Skin hydration or moisturization has been extensively highlighted to increase the COF [11,13,14,16,19,32,33]. This effect has been explained by capillary adhesion forces and an increase of the contact area leading to more adhesion [34,35]. From a tribological perspective, CHF lipids play an unclear role. Because adhesion decreased after skin was delipidized with ether [35], it could be assumed that lipids tend to increase the COF. Nevertheless, no overall correlation has been found between the lipids of the skin surface and the COF for most of the body regions except for the forehead and postauricular region which are sebum-rich areas [24,32]. Differences of lipid composition and quantity depending on the body region could explain the contradictory correlations observed between lipids and the COF [36,37].

Because of the natural biological diversity of humans, each fingerpad is unique. This elementary statement assumes that friction force differences are due to the diversity of finger properties. Moreover, it underlines the necessity of performing in vivo friction tests with a rather large number of individuals [38]. The diversity of fingerpad properties is a major concern in the field of tactile stimulator development. Indeed, such a device must be adapted and equally efficient from one individual to another. Another crucial issue is the stimulator's capacity to generate similar friction forces to those measured when the finger rubs ‘real’ surfaces. This last point underlines the kind of surfaces that need to be considered. Compared with precedent studies, this study follows the original approach of picking out counterparts that are defined from a perceptual perspective rather than from an engineering one. In the framework of psycho-perceptual researches, it has been shown that textures could be classified according to four dimensions depending on the perception of individuals when touching a surface. These dimensions of tactile perception have been defined as ‘softness’, ‘warmth’, ‘roughness’ (eventually divided in two subdimensions: fine and macro roughness) and ‘slipperiness’ [39]. Among them, only the latter listed dimension has been entirely related to friction forces occurring at the skin/surface interface. As friction modifiers, tactile stimulators are consequently convenient to simulate surfaces situated in a sticky/slippery scale (slipperiness dimension).

This study aims at characterizing the fingerpad properties of a rather large number of individuals and provides COF measurements of these fingers when they scan surfaces situated in the slipperiness dimension. Some counterfaces are ‘real’ (physical) surfaces, and others are ‘simulated’ ones by the use of a tactile stimulator named STIMTAC [40]. The goal of this study is to contribute giving answers to the following questions: What are the fingerpad properties' differences between individuals? When rubbing the same surface, what are the COF differences between individuals? What fingerpad properties govern the COF when they rub against physical surfaces? Do the COFs measured on a stimulator have the same range as the COFs encountered on physical surfaces?

2. Experiments and methods

2.1. Experiments overview

2.1.1. Participants

Twenty-six French volunteers (13 women and 13 men) participated in the experiments that were carried out. All procedures performed in studies involving human participants were in accordance with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. The subjects gave informed consent and provided information about their date of birth. None of them had been subjected to a similar experiment before and they were neither physiologically nor cognitively deficient. Individuals' age ranged from 34 to 56 years with an average of 42, and the mean age for men was 41.2, whereas the mean age for women was 42.8.

2.1.2. Global experiments procedure

Every participant was requested to follow the same global experiments procedure during approximately 45 min. This procedure was chronologically organized as follows. First, the subject had to stay calm for 5 min in a room where the temperature was 19 ± 1°C before washing his/her right forefinger with a common hydroalcoholic gel (Aniosgel 85 NPC) for 30 s in order to prevent pollution owing to product handling or sebum excess resulting from eventual physical activities just before the experiments. After the cleaning and drying of the subject's hands, SC physicochemistry analysis was performed (see §2.2.3). Then, friction experiments were conducted in a second room where temperature was kept at 20 ± 0.5°C (see §2.3). As the chemical composition of SC changes during the day [41], an important task was to perform friction experiments just after the characterization of the fingerpad's physicochemistry. Indentation tests were performed afterwards (see §2.2.2). Finally, the right forefinger of the participant was moulded to obtain its morphology and its roughness (see §2.2.1). The finger replica was made later, after the subject was released.

2.2. Fingerpad properties characterization

2.2.1. Shape and roughness

After hand cleaning and drying, the right forefinger's replica of each individual was realized in three steps. First, the subject pressed his/her finger on a high-viscosity silicone paste in order to create a roughly defined mould. Second, a low-viscosity silicone was trapped between the participant's finger and the mould. During this step, the mould was put into contact with the hinge of the participant's phalange but not against the fingerpad, in order to obtain a precise mould and prevent dermatoglyph deformation. Then, a polyurethane replica was made. The replica's topography was made by using an optical apparatus based on variations of focal length (InfiniteFocus G4, Alicona, Austria). The data were processed with the open source software Gwyddion 2.30. Two kinds of measurements were made: (i) the fingerpad's curvature radii R_main and R_{perpendicular} (respectively along and across the finger's principal axis) were used to calculate the geometric mean of the curvature radius

2.1

and (ii) after extraction of five profiles, the mean spatial period SP and the mean epidermal ridges R_t, i.e. the sum of the largest profile peak height and the largest profile valley depth (figure 1), were calculated. Note that R_t's mean value has been preferred to R_a in order to be more accurately related to the dermatoglyphs’ height.

Figure 1.

Three-dimensional overview of the fingerpad's surface. SP is the spatial period.

To validate the replica's process, comparison of a grooved aluminium plate (with dimensions similar to fingerpad in terms of spatial period and depth of valleys) and its replica was carried out. There was a 4% error for R_t and 1% for SP between the original and the replica.

2.2.2. Effective elastic modulus

A specific indentation device was implemented to evaluate the fingerpad's rigidity. This apparatus was mainly composed of a ring, an inductive displacement transducer rigidly connected to the ring, and a load gauge sensor (figure 2). During one of the tests, the subject placed her/his finger on the ring which was vertically guided with very low-stiffness elastic blades (7.8 × 10⁻² N mm⁻¹), and pressed her/his finger on the load sensor. As the ring had a 22 mm inner diameter, it stayed in contact with the phalange's extremities (see drawings included in figure 2), thus only the fingerpad was pressing the load sensor.

Figure 2.

Fingerpad indentation set-up and indentation curve (grey points) typically obtained. The dashed black curve indicates the loading curve fitting with respect to Hertz theory. Drawings show the fingerpad's pushing during the test.

This was an active test: the participant pressed her/his fingerpad by herself/himself on the load sensor's surface (loading and unloading). The only direction given to the subject was to reach a maximum load which had to be as close as possible to 0.5 N (similar to the loading encountered during friction tests, see §2.3.2). During the test, a gauge on a computer screen indicated continuously the normal load applied. The angle between the finger and the surface was about 25°, and loading speed (imposed by the subject) ranged from 0.9 to 3.5 mm s⁻¹. Prior to the real test, a 5 min training period took place in order to habituate the subject to use of the indentation device.

During the indentation, two simultaneous measurements were carried out: (i) the normal force P applied by the fingerpad on the polished stainless steel flat surface of the load sensor and (ii) the displacement h of the ring relative to the load sensor surface. These measurements led to a loading–unloading indentation curve for each subject.

Figure 2 highlights the indentation curve typically obtained. It shows a classically observed nonlinear behaviour [42] and a hysteresis between loading and unloading owing to the viscoelastic behaviour of the fingerpad.

Normally, the well-defined geometry of the indenter is used for determining the projected contact area and then the reduced elastic modulus of the tested material. In the present method, as the indenter is a flat surface, the current method cannot be used. Considering the beginning of the loading curve to be a purely elastic deformation, the loading measurement points until 0.4 N were fitted with Hertz's theory (figure 2) to calculate the reduced elastic modulus E* using

2.2

where P is the normal load (N), E^* is the reduced elastic modulus (Pa), h is the displacement (m), R is the radius of the equivalent sphere (m).

P and h were obtained from the indentation measurements. The radius R was extracted from the analysis of the finger's morphology (see §2.2.1): R was chosen to be equal to R_gm, which gave an identical contact area for an equivalent penetration depth. Then, the elastic modulus of the finger E_finger was determined according to the following equation:

2.3

where ν_finger is the Poisson's ratio of the fingerpad fixed to 0.5, as for a perfectly incompressible material, ν_steel is the Poisson's ratio of the stainless steel plate = 0.3, E_steel is the Young's modulus of the stainless steel = 210 GPa.

As pointed out by van Kuilenburg et al. [27], this elastic modulus has to account for the multilayered and non-homogeneous structure of the skin. Therefore, E_finger was more accurately defined as the fingerpad's effective elastic modulus E_eff.

2.2.3. Cutaneous hydrolipid film composition

The physicochemistry of the fingerpad's SC was characterized by Fourier transform infrared spectroscopy with attenuated total reflection (ATR-FTIR). Briefly, in ATR-FTIR spectroscopy analysis, the sample is placed on an infrared transparent crystal of high refractive index (the internal reflectance element, IRE) whose geometry allows total internal reflection. The internal reflectance results in an evanescent wave which is attenuated in regions where the sample absorbs the IR radiation.

In this study, the fingerpad's SC absorbance was measured in the mid-IR region (1000–4000 cm⁻¹) with a 2 cm⁻¹ resolution using 8700-Nicolet spectrometer equipped with a ZnSe IRE displaying a trapezoidal cut at 45°. Between each analysis, the 0.8 cm² surface of the IRE was gently cleaned with high purity ethanol. In ATR, the IR radiation penetration depth depends on the contact pressure between the sample and the IRE [41,43]. To minimize penetration depth variations from one subject to another, the experimenter applied with his own forefinger a nearly constant loading of 5 N on the subject's fingernail. The reason for holding the load in this way (lack of mechanical loading system) was to avoid causing the participant pain or discomfort. Pre-tests have shown that loading exceeding 3 N did not change spectrum peak intensity and position.

The spectra obtained in this study (figure 3) were very similar to those presented in the literature for human fingers or other parts of the human body in vivo [43] and for SC biopsies in vitro [25].

Figure 3.

Typical ATR-FTIR spectrum obtained. Arrows indicate bonding vibration bands appearing. : O–H symmetric stretching; and 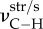: C–H asymmetric and symmetric stretching; : O–H bending and rocking; : C=O stretching; ν_aI and ν_aII: amide I and amide II bands.

ATR-FTIR spectral interpretation is much discussed in the literature in order to characterize the structure and composition of the SC. As regards the characterization of water quantity in the SC, the most appropriate technique is to calculate the band integrated intensity (peak area under the baseline). A comparison with the band integrated intensity and gravimetric measurements of SC in vitro has shown that the two measures were proportional as long as the water content was lower than 0.2 g g⁻¹ [44]. As regards the characterization of lipids, it must be noted that lipids’ IR absorbance signal is representative of a mixture of both intercellular lipids and skin surface lipids [25]. To compare the skin of different subjects, it is convenient to calculate the ratio of the integrated intensities which gives the lipids/water proportion in the SC [43].

Consequently, integrated intensities (peak surface under the baseline) , and were first calculated. Then, a water descriptor index representing the water quantity present on the fingerpad and a lipids/water descriptor index describing the lipids/water proportion were calculated.

The IR radiation depth of penetration d_p has been defined elsewhere [43] as

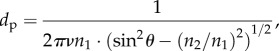2.4

where ν is the frequency of the incident radiation, θ is the angle of incidence (45°), n₁ = 2.43 and n₂ = 1.55 are the refractive indexes of the IRE crystal and the skin, respectively [44]. Considering the wavenumbers used, the penetration depth of the evanescent field in the fingerpad ranged from 0.6 to 1.1 µm. ATR-FTIR analysis was also located in the outer layer of the SC.

2.3. Friction tests

2.3.1. Scanned surfaces

Two sets of surfaces were considered in this study. The first set of surfaces consisted of two 40 × 40 mm² flat slabs of 4 mm thickness made of polymer: PTFE and acrylonitrile butadiene styrene (ABS) with a sticky coating. The roughness R_a of these slabs was 0.70 µm for the PTFE slab and 1.56 µm for the ABS slab. Prior to the friction experiments, all individuals had judged the ABS surface as being much more sticky than the PTFE one (thus perceived more slippery than the ABS-coated slab). In the following, the coated ABS and PTFE slabs will be thus respectively defined as ‘sticky surface’ and ‘slippery surface’. These two surfaces were adjoined on both sides of a larger plate in order to be scanned by the finger in a continuous way.

The second set of surfaces was based on the use of a tactile stimulator named STIMTAC [40]. The plate of STIMTAC (in beryllium copper coated with a polymer film with R_a = 1.23 µm) looks like a laptop computer touchpad (figure 4), but it vibrates with the help of piezoelectric actuators. The key concept of this stimulator's operation is based on the squeeze film air-bearing theory which is detailed in [45]. When one's finger rubs the vibrating plate, a thin layer of air is trapped between the plate and the fingerpad and leads to the lowering of friction force. The greater the vibration amplitude is (up to 2.3 µm), the thicker the layer of air between the plate and the fingerpad is, and thus the lower the friction force is. It must be mentioned that the lowering of the friction force has not been attributed to roughness modification owing to vibration but to an air-lubrication mechanism [1]. The friction force is modulated with time: at a given moment, vibration amplitude is the same all over the plate. However, as STIMTAC is equipped with sensors measuring the finger's position, the lowering of friction forces (i.e. plate's vibration) can be changed depending on the fingerpad's position on the plate. Consequently, one can program STIMTAC to lower the friction force differently from one position to another. In this study, the device was programmed to vibrate at the maximal amplitude when the finger was on one side of the plate while no vibration was applied when the finger scanned the other side. Simply put, these two sides of the vibrating plate will be respectively defined as ‘slippery surface’ (lowest friction force) and ‘sticky surface’ (highest friction force), even if STIMTAC does not produce different surfaces but different friction conditions.

Figure 4.

Friction measurement device during a test with STIMTAC.

To easily distinguish them, the first set of surfaces (polymer slabs) and the second set (STIMTAC use) were named ‘real surfaces’ and ‘simulated surfaces’, respectively.

2.3.2. Coefficient of friction measurements

A specific tribometer was implemented to measure the friction coefficient between the subject's fingerpad and a counterpart. This apparatus was constituted of a homemade sensor box allowing for simultaneous measurements of normal and tangential forces at a rate of 1000 samples s⁻¹. The normal load resolution was about 10 mN, and the tangential sensor had a 5 mN resolution and high stiffness. STIMTAC was rigidly fixed on the sensor box in order to perform friction tests with the simulated surfaces (figure 4). When performing friction tests with the real surfaces, the sticky and slippery adjoined slabs were placed on STIMTAC's vibrating plate that was switched off in this case (no vibration). With a constant speed of 4 mm s⁻¹, a linear DC motor moved the subject's arm which was held in a trough. The finger slid in the medial radial direction, from right to left and left to right (figure 4), and one test consisted of four cycles of 40 mm. Owing to the linear motor operating limits, the finger scanning speed was lower than the more spontaneous velocities encountered during natural active tactile exploration which are close to 40 mm s⁻¹ [46]. Nevertheless, the scanning speed used in this study was similar to those classically performed during passive tactile tests [18,19].

As the participant's finger was driven by the DC motor, the test was performed in passive touch conditions in terms of speed and sliding distance. Nevertheless, the subject exerted by herself/himself a force normal to the test surface, pressing her/his finger with a load of about 0.5 N. A gauge on a computer screen allowed the visualization of the actual loading in real time to help the subject stay in control. The angle between the finger and the scanned surface was about 25°. The friction tests were performed between the participant's right forefinger against real and then simulated surfaces. Before each test, the rubbed surfaces were cleaned with distilled water.

Figure 5 shows the typical curve of the COF versus the displacement obtained during one back-and-forth cycle. The COFs on the sticky and slippery surfaces (μ_stick and μ_slip, respectively) were calculated by taking into account the two mean values obtained in each direction of friction:

2.5

and

2.6

Figure 5.

Representation of a friction cycle (COF versus displacement of the finger) during a sliding test against simulated surfaces.

2.4. Statistical data treatment

All results are expressed as mean ± 1 standard deviation. The sets of data have been verified to follow the normal law with the Shapiro–Wilk test (p-value > 0.05). The variances were compared with the Fisher–Snedecor test (F-test). If the variances are not significantly different, the means are compared with the Student t-test. If the variances are different, the means are compared with the Welsh t-test. In the specific case of paired data (μ_stick and μ_slip for the same subject and the same set of surfaces), the difference in the two paired data is considered, and the t-test is applied to the mean difference using the null hypothesis. In order to test the linear correlation between two populations, the Pearson coefficient of correlation R is calculated and its square R², the coefficient of determination, demonstrates the correlation's strength in terms of percentage.

3. Results and discussion

3.1. Gender's influence on the fingerpad's properties

Substantial differences of fingerpad properties between women and men were encountered in this study. They are summarized in the following paragraphs that successively deal with the fingerpad's roughness, effective elastic modulus and then hydrolipid film composition.

Concerning the fingerpad's shape and roughness, the mean values of R_gm, SP and R_t calculated from the replicas' analysis of the 26 individuals are, respectively, 13 ± 3 mm, 458 ± 71 µm and 102 ± 26 µm. These values are consistent with those encountered in the literature [47]. Whereas other studies have shown women have less spaced epidermal ridges than men [48], there is no difference of SP between them in this study. However, our results suggest that men have higher epidermal ridges than women, with R_t values of 118 ± 25 and 86 ± 16 µm, respectively. This difference between women and men can be considered very significant (p-value < 0.001). To the best of our knowledge, this gender difference in fingerprint depth has never been previously reported.

The fingerpad's effective elastic modulus E_eff of all the participants reaches 70 ± 20 kPa with a very significant difference between men and women (F-test, p < 0.01). Women's fingerpads are stiffer than those of men: 82 ± 20 kPa compared with 59 ± 13 kPa. These values are in agreement with previous studies [11,28], but again, to the best of our knowledge, this difference of the fingerpads’ elastic modulus between men and women has never been previously reported. The range of elastic modulus values suggests that the maximum shear stress is located between 1.5 and 2.3 mm beneath the finger's surface. This observation justifies the denomination of effective elastic modulus used, which takes into account the stiffness of the SC, the epidermis, the dermis, the hypodermis and the underlying tissues also.

Figure 6 highlights the calculated D_W and D_L/W values. For all the participants, the results confirm the decrease of water quantity when the ratio of lipids to water rises. Clearly, women generally have a lower water content (and also greater lipids proportion) in the outer layer of the SC than men. The influence of gender on the amount of skin lipids and on skin hydration has not [24,32] or has rarely been observed in the literature [19]. The water descriptor index D_W is valued at 0.061 ± 0.055 (arb. units) with a significant difference between women and men (F-test, p < 0.01). Men have higher water content with 0.094 ± 0.062 (arb. units) than women with 0.029 ± 0.014 (arb. units) which agrees with Veijgen et al. [19]. The lipids/water index D_L/W reaches 0.122 ± 0.075 with a significant difference between men and women (F-test, p < 0.05). The hydrolipid film in women has a higher lipid-to-water ratio (0.15 ± 0.07) than that of men (0.09 ± 0.07). Moreover, men can have much larger values of D_W (up to 0.2) than women (no higher than 0.052), but D_L/W ranges are similar for men (from 0.03 to 0.25) and women (from 0.07 to 0.27). Some studies point out the softening of skin when hydration increases [11,27,29]: this result is consistent with the measurements obtained in this study which show lower effective elastic moduli and higher water contents for men compared with women.

Figure 6.

Water descriptor index D_W and lipids/water ratio descriptor index D_L/W measurements of the 13 women and 13 men subjects’ fingerpads.

3.2. Coefficient of friction's variability

The first line of table 1 highlights the mean and standard deviation values of the COFs related to the sticky and slippery surfaces (both real and simulated). As expected, μ_stick is higher than μ_slip. The difference between μ_stick and μ_slip is very high (t-test, paired data, p < 0.001) for both sets of surfaces.

Table 1.

COFs (measured on sticky surfaces: μ_stick; and measured on slippery surfaces: μ_slip) and TFC mean values and standard deviations of all subjects, women and men. Data are given for simulated and real surfaces separately.

	simulated surfaces			real surfaces
	μstick	μslip	TFC	μstick	μslip	TFC
all subjects	1.6 ± 0.7	0.9 ± 0.8	0.5 ± 0.3	2.4 ± 0.9	1.5 ± 1.0	0.5 ± 0.3
women	1.1 ± 0.4	0.4 ± 0.4	0.7 ± 0.2	1.9 ± 0.7	0.8 ± 0.6	0.6 ± 0.2
men	2.2 ± 0.6	1.5 ± 0.7	0.4 ± 0.3	3.0 ± 0.8	2.2 ± 0.9	0.3 ± 0.2

As depicted in figure 7, μ_stick and μ_slip can reach very different values from one subject to another. This dispersion supports the assumption that the diversity of the fingerpad's properties induces different friction behaviours between individuals even though the same surface is scanned. Most participants have μ_stick and μ_slip ranging respectively from 0.5 to 3 and from 0.1 to 2.4, whereas these COFs rise up to 5.5 and 3.7 for a few subjects. Although being extremely high, these values have nevertheless been reported elsewhere [18].

Figure 7.

COFs measured on sticky surfaces (μ_stick) relative to COFs measured on slippery surfaces (μ_slip) when rubbing the real and simulated surfaces for both women and men.

Women show lower COFs than men for each kind of surface, both for real and simulated surfaces (table 1 and figure 7). This difference is very significant (t-test, p < 0.01) for the four studied surfaces. This gender influence on the COF has been not [24,32,48] or rarely been indicated in the literature as far as the finger is concerned [19].

3.3. Concept of tactile frictional contrast

An overview of the 52 friction cycles collected (26 participants and the two surfaces' sets) leads to the observation of large variations of their global shapes. Without considering the algebraic values of μ_stick and μ_slip, some individuals show very large differences between these two COFs, whereas others show very close levels of μ_stick and μ_slip. While the counterparts and sliding conditions are the same, this means that subjects’ fingers are characterized by their propensity to frictionally distinguish two surfaces situated in the slipperiness dimension. To quantify this observation, the authors introduce the concept of tactile frictional contrast (TFC). By analogy with the optical contrast which quantifies the brightness difference between the darkest and the brightest levels in a picture, the TFC aims at quantifying the COF's difference when one's finger rubs two different surfaces. For a well-defined couple of surfaces, the TFC is thus an individual's feature. As this study focuses on surfaces' slipperiness, the TFC can be here defined as

3.1

The TFC has the convenience of being a dimensionless index ranging from 0 (no difference between μ_stick and μ_slip) to 1. The more μ_stick and μ_slip are different, the higher the TFC is. As the participants' TFC ranges from 0.03 to 0.89, it can be concluded that the differentiation of the friction force in the slipperiness dimension can be extremely different between individuals. It can be seen from table 1 that women's TFC is significantly higher than that of men both for real and simulated surfaces (t-test, p < 0.01). Moreover, results suggest that the highest COF values induce the lowest TFC values.

3.4. Friction related to fingerpads' properties

For both real and simulated surfaces, μ_stick and μ_slip are significantly negatively correlated to E_eff. The coefficients of determination R² range from 0.14 to 0.22 (t-test, p < 0.05), with a slightly higher correlation for the simulated surfaces. This correlation has been pointed out by Liu [49] with the help of spherical-shaped artificial fingers. His study shows the stiffer the material is, the lower the COF. Besides, the TFC is significantly correlated to E_eff only for the simulated surfaces with R² = 18% (t-test, p < 0.05). For the real surfaces, the correlation is not significant (p < 0.1).

The height of epidermal ridges R_t is significantly correlated with μ_stick and μ_slip for the two sets of surfaces. The coefficients of determination R² range from 0.32 to 0.42 (t-test, p < 0.01). This shows that at least 32% of the COF variance can be linearly related to the height of epidermal ridges when one's finger scans a more or less sticky surface. However, no correlation has been highlighted between R_gm or SP with both the COFs and the TFC for the four studied surfaces (t-test, p > 0.05).

While some papers examine separately the effect of skin hydration [13,16,19,33,37] and of the amount of lipids [24,32] on the COF, this study investigates these two parameters together. As regards lipids, Cua et al. [24,32] reveal a linear relationship between the COF and the amount of lipids in the skin. Nevertheless, our results do not show any correlation between the COFs and D_L/W. As regards the fingerpad's hydration, the literature points out an increase of the COF with skin moisturization [19,33]. In this study, D_W is correlated with μ_slip but not with μ_stick. Moreover, very significant correlations (R² = 0.7, t-test, p < 0.001) have been found between the two physico-chemical descriptors and the TFC, both for simulated and real surfaces. As shown in figure 8, a continuous decrease of the TFC is observed when D_W increases. Moreover, results point out an almost linear increase of the TFC with the lipids/water ratio until D_L/W is approximately 0.12 before reaching a plateau. Therefore, for surfaces situated in the slipperiness dimension, this study concludes to the predominance of fingerpads' hydrolipid film composition on individuals’ frictional differentiation of surfaces.

Figure 8.

Tactile frictional contrast (TFC) relative to D_W (a) and D_L/W (b) of women and men for both the simulated and the real investigated surfaces.

The absence of significant correlation between the COFs (μ_stick and μ_slip) could be explained by the studied tribocontact complexity. As tests have been performed with human subjects, no fingerpad properties remained constant from one friction test to another. Thus, one can assume that the COFs and the fingerpad properties are linked by a very complex transfer function including various couplings. Indeed, these properties are dependent on one another: D_W and E_eff, for instance [11,27,29].

3.5. STIMTAC efficiency in the slipperiness dimension

Considering table 1, it can be seen that real surfaces lead to slightly higher COFs than simulated ones, whatever the participants' subclass (all subjects, or women and men separately). However, figure 7 highlights that the COF measurement ranges are practically the same between the real and the simulated surfaces, both for μ_stick and μ_slip. Besides, the above-mentioned gender influence (higher COF for men than for women) is similarly encountered on both sets of surfaces. These results point to STIMTAC's efficiency in the simulation of sticky/slippery surfaces: it can achieve stimuli that induce similar friction forces to those encountered on these kinds of surfaces.

The two sets of surfaces show similar TFC values (table 1). Whatever the considered subclass of participants, the TFC is non-significantly different for the real and the simulated surfaces (t-test, p > 0.1). The TFCs of the two sets of surfaces are plotted in figure 9 where each point along the graph corresponds to a given participant. The two TFCs are linked with a linear relationship going through the origin with a slope close to 1 and R² = 0.73. Assuming that the finger/surface friction behaviour has a critical influence on tactile perception [7], STIMTAC could be exploited as a useful device, adapted to most individuals, to give the illusion of rubbing two distinct surfaces.

Figure 9.

Tactile frictional contrasts (TFCs) on simulated surfaces against TFCs on real surfaces. Each point corresponds to one participant, and the black line is the linear regression between the two measurements.

Moreover, figure 8 shows a very similar influence of the CHF's composition on the TFC for the two sets of surfaces. Remembering that the TFC is mainly dependent on the CHF's composition (see §3.4), the latter result indicates that STIMTAC accurately reproduces the impact of fingerpad properties on individuals’ frictional differentiation of sticky/slippery surfaces.

4. Conclusion

This study has provided in vivo friction measurements of 26 fingerpads with rubbing conditions which were rather similar to those encountered when spontaneous natural touching occurs. The scanned surfaces were situated at both ends of the slipperiness psycho-perceptual dimension (highly sticky and highly slippery surfaces). Physical surface and simulated ones with STIMTAC have been rubbed. In parallel, mechanical, physico-chemical and morphological feature characterization of the 26 studied fingerpads has been carried out. To the best knowledge of the authors, notable differences of the fingerpad properties between men and women have been highlighted for the first time. Women present lower epidermal ridge height and water content than men but a higher forefinger elastic modulus and lipids/water ratio.

With the same tribological modalities, the measured friction coefficients have been shown very different from one individual to another owing to large differences in their fingerpad properties. Nevertheless, difficulties have been encountered to correlate the COFs with the fingerpad's features. Furthermore, the new concept of TFC has been defined. With fixed tribological conditions and the same surface couple, this index accounts for one individual's feature and has revealed large differences between the studied subjects. For sticky/slippery surfaces, the TFC has been correlated with the hydrolipid film composition of the fingerpad skin. As a differential measurement, the TFC could be an interesting index in the field of tactile stimulator efficiency quantification as well as tactile perception.

For most participants, STIMTAC has allowed one to reach similar TFCs to those obtained with the physical surfaces, thus validating its use for research on tactile tribology and friction perception.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.