Dynamic footprint of sequestration in the molecular fluctuations of osteopontin

Abstract

The sequestration of calcium phosphate by unfolded proteins is fundamental to the stabilization of biofluids supersaturated with respect to hydroxyapatite, such as milk, blood or urine. The unfolded state of osteopontin (OPN) is thought to be a prerequisite for this activity, which leads to the formation of core–shell calcium phosphate nanoclusters. We report on the structures and dynamics of a native OPN peptide from bovine milk, studied by neutron spectroscopy and small-angle X-ray and neutron scattering. The effects of sequestration are quantified on the nanosecond– ångström resolution by elastic incoherent neutron scattering. The molecular fluctuations of the free phosphopeptide are in agreement with a highly flexible protein. An increased resilience to diffusive motions of OPN is corroborated by molecular fluctuations similar to those observed for globular proteins, yet retaining conformational flexibilities. The results bring insight into the modulation of the activity of OPN and phosphopeptides with a role in the control of biomineralization. The quantification of such effects provides an important handle for the future design of new peptides based on the dynamics–activity relationship.

1. Introduction

Intrinsically disordered proteins (IDPs) are capable of fulfilling many biological functions, despite entirely or partially lacking a unique three-dimensional structure (for recent reviews see, for example, [1,2]). The atomic thermal fluctuations of a protein can be related to the shape of the potential energy well within which the protein moves [3]. Compared to folded proteins, IDPs have an energy landscape with lower barriers between minima, enabling fast sampling of large areas of conformational space. The structural heterogeneity effectively provides an enlarged surface area through which specific inter- and intramolecular interactions are possible.

A disordered conformation can convey several functional benefits [1,2,4]. For example, IDPs are able to adapt to different environments and interact rapidly with one or more partners. One of the earliest suggestions [5–7] was that because of their unfolded and flexible conformation, caseins interact rapidly with nuclei of calcium phosphate to prevent precipitation of the mineral phase during the biosynthesis of milk. An unfolded conformation is a property of many of the proteins that are involved in biomineralization, a well-studied example being that of osteopontin (OPN) [8–11]. Naturally occurring OPN phosphopeptides formed by cleavage at or near residue 149 (OPN 1–149) [12] adopt a non-globular conformation in solution [13]. Biofluids are supersaturated with respect to the mineral phase of bones and teeth, but the N-terminal half of OPN inhibits hydroxyapatite formation by sequestering the precursor amorphous calcium phosphate phase to form thermodynamically stable calcium phosphate nanoclusters (CPNs) [14]. A CPN has a core–shell structure, where the core is amorphous calcium phosphate surrounded by a shell of OPN phosphopeptide chains [13,14]. The peptide interacts specifically with the core via the phosphorylated residues, and indeed unphosphorylated peptides are not able to form CPN [13,15]. Previous work with caseins and casein phosphopeptides, particularly with the β-casein 1–25 peptide, established the core, shell dimensions and masses of a casein CPN by contrast variation small-angle neutron scattering and other techniques [16–20]. An equilibrium thermodynamic model of CPN has shown how these dimensions can depend on the free energy of formation of the core and free energy of sequestration by the shell. This analysis also revealed another advantage of an unfolded conformation for creating stable equilibrium CPN structures, this being the ability to achieve a high density of packing of sequestering phosphopeptide chains on the core surface and thereby maximize the free energy of sequestration by the shell [8,13,14].

Despite significant advances in nuclear magnetic resonance (NMR) and other techniques, relatively little experimental protein dynamical information is presently available for IDPs [21–23]. Owing to their resistance to crystallization, the study of IDP structure by crystallography is presently infeasible. The IDP structure can be represented by an ensemble of transient conformational models, often determined by solution-based techniques such as NMR or small-angle X-ray scattering (SAXS) [24–26]. The resulting ensemble provides a representation of the heterogeneous conformational structures present, but neither NMR nor SAXS provide information on the rate of inter-conversion between transient states [27]. Furthermore, the disordered state may be affected by the non-physiological conditions under which the proteins are examined, as shown by discrepancies between in vivo and in vitro results [28]. Cellular protein concentrations of 300–400 mg ml⁻¹ are in fact much higher than those typically used for structure determination studies, and experimental evidence indicates that this has a large effect on disordered protein structure [29–31]. The structure of IDPs is often also affected by binding to a partner ligand. Some IDPs gain structure upon binding and undergo a disorder-to-order transition [32–34], while other observations support the existence of ‘fuzzy complexes’ where such transitions do not occur [35]. The latter was the case for a fuzzy complex with an OPN fragment, where an increase in disorder was observed when bound to heparin [36].

OPN has been called a molecule for all seasons [37]. It has a number of different roles including cell adhesion, signalling, migration and survival in many cell types, in addition to roles in immuno-modulation and biomineralization. OPN belongs to the family of small integrin-binding ligand, N-linked glycoproteins (SIBLINGs) [38]. The SIBLINGs are a sub-group of a larger, paralogous group of secreted proteins to which the caseins also belong [39,40]. Production of OPN by recombinant methods is complicated by the susceptibility of IDPs to proteolysis and the presence of significant and functionally important post-translational modifications in the native protein [12,41,42]. The length of the full OPN chain makes NMR assignments in the native protein somewhat difficult and has required work with labelled but (to-date) unphosphorylated and unglycosylated recombinant material. Fisher et al. [10] determined, using 1-D ¹H NMR and transverse relaxation times, that the solution structure of native OPN was consistent with that of an IDP. Kurzbach [36] combined electron paramagnetic resonance (EPR) and NMR techniques to show that different OPN compact and extended conformations can interconvert through cooperative phase transitions. Yamaguchi et al. [43] have shown that recombinant mouse OPN exhibits a transient long-range intramolecular interaction between its N- and C-terminal regions that can shield the central part of the chain from integrin interactions.

Neutron scattering in general provides access to molecular dynamics on the nanosecond–picosecond timescale and ångström length scale, dependent on instrumental resolution [44]. In native biological macromolecules, the neutron scattering signal is dominated by the strong incoherent contribution from hydrogen. Hydrogen atoms are distributed homogeneously across the protein backbone, and their motions can be said to represent the average motion of groups with which they are associated [45]. By measuring elastic neutron scattering with a very high-energy resolution as a function of the sample temperature and scattering vector—a technique denoted elastic incoherent neutron scattering (EINS)—the so-called apparent mean-squared displacement (MSD) can be extracted. This quantity can be obtained more easily than a full spectrum and provides information via an integral number of the amount of elastic scattering ‘lost’ due to the molecular mobility in the sample [22,46]. This technique is often used to obtain comparative information about protein dynamics in hydrated powders [47,48]. We focus on this apparent MSD technique regarding the protein dynamics in the present work, but will also discuss known limitations. We note that the advent of new spectrometers with very high flux at present and upcoming neutron sources will allow the extension of our study to overcome these limitations in the future. Here, we report on the structures and dynamics of a native OPN peptide from bovine milk in two different forms—by itself and as part of a CPN—studied by neutron spectroscopy, using a specific instrumental resolution of 4 ns, and SAXS and small-angle neutron scattering (SANS).

2. Material and methods

2.1. Sample preparation

In milk, OPN undergoes proteolytic processing by several different proteases, leading to a mixture (OPNmix) of different phosphopeptides [49]. OPNmix was isolated from bovine milk by the method of Sørensen et al. [49]. Gel filtration of OPNmix resolves the principal fraction, which is a more homogeneous mixture of N-terminal peptides ending between residues 145 and 153 of the mature protein sequence [49]. Here, and previously, we have described this mixture by the term OPN 1–149 [13].

Gel filtration was carried out using a column of Superdex 75 (S75) with a bed-length of 120 cm, at a flow rate of 0.5 ml min⁻¹. In total, 50 mg of OPNmix was dissolved in 5 ml of elution buffer (50 mM phosphate, 300 mM NaCl, 0.02% NaN₃, pH 7.0, H₂O solution). Fractions of 1 ml were collected and analysed by standard 12% polyacrylamide gel electrophoresis (SDS-PAGE) prior to pooling. The S75 column was calibrated with gel Biorad filtration standard, from which the apparent molecular mass of OPN 1–149 was determined [50]. Pure OPN 1–149 was exhaustively dialysed against H₂O, then D₂O, and subsequently freeze-dried and stored at −20 °C.

OPN CPNs were formed using the mixing method described previously by Holt et al. [13]. In the presence of an excess of OPN, the pH of a solution was raised slowly up to 7.4 by addition of calcium chloride followed by sodium phosphate salts of different basicity (mono-, di- and tri-sodium phosphates), while continuously mixing. The final concentrations were 30 mg ml⁻¹ OPN 1–149, 22 mM calcium, 20 mM phosphate, 1.5 mM NaN₃ (ionic strength 78 mM, pH 7.0).

The final solution contained a stoichiometric excess of phosphate centres (PCs) over calcium phosphate concentration. Nanocluster formation was completed in solutions of H₂O and D₂O. It should be noted that the stability of CPN formed with OPN in D₂O has been previously established [14]. Owing to the composition of the D₂O CPN buffer, contributions of the hydrogen atoms in the OPN 1–149 protein will dominate the incoherent neutron scattering signal.

2.2. Dynamic light scattering

Solution samples of OPN 1–149 and OPN CPN in H₂O buffers were tested at 25°C for homogeneity using a Malvern Zetasizer Nano instrument. The particle hydrodynamic diameter was determined from six individual measurements using automatically optimized conditions and protein mode analysis. The refractive indices and viscosities of the solutions were calculated from information provided for standard solutions on the instrument.

2.3. Circular dichroism

Circular dichroism (CD) spectra were obtained for OPN 1–149 at 20°C on a J-720 spectrometer (JASCO) at 0.5 mg ml⁻¹ (50 mM phosphate pH 7.4, 50 mM NaCl, H₂O). Spectra were recorded between 190 and 250 nm accumulating data over three runs with a bandwidth of 1 nm. The raw data were normalized for protein concentration and the number of OPN 1–149 residues.

2.4. Small-angle neutron and X-ray scattering

SANS data were collected at the small-angle neutron diffractometer D33 at the Institut Laue-Langevin (Grenoble, France). Samples containing 15 mg ml⁻¹ of OPN CPN in H₂O were filtered through a 0.22 µm Sartorius syringe filter into a Hellma Quartz cuvette (1 mm path-length). The incident neutron beam had a wavelength of 6 Å (δλ/λ = 10%). Data were recorded for a scattering wavevector q-range 0.04–0.12 nm⁻¹, where q = (4π sin θ)/λ and 2θ is the scattering angle.

SAXS experiments were performed at the I911-SAXS beamline at the MAX IV Laboratory (Lund, Sweden) [51]. The measurement parameters are summarized in table 1. Prior to measurements, the OPN 1–149 samples were exhaustively dialysed against the corresponding buffer (50 mM phosphate pH 7.4, 150 mM NaCl, H₂O solution), centrifuged and filtered (0.22 µm Sartorius syringe filter). The concentration was determined by UV absorption at 280 nm. Besides a 2.5 mg ml⁻¹ sample solution, a lower concentration of 1.5 mg ml⁻¹ was tested by SAXS and no OPN 1–149 concentration effects were observed. The sample measurements were carried out using a 1 mm capillary. An accessible q-range of 0.01–0.3 Å⁻¹ (summary of SAXS data parameters shown in table 1) was used. All frames were inspected for signs of radiation damage before averaging. Corresponding buffers from dialysis were measured before and after each sample, using the same measurement settings and the resulting curve subtracted from sample scattering.

Table 1.

SAXS data collection parameters.

parameter	value
sample to detector distance	1.45 m
wavelength	0.91 Å
q-range	0.1–3 nm−1
exposure time	6 frames, 10 s each
temperature	20°C
concentration	2.5 mg ml−1

2.5. Model-independent small-angle X-ray scattering data analysis

The experimental radius of gyration R_g and the forward scattering intensity I(0) were calculated from data at low q, according to the Guinier approximation:

2.1

For an unfolded protein, this approximation holds true for a narrow q-range where q.R_g < 1. The pair distribution function p(r) in real space was calculated by indirect Fourier transform using GNOM from the ATSAS package [52]. Analysis of p(r) allows the estimation of a maximum inter-particle distance (D_max), as well as R_g and I(0).

The Kratky plot (q².I against q) provides further model-independent information about the scattering particle. Globular particles typically show a well-defined maximum when plotted in this way, whereas for a disordered protein the Kratky plot should plateau at high q [24].

Calculation of the R_g for IDPs yields a single value that is an average for all conformations in solution. This average R_g can be analysed by the Flory equation, which relates the amino acid length of the IDP to a power law [53],

2.2

where N is the number of amino acid residues, R₀ is the persistence length of the chain and V is an exponential scaling factor. For chemically unfolded proteins (where it should be kept in mind that the structure typically remains less expanded than that of IDPs, due to the high charge of the latter), V and R₀ have been determined experimentally: 0.6 ± 0.028 and 1.93 ± 0.275, respectively [54]. Accurate predictions of the R_g of globular proteins can also be made according to the same relationship, where V and R₀ are equal to 0.39 and 0.35, respectively [55].

2.6. Ab initio modelling and flexibility analysis

The software used for each different step of the analysis is summarized in table 2. Using ab initio modelling to fit the SAXS data, it is possible to obtain an average view of the conformational space occupied by a protein in solution. Overall OPN 1–149 scattering envelopes were obtained from two different ab initio approaches: dummy atom and dummy residue modelling from the DAMMIF [56] and GASBOR [57] software, respectively. The DAMMIF assembly of closely packed dummy atoms is packed within a sphere which has a diameter equal to the D_max, determined by the indirect Fourier transform with GNOM.

Table 2.

Software used for SAXS data analysis and visualization.

process	software
primary data reduction	Primus
data processing	GNOM
ab initio modelling	DAMMIF/DAMMAVER
ensemble generation	EOM
three-dimensional graphics	Pymol

Using simulated annealing, the software searches for a conformation within the defined sphere that matches the experimental data. This approach can find different solutions that fit the data [58,59]. Twenty independent DAMMIF computations were performed and the models were averaged using DAMAVER [56]. A filtered final model was produced, by removing low occupancy space (electronic supplementary material, figure S5 shows the fit to the scattering data).

The flexibility of OPN 1–149 was further analysed using the ensemble optimization method EOM from the ATSAS package [24]. EOM exploits a genetic algorithm to create a large heterogeneous ensemble of models based on the amino acid sequence. A pool of 10 000 conformers was created, from which an ensemble of 20 structures were picked by minimization of the discrepancy between the calculated scattering profile and the experimental scattering curve. Analysis of the resulting data provided information on the size distribution of the protein, and the 20 protein conformers that most accurately represent the ensemble as a whole.

Predictions of OPN 1–149, tau and maltose binding protein (MBP) backbone flexibility were also made using the Dynamine predictor with the corresponding amino acid sequences [60]. Tau was chosen for comparison to an IDP, while the MBP provides a comparison to a globular protein of a similar size (both taken from Gallat et al. [47]). Dynamine functions by comparing sequence information with a database of recorded NMR spectra. It predicts an average S² value for every residue in a given sequence, where S² describes how restricted the movement of the atomic bond N–H protein backbone vector is with respect to the molecular reference frame. A value of 1 reflects complete order in a stable conformation, while a value of 0 means random bond vector movement (highly dynamic). Values of S² less than 0.8 are considered to indicate a flexible region [60]. It should be noted that S² predicted using DynaMine are on an absolute scale, allowing for comparison between predictions for different proteins.

2.7. Elastic incoherent neutron scattering

Lyopholized powders (150 mg) of OPN 1–149 and OPN CPN were rehydrated over pure D₂O until a level of 0.44 g of D₂O per gram of protein was reached, as determined by weighing. A highly similar system, namely the casein CPN found in milk, is hydrated with 0.35 g H₂O per gram of protein [61]. By comparison, the hydration level used in this experiment is considered appropriate. This was further confirmed by re-hydration of the same samples to 0.6 g D₂O per gram of protein, at which point the observed motions exited the window of the spectrometer.

Samples were sealed in a flat aluminium sample holder. Hydrated powder samples were chosen so that global motions (diffusion and rotation of the entire molecule, significant in the experimental energy window chosen) are suppressed on the chosen time scale, while the humidity ensures a functional sample environment.

EINS experiments were carried out on the backscattering IN16 spectrometer at the Institut Laue-Langevin (ILL, France). An instrumental resolution of 0.9 μeV was used, corresponding to motions occurring on the nanosecond timescale. Specifically, the scattering recorded in the elastic fixed energy window corresponds to a time scale of approximately 4 ns. This means that all molecular motion in the sample occurring on the relaxation or vibration times slower than 4 ns appears as elastic scattering. Conversely, no motion on time scales significantly faster than 4 ns contributes to the recorded elastic intensity. The wavelength of the incident neutron beam was 6.27 Å, corresponding to a measured q-range of 0.02–1.9 Å⁻¹. IN16 uses a configuration with 22 detector tubes covering the accessible angular range. The measured flux was normalized using a beam monitor determining the incident neutron flux. The individual detector count rates were normalized by the relative detector efficiency obtained from the sample scattering signal at 10 K. Each sample was inserted into an orange ILL cryostat at room temperature before decreasing to 10 K. The sample was held at an angle of 135° with respect to the incident neutron beam. Elastically scattered neutrons were continuously counted whilst ramping from 10 to 300 K, at a rate of 0.2 K min⁻¹.

Taking only incoherent neutron scattering into account, the inelastic scattering law can be described as a function of q and the frequency ω (ħω is the energy exchange experienced by the sample):

2.3

The intermediate scattering function is

2.4

For N hydrogen atoms in position R, the van Hove auto-correlation function g(r, t) can be described as

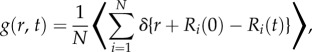2.5

where δ is a Dirac function, R_i(0) and R_i(t) are the position vectors for atomic motions with no preferential orientation and no time dependence on the instrumental resolution. By introducing the so-called apparent MSD 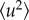and assuming that

2.6

the elastic scattering intensity can be described using the Gaussian approximation, analogue to the Guinier approximations used for small-angle scattering, where the characteristic length described by the motion of the particle is

2.7

The elastic scattering intensity is then approximated by

2.8

For an elastic temperature scan, equation (2.8) defines the apparent MSD 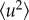, caused by thermal vibrations at low temperatures and a superposition of vibrations and diffusive motions at high temperatures. It is emphasized that  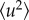by this definition is an apparent quantity not directly related to a physical picture, but providing a convenient way of expressing the loss of elastic intensity caused by an enhancement of the molecular mobility in the sample [22]. The obtained 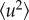are connected to the spatial extent of the atomic thermal motions and include both vibrational and diffusive dynamics. The considerations regarding the MSDs may be generalized, since a backscattering spectrometer in principle can access the Fourier transform of the actual time-dependent MSD, limited by the resolution time of the instrument. This generalized MSD contains information on the geometry of confinement of diffusive motions. However, such generalization is beyond the scope of the present analysis. The Gaussian approximation is valid for 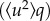< 2 and at low temperatures where diffusive motions are entirely absent [48]. We have extracted atomic MSDs from the q-dependency of the elastic intensity, in accordance to equation (2.8) (see also the electronic supplementary material, figure S9), for the range of q where the equation is valid. The elastically scattered neutrons of the empty cell I_(empty,T)(q) were also recorded in a similar manner for subtraction of sample holder effects. Elastic contributions from the sample scattering were then obtained according to the formula

2.9

where I_(sample,T)(q) is the normalized intensity of the neutrons scattered from the sample at temperature T, and I_(total,T)(q) is the measured sample intensity. The denominator in equation (2.9) represents the intensity averaged at the lowest measured temperature (10 K), where trans is the experimentally measured sample transmission. Effective mean force constants that describe the protein resilience (including anharmonic dynamics of the proteins) were obtained from the slope of 〈u²〉 versus temperature, according to

2.10

The effective force constant in this context is to be understood in terms of a quasi-harmonic approximation and the definition by Zaccai [22,45]. The samples were probed for crystalline ice formation using the in situ diffraction setting on IN16. No Bragg peaks were observed (see also the electronic supplementary material, figures S7 and S8), corresponding to a lack of bulk water. The atomic MSDs were extracted from the normalized data using the program LAMP provided by the ILL [62], from the q-dependency of the elastic intensity described by the Gaussian approximation.

3. Results and discussion

3.1. OPN 1–149 displays biophysical properties of a non-globular protein

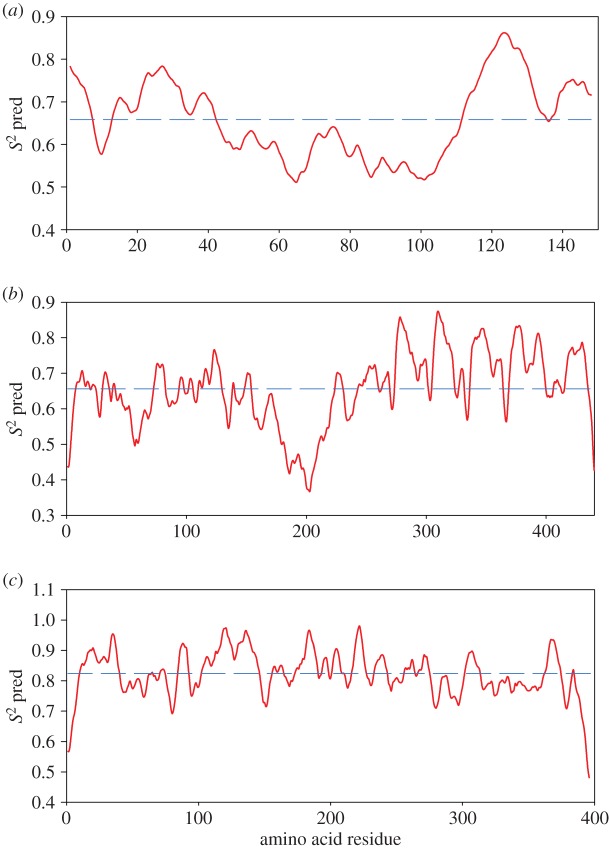
Tau and OPN 1–149 both show similar S² values below 0.8, indicative of a highly flexible protein. Significantly higher values were obtained for the globular MBP (figure 1). Further bioinformatic analysis by a charge-hydropathy plot and the IUpred algorithm also predict a mainly disordered structure for the OPN1–149 amino acid sequence (see electronic supplementary material, figures S1 and S2).

Figure 1.

DynaMine [60] predicted S² values for (a) bovine OPN 1–149, sequence Uniprot ID P31096; (b) the disordered tau protein, sequence Uniprot ID P10636; and (c) folded MBP, sequence Uniprot ID 17840E3. The average value of S² is indicated for each graph with a dashed line. (Online version in colour.)

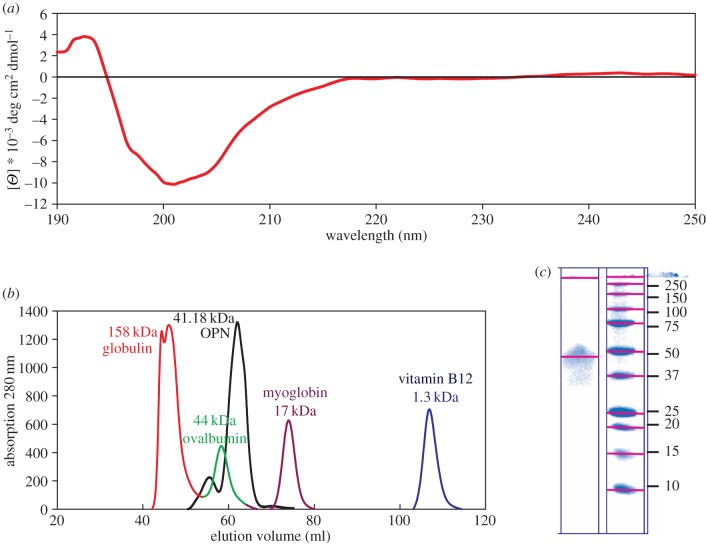
CD and analytical size exclusion chromatography (SEC) are in agreement with an IDP structure for OPN 1–149. The CD spectrum indicates a lack of any secondary structure elements (figure 2a).

Figure 2.

Biophysical characterization of OPN 1–149 in solution. (a) CD spectrum collected at room temperature, showing a lack of secondary structure elements. (b) UV absorption spectra of eluted volume from analytical S75 column. The OPN 1–149 peak corresponds to a molecular mass of 41.18 kDa. (c) SDS-PAGE (12%) analysis of purified OPN 1–149 protein (left column) and molecular weight ladder (units shown in kDa). (Online version in colour.)

By comparison to a reference set of globular proteins, OPN 1–149 migrates down an S75 gel filtration column as a protein with a much higher molecular weight (44 kDa) than expected (18 kDa) (figure 2b). The ratio of the apparent to the theoretical molecular weight is 2.44, where a ratio of 2.2–2.8 is typically expected for disordered proteins [63]. This apparent disagreement in observed and expected molecular weight is consistent with SDS-PAGE results, as typically happens for IDPs [35] (figure 2c). Combined biophysical evidence strongly supports a disordered protein structure for OPN 1–149 in solution.

3.2. Small-angle X-ray scattering data for dilute solution confirms IDP structure of OPN 1–149

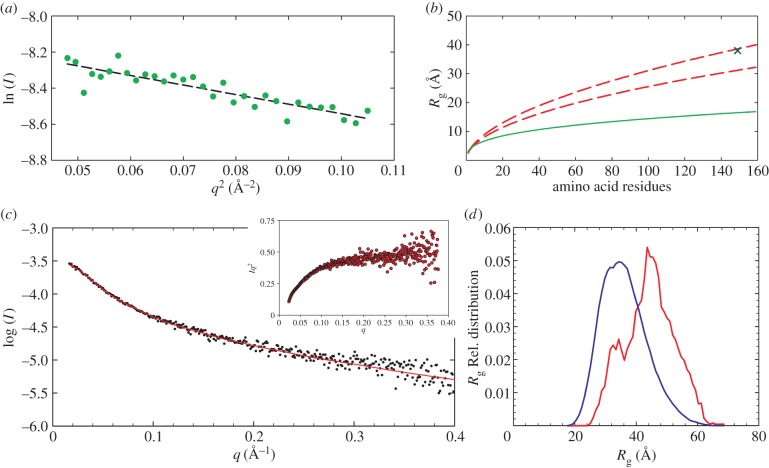
Model-independent SAXS analysis. Determination of the R_g by SAXS yields a single value that for IDPs represents an average of all conformations present in the solution. The Flory equation can be adapted to yield the R_g of globular and chemically denatured proteins (see equation (2.2)) and hence a comparison of the compactness between the determined R_g can be obtained. The R_g of OPN 1–149 derived from the Guinier plot was 38.6 Å, which is in close agreement with the 39.2 Å value obtained by the indirect Fourier transform method (figure 3 and table 3).

Figure 3.

(a) Determination of the R_g by Guinier analysis (38.6 ± 2.5 Å). (b) Comparison of the experimentally determined R_g (cross point) with the expected R_g of chemically denatured proteins (between dashed lines) determined by the Flory equation (see Materials and methods for parameters) according to the method of Kohn et al. [54]. The region between the two lines represents the confidence interval of the Flory equation. The expected R_g for globular proteins is shown by the lower continuous line [55]. (c) Fit to the scattering curve of the final ensemble to the experimental data points. The inset shows the Kratky plot. (d) Histogram depicting a comparison between the initial ensemble as a bell-shaped curve, and the bimodal final ensemble that best fits the experimental data. (Online version in colour.)

Table 3.

Parameters of OPN 1–149 determined by analysis of the SAXS data.

parameter	value
I0 from Guinier	27.59 ± 0.51
Rg from Guinier	37.90 ± 0.08 Å
Dmax	12.44 nm
I0 from p(r)	27.91 ± 0.10
Rg from p(r)	39.20 ± 0.023 Å

The R_g observed for OPN 1–149 is closer to those expected for chemically unfolded proteins then those observed for globular proteins (see figure 3b) [64,65]. The disordered state of OPN 1–149 is also corroborated by the asymmetric shape of the p(r) distribution (figure 4) [66]. Further model-independent evidence of the disordered nature of OPN 1–149 can be observed in the Kratky plot (figure 3c). For a folded protein a bell-shaped curve with a defined maximum would be expected instead the Kratky plot plateaus at high q [67,68]. These overall parameters suggest a disordered and elongated shape of OPN 1–149 in solution.

Figure 4.

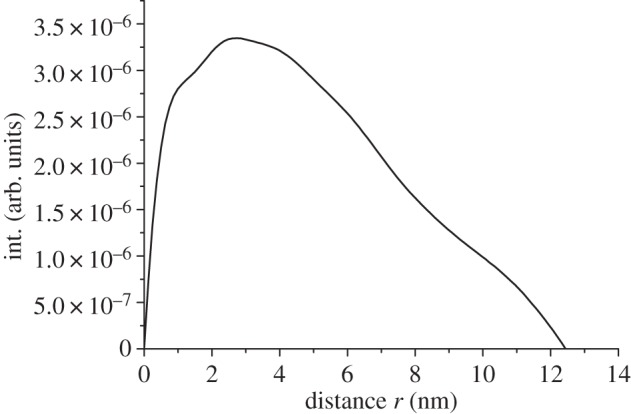
The p(r) distribution of OPN 1–149 determined by analysis of the SAXS data by the GNOM program.

3.2.1. Ab initio modelling of small-angle X-ray scattering data

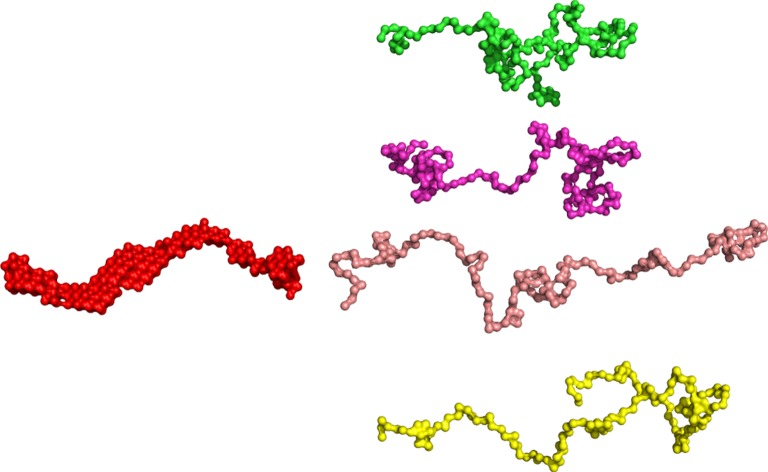
The 20 DAMMIF models for OPN 1–149 were compared with DAMSUP, where the highest normalized spatial discrepancy observed was 1.343. The final averaged model represents the most populated region of the solution-spread model, shown in figure 5. The resulting structure shows an elongated particle, and is similar to structures obtained for other disordered proteins (figure 5) [65].

Figure 5.

(Left) Ab initio reconstruction of the OPN 1–149 scattering envelope using DAMMIF yields a single structure which represents an elongated protein in solution. (Right) Open and compact representations of the distribution of models produced by the ensemble optimization method. (Online version in colour.)

Ab initio modelling using the dummy residue approach provides qualitatively similar results (electronic supplementary material, figure S3). The computed models provide a good fit to the data, with GASBOR producing slightly higher χ²-values compared with the DAMMIF models (electronic supplementary material, figure S4). This is expected as the dummy residue approach represents more realistic description of the different conformers present in a solution for IDPs. The obtained models do not provide high-resolution structural models but do show the high area of conformational space sampled by OPN 1–149. Further, the scattering envelopes obtained by ab initio techniques agree with obtained model-independent data from the Kratky plot and the radii of gyration obtained from the p(r) distribution and the Guinier plot (figure 4). That OPN 1–149 is disordered is in close agreement with data obtained for other OPN fragments and the full-length protein [10,11].

3.2.2. EOM analysis of protein flexibility

IDP structures have a heterogeneous distribution, from Gaussian chains to more compact folded conformations. SAXS measures the form factor of a sample, but for IDPs the fluctuations between form factors are much higher than the SAXS time resolution. To extend the information attainable for OPN 1–149, the SAXS data were analysed using EOM [24]. The selected EOM ensemble of 20 structures generated for OPN 1–149 produced a good fit to the experimental data with χ² of 1.31 (figure 3c,d).

The best-fit ensemble shows a somewhat bimodal although wide ranging distribution of the R_g (figure 3c). The distribution of the radii peak at higher values than the random pool, indicative of a preference to a somewhat open or extended conformation. The peak for lower R_g however also indicated that the protein exists in a more compact state, in agreement with previous observations on recombinant quail OPN, obtained by a combined spectroscopic approach (NMR and EPR) [23]. Representations of the compact and open structures produced by EOM are shown in figure 5. The models obtained by the different modelling techniques are shown in the electronic supplementary material, figure S10 on the same scale, highlighting that the size and shape of the DAMMIF and GASBOR models are an average of the extended and collapsed models determined by EOM.

3.3. Small-angle neutron scattering of calcium phosphate nanoclusters

Dynamic light scattering and small-angle neutron scattering measurements were performed to assess the extent of CPN formation and the solution mono-dispersity prior to EINS experiments. An R_g of 205 ± 5 Å was extracted from the Guinier plot obtained from SANS in H₂O (figure 6) for the formed CPN, in close agreement with previously obtained results [13,14]. The DLS measurements (see also the electronic supplementary material, figure S6) show contributions from smaller particles (R_H = 1.9 nm) and a large fraction (R_H = 23.1 nm), corresponding to the free OPN 1–149 peptide and OPN CPN, respectively.

Figure 6.

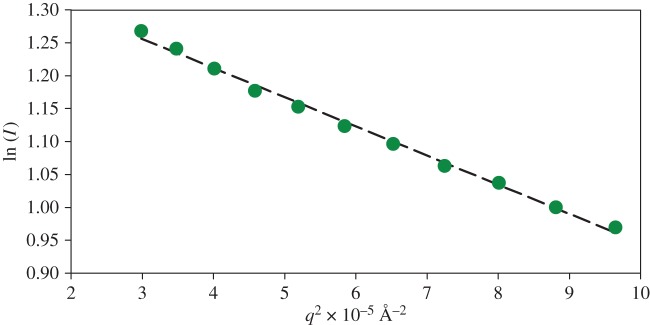
Guinier plot of OPN CPN SANS data. The R_g (205 ± 5 Å) was extracted from the slope of the dashed line which fits the points satisfying q.R_g < 1.3. (Online version in colour.)

3.4. Osteopontin dynamics and the effects of calcium phosphate sequestration in hydrated protein samples

Analysis of protein dynamics was carried out on hydrated powder samples, in order to suppress the protein centre of mass motion with which the internal molecular motions would otherwise be convoluted. This restriction simplifies the analysis and reduces the requirements for the neutron flux on the sample, which is often a limiting factor of studying biological systems with neutrons. At hydration levels of 0.43 gram D₂O per gram of protein, internal motions in the powder are similar to the internal motions in solution [69]. The fixed window elastic temperature scan provides a cost efficient approach to obtain a characteristic quantity regarding the flexibility of a protein on a given timescale, without imposition of complex models.

As outlined in the methods section, EINS yields the so-called apparent MSDs, determined from the elastic component of the incoherent dynamic structure factor [44,45]. With some limitations, the apparent MSD allows for a comparison with a quantity that can be directly obtained from measured data of different proteins or different conformations of proteins. At increased temperatures, the MSD includes diffusive motions, which correspond to the resolution of the instrument used [22]. The limitations are given by the fact that a further separation of the recorded signal into contributions from diffusive and vibrational motions, and the further characterization of the diffusive length and time scales, would require to record data at energy transfers different from zero at all scattering vectors. Despite these limitations the apparent MSD technique has nonetheless been proved useful to compare the dynamics of different classes of proteins. Gallat et al. [47] showed that the intrinsically disordered tau protein behaves in a more dynamic manner compared with MBP, a globular protein of similar molecular mass. The conclusions, drawn by Gallat and co-workers, that a disordered protein behaves more dynamically then a folded counterpart, have been confirmed by quasi-elastic neutron studies of the intrinsically disordered β-casein [70,71].

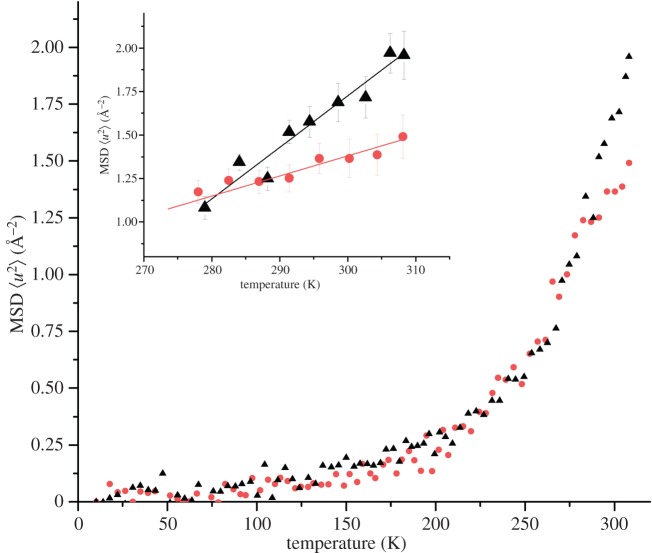
EINS data of OPN 1–149 and OPN CPN were recorded as a function of temperature against the angular dependency of scattering intensity, known as a fixed window EINS temperature scan (see ‘Material and methods’). The apparent MSD was extracted from the slope of the fitted straight lines on a logarithmic plot of the elastic scattering intensities versus the scattering vector squared. Figure 7 shows the obtained MSDs plotted as a function of temperature and the effective force constants are summarized in table 4.

Figure 7.

EINS data indicates a difference in protein flexibility when in free and nanocluster form. MSDs as a function of temperature of OPN 1–149 (black triangles) and OPN CPN (dots), hydrated to 0.44 g D₂O per gram of protein, from IN16 neutron spectroscopy data. Inset: effective force constants were extracted from the highlighted slopes above 270 K. (Online version in colour.)

Table 4.

Effective force constants extracted from points above 270 K.

sample	〈k′〉 (N m−1)
OPN 1–149	0.083 ± 0.009
CPN	0.156 ± 0.019 Å
Tau [47]	0.096
MBP [47]	0.185

Figure 7 shows the characteristic transitions first observed for proteins by Doster et al. [72,73]: below 100 K, contributions mainly come from harmonic vibrations; above around 150 K, there is a second slope caused by methyl rotational transitions; and the third slope, around 180 K, corresponds to the onset of anharmonic motions in the water coupled region. We emphasize that the extracted effective force constants, being defined by the change of the apparent MSD with temperature, reflect a resilience to an increase of the diffusive mobility with increasing temperature. The term resilience by this definition is not to be confused with mechanical stiffness.

The results obtained for both free OPN 1–149 and OPN CPN show typical two well model behaviour, previously observed in other hydrated protein samples examined by EINS [46,74,75]. Identical MSDs were obtained at temperatures below 230 K, where atoms are trapped in a low harmonic well. According to the two-well model, at higher temperatures both OPN 1–149 and OPN CPN start to sample the harmonic and anharmonic wells causing a rapid increase in measured MSDs values. At higher temperatures, the MSD of OPN 1–149 is higher than that of OPN CPN, indicative of increased dynamics of free OPN 1–149. This behaviour is similar to that previously found in dynamics studies of β-casein which stiffens upon binding to calcium ions (although in this case partial folding was also observed in the bound protein) [70]. When comparing CPN-forming phosphopeptide dynamics, however, the number and distribution of clustered regions of phosphorylated residues ([14]; PC) must be kept in mind. Proteins such as β-casein and OPN bind to the inorganic core of CPN through PCs, which act like anchor points to calcium phosphate, restricting the chain displacements. While the human β-casein contains a single PC close to the N-terminal, OPN 1–149 contains three PCs simultaneously associated with the core in CPN [13].

The associated effective force constants 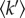were extracted from the data above 270 K (figure 7 inset and table 4). The value is almost twice as large for OPN 1–149 compared with that obtained for OPN CPN. The observed increase in the effective force constant indicates that OPN 1–149 becomes more resilient upon sequestration of calcium phosphate. This is consistent with internal packing in the CPN, where the three PCs can further anchor the protein chain. Table 4 additionally shows that the resilience of hydrated OPN is in close agreement with previously measured force constants of the Tau protein. The flexibility of OPN in CPN is somewhat reduced, yet remains larger then observed in globular proteins. Therefore, the peptides on the nanocluster shell are still able to occupy a comparably larger conformational space than folded counterparts.

4. Conclusion

The dynamical behaviour observed for OPN 1–149 is in agreement with results obtained by other techniques on the intrinsically disordered β-casein, and furthermore agrees well with other EINS fixed window temperature scans performed on the intrinsically disordered Tau protein [70,71]. This suggests that an increased dynamical behaviour, compared to globular proteins, may be a functionally required property of IDPs. Upon sequestration of calcium phosphate by OPN 1–149, 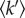decreases significantly yet the in silico protein backbone dynamic calculation of S² does not take this into account. When considering the dynamical properties of IDPs the amino acid sequence and protein structure must be considered, but also the state of the protein and its molecular environment, including the presence of binding and crowding agents.

Disordered proteins can undergo disorder-to-order transitions upon binding to other molecules, but can also retain substantial conformational flexibility as shown here for OPN CPN. Given that previous work [11] showed that the flexibility of OPN increases upon binding to heparin, structural and dynamical changes are clearly strongly dependent on the molecular partner. For both calcium phosphate and heparin, the order or disorder induced is not described by formation of secondary structural elements, but rather OPN peptide occupation of conformational space. Such behaviour of IPDs has previously been simulated by computational studies, which showed that under crowding conditions the calculated R_g of unfolded proteins decreases [76].

Finally, in the context of biomineralization, the increased dynamics of OPN allows the rapid sequestration of amorphous calcium phosphate while still maintaining a disordered state. This enables peptide packing around the CPN core and may be of benefit for further CPN interactions [77]. It is known that OPN 1–149 forms CPN, unlike the full-length OPN [13]. It was previously suggested [13] that the relatively short number of phosphorylated residues per PC for OPN 1–149 stabilizes binding to amorphous calcium phosphate, while longer PCs are prone to binding crystalline phases. The lower resilience of OPN 1–149 compared with the full-length OPN is important for the modulation of function, namely allowing for three PCs to sample a compact conformational space and collectively find favourable calcium-binding positions.

Data accessibility

Neutron data are made available at: http://dx.doi.org/10.5291/ILL-DATA.8-04-706.

Authors' contributions

S.L., S.C.M.T. and M.H. carried out sample preparation work. S.L., T.S., T.N. and S.C.M.T. carried out scattering data collection. S.L., G.Z. and T.S. carried out the analyses of the EINS data. S.L. carried out analysis of the SAXS data. All authors participated in the overall design of the study, planning of the experimental strategies and helped draft the manuscript. S.C.M.T. and G.Z. coordinated the study. All authors gave final approval for publication.

Funding

S.L. and S.C.M.T. would like to thank Keele University (EPSAM), the ILL and Lund University for financial support. T.N. acknowledges financial support from the Swedish Research Council.

Competing interests

The authors have no competing interests.