Fast nastic motion of plants and bioinspired structures

Abstract

The capability to sense and respond to external mechanical stimuli at various timescales is essential to many physiological aspects in plants, including self-protection, intake of nutrients and reproduction. Remarkably, some plants have evolved the ability to react to mechanical stimuli within a few seconds despite a lack of muscles and nerves. The fast movements of plants in response to mechanical stimuli have long captured the curiosity of scientists and engineers, but the mechanisms behind these rapid thigmonastic movements are still not understood completely. In this article, we provide an overview of such thigmonastic movements in several representative plants, including Dionaea, Utricularia, Aldrovanda, Drosera and Mimosa. In addition, we review a series of studies that present biomimetic structures inspired by fast-moving plants. We hope that this article will shed light on the current status of research on the fast movements of plants and bioinspired structures and also promote interdisciplinary studies on both the fundamental mechanisms of plants' fast movements and biomimetic structures for engineering applications, such as artificial muscles, multi-stable structures and bioinspired robots.

1. Introduction

When one thinks of fast movement, plants do not usually come to mind. The movements of most plants [1] typically involve a tropism, the growth or turning movement of a biological organism in response to a direction-dependent stimulus, and are normally only notable over the course of hours or days. Classic examples of tropisms include phototropic movements towards light, directional growth or reorientation in response to gravity (gravitropism) and touch-sensitive growth of the roots (an example of thigmotropism) [1–5]. In addition to tropisms, some carnivorous plants trap prey using nastic movements, or direction-independent, reversible orientational changes in response to direction-independent stimuli. Among these, of particular interest is the Venus flytrap (Dionaea) which, upon consecutive triggering of the sensitive hairs on its namesake trap, can close a trap in less than a fraction of a second to capture its arthropod prey. This unusual plant, living in bogs with nutrient-deficient soil, was first discovered in 1760 by the North Carolina colonial governor Arthur Dobbs and was considered as ‘the great wonder of the [plant] kingdom’. Later, Darwin [6] systematically investigated the mechanisms of the Venus flytrap's fast movement and called the plant ‘one of the most wonderful in the world’.

The movements of live plants are typically classified into two categories, tropistic and nastic movements [7]. Tropistic movements refer to directional movements in response to external stimuli that have certain directionality (e.g. gravity, light and mechanical touches). For example, the development of tendrils may depend on where and how they touch an object that acts as a support, so this type of movement is tropistic (termed thigmotropic movement or thigmotropism, where the prefix ‘thigmo’ denotes touch responsive [8]). In contrast, nastic movements refer to direction-independent mechanical movements in response to external stimuli [9]. For instance, the way that a Dionaea trap closes usually does not depend on where and in what direction the sensitive hairs are touched, so it is an example of a nastic (or more specifically, thigmonastic) movement. On the other hand, researchers have also distinguished between active and passive systems among plant movements [10]. Action potentials are typically involved in active movements, whereby the live tissues or cells can actively deform in response to the stimuli by the transport of ions and fluids or the change in membrane permeability, often assisted by mechanical principles such as buckling, swelling or cavitation [7,11]. In contrast, passive movements refer to configurational changes of dead tissues that occur in response to environmental changes [12–14]. Because of the vast amount of literature on plants' movement, we choose to focus primarily on fast, nastic movements, and by ‘fast movement’, we refer to any movement that takes place in few seconds or less.

Although it has been known for centuries that certain plants are capable of fast movement, the exact biomechanical, biochemical and electrophysiological mechanisms which drive their fast movement have only begun to be comprehensively understood in recent years. For a more detailed overview of existing knowledge of these mechanisms, the readers may refer to some recent review articles on fast-moving plants [11,15–23]. It is also worth noting that plant biomechanics and mechanobiology have garnered increasing attention from the scientific community, as they represent ‘convergent paths to flourishing interdisciplinary research’ [23]. In the past decades, the role of mechanical forces, both internal and external, has been considered critical in the shaping of biological shapes, such as in stem cell differentiation [24], embryonic morphogenesis [25–28], cancer cell migration [29], plant morphogenesis [3,5] and touch-sensitive responses of plants [9]. In this review, nevertheless, our focus is on the mechanically stimulated movement of plants.

The mechanical sensing, actuation and movement in plants have since become sources of inspiration in biomimetic design, which have a wide range of engineering applications, including structural mechanics, biomedical engineering and chemical engineering. In this article, we review the characteristics and mechanisms of several representative fast-moving plants and some recent developments of engineering structures inspired by these plants. It is foreseeable that interdisciplinary collaborations between biologists, physicists, chemists, mathematicians and engineers will bring forth new insights that ultimately lead to a unified picture of how these non-muscular systems operate. We hereby hope that our work can promote further interdisciplinary studies on the movements of plants as well as the advancement of bioinspired and biomimetic technologies.

2. Fast movement of the Venus flytrap

In this section, we examine the important structures and features of the Venus flytrap and review the biomechanical, chemical and electrophysiological mechanisms behind its fast movement. Further study of these mechanisms will contribute to more comprehensive understanding of the nastic movements of plants.

2.1. The structural features of the Venus flytrap

The most spectacular feature of the Venus flytrap, is the ‘open mouth’, a pair of leaves that traps arthropods to nourish the plant. As shown in figure 1a, the modified leaves of the Venus flytrap have two parts, the upper and lower leaf. The lower leaf, also known as the petiolus, has an expanded leaf-like structure [31]. The upper leaf has three main features: a shell-like ‘open mouth’ composed of a pair of symmetrical lobes, three to five (typically three) sensitive hairs (figure 1b) on the inner side of each lobe and cilia, the numerous interlocked ‘teeth’ located on the border of each lobe. When an external force is applied to the trigger hairs, the trap swiftly closes. Usually, two consecutive touches are needed to trigger this rapid closure, a mechanism that helps ensure the plant does not waste energy on capturing non-prey. This movement can also be triggered by other external stimuli, such as electricity or heat [32–34]. In addition, upon mechanical stimulation, touch receptors, the small trichomes located on the outer leaves and stems of the Venus flytrap, generate action potentials that can sensitize the trigger hairs for contact [35].

Figure 1.

Images of Dionaea (a) and (b) and Aldrovanda (c–g). (a) The modified leaves of Dionaea are divided in two parts, the upper (ul) and the lower leaf (ll). (b) The upper leaf has two lobes which centre is brightly coloured red and contains three sensitive trigger hairs (arrows). The free edge of each lobe is lined with spine-like projections or cilia. (a,b) Adapted from [8]. (c) Photograph of a node of an Aldrovanda vesiculosa whorl with eight leaves (photograph © Dr Barry Rice, Sierra College, Rocklin, CA). (d,e) Microphotographs of a trap in open and closed configurations, respectively. The oval lobes are approximately 5 mm long. (f,g) Models of the trap in open and closed configurations, respectively. (d–g) Adapted from [30]. (Online version in colour.)

2.2. Biomechanics of fast movements in the Venus flytrap

The physical mechanisms behind the trap of the Venus flytrap are highly complex and remain incompletely understood. Through systematic observation and experimentation, Darwin [6] discovered that the inner layers of the Venus flytrap's lobes contract during closure, whereas the entire leaf's shape changes from convex to concave. Following these observations, researchers have proposed that the trap is mechanically bistable, with two stable states, i.e. the open and closed configurations, and an intermediate state [31,36,37].

Following Darwin, several additional explanations have been proposed for the underlying mechanisms behind this trap closure. Brown [38] proposed that trap closure is caused by the expansion of the outside of the lobes, and furthermore, that the opposite expansion of the inner surface of the lobes drives the reopening process of the Venus flytrap. Inspired by Darwin's hypotheses, Forterre et al. [36] used modern experimental technology to examine the biomechanics of leaf closure. Using elasticity theory, they proposed that a dimensionless parameter, α = W⁴κ²/h² (where W denotes the size of the lobe, h is the thickness and κ is the curvature), controls bistability (figure 2a–c). To test this hypothesis, Forterre and co-workers drew arrays of submillimetric ultraviolet-fluorescent dots on the surface of the leaves and irradiated the plant to fluoresce the dots, with the movements of these dots recorded by high-speed camera during trap closure. From these experiments, the researchers inferred that the main source of the fast and dramatic closure of the trap is the bistable, doubly curved structure of the leaves, which snap-buckle to reverse their Gaussian curvature upon closing. Moreover, the sudden change of intrinsic curvature along the direction perpendicular to the midrib was determined to be the main source of the driving force behind trap closure, verified by measuring the strain field upon closure. The experiments also showed that the speed of the lobe during closure increases as a function of α (figure 2d).

Figure 2.

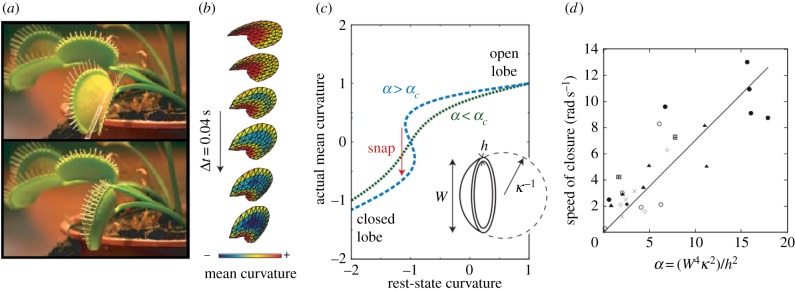
Snap-buckling of the Venus flytrap (Dionaea muscipula). (a) Venus flytrap in its open and closed states, shown in the upper and lower panel, respectively. (b) Computational reconstruction of trap lobe during closure from experimental data. (c) The mean curvature as a function of the dimensionless parameter α = W⁴κ²/h². For α < α_c. No multistability is predicted when α < α_c. When α > α_c, the system goes through a region featuring multistability where a ‘snap-through’ motion occurs. (d) Average speed of trap closure as a function of α. Adapted from [11] and [36]. (Online version in colour.)

While Forterre and co-workers demonstrated that the fast motion of the Venus flytrap involves a snap-buckling instability of the shell-like geometry of the lobes, the cell and tissue scale sources of this active movement remain poorly understood. To address these concerns, Colombani & Forterre [39] studied the cell scale in vivo measurements of the pressure and other poroelastic properties using a microfluidic pressure probe. Their initial results shed light on the time course of cellular pressure and volume change during plant movement, as well as membrane permeability and Young's modulus. The determined poroelastic time of 20–150 s, much too large to account for rapid closure of the trap, suggests that some other cellular property (e.g. pre-stress of mesophyll cells) rather than active, osmotically driven water transport between cells could be the cell scale source of rapid trap closure. Additional studies are necessary to fully understand the exact nature of this source.

In addition, Markin et al. [40] proposed a hydroelastic curvature model to interpret the mechanism of the active movement of the Venus flytrap. Here, based on the assumption that the trap possesses curvature elasticity and consists of outer and inner hydraulic layers where different hydrostatic pressures can build up, the natural principal curvatures are determined by the hydraulic states of the two layers of the plant, which are in turn defined by their differing hydrostatic pressures. Similar to a bimetallic couple, this so-called bilayer couple can change shape rapidly in response to triggering of the sensitive hairs of the plant. This change is thought to occur through transportation of water via aquaporins between the two layers. Yang et al. [37] further developed a mathematical model to simulate the closing and opening dynamics of the Venus flytrap from the nonlinear dynamics and control perspective. In a separate study, Joyeux [41] presented an elasticity model of the Venus flytrap by accounting for the anisotropic nature of the strain field of the trap and assuming that the open geometry is the minimum energy state, which embodies improvement over the previous model [42] developed by Joyeux and co-workers. More recently, Pandolfi et al. [43] showed that this movement is intimately dependent on gravity, which has not been considered before; however, the detailed biophysical mechanism remains inconclusively explained and requires further examination.

2.3. Different ways of triggering the Venus flytrap

The Venus flytrap can be triggered in a number of ways. In nature, the trigger mechanism is mechanical stimulation, in which two consecutive touches on the sensitive hairs within around 30 s lead to closure. These touches can be on the same hair or on separate hairs. Each touch generates an electrical signal, which transmits between the lobes and the midrib of the trap. In addition to the typical two touches, a single sustained touch to one trigger hair can also close the trap, if two electrical signals are generated about 2 s apart in the same manner [44]. Furthermore, there exists a temperature dependence of mechanically stimulated closure, with evidence suggesting that higher temperatures result in a greater sensitivity to mechanical stimulation [32].

External electrical stimulation, involving the transmission of electrical charge between a lobe and the midrib by means of electrodes and a charged capacitor can also induce closure. At room temperature, a total charge of about 14 µC [33], applied at once or in smaller increments, also causes the Venus flytrap to close, though the exact amount of charge required increases with trap size and decreases at higher temperatures. Closure by repetitive application of smaller charges demonstrates electrical memory in the Venus flytrap (see section Electrophysiology behind the Venus flytrap's fast movement), subject to a time interval similar to that associated with mechanical stimulation [31].

The Venus flytrap also closes in response to optical stimulation in the mid-infrared region. The snapping mechanism can be triggered with 7.35 µm radiation from a continuous-wave laser directed at the interior of a Venus flytrap. Furthermore, electrical signals are found to propagate in the Venus flytrap concurrently with each optical stimulation, in the same manner observed in mechanical stimulation [45]. Also noteworthy are recent experiments involving chemical stimuli of trap closure. Volkov et al. [46] showed that application of 10 µl of ether or chloroform on the midrib induces slow (10 s) closure of the trap, and similarly, that application of 10 µl of chloroform directly on the sensitive hairs can induce closure as fast as mechanical stimulation of the hairs.

2.4. Biochemistry behind the Venus flytrap's fast movement

A number of plant hormones have been identified and linked to several key properties of the Venus flytrap and its prey-catching and digesting mechanisms. In plants, lipid-based hormone signals known as jasmonates regulate defence mechanisms in response to abiotic and biotic stresses. In contrast, these jasmonates play a role in nutrition retrieval for the Venus flytrap: the phytohormone jasmonic acid and coronatine (the molecular mimic of the isoleucine of jasmonic acid) are jasmonates involved in the secretion of digestive enzymes. Perez et al. demonstrated that spray application of these jasmonates on just one leaf can trigger secretion of digestive enzymes throughout a Venus flytrap without any mechanical stimulation, indicating that these jasmonates are systemic in nature [47]. In addition, the researchers showed that jasmonates are involved in the trap-closing mechanism. They also showed that isolated traps from D. muscipula can be induced to close when aqueous-phase extracts containing 12-oxo-phytodienoic acid are adsorbed on the leaves. In these experiments, the total quantity of bioactive substance, as opposed to the concentration, influences closure. One hypothesis suggests that this bioactive trap-closing chemical may be secreted stepwise in response to each action potential, inducing trap-leaf closure past a specific threshold [33,48]. This hypothesis would thereby link the observed memory effect associated with the accumulation of stimuli to the accumulation of this chemical.

Abscisic acid (ABA) is also involved in the trap-closing mechanism. ABA is a plant hormone that activates anion channels to close stomata, reducing transpiration. ABA is produced in plants in response to low water availability. In D. muscipula, ABA has been shown to lower trap sensitivity to mechanical stimuli. Compared with well-watered Venus flytraps, both ABA-sprayed and water-deficient traps require additional mechanical stimulation to trigger fast trap closure [47].

2.5. Electrophysiology behind the Venus flytrap's fast movement

The Venus flytrap's rapid closure is typically triggered by consecutive mechanical stimuli within a window of 30 s on the one or multiple sensitive hairs. It is known that such mechanical stimulation activates certain ion channels to generate both a receptor potential and an action potential, which may be responsible for the opening of fluid channels between different hydraulic layers. Nevertheless, two consecutive stimuli only put the trap into a semi-closed state. Without any further stimulations, the trap will gradually reopen in a few hours. In the case where a trapped insect keeps struggling and stimulating the sensitive hairs, the trap will close tighter and tighter until it is fully sealed, upon which the digestive fluids are secreted to help digest the nutrients.

As mentioned before, an alternative way to trigger closure is by applying an electrical pulse above a threshold value between the upper layer of one lobe and the midrib. In such an experiment, the polarity is critical, because an electrical pulse with inverted polarity does not trigger trap closure [40]. Whether triggered mechanically or electrically, the rapid closure of the Venus flytrap always follows the generation of receptor and action potentials [33]. There are usually three phases during closure: a mechanically silent phase (no notable movement), an accelerating movement phase and a fast movement phase [21,33]. Volkov et al. [31] employed a high-speed data acquisition device to record the duration and amplitude of the action potentials and showed that the duration of an action potential in the Venus flytrap is typically about 1.5 ms. Furthermore, the researchers [31] used the ion channel uncouplers and blockers to explore the mechanisms of different closure phases. They found that both ion channel uncouplers and blockers can increase the time delay of trap closure dramatically while decreasing the speed of closure.

It is also interesting to note that the Venus flytrap exhibits short-term electrical memory [44], i.e. separate electrical pulses, each of which is less than the threshold and within a time window of no more than 50 s, can initiate closure as long as the sum of electrical stimulus exceeds the threshold value. Volkov and co-workers demonstrated that this stimuli threshold is temperature-dependent, with a charge threshold between 8 and 9 µC (with a larger electrical threshold corresponding to larger traps) at room temperature compared with only 4.1 µC at 28–36°C [44]. This electrical memory was also demonstrated to be time-dependent through application of below-threshold electric shocks separated by a 15 s interval, with decreased number of below-threshold electric shocks required for closure of the trap with increasing current of each shock. Researchers have also begun to discover the biomolecular components underlying this electrical memory. Ueda et al. [48] demonstrated that there exists a threshold of accumulated biometabolite for stimulating trap closure. Using bioassays to separate Dionaea extracts, a bioactive polysaccharide was identified that is capable of triggering trap closure in the absence of any external mechanical or electrical stimuli. The molecular electronics and different electrical characteristics of the complete hunting cycle (the open state, closed state, locked state, constriction and digestion state, and semi-open state) were further examined [34,49]. Putting the results from these studies together, it is promising that a more comprehensive understanding of the biological electronic system and the associated ‘memory’ and actuation mechanisms in plants such as Dionaea might be achieved. Furthermore, while there are clear parallels to be drawn between the electrical signals in plants and animals, additional studies are required to elucidate the unique physiological origins and functions of these signals in plants [50].

3. Comparative biomechanics on active plant traps

The mechanics of movements in D. muscipula differ from those in the underwater carnivorous traps Aldrovanda vesiculosa and Utricularia. Poppinga and Joyeux compared the biomechanical mechanisms of Aldrovanda and Dionaea by modelling the Aldrovandas trap as a pair of thin elastic shells hinged to the midrib [30] (figure 1c–g). The midrib connecting the two lobes can bend inward in the closed configuration. This study indicates that the Aldrovanda's trap closure is due to swelling and shrinking [51] of tissues in or around the midrib, rather than mechanical buckling that takes place in Dionaea muscipula. Moreover, the model suggests that this mechanism is the source of the rapid speed of trap closure in Aldrovanda, i.e. a large opening or closing movement of the trap can result from a relatively small bending deformation of the midrib, in contrast with the snap-buckling of convex to concave curvature seen in the lobes of Dionaea. More recently, Joyeux [41] proposed a precise mechanism for the action of motor cells surrounding the midrib of an Aldrovanda trap that could lead to closing and opening of the trap. This new model confirms that the reversible movements of Aldrovanda trap can be controlled by the swelling and shrinking of the motor cells near the midrib, in contrast to the irreversible mechanism operating in Dionaea traps where mechanical buckling plays a dominant role.

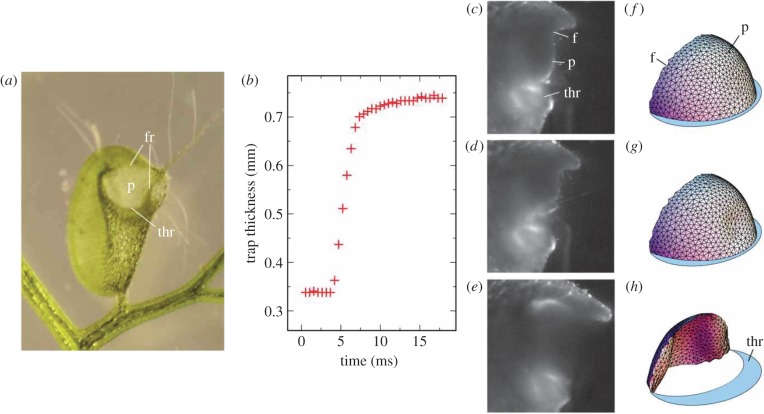
Bladderwort (Utricularia) traps also employ a mechanical buckling mechanism that differs from that of Dionaea [52]. Utricularia's suction traps are among the most complicated of all active traps in the plant kingdom [42]. The trap is composed of a hollow trap body, a ‘trap door’ (which grants entrance to the trap body's interior), and four outward facing trigger hairs located on the trap door [42]. During the trap-setting phase, active cells pump water out of the trap body through two-armed glands, termed bifids, creating a negative pressure differential up to −16 kPa [53,54] between the interior and exterior of the trap body. As a result, the thin walls of Utricularia become concave (modelled as spherical) with stored elastic energy in the doubly curved shell of the trap body. Joyeux et al. [42] modelled this buckling scenario like a trap door. The researchers also showed that this buckling can also be initiated by a local deformation of the shell from mechanical stimulation of the trigger hair. Figure 3 further suggests that the swinging motion of the panel starts with local curvature inversion, and that the ‘door’ acts like a flexible valve that flips under external pressure (and changes curvature from concave to convex) [42]. Additionally, Utricularia traps fire not only upon mechanical stimulation of the trigger hairs, but also spontaneously to capture small organisms and detritus (e.g. phytoplankton or bacteria) which are too small to mechanically trigger the trap [55]. This spontaneous action occurs through mechanical oscillations of regular pumping and mechanical buckling of the trap door. The underlying mechanisms of the spontaneous firing could inspire biomimetic design of engineering structures that are capable of autonomous elastic deformation.

Figure 3.

(a) Utricularia inflata in untriggered, set configuration (adapted from [52]). Note that the trap, approximately 3 mm wide, has concave curvature of its walls owing to the negative internal pressure in set configuration. (b) Experimentally determined time course behaviour of trap thickness during trap closure following mechanical stimulation of one of the trigger hairs. (c–e) Time course behaviour of door opening of Utricularia australis trap at 0, 7.6 and 8.6 ms following mechanical stimulation of trigger hairs, respectively. (f–h) Computational reconstruction of the trap door in set configuration (f), at the initial stages of buckling (g), and in the process of curvature inversion (h) door in set condition, at the onset of buckling, and while swinging open, respectively. (b–h) Adapted from [42]. ‘p’ and ‘f’ denote the panel and the frame of the door, respectively; ‘thr’ denotes the threshold (following the conventions in [19]). (Online version in colour.)

Furthermore, Llorens and co-workers developed a model to simulate the dynamical process of Utricularia's trap closure by considering hydrodynamics, buckling of the door and deformation of the trap body. This comprehensive treatment can predict the main mechanical features of the Utricularia's trap closure, namely triggered closure and spontaneous firing. Firing and resetting of traps in Utricularia are associated with water flow and trap volume changes, the mechanism of which has been studied experimentally by Lubomir Adamec. The experimental data suggest that only a direct recording of a physiological activity in trigger hairs of a stimulated Utricularia trap can determine whether or not the mechanical stimulus results in an action potential (such as in D. muscipula and Aldrovanda vesiculosa), which could serve as an electrical signal for the trap-door buckling [56]. Bartosz J. Plachno et al. studied the relationship between trap anatomy and its firing–resetting efficiency in nine Australian Utricularia species and found that the trap firing–resetting rate, while conceivably dependent on trap thickness, did not seem to depend on the number of cell layers in the trap wall, as quantitative functional trap characteristics of the three to four cell layer thick traps of U. volubilis were similar to those of the two to three cell layer thick traps of U. dichotoma [57].

4. Catapult-flypaper traps

Sundews (Drosera) are mostly known for capturing prey with sticky traps. However, one recently discovered sundew (Drosera glanduligera, Droseraceae) demonstrates fast motion for the capture of prey. Upon sensing prey with its touch-sensitive snap-tentacle heads, Drosera glanduligera catapults prey using outstretched snap-tentacles (as shown in figure 4a) onto adjacent sticky glue-tentacles (figure 4b,c) in as little as 75 ms [58–60]. These sticky glue-tentacles then slowly fold up and surround the prey over several minutes to several hours while digesting the prey with secreted digestive enzymes. The rapid catapulting movement of the snap-tentacle is considered to be primarily owing to change in hydraulic pressures within the tentacle. Two possible mechanisms of this hydraulic pressure change have been proposed [58]: rapid transport of water from cells in the adaxial half of the tentacle to cells in the abaxial half, resulting in adaxial contraction and abaxial extension and the fast catapulting movement; or, a sudden loss of turgor pressure in adaxial cells, followed by tentacle bending owing to pre-stress of the abaxial surface to release the elastic energy stored in the epidermal cells on the adaxial side. However, further investigations are needed to test these hypotheses and elucidate the operating mechanisms of the fast catapulting motion of the snap-tentacles. Notably, unlike the snap-through movement of the Venus flytrap, the catapulting movement of the snap-tentacles is irreversible, possibly because non-recoverable fracture of the epidermal cells occurs in the hinge zone of the snap-tentacle upon initiation of movement [58]. Some other flypaper traps, such as Pinguicula [61,62], less mobile in nature, are nevertheless not reviewed in detail in this article.

Figure 4.

Trap leaves of Drosera glanduligera (adapted from [58]). (a) Drosera glanduligera in its natural habitat; note the radially long, outward extending, non-sticky snap-tentacles and the shorter glue-tentacles they snap towards. (b) An example of cultivated Drosera glanduligera. (c) Drosera glanduligera with a captured fruit fly, stuck within the concave interior of the trap. (Online version in colour.)

5. Other fast movements in plants

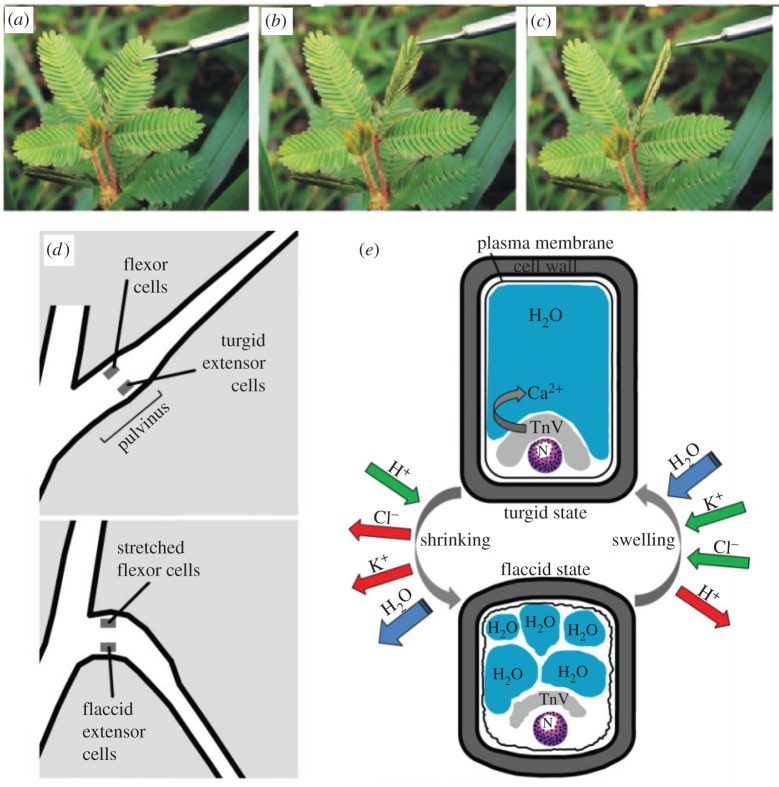
Besides these carnivorous plants with active traps, there are other plants that can move at a comparably dramatic speed. Because the main focus of this review article is on the fast, nastic movements mostly discovered in carnivorous plants, here we mention only a few examples of other types of fast movements in plants. Interested readers can refer to some excellent review articles [11,18]. As yet another well-known moving plant, Mimosa pudica exhibits a rapid, defensive response to external stimuli, such as the closing of its leaves (figure 5a–c) and bending of its pulvinus, the joint-like thickening of the plant near the bottom of a leaf or leaflet where the plants ‘motor cells’ reside. [8,22] (figure 5d). These motor cells, divided into flexor and extensor cells on the ventral and dorsal side of the leaf, respectively, regulate the volume and shape according to their relative turgor pressure. Upon mechanical stimulation of the plant, an action potential is initiated which propagates a signal from the site of the stimulus to the pulvinus. This results in another action potential which initiates the differential transport of K⁺ and Cl^–, leading to a change in turgor pressure in the cells (figure 5e). Consequently, the water potential in the extensor cells increases, resulting in loss of water and shrinkage of the cells, with the opposite occurring in the flexor cells, which swell to a turgid state. As a result, the leaflet folds up, ensnaring the trapped prey within. Calcium ions are also shown to play an important role in this nastic movement [8,63,64]. More recently, Song et al. [65], using advanced bioimaging techniques including two-dimensional X-ray microimaging and three-dimensional X-ray tomography, non-destructively monitored the pulvinis at a high resolution to analyse the morphological characteristics of the pulvinis in real time.

Figure 5.

Thigmonastic movement of leaflets and schematics of mechanisms in Mimosa pudica. (a) Leaflets open; (b) leaflets closing owing to touch-induced changes in cell turgor of cells within the pulvinus, a structure located at the base of each leaflet. (c) Leaflets closed. The time-lapse between each photograph is about 1 s. (a–c) Adapted from [8]. (d) Cartoon illustrates the mechanism of leaf movement in M. pudica before (top panel) and after (bottom panel) application of stimulus. Note the corresponding states of the flexor and extensor cells in each condition, which implies that the extensor cells are the primary effector of pulvinus bending. (e) Cartoon illustrates turgor changes in an extensor cell and the resulting shape changes of the cell as it changes between turgid (above) and flaccid (below) states; here, N denotes the cell nucleus. The primary ionic movements underlying these turgor changes are shown: when the leaves are mechanically simulated, adenosine triphosphate (ATP) dephosphorylating H⁺ pumps (green) allow for the rapid outward flux of K⁺ and Cl^– ions, which in turn trigger outward osmotic movement of water. Tannin-rich vacuoles (TnV) store Ca²⁺ to regulate K⁺ flux. (d,e) Adapted from [8,22]. (Online version in colour.)

In contrast to the plant-initiated, hydraulically driven movements of M. pudica, some plants use purely mechanical mechanisms to achieve rapid movements. Among such plants, a variety of mechanisms exist to achieve the fast dispersion of small solid objects, such as spores, pollen or seeds [11,12,18,66]. For example, the stamen of the bunchberry dogwood (Cornus canadensis) has evolved a trebuchet-like method for ‘catapulting’ their pollen skywards after the flower opens [66], and the sphagnum moss can shoot its spores out like an airgun using built-up internal pressure [67]. Yet another example of projectile motion is the release of fern spores [68,69], where through a cavitation catapult mechanism, generation of bubbles causes rapid cell expansion, inducing dramatic bending of the annulus cells and subsequently converting stored elastic energy into kinetic energy [11,69].

Last but not least, a number of plants also exhibit thigmonastic movements in their reproductive parts such as the floral organs and fruits [8,19,70–74]. For example, when touched gently, the stamens of the moss rose, Portulaca grandiflora can bend within less than a second and return to the original positions in about 5 min [70], similar to the thigmonastic movement of Mimosa leaves in terms of the response times. Orchids have also evolved remarkable actuating structures and morphologies, such as sexually dimorphic flowers, to induce insects to cross-pollinate for them [72,74]. Such touch-sensitive movements of the reproductive organs represent an active adaption to enhance cross-pollination by transporting the pollen grains to arthropods (such as bees) and birds who serve as pollinators. Interesting questions then naturally arise about how these plants and their pollinators have co-evolved over millions of years. Addressing the molecular and biophysical mechanisms in these thigmonastic movements may help elucidate the coevolutionary relationships between the species of flowering plants and the pollinators as well as provide information about the evolution paths of these versatile floral morphologies [8].

6. Engineered actuating structures inspired by fast-moving plants

Fast-moving plants, as examples of dynamically morphing biological structures, are good model systems in the field of biomimetics, a relatively new discipline that takes inspiration from biology for problems in engineering. For example, the leaves of the Mimosa plant, which contract upon certain external stimuli (physical, heat, chemical, etc.), have inspired research into structures that can change on demand between flexible and stiff states through changes in hydraulic pressure [75]. In particular, D. muscipula, the Venus flytrap, has drawn strong interest from engineers and plant biologists alike. The quick sensing and closing properties of Dionaea have inspired a number of imitative designs with potential applications in drug delivery systems, artificial muscles and shape-changing structures [76–79].

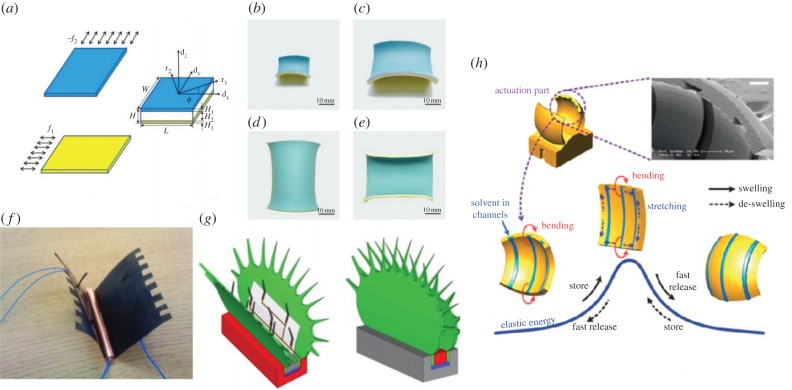
Holmes & Crosby [76] used mechanical buckling of plates (in a two-dimensional analogue of Euler buckling) and biaxial compressive loads to fabricate an array of lens-like bistable shells, shown in figure 6. A layer of biaxially pre-stretched polydimethylsiloxane (PDMS), which is patterned with periodic arrays of holes, is topped via spin coating by a thin film of uncured PDMS. The two layers of PDMS are then bonded via cross-linking. The micro-lenses formed by this process can possess either a concave or convex shape; a characteristic snap-through movement, similar to that of the Venus flytrap, occurs upon transition between the shapes. The focal point of each micro-lens is either above the structure surface (when the micro-lens is convex) or below the structure surface (when the micro-lens is concave). The researchers demonstrated finely tunable mechanical properties of the micro-lens structure through tuning of the geometric properties of the structure, e.g. lens size and spacing between adjacent lenses.

Figure 6.

Shown is a diagram of ‘snap-through’ transition of the micro-lens structure. The surface of a concave micro-lens (b₁) undergoes snap-through transition to a convex shape (b₂) in approximately 30 ms. Adapted from [76]. (Online version in colour.)

Chen et al. [79] studied the geometrical and mechanical properties of a bistable strip (figure 7a–e). They proposed a theoretical model for the large deformation of shell structures by the conformation of a strip on the doubly curved surface of a torus. The theory captures the main feature of the competition between bending and stretching energy of an elastic plate when the Gaussian curvature changes. In addition, they fabricated a physical model of a bistable structure by uniaxially pre-stretching two rubber sheets in perpendicular directions, ‘sandwiching’ a much thicker rubber sheet between the two pre-stretched sheets and bonding the three sheets together. Using the theoretical model, the researchers identified two dimensionless parameters (related to the mechanical forces and geometry) that control the bistable behaviour of the system. In particular, the geometric parameter, 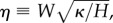also discussed by Armon et al. [13] in an independent study, is equivalent to α^1/4 (where α is the geometrical parameter that controls the elastic energy barrier in the Venus flytrap's closure [36]). Their work quantified the conditions for bistability, providing a mathematical framework for the study of bistable and multi-stable structures, with application in artificial muscles, bioinspired robots and shape-changing structures. Subsequent finite-element simulations and experiments further support the validity of the theory [80–82]. Based on this mechanical principle, bistable helical ribbons have been designed which can morph from one helical shape to the other upon certain external stimulus [81].

Figure 7.

(a) Schematic of the bench-top experiments: two pieces of latex rubber sheets (blue and yellow) were pre-stretched along perpendicular directions and a thicker elastic strip is sandwiched in-between. Upon release, the bonded multilayer composite will deform into one of the following shapes in (b–e). (b) A saddle shape when the composite layer is narrow enough. (c) A saddle shape when the composite layer is thick enough. (d) A stable, nearly cylindrical shape when the composite layer is wide and thin enough. (e) The other stable shape (bending upwards) for the same sheet as in (d). (a–e) Adapted from [79]. (f) The robotic Venus flytrap (VFT) with a pair of lobes (traps), embedded spine (copper roll), IPMC trigger fingers and lead wires for sensing and actuation. (g) Schematics of a robotic VFT in an open and closed configuration (adapted from [77]). (h) Snap-buckling of the doubly curved hydrogel device by swelling of the lobes from solvent in the microfluidic channels. Note the characteristic shape changes and reversal of curvature that occur during actuation of the device. Scale bar, 100 µm. Adapted from [78]. (Online version in colour.)

Hydrogel polymers, which swell and contract in response to a wide range of input stimuli (chemical, temperature, mechanical), can lead to a variety of sensing and actuating systems with a wide range of engineering applications [83]. Inspired by Dionaea, Lee et al. [78] fabricated a jumping microgel device as illustrated in figure 7h, using the sensing–actuating properties of hydrogel to engineer a microgel jumping device that generates a snapping motion within 12 ms. The researchers created a doubly curved shape from hydrogel and employed elastic instability to create the snap-buckling mechanism responsible for the quick actuation of the device. Upon swelling, the microgel legs of the device snap-buckle, resulting in a rapid jump. The power density of this device, at 34.2 mW g^–1, approaches that of human muscle. Also inspired by Dionaea, Gracias and co-workers [84,85] have designed and fabricated smart photo-patterned bilayer hydrogel actuators. These hydrogel actuators exhibit external stimuli-dependent swelling behaviour, which, employed in a bilayer design, can act as a hinge for a Venus flytrap-like actuator. Santulli et al. [86], combining hydrogel polymer with braided fibres, developed and characterized actuators with tunable stiffness and force generation capacity.

In order to understand the behaviour of these hydrogel devices, the underlying behaviours and properties of the hydrogel must be characterized and quantified. Stoychev et al. [87] explored the folding behaviour of rectangular hydrogel bilayers on a substrate, characterizing the effects of both non-homogeneous swelling and adhesion of the hydrogel to the substrate. The capillary forces that drive liquid absorption-based hydrogel actuation have been reviewed by Roman & Bico [88]. Nevertheless, many properties and behaviours of hydrogel structures remain to be explored.

Hydrogel composites allow for the design of complex, dynamically morphing pre-programmed shapes. Erb et al. [89], inspired by the shape changes in natural seed dispersal units and carnivorous plants, designed hydrogel composites with embedded structural reinforcements which can deform into complex, bioinspired shapes, such as a twisting seed pod. Hydrogels and other polymers may also be used with origami design principals, combining the sensing–actuating properties of polymers with the pre-programmed, dynamically tunable properties of origami designs. For instance, Wei et al. [90] designed hybrid hydrogels that can dynamically morph into specific shapes, including helical sheets with reversible chirality, whereas Ryu et al. developed photo-origami designs which, in reaction to certain wavelengths of light, fold into precise three-dimensional structures from two-dimensional sheets [91]. Origami designs incorporating stiff plate elements [92] and biomimetic leaf folding patterns [93] might also be used towards the development of novel actuators.

In addition, ionic polymer–metal composites (IPMCs) have garnered much interest from the scientific community for both their biomimetic sensor and actuator properties [94]. IPMCs exhibit characteristic sensing and mechanical bending in an electrical field, actions that strongly resemble the sensing and bending capabilities of the leaves of the Venus flytrap. IPMCs also have potential medical and industrial applications; this study of IPMCs focuses on further modelling of IPMC actuators and development of application prototypes [95–97]. Because of the similarities between the two, studies of the bending and sensing mechanics behind IPMC actuators and Venus flytrap mechanics go hand in hand. As illustrated in figure 7f,g, a novel flytrap-inspired robot was fabricated by Shahinpoor using IPMC artificial muscles as distributed sensors and actuators [77]. A conductive copper spine served as a ‘midrib’, which transmitted the signals sensed by the IPMC trigger hair to the solid-state relay system and to activate a small dynamic voltage generator capable of actuating the robotic trap. When certain stimuli were applied to the IPMC trigger hairs, the functioning of the voltage generator can cause the flytrap robot to close. Such biomimetic design of smart systems/structures, integrated with functional sensors and actuators, can be potentially useful in a number of engineering applications [21].

The hydraulic redistribution-driven movements of plants have also influenced the development of osmotically actuating, shape-changing structures. Sinibaldi et al. [98], inspired by osmotic-driven plant movements, modelled the dynamic behaviour of two implementations of the osmotic actuator concept. Both models were formulated on the basis of two chambers, a reservoir chamber (RC) filled with solute and actuation chamber filled with solute and solvent, which are separated by a solute-impermeable osmotic membrane. The two models are different in their implementation of the actuator: the first has actuation work stored through the elastic deformation of a spring by a piston that displaces through solvent flux; the second has actuation work stored through the elastic deformation of a non-permeable bulging membrane. These models represent preliminary steps towards understanding towards the development of biomimetic, biorobotic solutions inspired by plant movement.

There are additional examples of morphing structures inspired by the hydraulic redistribution-driven plant movement. Inspired by the hydraulic movements of D. muscipula and M. pudica, Pagitz et al. developed a model for morphing structures driven by pressure-actuated cellular structures [99]. The researchers further refined this model by introducing a shell-like structure that can, through its characteristic ‘snap-through’ morphology, change the sign of its Gaussian curvature [100]. These shape-changing structures, driven by multilayer cellular pressure actuation, have potential applications in aerospace engineering, automobile engineering, architectural design, etc. Moreover, Freeman [101,102] designed biomimetic flexible morphing membranes, so-called engineered nastic membranes, for on-demand change of aircraft wing shape during flight. Upon introduction of adenine triphosphate (ATP) to these nastic membranes, proton pumps are activated which move select ions across the membrane into a cylindrical inclusion (analogous to protons being pumped into the intracellular space). The resulting electrochemical gradient activates co-transporters and exchangers located in the nastic membrane, which drive the ions back out of the inclusion and down their electrochemical gradient while concurrently using this ionic flux to move fluid into the inclusion. This inward flow of fluid results in expansion of the cylindrical inclusion until fluid pressures are equalized and hydrostatic equilibrium reached and is responsible for the dynamic morphology of the structure. Detailed analysis of the mechanical, morphological and electrochemical properties of this bioinspired actuator in ABAQUS for the surrounding polymer and UFLUID for the driving transport processes revealed that various properties, including slow reaction time, difficulty in upwards scaling and limited displacement prevented this design from application in its original purpose of morphing aircraft wings; however, the design showed promising applications in enhanced osmotic actuation, water purification through protein-driven selective transport and highly targeted drug or vaccine delivery devices, which burst and release their contents upon contact with the proper stimulus in the body. More recent developments to this design by Freeman & Leiland [102] incorporated the use of voltage-gated ion channels for the control of activation and a novel dual activation chamber design capable of simultaneous swelling and shrinking, with potential applications in biomorphic structures.

The mechanical principles demonstrated by moving plants also have potential application in systems engineering. Recently, Lenau & Hesselberg [103] studied the self-organization principles demonstrated in stimulated motion plants. They divided the plant motions into three categories (according to the purpose): dispersal of spores, pollen or seeds (e.g. sphagnum mosses); obtainment of nutrients (e.g. carnivorous plants such as Dionaea) and protection of vital organs or obtainment of optimal light and temperature conditions (e.g. Mimosa). They outlined the self-organization principles behind sun-tracking plants, i.e. detect sunlight, communicate this signal to an actuator, and perform a motion to optimize internal and external conditions based on the amount of sunlight, and showed that these design principles could be applied to the design of window blinds that open and close based on the amount of sunlight or solar energy devices that track the sun's position through the sky in order to maximize exposure. These designs for sun-tracking devices have potential applications in energy conservation on an industrial or consumer scale. Also inspired by the sun-tracking movements of plants, Dicker and co-workers [104] developed a biomimetic analogue of the sun-tracking leaves of the Cornish mallow (Lavatera cretica), which reversibly move the plane of the leaf to be perpendicular to available sunlight, termed diaheliotropic movement. As shown in figure 8, the designed biomimetic photo-actuator consists of a reversible photobase as the sensor and pH-sensitive hydrogels as the actuator. The photobase 4,4-bis(dimethylamino)triphenlmethane leucohydroxide (malachite green carbinol base) is stored in a pair of artificial leaf veins which limit light exposure via shades oriented 45° to the tube surfaces and changes pH when exposed to UV light. Upon pH change, the pH-sensitive hydrogel, an epoxy hydrogel described by Yoshioka & Calvert [105], reversibly swells within a pair of novel flexible matrix composite (FMC) tubes in a twisted double T joint configuration. Owing to the twisted double T joint configuration of the tubes and limited light exposure of the artificial leaf veins, the biomimetic photo-actuator continues to bend until the light exposure of the photobase is maximized, analogous to the sun-tracking movements of plants. This biomimetic sun-tracking device acts as a proof of concept for chemical sensing, control and actuation with potential applications in solar tracking for solar power generation.

Figure 8.

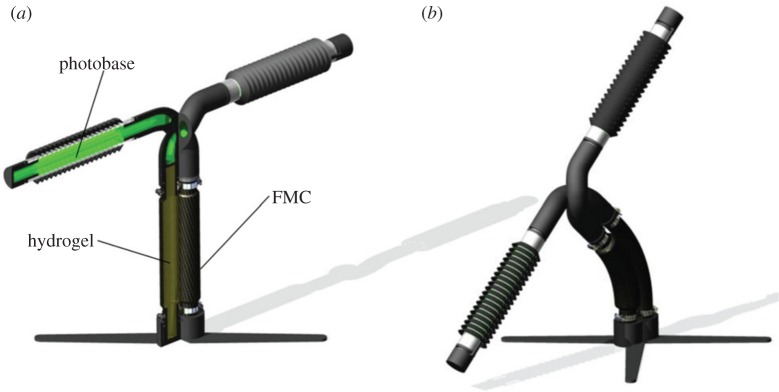
(a) Un-actuated device with quarter section removed to reveal internal structure. (b) Full device in actuated state showing orientation towards the light source. Adapted from [104]. (Online version in colour.)

7. Conclusion

Plants with fast thigmonastic movements have evolved the capability to quickly and dramatically alter their shapes in response to certain external stimuli. Although these mechanically induced active movements may appear to serve different purposes, from a protective mechanism (e.g. the folding of Mimosa leaflets) to a hunting function (for example, the rapid closure of the traps of Dionaea, Utricularia and Aldrovanda), some common ground exists. For instance, recent investigations have started to show that most thigmonastic movements result from differential changes of turgor pressure in the tissues, and the opening of certain key ion channels is often involved [8]. While some biophysical and biochemical mechanisms behind the fast motions of plants have been extensively studied, many questions remain unanswered. For example, how the action potentials are generated through the touch receptors in Dionaea remains to be investigated. Moreover, the source and role of action potentials in fast-moving plants, especially in carnivores other than Dionaea, are not completely understood. The coupling between these action potentials and molecular-level activities (which drive macroscopic movement) also remains not well understood. In Dionaea, recent studies suggest that it is the speed of ion transport, instead of water transport, that constrains the speed of osmotic flows; therefore, alternative mechanisms of perturbing the water potential in cells should be searched for [11]. Last but not least, the roles of actin cytoskeleton, microtubules and auxin during these active movements require elucidation.

Understanding the molecular, biomechanical, biochemical and electrophysical mechanisms among the diverse types of movements in plants may be the key to reveal the universal mechanisms governing plants' movements and how they evolve as a result of adaption to the ever-changing living environments [106]. However, it remains a grand challenge how to develop more realistic, multi-scale biomechanical models that incorporate various factors at the molecular, cellular, tissue and organism level. The difficulty in bridging the physical and biological aspects of the problem also arises from the fact that there is a lack of effective non-invasive experimental techniques for measuring the stresses inside cells and monitoring the transport of fluids (not to mention ions) inside the plant cells during these rapid movements [11]. The recent in vivo measurement of pressures and poroelastic properties in cells of Dionaea [39] and the measurement of mechanical stresses in developing embryos [107] seem to have paved way for further breakthroughs in investigating the underlying mechanisms in fast-moving plants. In addition, the comparisons between the behaviours and operating mechanisms in the moving plants, Mimosa, Dionaea, Aldrovanda, Utricularia and Drosera also bring forth interesting questions from the evolutionary biology and comparative biomechanics perspectives that remain to be addressed. The study of fast-moving plants will not only foster integration of physics, chemistry, biomechanics and molecular biology to address intriguing mechanisms involved in plants' fast motions, but also inspire various kinds of biomimetic designs for engineering applications.

Author contributions

Q.G., E.D., X.H., and Z.C. generated the idea for the manuscript, performed literature searches, helped to draft and edit it. S.X. and E.C. also performed literature searches, helped to draft and edit it.

Competing interests

The authors have no financial or personal relationships with other people or organizations that might inappropriately influence or bias the work.

Funding

This work is in part supported by the National Science Foundation of China (grant no. 11102040), Projects of International Cooperation and Exchanges NSFC (grant no. 11201001044) and Fujian University of Technology Research Fund (grant no. GY-Z15006). Z.C. acknowledges support from the Society in Science—Branco Weiss fellowship, administered by ETH Zürich.