A frequency-based hypothesis for mechanically targeting and selectively attacking cancer cells

Abstract

Experimental studies recently performed on single cancer and healthy cells have demonstrated that the former are about 70% softer than the latter, regardless of the cell lines and the measurement technique used for determining the mechanical properties. At least in principle, the difference in cell stiffness might thus be exploited to create mechanical-based targeting strategies for discriminating neoplastic transformations within human cell populations and for designing innovative complementary tools to cell-specific molecular tumour markers, leading to possible applications in the diagnosis and treatment of cancer diseases. With the aim of characterizing and gaining insight into the overall frequency response of single-cell systems to mechanical stimuli (typically low-intensity therapeutic ultrasound), a generalized viscoelastic paradigm, combining classical and spring-pot-based models, is introduced for modelling this problem by neglecting the cascade of mechanobiological events involving the cell nucleus, cytoskeleton, elastic membrane and cytosol. Theoretical results show that differences in stiffness, experimentally observed ex vivo and in vitro, allow healthy and cancer cells to be discriminated, by highlighting frequencies (from tens to hundreds of kilohertz) associated with resonance-like phenomena—prevailing on thermal fluctuations—that could be helpful in targeting and selectively attacking tumour cells.

1. Introduction

In the human body, there are trillions of (10 – 100 µm in size) cells: they have all the same structure and all originate from a single fertilized egg, the zygote, that differentiates into specialized cells. The structure of the human cell is a complex factory that makes proteins, including tissue materials [1]. It is constituted by three mechanically relevant systems: the cell membrane—the wall of the factory— a very deformable (0.1–1 kPa), approximately 10-nm-thick lipid bilayer; the membrane-confined viscoelastic gel-like cytosol; and the cytoskeleton—the bearing structure of the cell—an elastic network of protein filaments, embedded in the cytosol and anchored to the membrane, that maintains the cell's shape, protects the cell, enables cell motion (migration and adhesion), and mediates inner and outer loads. The main kinds of cytoskeletal filaments are microtubules (25-nm-diameter tubes made up of spiralling tubulin in two-part subunits), actin filaments (7-nm-diameter twisted double strands of the protein actin) and intermediate filaments (10-nm-diameter interwoven rope-strands), cell spreading and motility being driven by the assembly (polymerization) and disassembly (depolymerization) of branched actin filaments [2,3].

Overall, the cell behaves as a viscoelastic system [4–7]. However, differently from inorganic materials, biological soft matter is inhomogeneous and generally hierarchically organized [8–12] and thus reacts to mechanical stimuli by simultaneously involving several cell districts and processes, as well as protein filaments and supra-molecular and molecular structures present at different scale levels. The hierarchical organization of the cell works as a complex transducer device that converts macro-mechanical signals (pressure gradients, oscillation of organelles, etc.) to activate a biomechanical orchestra that steers a cascade of biochemical and physical coordinated events which govern the mechanobiology and the mechanosensing of the whole cell, regulating differentiation, growth, morphogenesis and—through polymerization/depolymerization-based cytoskeleton structural rearrangements—migration and adhesion phenomena affecting both single-cell dynamics and macroscopic behaviours of tissue and tumour masses [13–16].

Several scientific papers have in the last two decades been devoted to the study of the effects of mechanical stimuli on human cells, leading to a number of biological behaviours being observed whose essential processes are often still obscure or only partially understood. It has been, for example, observed that the effect of ultrasound upon single cells is significantly influenced by the frequency and the energy density applied [17]. Cell membrane damage was observed after ultrasound treatment in human blood cells and leukaemic cell lines [18], experimental studies demonstrating that malignant cells are sometimes much more susceptible and prone to be killed than normal cells when subjected to ultrasound exposure [19,20]. Depending on cell type and the sonication protocol, ultrasound seems to be able—if adequately modulated—to decrease cancer cell growth as well as to increase and stimulate wound healing [17]. In particular, increases in the proliferation rate for hcMEC and MDCK healthy cells after application of ultrasound at various energy density levels and prescribed frequencies have been experimentally observed and, after ultrasonic exposure, HT29 monitored cancer cells have exhibited cell death (apoptosis) [17]. Additionally, it has been seen that ultrasound inhibits cell proliferation of human myelomonocytic lymphoma U937 cells and stimulates MCF-7 breast cancer cells to undergo apoptosis [21,22], although the same investigators admit that ‘the molecular mechanism of ultrasound-induced apoptosis has not yet been clearly understood’. Recently, however, Mizrahi et al. [23] have experimentally observed significant cytoskeleton reversible remodelling dynamics when human airway smooth muscle cells were exposed to low-intensity ultrasound, these physical changes being caused by very small strains (10⁻⁵) at ultrasonic frequencies (10⁶ Hz) close to those caused by relatively large strains (10⁻¹) administered at physiological frequencies (10⁰ Hz).

The biologically relevant motion of intracellular particles, induced by ultrasonic waves, has been hypothesized to play a key role in the mechanism underlying the relative displacement between cell organelles and cytoplasm as an effect of the different inertias of the media. Although the question of how the mechanical vibrations act on the biological cell behaviour remains substantially an open issue, a study by Or & Kimmel [24] theoretically explores the possibility of resonance-like phenomena and suggests that mechanically induced oscillations—larger than maximal thermal fluctuations—might kindle high-frequency (compatible with low-intensity therapeutic ultrasound (LITUS) ranges) strain regimes, potentially able to determine fatigue-like phenomena in cells. In particular, the frequency resonance hypothesis assumes that the absorption of ultrasound by proteins and protein complexes may directly alter signalling mechanisms within the cell, determining conformational shift or disrupting multimolecular complexes at critical frequencies around both 45 kHz and 1 MHz [25].

On the other hand, very recently, experimental studies have been performed on individual cancer and healthy cells of different types, demonstrating that the former were about 70% softer than the latter [26–36]. It seems that the increase in cell deformability is directly related to cancer progression, as observed by Ketene et al. [34] in the case of a transformed phenotype from a benign (non-tumorigenic) cell to a malignant (tumorigenic) one. Ploidinec et al. [37], by resolving the nanomechanical signatures of defined stages of tumour progression, also highlight that cancer evolution is associated with a significant softening of tumour epithelial cells in comparison with normal mammary epithelium, including metastasis, hypothesizing that metastatic cells gain their migration capabilities by acquiring a certain degree of flexibility and deformability to escape their original niche. As assumed by Pachenari et al. [38], metastatic cells could be induced to become mechanically softer than healthy cells to pass through rigid capillaries whose diameters are smaller than tumour cells, this deformability playing a crucial role in the potency of tumour cells to form neoplastic foci. This seems to be corroborated by experiments, as found by Abdolahad et al. [39], who show that the fraction of entrapment of higher metastatic cancer cells (in carbon nanotubes) is significantly greater than lower metastatic grades.

These results, which seem to be confirmed regardless of the cell lines examined and independent of the specific measurement technique used for determining the mechanical properties (Atomic Force Microscopy, optical tweezers, etc.), lead to possible new scenarios for biomechanical applications in medicine [40]. At least in principle, the above-mentioned differences in cell stiffness might be exploited to create mechanical-based targeting strategies for discriminating neoplastic transformations within human cell populations, paving the way for innovative complementary tools for cell-specific molecular tumour markers and, hopefully in the future, for possible applications in diagnosis and treatment of cancer diseases.

By recalling the above-mentioned experimental evidence for the discrepancies in deformability between tumour and normal cells, with the aim of at an early stage characterizing—and gaining insights into—the frequency response of single-cell systems to mechanical stimuli (typically LITUS), a generalized viscoelastic paradigm which combines classical (say Voigt, Maxwell and standard linear Kelvin (SLK)) and spring-pot-based models is introduced for modelling the problem (§2), by starting from the work by Or & Kimmel [24]. To this purpose, any detail relating to the complex structural organization of the cells in which the nucleus, cytoskeleton, elastic membrane and gel-like cytosol govern and interact with the cascade of events at the basis of the mechanobiology of the system has necessarily been neglected.

After preliminary sensitivity analyses aimed to catch both qualitative and quantitative remarks on mechanically stimulated single-cell systems (see §3), the viscoelastic modelling was confined to cell lines whose mechanical properties have been experimentally measured in the literature with reference to healthy cells and their cancer counterparts. The theoretical results, illustrated in §4, will show that the differences in stiffness—at least in principle—allow us to mechanically discriminate between tumour and normal cells, the critical frequencies associated with oscillation magnitude peaks (from tens of kilohertz to hundreds of kilohertz) confirming that mechanical resonance-like phenomena can prevail with respect to thermal fluctuations and thus could be helpfully used for targeting or ad hoc altering the functions of tumour cells.

2. Frequency response of one-dimensional single-cell viscoelastic systems

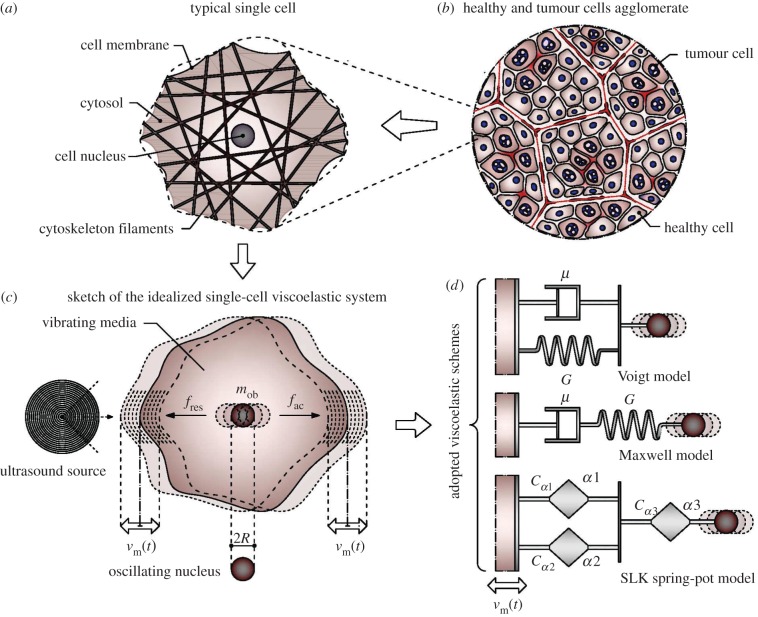
By starting from an approach recently proposed by Or & Kimmel [24] to analyse a vibrating cell nucleus in a viscoelastic environment excited by LITUS, let us consider the single-cell dynamics through an oscillating mass embedded in a viscoelastic medium (figure 1). A spherical rigid object with radius R is therefore considered to represent the nucleus, in which the whole mass of the cell is assumed to be concentrated, and the cell is also assumed to behave as a homogeneous and isotropic viscoelastic medium: in this way, the system can be characterized by one degree of freedom activated by a prescribed time-varying LITUS-induced velocity law of the form

2.1

where v_m is the velocity assigned to the medium, v_m0 represents the complex velocity phasor and ω₀ = 2πf is the angular frequency of the oscillations, f being the frequency measured in hertz. By essentially following the strategy suggested in the above-mentioned work, the equation of motion can be written as

2.2

where t is the time, f_m represents the inertial force, m_ob is the nucleus mass whose density is ρ_ob, and u_ob is the associated displacement. Furthermore, f_ac is the basic driving force in the system, due to the acoustic pressure gradients that are induced by the ultrasound transducer. In this case, where the object is very small compared with the acoustic wavelength, the acoustic force can be assumed to have the simple form of a force which would act on a sphere of the same size in the absence of the object [41]; this permits us to write

2.3

where ρ_m is the density of the medium. Dimensional analyses suggest that the convective term is small and therefore, in equation (2.3), the absence of spatial variability allows us to use regular time-differentiation d/dt instead of the substantial derivative D/Dt [24].

Figure 1.

Cartoon of the idealized single-cell system: (b) healthy and tumour cells agglomerate; (a) typical cell unit, with nucleus and cytoskeleton structure embedded in the cytosol and confined by the lipid bilayer cell membrane; (c) idealized single-cell system with cell nucleus oscillating in a viscoelastic environment under the action of a radiating ultrasound source; and (d) adopted viscoelastic schemes (Voigt, Maxwell and generalized spring-pot-based SLK models).

Finally, f_res is the response force which is applied on the object by its surroundings as a result of their relative motion; as a consequence, the response force depends upon the rheological properties of the medium in which the object is embedded. In particular, in order to have a fundamental insight on different—and more complex—behaviours of single-cell systems, this force will be written as parametrically depending on several geometrical and mechanical features of interest. The analyses will be conducted by adopting two quasi-standard viscoelastic models, the classical Voigt and Maxwell ones, and finally considering a generalized SLK model, where the dashpot and springs are substituted by the so-called spring-pot systems, widely adopted in several recent studies to interpret peculiar responses of biological structures [42].

Additionally, differently from the strategy used by Or & Kimmel [24] to solve the differential problem at hand, the Laplace transform will be used here by exploiting the well-known classical relationship between the Laplace and Fourier transforms, that is, enabling us to directly obtain the response of the systems in terms of frequency.

With reference to the initial conditions, in all the cases the object is initially at rest, that is,

2.4

Then, by Laplace transforming equation (2.2), one obtains

2.5

where all the transformed terms are denoted with capital letters and s is the Laplace variable. As a consequence, in equation (2.5) F_ac is the Laplace transform of the acoustic force f_ac in equation (2.3), leading to

2.6

2.1. Cells behaving as a quasi-standard Voigt model

In the Voigt idealization, viscous and elastic elements are connected to each other in parallel (figure 1). The response force is then obtained by simply summing up the contributions of the two elements as follows:

2.7

where f_µ is the viscous force response and f_G represents the elastic contribution. In particular, the viscous term is modelled here following Basset [43] and Landau & Lifshitz [44], as also suggested by Or & Kimmel [24] for the case of rapid vibration of a rigid object in viscous fluids. The explicit expression can thus be written as

2.8

with μ and v the dynamic and the kinematic viscosities of the medium, respectively, and the velocities It is worth highlighting that the structure of the viscous response force assumed here differs from the classical Stokes force because in equation (2.8) there are frequency-dependent terms and, additionally, there appears to be a spurious inertial contribution that Brennen [45] termed added mass, that is, p (p = 2 in this case) is the number of elements in parallel, here used to solve the ambiguous situation raised by Or & Kimmel [24], so avoiding the duplication of the added mass contribution in the viscoelastic system at hand.¹

With reference to the elastic force, f_G, as proposed by Ilinskii et al. [46], is explicitly written as follows:

2.9

Analogously to the previous case, the elastic response differs from the classical Hooke law: in fact, rigorously speaking it does not represent a pure elastic contribution and—to take into account the effects of rapid fluctuations determined by the dynamic interaction of the system with the environment which drive the response towards the actual physical behaviour—additional terms appear in (2.9). In particular, these contributions are here constituted by the so-called virtual friction (a dissipative term represented by ) and, again, the added mass (an inertial term), as suggested by Ilinskii et al. [46]. In equation (2.9), G is the elastic shear modulus of the medium, assumed to be about a third of the corresponding Young's modulus as a consequence of the hypothesis of incompressibility, while u_m represents the vibrational displacement of the medium. Hereinafter, the following parameters are conveniently introduced:

2.10

and

2.11

and a further dimensionless constant is also defined as follows:

2.12

with Finally, the quasi-standard Voigt viscoelastic constitutive law is written as

2.13

Laplace transforming the response force (2.13), one has

2.14

and, replacing (2.14) and (2.6) in (2.5) and after some algebraic manipulations, the final form of the equation is obtained as

2.15

where ΔU = U_ob − U_m. By solving equation (2.15), the in-frequency analytical solution in terms of amplitude of the relative displacement ΔU between the cell nucleus and the environment hence takes the form

2.16

2.2. Cells behaving as a quasi-standard Maxwell model

In the Maxwell system, viscous and elastic elements are connected in series (figure 1). In order to obtain the response in terms of relative displacement ΔU, one has to start by imposing the isostress condition, that is,

2.17

and then to write the compatibility condition, that is, that the sum of the relative displacement due to the elastic and to the viscous components equates to the relative displacement

2.18

where F_µ and F_G constitute the Laplace transforms of the viscous and the elastic response forces given in equations (2.8) and (2.9), respectively. As a consequence, one has

2.19

from which viscous and elastic components of the relative displacement are separately given as

2.20

By recalling F_res from equation (2.5) and by taking into account equation (2.20), the analytical solution for the frequency response of the quasi-standard Maxwell system is finally obtained as follows:

2.21

2.3. Cells behaving as a spring-pot-based quasi-standard linear Kelvin model

2.3.1. Spring-pot model involving virtual friction and added mass

The so-called spring-pot model is a viscoelastic system in which the constitutive law is defined through fractional derivatives. The concept of the fractional derivative can be dated back to 1695 during correspondence between de L'Hospital and Leibniz. Their purpose was to give an answer to the famous question: ‘What does the derivative dⁿf(x)/dxⁿ mean if n = 1/2?’. From that time, a branch of mathematics named fractional calculus has been developed and it is to date considered a generalization of the commonly used integer-order differentiation and integration. The basic idea is to look at a fractional derivative as the inverse operation of a fractional integral, as suggested by Riemann–Liouville. Caputo [47] developed a concept of the fractional derivative, namely , which could be used in the ‘real world’:

2.22

where f(t) is integrable in [a, t] and Γ is the Euler Gamma function.

The idea to use fractional derivatives in viscoelasticity can be traced back to the work by Nutting [48]. He noted that, from the best fitting of experimental curves, the relationship between deformation and time could be described by a power law, i.e. 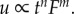In 1949, Blair & Caffyn [49] justified analytically this experimental law through fractional derivatives, introducing a new analytical model in viscoelasticity: the spring-pot model. Successively, a number of scientific papers have been produced for approaching viscoelastic problems in several classical as well as pioneering engineering and physical fields (e.g. [42,50]).

For this purpose, the spring-pot model is substantially that firstly introduced by Blair & Caffyn [49], but it is here generalized to take into account the virtual friction and the added mass by means of the suitable introduction of additional contributions. In particular, the response spring-pot force f_SP is defined as follows:

2.23

in which 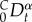represents Caputo's fractional time-derivative of order α, with defined over the time interval (0, t), C_α is a frequency-dependent coefficient re-written by following Koeller [51]:

2.24

while the dissipative and the inertial terms were included by assuming for them the following simplest form:

2.25

in this way obtaining that in the limit cases, say α = 0 and α = 1, the Or & Kimmel [24] elastic and viscous models are, respectively, reproduced.

Therefore, by substituting equation (2.23) into equation (2.5) and additionally exploiting the fractional derivative rule which leads to the Laplace transform preserving the ordinary (integer) derivative law for the Laplace variable, i.e. , the spring-pot frequency response of the system is finally obtained in terms of relative displacement as follows:

2.26

2.3.2. Generalized standard linear Kelvin model incorporating spring-pot systems

Among the fundamental viscoelastic schemes, SLK models are often used to enrich Voigt and Maxwell ones by building up in series a Voigt system and an elastic spring. An alternative to this configuration is represented by the Maxwell–Wiechert model—a Maxwell system in parallel with an elastic spring—from which the most general form of the linear viscoelastic scheme can be derived through the Prony series method. However, both of the above-mentioned models can be seen as special cases of the so-called standard linear solid systems [4].

Since spring-pot can be physically thought of as a viscoelastic system with the special capability of smoothly generating intermediate behaviours as the constitutive parameter α moves from zero (purely elastic behaviour) to 1 (purely viscous behaviour), a generalized SLK model is here defined by substituting a spring-pot to each dashpot and spring in the classical SLK model, as illustrated in figure 1. In this straightforward way, by also suitably including the additional terms of virtual friction and added mass, a powerful low-parameter linear viscoelastic system is finally obtained and the related in-frequency response derived in closed-form: as a result, all the above-mentioned simpler viscoelastic schemes and analytical solutions, including those given in [24], are found as limit or special cases of this generalized spring-pot-based SLK system.

Therefore, let us consider the generalized quasi-SLK model as illustrated in figure 1. Owing to the configuration of spring-pot elements, it is possible to write forces and displacements as follows:

2.27

and

2.28

where f_SLK is the resultant force of the entire system, f_P = f_SP1 + f_SP2, f_SP1, f_SP2 and f_SP3 representing the forces due to the three spring-pots shown in figure 1, whose explicit expressions are given in equation (2.23). Also, the terms appearing in (2.28) are the displacements, being Δu_P = Δu_SP1 = Δu_SP2.

By Laplace transforming f_P and f_SP3, the fractional derivative rule 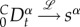gives

2.29

and

2.30

After standard manipulations, it is possible to obtain

2.31

and

2.32

By recalling F_res from equation (2.5), one finally attains the analytical solution of the in-frequency response of the generalized SLK system as follows:

2.33

The obtained generalized SLK model, which also takes into account virtual friction and added mass, is then capable of reproducing all the viscoelastic models presented in [24], including viscous and elastic ones; additionally, modulating the spring-pot parameters—say the order of the fractional derivative α—a vast number of viscoelastic ‘intermediate’ systems might be obtained, as summarized in table 1 for some selected cases that will be afterwards used in the simulations.

Table 1.

Synoptic frame illustrating how to set the parameters characterizing the proposed generalized quasi-SLK viscoelastic model, in order to replicate elastic, viscous, Voigt (V), Maxwell (M) and standard linear Kelvin (SLK) limit cases, as well as the three intermediate chosen configurations, SLK_1, SLK_2 and SLK_3, employed to perform the subsequent analyses.

	α1		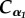α2		α3
elastic	0	→∞	—	—	0	c0G
viscous	0	→∞	—	—	1	c1µ
V	0	c0G	1	c1µ	0	→∞
M	0	→0	1	c1µ	0	c0G
SLK	0	c0G	1	c1µ	0	c0G
SLK_1	0.5	C0.5	1	c1µ	0	c0G
SLK_2	0	c0G	0.5	C0.5	0	c0G
SLK_3	0	c0G	1	c1µ	0.5	C0.5

3. Sensitivity analyses: qualitative insights into and the resonance hypothesis of single-cell dynamics

With the aim of deriving both quantitative information and qualitative insights into the frequency response of single-cell systems through simple (one degree of freedom) viscoelastic schemes, sensitivity analyses have been performed by generalizing some models successfully employed by Or & Kimmel [24]. To explore possible different behaviours and enrich the in-frequency responses of these single-cell systems, a wide class of viscoelastic paradigms have been in particular considered by introducing a new generalized SLK model and constructing related analytical solutions. To gain realistic physical results, the mechanical properties of actual cells have been deduced from consolidated literature data and, to untie the key aspects of the cell response from the specific choice of the viscoelastic model, the sensitivity analyses have been conducted by querying different schemes.

Actually, to measure physical and in particular biomechanical properties at a single-cell-scale level (i.e. stiffness, ultimate strain, strength, toughness, etc.) is a difficult and often challenging task. This is fundamentally due to several obstacles that might emerge when dealing with complex microstructures characterizing living systems, difficulties essentially arising from the fact that, during the test, intrinsic changes of the biological structure, movements of its mechanical apparatus and biochemical responses can all in principle interfere with the actual property being measured. Furthermore, for example at the single-cell scale, mechanical features may be drastically different from one site to another, as a consequence of reorganization dynamics activated by adhesion, migration and polymerization–depolymerization processes which change the internal configuration of the cytoskeleton and, as a result, may determine non-homogeneous distribution of stiffness and deformation [2,3,52]. In this respect, Lekka et al. [31] show, for instance, that depth of indentation, the substrate on which the cells are spread, the load rate as well as the position and time of cell poking might all influence the stiffness atomic force microscopy measurements. This implies that the physical measurements generally can be strongly dependent on the technique used and, as a consequence, quantitative estimations may cover wide ranges. Several experimental tests [26–36,53] have in fact shown that Young's modulus of the cytoplasm of different (healthy and cancer) cell lines can oscillate from about 100 Pa to 10 kPa. Also, the size of the cell nucleus is of the order of a few micrometres and may depend on the cell size [54]. Further studies on the overall cell viscosity demonstrated that rheological properties may span over five orders of magnitude, probably because of the effect of the high dependence of the response on frequency bands and measurement techniques. Indeed, as highlighted in the paper by Or & Kimmel [24], while the viscosity of aqueous cytoplasm was found to be similar to that of water in fibroblasts, say μ = (1.3 ± 0.1) × 10⁻³ Pa s [55], and slightly higher in smooth muscle cells, e.g. μ = (12.5 ± 5.5) × 10⁻³ Pa s [56], the apparent viscosity of blood granulocytes was instead estimated to be substantially higher, with about μ = (210 ± 100) Pa s [57].

This said, by taking into account the above-mentioned literature experimental results which suggest that the measured mechanical features of cells can oscillate within wide ranges, the sensitivity analyses of the frequency response of single-cell units have been performed by making variable the overall cell Young's modulus, the viscosity of the cytosol and the nucleus size in a way to cover the whole range spanned by the literature biomechanical data for different cell lines. Except for the information used here for parametrically describing the cell stiffness, the remaining physical data used for the analytical simulations are mainly referred to those suggested in [24].

Thus, with respect to the notations already introduced to describe the key parameters in the proposed generalized SLK viscoelastic model, all the analyses have been conducted by using the vibration velocity amplitude of the medium v_m0 = 0.12 ms⁻¹, derived for a plain progressive wave with acoustic intensity of 1 W cm⁻² to which is associated an intensity with speed of sound c = 1500 ms⁻¹ at room temperature [58]. The mass density of the medium is taken to be that of water at room temperature, the nucleus being considered 30% more dense than the environment, as generally assumed in the literature [59].

In particular, the analyses have been performed by making reference to six representative viscoelastic schemes, say Voigt, Maxwell, SLK and three further generalized SLK models modified by, respectively, placing in position 1, 2 and 3 spring-pots with α = 0.5, all enhanced by introducing the effects of virtual friction and added mass.

The analytical results have been obtained by making use of the symbolic code Wolfram Mathematica [60] and have been plotted in the frequency domain of interest for possible applications in biomedical engineering, that is, 1 kHz ≤ f ≤ 100 MHz, showing the frequency response of the systems in terms of relative displacement amplitude, |ΔU|, which represents, in the time domain, the amplitude of the ultrasound-induced relative oscillations between the cell nucleus and its environment.

The most significant results are all summarized in figures 2–4, where cell stiffness, viscosity and nucleus size have been separately assumed to vary over the ranges experimentally reported in the scientific studies; in each group of sensitivity analyses the other complementary parameters were kept fixed and were chosen equal to those most commonly encountered in the literature, that is, Young's modulus E = 2100 Pa [26], the mean nucleus radius R = 1 µm [1] and the viscosity of water μ = 10⁻³ Pa s [24].

Figure 2.

Sensitivity analyses for the frequency response of the cyclic displacement amplitude of a spherical object (R = 1 µm) with respect to its surroundings with low viscosity (μ = 10⁻³ Pa s) and varying Young's modulus (E = 100, 500, 1000, 5000, 10 000 Pa): (V) Voigt; (M) Maxwell; (SLK) standard linear Kelvin; (SLK_1) generalized SLK with spring-pot in position 1, (SLK_2) 2 and (SLK_3) 3, with α = 0.5.

Figure 3.

Sensitivity analysis for the frequency response of the cyclic displacement amplitude of a spherical object (R = 1 µm) with respect to its surroundings with stiffness (E = 2100 Pa) and varying viscosity (μ = [10⁻³ ∼ 10] Pa s): for abbreviations see figure 2.

Figure 4.

Sensitivity analysis for the frequency response of the cyclic displacement amplitude of a spherical object with respect to its surroundings with stiffness (E = 2100 Pa), viscosity (μ = 10⁻³ Pa s) and varying size of the object (R = 0.1, 1, 5, 10, 20 µm): for abbreviations see figure 2.

In particular, in figure 2 the frequency response of the relative displacement between the environment and the embedded spherical object representing the cell nucleus, with radius R = 1 μm, is shown by assuming low viscosity (i.e. μ = 10⁻³ Pa s) and varying cell stiffness through five selected Young's moduli, coherently deduced from the literature and ranging from E = 100 Pa to E = 10 kPa. Analogously, figures 3 and 4 illustrate again the results in terms of displacement amplitude versus frequency, for the six viscoelastic models, respectively, assuming stiffness fixed to E = 2100 Pa and varying viscosity (choosing five values in the range μ = 10⁻³ Pa s to μ = 10 Pa s) and nucleus radii spanning the actual physical range, that is, from R = 0.5 µm to R = 10 µm.

The analytical outcomes obtained from the sensitivity analyses allow us to highlight some relevant preliminary remarks which guide the subsequent simulations performed by specializing the viscoelastic models in order to discriminate mechanical frequency responses of healthy and cancer cells. In particular, the most significant results can be summarized in the following points.

First of all, some relevant qualitative behaviours can be recognized in the results shown in figures 2–4, all represented by plotting relative displacement amplitude versus frequency, that is: (i) increasing peak frequencies and associated decreasing maximum displacements as stiffness of the system increases (figure 2), (ii) decreasing maximum displacement peaks with moderate frequency shifts as viscosity increases, with some slight differences in Voigt and SLK_3 models that leave the trend unaltered, as shown in figure 3, and (iii) increasing maximum displacement peaks with decreasing corresponding frequencies as the cell size increases (i.e. the nucleus radii increase), as illustrated in figure 4.

Importantly, with the exception of the sole limit cases (extremely large or small cell nuclei, significantly low elastic moduli and highest viscosity values), in all the investigated models, the results show that the peak frequency and the corresponding maximum vibrational amplitudes |ΔU| can be recognized to lie within the range 10⁴ – 10⁶ Hz, an interval analogous to that found in the experiments by Johns [25] and Lejbkowicz & Salzberg [20], which thus confirms that resonance-like responses can be obtained by stimulating cells with ultrasound.

In agreement with the Or & Kimmel outcomes [24], the obtained results derived by conducting the simulations with different viscoelastic models, where the Young's modulus variation has been additionally taken into account, confirm that mechanical (e.g. ultrasound-induced) vibrations |ΔU| are mostly comparable to or greater than spontaneous thermal fluctuations. This happens for both the case of a purely elastic solid, where—according to Ohshima & Nishio [61]—the mean square displacement with respect to its equilibrium position can be analytically assumed to obey the equation and viscous media, in which the mean relaxation distance is [62], where k_B is the Botzmann constant, T is the absolute temperature and v₀ is the initial velocity. To prove this numerically, it is sufficient to verify that, by making the cell nucleus radii and both the elastic and the viscous moduli appearing in the equations above variable in the ranges of interest, the codomain of the square root of the mean square displacement is (2 × 10⁻¹⁰, 9 × 10⁻⁹) and the codomain of the mean relaxation distance is (6 × 10⁻¹⁵, 2 × 10⁻⁸), the upper bounds of both the intervals giving values comparable to or smaller than the peaks of mechanical vibration amplitudes theoretically obtained from the sensitivity analyses (figures 2–4).

Moreover, it has been experimentally demonstrated that cyclic loads at low frequencies, associated with strain levels in the range (10⁻², 10⁻¹), may induce mechanical and configurational alterations or rupture in living cells (see table 1 in [24]). Analogous effects can also be observed at relatively high frequencies, in the case of ultrasound-stimulated cells, as experimentally shown by Lejbkowicz & Salzberg [20] and Mizrahi et al. [23]. In particular, Mizrahi et al. [23] show that these physical changes are caused by very small strains (10⁻⁵) at ultrasonic frequencies (10⁶ Hz) and are close to those caused by relatively large strains (10⁻¹) at physiological frequencies (10⁰ Hz). With respect to this work, by taking into account the relative displacement peaks between the cell nucleus and the environment obtained from analytical results, a rough estimate of the equivalent uniaxial strain can be calculated as 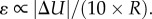Therefore, by considering that cell nuclei may vary within the range (2 × 10⁻⁷, 10⁻⁵) m and vibrational displacement amplitudes are found ranging from 10⁻⁹ m to 10⁻⁷ m (with the exception of the extreme cases of fluid-like behaviours), strains from 10⁻⁵ up to 10⁻¹ can be reached. As a consequence, at the ultrasound frequencies (and/or by increasing the ultrasound radiation intensity), after a few seconds of exposure, cell configurational alterations or disruptions due to fatigue-like phenomena might actually be expected.

Importantly, the peak frequencies theoretically obtained by means of the implemented viscoelastic models may span from tens of kilohertz to 1 MHz, both being the frequency extreme values of this interval involved as critical frequencies at which it has been experimentally observed that cells show relevant biological responses as a result of prevailing mechanical effects on thermal ones [17,25].

Further details of the results can be found in the captions to the figures.

4. Frequency-based detection of cancer and healthy cells at the single-cell level

On the basis of the sensitivity analyses, it has been demonstrated above—by means of theoretical arguments—that single cells, modelled through different elementary viscoelastic systems, exhibit frequencies (from tens to hundreds of kilohertz) associated with oscillation magnitude peaks which confirm that mechanical resonance-like phenomena induced by ultrasound can prevail with respect to thermal fluctuations, a fact that also suggests that the cell structural response can be recognized as a candidate for playing a key role in some experimentally observed biological effects [17,20,23,25].

On the other hand, as recalled above, independent literature results have in recent years shown that, regardless of measurement techniques and cell lines, cancer cells are always significantly softer than their healthy counterparts, a fact ascertained by biologists (table 2). Given that there are very few common factors shared by tumour cells (this is the main reason for the success of molecular markers) this stiffness discrepancy between normal and tumour cells constitutes an extremely relevant property.

Table 2.

Actual stiffness for different lines of healthy and cancer cells, measured by means of several techniques, as described in the references reported in the first column.

			stiffness (kPa) ± s.d.
investigator	year	cell line	healthy	cancer
1. Lekka et al. [31]	2012	human bladder HCV29	3.09 ± 0.42
		human bladder T24		0.83 ± 0.27
2. Rebelo et al. [32]	2013	human kidney non-tumorigenic RC-124	9.38
		human kidney carcinoma A-498		7.41
		human kidney adenocarcinoma ACHN		2.48
3. Lekka et al. [30]	2012	human prostate non-tumorigenic PZHPV7	3.09 ± 0.28
		human prostate metastatic carcinoma LNCaP		0.45 ± 0.21
		human prostate metastatic carcinoma Du145		1.36 ± 0.42
		human prostate adenocarcinoma PC-3		1.95 ± 0.47
		human breast normal A184A1	2.26 ± 0.56
		human breast cancer T47D		1.20 ± 0.28
		human breast adenocarcinoma MCF7		1.24 ± 0.46
4. Prabhune et al. [33]	2012	human thyroid S748	2.211 ∼ 6.879
		human thyroid anaplastic carcinoma S277		1.189 ∼ 1.365
5. Ketene et al. [34]	2012	mouse early ovarian surface epithelia MOSE		0.549 ± 0.281
		mouse late ovarian surface epithelia MOSE		1.097 ± 0.632
6. Nikkhah et al. [35]	2010	human breast normal mammary epithelium MCF10A	1.13 ± 0.84
		human breast metastatic tumour MDA-231		0.51 ± 0.35
7. Faria et al. [36]	2008	human prostate benign BPH	2.797 ± 0.491
		human prostate adenocarcinoma PC-3		1.401 ± 0.162
		human prostate metastatic carcinoma LNCaP		287 ± 52
8. Lekka et al. [29]	1999	human epithelial normal Hu609	9.7 ± 3.6
		human epithelial normal HCV29	7.5 ± 3.6
		human epithelial cancerous Hu456		1.0 ± 0.6
		human epithelial cancerous T24		0.8 ± 0.4
		human epithelial cancerous BC3726)		0.3 ± 0.2
9. Li et al. [28]	2008	human breast epithelial non-malignant MCF10	1.15 ± 0.52
		human breast epithelial malignant (MCF-7)		0.614 ± 0.237
10. Cross et al. [26]	2007	human lung benign carcinoma	2.10 ± 0.79
		human lung tumoral carcinoma		0.56 ± 0.09
		human breast benign ductal adenocarcinoma	1.93 ± 0.50
		human breast tumoral ductal adenocarcinoma		0.5 ± 0.08

With the aim of both gaining information about the possibility of mechanically targeting healthy and cancer cells and quantitatively estimating the frequency bands at which detection could in principle be realized, in this section the viscoelastic schemes, already used above for the sensitivity analyses, are specialized with reference to the stiffness values actually experimentally measured and reported in the literature for a number of healthy and cancer cell lines (table 2). In particular, as an example, figure 5 illustrates how benign and tumour mesothelial cells extracted from carcinoma of the lung [26] would behave in terms of relative displacement amplitude versus frequency. The outcomes show that, in all the six examined viscoelastic models, the difference in stiffness between the results is sufficient for recognizing the corresponding significant frequency shifts defined as in-frequency distances between the resonance-like oscillation magnitude peaks. Importantly, a relevant difference is also reflected in the graphics of the obtained results in terms of relative displacement amplitudes, which would in principle ensure the possibility of selectively targeting tumour cells if—for example, by means of ultrasound—the radiation is applied at a prescribed intensity and at a frequency close to the resonance-like frequency of the cancer single-cell system, an effect amplified by the fact that, due to the frequency shift described above, the normal cell always exhibits a smaller displacement amplitude at the tumour critical frequency.

Figure 5.

Frequency response, in terms of relative displacement amplitude versus frequency, of healthy (H) and cancer (C) mesothelial cells extracted from carcinoma of the lung, simulated through the proposed viscoelastic schemes: (R = 1 µm; μ = 10⁻³ Pa s; measured cancer Young's modulus: E = 560 Pa; measured healthy Young's modulus: E = 2100 Pa). The six graphics refer to the following models: (V) Voigt; (M) Maxwell; (SLK) standard linear Kelvin; (SLK_1) generalized SLK with spring-pot in position 1, (SLK_2) 2 and (SLK_3) 3, with α = 0.5. The grey regions highlight the difference in frequency between peaks in cancer and healthy cells. Dashed lines represent the displacement amplitudes corresponding to the thermal fluctuations, always smaller than the mechanical ones.

To stress this aspect, figure 6 collects—in the form of histograms—all the theoretical outcomes obtained by making reference to the viscoelastic properties experimentally measured in numerous independent literature works for six healthy and cancer cell lines (table 2). In particular, the results are summarized by highlighting—for each cell line—the difference in frequencies at which the oscillation amplitude peak occurs, in both cancer and healthy cells, and averaging the results—for the sake of simplicity—over each viscoleastic scheme adopted for performing the simulations. The bar chart confirms the possibility of observing the relevant differences, in terms of resonance-like frequencies, by comparing cancer and healthy cell mechanical responses; these differences are registered for all the cell lines examined, regardless of the implemented viscoelastic model and at frequencies always compatible with LITUS.

Figure 6.

Bar chart with a synopsis of the theoretically derived in-frequency responses of healthy and cancer cells whose mechanical properties have been experimentally measured: the histograms compare peak frequencies for each tumour and normal cell line pair examined, by averaging over all the results obtained from the six viscoelastic schemes used. The first column reports the cell type and the corresponding literature reference from which the data are deduced; the last two columns give some quantitative results in terms of the ratio between maximum ((Δf)_max/f_H) and minimum ((Δf)_min/f_H) frequency shifts over the reference resonance-like frequency of the healthy cell, for each cell line.

Finally, by keeping in mind possible practical uses for targeting tumour cells, the last two columns in figure 6 report a synopsis of the most important quantitative results obtained from the analyses performed, showing that both the ratios Δf/f_H between the maximum and minimum frequency shifts and Δf = f_H − f_C over the reference healthy resonance frequency f_H (occurring with respect to SLK_1 and Voigt viscoelastic models) would allow in principle the peak frequencies in a real case to be quantitatively discriminated. As a matter of fact, the reference healthy frequencies f_H are indeed about 40 – 400 kHz, while the frequency shifts oscillate between about 20 and 250 kHz. This seems to explain the experimental findings in [20] and also to suggest that, for a practical (therapeutic) purpose, a biomedical device could be designed to selectively determine ultrasound-induced large vibrations in tumour cells, once wave frequencies were tuned from 25% to 60% of the reference healthy frequency.

5. Conclusion, limitations and future perspectives

Cancer is a genetic disorder that involves the transformation of benign body cells into malignant rapidly dividing cells through abnormal changes called hyperplasia and dysplasia. In hyperplasia, there is an increase in the number of cells that generally leaves organs or tissues normal when observed under a microscope; in dysplasia, the process is still accompanied by an altered proliferation programme, but the cells look generally abnormal. However, rigorously speaking, hyperplasia and dysplasia may or may not become cancer, even if they represent propaedeutic steps towards cancer disease.

Tumours are constituted by a complex mix of neoplastic (cancer) and normal (healthy) cells. At this scale, regardless of the cell line, there are very few common factors in solid tumours: two of these are the overall abnormal growth of the tissues and the anomalous regression in cell differentiation, prodromal to cell spread and metastasis. To distinguish between anomalous malignant and benign cell growth is however often impossible in small tissues.

To date, in the absence of alternative ways for recognizing and targeting cancer cells, molecular markers are widely employed to detect tumours. As a matter of fact, non-specialized, back-differentiated and generally potentially metastatic cells are in the vast majority of the cases excluded by this type of targeting, because molecular markers need to deal with highly specialized cells, which are normally less aggressive than their non-specialized counterparts. However, regression towards less specialized cell types often camouflages cancer cells as normal less differentiated cells, a fact that generally forces the markers to be changed.

In this study, by exploiting some consolidated literature results that have demonstrated that tumour cells are significantly softer than the healthy ones, independent of the cell line and regardless of the measurement techniques used for determining the cell stiffness, the frequency response of single-cell systems has been investigated by using both consolidated and generalized spring-pot-based viscoelastic schemes. After conducting a sensitivity analysis with respect to the cells' physical and geometrical parameters, the theoretical models have been finally specialized to cancer and healthy cells, whose mechanical properties were ex vivo or in vitro experimentally measured.

The results have shown that a mechanical-based means of targeting cancer and healthy cells may actually be envisaged. The theoretical outcomes have in fact highlighted that, for all the cell lines examined and independently of the viscoelastic scheme adopted to simulate the cells' response, normal and tumour cells' peak frequencies can be clearly distinguished. Importantly, they mostly fall within the range (10⁴, 10⁶) Hz, an interval compatible with LITUS, which is already widely employed for medical applications. Peak frequency values outside this interval are found for the sole cases associated with extreme limit situations, that is, both when the cells behave as fluid-like (Maxwell) viscoelastic materials and exhibit the highest elastic modulus and/or large nucleus sizes (in this case, the peak frequency tends to disappear) and when the cells behave as Voigt viscoelastic systems and contemporaneously are characterized by the lowest stiffness or highest viscosity (in this case, the peak frequencies move towards frequencies slightly lower than 10⁴ Hz). It is worth noting that both these theoretical limit situations are quite unrealistic, because they assume that essentially the cells would behave as a viscous fluid; in the first case the Maxwell model intrinsically representing a fluid-like material and in the second case the Voigt model with high viscosity and low stiffness still representing a fluid-like behaviour.

Nevertheless, some potential limitations of the proposed modelling approach have to be highlighted.

First, a recent experiment seems to have ascertained that the mechanical properties might intrinsically change in cancer cells when they are found in suspension (or non-spread) and adherent, as a result of specific active cytoskeleton-mediated features [63]. In particular, these structural changes, which would seem to be induced by the reorganization of cytoskeletal intermediate filaments and promoted by specific oncogenes when adherent cancer cells recognize the extra-cellular matrix (ECM), would determine an overturning of the stiffness ratio between tumour and healthy cells, the former becoming stiffer than the latter [63]. Although this stiffness overturning could be attributed to the specific action of the oncogene SV40T and not to the fact that the tumour and healthy cells change their stiffness ratio in adherent and suspended situations (as also experimentally proved by Haghparast et al. [64]), a stiffening of cancer—and mainly metastatic—cells found in some in vivo situations does not impede using the principle of exploiting stiffness discrepancies between normal and tumour cells to discriminate among them. In fact, the above proposed mechanical strategy could still be used by expecting the relative position of the peaks' frequency to be inverted, as also numerically demonstrated in figure 7, where the results are obtained by simulating the viscoelastic responses of the cells according to the experimental data reported in [63].

Figure 7.

In-frequency responses of healthy (blue) and tumour (purple) single cells, according to Voigt, Maxwell, SLK and three different spring-pot-based SLK viscoelastic models, namely SLK_1, SLK_2 and SLK_3. Cell lines are skin fibroblasts immortalized (BJhTERT and BJhTERT + SV40 T), as reported in [63]. In all the graphics, dashed lines refer to viscoelastic responses associated with low viscosity, while solid lines refer to high viscosity, the responses for these two cases, in terms of displacement amplitude, being, respectively, represented on two different scales on the ordinates at the left and right sides. Note that, in the vast majority of cases, it is possible to find a significant in-frequency distance between healthy and tumour peaks, as highlighted by the double-headed arrows. (Online version in colour.)

Most importantly, the assumed single-cell viscoelastic models do not consider the actual constraints which cells sense as the effect of the presence of both the ECM and other surrounding cells, a condition which the cells actually experience when they in vivo inhabit masses or tissues. Despite the collective mechanical behaviour of cell agglomerates and tissues underlying the scope of this work, it can be inferred that these constraints due to the in vivo dense cell population might be thought of, at least in the first approximation, as equivalently represented by an overall stiffening of the whole system. As a consequence, an overall shift towards higher frequencies should be expected for maximum relative displacement peaks of both normal and cancer cells, the possibility of in-frequency discrimination among benign and malignant cells, as well as the other qualitative information, remaining preserved. However, at the tissue level, where the cells are not only collectively subjected to constraints but also dynamically interact through the ECM, activating complex biochemical signals and mechanically sensing ECM rigidity and in situ vascular pressure, overall modifications of the cell cytoskeleton organization can occur. In this respect, it is worth highlighting that the authoritative work by Paszek et al. [65] has shown that tumour tissues are stiffer than normal tissues, with ranges of measured Young's moduli compatible (but inverted) with respect to those found for single-cell systems, that is, from hundreds of pascals to a few kilopascals. However, analogously to the case discussed above with reference to the experimental findings reported in [63], the overturning of the elastic moduli could still be theoretically exploited for targeting tumour tissues.

In conclusion, possible ways of overcoming the intrinsic limitations of the single-cell paradigm and extending the proposed idea to more realistic in vivo situations have been glimpsed. Moreover, with reference to single cells, the obtained results have effectively shown that it is possible, at least in principle, to mechanically discriminate between tumour and normal cells by exploiting their experimentally measured stiffness discrepancies—for instance stimulating cells through LITUS—frequency peaks and vibration amplitudes being recognized and quantitatively appreciated in the presence of cancer and healthy cells.

Although the outcomes are to date only theoretically derived, it is felt that—if the predictions were experimentally confirmed—this study might open the way for envisaging alternative strategies for the diagnosis and therapy of cancer diseases, both by designing pioneering generations of mechanically based tumour markers and by taking advantage of the resonance-like phenomena to selectively attack malignant cells.

Competing interests

We declare we have no competing interests.

Funding

M.F. is supported by Campania Bioscience (PO-FESR 2013 DRC n.124-2013—‘Innovative therapies for Inflammatory, metabolic, neoplastic and geriatric diseases’), in the framework of the research project ‘Single-cell mechanics as a complementary tool for cancer therapy and diagnosis’—FIRB-RBFR08XXHJ, Italian Department of Education, University and Research, at the Interdisciplinary Research Center for Biomaterials (CRIB), University of Napoli Federico II. N.M.P. is supported by the European Research Council with the following grants: ERC StG Bihsnam on ‘BioInspired hierarchical super-nanomaterials’, ERC PoC Replica2 ‘Large-area replication of biological antiadhesive nanosurfaces’, and ERC PoC Knotouth, as well as by the European Union and by the Provincia Autonoma di Trento, within the Graphene Flagship. L.D. is supported by grant PIAPP-GA-2013–609758-HOTBRICKS, ‘Mechanics of refractory materials at high temperature for advanced industrial technologies’, from the EU through the FP7 programme, and by NSF grant no. DMS-0635983.