Introduction:
Emergency physicians, like other specialists, are faced with different patients and various situations every day. They have to use ancillary diagnostic tools like laboratory tests and imaging studies to be able to manage them (1-8). In most cases, numerous tests are available. Tests with the least error and the most accuracy are more desirable. The power of a test to separate patients from healthy people determines its accuracy and diagnostic value (9). Therefore, a test with 100% accuracy should be the first choice. This does not happen in reality as the accuracy of a test varies for different diseases and in different situations. For example, the value of D-dimer for diagnosing pulmonary embolism varies based on pre-test probability. It shows high accuracy in low risk patient and low accuracy in high risk ones. The characteristics of a test that reflects the aforementioned abilities are accuracy, sensitivity, specificity, positive and negative predictive values and positive and negative likelihood ratios (9-11). In this educational review, we will simply define and calculate the accuracy, sensitivity, and specificity of a hypothetical test.
Definitions:
Patient: positive for disease
Healthy: negative for disease
True positive (TP) = the number of cases correctly identified as patient
False positive (FP) = the number of cases incorrectly identified as patient
True negative (TN) = the number of cases correctly identified as healthy
False negative (FN) = the number of cases incorrectly identified as healthy
Accuracy: The accuracy of a test is its ability to differentiate the patient and healthy cases correctly. To estimate the accuracy of a test, we should calculate the proportion of true positive and true negative in all evaluated cases. Mathematically, this can be stated as:
Sensitivity: The sensitivity of a test is its ability to determine the patient cases correctly. To estimate it, we should calculate the proportion of true positive in patient cases. Mathematically, this can be stated as:
Specificity: The specificity of a test is its ability to determine the healthy cases correctly. To estimate it, we should calculate the proportion of true negative in healthy cases. Mathematically, this can be stated as:
Examples:
Scenario 1
Imagine we have a sample of 100 cases, 50 healthy and the others patient. If a test can be positive for all patients and be negative for all the healthy ones, it is 100% accurate. In figure 1, arrow shows the test and it has been able to differentiate the healthy and patient exactly. In this example, the sensitivity of the test is 50 divided by 50 or 100% and its specificity in determining the healthy people is 50 divided by 50 or 100%.
Figure 1.
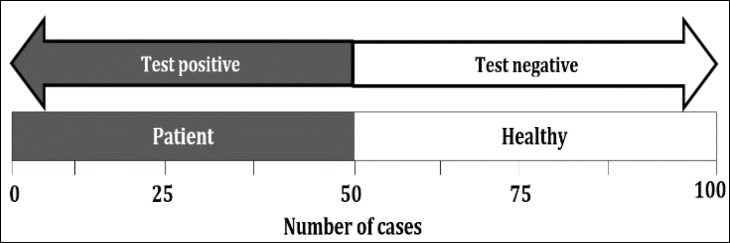
A schematic presentation of an example test with 100% accuracy, sensitivity, and specificity
Taking into account the mentioned statistical characteristics, this test is appropriate for both screening and final verification of a disease.
Scenario 2
If the test can only diagnose 25 out of the 50 patients and has reported the others as healthy (Figure 2); accuracy, sensitivity, and specificity will be as follows:
Figure 2.

A schematic presentation of an example test with 75% accuracy, 50% sensitivity, and 100% specificity.
Accuracy: Of the 100 cases that have been tested, the test could determine 25 patients and 50 healthy cases correctly. Therefore, the accuracy of the test is equal to 75 divided by 100 or 75%.
Sensitivity: From the 50 patients, the test has only diagnosed 25. Therefore, its sensitivity is 25 divided by 50 or 50%.
Specificity: From the 50 healthy people, the test has correctly pointed out all 50. Therefore, its specificity is 50 divided by 50 or 100%.
According to these statistical characteristics, this test is not suitable for screening purposes; but it is suited for the final confirmation of a disease.
Scenario 3
This time we will assume that the test has been able to identify 25 of the 50 healthy cases and has reported the others as patients (Figure 3). In this scenario accuracy, sensitivity and specificity will be as follows:
Figure 3.
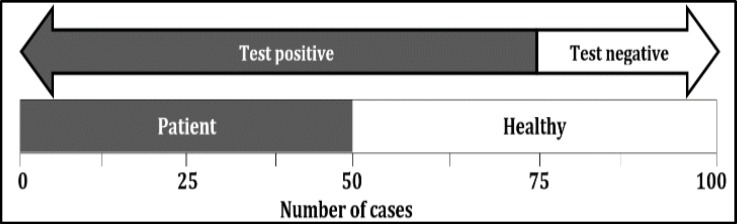
A schematic presentation of an example test with 75% accuracy, 100% sensitivity, and 50% specificity.
Accuracy: Of the 100 cases that have been tested, the test could identify 25 healthy cases and 50 patients correctly. Therefore, the accuracy of the test is equal to 75 divided by 100 or 75%.
Sensitivity: From the 50 patients, the test has diagnosed all 50. Therefore, its sensitivity is 50 divided by 50 or 100%.
Specificity: From the 50 healthy cases, the test has correctly pointed out only 25. Therefore, its specificity is 25 divided by 50 or 50%.
According to these statistical characteristics, this test is suited for screening purposes but it is not suitable for the final confirmation of a disease.
Acknowledgments:
We would like to thank Dr. Saeed Safari and Dr. Mahmoud Yousefifard for their invaluable helps.
Conflict of interest:
None
Funding support:
None
Authors’ contributions:
All authors passed four criteria for authorship contribution based on recommendations of the International Committee of Medical Journal Editors.
References
- 1.Aminiahidashti H, Hosseininejad SM, Montazer H, et al. Diagnostic Accuracy of Ascites Fluid Gross Appearance in Detection of Spontaneous Bacterial Peritonitis. Emergency. 2014;2(3):138–40. [PMC free article] [PubMed] [Google Scholar]
- 2.Ojaghi Haghighi SH, Morteza Begi HR, Sorkhabi R, et al. Diagnostic Accuracy of Ultrasound in Detection of Traumatic Lens Dislocation. Emergency. 2014;2(3):121–4. [PMC free article] [PubMed] [Google Scholar]
- 3.Taghizadieh A, Ala A, Rahmani F, Nadi A. Diagnostic Accuracy of Chest x-Ray and Ultrasonography in Detection of Community Acquired Pneumonia; a Brief Report. Emergency. [In press] [PMC free article] [PubMed] [Google Scholar]
- 4.Amini A, Eghtesadi R, Feizi AM, et al. Sonographic Optic Nerve Sheath Diameter as a Screening Tool for Detection of Elevated Intracranial Pressure. Emergency. 2013;1(1):15–9. [PMC free article] [PubMed] [Google Scholar]
- 5.Heydari F, Esmailian M, Dehghanniri M. Diagnostic Accuracy of Ultrasonography in the Initial Evaluation of Patients with Penetrating Chest Trauma. Emergency. 2014;2(2):81–4. [PMC free article] [PubMed] [Google Scholar]
- 6.Kariman H, Joorabian J, Shahrami A, Alimohammadi H, Noori Z, Safari S. Accuracy of emergency severity index of triage in Imam Hossein hospital-Tehran, Iran (2011) J Gorgan Uni Med Sci. 2013;15(1):115–20. [Persian] [Google Scholar]
- 7.Alavi-Moghaddam M, Safari S, Najafi I, Hosseini M. Accuracy of urine dipstick in the detection of patients at risk for crush-induced rhabdomyolysis and acute kidney injury. Eur J Emerg Med. 2012;19(5):329–32. doi: 10.1097/MEJ.0b013e32834dd2ef. [DOI] [PubMed] [Google Scholar]
- 8.Shojaee M, Faridaalaee G, Yousefifard M, et al. New scoring system for intra-abdominal injury diagnosis after blunt trauma. Chin J Traumatol. 2014;17(1):19–24. [PubMed] [Google Scholar]
- 9.Šimundić A-M. Measures of diagnostic accuracy: basic definitions. Med Biol Sci. 2008;22(4):61–5. [PMC free article] [PubMed] [Google Scholar]
- 10.Altman D, Bland J. Statistics Notes: Diagnostic tests 1: sensitivity and specificity. BMJ. 1994;308(6943):1552. doi: 10.1136/bmj.308.6943.1552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Davidson M. The interpretation of diagnostic tests: A primer for physiotherapists. Aust J Physiother. 2002;48(3):227–32. doi: 10.1016/s0004-9514(14)60228-2. [DOI] [PubMed] [Google Scholar]


