Abstract
In nature, animals often ignore socially available information despite the multiple theoretical benefits of social learning over individual trial-and-error learning. Using information filtered by others is quicker, more efficient and less risky than randomly sampling the environment. To explain the mix of social and individual learning used by animals in nature, most models penalize the quality of socially derived information as either out of date, of poor fidelity or costly to acquire. Competition for limited resources, a fundamental evolutionary force, provides a compelling, yet hitherto overlooked, explanation for the evolution of mixed-learning strategies. We present a novel model of social learning that incorporates competition and demonstrates that (i) social learning is favoured when competition is weak, but (ii) if competition is strong social learning is favoured only when resource quality is highly variable and there is low environmental turnover. The frequency of social learning in our model always evolves until it reduces the mean foraging success of the population. The results of our model are consistent with empirical studies showing that individuals rely less on social information where resources vary little in quality and where there is high within-patch competition. Our model provides a framework for understanding the evolution of social learning, a prerequisite for human cumulative culture.
Keywords: social learning, competition, producer–scrounger game, agent-based model
1. Introduction
Animals rely on current information about their environment, which they gain by directly interacting with their environment (individual learning) or by observing others (social learning). Theoretically, social learning has many benefits. In particular, it allows animals to learn behaviours that have been tested and retained by others, and these should have higher expected returns than untried new behaviours [1–5]. Social learning also has evolutionary consequences by facilitating local adaptation, and it is a requisite mechanism for the evolution of culture [1,6,7] including cumulative culture in humans. A recent tournament model demonstrated a consistent competitive advantage for individuals relying primarily on social learning [2]. Together these arguments suggest that social learning should be ubiquitous in nature, but observational and experimental evidence for example from goats [8], honeybees [9] and guppies [10] suggests that animals often opt for individual learning even when social information is available.
Social learning theory often focuses on how individuals are expected to deploy social learning strategies in a foraging context [11–13]. Models have explored the relative effectiveness of individual and social learning in spatially heterogeneous or temporally fluctuating environments [1,7,14], or when and where individuals should selectively use social learning [2,15,16]. In order to reproduce the coexistence of learning strategies seen in nature, models generally attribute either costs [7,14,15,17] or learning errors [2,15,18] to social learning (reviewed in [19]). The costs of social learning have been attributed to the development and maintenance of a sophisticated behavioural repertoire and nervous system [14]; to a metabolic cost for searching or joining [18]; or to acquiring inappropriate or outdated information [2]. Some models just assume arbitrary costs [7,17]. Previous models have shown that the fitness of learning strategies is frequency-dependent [6]. Although these models generate the mixed-learning strategies seen in nature, there is little empirical evidence for either the costs or low fidelity of social learning when compared with individual learning [20–22]. Thus, the wide use of individual learning in nature remains poorly explained.
Despite the common use of a foraging framework to study social learning, relatively little theoretical attention has been paid to the impact of competition. This is despite the recognition, since Malthus [23,24], that competition plays a fundamental role in shaping populations and behaviour. Resource competition should disproportionately affect social learners, since by copying others social learners are more likely to be forced to share resources in depleted patches. By contrast, directly sampling the environment allows individual learners to find unexploited patches. The argument is the same if individuals copy complex foraging behaviours rather than foraging patch choices. Two individuals that use the same behaviours will exploit similar resources, while an individual that innovates can access resources that are unused by others.
Social learning models [2] often assume that resource quality is highly variable and that resources within patches are unlimited. The latter assumption implies that there is no competition and is usually made to simplify model dynamics. However, in nature competition is ubiquitous [24–26]. Consider for example mate-choice preferences, nesting, feeding and oviposition sites. All represent cases of limited resources (mates, space, food or a combination). Where resources are sufficiently large or abundant, individuals experience little competition. Where resources are less abundant, individual success in resource acquisition is negatively impacted by competition. In addition to resource abundance, resource distribution should also affect the impact of competition on social learning. Where resource quality varies widely, the costs of sharing resources should be outweighed by the advantages of using others to find highly profitable patches. However, where there is little variation in resource quality, individuals may do best by identifying unused patches.
Where individuals compete for access to resources using aggression [27], resources can be lost or the net gain can be reduced by the physiological costs of contest. For example, house sparrows (Passer domesticus) foraging in small patches aggressively drive competitors away from resources. Dominant individuals forage less efficiently because they invest time in this resource-guarding behaviour, and subordinate individuals may fail to forage at all [28]. Thus, fewer resources are collected from patches with more foragers. By contrast, in pure exploitative competition individuals simply divide rewards rather than engaging in conflict. Thus, the distribution of resources can affect learning or foraging strategies in several ways; highly clumped and variable resources are more divisible but also potentially more likely to be contested than evenly spread resources. By using environmentally appropriate learning strategies in a frequency-dependent manner, individuals should be able to mitigate the effect of competition. Therefore, competition deserves consideration in learning models: it is important to understand how learning strategies compete against each other [29].
To study how competition affects the success of individual and social learning, we developed an agent-based model, where individuals forage for resources divided among patches. Patches contain different amounts of resource, which can change over time. Individuals learn about patches by direct exploration (individual learning) or by observing another individual that has visited that patch (social learning). Our model is akin to the classical producer–scrounger game [11]: individual learners produce new knowledge about the system, and social learners exploit the knowledge that others have produced. In contrast to earlier social learning models, resources are limited and individuals foraging at the same patch compete to collect them.
We use this model to ask the following questions: (i) does competition reduce the effectiveness of social learning relative to individual learning, (ii) does environmental stability or variation in resource quality affect the relative effectiveness of social learning and individual learning, and (iii) how is the mean individual foraging success affected by different proportions of social learning in a group?
2. Material and methods
We used agent-based stochastic simulations to study the relative fitness of individual and social learning in different environments and under different competition strengths. We describe our model as if the information that individuals must learn is the location of resources that are distributed among patches. However, the model is equally appropriate if individuals must learn foraging strategies that offer different resource pay-offs, similar to the multi-armed bandit model used by Rendell et al. [2].
(a). The model
We modelled an environment comprised of patches. Each patch has a resource value, which describes the amount of resources that one insatiable individual foraging alone could collect from that patch in a single time step. We drew the resource value for each patch independently from a gamma distribution. In each time step, the resource value of each patch changes with probability τ. If the resource value changes, a new resource value for that patch is drawn independently from the same gamma distribution. We used different gamma distributions to study environments with different resource distributions. We set the parameters of each gamma distribution so that the expected resource value in any patch was the same in all environments (here set to 4), but the variability among patches differed among environments. Thus, each environment we studied could be fully characterized by the number of patches, the rate of change τ and the evenness G of the resource distribution. We measured G using the Gini index [30], which is widely employed by economists to measure wealth inequality (see the electronic supplementary materials). The Gini index can range from G = 0 (if all patches have the same resource value) to G = 1 (if all resources are concentrated in a single patch). We studied values between G = 0.14, where there is little variability among patches, and G = 0.83, where most patches are poor and a few patches are very rich (electronic supplementary material, table S1).
Individuals in our model collect resources from patches. Individuals can collect resources only from patches that they know about, and they learn about patches in one of two ways. Each individual is either an individual learner or a social learner. A social learner observes a randomly selected exploiting individual, and learns the amount of resources that individual collects from the patch it is currently exploiting. An individual learner observes a randomly selected patch, and learns the amount of resources that individuals in that patch are currently collecting. If no individuals are exploiting the patch, the individual learner learns the full resource value of the patch. We call the amount the individual learns the anticipated reward of the patch. When an individual first learns about a patch, the anticipated reward is the amount that is currently being collected, and is not corrected for the added competition that will occur if the individual joins exploiters in the patch. In nature, animals may or may not be able to adjust anticipated rewards for anticipated competition. We have chosen this formulation because it ensures that social and individual learners obtain equally accurate information. Thus, there is no implied penalty on the quality of information obtained by social learners. An individual that has learned the anticipated reward of a patch maintains that information until it is updated (for example, if it visits that patch to forage or if it learns about the patch again) or until the individual dies. Thus, if the resource value or number of individuals using a patch changes, an individual's anticipated reward from that patch will be incorrect until it is updated.
Time in our model is divided into steps that we call rounds. In each round, each individual either learns (with probability β) or exploits resources from patches it has previously learned about (with probability 1 − β). We set β = 0.2, which was found to be most advantageous for individual learners in a previous model [31]. If an individual exploits, it visits the patch that it knows about and from which it anticipates the highest reward. It collects an amount of resources p from that patch, where
Here, π is the resource value of the patch, n is the number of individuals that visit the patch in that round, u describes the maximum resources that an individual can collect in a single round (e.g. due to satiation) and c scales the strength of competition between individuals in a patch (e.g. [32,33]). If c = 0, then individuals are not affected by other individuals in the same patch and receive p = π (i.e. there is no competition). Where c = 1 individuals receive exactly p = π/n (i.e. there is full exploitative competition), and where c > 1 individuals receive less than p = π/n (i.e. there is interference competition).
Every individual that exploits a patch updates its anticipated reward of that patch according to the amount of resources it has collected. If an individual is selected to exploit but has not yet learned about any patches, then it does nothing in that round.
In each round, each individual in the population dies with probability d = 0.02. Any individual that has survived its first 100 rounds dies after its 100th round. Thus, the life expectancy of individuals is 43.37 rounds. When an individual dies, a new individual with no knowledge of the environment is immediately born to replace it. Thus, the population size is constant.
(b). Analysis 1: frequency-dependent effects of social and individual learning without and with competition
Our first goal was to understand how the relative fitness of individual and social learners depends on the frequencies of each strategy. This is important because frequency dependence is needed to explain how learning strategies coexist in nature, and the source of this frequency dependence is still poorly understood. The relative amount of resources collected by an individual is a performance measure that is commonly used as fitness proxy in foraging theory [2,34], and we used this here. We ran simulations with 100 patches and 100 individuals. We initialised each simulation with a fixed frequency of individual learners, and we iterated 104 model rounds. To maintain fixed frequencies of each learning strategy, we assumed that whenever an individual died it was immediately replaced by the birth of a new individual with the same learning strategy. In each of the last 2500 rounds of each simulation, we recorded the average resources collected by each individual or social learner. We conducted 100 simulations for each frequency of individual learners in the set {0.01, 0.1, 0.2, … , 0.9, 0.99} and evenness in the set G ∈ {0.14, 0.83} both without (c = 0) and with (c = 1) competition. In all simulations, we set u = ∞ (i.e. individuals can collect up to the full resource value of the patch they visit).
(c). Analysis 2: the effect of environmental parameters on the fitness of learning strategies
The approach above allows us to predict the frequency of individual learning in the population at which each social or individual learner collects the same amount of resources. We expect this to be the frequency at which the strategies coexist [6]. However, this approach is computationally intensive. Therefore, to understand how competition affects the fitness of learning strategies across a broad range of environmental conditions, we used an evolutionary algorithm. As above, we modelled systems with 100 patches and 100 individuals. We initialized each population with 50 individual and 50 social learners, and we iterated 104 model rounds. When an individual in the population died, it was immediately replaced by the offspring of a surviving individual. The probability that each surviving individual was selected as the parent was proportional to the average resources per round that the individual had collected over the course of its lifetime. This translation of resources collected to reproductive potential has been used in previous studies of individual and social learning [2]. Offspring inherited their learning strategy from their parent, and with probability 0.01 that their learning strategy mutated to the opposite strategy. Mutation prevents strategies from becoming fixed due to stochastic drift. We conducted 100 simulations for each combination of G ∈ {0.14, 0.16, 0.18, 0.20, 0.22, 0.24, 0.27, 0.30, 0.34, 0.37, 0.41, 0.45, 0.50, 0.54, 0.59, 0.63, 0.68, 0.72, 0.76, 0.80, 0.83}, τ = 10i for i ∈ {−4, −3.9, −3.8, …, 0}, c = 1 and u ∈ {2, 4, 40, ∞} (for results when u < ∞, see the electronic supplementary material, figure S3). We calculated the average frequency of individual learners in the population over the last 2500 rounds of each simulation.
This analysis assumes that each forager is either an individual learner or a social learner, and uses only that learning strategy. In the electronic supplementary materials, we analyse a similar model in which each individual can use a combination of the two learning strategies (electronic supplementary material, figure S2).
(d). Analysis 3: the effect of competition strength on the fitness of learning strategies
To understand how competition strength affects the fitness of individual and social learners, we used the evolutionary approach from analysis 2. We conducted 100 simulations for each combination of c ∈ {0.01, 0.6, 1, 1.6, 2.5}, G ∈ {0.14, 0.83}, u = ∞ and τ = 0.01. When c = 0.01, each individual has very little effect on the resources collected by other individuals in the patch (i.e. competition is weak). When c = 2.5, there is strong interference competition: two individuals foraging in the same patch collect only 35% of the resources that a single individual would collect alone. As in analysis 2, we iterated simulations for 104 rounds, and we calculated the mean frequency of individual learners in the population over the last 2500 rounds.
(e). Analysis 4: the effect of social learners on mean individual foraging success
In analyses 1–3, we asked how environmental parameters and competition strength affect the stable frequency of social learners in a population. In this final analysis, we asked how the frequency of social learners affects mean individual foraging success. We defined mean individual foraging success as the average resources collected per individual per foraging round. Using the approach from analysis 1, we conducted simulations in which the frequency of social learners was fixed at f. We conducted 100 independent simulations over 104 rounds, and averaged the mean individual foraging success in populations with f ∈ {0.01, 0.1, 0.2, … , 0.9, 0.99} over the last 2500 rounds. Then, using the approach from analyses 2 and 3, we conducted 100 additional simulations in which the frequency of social learners was allowed to evolve. We iterated simulations for 104 rounds and calculated the mean evolved frequency of social learners and the mean individual foraging success in the evolved population over the last 2500 rounds of each simulation. We compared the mean individual foraging success in evolved populations to that in populations with fixed frequencies of social learning. We conducted this analysis for populations and environments characterized by each combination of τ ∈ {0.01, 0.1}, c ∈ {0.6, 1, 1.6}, u ∈ {2, ∞} and G = 0.83.
3. Results
(a). Competition enables the coexistence of learning strategies
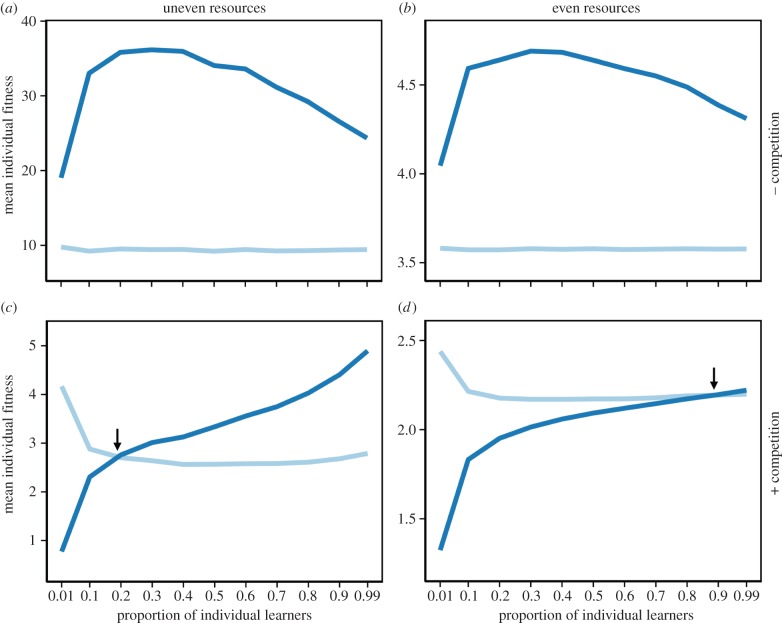
When there is no competition, social learners collect more resources than individual learners regardless of the relative frequency of the two strategies (figure 1a,b). Thus, social learners will outcompete and exclude individual learners from the population. With competition, however, there is frequency dependence and each strategy is favoured when is it rare (figure 1c,d). The frequency at which the two strategies have the same fitness, and thus at which they should coexist, depends on the resource distribution (cf. figure 1c,d).
Figure 1.
Mean individual fitness, measured as the average amount of resources collected, for individual (light grey line) and social (dark grey line) learners in simulations without (a,b) and with (c,d) competition. Without competition, social learners are always fitter than individual learners. With competition, each strategy is more fit than the other when it is rare. Arrows indicate the evolutionarily stable proportion of individual learners in the population. Resources are unevenly (G = 0.14) distributed in (a,c) and evenly (G = 0.83) in (b,d). (Online version in colour.)
(b). Stable and highly skewed resources favour social learning
With competition, social learning is favoured when resources are unevenly distributed and highly predictable (figure 2). This is because foragers gain higher returns by identifying and exploiting high-quality patches, even if they must share those patches with others. If resources are more evenly distributed, individual learning is favoured. In this case, foragers do better by spreading themselves evenly among patches and avoiding competition. Rapidly changing patch quality also favours individual learning. In this case, the information held by others quickly becomes obsolete. The slightly better information a forager obtains by learning from others is not worth the competition it faces from the individual it has copied. We found qualitatively similar effects of resource distribution and rate of environmental change using a model in which each individual was allowed to employ a mixture of individual and social learning (electronic supplementary material, figure S2).
Figure 2.
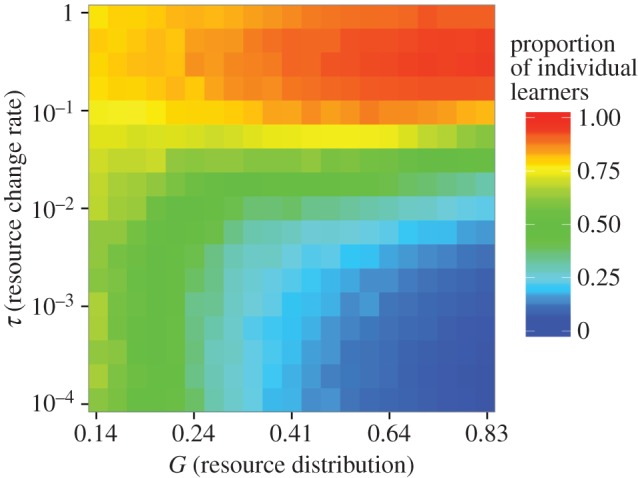
Mean proportion of individual learning as a function of the evenness of resources among patches (x-axis) and the rate at which resources change over time (y-axis). The x-axis represents increasing unevenness in resource distribution (Gini index G), and the y-axis represents the probability that the resource value of a patch offers changes in any round. Social learning becomes common when resources are stable and unevenly distributed. Results shown here are for u = ∞. We obtained qualitatively similar results for other values of u (electronic supplementary material figure S3). (Online version in colour.)
The steady state for social learning in analysis 2 does not precisely match the predictions of analysis 1. This is due to the effect of mutation in analysis 2. Symmetrical mutation pushes the ratio of social and individual learners towards 50%. When selection is weak (e.g. on the lower left side of figure 2), the steady state in the evolutionary model is close to 50%. When selection is strong (e.g. on the right side of figure 2), the results of the evolutionary analysis are similar to the predictions of analysis 1.
(c). Competition favours individual learning
Social learning dominates when competition is very weak, regardless of resource distribution (figure 3). This is because every individual can collect nearly the full resource value from a patch regardless of how many individuals are present, so there is little disadvantage in joining others. With increasing competition, there is more incentive to find unexploited patches and consequently individual learning increases. The more evenly resources are distributed, the faster the proportion of social learning decreases with increasing competition.
Figure 3.
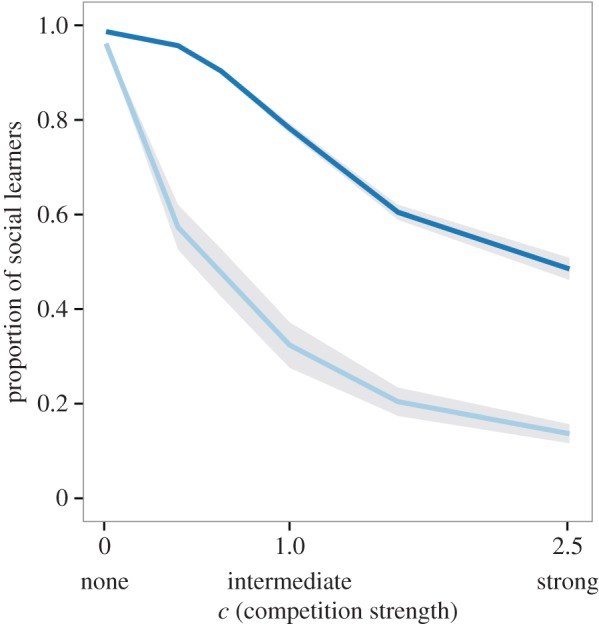
Mean proportion of social learners under different competition strengths (c = 0.01, 0.6, 1, 1.6, 2.5) with slowly changing (τ = 0.01) evenly (light grey, G = 0.14) and unevenly (dark grey, G = 0.83) distributed resources. With increasing competition, there is more individual learning. At high levels of competition, social learning remains common only if resources are unevenly distributed. Shaded areas indicate 1 s.d. around the mean. (Online version in colour.)
(d). Social learning lowers mean individual foraging success
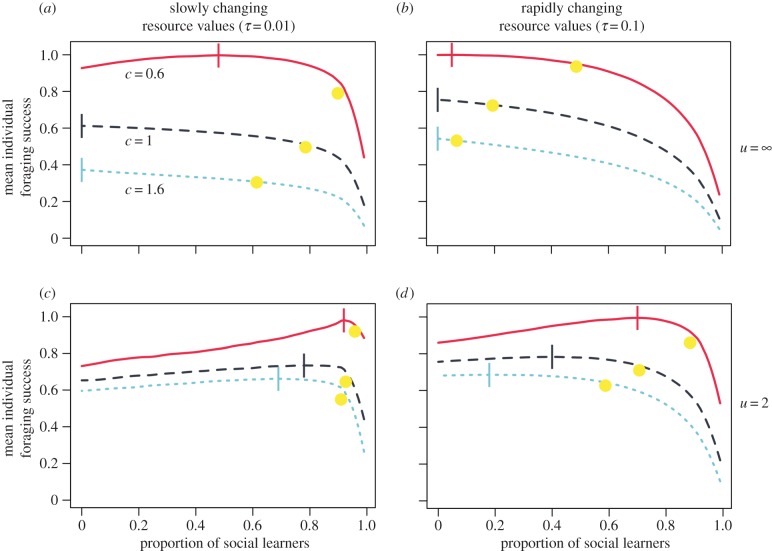
Figure 4 shows how the mean individual foraging success depends on the frequency of social learners under different sets of conditions. The vertical score on each line shows the frequency of social learners that maximizes the mean individual foraging success. If one forager can collect all of the resources from any patch it visits and there is complete exploitation or interference competition (i.e. if c ≥ 1 and u = ∞), then the mean individual foraging success is maximized when all foragers are individual learners. This is true because every social learner reduces the success of the foragers it copies by at least as much as it collects itself. If multiple foragers in a patch can sometimes collect more total resources than one forager could collect alone (i.e. if c < 1 or u < ∞), then some social learning can increase the mean individual foraging success. In this case, an individual learner that discovers an unexploited high-value patch may be unable to exploit all of the resources in that patch. By following that individual, social learners can find the high-value patch and access the unexploited resources more quickly than individual learners can. These social learners gain more by copying than the patch finders lose by being copied. Thus, the mean individual foraging success is higher in a population with some social learners than in a population with all individual learners.
Figure 4.
Mean individual foraging success as a function of the frequency of social learners and the competition strength (solid: c = 0.6, dashed: c = 1, dotted: c = 1.6). Resources were unevenly distributed (G = 0.83) and resource values changed at rates τ = 0.01 (a,c) or τ = 0.1 (b,d). In (a,b), one individual foraging alone can collect the full resource value from any patch it visits (i.e. u = ∞). In (c,d), an individual can collect a maximum of two units per round (i.e. u = 2). Vertical lines show the frequency of social learning at which mean individual foraging success is maximized. Dots show the frequency of social learning that evolves. When competition is weak or when individuals can collect only limited resources, social learning can increase the mean individual foraging success in the population. However, social learning always evolves until it begins to lower mean individual foraging success. To facilitate comparison between panels, we scaled mean individual foraging success so that a value of 1 represents the maximum achieved by any population in that environment. Foraging success functions were smoothed with a locally weighted regression using a nearest-neighbour approach. (Online version in colour.)
If the frequency of social learning in a population is allowed to evolve, the mean individual foraging success at the evolved frequency (dots in figure 4) can be higher or lower than in a population of all individual learners. Nonetheless, the frequency to which social learning evolves always exceeds the frequency that maximizes the mean individual foraging success. Thus, at the frequency to which they evolve, social learners negatively affect the mean foraging success in their system.
4. Discussion
Our results demonstrate that in contrast to a competition-free world, which favours social learning, competition for resources can promote mixed individual and social learning strategies. Social learning is highly effective where resources are unevenly distributed because it allows individuals to quickly find good but densely occupied patches. Even with competition, pay-offs in these patches can be higher than in randomly sampled patches. By contrast, when patches vary little in quality, individual learning is advantageous. In this case, there are no patches with extremely high resource values, and individual learning allows foragers to find unoccupied patches and so to avoid competition. Moreover, where environmental turnover is high and resource predictability is low, information quickly becomes outdated. When information is less accurate, the positive effect of collecting information from other foragers becomes small relative to the negative effect of competing with those foragers for resources, and individual learning is again advantageous. Thus, social learning is favoured where resource distribution is uneven yet predictable, and individual learning is favoured where resource distribution is even and/or unpredictable.
Previous social learning models have typically not incorporated competition (e.g. [2,6,7,14–16]). Instead, they have explained the coexistence of individual and social learning strategies by attributing arbitrary costs, low fidelity or inefficiencies to social learning [2,6–10]. Given that competition is ubiquitous in nature it is commonly incorporated in foraging models, for instance in ideal-free distribution [35] and producer–scrounger games [33]. Our analysis demonstrates the importance of including competition in models of social learning: models that ignore competition may give incomplete or misleading results.
The results from our competition-based learning model are consistent with what we find in nature. Sticklebacks (Pungitius pungitius), for example, use individual learning to make foraging decisions when competition is high, but rely almost entirely on social learning when competition is low [36]. Honeybees (Apis mellifera) rely heavily on social information when foraging resources are unevenly distributed and are more likely to use individual information when resources are evenly distributed [20]. Foraging returns for rats (Rattus norvegicus) are likely to be highly variable because some potential food items are harmful or fatal, and rats exhibit strong preferences for socially learned food items [37]. By contrast, herbivores like goats experience homogeneous resource distributions and rely on individual information when exhibiting grazing preference [8].
In our model, social learning can evolve to high frequencies. This is true because social learning can be advantageous to individuals. However, in a classic thought experiment, Rogers [6] predicted that social learning at its evolutionarily stable frequency would have no effect on population mean fitness. This has become known as Rogers' paradox [15]. It is a paradox because most researchers believe that the capacity for social learning to increase population mean fitness explains the evolution of culture, and if Rogers' prediction holds this cannot be true. Rogers' model assumes that the fitness of individual learners does not depend on the frequency of social learners. Because the fitness of social learners is reduced as they become more common, social learners increase in the population only until they have the same fitness as individual learners. Therefore, at the stable state, the mean fitness of the population with social learners is the same as the mean fitness of the population without them. In the presence of competition, the frequency of social learners does affect the fitness of individual learners. In this case, social learning at its evolved frequency can either increase or decrease population mean fitness relative to populations with all individual learners, as we show here. Thus, competition offers a resolution to Roger's paradox. Interestingly, the evolved frequency of social learning is always greater than is necessary to maximize the population mean fitness. Thus, at the evolved frequency of social learning, individuals that use social learning beyond the optimal frequency have a negative effect on population mean fitness.
We have restricted our analysis to cases in which within-patch resource collection by individuals is either strictly independent (i.e. c = 0) or competitive (i.e. c > 0). In nature, resource collection can also be cooperative (i.e. c < 0). In this case, two or more individuals working together can access resources that one individual could not access alone. Cooperative foraging has been observed in mammals [38], birds [39], spiders [40], possibly fish [41] and is common in eusocial insects [42]. If foraging is cooperative, evolutionarily stable frequencies of social learning might not reduce mean individual foraging success. However, cooperative foraging is likely to be a derived trait that evolves from simpler intraspecific interactions. Thus, as cooperative foraging evolves, social learning may still pass through a stage in which it reduces the fitness of its population.
The ability to learn from others is a prerequisite for the evolution of culture [1,6,7,43,44], including the cumulative culture that has made humans so successful. We have shown that the evolution of social learning is shaped by competition. This result provides an important new context for future studies of cultural evolution.
Supplementary Material
Acknowledgement
The authors thank two anonymous referees for comments on the manuscript, and the University of Manchester EPS for access to the HTCondor computer cluster.
Authors' contributions
M.S. generated the model. All authors contributed to the study design, analyses and the manuscript.
Competing interests
We declare we have no competing interests.
Funding
S.S. was supported by a Royal Society URF and M.S. by a Royal Society Research Grant.
References
- 1.Boyd R, Richerson PJ. 1985. Culture and the evolutionary process. Chicago, IL: University of Chicago Press. [Google Scholar]
- 2.Rendell L, et al. 2010. Why copy others? Insights from the social learning strategies tournament. Science 328, 208–213. ( 10.1126/science.1184719) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Giraldeau L-A, Valone TJ, Templeton JJ. 2002. Potential disadvantages of using socially acquired information. Phil. Trans. R. Soc. Lond. B 357, 1559–1566. ( 10.1098/rstb.2002.1065) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thornton A, Clutton-Brock TH. 2011. Social learning and the development of individual and group behaviour in mammal societies. Phil. Trans. R. Soc. B 366, 978–987. ( 10.1098/rstb.2010.0312) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Galef BG, Laland KN. 2005. Social learning in animals: empirical studies and theoretical models. Bioscience 55, 489–499. ( 10.1641/0006-3568%282005%29055%5B0489:SLIAES%5D2.0.CO%3B2) [DOI] [Google Scholar]
- 6.Rogers AR. 1988. Does biology constrain culture. Am. Anthropol. 90, 819–831. ( 10.1525/aa.1988.90.4.02a00030) [DOI] [Google Scholar]
- 7.Feldman MW, Aoki K, Kumm J. 1996. Individual versus social learning: evolutionary analysis in a fluctuating environment. Anthropol. Sci. 104, 209–231. ( 10.1537/ase.104.209) [DOI] [Google Scholar]
- 8.Baciadonna L, McElligott AG, Briefer EF. 2013. Goats favour personal over social information in an experimental foraging task. PeerJ 1, e172 ( 10.7717/peerj.172) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Grüter C, Balbuena MS, Farina WM. 2008. Informational conflicts created by the waggle dance. Proc. R. Soc. B 275, 1321–1327. ( 10.1098/rspb.2008.0186) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kendal RL, Coolen I, Laland KN. 2004. The role of conformity in foraging when personal and social information conflict. Behav. Ecol. 15, 269–277. ( 10.1093/beheco/arh008) [DOI] [Google Scholar]
- 11.Barnard CJ, Sibly RM. 1981. Producers and scroungers: a general model and its application to captive flocks of house sparrows. Anim. Behav. 29, 543–550. ( 10.1016/S0003-3472(81)80117-0) [DOI] [Google Scholar]
- 12.Giraldeau L-A, Caraco T. 2000. Social foraging theory. Princeton, NJ: Princeton University Press. [Google Scholar]
- 13.Arbilly M, Motro U, Feldman MW, Lotem A. 2011. Evolution of social learning when high expected payoffs are associated with high risk of failure. J. R. Soc. Interface 8, 1604–1615. ( 10.1098/rsif.2011.0138) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wakano JY, Aoki K. 2006. A mixed strategy model for the emergence and intensification of social learning in a periodically changing natural environment. Theor. Popul. Biol. 70, 486–497. ( 10.1016/j.tpb.2006.04.003) [DOI] [PubMed] [Google Scholar]
- 15.Enquist M, Eriksson K, Ghirlanda S. 2007. Critical social learning: a solution to Rogers's paradox of nonadaptive culture. Am. Anthropol. 109, 727–734. ( 10.1525/AA.2007.109.4.727) [DOI] [Google Scholar]
- 16.Hamblin S, Giraldeau LA. 2009. Finding the evolutionarily stable learning rule for frequency-dependent foraging. Anim. Behav. 78, 1343–1350. ( 10.1016/j.anbehav.2009.09.001) [DOI] [Google Scholar]
- 17.Kameda T, Nakanishi D. 2002. Cost–benefit analysis of social/cultural learning in a nonstationary uncertain environment. An evolutionary simulation and an experiment with human subjects. Evol. Hum. Behav. 23, 373–393. ( 10.1016/S1090-5138(02)00101-0) [DOI] [Google Scholar]
- 18.Afshar M, Giraldeau L-A. 2014. A unified modelling approach for producer–scrounger games in complex ecological conditions. Anim. Behav. 96, 167–176. ( 10.1016/j.anbehav.2014.07.022) [DOI] [Google Scholar]
- 19.Aoki K, Feldman MW. 2014. Evolution of learning strategies in temporally and spatially variable environments: a review of theory. Theor. Popul. Biol. 91, 3–19. ( 10.1016/j.tpb.2013.10.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wray MK, Klein BA, Seeley TD. 2012. Honey bees use social information in waggle dances more fully when foraging errors are more costly. Behav. Ecol. 23, 125–131. ( 10.1093/beheco/arr165) [DOI] [Google Scholar]
- 21.Webster MM, Laland KN. 2008. Social learning strategies and predation risk: minnows copy only when using private information would be costly. Proc. R. Soc. B 275, 2869–2876. ( 10.1098/rspb.2008.0817) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McLinn CM, Stephens DW. 2010. An experimental analysis of receiver economics: cost, reliability and uncertainty interact to determine a signal's value. Oikos 119, 254–263. ( 10.1111/j.1600-0706.2009.17756.x) [DOI] [Google Scholar]
- 23.Glass DV, Appleman P. 1976. Thomas Robert Malthus: an essay on the principle of population (1798). Popul. Stud. (NY). 30, 369 ( 10.2307/2173616) [DOI] [Google Scholar]
- 24.Gause GF. 1934. The struggle for existence. Baltimore, MD: The Williams & Wilkins Company. [Google Scholar]
- 25.Elton CS. 1946. Competition and the structure of ecological communities. J. Anim. Ecol. 15, 54–68. ( 10.2307/1625) [DOI] [Google Scholar]
- 26.Hassell MP, Varley GC. 1969. New inductive population model for insect parasites and its bearing on biological control. Nature 223, 1133–1137. ( 10.1038/2231133a0) [DOI] [PubMed] [Google Scholar]
- 27.Miller RS. 1967. Pattern and process in competition. Adv. Ecol. Res. 4, 1–74. ( 10.1016/S0065-2504(08)60319-0) [DOI] [Google Scholar]
- 28.Johnson CA, Giraldeau LA, Grant JWA. 2006. Intensity of interference affects the distribution of house sparrows, Passer domesticus, at food patches. Anim. Behav. 71, 965–970. ( 10.1016/j.anbehav.2005.10.003) [DOI] [Google Scholar]
- 29.Fawcett TW, Hamblin S, Giraldeau LA. 2013. Exposing the behavioral gambit: the evolution of learning and decision rules. Behav. Ecol. 24, 2–11. ( 10.1093/beheco/ars085) [DOI] [Google Scholar]
- 30.Ceriani L, Verme P. 2011. The origins of the Gini index: extracts from Variabilità e Mutabilità (1912) by Corrado Gini. J. Econ. Inequal. 10, 421–443. ( 10.1007/s10888-011-9188-x) [DOI] [Google Scholar]
- 31.Castro L, Toro MA. 2012. Imitation or innovation? Unselective mixed strategies can provide a better solution. Theory Biosci. 131, 273–279. ( 10.1007/s12064-012-0161-4) [DOI] [PubMed] [Google Scholar]
- 32.Sutherland WJ. 1983. Aggregation and the ‘Ideal Free’ distribution. J. Anim. Ecol. 52, 821–828. ( 10.2307/4456) [DOI] [Google Scholar]
- 33.Beauchamp G. 2000. Learning rules for social foragers: implications for the producer–scrounger game and ideal free distribution theory. J. Theor. Biol. 207, 21–35. ( 10.1006/jtbi.2000.2153) [DOI] [PubMed] [Google Scholar]
- 34.Stephens DW, Brown JS, Ydenberg RC (eds). 2007. Foraging: behavior and ecology. Chicago, IL: The University of Chicago Press. [Google Scholar]
- 35.Tregenza T. 1995. Building on the ideal free distribution. Adv. Ecol. Res. 26, 253–302. ( 10.1016/S0065-2504(08)60067-7) [DOI] [Google Scholar]
- 36.Webster MM, Laland KN. 2012. Social information, conformity and the opportunity costs paid by foraging fish. Behav. Ecol. Sociobiol. 66, 797–809. ( 10.1007/s00265-012-1328-1) [DOI] [Google Scholar]
- 37.Galef B, Whiskin EE. 2001. Interaction of social and individual learning in food preferences of Norway rats. Anim. Behav. 62, 41–46. ( 10.1006/anbe.2000.1721) [DOI] [Google Scholar]
- 38.Courchamp F, Rasmussen GSA, Macdonald DW. 2002. Small pack size imposes a trade-off between hunting and pup-guarding in the painted hunting dog Lycaon pictus. Behav. Ecol. 13, 20–27. ( 10.1093/beheco/13.1.20) [DOI] [Google Scholar]
- 39.Nawab A. 2005. Common mynas Acridotheres tristis robbing the eggs of a nightjar Caprimulgus sp. Indian Birds 1, 120–121. [Google Scholar]
- 40.Pasquet A, Krafft B. 1992. Cooperation and prey capture efficiency in a social spider, Anelosimus eximius (Araneae, Theridiidae). Ethology 133, 121–133. ( 10.1111/j.1439-0310.1992.tb00826.x) [DOI] [Google Scholar]
- 41.Motta PJ, Wilga CD. 2001. Advances in the study of feeding behaviors, mechanisms, and mechanics of sharks. Environ. Biol. Fishes 60, 131–156. ( 10.1023/A:1007649900712) [DOI] [Google Scholar]
- 42.Czaczkes TJC, Atnieks FLWR. 2013. Cooperative transport in ants (Hymenoptera : Formicidae) and elsewhere. Myrmecol. News 18, 1–11. [Google Scholar]
- 43.Laland KN, Hoppitt W. 2003. Do animals have culture? Evol. Anthropol. 12, 150–159. ( 10.1002/evan.10111) [DOI] [Google Scholar]
- 44.Claidière N, Sperber D. 2010. Imitation explains the propagation, not the stability of animal culture. Proc. R. Soc. B 277, 651–659. ( 10.1098/rspb.2009.1615) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.