Rapid 3D Dynamic Arterial Spin Labeling with a Sparse Model-Based Image Reconstruction

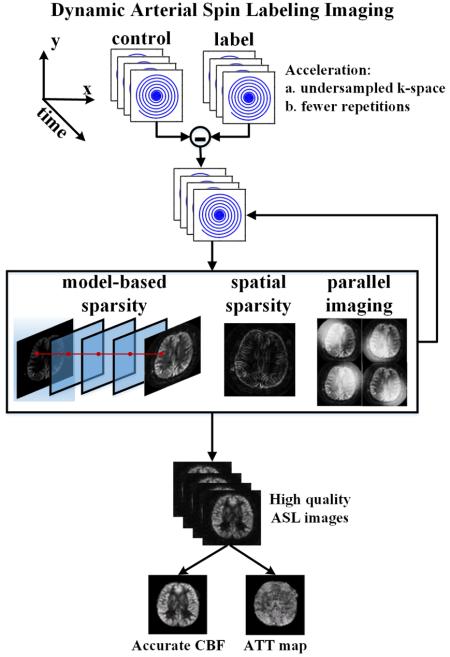
Abstract

Dynamic arterial spin labeling (ASL) MRI measures the perfusion bolus at multiple observation times and yields accurate estimates of cerebral blood flow in the presence of variations in arterial transit time. ASL has intrinsically low signal-to-noise ratio (SNR) and is sensitive to motion, so that extensive signal averaging is typically required, leading to long scan times for dynamic ASL. The goal of this study was to develop an accelerated dynamic ASL method with improved SNR and robustness to motion using a model-based image reconstruction that exploits the inherent sparsity of dynamic ASL data. The first component of this method is a single-shot 3D turbo spin echo spiral pulse sequence accelerated using a combination of parallel imaging and compressed sensing. This pulse sequence was then incorporated into a dynamic pseudo continuous ASL acquisition acquired at multiple observation times, and the resulting images were jointly reconstructed enforcing a model of potential perfusion time courses. Performance of the technique was verified using a numerical phantom and validated on normal volunteers on a 3-Tesla scanner. In simulation, a spatial sparsity constraint improved SNR and reduced estimation errors. Combined with a model-based sparsity constraint, the proposed method further improved SNR, reduced estimation error and suppressed motion artifacts. Experimentally, the proposed method resulted in significant improvements, with scan times as short as 20 seconds per time point. These results suggest that the model-based image reconstruction enables rapid dynamic ASL with improved accuracy and robustness.

1. Introduction

Arterial spin labeling (ASL) (Detre et al., 1992) is a non-invasive and non-contrast perfusion imaging method for magnetic resonance imaging (MRI). By deriving perfusion data from the natural MR signal of magnetically tagged blood, instead of from an extrinsic contrast agent, ASL provides a safer option for assessing tissue perfusion in patients at risk of nephrogenic systemic fibrosis (Hasebroock and Serkova, 2009) and a preferable option in other situations, such as when imaging infants and children. Cerebral blood flow (CBF) maps estimated using ASL are consistent with dynamic susceptibility contrast (DSC) results and have been widely applied to cerebrovascular studies, such as stroke (Wang et al., 2012) and Alzheimer’s disease (Yoshiura et al., 2009). ASL is also preferable for studies requiring repeated perfusion assessments in a short period of time, such as functional MRI (Borogovac and Asllani, 2012; Detre and Wang, 2002). The absolute quantification of blood flow in ASL directly reveals physiological changes (Asllani et al., 2009; Rusinek et al., 2011).

Since the blood magnetization is “labeled” upstream of the volume of interest, a portion of the ASL signal decays before arterial blood flows into the imaging slab, and the acquired signal thus depends on the tagged blood arrival time, called the arterial transit time (ATT), which in turn depends on both the blood flow velocity and the distance between the tagging plane and the imaged region. However, most ASL studies follow the single post label delay (PLD) protocol, which results in a “static” 2D/3D ASL image. It cannot provide a subject-dependent ATT map and requires a simplified ASL model, which may result in errors in CBF quantification (Dai et al., 2012; Qiu et al., 2010). A PLD longer than the ATT can ensure the blood bolus has flowed into surrounding tissue and reduces estimation error (Alsop and Detre, 1996), but this method may miss the peak ASL signal and requires prior knowledge of the ATT.

A multiple-PLD protocol can measure multiple phases of ASL perfusion and fully characterize the ASL dynamic model. It can improve CBF accuracy and provide rich hemodynamic information, such as ATT for characterizing cerebrovascular diseases (Macintosh et al., 2012). But, the intrinsically low SNR of ASL can require extensive signal averaging, and thus a multiple-PLD protocol may become prohibitively time-consuming.

Dynamic ASL imaging can be accelerated in two ways: (1) acquiring undersampled k-space data, and (2) reducing the number of averages. However, accelerating ASL data acquisition in this way comes at the cost of reduced image quality and CBF accuracy using conventional techniques.

In this work, we propose a method to accelerate dynamic 4D ASL images, which maintains the image quality and provides accurate and robust parameter quantification. First, we use a rapid and efficient data acquisition method: single-shot 3D turbo spin echo (TSE) imaging with a spiral k-space trajectory. (Other readouts can be used, such as 3D GRASE (Wang et al., 2013).) Spiral TSE parallel imaging is a very rapid imaging method, enabling rapid 3D scanning. Second, we incorporate a dual-density spiral trajectory and non-Cartesian parallel imaging, which enable single-shot 3D scanning with the desired spatial resolution. Single-shot scanning saves time and is more robust to motion and physiological variations than interleaved scanning. With a dual-density trajectory, our design is also less vulnerable to T2-blurring and susceptibility artifacts, compared to conventional single shot constant-density spiral scanning, which requires a long readout to achieve spatial coverage and resolution (Meyer et al., 2011). However, there is an SNR penalty at high acceleration rates using parallel imaging. Therefore, we also incorporate a third technique: compressed sensing (Lustig et al., 2007), which exploits sparsity of the data and grew out of earlier research in nonlinear denoising methods. Compressed sensing can recover the ASL signal from an acquisition with undersampled k-space and fewer averages. Thus, it is an intriguing option for accelerated ASL image reconstruction (Zhao et al., 2013, 2012). In this work, we combine a 3D single-shot stack-of-spirals k-space trajectory, parallel imaging and compressed sensing for highly accelerated image acquisition with excellent SNR.

For dynamic ASL, we certainly need high acceleration and high SNR, not only for the perfusion images, but also for the resulting parameter maps. The first step in applying compressed sensing to ASL image reconstruction is to enforce a spatial sparsity constraint. This is a promising technique in its own right, and can be used to accelerate ASL image acquisition for each time point separately. Related research into spatial constraints include methods to improve ASL image quality using spatial filters, wavelet sparsity (Bibic et al., 2010) and independent component analysis (J. a. Wells et al., 2010). Fortunately, the dynamic ASL problem is even richer with opportunities for compressed sensing. The key hypothesis of this paper is that for dynamic ASL perfusion imaging, the similar spatial structure of images at different delay times and prior information about their temporal evolution can be exploited to improve image quality and perfusion parameter estimation. By using the sparsity of dynamic ASL perfusion images in the domain of a perfusion model, we can efficiently use the relationship between different time frames and not just reconstruct each frame separately. The resulting image reconstruction suppresses both random noise and artifacts, because they do not conform to the underlying perfusion model. The proposed method results in rapid and robust dynamic ASL imaging, as demonstrated below.

2. Methods

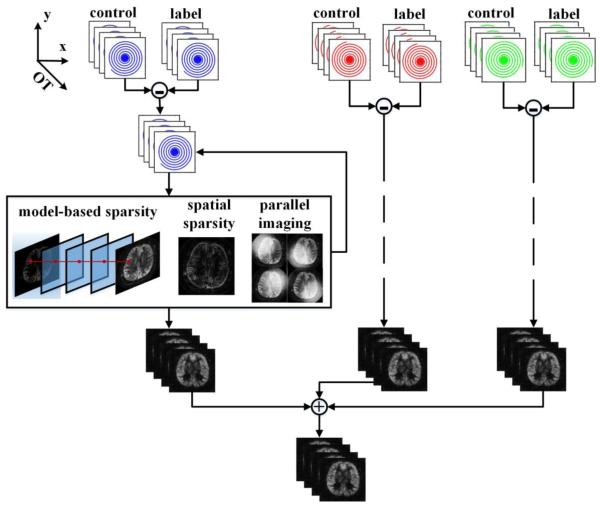
In dynamic ASL, perfusion images with the same CBF information are measured at multiple observation times (OTs). These measurements are conventionally reconstructed separately. But they can be reconstructed more efficiently by combining all of the dynamic frames with an ASL dynamic model.

2.1. Theoretical framework

2.1.1. Dictionary representation

Compressed sensing recovers images from noise or noise-like artifacts using a sparsity-promoting image reconstruction. This constrained optimization problem is usually solved by introducing Lagrange multipliers:

$$\widehat{x}=\text{arg}{\text{min}}_{\text{x}}\Vert F\mathit{x}-\mathit{y}{\Vert }_2+\lambda \Vert R\left(x\right){\Vert }_p$$ (1)

where x is the target image and y is the acquired data. F is a Fourier transform operator that includes the k-space sampling trajectory and under-sampling pattern. R(x) is the representation of x in the sparse transform domain, constrained in the minimization with norm p. λ is a regularization parameter.

Suppose the signal x can be represented by a linear combination of a few elements in the dictionary D, which contains n prototypes, D = {d₁,d₂, …, d_n}:

$$x=\sum _{i=1}^n{s}_i{d}_i+ϵ$$ (2)

where ϵ is the error tolerance, which limits the sparsity of the representation. s_i is the coefficient of prototype d_i and is an element of a sparse coefficient vector s = {s₁,s₂, …, s_n}, where most elements are zeros. Compressed sensing improves image quality by enforcing the sparsity of s, while maintaining data fidelity:

$$\widehat{x}=\text{arg}{\text{min}}_{\text{x}}\Vert F\mathit{x}-\mathit{y}{\Vert }_2+\lambda \Vert \mathit{s}{\Vert }_p$$ (3)

Additional sparsity constraints can be used to improve image quality. The total variation (TV) constraint is commonly used for noise suppression and image recovery. Based on an assumption that the object is piece-wise smooth, TV suppresses noise-like artifacts and maintains edge structure. With this additional constraint, the cost function becomes:

$$\widehat{x}=\text{arg}{\text{min}}_{\text{x}}\Vert F\mathit{x}-\mathit{y}{\Vert }_2+{\lambda }_1\Vert \mathit{s}{\Vert }_{p1}+{\lambda }_2\Vert TV\left(\mathit{x}\right){\Vert }_{p2}$$ (4)

2.1.2. ASL Model and over-complete dictionary

K-SVD (Aharon et al., 2006) is an algorithm for generating an over-complete dictionary D, which contains more prototypes than the dimension of the signal x. Compared with an orthogonal dictionary, such as one obtained by principle component analysis (PCA) (Huang et al., 2012), an over-complete dictionary leads to a sparser representation of the signal and improves compressed sensing performance on a signal of limited dimension, such as dynamic ASL, where only a few OT encoding steps are present because of the limited scan time.

The K-SVD algorithm builds up the signal prototype dictionary iteratively from a training data set. Because each tissue pixel will follow a valid ASL signal evolution pattern (Fig. 1), it can be described by prototypes based on the ASL dynamic model. Therefore, we trained the K-SVD dictionary with a synthetic dataset generated from an ASL signal model. By using a large number of signal prototypes representing the realistic range of possible ASL parameters, we can represent any expected signal. The K-SVD algorithm then distills the representation down to a smaller dictionary that can still represent any expected signal accurately as a linear combination of a small number of signal prototypes.

Fig. 1.

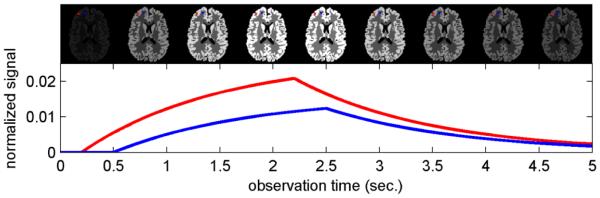
Evolution of dynamic ASL signals in a numerical phantom illustrating the underlying assumptions of this work. The signal from an individual pixel is temporally slowly varying. The dynamic signals in different pixels (blue and red) follow the same nonlinear perfusion model with different parameter values.

The following single-compartment perfusion model (Buxton et al., 1998; Dai et al., 2012) was used to generated the training data:

$$\Delta M\left(t\right)=2M_0\alpha f{T}_1\text{exp}\left(-\frac{\Delta t}{T_{1,b}}\right)Q\left(t\right)$$ (5)

$$Q\left(t\right)=\{\begin{array}{cc}0\hfill & 0<t<\Delta t\hfill \\ 1-\text{exp}\left(-\frac{t-\Delta t}{T_1}\right)\hfill & \Delta t\le t\le \Delta t+\tau \hfill \\ \text{exp}\left(-\frac{t-\tau -\Delta t}{T_1}\right)-\text{exp}\left(-\frac{t-\Delta t}{T_1}\right)\hfill & \Delta t+\tau \le t\hfill \end{array}\phantom{\}}$$ (6)

where ΔM is the dynamic ASL signal.

When generating the training data, we assumed α, the labeling efficiency, is 0.9; T₁, the longitudinal relaxation time of brain tissue, is 1500 ms (Alsop et al., 2015); and T_1,b, the longitudinal relaxation time of blood, is 1660 ms (Lu et al., 2004). M₀, the equilibrium magnetization of blood, was normalized to 1. Observation times t and blood bolus duration τ were set to the values used in the dynamic ASL experiment. To cover a range of possible acquired signals, the training data included 9600 ASL dynamic signals with CBF (f) 1-120 ml/100g/min and ATT (Δt) 50-4000 ms. The K-SVD algorithm generated 256 prototypes.

2.1.3. Compressed sensing solver

This image reconstruction problem is a nonlinear optimization problem. We apply the following four steps to solve this problem, as shown in Fig. 2:

Fig. 2.

Overview of model-based reconstruction. The acquired data corresponding to each spiral interleaf are processed separately. Each label image dataset is subtracted from the corresponding control image dataset to generate k-space data with ASL contrast. The ASL images are recovered in a model-based iterative reconstruction by pursuing model-based sparsity, spatial sparsity and data consistency across multiple-channel measurements.

1) Define x as the ASL perfusion-weighted image. The complex k-space data is subtracted pair-wise to get the data with ASL contrast. x0 is initialized by gridding and zero padding.

2) The multi-OT ASL images are projected onto the pre-trained dictionary D pixel by pixel. Orthogonal matching pursuit is used to enforce sparsity in the over-complete dictionary.

$$\begin{array}{cc}\hfill & \text{minimize:}\Vert \mathit{s}{\Vert }_0\hfill \\ \hfill & \text{subject}\text{to}\Vert \mathit{x}-\mathit{sD}\Vert <ϵ\hfill \end{array}$$ (7)

Q represents an image with sparsity enforced in the domain of the model-based dictionary:

$$\mathit{Q}=\mathit{sD}$$ (8)

3) The TV constraint is enforced by a shrinkage with a penalty method (Lingala et al., 2011).

$$\mathit{P}=\frac{TV\left(x\right)}{\Sigma \Vert TV\left(x\right){\Vert }_2}\text{max}\left(\Sigma \Vert TV\left(x\right){\Vert }_2-\frac{{\lambda }_2}{\beta },0\right)$$ (9)

4) A least-square function is solved by the conjugate gradient method to maintain data fidelity and enforce the constraints of model-based sparsity Q and total variation P.

$$\widehat{x}=\text{arg}{\text{min}}_{\text{x}}\Vert F\mathit{x}-\mathit{y}{\Vert }_2+{\lambda }_1\Vert \mathit{x}-\mathit{Q}{\Vert }_2+{\lambda }_2\Vert TV\left(\mathit{x}\right)-\mathit{P}{\Vert }_2$$ (10)

If in-plane k-space is undersampled for acceleration, we can recover the image by using information from multiple channels. SPIRiT (Lustig and Pauly, 2010) is an autocalibrated parallel reconstruction method that can be used with non-Cartesian trajectories. When using undersampled k-space, we combine the calibration consistency penalty and data fidelity terms:

$$\widehat{x}=\text{arg}{\text{min}}_{\text{x}}\Vert F\mathit{x}-\mathit{y}{\Vert }_2+{\lambda }_1\Vert \mathit{x}-\mathit{Q}{\Vert }_2+{\lambda }_2\Vert TV\left(\mathit{x}\right)-\mathit{P}{\Vert }_2+{\lambda }_3\Vert (\mathit{G}-I)x{\Vert }_2$$ (11)

where G is the SPIRiT calibration kernel.

Step 2-4 are repeated until the stopping criterion (improvement of cost function is less than 0.01% or maximum number of iterations) is satisfied.

2.2. Pulse-sequence design

2.2.1. Blood Tagging

Pseudo continuous arterial spin labeling (pCASL) (Dai et al., 2008) was used to tag and build the blood bolus. It achieves flow-driven inversion by repeating small flip angle RF pulses and gradients. The RF pulse train was built by repeating Hanning pulses of 500 µs duration with a 500 µs gap between them. The mean B1 amplitude was 1.63 µT, the slice-selective gradient amplitude was 5 mT/m, and the mean gradient amplitude was 0.2 mT/m, corresponding to η_b = 7% (Wu et al., 2007). Control and label scans were switched by controlling the phase of RF pulses. The tagging plane was placed 80 mm below the anterior commissure-posterior commissure line.

2.2.2. Background suppression

Background suppression was used in some experiments to reduce background artifacts and stabilize images (Dai et al., 2010; Maleki et al., 2011; Ye et al., 2000). A slab-selective saturation RF pulse with duration 10 ms was applied before the pCASL tagging pulse train. Two non-selective hyperbolic secant inversion pulses with duration 10 ms were applied after the pCASL tagging pulses and before data acquisition. The intervals between background suppression RF pulses were pre-calculated to minimize the maximum residual signal in white matter, gray matter, blood and CSF, with T1=1000, 1500, 1660 and 4200 ms at 3T, respectively.

2.2.3. Vessel Suppression

Adiabatic BIR-4 preparation pulses were used to suppress the vascular blood signal, because the intravascular signal often manifests as a bright spot in subtracted perfusion images and can result in over-estimation of CBF. To reduce the RF pulse duration and T₂ weighting, a single lobe crusher was used with gradient amplitude 22 mT/m, duration 5000 μs, and rise time 440 μs. For laminar blood flow, the maximum vessel velocity is 1.5 cm/s at the first zero-crossing of the attenuated sinc function (Duhamel et al., 2003).

2.2.4. Imaging Data

k-space data were collected with a stack-of-spirals trajectory using a 3D turbo spin echo (TSE) pulse sequence (Dai et al., 2008; Fielden et al., 2015). In-plane spiral readout gradients were inserted between hard RF refocusing pulses and phase encoding along the slice direction was performed centrically (Fig. 3a). Each echo in a particular TSE echo train collected the same spiral interleaf, with a collection of through-plane phase encodings sampled during the echo train. RF chopping between averages was used to achieve a better slab selection profile by rotating the phase of refocusing RFs by 180 degrees on even averages (Mugler, 2014). Two dummy scans were performed before ASL data collection to build up the steady state for the background signal.

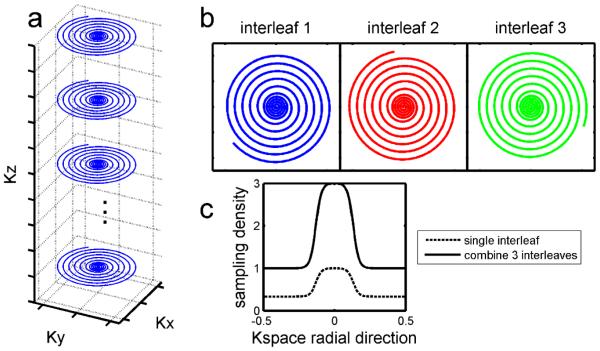
Fig. 3.

Dual-density 3D spiral k-space trajectory. In this 3D spiral TSE pulse sequence, each echo train samples a particular spiral interleaf while the z direction is encoded with a centric view order (a). Each dual-density spiral interleaf fully samples the center of k-space (dashed line in c), providing auto-calibration data for parallel image reconstruction. With different initial spiral angles (b), multiple interleaves can be combined into an oversampled k-space (solid line in c) and reconstructed by a simple gridding method for comparison with accelerated image reconstruction methods.

2.2.5. Single-shot parallel imaging

Parallel imaging was used to accelerate ASL imaging by exploiting redundant information among multiple receiver channels. A dual-density spiral trajectory was used to acquire k-space, with Nyquist sampling during the first 1/4 of the readout and under-sampling by a factor of 3 during the rest of the readout. The dual-density design covers a larger k-space area than a Nyquist-sampled constant-density spiral with similar readout length. Therefore, it enables single-shot imaging, reduces scan time, and improves motion robustness.

By rotating the spirals, multiple dual-density spirals can be combined to form an oversampled k-space (Fig. 3b and Fig. 3c). This data can be reconstructed by gridding in k-space, yielding a reference image reconstructed using a standard method. This reference image is similar to a conventional multiple-shot spiral scan and it will be compared to the proposed reconstruction using parallel imaging and compressed sensing methods.

2.3. Simulations

To demonstrate the performance of compressed sensing with a model-based constraint, a numerical phantom was used to mimic dynamic ASL imaging and CBF estimation. A high resolution T1 weighted image was segmented based on tissue probability maps (Ashburner and Friston, 2005) with published software SPM12 (http://www.fil.ion.ucl.ac.uk/spm/). White matter (WM) and grey matter (GM) ROIs were selected and their CBFs were assumed to be 20 and 50 ml/100g/min, respectively. This simulated CBF map was smoothed by a Gaussian kernel to provide a more realistic transition between tissues and to reduce the spatial resolution. The dynamic perfusion signal of each pixel was generated based on the local CBF value and calculated by the ASL dynamic model outlined above. Nine perfusion images were simulated at OT = 600, 1100, 1600, 2100, 2600, 3100, 3600, 4100 and 4600 ms. Other parameters were chosen as follows: normalized equilibrium blood signal M₀ = 1, tissue blood partition coefficient λ = 0.9, tissue T₁ = 1500 ms, blood T_1,b = 1660 ms, tagged bolus duration τ = 2000 ms.

The noiseless dynamic ASL images were projected onto the trained dictionary, so as to verify the accuracy and sparsity of the model-based dictionary. For noisy ASL images, we hypothesized the signal could be recovered by enforcing its sparsity on the dictionary. We tested this hypothesis by representing the noisy dynamic ASL images with only a few significant dictionary coefficients.

To test the performance of the model-based constraint with modest random variation of the object, we simulated an acquisition with random head motion. At OT = 3600 ms, the control images were independently translated in both the x and y directions by a random distance between −10 and 10 mm in 5% of the repetitions. Independently, 5% of label images were subjected to similar motion. Without background suppression, the control and label images have about 100-fold higher signal than the ASL signal. The mismatch between control and label images resulted in edge enhancement in the difference images, which typically dominated image contrast. Images acquired at other OTs were assumed to be motionless.

To verify the noise suppression of the proposed method, Gaussian noise was added, with σ = 0.002. The SNR was less than 10 based on the highest signal in all perfusion images and was lower for the early/late OTs and low perfusion regions. These images were transformed to k-space and reconstructed by the compressed sensing method. Spatial sparsity and model-based sparsity have separate effects on image quality. To verify additional improvement by introducing model-based sparsity, we reconstructed ASL images using spatial sparsity first and selected the Lagrange multiplier with the best performance. Then, the model-based constraint was added and evaluated.

Image structures and artifacts were also evaluated via root mean squared error (RMSE) and structural similarity index (SSIM) (Wang et al., 2004), compared to noiseless and motionless images.

2.4. In Vivo Measurements

Healthy volunteers were imaged on a 3 Tesla Siemens Trio scanner (Erlangen, Germany) with a 12-channel head coil receiver array and body coil transmission. The scans followed the protocol approved by the University of Virginia and written informed consent was obtained from each subject.

2.4.1. Lower SNR dynamic ASL protocol

To study the performance proposed method in an accelerated acquisition with associated lower SNR, we performed dynamic ASL with single-shot dual-density spiral trajectories and without background suppression. Six volunteers were imaged with following protocol.

For the multiple-OT ASL measurements, single-shot dual-density spiral scanning was used with an in-plane acceleration factor of 2. The spiral readout duration was 6 ms and the FOV was 200 mm, which gave a nominal spatial resolution of 4.5 × 4.5 mm². The whole brain was covered by 24 slices with thickness 4.5 mm. Four pairs of control and label images were averaged to improve SNR. Three repetitions of the dual-density spiral were performed with different initial spiral angles. TR was 5 s and TE was 22 ms. For each OT measurement, the scan time was about 2 minutes. We acquired 9 OT measurements sequentially with total scan time about 18 minutes.

To observe the early perfusion signal of a 2000 ms blood bolus, 9 OTs were designed by varying pCASL tagging durations and PLDs (Table 1). The entire bolus will be observed if the Design OT of the first time point is less than the ATT. More general designs related to this method have been reported for Hadamard tagging design (Dai et al., 2013; J. A. Wells et al., 2010).

Table 1.

Observation Time Design (ms)

Design OT	600	1100	1600	2100	2600	3100	3600	4100	4600
Bolus Duration	500	1000	1500	2000	2000	2000	2000	2000	2000
Sequence PLD	100	100	100	100	600	1100	1600	2100	2600

To improve CBF estimation, a saturation recovery sequence with the same 3D stack-of-spirals sequence and the same resolution was employed to measure a T₁ map. This sequence used two averages and was repeated 5 times with different TRs (1s, 2s, 3s, 4s and 5s) to acquire images with different T₁ weighting.

A T₁ map was calculated from the saturation recovery scans with multiple TRs. The images from each TR were reconstructed by SPIRiT. The equilibrium magnetization of the brain signal M₀ and the T₁ map was estimated by minimizing the least squared error of the saturation recovery equation:

$$M_{sat}=M_0\left(1-\text{exp}\left(-\frac{TR}{T_1}\right)\right)$$ (12)

To evaluate the performance of the proposed image reconstruction method, volunteer data were also reconstructed by a gridding method and a parallel imaging method with SPIRiT reconstruction. The residual error in CBF calculation and the SNR from the highest perfusion signal measurement were analyzed by the Wilcoxon signed-rank test. Two ROIs were chosen based on the T1 map: white matter (WM) 10-1300 ms and grey matter (GM) 1300-1900 ms.

To test the improvement in the CBF map by the proposed method, we compared the different reconstruction methods in a low SNR case. Low SNR images were obtained by using 1/3 of the data, where the first repetition of the dual-density spiral acquisition was chosen from the three repetitions. The gridding method, the parallel image reconstruction and the proposed method were used to reconstruct the ASL images, which provided the low SNR CBF maps. Because DSC images were not available, we treated the CBF map from all available ASL data as a high SNR gold standard. By comparing the similarity of CBF maps between high SNR and low SNR cases, we evaluated the performance of reconstruction methods and analyzed the results by the Wilcoxon signed-rank test across six volunteers.

2.4.2. Accelerated dynamic ASL protocol

Two additional experiments were performed to demonstrate accelerated dynamic ASL with background suppression, dual-density readouts and model-based image reconstruction.

The 3D stack-of-spirals trajectory was implemented with single-shot dual-density spirals with 7.2-ms readouts. These slightly longer dual-density readouts provided the same 4×4 mm² in-plane resolution while also providing calibration data necessary for autocalibrated parallel image reconstruction. The FOV was 200 mm and the in-plane resolution was 4×4 mm². 24 slices with thickness 4 mm were acquired. TR was 5.0-5.5 s and TE was 23 ms. Three repetitions of the dual-density spiral trajectory were acquired with different spiral rotation angles. Two averages resulted in scan time of approximately 60 s per OT measurement.

Nine measurements were acquired with OTs = 800, 1300, 1800, 2300, 2800, 3300, 3800, 4300 and 4800 ms. To observe the early perfusion signal of a 1800 ms blood bolus, 9 OTs were designed by varying pCASL tagging duration and PLD (Table 2).

Table 2.

Observation Time Design (ms)

Design OT	800	1300	1800	2300	2800	3300	3800	4300	4800
Bolus Duration	300	800	1300	1800	1800	1800	1800	1800	1800
Sequence PLD	500	500	500	500	1000	1500	2000	2500	3000

To quantify CBF, the equilibrium blood signal M₀ was measured by the same sequence at TR = 6 s, but without background suppression and flow suppression.

To validate the trade-off between acceleration and image quality, data from three repetitions of dual-density spiral scans were processed separately. When all three repetitions were included, ASL images were acquired in 60 s per OT measurement. When two of the three repetitions were used, scan time was 40 s per OT measurement, and when only one repetition was used, scan time reduced to 20 s per OT measurement.

2.4.3. CBF quantification

ASL images ΔM_i from multiple observation times OT_i were fitted to the dynamic ASL model with minimization of the least squared error, resulting in CBF and ATT.

Image reconstruction and data analysis were performed in MATLAB 2012b (The MathWorks, Inc.) on a 4x GTX 680 Workstation (Amax Information Technologies, Inc.) with 12 CPUs (Intel Xeon E5-2640 2.50GHz Processor LGA2011).

3. Results

3.1. Simulations

Simulated multi-OT ASL images represented by the over-complete dictionary and the associated approximation errors are shown in Fig. 4. The noiseless ASL signal was accurately approximated using just a few prototypes in the dictionary (Fig. 4a). More prototypes yielded improved signal approximation but also tend to approximate the noise, because of the low SNR of the ASL signal (Fig. 4b). In Fig. 4c, a noisy ASL signal (RMSE = 1.84e-3) was projected onto the dictionary and then represented by a few primary prototypes, which suppresses noise and recovers the signal (RMSE = 5.8e-4).

Fig. 4.

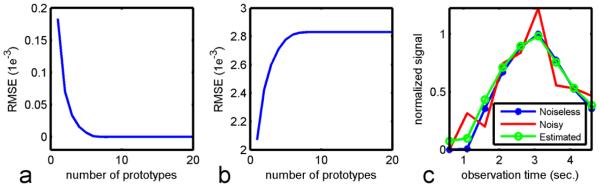
The trained dictionary represents the ASL signal. For noiseless data (a), only a few prototypes are needed to represent the signal with high accuracy. For noisy data (b), image denoising can be performed by projecting the signal onto a few prototypes. One selected ASL pixel illustrates that a dictionary representation can approximate the noiseless signal more accurately than the noisy signal itself (c).

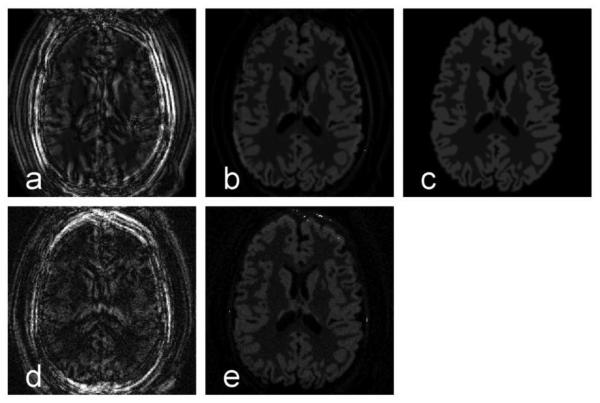
Fig. 5 shows that the model-based constraint reduced random artifacts. Modest rigid bulk motion resulted in ring-like artifacts around the brain and bright spots in the CSF region, as shown in noiseless ASL (a). Because this random motion artifact did not follow the ASL signal decay model, it was suppressed by the model-based dictionary (b). As a reference, the noiseless and motionless image is shown in (c). Similarly, in noisy data (d), the motion artifact and background noise were suppressed by projecting the dynamic signal onto the dictionary (e). Some motion artifacts remain near the CSF region, because some random noise and motion were dominant in the region with low perfusion signal. Some of these random variations fit the ASL model and thus were represented by the dictionary.

Fig. 5.

Model-based sparsity reduces artifacts in multi-OT ASL images. In the noiseless case, one of the dynamic ASL images contained motion artifacts (a) from subtraction between control and label images. By projecting the multi-OT signal onto the model-based dictionary, the motion artifact was reduced dramatically (b), because its dynamic pattern was distinct from the ASL model. As a reference, the noiseless and artifact-free image is shown in (c). Similar results were seen with noisy data (d, e). All images are windowed the same, demonstrating the magnitude of the motion artifacts.

The performance of constrained image reconstruction depends on the choice of Lagrange multipliers. To demonstrate the image quality improvement achieved by enforcing model-based sparsity, the multipliers were chosen in two steps. First, with a spatial constraint only, we searched for the best TV weight minimizing RMSE. It was an “L-curve” as shown in Fig. 6 (left) and the minimum RMSE was achieved with the TV weight 0.0033. Then, model-based sparsity was performed with images at 9 OTs and combined with this “best” TV. From Fig. 6 (right), the RMSE was further reduced and K-SVD achieved its best performance at weight 1.4.

Fig. 6.

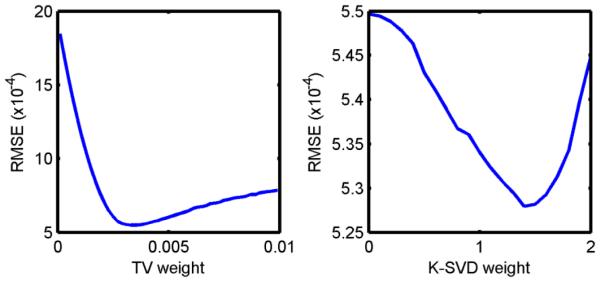
Regularization parameter searching in compressed sensing. Left: RMSE changed with spatial TV weights only. Based on the RMSE, the best TV weight was fixed at 0.0033. By adding the K-SVD constraint, the error is further reduced (right).

The above results are more clearly demonstrated in simulated ASL images (Fig. 7). Spatial TV (b) suppressed noise and improved the ASL image SNR. Model-based reconstruction (c) enforced the signal changes in OT encoding space towards the dynamic model and suppressed noise along the OT encoding dimension. The combination of the above two types of sparsity (d) improved the image quality further. Initial noisy (a) and ideal (e) images are also shown for reference.

Fig. 7.

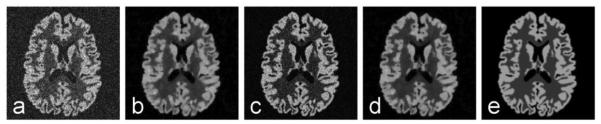
Simulated ASL images reconstructed by compressed sensing. The complex Gaussian noise in initial images (a) was suppressed by the compressed sensing reconstruction with spatial TV constraint (b) and model-based sparsity (c). By combining spatial and model-based sparsity, the image quality is improved further (d). The noiseless image (e) is shown for reference.

Quantitation of local SNR and estimation error are shown in Table 3. For all ROIs, the compressed sensing reconstruction increased the SNR and the model-based sparsity improved it further. Compared with the noiseless ASL signal, compressed sensing with spatial TV and model-based K-SVD constraints increased the image similarity, reduced the error from background noise in images by a factor of 3.8, and reduced the residual in perfusion maps by a factor of 2.4.

Table 3.

Improvement of ASL image quality and CBF maps by compressed sensing.

	SNR WM	SNR GM	Image SSIM	Image RMSE (e-4)	CBF RMSE	CBF fitting residual (e-4)
Initial	3.4	6.4	0.42	20.0	8.2	61.4
TV	25.4	45.0	0.71	5.5	5.9	25.3
Model	5.7	14.0	0.55	11.7	7.1	37.5
TV+Model	27.7	52.1	0.73	5.3	5.3	25.2

3.2. Experiments

Fig. 8 shows one slice from a dynamic ASL 3D image set acquired with a dual-density spiral trajectory and without background suppression. The conventional non-Cartesian gridding reconstruction (a) resulted in high background noise and motion artifacts. Parallel reconstruction with SPIRiT (b) reduced noise and stabilized the image. As in the simulations, the model-based reconstruction (c) suppressed the noise in the background and improved the SNR of experimental ASL images.

Fig. 8.

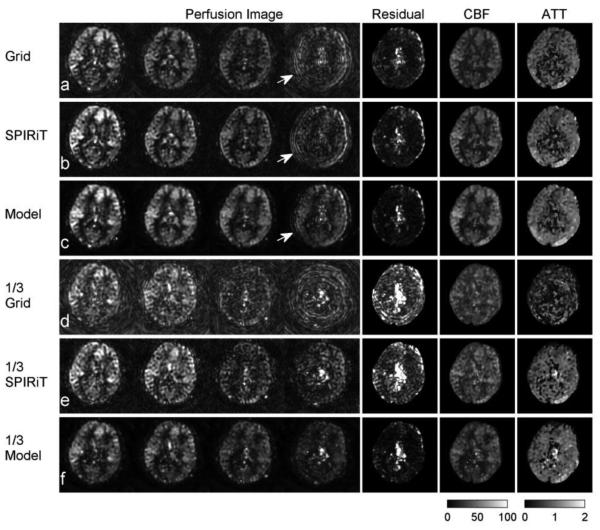
Dynamic pCASL perfusion images from selected OTs (2600, 3100, 3600, 4100 ms) in a normal volunteer. The gridding reconstruction (a) shows high motion artifacts and background noise. The SPIRiT reconstruction (b) eliminated many of the artifacts in the gridding reconstruction. The model-based reconstruction suppressed background noise and reduced the estimation error in the CBF (c). As the arrow highlights, the motion artifacts obtained using the gridding method (a) and SPIRiT reconstruction (b) were suppressed when the model-based sparsity constraint was used (c). When using only 1/3 of the acquired data and reducing the scan time to 40s at each OT, the SNR of perfusion images dropped substantially in the Grid (d) and SPIRiT (e) reconstruction and there was more fitting error, as shown by the CBF calculation residual. Again, the proposed method improved the images, reduced the fitting error, and provided a similar CBF map to the high-SNR results (f). Units: Dynamic model fitting residual (a.u.). CBF maps (ml/100g/min). ATT maps (seconds).

The proposed method also corrected artifacts. As highlighted by the arrows in Fig. 8, the brain had a slight mismatch between control and label measurements, which resulted in ring-like motion artifacts. Because the motion occurred irregularly, the model-based constraint reduced the artifact because it had a poor representation in the model-based dictionary. The model-based constraint can suppress motion at a single OT, because the model information can be provided by images at other OTs. If more of the ASL images contained artifacts or the artifacts were more severe, the proposed method might fail to detect the perfusion signal.

The CBF maps are shown on the right of Fig. 8. In the residual maps of CBF fitting, the proposed method reduced the residual in GM and WM regions, compared with the gridding and parallel image reconstructions. It also reduced the error from CSF, which does not contain perfusion signal, and the edge of brain, which exhibits motion artifacts.

To show the improvement in accuracy of the proposed method, we considered the high SNR result from all the acquired data to be a gold standard and compared the CBF map from only one third of acquired data to it, which reduced the total scan time from 18 minutes to about 6 minutes for nine OTs. A conventional gridding reconstruction (d) is not feasible for this data set, because k-space is undersampled and thus the resultant images would suffer from aliasing. The model-based reconstruction (f) was more stable, had higher SNR, and lower fitting error than the parallel image reconstruction (e). The proposed method results in a CBF map that provides a much closer approximation to the high SNR results (a, b, c).

Fig. 9 shows the statistical analysis of the six volunteers’ images with the low SNR protocol. Fig. 9a shows SNR improvement using the proposed method. In the gray matter region, the proposed method significantly improved the SNR (P < 0.05) compared with gridding and parallel image reconstruction. Fig. 9b shows the model fitting residual of CBF estimation in the volunteers. The proposed method resulted in less estimation error versus parallel and gridding reconstruction in white matter (P <0.05). Also, significant improvement was achieved in the grey matter compared with parallel imaging. Treating the high SNR CBF map from all available data as a gold standard, the CBF maps from only 1/3 of data were evaluated by the similarity index, as shown in Fig. 9c. The proposed method resulted in significantly higher similarity to the high SNR results.

Fig. 9.

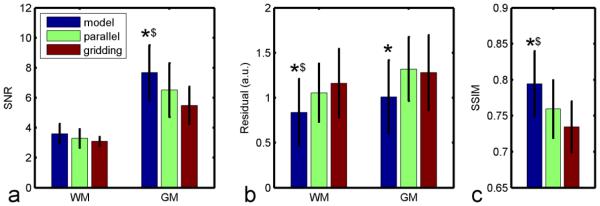
ASL image SNR and CBF estimation residual in volunteers (N = 6, mean ± standard deviation). ROIs of grey matter (GM) and white matter (WM) were chosen based on T1 value. Compared with gridding and parallel image reconstruction, the proposed method improved SNR (a) and reduced estimation residuals (b) significantly. With 1/3 of the data, the proposed method also provided better structural similarity to the high SNR results (c). (In the same ROI, * P < 0.05 versus the parallel reconstruction method; ^$ P < 0.05 versus the gridding method).

Figures 10 and B show the experimental results using the accelerated dynamic ASL protocol with single-shot 3D stack-of-spiral k-space trajectories and background suppression. The proposed method reduced the background noise and model regression residual in the 60 s / OT scan. With an acceleration factor of 1.5, the proposed method largely maintained the image quality and accuracy of the CBF map when the scan time was reduced to 40 s / OT. Acceleration by a factor of 3 further reduced the scan time to 20 s per OT measurement. It resulted in more error in the CBF calculation, but even this short scan time yielded high quality for the ASL images and CBF map.

Fig. 10.

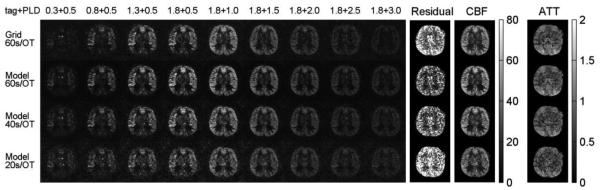
Accelerated dynamic ASL with model-based reconstruction, single-shot 3D spiral k-space trajectories and background suppression. With a scan time of 60 s / OT measurement, the model-based reconstruction reduced the background noise and model residual (mean residual = 4.6e-6), compared with conventional gridding reconstruction (mean residual = 7.1e-6). The proposed method maintained the image quality with a scan time of 40 s / OT (mean residual = 5.7e-6) and provided moderate image quality with a 20 s / OT measurement (mean residual = 9.5e-6). Units: Dynamic model fitting residual (a.u.). CBF maps (ml/100g/min). ATT maps (seconds).

In Figure 11, we show the 3D coverage of dynamic ASL results in the second case (Appendix Fig. B), with 20s per frame scan and model-based reconstruction. The accelerated protocol had somewhat lower SNR in the white matter region as expected. Nonetheless, the proposed method yielded high quality dynamic 3D ASL images and parameter maps from nine perfusion phases in three minutes.

Fig. 11.

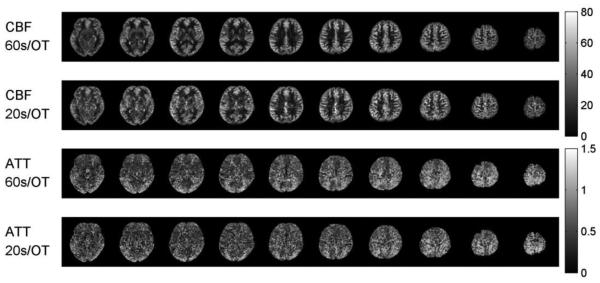
3D CBF and ATT maps for the second case of accelerated dynamic ASL. CBF maps (ml/100g/min). ATT maps (seconds).

4. Discussion

This work presents a model-based image reconstruction for dynamic ASL perfusion imaging. The method was combined with single-shot 3D spiral acquisition and parallel imaging, yielding whole-brain dynamic ASL image acquisition in 20 seconds per time frame with an acceleration factor of 3. In this method, prior knowledge of the dynamic ASL signal time course was exploited to distinguish the ASL signal from noise and random motion artifacts. This model-based image reconstruction method improved ASL image quality and robustness and yielded accurate CBF estimates.

One contribution of this work is the demonstration of the acceleration of spiral k-space scanning methods using non-Cartesian parallel image reconstruction. This enables single-shot 3D spiral ASL image acquisition with sufficient spatial resolution, which in turn increases robustness to motion. The value of single-shot 3D imaging using parallel imaging has previously been demonstrated using 3D GRASE techniques (Wang et al., 2013). This work demonstrates further improvements in image quality and parameter map accuracy by combining parallel imaging with model-based compressed sensing reconstruction.

As a reconstruction strategy, the proposed method is compatible with most current techniques in dynamic ASL. While this study focused on spiral scanning, the proposed method could easily be adapted to use Cartesian readouts, such as 2D echo planar imaging or 3D GRASE. Background suppression was used in some of our experiments to further suppress artifacts and improve image quality. While the model-based reconstruction intrinsically suppresses artifacts, motion compensation would further improve the robustness of the method. The method could be combined with new RF labeling pulse techniques, such as Hadamard encoding (Dai et al., 2013; J. A. Wells et al., 2010).

Model-based sparsity assumes the signal in each pixel follows a given dynamic ASL model, with the parameters of the model varying from pixel to pixel. Although CBF is a linear scale factor in the dynamic model used in this study, the model is a nonlinear function of ATT. Therefore, we used a dictionary learning method, which provides a general approach for model-based reconstruction. This method can easily be adapted to other ASL models. Here, we chose the basic CASL model (Buxton et al., 1998). An improved model could describe perfusion more accurately, for example by including an arterial input function (AIF) with dispersion (Calamante, 2013) or a measured AIF (Petersen et al., 2006), but a complex dynamic perfusion model could also require higher image quality and more OT measurements to estimate the parameters precisely, thus increasing imaging time.

The K-SVD method enforces the sparsity of the low-dimensional signal of ASL using an over-complete dictionary. The training data set included signal prototypes based on all reasonable values of the perfusion parameters (CBF and ATT). More accurate parameter ranges can be determined based upon a particular application, which would improve the sparsity and accuracy of representation in the dictionary. More prototypes in the K-SVD dictionary may further improve the sparse representation, but would also increase the computational complexity for the orthogonal matching pursuit and prolong image reconstruction time. Moreover, in our work, minor differences were noticed between dictionary sizes ranging from 32 to 512. Other parameters in the perfusion model are assumed as prior knowledge, which are conventionally used in model fitting. The dictionary is resistant to the error of scaling parameters, such as labeling efficiency, because the ‘learning’ process of the elements in dictionary is normalized. This is also true for the DC component, which is removed before dictionary training. Error of other parameters, such as T₁, can be seen as errors in the model in the training step. This kind of error could make the dictionary converge to the wrong prototypes, which could spread into both ATT and CBF maps.

In this work, we used direct model fitting to calculate CBF and ATT. The proposed dictionary training can be also seen as a method to further simplify the model. To further improve the estimation, we could use a simple model to constrain the reconstruction, and then use a more comprehensive model for quantification, which could account for variations in model parameters. For example, it has been reported that a Bayesian model can improve the estimation of CBF (Chappell et al., 2009; Santos et al., 2011). These methods could be combined with the proposed method to improve estimation of perfusion parameters.

The TV sparsity used in this study is a technique commonly used in MR anatomical image reconstruction. However, the weight of the TV sparsity term was carefully chosen in this study for ASL images. The optimal weights for the sparsity terms depend on the SNR level and the amount of motion, but we did not adapt the weights on an image-by-image basis. An improperly weighted sparsity term can result in either image artifacts (by overweighting sparsity) or limited improvement (by underweighting sparsity). This is a limitation of the algorithm proposed in this paper, and more generally in many constrained image reconstruction methods. The best strategy for choosing regularization parameters is still an open question.

In the compressed sensing reconstruction, the model-based sparsity limits the way we prepare the initial k-space data . Perfusion contrast in ASL is obtained by subtracting tagged images from control images. The low SNR in perfusion images makes it difficult to distinguish signal from noise. Therefore, to maximize the performance of spatial sparsity, one might propose to apply the compressed sensing reconstruction to control and label images separately prior to subtraction. However, because the ASL signal is less than 1% of normal MR images, the dynamic evolution of ASL is too small to extract from the background signal before subtraction, so it would be difficult to exploit model-based sparsity based on component images. Therefore, in this work, we subtracted the k-space data of the label images from that of the control images as the first step in the image reconstruction. This complex subtraction may be less robust than magnitude subtraction, because it is more sensitive to variations in signal phase.

This work used a pCASL tagging method with the length of the tagging pulse reduced for early observation times. This tagging scheme made it possible to begin measuring the ASL signal when only part of the blood bolus has arrived at the tissue of interest (Table 1). This in turn makes it possible to catch the rising edge of the perfusion signal and to detect short ATT values. So, changing the length of the tagging pulse has advantages in the design of dynamic pCASL experiments, but it does change the perfusion bolus duration. The alternative would be a more conventional design with constant perfusion bolus duration and variable post-label delay. The reliability and accuracy of this variable perfusion bolus technique should be further evaluated in a future study.

The acceleration factors quoted throughout are defined based on k-space undersampling factors, and thus measure the reduction in the minimum scan time relative to a fully-sampled scan that uses a conventional image reconstruction. This is one measure of the performance of the proposed method, but it is also important to consider the effect of the method on the SNR of the ASL images and on the accuracy of the resulting CBF maps. While it is clear that the method improves the apparent SNR for a given scan time, it is more difficult to make general statements about how the SNR varies with scan time. Because compressed sensing is a not a linear algorithm, the model-based reconstruction has more effect on the first and last frames of a dynamic image set than on the central high-SNR frames, as shown in Figs. 10, A and B. In addition, because the proposed method can reduce motion artifacts, this can also contribute to an improvement in the apparent SNR. Experimentally, we observed that the CBF accuracy is clearly better with an acceleration factor of 1.5 using the proposed method than with fully sampled data reconstructed using gridding. This is quantified by the mean CBF fitting residual in the captions of Figs. 10 and B. With an acceleration factor of 3, the accuracy is somewhat lower in Fig. 10 and slightly lower in Fig. B. Thus, based on this data, it appears that an acceleration factor between 2 and 3 is possible using this method without loss of accuracy, but more studies would be needed to confirm this.

This study used equally spaced observation times. However, CBF estimation accuracy might be improved by optimal observation-time design (Xie et al., 2008; Zhao and Meyer, 2013, 2012). Non-equally-spaced sampling in the parameter encoding space might break the assumptions of some sparsity constraints, such as temporal TV, but it can be adapted into model-based sparsity by proper dictionary training.

The computation time for the proposed model-based image reconstruction is relatively long, which is true of many compressed sensing techniques. For four-channel data, the computation time with the current MATLAB implementation is about 20 minutes for one slice at nine time points. This would be a significant limitation in a clinical setting. The computation time can be reduced by optimizing the algorithm, implementing it in C/C++, and employing a graphics processing unit (Murphy et al., 2012).

The numerical phantom used in the simulations was used only to prove the concept of model-based reconstruction, and it has some limitations as a general ASL phantom. One limitation is that experimental ASL images have greater partial volume effects at tissue interfaces than the phantom. Using a tissue probability map directly rather than using it for image segmentation could generate a more accurate low-resolution ASL image. However, the proposed method enforces model-based sparsity at each pixel. Therefore, partial volume effects should have a minor impact on the conclusions drawn from the simulations. A related point is that an improved model including partial volume effects (Chappell et al., 2011) could be incorporated into the proposed method and could improve the quantification of CBF.

5. Conclusions

This work introduces model-based compressed sensing to improve ASL image quality and CBF accuracy. By enforcing sparsity in the observation-time encoding domain, noise and motion artifacts were suppressed and the estimated CBF maps were more accurate. When combined with single-shot 3D spiral scanning and background suppression, the proposed method reduces the scan time of whole-brain dynamic ASL to as short as 20 seconds per time frame.

7. Appendices

7.1. Standard dynamic ASL protocol

The proposed method focuses on new image reconstruction techniques. It was validated by comparing it to a standard ASL imaging protocol with background suppression and conventional image reconstruction. Two volunteers were imaged with the following protocol.

The 3D stack-of-spirals trajectory was implemented with three interleaved constant density spirals with 6-ms readouts. The FOV was 200 mm and the in-plane resolution was 4×4 mm². 24 slices with thickness 4 mm were acquired. TR was 5.0-5.5 s and TE was 23 ms. Control and label images were acquired with two averages, resulting in a scan time of approximately 60 s per OT measurement. Nine measurements were acquired with the OTs given in Table 2.

Fig. A shows the performance of model-based image reconstruction on two volunteers’ dynamic ASL scans with background suppression and constant-density spiral readouts. With background suppression, ASL images have good SNR at PLD = 0.5, 1.0 and 1.5 seconds, with a 60 s scan per OT measurement. Compared with the standard ASL reconstruction method, the proposed method further suppressed the background noise in the ASL images (as highlighted by the arrows in the first volunteer’s results) and provided better contrast between white matter and gray matter. It also recovered missing structures, as highlighted by the arrows in the second volunteer’s results. More importantly, the proposed method largely reduced the residual in the model regression in both cases, corresponding to more accurate CBF and ATT maps.

Fig. A.

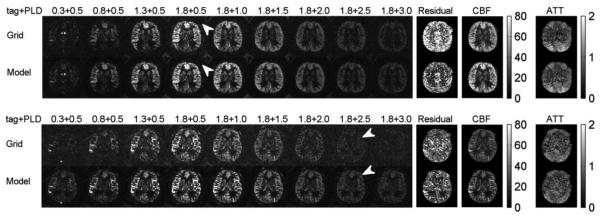
Performance of model-based image reconstruction on dynamic ASL images with background suppression for two volunteers. Each image was reconstructed using the standard gridding method and the proposed method. For each subject, the top two rows show ASL images at 9 OTs, and the bottom two rows show the CBF and ATT maps calculated from these images using different methods. The arrows illustrate regions with improved SNR with the proposed method. With the model-based constraint, the proposed method suppressed the background noise and reduced the residual in perfusion model regression. Units: Dynamic model fitting residual (a.u.), CBF maps (ml/100g/min) and ATT maps (seconds).

7.2. Additional results using the accelerated dynamic ASL protocol

Fig. B shows the results from a scan of a second volunteer using the accelerated dynamic ASL protocol. The results can be compared to those of Fig. 10.

Fig. B.

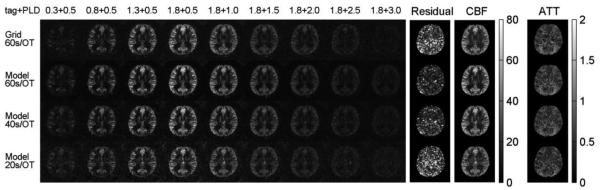
Second case of accelerated dynamic ASL with model-based reconstruction, single-shot 3D spiral k-space trajectories and background suppression. Results from the first case are shown in Fig. 10. The residual in the 60s scan and conventional reconstruction with gridding method (mean residual = 4.2e-6) was reduced by the model-based constraint (mean residual = 2.3e-6). The quality of images was maintained with 40 s / OT (mean residual = 2.7e-6) and 20 s / OT (mean residual = 4.3e-6). Units: Dynamic model fitting residual (a.u.). CBF maps (ml/100g/min). ATT maps (seconds).