Estimation of effect size distribution from genome-wide association studies and implications for future discoveries

Abstract

We report a set of tools to estimate the number of susceptibility loci and the distribution of their effect sizes for a trait on the basis of discoveries from existing genome-wide association studies (GWASs). We propose statistical power calculations for future GWASs using estimated distributions of effect sizes. Using reported GWAS findings for height, Crohn’s disease and breast, prostate and colorectal (BPC) cancers, we determine that each of these traits is likely to harbor additional loci within the spectrum of low-penetrance common variants. These loci, which can be identified from sufficiently powerful GWASs, together could explain at least 15–20% of the known heritability of these traits. However, for BPC cancers, which have modest familial aggregation, our analysis suggests that risk models based on common variants alone will have modest discriminatory power (63.5% area under curve), even with new discoveries.

Although GWASs have been successful in identifying susceptibility loci for over 125 complex traits in humans, the variants discovered thus far explain only a modest proportion of the heritability of these traits¹. The debate over the value of conducting more GWASs with current genotyping platforms has contrasted the benefits of discovering new regions for understanding biology with the diminishing returns of identifying new loci that have progressively smaller estimated effect sizes and thus marginal value for risk prediction^2,3. Nevertheless, the research community is converging into consortia for large meta-analyses, which promise to discover additional loci missed in the first generation of GWASs owing to relatively small sample sizes. Already, large-scale pooling and meta-analyses of common diseases and traits have successfully found additional new loci. The falling cost of fixed-content array genotyping technology is also fueling efforts to launch new GWASs. In addition, development of next-generation genotyping and sequencing platforms, together with the completion of 1,000 Genomes Project, will soon enable the investigation of uncommon and rare variants.

As data from recent GWASs suggest, complex traits are associated with a spectrum of susceptibility loci that contribute to heritability. Once the first studies have been conducted, a challenge for second-generation GWASs is that the undiscovered susceptibility loci are expected to have smaller effect sizes, because those with large effect sizes—the low-hanging fruit—have already been detected. How large should future GWASs be to detect a substantial number of as-yet-unidentified susceptibility loci?

Standard power calculations are inadequate for addressing the potential discoveries of future GWASs because they evaluate the probability of detecting a single susceptibility locus with a fixed effect size. Here, in contrast, we calculate the expected number of discoveries for future GWASs by integrating power over the number of unidentified susceptibility loci that probably exist, accounting for the distribution of relative risk and allele frequency.

One of the early promises of the GWAS approach was more accurate models for risk prediction based on genetic profiles⁴. Theoretical calculations based on estimates of total genetic variances have indicated that the potential benefit of such models could be large for chronic diseases such as breast cancer⁵. Recent reports, however, have noted that the known common susceptibility loci do not discriminate well for risk prediction^6–10. Some have speculated as to how many additional common loci, with specific effect sizes, would be required to substantially improve the risk model in the future^6,7,11. However, no report, to our knowledge, has used empirical evidence to assess the number of loci that are likely to be associated with a given disease, and the distribution of their effect sizes.

We show here how to use data from existing GWASs to evaluate the power and risk-prediction utility of future studies. To demonstrate and validate the utility of the method, we estimate the distribution of effect sizes for common SNPs identified in several recent GWASs. The distribution of effect sizes seen in current GWASs is skewed because of the bias in favor of larger effect sizes, for which power is greater. We correct for such bias by relying on the observation that the number of susceptibility loci with a given effect size that could be expected to be discovered in a GWAS is proportional to the product of the power of that study with that effect size and the total number of underlying susceptibility loci that exist with similar effect size. We obtain an estimate of the number of susceptibility loci with different effect sizes for a trait, using the number and empirical distribution of observed effect sizes of known loci and the power of the original discovery samples at those effect sizes. We report nonparametric and parametric methods for extracting information from published GWASs and describe how to use these estimates to evaluate power and risk-prediction utility.

We apply these methods to publicly available data from GWASs of height, Crohn’s disease and three cancer sites: breast, prostate and colorectal. On the basis of the estimated distribution of effect sizes, we project sample sizes required for a GWAS to identify these associations. For Crohn’s disease and the cancers, we estimate the discriminatory accuracy of risk models. Our projections provide insight into the scale of effort that GWASs will require for both discovery and risk prediction using common variants. Potential applications of the methods for studies of rare variants are also discussed.

RESULTS

Height

Adult height is known to be highly heritable, and 80–90% of its variance can be explained by genetics¹². Three recent large GWASs reported 54 susceptibility loci for height from a total of 63,000 subjects of European ancestry^13–15. Although many of these 54 detected loci reached genome-wide significance in the initial scans of between 13,000 and 31,000 subjects, others were discovered in follow-up genotyping of promising signals. In this report, we have included 30 loci that reached genome-wide significance (P < 10⁻⁷) in the initial scans, to obtain an unbiased estimate of effect sizes (Supplementary Table 1) based on the replication sets. Although this strategy excludes some susceptibility loci, our estimation method was not biased for selection of SNPs, as it automatically adjusts for power to accommodate the chosen selection strategy.

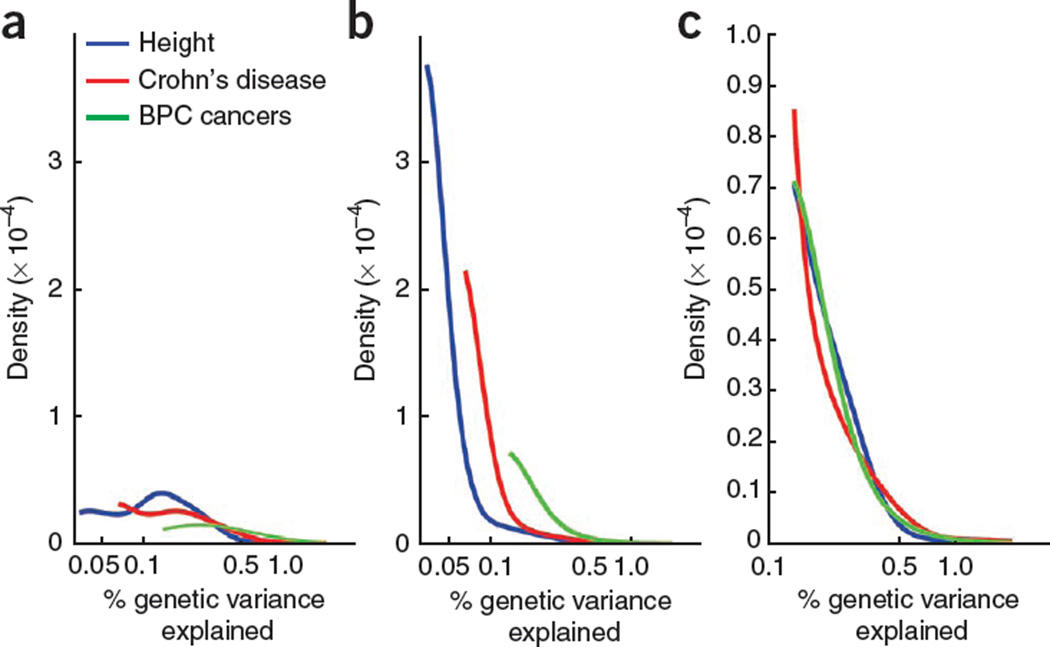
Figure 1 shows the effect of adjusting for power for the identified susceptibility loci in estimating the density of all underlying SNPs. The density of the effect sizes for the observed SNPs initially increases with decreasing effect sizes, reaches a peak and then decreases at the lowest size range. The estimated density of effect sizes for all underlying SNPs, in contrast, continues to increase at an accelerating rate as the effect size decreases. The density of the currently identified SNPs is biased, compared to the density of all underlying SNPs, owing to the lower probability that SNPs with smaller effect sizes will be identified.

Figure 1.

Nonparametric estimates for distributions of effect sizes for susceptibility loci. (a) Curves based only on observed susceptibility loci; these curves are distorted because loci with larger effect sizes are more likely to have been detected. (b) Curves based on estimated susceptibility loci, representative of the population of all susceptibility loci. (c) Estimated nonparametric distributions after normalization over the common observed range for the three traits.

We estimate that 201 (95% confidence interval (CI): 75, 494) SNPs exist for height in the range of effect sizes observed in current GWASs and that, together, they could explain approximately 16% (95% CI: 11%, 31%) of genetic variance for adult height (Table 1). This estimated distribution of effect sizes suggests that the cumulative number of loci that could be expected to be discovered in future GWASs increases linearly¹⁶ with increasing sample size, whereas the associated percentage of genetic variance explained increases at a decelerating rate, because the additional loci discovered in larger studies will tend to have smaller effect sizes (Table 2). Sample size calculations based on the estimated distribution of effect sizes suggest that it is important for study designs to account for already identified loci from past studies if they are to have sufficient power to detect novel loci (Table 3). For example, the calculations show that whereas the first GWAS of height would have required a sample size of n = 24,800 for the detection of 25 loci with 80% power, a new study would require a sample size of n = 40,100 for the discovery of the same number of new loci with similar power, given that many loci are now already known for height. Further, we find that the effect on the expected number of discoveries from increasing the density of genotyping platforms is relatively modest for white populations but possibly substantial for African-American populations (Supplementary Table 2).

Table 1.

Estimated numbers of common susceptibility SNPs, and associated genetic variances explained, for three complex traits

	Estimated number of total loci (95% CI)	Total GVa explained by estimated loci (95% CI)	Observed range of effect sizes (% GV)
Height	201 (75, 494)	16.4 (10.6, 30.6)	0.04–1.13
Crohn’s disease	142 (71, 244)	20.0 (15.7, 28.0)	0.07–1.96
BPCb cancers	67 (31, 173)	17.1 (11.6, 35.8)	0.14–1.82

All the projections were performed using a nonparametric method and are restricted to the range of observed effect sizes for known susceptibility SNPs (shown in the last column).

^aAll genetic variances (GV) are shown as a percentage of the total variance of the trait attributable to heritability. For Crohn’s disease and BPC cancers, the variance due to heritability is computed from estimates of sibling relative risk using a log-normal model for risk⁵.

^bAll estimates should be interpreted as averages over the three cancers.

Table 2.

Cumulative number of susceptibility loci expected to be discovered from a single-stage GWAS with increasing sample sizes

Height			Crohn’s disease			BPCc cancers
Sample size	Expected number of discoveries	Expected GVa explained	Sample sizeb	Expected number of discoveries	Expected GV explained	Sample sizeb	Expected number of discoveries	Expected GV explained
25,000	27.4	6.6	10,000	26.0	11.1	10,000	2.8	2.8
50,000	74.6	10.3	20,000	64.4	14.6	20,000	10.1	5.8
75,000	125.7	13.2	30,000	108.2	17.7	30,000	21.2	8.7
100,000	161.6	14.9	40,000	132.7	19.3	40,000	33.6	11.4
125,000	182.9	15.7	50,000	140.1	19.8	50,000	44.5	13.5

The projections were obtained by accounting for the estimated distribution of effect sizes for the traits. All calculations are based on a significance level for discovery of 10⁻⁷.

^aAll genetic variances (GV) are shown as a percentage of the total variance of the trait attributable to heritability. For Crohn’s disease and BPC cancers, the variance due to heritability is computed from estimates of sibling relative risk using a log-normal model for risk⁵.

^bSample size assumes 50% affected individuals and 50% controls.

^cAll estimates should be interpreted as averages over the three cancers.

Table 3.

Sample size required for detecting novel loci in first or later studies

Height		Crohn’s disease		BPC cancers
No. of novel loci	Sample size (first study/later study)	No. of novel loci	Sample size (first study/later study)	No. of novel loci	Sample size (first study/later study)
25	24,800/40,100	15	6,700/14,000	5	15,500/25,100
50	39,800/53,000	30	11,900/18,300	10	21,700/31,000
75	52,100/65,300	45	16,300/21,900	15	26,600/35,900
100	63,900/79,100	60	19,800/25,300	20	31,000/40,600
125	77,000/96,800	75	23,100/28,900	25	35,100/45,400

Shown are sample sizes required for a single-stage GWAS to have 80% probability of detecting the specified number of novel loci (or more), when it is either the first study (all loci will be novel) or a later study (‘novel’ loci exclude known susceptibility loci detected in earlier studies), with a significance level of 10⁻⁷. For ‘later studies’, only SNPs used for the estimation of the effect size distribution were excluded. For a number of these traits, there are known additional loci, and thus the sample-size requirement for later studies is expected to increase when all known susceptibility loci are accounted for.

Crohn’s disease

Crohn’s disease is a common inflammatory bowel disease that has high heritability, with a sibling relative risk (λ_sib) estimated at between 20 and 35. A recent multistage genome-wide association study with 13,532 subjects of European ancestry has identified ~30 independent susceptibility loci for this trait¹⁷. The first stage was a scan of 3,230 affected individuals and 4,829 control subjects; in a second stage, 74 independent regions (P < 5 × 10⁻⁵) were genotyped in 2,325 additional affected people and 1,809 population-based controls, alongside 1,339 independent case-parents trios. In the present study, we included 32 susceptibility SNPs that reached genome-wide significance in the combined analysis of first- and second-stage population-based studies, and we obtained estimates of their effect sizes from the independent case-parent trios. We calculated the power of the SNPs at the estimated effect size, following the two-stage design with alpha levels of 5 × 10⁻⁵ for the first stage and 10⁻⁷ for the second stage (Supplementary Table 3). We excluded five outlier SNPs that had extremely small effect sizes compared to the rest (see Supplementary Note for sensitivity analysis).

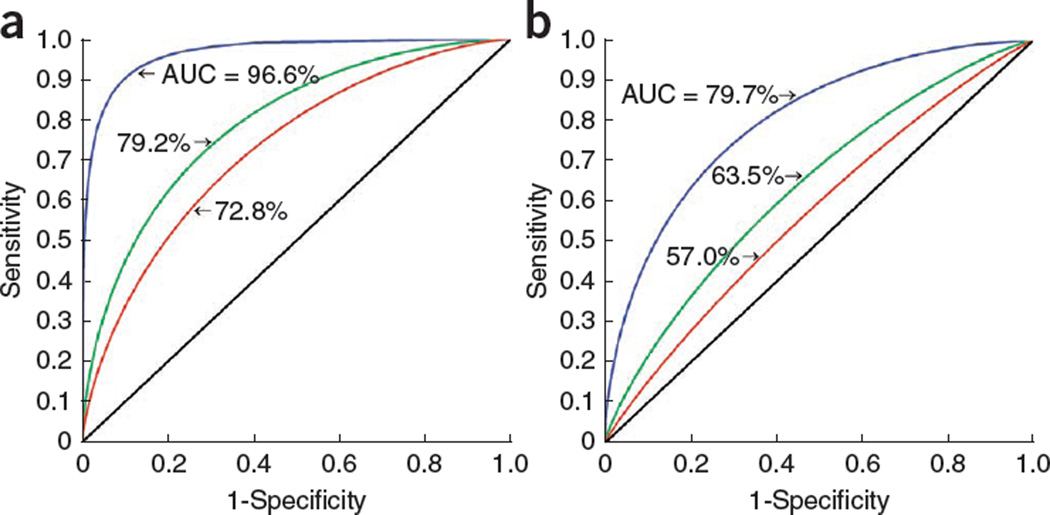
We estimated that a total of 142 (95% CI: 71, 244) independent susceptibility loci exist for Crohn’s disease within the range of effect sizes seen in the current GWASs. These loci together could explain 20% (95% CI: 16%, 28%) of genetic variance for the trait. On the basis of the estimated distribution of effect sizes, we projected that a future risk model for Crohn’s disease that could include all of the 142 estimated loci would have an area-under-curve (AUC) value (Fig. 2) of 79.2% (95% CI: 76.4%, 83.2%). In contrast, the AUC is 72.8% for a model that includes only ~30 currently known SNPs, and 96.6% for an idealized model that could explain the majority of genetic variance of Crohn’s disease.

Figure 2.

Receiver operating characteristic curves for genetic risk models. (a,b) Curves for Crohn’s disease (a) and BPC cancers (b). AUC is a measure of the discriminatory power of the risk model. Blue, a theoretical genetic risk model that explains all of the known familial risk of the trait. Green, a risk model that includes all of the susceptibility loci (142 for Crohn’s disease and 67 on average for BPC cancers) estimated to exist within the range of effect sizes seen in the current GWASs. Red, a risk model that includes only known susceptibility loci (~30 for Crohn’s disease and ~7 on average for each of the BPC cancers), which we used to estimate the distribution of effect sizes of these traits. Black, reference line corresponding to a model without discriminatory power in which cases have the same distribution of risk as controls.

Breast, prostate and colorectal cancers

BPC cancers are common and are known to have modest heritability, with estimated sibling relative risks between 2 and 3 (ref. 18). Recent GWASs have reported susceptibility loci for each cancer with comparable ranges of effect sizes. Compared to height and Crohn’s disease, however, fewer loci have been discovered. Assuming a similar genomic architecture for each, we improved precision by obtaining averaged estimates for the number and distribution of effect sizes over these three traits. Our analysis included 20 susceptibility loci for cancers, reported in studies based in the UK^19–21; five of these loci are associated with breast, five with prostate and ten with colorectal cancers (Supplementary Table 4). All three case-control studies used selective sampling of cases by family history or age at onset, or both, ostensibly rendering standard power calculations inappropriate. We used power estimates for the breast cancer SNPs reported in the original publication and obtained effect size estimates for the same SNPs using only the third stage of the study. Similarly, for colorectal cancer, we used the power estimates for ten SNPs and the corresponding effect size estimates from the replication study. As no power estimates were reported in the prostate cancer study, we obtained an effective sample size for this study by equating expected and observed number of discoveries, under the assumption that the effect size distribution for prostate cancer is the same as that estimated from the pooled colorectal and breast cancer susceptibility SNPs, and then used this effective sample size to evaluate the power of the five individual prostate cancer SNPs.

We estimated that for each BPC cancer, there exist, on average, 67 (95% CI: 31, 173) susceptibility loci within the range of effect sizes seen in the current GWASs, and that these loci together could explain 17% (95% CI: 12%, 36%) of genetic variance for each cancer. We estimated that a risk model based on 67 loci can achieve an AUC value of 63.5% (95% CI: 61.2%, 69.1%). The corresponding estimate of AUC for models that include only the five to ten susceptibility loci initially identified for the BPC cancers is, on average, 57.0%.

External validation

We validated the proposed methodology and associated projections using several sources of independent data (Table 4). To carry out this validation, we used the estimated distribution of effect sizes we obtained in the studies described above to project the number of loci expected to be discovered in these additional data sources, on the basis of their sample sizes and study designs. We projected the total number of loci expected to be discovered in the Cancer Genetic Markers of Susceptibility (CGEMS) two-stage breast and prostate cancer studies^22,23; these were two US-based studies that we purposefully did not use to select loci for estimating distribution of effect sizes of BPC cancers. We also projected the number of novel loci expected to be discovered in the most recent Cancer Research UK (CRUK) three-stage prostate cancer study²⁴, which included additional data beyond that of the two-stage study²⁰ we used to select loci for BPC cancers. For height, we projected the number of additional loci expected to be discovered after inclusion of the second-stage data in the study in ref. 13, from which we had only used the first-stage data for selection of susceptibility loci. For each outcome, the projected number of novel signals closely approximates the observed number of discoveries. Finally, we prospectively projected the total number of height loci expected to be discovered in a meta-analysis of about 130,000 subjects by the Genomewide Investigation of Anthropometric Measures (GIANT) consortium. Findings from the GIANT consortium (J. Hirschhorn, Harvard Medical School, personal communication) are expected to be reported soon.

Table 4.

Expected and observed numbers of discoveries in external data sets

	Expected number of discoveriesa	Observed number of discoveries
Cancer
Total number of discoveries in CGEMS prostate two-stage study	2.7	5
Total number of discoveries in CGEMS breast two-stage study	3.0	3
Number of additional discoveries in the latest CRUK prostate studyb	9.5	7–9c
Height
Number of additional discoveries in ref. 13 after inclusion of stage 2d	9.3	11
GIANT consortiume	186	Not available

Data sets used for this validation exercise were not used in selection of loci for estimating effect size distribution. All calculations are based on a genome-wide significance of 10⁻⁷.

^aObtained using the externally estimated distributions of effect sizes, along with sample size and study design of the specified studies.

^bData from only five prostate cancer loci discovered from the original CRUK prostate study contributed to the estimation of the distribution of effect sizes of BPC cancers. Here, expected number of additional discoveries is calculated as the difference between expected number of discoveries with and without the third-stage data.

^cStudy reported discovery of nine independent susceptibility SNPs from seven different chromosomal regions.

^dData from only 20 loci discovered in the first stage of this study contributed to estimation of the distribution of effect size for height.

^eProspective projection for a meta-analysis of GWAS data for 130,000 subjects.

DISCUSSION

The expected number of discoveries from future GWASs, as well as the projected impact of the findings on individualized risk models, depend on the number and distribution of effect sizes for underlying susceptibility loci. In this report, we have proposed a method to project estimates for the distribution of effect sizes of undiscovered loci using estimates of effect sizes of known susceptibility SNPs, together with the power of the studies reporting the loci. We show how such estimates can be used to estimate power and sample-size requirements for future studies—either new GWAS scans or meta-analyses. We have validated our method using existing GWASs of common variants associated with a range of common traits—namely, Crohn’s disease, height and three common cancers. It is likely that future studies with larger sample sizes will discover a set of variants with effect sizes smaller than those currently seen. When such data become available, our method can be used to project additional loci in an extended range of effect sizes.

In our results, the projected numbers of common susceptibility SNPs associated with height and Crohn’s disease exceed the number for BPC cancers, which is consistent with reported heredity for each of these traits. Overall, we observed that the shapes of the estimated distributions of effect sizes for each trait were similar across phenotypes—notably, all had an increasingly large number of susceptibility loci at decreasing effect sizes²⁵. When we considered fitting alternative parametric models (Supplementary Table 5), we observed that an exponential distribution, which implies the number of susceptibility loci increases at an exponential rate with decreasing effect sizes, estimated a considerably smaller number of total susceptibility loci than the nonparametric estimator. In contrast, a Weibull distribution with number of loci increasing at a faster-than-exponential rate with decreasing effect size provided estimates much closer to that obtained from the nonparametric method. In this regard, the results based on current GWASs point toward a model for distribution of effect sizes for complex traits that suggests a large number, possibly thousands, of susceptibility loci with very small effect sizes³.

Most often, researchers have evaluated the power of studies to detect single SNPs with different effect sizes or allele frequencies. Typically, the methods do not account for the number of SNPs that are likely to exist with different effect sizes. A few earlier reports have described power calculations for genetic association studies that reflect uncertainties regarding linkage disequilibrium^26,27 and allele frequencies^26,28 integrating over empirically estimated distributions of the parameters. Our method is designed to assess the number of discoveries expected on the basis of power calculations that are integrated over the estimated number of loci and their likely distribution of effect sizes. Our sample-size calculations show the importance of accounting for previous discoveries (Table 3). The method can use results from calculations of power to detect single SNPs with fixed effect sizes, making use of standard tools such as CaTS and GWASpower²⁹ together with an estimated distribution of effect sizes to assess the integrated power of a study over the catalog of different SNPs.

GWASs are conducted using surrogate markers and rarely identify the functional variant directly; one should take this into account when interpreting the estimates of effect size distribution and the associated power calculations for future studies. The majority of GWASs used in this report used commercial fixed genotyping platforms (Affymetrix, Perlegen and Illumina), which provide adequate coverage of HapMap Phase II SNPs with minor allele frequency (MAF) > 5%. Select studies^14,17 employed imputation, which can monitor ~2.5 million SNPs included in HapMap Phase II. So far, fine mapping studies of the reported loci have provided no conclusive examples of new common alleles with substantially higher effect sizes. Thus, it is unlikely that denser platforms with more common variants (MAF > 5%) will substantially alter the risk estimates for common variants in people of European background. In contrast, if the same platforms are used for a different population, resulting in lower coverage, then we can expect to see substantially smaller effect sizes even if the distributions for the underlying causal variants are comparable between the populations (Supplementary Table 2). It is possible that next-generation genotyping and sequencing platforms, which will efficiently interrogate uncommon and rare variants, could magnify the effect sizes for some of the estimated loci that are currently being represented by common variants owing to synthetic association³⁰ (Supplementary Table 6).

There is uncertainty in the estimates of effect size distribution and the associated projections for future studies. We provide estimates of uncertainty owing to chance variation in the set of existing loci because of the randomness of the data that led to the initial discoveries. There can also be systematic errors. To avoid bias, it is crucial that the power of the existing studies that led to the discovery of the observed loci is evaluated in an unbiased fashion. Steps should be taken to avoid overestimation of effect sizes, as well as of corresponding power, owing to winner’s curse^31,32. Sometimes precise design and selection criteria may not be well defined in published studies. Accordingly, the sensitivity of the estimates should be analyzed, and these sensitivity analyses should be consistent with the apparent design of the original studies (Supplementary Table 7).

Our method can be performed using only summary data from published GWASs as long as there is enough information to allow unbiased evaluation of power to detect loci in the observed range of effect sizes. For a simple one-stage or multi-stage GWAS with additional replication data, power calculations can be done externally. However, for more complex studies characterized by complicated sampling and selection criteria, power calculations by independent researchers may not be possible. Thus, we suggest that journals encourage inclusion of power calculations with the original findings. To this end, we have developed a toolbox, INPower (see Methods), that can integrate the distribution of effect sizes into power calculations for future studies.

Using the estimated distributions of effect sizes, we can project the potential utility of risk models for Crohn’s disease and BPC cancers by assessing the likely upper bound of discriminatory power. Recently, reports^7,11 have speculated on the number of susceptibility SNPs with certain effect sizes that will be needed to achieve an AUC of ~80% for a risk model. Given the paucity of findings thus far, we estimate that such a large number of loci with the inferred effect sizes probably do not exist. It appears that for a trait like breast cancer, which is known to have a modest genetic component, one could optimistically expect to achieve an AUC of approximately 63.5% (95% CI: 61.2, 69.1) for a purely genetic risk model with common variants. In contrast, for a trait like Crohn’s disease, which is highly familial, a risk model based on the already identified ~30 loci has higher discriminatory power (AUC = 72.8%). Discoveries from additional studies can further improve the discriminatory power of genetic models, but we project that the AUC for risk models that would include these additional discoveries is unlikely to exceed 79.2%. As noted above, it is possible that future studies of rare variants will magnify the effect size for some of the estimated loci and thus increase the discriminatory power for risk models as well.

In this report, we describe the application of this method using data from GWASs. The general concepts and principles we outline, however, are potentially applicable to findings from future studies with different features, such as those using next-generation sequencing and new, denser types of genotyping platforms. Our method can be applied to studies that test rare variants in regions across the genome^33,34 if an effect size is used that captures the total genetic variance explained by multiple rare variants within a region. Once discoveries from the first set of studies of rare variants become available, our method can be potentially used to project the number of additional loci containing rare susceptibility variants that could be discovered from subsequent studies.

In summary, our method uses existing GWAS data to project the likely number of discoveries from future GWASs. Thus, we provide investigators with an additional tool to determine the utility of further studies. Accordingly, the method should be useful for justifying additional scans as well as meta-analyses designed to identify novel regions that can add insights into the genetic epidemiology of a disease or a trait.

ONLINE METHODS

Definition of effect size

Throughout this article, we define the effect size (ES) for a susceptibility SNP marker (SSM) as

$$\mathrm{E}\mathrm{S}=2{\beta }^{2}f(1-f),$$

where the coefficient β measures the regression effect—for example, log odds-ratio in a logistic model—of the locus per copy of the variant allele, and f denotes the MAF. The effect size, as defined above, corresponds to the contribution of the locus to the genetic variance of the trait under Hardy-Weinberg equilibrium and an additive polygenic model. Notably, under modest assumptions, the power to detect the locus using the commonly employed trend test can be shown to depend on β and f only through the quantity ES. Thus, the effect size for an SSM, as defined above, determines its contribution to the total genetic variance of the trait as well as the statistical power to detect it in an association study.

Estimation of the distribution of effect sizes

The basic idea behind the proposed approach can best be seen by considering the problem of estimating a histogram to describe the frequency distribution of the effect sizes for the underlying SSMs. Suppose ES₁, … , ES_K are the observed effect sizes for K known SSMs for a trait. Suppose we divide the range of the effect sizes into l = 1, … , L bins and our goal is to estimate M_l for l = 1, … , L, the total number of underlying SSMs that fall into the different bins. Now suppose a GWAS (or a group of such studies) has detected K_l for l = 1, … , L loci in these L bins. Now if pow(N, l) denotes the power of the study to detect an SSM in the lth bin, assuming that power for all the SSMs within a bin is approximately the same, then it is evident that for each bin, the observed count K_l follows a binomial distribution with n = M_l and P = pow(N, l), with the expectation that E(K_l) = M_l pow(N, l). Thus, we can naturally estimate M_l as

$$M_l=\frac{K_l}{\text{pow}(N,l)}.$$

With this basic ingredient in mind, we consider a modification of the estimation method using parametric and nonparametric smoothing techniques that avoid the arbitrary definition of ‘bins’ required in the histogram approach.

Parametric method

We assume a parametric form—for example, exponential or Weibull distribution—for the density of effect sizes of all underlying susceptibility SNPs. Let f_θ (ES) represent such a parametric density, where the associated parameters θ need to be estimated from the data. The observed effect sizes in a study are typically left-truncated, as power to detect loci with effect sizes below a certain threshold, say C, is practically zero. In our method, we choose the truncation point C in such a way that the power for the existing studies below this threshold is less than 1%. We then obtain an estimate of θ based on all the observed effect sizes above this threshold by maximizing the weighted truncated log-likelihood

$$l=\sum _{k:\mathrm{E}{\mathrm{S}}_k>C}\frac{1}{\text{pow}(N,\mathrm{E}{\mathrm{S}}_k)}\text{log}\frac{f_{\theta }(\mathrm{E}{\mathrm{S}}_k)}{\underset{\mathrm{E}\mathrm{S}>C}{\int }{f}_{\theta }(\mathrm{E}\mathrm{S})}.$$

Once an estimate of θ is obtained, then an estimate of M, the total number of loci in the observed range of effect size (ES > C) is obtained by equating the observed number K and expected number of discoveries under the estimated distribution of effect sizes, using the equation

$$K=M\sum _{k:\mathrm{E}{\mathrm{S}}_k>C}\frac{f_{\hat{\theta }}(\mathrm{E}{\mathrm{S}}_k)}{\underset{\mathrm{E}\mathrm{S}>C}{\int }{f}_{\hat{\theta }}(\mathrm{E}\mathrm{S})}\text{pow}(N,\mathrm{E}{\mathrm{S}}_k).$$

Finally, the estimates of the number of underlying loci for each of the observed effect sizes are obtained as

$${\hat{M}}_{\mathrm{E}{\mathrm{S}}_k}=\hat{M}\frac{f_{\hat{\theta }}(\mathrm{E}{\mathrm{S}}_k)}{\sum _{l:\mathrm{E}{\mathrm{S}}_l>C}{f}_{\hat{\theta }}(\mathrm{E}{\mathrm{S}}_l)},\mathrm{E}{\mathrm{S}}_k>C.$$

Nonparametric method

We used the kernel smoothing technique to obtain a nonparametric estimate of effect size distribution. For each of the identified SSMs with a unique effect size ES, we first estimate the number of underlying SSMs with similar effect sizes as 1/pow(N, ES) where pow(N, ES) denotes the power to detect the SSM having the effect size ES with sample size N, and then smooth these ‘raw counts’ using the locally linear kernel smoothing technique to reduce the variability of the estimates. In this procedure, the estimate for the number of SSMs at each of the observed effect sizes ES is obtained as

$$\hat{M}(\mathrm{E}\mathrm{S})=\frac{\sum _{\mathrm{E}{\mathrm{S}}_k\in N_{\lambda }(\mathrm{E}\mathrm{S})}w(\mathrm{E}{\mathrm{S}}_k-\mathrm{E}\mathrm{S})/\text{pow}(N,\mathrm{E}{\mathrm{S}}_k)}{\sum _{\mathrm{E}{\mathrm{S}}_k\in N_{\lambda }(\mathrm{E}\mathrm{S})}w(\mathrm{E}{\mathrm{S}}_k-\mathrm{E}\mathrm{S})},$$

which is a weighted average of 1/pow(N, ES_k) for all the identified SSMs in a neighborhood N_λ (ES) of ES where the weights decrease smoothly according to a specified function w(x) with the increasing distance between ES_k and ES. Once we obtain estimates of M̂ (ES_k), k = 1,…, K for the observed effect sizes, we can obtain an estimate of the total number of underlying SSMs in this range simply as $M=\sum _k\hat{M}(\mathrm{E}{\mathrm{S}}_k)$.

Power calculations for existing studies

For the above calculations for estimation of effect size distribution, it is crucial that the power of the studies that have led to the discovery of existing loci is evaluated in an unbiased fashion. It is particularly important to avoid the problem of ‘winner’s curse’^31,32,35,36, which could lead to overestimation of effect sizes and powers. When the set of identified SNPs comes from multiple studies, published separately without any meta-analysis, the power for an identified SSM should be defined as the probability of it being detected in at least one of those studies. Assuming the studies are independent, such probabilities can be computed as

$$P(\mathrm{E}\mathrm{S})=1-\prod _{\text{study}}\{1-{\text{pow}}_{\text{study}}(N_{\text{study}},\mathrm{E}\mathrm{S})\}.$$

Evaluating power of a new GWAS using estimates of the distribution of SSMs

Let X denote the random variable indicating the total number of SSMs that could be identified in a GWAS of sample size N. Given the estimates of the range of effect sizes, ES₁, … , ES_K, and the corresponding estimates of the frequencies of total number of SSMs that exist with those effect sizes, M̂ (ES₁),…, M̂ (ES_K), we can write

$$X=X_1+\dots X_K,$$

where each X_k, the number of SSMs that could be identified with the particular effect size ES_k, can be shown to follow a binomial distribution with n = M̂ (ES_k) and P = pow(N,ES_k). We note that standard power calculation tools can be used to evaluate pow(N,ES_k), which denotes the power of the study to detect a fixed SSM with effect size ES_k. In this step, one can also account for coverage of a genotyping platform with known r² distribution. One can analytically calculate power for a fixed SNP and fixed r² as p(r²) = pow(N,r² × ES_k) and then integrate it over the known r² distribution for a genotyping platform. We can evaluate the probability distribution of X, decomposed as a sum of independent binomial random variables as above, to obtain an assessment of power that automatically accounts for the distribution of effect sizes. For example, we evaluated Pr (X ≥ k) to estimate the power of a study to detect at least k loci. We also estimated $E(X)=\sum _k\hat{M}(\mathrm{E}{\mathrm{S}}_k)\text{pow}(N,\mathrm{E}{\mathrm{S}}_k)$ to assess the number of loci expected to be discovered in a study of size N. Moreover, one can evaluate the power of a GWAS for identifying ‘novel’ loci by simply subtracting the number of already identified loci from M̂ (ES_k), k = 1,…,K in all the calculations of the binomial probabilities.

Evaluating total genetic variance explained

Estimating the distribution of effect sizes for SSMs is also useful for evaluating the percentage of heritability that could potentially be explained using findings from future GWASs. Letting ${\sigma }_G^2$ be the total genetic variance (GV) of a trait, we use

$$\mathrm{G}\mathrm{V}=\sum _k\mathrm{E}{\mathrm{S}}_k\hat{M}(\mathrm{E}{\mathrm{S}}_k)$$

to estimate how much of the GV can be explained by all of the SSMs that potentially exist in the range of effect sizes that has already been observed in the current generation of association studies.

Genetic risk distribution and its discriminatory power

To evaluate the AUC for discriminatory power of risk, we followed ref. 5 by assuming that the genetic risk follows a log-normal distribution with mean μ and s.d. σ for the general population and with mean μ + σ² and s.d. σ for affected individuals. We set μ = −σ²/2 so that the expected mean of the population risk is equal to 1 and the risk distributions are characterized by only one parameter σ. For each trait, three sets of receiver operating characteristic curves are obtained for three different choices of σ²: (i) the total genetic variance that could explain all the familial risk for a trait; (ii) the genetic variance explained by the estimated susceptibility loci; and (iii) the genetic variance explained by currently known susceptibility loci. We use the relationship λ²_sib = exp(σ²), where λ_sib denotes sibling relative-risk, to obtain an estimate of the total genetic variance that could explain all the familial risk of a trait.

Parametric bootstrap for variance estimation

A parametric bootstrap method was implemented to obtain variability for the estimates presented in this paper. In each bootstrap (BS) replication, we generate a random number of ‘observed’ loci, say denoted by K^BS(ES_k), for each effect size ES_k, by sampling from a binomial distribution with n = M̂ (ES_k) and P = pow(N,ES_k), where M̂ (ES_k) are estimates of the total number of susceptibility loci from the original data. For each BS replicate, we then recompute all of the estimates of interest based on the new random draw of observed loci. The 95% confidence intervals presented with the estimates in the Results and Discussion were constructed by selecting the 2.5th and 97.5th percentiles of bootstrap estimates obtained from 100 replicates.