Abstract
Approximate Bayesian computation (ABC) is useful for parameterizing complex models in population genetics. In this study, ABC was applied to simultaneously estimate parameter values for a model of metapopulation coalescence and test two alternatives to a strict metapopulation model in the well-studied network of Daphnia magna populations in Finland. The models shared four free parameters: the subpopulation genetic diversity (θS), the rate of gene flow among patches (4Nm), the founding population size (N0) and the metapopulation extinction rate (e) but differed in the distribution of extinction rates across habitat patches in the system. The three models had either a constant extinction rate in all populations (strict metapopulation), one population that was protected from local extinction (i.e. a persistent source), or habitat-specific extinction rates drawn from a distribution with specified mean and variance. Our model selection analysis favoured the model including a persistent source population over the two alternative models. Of the closest 750 000 data sets in Euclidean space, 78% were simulated under the persistent source model (estimated posterior probability = 0.769). This fraction increased to more than 85% when only the closest 150 000 data sets were considered (estimated posterior probability = 0.774). Approximate Bayesian computation was then used to estimate parameter values that might produce the observed set of summary statistics. Our analysis provided posterior distributions for e that included the point estimate obtained from previous data from the Finnish D. magna metapopulation. Our results support the use of ABC and population genetic data for testing the strict metapopulation model and parameterizing complex models of demography.
Keywords: approximate bayesian computation, Daphnia magna, extinction rate, metapopulation
Introduction
With the increase in computational power over the last few decades, studies in population genetics have increasingly relied on model-based inference. Studies that seek to parameterize complex models of historical population demography typically proceed along one of two pathways. In cases where a likelihood function is tractable, maximum-likelihood estimates for demographic parameters (e.g. effective population sizes and migration rates) can be obtained by heuristically searching parameter space using Markov chain Monte Carlo (MCMC) methods (e.g. Beerli & Felsenstein 1999; Nielsen & Wakeley 2001). For more complicated models, likelihood functions may not always be available. In these situations, approximate Bayesian computation (ABC) has proven to be a useful approach for identifying the range of demographic parameters consistent with empirical observations. Application of ABC methods to the inference of historical demography has been particularly fruitful (see Chan et al. 2006; Bertorelle et al. 2010; Csilléry et al. 2010), and this framework has provided a means of testing the support for alternative (potentially complex) models of demographic history (Hickerson et al. 2006; Shriner et al. 2006; Peter et al. 2010).
To date, ABC has been used mostly for questions in population genetics, but its utility can extend to other fields, including ecology and epidemiology (see Beaumont 2010). In the field of molecular ecology, ABC proceeds through three primary steps: constructing, fitting, and improving a model of population history (Csilléry et al. 2010). For population genetics applications, models are usually rooted in coalescent theory (Kingman 1982). Researchers have developed coalescent simulation packages that allow for recombination, population size changes, and population subdivision (e.g. ms; Hudson 2002). The speed with which large numbers of simulations can be generated on modern computer systems is a primary benefit of the use of coalescent models for ABC. Essentially, ABC begins with data collected from a field system of interest and a model of system dynamics. Millions of simulations of the specified model (or models) are conducted by randomly drawing parameter values from prior distributions. Following the generation of simulated data sets, summary statistics are calculated for both the observed and simulated data. Under the simplest approaches, posterior distributions for the parameters of the model are approximated by the randomly drawn parameter values resulting in summary statistics that are close to the observed values (see Bertorelle et al. 2010 for a more detailed explanation).
This study focuses on the Finnish Daphnia magna metapopulation, a system that has been the subject of intensive research for the past 30 years. Levels of population subdivision among occupied and newly colonized pools (Haag et al. 2005, 2006) suggest that gene flow between habitats is limited and that founding events typically involve a small number of individuals sampled from a single occupied population (i.e. propagule-pool recolonization; Slatkin 1977). Work in this system has also helped to provide an estimate of the average yearly extinction rate (Pajunen & Pajunen 2003), documented inbreeding depression in natural populations (Haag et al. 2002), examined relationships between population age and genetic diversity/divergence (Haag et al. 2005), and more recently, shown positive influences of genetic diversity on a population’s ability to resist the spread of parasitic infection (Altermatt & Ebert 2008). Most observations from this system generally support the application of a metapopulation model (Hanski & Ranta 1983; Pajunen & Pajunen 2003), but the long-term persistence of some populations raises the possibility that some pools may be inherently less susceptible to extinction (Pajunen & Pajunen 2003).
In this study, we used multilocus microsatellite data to compare models of population dynamics in the Finnish metapopulation. In the first model, all populations were subject to the same rate of extinction; this model therefore represented a strict Levins (1969) metapopulation model. In the second model, one population was protected from local extinction (a persistent source). In the final model, extinction rates for individual populations were drawn from a distribution, and we included the mean and standard deviation of that distribution as parameters in the model (variable e). The distinction between these representations is in the level of genetic diversity maintained in the system. Under the metapopulation and variable e models, all populations have been recolonized in the recent past, so their genetic diversity is determined primarily by the rate of extinction in the metapopulation and its influence on expected population age. By contrast, in the persistent source model, the genetic diversity of the source population is determined by its effective size. The source then serves as a regional pool of diversity that is distributed, through migration and recolonization, to extinction-prone populations in the system. In addition to comparing these models, we used ABC to estimate parameter values for the best-fit model, including the subpopulation genetic diversity (θS), the rate of gene flow among patches (4Nm), the founding population size (N0), the metapopulation extinction rate (e) and its standard deviation (σe). Some previous studies have used population genetic data to test the metapopulation model (Lamy et al. 2012) or identify source populations in natural systems (Dias et al. 1996; Barson et al. 2009). Our study is unique in that, to our knowledge, it is the first to use ABC to explicitly test a metapopulation model in a well-studied field system, while simultaneously estimating parameter values for the system. Our results highlight the promise of ABC methods to rapidly provide plausible distributions for parameters that are difficult to estimate (e.g. extinction rate), even in complex demographic settings like metapopulations.
Methods
Study site and sampling
In July 2009, fourteen populations of Daphnia magna were collected from Storgrundet (59.822°N, 23.261°E), a rocky island in the Tvärminne archipelago off the southern coast of Finland. Sampled populations were preserved in 95% ethanol and returned to the University of Georgia for processing. Genomic DNA was extracted from individuals using a Puregene (Gentra Systems, Inc.) isolation protocol. Forty-eight individuals from each population were genotyped at fourteen microsatellite loci (see Colson et al. 2009 for primers). These fourteen loci were amplified in a total of six polymerase chain reactions (PCR) and further pooled for genotyping into four submissions per individual (multiplex groupings are given in Table S1, Supporting information).
Amplifications were conducted in 12.5 lL volumes consisting of 1 × GoTaq colourless dye (Promega Corp.), 1.5 mM MgCl2, 800 μM dNTPs, 500 μM of each primer in the amplified group and 0.5 U GoTaq polymerase (Promega Corp.). All fragments were amplified using the following thermal profile: 94 °C for 4 min, followed by 35 cycles of 94 °C for 30 s, 53 °C for 30 s, and 72 °C for 30 s and a final elongation at 72 °C for 4 min. Genotyping runs were conducted on an ABI 3730 (Applied Biosystems, Inc.) at the Georgia Genomics Facility (University of Georgia) using GeneScan Rox 500 size standard (Applied Biosystems, Inc.). Microsatellite alleles were scored using panels designed in GeneMarker v. 1.6 (SoftGenetics, LLC). The samples and genetic data considered in this article are shared with a previous study in the Finnish D. magna metapopulation (Robinson et al. 2012a,b).
Alleles at eight of the fourteen sampled loci showed the influence of flanking mutations on allele size. That is, they differed by noninteger numbers of repeat units. To determine the true number of microsatellite repeats, we cloned and sequenced representative alleles. For cloning, individuals homozygous for questionable alleles were amplified, under the conditions outlined previously, using primers without fluorescent tags. TOPO TA cloning kits (Invitrogen) were then used to transform E. coli cells with the resulting amplification products, according to manufacturer specifications. Successfully transformed colonies were subjected to PCR, and products were cycle sequenced using ABI Big Dye Terminator sequencing reactions (Applied Biosystems Inc.). DNA sequencing was performed at the Georgia Genomics Facility (University of Georgia). Sequenced alleles at each microsatellite locus were aligned using CodonCode Aligner (CodonCode Corp.) and visual counts of the repeat motif (Table S1, Supporting information) were made. Inspection of these sequences revealed that insertions in flanking regions (often in homopolymeric stretches) were typically responsible for unexpected allele sizes (J. Robinson, results not shown).
The inclusion of insertions in the flanking regions would most likely serve to increase the effective mutation rate of the loci used in our analysis to levels higher than the estimate we employed in our simulation models (estimated in D. pulex; Seyfert et al. 2008). Insertions that occur outside of the repeat region are also probably governed by a mutational model other than that assumed in our analysis. This additional source of mutation (and the elevated allelic diversity at some loci associated with a higher rate of electrophoretically detectable mutation) could bias our analysis towards models and parameter estimates that are associated with high diversity in the Daphnia populations (e.g. larger local and/or founding effective sizes, greater migration and reduced extinction rate). To limit mutations in the data set to those that occur within the repeat region of the microsatellite locus, allelic sizes were recoded to reflect similarities or differences in the number of repeat units, before being used for the ABC analysis. For instance, alleles took all possible values between 328 and 334 bp at the dinucleotide repeat locus WFes0007834 (Table S1, Supporting information). After sequencing, it was apparent that many of these alleles shared repeat numbers, but had additional mutations in the flanking regions. As a result, these seven alleles were binned into three allelic classes based on the number of repeats (allele sizes 330, 332, and 334). Because this practice involved grouping alleles of different absolute size, observed values of diversity statistics associated with allelic richness were reduced (i.e. the number of alleles, K). In total, we recoded twelve alleles across eight of the sampled loci. All allele sizes were converted to a relative number of repeats measure by subtracting the size of the smallest observed allele from all allele calls, dividing by the length of the repeat motif and adding one. While the binned data set produced summary statistics that were generally similar in magnitude to the raw data (see Fig. S1, Supporting information), we performed ABC analyses on both data sets to determine how robust our conclusions were to the exclusion of flanking region mutations.
Coalescent simulations
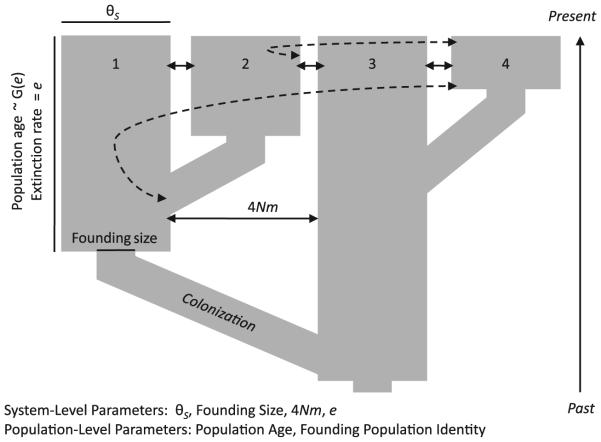
Coalescent simulations for ABC analysis were performed using ms (Hudson 2002). The simulations were designed to represent coalescence in a metapopulation with small founding sizes and frequent local extinction. To represent the recolonization of a habitat, we specified the timing and magnitude of population size changes (ms argument -en) and the timing of population splitting (ms argument -ej; looking forward in time). Looking backwards in time, our simulations model population recolonization as a stepwise reduction in population size to N0 (the number of diploid founding individuals) at time t, followed by the movement of all lineages to an extant population at time t + 1 generations in the past (Fig. 1).
Fig. 1.
Graphical representation of the simulated coalescent model, with four populations instead of the 14 considered in our analysis. Subpopulation effective sizes (width of population bars), pairwise migration rates (solid and dotted arrows), and founding population sizes (width of small boxes in the history of each population) were constrained to be equal across the system. The model illustrated corresponds to the strict metapopulation model or the variable e model, as all patches were recolonized in the recent past.
Five parameters were varied among the coalescent simulations conducted. These parameters included the effective size of the present-day subpopulations, NS (all fourteen assumed to be of equal size); the number of effective migrants exchanged among populations per generation, 4Nm (rates assumed to be equal across the system); the population size associated with recolonization, N0 (constant across space and time); the mean rate of extinction, e, which determines the expected age of a population in years (=1/e); and the standard deviation of e across populations, σe (variable e model only). To translate age in years to age in generations, we assume five Daphnia magna generations per year (D. Ebert, pers. comm.). One million simulations were carried out under each of three alternative models, one in which all patches were subject to the same rate of local extinction (strict metapopulation model), another in which one of the fourteen populations maintained a constant size (persistent source model), and a third model that allowed for population-specific extinction rates (variable e model). Prior distributions for the free parameters of the models are provided in Table 1, along with the biological reasoning behind their specification. Our primary interest was in providing an estimate of the rate of local extinction, so we utilized a uniform prior spanning all possible values for this parameter (U:0.001–0.999). Other parameters are unbounded biologically, so we chose priors that generously spanned the reasonable ranges based on previous data obtained in this system. Data sets produced by ms were converted to microsatellite genotype data using a published Perl script (Pidugu & Schlötterer 2006). Summary statistics for the ABC analysis were then calculated for each of the resulting data sets.
Table 1.
Prior distributions for model parameters. For each parameter, the uniform distribution from which simulated parameter values are drawn is given, along with a biological explanation for the bounds of the distribution
| Parameter | Prior | Explanation |
|---|---|---|
| θ S | U(0.01 – 0.5) | Corresponds to minimum and maximum subpopulation effective sizes of <50 and >1500 individuals, respectively. |
| 4Nm | U(0.5 – 9.0) | Observed FST among populations ~ 0.27 (Haag et al. 2005). Corresponds to expected FST between 0.1 and 0.67. |
| N0 | U(1 – 100) | Estimated founding size in Finnish metapopulation is 1.7 genotypes per founding event (Haag et al. 2005). |
| e | U(0.001 – 0.999) | As it is a rate, e is naturally bounded by 0 and 1. |
| σ e * | U(0.01– 0.25) | Lower bound – near constant extinction rate across all populations; Upper bound – approaches a uniform distribution of rates. |
Only included in the variable e model simulations.
Summary statistics
We calculated a total of 19 data summaries for both the observed data from the Finnish metapopulation and our simulated data sets. These statistics included the total number of alleles in the data set (K), the mean and range (across loci) of system-wide variance in repeat number (σ2AS; Di Rienzo et al. 1994), the mean and range (across loci) of system-wide number of pairwise differences in repeat number (τ; adapted for microsatellite data sets from Rogers 1995), the mean values of FST (across pairwise comparisons among populations) and FIS (across populations), and four quantiles (25%, 50%, 75%, 100%) describing the distributions of K, σ2AS, and τ, calculated for each locus in each population (14 loci × 14 populations = 196 values for each statistic).
Ideally, statistics used for the purpose of ABC should be minimally correlated with one another (Hickerson et al. 2006). However, the neural network method reduces the dimensionality of the data set, thereby limiting the influence of correlation among summary statistics, and fits a nonlinear regression between summary statistics and simulated parameter values (Blum & François 2010). For this reason, correlations among the selected summary statistics were not assessed, and all 19 were included in the analyses.
Data analysis
Summary statistics for the simulated and observed data sets were calculated, and all ABC analyses were performed using the R statistical computing environment (R Development Core Team 2012), and the R packages: ‘abc’ (Csilléry et al. 2012), ‘Geneland’ (Guillot et al. 2005), ‘nnet’ (Venables & Ripley 2002), ‘quantreg’ (Koenker 2009) and ‘SparseM’ (Koenker & Ng 2009). The latter three packages are required dependencies of the ‘abc’ package. The scripts used to generate, process and analyse the simulated data sets are available from the corresponding author on request.
In ABC, the ratio of acceptances under competing models with equal prior probability can be used to assess relative support for the models (Pritchard et al. 1999). Under the simplest approach (i.e. the rejection method), the proportion of accepted data sets simulated under each model is an estimate of the posterior probability of the model. For the purposes of our project, we used the ‘postpr()’ function in the ‘abc’ R package (Csilléry et al. 2012), using the neural network and multinomial logistic regression methods, with tolerance set at 25% and 5%, respectively, to determine the most appropriate model. Using these methods, posterior model probabilities are predicted through the use of a nonlinear regression between model index and summary statistics (see Cornuet et al. 2008; Bertorelle et al. 2010; and Csilléry et al. 2012 for a more detailed explanation). At the two tolerance levels employed, the closest 750 000 or 150 000 (respectively) simulated data sets were used to determine posterior model probabilities. We also calculated Bayes factors, as the ratio of the predicted model probabilities. Bayes factors are similar to likelihood ratios, but can be applied to non-nested models, are generally more conservative than P-values and are easily applied when more than two models are compared (i.e. multiple comparisons are not a concern; Kass & Raftery 1995).
To assess the ability of our summary statistics to differentiate between models, we used a leave-one-out cross-validation approach, as implemented by the ‘cv4postpr()’ function in the ‘abc’ R package (Csilléry et al. 2012). We ran 100 cross-validation replicates per model, using a multinomial logistic regression for model selection (5% tolerance). For each replicate, one simulated data set from the reference table (3 000 000 total data sets) is ‘left out’ of the training data and the ABC approach is used to classify the model into one of the three alternatives. This analysis provides an estimate of the type I (false positive, choosing the focal model for data simulated under an alternative) and type II (false negative, choosing an alternative for data simulated under the focal model) error rates of our model selection approach.
Following our model selection analysis, we used ABC to estimate parameter values for θS, 4Nm, N0, e and σe (if necessary) using only the data sets simulated under the selected model (1 000 000 simulations). ABC methods assume that the summary statistics calculated from simulated data sets are sufficient for estimation of the parameters used to generate the data. Under the simplest approach, the simulations that produce summary statistics closest to the observed data (in Euclidean space) provide an approximate sample from the posterior distribution. Beaumont et al. (2002) introduced the more widely used local linear regression approach, where a linear relationship between parameter values and summary statistics is estimated via weighted regression and parameter values are adjusted towards their expected values (given the observed summary statistics) using the slope of the regression (see Bertorelle et al. 2010 for a more complete explanation).
In this study, we used the neural network method for nonlinear correction as implemented in the ‘abc’ R package (Csilléry et al. 2012). The neural network method corrects for nonlinearity in the regression between parameter values and summary statistics, allowing the use of a larger fraction of the simulated data and easing the computational burden of ABC (Blum & François 2010). Other approaches (e.g. local linear regression; Beaumont et al. 2002) typically consider smaller portions of the simulated data for parameter estimation (tolerance ~1%). Another advantage of the neural network implementation is that it addresses the ‘curse of dimensionality’, where increasing the number of summary statistics used decreases the accuracy of the ABC approach (Beaumont 2010). The method projects a potentially highly dimensional set of summary statistics onto a much smaller number of ‘hidden layers’ and then uses these projected values for nonlinear regression (Blum & François 2010). We used a 25% tolerance level (i.e. considering the closest 250 000 data points) to estimate posterior distributions for the parameters of the best model. For the purposes of this analysis, the defaults of ten neural networks and five hidden layers were used. For comparison, we also applied the more widely used local linear regression method (Beaumont et al. 2002), with a 5% tolerance level, to estimate parameter values for the best model.
All simulated parameter values were logit transformed for estimation of their posterior distributions (a common practice in ABC; Bertorelle et al. 2010). Under the rejection approach, transformations are not necessary, as the posterior distribution is given by the distribution of parameter values used to simulate the accepted data sets. However, when regression methods (local linear regression–Beaumont et al. 2002; nonlinear conditional heteroscedastic regression–Blum & François 2010) are employed, the parameter adjustments may result in support for values outside the bounds of the prior (that were not simulated in the generation of the reference table). In our analysis, the bounds of the prior distribution for each parameter were used to normalize parameter values to a scale of 0–1. Then, a logit transformation [log(p/(1-p))] was applied to the normalized values for the regression step. Transformed values were adjusted towards their expected value based on the slope of the regression between parameters and summary statistics (see Blum & François 2010) and back transformed to their original scale. After back transformation, the density of the accepted and adjusted parameter values gave the posterior distribution for the parameter. All steps associated with parameter estimation were performed using the ‘abc’ function in the ‘abc’ R package (Csilléry et al. 2012).
As a post hoc measure of the quality of our parameter estimates, we used the data sets simulated under the appropriate model to calculate coefficients of determination (R2) between each of the free parameters of our model and the 19 summary statistics. These coefficients show the proportion of the variance in the parameter values explained by individual summaries of the data (Bertorelle et al. 2010). There is no clear threshold value below which a summary statistic can be considered uninformative, as reliable parameter estimates may be attainable even if the proportion of the explained variance is relatively low (Bertorelle et al. 2010).
Bertorelle et al. (2010) recommend the use of pseudoobserved data sets (‘PODS’) for quality control in ABC applications. We used this posterior predictive approach to test the fit of our selected model by simulating 1000 PODS using parameter values drawn from posterior distributions. Summary statistics were standardized, as in all analyses using the ‘abc’ package, by utilizing the median absolute deviation as a measure of the standard deviation (Csilléry et al. 2012). Euclidean distances between the standardized summary statistics and the empirical data were calculated, and the distribution of these distances was compared with the distributions of distances from data sets simulated for ABC. Additionally, we compared the distributions of the 19 summary statistics calculated from PODS to the observed values from the D. magna system.
Results
Our model selection analysis supported the persistent source model over the strict metapopulation and variable e models in the Finnish D. magna system. Using the neural network method with tolerance set to 25% (i.e. considering the 750 000 simulated data sets that produced summary statistics nearest those observed in the Finnish samples), the posterior probability of the persistent source model was 0.769. Similarly, using a multinomial logistic regression with the closest 150 000 data sets (5% tolerance), the posterior probability was 0.774. Bayes factors were 6.44 and 6.10 in favour of the persistent source model for the neural network and logistic regression methods, respectively (Table 2). Cross-validation indicated that our model selection analysis was not capable of differentiating between models simulated under the strict metapopulation and variable e models, with data sets simulated under both models more often assigned to the strict metapopulation model. Nonetheless, our approach showed consistent ability to identify data simulated under the persistent source model. The misclassification rates from this analysis provide an estimate of type I and type II errors. A total of 22 of the 100 cross-validation replicates of the persistent source model were classified to the strict metapopulation or variable e models (type II error = 22%). Similarly, of the 200 cross-validation replicates that considered data sets simulated under the strict metapopulation or variable e models, 14 were misclassified to the persistent source model (type I error = 7%).
Table 2.
Model selection results. Proportions of accepted data sets, predicted posterior probabilities, and Bayes factors (comparing each model to the strict metapopulation model) for the three models considered in our analysis (strict metapopulation, persistent source, and variable e) using (a) the neural network approach with 25% tolerance and (b) the multinomial logistic approach with 5% tolerance
| Proportion accepted |
Posterior probability |
Bayes factor |
|
|---|---|---|---|
| (a) | |||
| Metapopulation | 0.0965 | 0.1194 | 1.00 |
| Persistent source | 0.7797 | 0.7689 | 6.44 |
| Variable e | 0.1234 | 0.1116 | 0.93 |
| (b) | |||
| Metapopulation | 0.0742 | 0.1269 | 1.00 |
| Persistent source | 0.8546 | 0.7740 | 6.10 |
| Variable e | 0.0713 | 0.0991 | 0.78 |
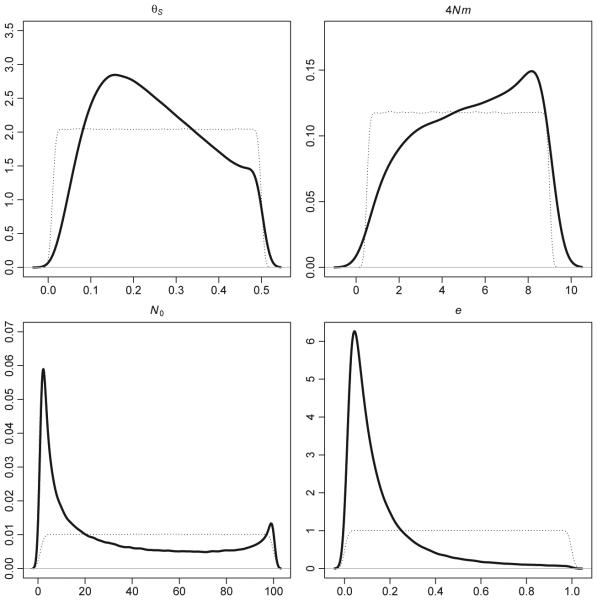
Because of the consistent support for the persistent source model and the moderate type I error rate, we used only those data sets simulated under this representation to estimate parameter values. These estimates, along with 95% highest probability density (HPD) intervals are provided in Table 3. Additionally, the prior and posterior distributions for θS, 4Nm, N0 and e, from the neural network method are plotted in Fig. 2. Posterior distributions from the local linear regression method were similar to those obtained using neural networks and are summarized in Table 3b and plotted in Fig. S2 (Supporting information). Visual inspection of the posterior distributions for these parameters shows divergence from the prior for all parameters except 4Nm. For this parameter, the posterior distribution was similar to the prior, but with increased probability density at higher values. For all parameters, the 95% HPD intervals contain most of the range of values specified in the prior distribution (Table 3). We performed additional simulations (data not shown) in which we expanded the priors to determine if the credible intervals of the posterior were being determined by the range of our priors and found this was indeed the case. In addition, in sets of simulations in which we used extremely wide, highly unrealistic priors for all the unbounded parameters, θS, 4Nm and N0, we found posterior distributions for e that exhibited a maximum close to 1.
Table 3.
ABC parameter estimates. Estimates were obtained using (a) the neural network methodology with tolerance set to 25% (250 000 datasets), and (b) the local linear regression methodology with tolerance set to 5% (50 000 datasets). The point estimates reported are the weighted means, medians, and modes from the posterior distributions, 95% HPD intervals are also reported. Only datasets simulated under the persistent source model were used for parameter estimation
| Parameter | Mean | Median | Mode | Lower 95% |
Upper 95% |
|---|---|---|---|---|---|
| (a) | |||||
| θ S | 0.2522 | 0.2391 | 0.1497 | 0.0531 | 0.4873 |
| 4Nm | 5.3778 | 5.5619 | 8.6931 | 0.9794 | 8.9029 |
| N0 | 35.0993 | 22.7117 | 3.2205 | 1.2968 | 98.8705 |
| e | 0.1656 | 0.1009 | 0.0387 | 0.0133 | 0.7228 |
| (b) | |||||
| θ S | 0.2560 | 0.2448 | 0.1551 | 0.0482 | 0.4894 |
| 4Nm | 4.9235 | 4.9084 | 4.2524 | 0.8942 | 8.8253 |
| N0 | 35.3452 | 23.8612 | 3.8013 | 1.3138 | 98.5094 |
| e | 0.1982 | 0.1308 | 0.0505 | 0.0142 | 0.7617 |
Fig. 2.
Prior (dotted lines) and posterior distributions (solid lines) estimated for the four parameters of the persistent source model. Estimates are from an ABC analysis considering only the data sets simulated with a persistent source population and using the neural net methodology with a tolerance of 25% (250 000 data sets).
We interpret this result as an effect of model misspecification. Given broader priors, realistic parameter combinations occur infrequently in the simulations and are overwhelmed by combinations with extreme values for θS, 4Nm and N0. Simulations with realistic parameter values thus make only a minor contribution to the reduced extinction rate and realistic migration rates and founding sizes and a model with much larger founding sizes and migration rates that includes unrealistically high extinction rates. Given the implausibility of the extinction rates estimated using broader priors, we report the results from simulations using the priors shown in Table 1, which allow for a broad range of extinction rates while imposing realistic limits on the other parameters of the model.
Our practice of binning alleles did influence the model selection results. When the raw data were considered, the proportion of accepted data sets simulated under the persistent source model was still much larger than that of the alternatives (Table S2, Supporting information). However, the multinomial logistic regression resulted in a posterior probability of 0.922 for the strict metapopulation model (Table S2, Supporting information). Nonetheless, parameter estimates were similar (albeit with lower θS, lower N0, and higher e) when using the raw allele calls (Table S3, Supporting information). In particular, the estimate of extinction rate (our focal parameter) was only slightly higher than the values estimated using the binned data set. Because flanking mutations would tend to inflate the overall rate of mutation above that applied in our analysis, we focus our discussion on analyses performed on the binned data set.
Coefficients of determination calculated between each of the parameters of our model and the summary statistics are given in Table 4. These coefficients indicated that some of the selected data summaries provided reliable information for the estimation of θS, 4Nm and e, with comparatively little information for estimation of N0. For N0, only four statistics had coefficients of determination greater than 0.01.
Table 4.
Coefficients of determination (R2) for summary statistics. Parameters included the population diversity parameter (θS), the number of migrants exchanged among populations per generation (4Nm), the founding population size (N0), and the extinction rate (e). Values were calculated using only data-sets simulated under the persistent source model
| θ S | 4Nm | N0 | e | |
|---|---|---|---|---|
| Mean system- wide τ |
0.27895 | 0.01524 | 0.00086 | 0.00345 |
| Range of system- wide τ |
0.15234 | 0.00241 | 0.00233 | 0.00157 |
| Mean system- wide σ2 AS |
0.12183 | 0.12215 | 0.00002 | 0.00013 |
| Range of system- wide σ2 AS |
0.06925 | 0.09093 | 0.00000 | 0.00002 |
| Total number of alleles (K) |
0.54840 | 0.01980 | 0.00721 | 0.15164 |
| Mean FST | 0.06772 | 0.00104 | 0.00371 | 0.00661 |
| Mean FIS | 0.18903 | 0.00143 | 0.00530 | 0.01157 |
| Quantiles | ||||
| τ | ||||
| 25% | 0.27726 | 0.00174 | 0.00717 | 0.01295 |
| 50% | 0.33758 | 0.00017 | 0.00026 | 0.02219 |
| 75% | 0.08674 | 0.00124 | 0.00432 | 0.02321 |
| 100% | 0.21657 | 0.00130 | 0.00614 | 0.03091 |
| σ2 AS | ||||
| 25% | 0.28630 | 0.00092 | 0.00779 | 0.03407 |
| 50% | 0.09205 | 0.00775 | 0.00002 | 0.03075 |
| 75% | 0.14899 | 0.00277 | 0.01113 | 0.04540 |
| 100% | 0.22278 | 0.00545 | 0.01959 | 0.07360 |
| K | ||||
| 25% | 0.27226 | 0.00298 | 0.02742 | 0.05783 |
| 50% | 0.40181 | 0.00001 | 0.00483 | 0.05171 |
| 75% | 0.00003 | 0.01648 | 0.01552 | 0.00041 |
| 100% | 0.00549 | 0.00755 | 0.00050 | 0.00004 |
PODS simulated under the persistent source model, using parameter values drawn from the posterior distributions, produced sets of summary statistics that were closer to our observed data than those produced in the generation of our reference table (Fig. 3). The mean and median Euclidean distances between our observed data and the standardized summary statistics for PODS were 14.59 and 13.13, respectively (compared with 22.31/21.23 for the strict metapopulation model, 16.33/15.56 for the persistent source model and 21.84/21.16 for the variable e model). Comparison of individual summary statistics indicated that for most data summaries, our observed values were located in the central mass of the distribution seen in our PODS (Table 5; Fig. S1, Supporting information). There was one exception to this rule, the observed maximum population and locus-specific variance in repeat number was located in the tail of the distribution of values obtained through the simulation of PODS. Aside from this statistic, summaries calculated from simulated data agreed well with the observed data from Finland (Fig. S1, Supporting information).
Fig. 3.
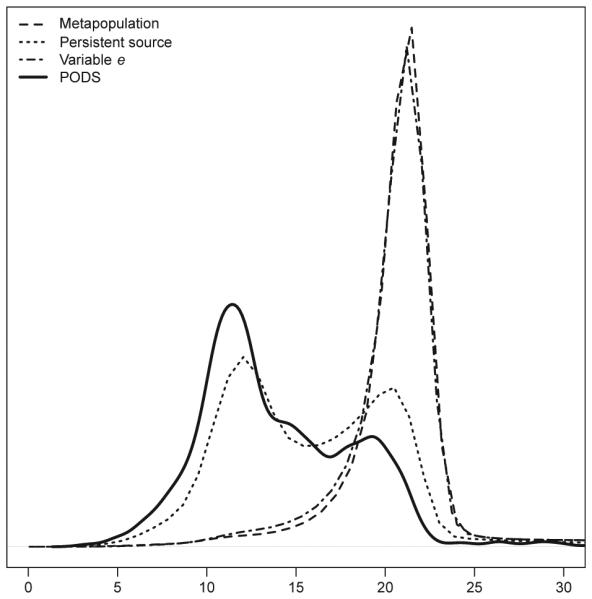
Euclidean distances between standardized summary statistics from simulated and observed data. Distances for simulations conducted under a strict metapopulation model (dashed line; n = 1,000,000), a persistent source model (dotted line; n = 1,000,000), a model that allowed among population variation in extinction rate (dot-dashed line; n = 1,000,000), and pseudo-observed data sets (PODS) simulated under the persistent source model with parameter values drawn from posterior distributions (heavy solid line; n = 1000) are shown.
Table 5.
Observed values of summary statistics. These statistics were calculated from the binned microsatellite data set obtained for the 14 D. magna populations
| Statistic | Value | |
|---|---|---|
| Mean system-wide τ | 0.1775 | |
| Range of system-wide τ | 0.4945 | |
| Mean system-wide σ2 AS | 0.3084 | |
| Range of system-wide σ2 AS | 1.2493 | |
| Total number of alleles (K) | 44 | |
| Mean FST | 0.2378 | |
| Mean FIS | −0.0395 | |
| Quantiles | ||
| Population and locus-specific τ | 25% | 0 |
| 50% | 0 | |
| 75% | 0.3208 | |
| 100% | 1.0098 | |
| Population and locus-specific σ2 AS | 25% | 0 |
| 50% | 0.0369 | |
| 75% | 0.2028 | |
| 100% | 3.8476 | |
| Population and locus-specific K | 25% | 1 |
| 50% | 2 | |
| 75% | 2 | |
| 100% | 4 |
Discussion
Our application of the ABC methodology to the complex demographic history of a metapopulation was largely successful. Our model comparison favoured a model that included a persistent source population over the strict metapopulation and variable e models. This finding is, in part, supported by previous studies in the Finnish metapopulation. For instance, the rate of extinction in individual patches appears to decline with population age and, in nearly 30 years worth of data collection in the system, there are several populations in which extinction has not yet been recorded (Pajunen & Pajunen 2003). Our posterior distribution for extinction rate under the persistent source model included substantial posterior density below the previous estimate from the long-term ecological survey of Pajunen & Pajunen (2003). Depending on the measure of central tendency employed, point estimates from our analysis range from substantially lower than, to nearly identical to the previous estimate (Table 3). Comparisons of the distribution of summary statistics calculated for PODS with their values in the Finnish Daphnia magna metapopulation suggest a good fit between our model and the observed data.
In the strictest sense, a metapopulation is defined as a set of semi-isolated populations, each of which is subject to local extinction and recolonization. In Levins’ (1969) original description of the model, all populations are assumed to have the same yearly probability of extinction. This assumption sets up an expectation of geometrically distributed population ages (Pannell & Charlesworth 2000), as the history of each individual population can be thought of as a series of extinction trials. Our ABC analysis suggests that the persistent source model is a better representation of the dynamics of the Finnish Daphnia metapopulation. In the present context, these source populations are not necessarily equivalent to sources as defined by Pulliam (1988). In his definition, sources experience a net flux of individuals out of the population, while sinks are maintained through immigration, despite a reproductive deficit. Our use of the term ‘source’ refers more to the yearly probability of extinction in the patch rather than the net movement of individuals into or out of the population.
The physical properties of the habitat patches in this system (distance from the island shoreline, depth, volume) may influence the susceptibility of the inhabitant populations to local extinction. Haag et al. (2005) found a positive correlation between population age and distance to the sea in D. magna and its congener Daphnia longispina. They also documented a relationship between pool volume and population age in D. longispina, but not in D. magna. It is also possible that the genetic diversity of the population itself plays a role in determining extinction probability, either through an enhanced ability to deal with environmental perturbations (Pajunen & Pajunen 2003) or through increased resistance to parasite spread (Altermatt & Ebert 2008). Regardless of the mechanism, our study suggests that ‘source’ populations in the system substantially contribute to the maintenance of system-wide genetic diversity.
Some previous studies have attempted to test the suitability of the metapopulation model or identify source and sink populations (sensu Pulliam 1988) using genetic data. However, the predictions for the genetic composition of sinks differ depending on the specifics of the system. For instance, Charlesworth (2003) hypothesized that the diversity of a source-sink system would be driven primarily by the source, as most lineages present in sinks would be recently derived from the source. However, if sink populations receive migrants from multiple genetically differentiated sources, they might have higher allelic diversity (Dias et al. 1996). In fact, comparisons of the levels of diversity in source and sink populations are not sufficient to differentiate between habitat types, as diversity also depends on migration rates connecting populations of the same type, and in some cases, small sinks may be more diverse than large sources (Rousset 1999). Nonetheless, previous studies have employed approaches that seem promising for application in these sorts of systems.
For instance, in their analysis of microsatellite variation in populations of the guppy Poecilia reticulata, Barson et al. (2009) used the software package BAPS (Corander et al. 2003) to calculate the proportion of each individual’s genotype that was introduced through immigration from other populations. Using these data, they were able to assign source or sink labels to their populations by subtracting total emigration from total immigration. Their results showed that, as expected, upstream populations constituted sources of migrants but downstream sink populations were often more diverse (Barson et al. 2009). More recently, Lamy et al. (2012) used temporal changes in allele frequency in populations of the freshwater snail Drepanotrema depressissimum to test the metapopulation model against alternative representations. In their analysis, they found that extinction rate was probably much lower than had previously been estimated, as most of the populations involved in apparent extinctions did not show significant genetic divergence before and after putative extinction events (Lamy et al. 2012). In this case, the detection probability is low for aestivating snails during dry periods, leading to inflated estimates of the extinction rate (Lamy et al. 2012). Similarly, the substantial posterior support for a reduced extinction rate estimated in the present analysis may be explained by the persistence of Daphnia resting eggs in populations that are thought to be extinct (see below). The estimation of immigration and emigration rates through Bayesian population assignment (Barson et al. 2009) and studies of temporal changes in allele frequency on either side of a putative extinction event (Lamy et al. 2012) provide complementary approaches to the use of ABC to compare strict metapopulation models with alternative representations. Our study shows that ABC can provide a rapid method by which a strict metapopulation model can be tested, and in this case, rejected.
It is important to note that the persistent population(s) implicated by our analysis does not necessarily exist on Storgrundet. Persistent populations of D. magna on other islands might serve as a regional pool of diversity for the archipelago as a whole. Additionally, if interisland movements occur frequently, immigration from the unsampled populations that make up the remainder of the Finnish D. magna metapopulation could bias our approach towards accepting the persistent source model, as we expect genetic diversity to be higher in the system under this model. Given this potential bias and the large number of islands off the southern Finnish coast, we cannot reject a strict metapopulation at the scale of the archipelago. However, we feel confident in our ability to reject at least one scenario: a strict metapopulation on the island of Storgrundet, in isolation from the rest of the archipelago.
One of the most difficult parameters to estimate in a metapopulation is the rate of local extinction. Previous estimates in the D. magna system are the result of nearly 20 years worth of twice yearly sampling (Pajunen & Pajunen 2003). Our study, using snapshot genetic data, provided a range of credible extinction rates (95% HPD = 0.013 - 0.723) that includes the point estimate of Pajunen & Pajunen (2003; e = 0.161). Depending on whether the mode, median or mean is used as a point estimate, we obtain a value that is below (mode = 0.039, median = 0.101), or essentially identical (mean = 0.166) to the previous estimate. As a post hoc assessment of the agreement between our parameter estimates and that provided by Pajunen & Pajunen (2003), we used exact binomial tests, with the observed number of extinctions and the number of occupied pools (data given in Table 2 of Pajunen & Pajunen 2003), to calculate 95% confidence intervals on the yearly estimate of extinction rate. These confidence intervals, along with our point estimates and that of Pajunen & Pajunen (2003) are plotted in Fig. S3 (Supporting information). The confidence intervals included the mode of the posterior distribution in five of the 16 years of observation. Point estimates from the median and mean were more consistent with the data from Finland, and were included in the confidence intervals calculated for nine and 12 of the 16 years, respectively. It is notable that even the estimate of Pajunen & Pajunen (2003) is not included in confidence intervals from all 16 years worth of observations (12 of the 16; Fig. S3, Supporting information).
There are a number of factors that need to be considered when interpreting the results of our analysis. For instance, immigrant alleles in this system are at a selective advantage in local populations, leading to an increase in the apparent rate of migration (Ebert et al. 2002). Apparent gene flow could be as much as 35-fold higher than the actual rate of movement of individuals as little as 2 years after an immigration event (Ebert et al. 2002). Unsampled, or ‘ghost’, populations might also have an influence on our estimates of gene flow (Beerli 2004). In the context of a metapopulation with frequent local extinction, ghost populations may include now extinct populations that served as sources of migrants and colonists into currently occupied habitat patches. Incorporation of unsampled populations in ABC analyses requires only that additional populations are included in the simulated data sets and removed before analysis (Beerli 2004; Estoup & Guillemaud 2010). We chose not to include the effects of unsampled populations in our analysis, in part because all filled pools on Storgrundet were exhaustively sampled for D. magna, making it highly unlikely that an extant population on this island was overlooked. However, if interpopulation movements are common in this system, extinct ghost populations could still inflate our estimates of gene flow and potentially bias our model selection analysis in favour of the persistent source model.
The bias associated with ghost populations or interisland migration might also lead to an underestimate of the extinction rate in the system. Alternatively, the lower point estimates from our analysis may be more characteristic of the dynamics in these populations than the estimate provided by Pajunen & Pajunen (2003) or the mean of the posterior distribution. In their ecological survey, populations were assumed to be extinct when D. magna were absent from a habitat patch for two consecutive years (Pajunen & Pajunen 2003). This is a reasonable assumption in these rock pools, where desiccation and freeze/thaw cycles provide numerous cues for emergence from resting eggs. However, in more stable bodies of water, the diapausing eggs of zooplankton are known to remain viable in sediments for very long periods of time (e.g. Carvalho & Wolf 1989; Hairston et al. 1995). If this were the case in the Tvärminne archipelago, the assumptions of Pajunen & Pajunen (2003) might lead to an overestimate of the extinction rate in the system.
Finally, our model of coalescence in a metapopulation is not the only way to simulate data from such a system. Wakeley & Aliacar (2001) developed a metapopulation coalescent model and identified two separate phases of the coalescent process (the scattering and collecting phases). When using the Wakeley & Aliacar (2001) model, both phases are simulated if more than a single sequence or allele is sampled per deme. This model was not employed in our analysis because its application in software packages like ms (Hudson 2002) requires either that the scattering phase be simulated separately or that samples are reduced to a single allele or sequence per deme. Our analysis required larger samples, to estimate within-population values for several summary statistics. Shriner et al. (2006) applied the collecting phase of the model derived by Wakeley & Aliacar (2001) to HIV samples taken from within individuals. Their analysis tested the metapopulation model against six alternatives (including negative frequency-dependent selection, positive selection, exponential growth, etc.) and found that it best explained the observed data. These results show the promise of applying the metapopulation coalescent, but its widespread use will most likely await its inclusion in user-friendly software designed with ABC in mind (e.g. DIY ABC; Cornuet et al. 2008). In this study, the coalescent history we simulated appears to have captured the dynamics of the system, given the similarity between summary statistics calculated from the empirical data and those calculated from PODS (Fig. S1, Supporting information).
Approximate Bayesian computation holds great promise for inference in complex demographic systems like metapopulations. Of the data sets that most closely resembled the data collected from the Finnish Daphnia populations, a large majority were simulated under the persistent source model (Table 2). Our data were also able to provide an independent estimate of the rate of local extinction in the system. Application of ABC to more complicated demographic histories will require that informative data summaries are identified for all parameters of interest, but recent advances like the incorporation of feed-forward neural networks (Blum & François 2010) may greatly improve the ability of ABC to rapidly and accurately parameterize complex models of population history.
Supplementary Material
Acknowledgements
The authors thank D. Ebert and C. Haag for assistance with microsatellite primers and sample locations. Thanks also to M. Reinikainen, A. Ruuskanen, and others at the Tvärminne Zoological Station, without whom sample collection would not have been possible. The authors would additionally like to thank R. Eytan, C. Zakas, M. Meyers, T. Kartzinel, K. Bockrath, and C. Ewers for helpful discussions of the underlying coalescent model. We also appreciate conversations with M. Hickerson concerning the results of our analyses. K. Robinson provided numerous helpful comments on early drafts of the manuscript and assisted in field collections. We also gratefully acknowledge the input of two anonymous reviewers and F. Rousset, for comments that substantially improved the manuscript. ABC simulations and analysis were facilitated by the computational resources provided by the Department of Genetics at the University of Georgia and the help of D. Brown. This research was supported by a Ruth L. Kirschstein Training Grant from the National Institutes of Health, the Kirby and Jan Alton Fellowship, and the University of Georgia Department of Genetics.
Footnotes
The research detailed in this manuscript constituted one chapter from the doctoral dissertation research of J.R. As such, J.R. contributed to all aspects of the project, from initial design, to sample collection, genotyping, simulation design and analysis, and manuscript preparation. D.H. assisted with the design of coalescent models for A.B.C. and provided comments on numerous drafts of the manuscript. J.W. assisted with lab work and the design of coalescent models. J.W. also provided funding for travel and genotyping.
Data accessibility
Sample locations and microsatellite genotypes (both raw and binned allele calls) are shared with a previous publication from our group (Robinson et al. 2012a) and are available from the Dryad data repository at doi:10. 5061/dryad.0dn7s (Robinson et al. 2012b).
Supporting information
Additional supporting information may be found in the online version of this article.
References
- Altermatt F, Ebert D. Genetic diversity of Daphnia magna populations enhances resistance to parasites. Ecology Letters. 2008;11:918–928. doi: 10.1111/j.1461-0248.2008.01203.x. [DOI] [PubMed] [Google Scholar]
- Barson NJ, Cable J, Van Oosterhout C. Population genetic analysis of microsatellite variation of guppies (Poecilia reticulata) in Trinidad and Tobago: evidence for a dynamic source-sink metapopulation structure, founder events and population bottlenecks. Journal of Evolutionary Biology. 2009;22:485–497. doi: 10.1111/j.1420-9101.2008.01675.x. [DOI] [PubMed] [Google Scholar]
- Beaumont MA. Approximate Bayesian computation in evolution and ecology. Annual Review of Ecology, Evolution, and Systematics. 2010;41:379–406. [Google Scholar]
- Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162:2025–2035. doi: 10.1093/genetics/162.4.2025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerli P. Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations. Molecular Ecology. 2004;13:827–836. doi: 10.1111/j.1365-294x.2004.02101.x. [DOI] [PubMed] [Google Scholar]
- Beerli P, Felsenstein J. Maximum-likelihood estimation of migration rates and effective population numbers in two populations using a coalescent approach. Genetics. 1999;152:763–773. doi: 10.1093/genetics/152.2.763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertorelle G, Benazzo A, Mona S. ABC as a flexible framework to estimate demography over space and time: some cons, many pros. Molecular Ecology. 2010;19:2609–2625. doi: 10.1111/j.1365-294X.2010.04690.x. [DOI] [PubMed] [Google Scholar]
- Blum MGB, François O. Non-linear regression models for Approximate Bayesian Computation. Statistics and Computing. 2010;20:63–73. [Google Scholar]
- Carvalho GR, Wolf HG. Resting eggs of lake-Daphnia I. distribution, abundance and hatching of eggs collected from various depths in lake sediments. Freshwater Biology. 1989;22:459–470. [Google Scholar]
- Chan YL, Anderson CNK, Hadly EA. Bayesian estimation of the timing and severity of a population bottleneck from ancient DNA. PLoS Genetics. 2006;2:e59. doi: 10.1371/journal.pgen.0020059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth D. Effects of inbreeding on the genetic diversity of populations. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2003;358:1051–1070. doi: 10.1098/rstb.2003.1296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colson I, Du Pasquier L, Ebert D. Intragenic tandem repeats in Daphnia magna: structure, function and distribution. BMC research notes. 2009;2:206. doi: 10.1186/1756-0500-2-206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corander J, Waldmann P, Sillanpää MJ. Bayesian analysis of genetic differentiation between populations. Genetics. 2003;163:367–374. doi: 10.1093/genetics/163.1.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornuet JM, Santos F, Beaumont MA, et al. Inferring population history with DIY ABC: a user-friendly approach to Approximate Bayesian Computation. Bioinformatics. 2008;24:2713–2719. doi: 10.1093/bioinformatics/btn514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csilléry K, Blum MGB, Gaggiotti OE, François O. Approximate Bayesian Computation (ABC) in practice. Trends in Ecology & Evolution. 2010;25:410–418. doi: 10.1016/j.tree.2010.04.001. [DOI] [PubMed] [Google Scholar]
- Csilléry K, François O, Blum MGB. abc: an R package for approximate Bayesian computation (ABC) Methods in Ecology and Evolution. 2012;3:475–479. doi: 10.1016/j.tree.2010.04.001. [DOI] [PubMed] [Google Scholar]
- Di Rienzo A, Peterson AC, Garza JC, Valdes AM, Slatkin M, Freimer NB. Mutational process of simple-sequence repeat loci in human populations. Proceedings of the National Academy of Sciences, USA. 1994;91:3166–3170. doi: 10.1073/pnas.91.8.3166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dias PC, Verheyen GR, Raymond M. Source-sink populations in Mediterranean Blue tits: evidence using single-locus minisatellite probes. Journal of Evolutionary Biology. 1996;9:965–978. [Google Scholar]
- Ebert D, Haag CR, Kirkpatrick M, Riek M, Hottinger JW, Pajunen VI. A selective advantage to immigrant genes in a Daphnia metapopulation. Science. 2002;295:485–488. doi: 10.1126/science.1067485. [DOI] [PubMed] [Google Scholar]
- Estoup A, Guillemaud T. Reconstructing routes of invasion using genetic data: why, how and so what? Molecular Ecology. 2010;19:4113–4130. doi: 10.1111/j.1365-294X.2010.04773.x. [DOI] [PubMed] [Google Scholar]
- Guillot G, Mortier F, Estoup A. Geneland: a program for landscape genetics. Molecular Ecology Notes. 2005;5:712–715. [Google Scholar]
- Haag CR, Hottinger JW, Riek M, Ebert D. Strong inbreeding depression in a Daphnia metapopulation. Evolution. 2002;56:518–526. [PubMed] [Google Scholar]
- Haag CR, Riek M, Hottinger JW, Pajunen VI, Ebert D. Genetic diversity and genetic differentiation in Daphnia metapopulations with subpopulations of known age. Genetics. 2005;170:1809–1820. doi: 10.1534/genetics.104.036814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag CR, Riek M, Hottinger JW, Pajunen VI, Ebert D. Founder events as determinants of within-island and amongisland genetic structure of Daphnia metapopulations. Heredity. 2006;96:150–158. doi: 10.1038/sj.hdy.6800774. [DOI] [PubMed] [Google Scholar]
- Hairston NG, Jr, Van Brunt RA, Kearns CM, Engstrom DR. Age and survivorship of diapausing eggs in a sediment egg bank. Ecology. 1995;76:1706–1711. [Google Scholar]
- Hanski I, Ranta E. Coexistence in a patchy environment: three species of Daphnia in rock pools. The Journal of Animal Ecology. 1983;52:263–279. [Google Scholar]
- Hickerson MJ, Dolman G, Moritz C. Comparative phylogeographic summary statistics for testing simultaneous vicariance. Molecular Ecology. 2006;15:209–223. doi: 10.1111/j.1365-294X.2005.02718.x. [DOI] [PubMed] [Google Scholar]
- Hudson RR. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
- Kass RE, Raftery AE. Bayes factors. Journal of the American Statistical Association. 1995;90:773–795. [Google Scholar]
- Kingman JFC. On the genealogy of large populations. Journal of Applied Probability. 1982;19:27–43. [Google Scholar]
- Koenker R. quantreg: quantile regression. R package (version. 4.44) 2009 http://CRAN.R-project.org/package=quantreg.
- Koenker R, Ng P. SparseM: sparse linear algebra. R package (version. 0.83) 2009 http://CRAN.R-project.org/package=SparseM.
- Lamy T, Pointier JP, Jarne P, David P. Testing metapopulation dynamics using genetic, demographic and ecological data. Molecular Ecology. 2012;21:1394–1410. doi: 10.1111/j.1365-294X.2012.05478.x. [DOI] [PubMed] [Google Scholar]
- Levins R. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bulletin of the Entomological Society of America. 1969;15:237–240. [Google Scholar]
- Nielsen R, Wakeley J. Distinguishing migration from isolation: a Markov Chain Monte Carlo approach. Genetics. 2001;158:885–896. doi: 10.1093/genetics/158.2.885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pajunen VI, Pajunen I. Long-term dynamics in rock pool Daphnia metapopulations. Ecography. 2003;26:731–738. [Google Scholar]
- Pannell JR, Charlesworth B. Effects of metapopulation processes on measures of genetic diversity. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2000;355:1851–1864. doi: 10.1098/rstb.2000.0740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter BM, Wegmann D, Excoffier L. Distinguishing between population bottleneck and population subdivision by a Bayesian model choice procedure. Molecular Ecology. 2010;19:4648–4660. doi: 10.1111/j.1365-294X.2010.04783.x. [DOI] [PubMed] [Google Scholar]
- Pidugu S, Schlötterer C. ms2 ms.pl: a PERL script for generating microsatellite data. Molecular Ecology Notes. 2006;6:580–581. [Google Scholar]
- Pritchard JK, Seielstad MT, Perez-Lezaun A, Feldman MW. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Molecular Biology and Evolution. 1999;16:1791–1798. doi: 10.1093/oxfordjournals.molbev.a026091. [DOI] [PubMed] [Google Scholar]
- Pulliam HR. Sources, sinks, and population regulation. The American Naturalist. 1988;132:652–661. [Google Scholar]
- R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2012. [Google Scholar]
- Robinson JD, Haag CR, Hall DW, Pajunen VI, Wares JP. Genetic estimates of population age in the water flea, Daphnia magna. The Journal of Heredity. 2012a;103:887–897. doi: 10.1093/jhered/ess063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson JD, Haag CR, Hall DW, Pajunen VI, Wares JP. Data from: genetic estimates of population age in the water flea, Daphnia magna. Dryad Digital Repository. 2012b doi: 10.1093/jhered/ess063. doi:10.5061/ dryad.0dn7s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers AR. Genetic evidence for a Pleistocene population explosion. Evolution. 1995;49:608–614. doi: 10.1111/j.1558-5646.1995.tb02297.x. [DOI] [PubMed] [Google Scholar]
- Rousset F. Genetic differentiation within and between two habitats. Genetics. 1999;151:397–407. doi: 10.1093/genetics/151.1.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyfert AL, Cristescu MEA, Frisse L, Schaack S, Thomas WK, Lynch M. The rate and spectrum of microsatellite mutation in Caenorhabditis elegans and Daphnia pulex. Genetics. 2008;178:2113–2121. doi: 10.1534/genetics.107.081927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shriner D, Liu Y, Nickle DC, Mullins JI. Evolution of intrahost HIV-1 genetic diversity during chronic infection. Evolution. 2006;60:1165–1176. [PubMed] [Google Scholar]
- Slatkin M. Gene flow and genetic drift in a species subject to frequent local extinctions. Theoretical Population Biology. 1977;12:253–262. doi: 10.1016/0040-5809(77)90045-4. [DOI] [PubMed] [Google Scholar]
- Venables WN, Ripley BD. Modern Applied Statistics with S. 4th. Springer; New York, NY: 2002. R package ver. 7.3-1. [Google Scholar]
- Wakeley J, Aliacar N. Gene genealogies in a metapopulation. Genetics. 2001;159:893–905. doi: 10.1093/genetics/159.2.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.