Moderated mediation analysis: An illustration using the association of gender with delinquency and mental health

Abstract

Purpose

When researchers find an association between two variables, it is useful to evaluate the role of other constructs in this association. While assessing these mediation effects, it is important to determine if results are equal for different groups. It is possible that the strength of a mediation effect may differ for males and females, for example – such an effect is known as moderated mediation.

Design

Participants were 2532 adolescents from diverse ethnic/racial backgrounds and equally distributed across gender. The goal of this study was to investigate parental respect as a potential mediator of the relationship between gender and delinquency and mental health, and to determine whether observed mediation is moderated by gender.

Findings

Parental respect mediated the association between gender and both delinquency and mental health. Specifically, parental respect was a protective factor against delinquency and mental health problems for both females and males.

Practical implications

Demonstrated the process of estimating models in Lavaan, using two approaches (i.e. single group regression and multiple group regression model), and including covariates in both models.

Introduction

Both impaired mental health functioning (e.g., depression, anxiety) and delinquent behavior (e.g., aggression, truancy) are common among adolescents (Achenbach & McConaughy, 1997; Cicchetti & Toth, 1991). Epidemiological data suggests that 18% of adolescents experience symptoms of depression (Rushton et al., 2002; Saluja et al., 2004).

Early onset of depression is a risk factor for adult depression (Pine et al., 1998), and early delinquency is associated with poor educational attainment, criminal behaviors, dependence on public assistance and early pregnancies (Cote et al., 2001; Fontaine et al., 2008; Moffitt et al., 2001; Odgers et al., 2008; Schaeffer et al., 2006). There is robust evidence in the literature that females more often report more symptoms of depression and anxiety, whereas males tend to report more delinquency (see Albano and Kain, 2005; Moffit et al., 2001 for reviews). Still, mechanisms through which observed gender differences occur are not well understood. There is preliminary evidence that parental respect might be a protective mechanism against delinquency (Unger et al., 2002; 2006; Gil et al., 2000), although whether this is also the case for anxiety and depressive symptoms is unknown.

Mediation effects are increasingly seen as important in psychological research. A mediation effect occurs when a third variable explains the relationship between two other variables. Figure 1 shows a model, in which a predictor (x) is found to be associated, and presumed to be causally associated, with an outcome (y). The size of the effect from x to y is the total effect and is labelled c.

Figure 1.

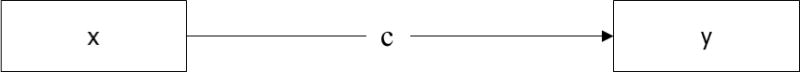
Path diagram showing the effect from predictor (x) to outcome (y).

A mediating variable, m, can be added to this model, as shown in Figure 2. Variable m is hypothesized to be a measure of the mechanism by which the predictor x has its effect. The direct effect from x to y is now labelled c′. The effect from x to m is labelled a, and the effect from m to y is labelled b. The size of the effect from x to y is reduced by the total amount of the indirect effect, which is found as the product of a and b. Therefore:

$$c=\mathit{ab}+c\prime$$

Figure 2.

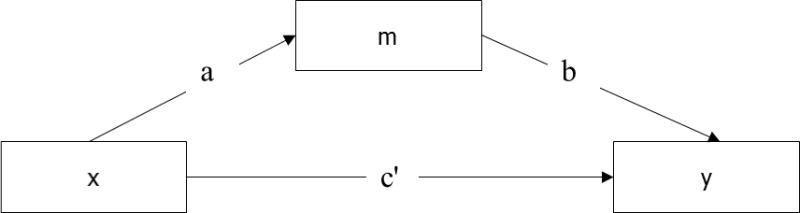
Path diagram showing mediation effect.

Researchers are typically interested in the indirect effect (found as ab) which explains the extent to which the effect of x is mediated by m. To estimate the standard error and hence confidence intervals and p-value, bootstrapping is used, as the effect ab is not normally distributed (MacKinnon et al., 2007, Shrout and Bolger, 2002).

The use of moderator analyses also has a long history in psychological research through its use in analysis of variance (typically referred to as an interaction effect). A moderator effect occurs when the effect of one predictor is changed by a second predictor. For example, the association between gender and delinquency may vary as a function of parental monitoring (or, equivalently, the effect of parental monitoring may vary as a function of gender). To fully disentangle the nature of the relationships between variables it may be necessary to combine these two approaches. James and Brett (1984) introduced the term ‘moderated mediation’ for the situation in which a moderator is added to a mediation model, however there are several different ways in which a moderator may influence a mediational relationship (see Preacher et al., 2007).

This paper presents an example of moderated mediation in which an independent variable functions as a moderator of the path labelled b in Figure 2 using a sample of 2532 adolescents. Gender is treated as an exogenous variable, with parental respect as a mediating variable, and have two outcome variables: delinquency and mental health. In addition, gender acts as a moderator of the relationship between parental respect and the outcome variables, hence this is a moderated mediation model. Two equivalent models are demonstrated to estimate the parameters of the moderated mediation effect. Recognizing alternative equivalent ways to parameterize a model may be seen as a problem (Hershberger, 1994, Hershberger, 2006, Raykov and Marcoulides, 2001), however the ability to respecify a model in different, but equivalent, ways allows us to easily relax assumptions, and to extend models in different ways.

Finally, little attention is paid in the methodological literature on moderator and mediator effects to confounding variables. If a variable (Z) is a predictor of all variables in a mediation model, then it is possible that spurious mediation effects will be found if this variable is not controlled. The paper demonstrates how confounding variables can be controlled for in statistical models of moderated mediation. All analyses use the Lavaan (Rosseel, 2012) package within the R statistical environment (R Development Core Team 2014) which is free and open source (other software which can analyze multiple group structural equation models and allow non-linear parameter constrains can also be used, including Mx/openMx, Lisrel, EQS, or Mplus [note that if a software package is not mentioned this should not be taken to imply that it cannot estimate such models, it is just that we are not sufficiently familiar with its capabilities at the time of writing]).

Method

Procedure

Data for the present study come from the 6^th wave of a longitudinal investigation of two cohorts of youth (D’Amico et al., 2012), originally recruited from middle schools in the Los Angeles, California, metropolitan area. Participants were 2532 adolescents who completed a web-based survey between May 2013 and April 2014 and provided complete data for all predictors in the analysis. A Certificate of Confidentiality was obtained, and all procedures were approved by the individual schools, the school districts, and the institution’s review board. See D’Amico et al., 2012 for more details on procedures.

The sample was 46% male and mean age was 16.2 years (sd 0.74, range 14–18). The race/ethnicity composition was 44% Hispanic, 31% non-Hispanic white (hereafter ‘white’), 21% Asian, and 14% other.

Measures

Sociodemographic variables included age, gender, educational attainment of the respondent’s mother, and race/ethnicity (Hispanic, Asian, other race, and White).

Delinquency was a summary score of 12 items indicating the frequency of different behaviors representing this construct (Tucker et al., 2002). Participants were asked how often they had done each of the following 12 things over the past year: skipped school; broken into property; stolen from a store; been sent out of the classroom; gotten into trouble with police; damaged others’ property on purpose; run away from home; been involved in fights; been suspended from school; cheated on a test; sold drugs; driven a car under the influence (1 = not at all to 6 = 20 or more times). Higher scores indicate more involvement in these behaviors (α=0.86).

Mental Health Functioning was measured with the Mental Health Inventory (MHI-5; Stewart et al., 1992). The MHI-5 evaluates general mental health by assessing frequency (1=all the time to 6=never) of the following domains of mental health: anxiety (i.e. “How much of the time have you been a very nervous or anxious person?”); general positive affect (i.e. “How much of the time have you felt calm or peaceful?”; “How much of the time have you been a happy person?”); depression (i.e. “How much of the time have you felt downhearted or blue?”); and behavioral/emotional control (i.e. “How often have you felt so down in the dumps that nothing could cheer you up?”). The MHI-5 has been used in studies of adolescents (Tanielian et al., 2009; Theunissen et al., 2011). Higher scores correspond to better mental health (α=0.75).

Respect for Parents was assessed by a four item questionnaire adapted from Unger and colleagues (Unger et al., 2002) and used in previous studies (Shih et al., 2010; 2012). Participants were asked to respond on a 4-point Likert scale ranging from 1=strongly disagree to 4=strongly agree to questions measuring how important it was to participants that they care (i.e. “I will take care of my parents when they are old”), respect (i.e. “It’s important to respect my parents) and honor their parents (i.e. “It is important to honor my parents”) in addition to being a good person (i.e. “I will take care of my parents when they are old”). Higher scores indicate greater respect (α=0.91).

Results

Statistical analysis

A very brief introduction to regression models in Lavaan is presented first. The paper demonstrates that a difference between two groups can be tested using a regression framework or a multiple group framework using gender as predictor and delinquency as outcome. Then a moderator model is shown, which can be fitted as a single group using a multiplicative interaction term, or fitted as multiple groups. Next a mediation model is fit, with gender as predictor, delinquency as outcome, and parental respect as mediator. The mediation model is then adapted to a moderated mediation model. Again, two different, but equivalent, approaches are demonstrated – that of a multiplicative interaction term and a multiple groups approach. One advantage of a structural equation modeling approach is how straightforwardly it is possible to move from a single outcome to multivariate outcomes; this is demonstrated by adding mental health as a second outcome, and show how multivariate hypotheses can be tested using a Wald test. Finally, show how additional control variables can be added to the model and it is shown how this may alter conclusions.

Models in Lavaan

Estimating a structural equation model using the Lavaan package involves three steps. First, the model is set up using Lavaan syntax. Throughout this paper this setup is referred to as modelx. Second, the model is estimated using one of the estimation functions available in Lavaan. In this paper, the sem() function is used. The sem() takes as minimum arguments the name of the model, and the name of the dataset that the model is to be applied to (d is used throughout this paper). The fitted model is named fitx. Finally, the summary() function is applied to the fitted model to examine the results.

The effect of gender on delinquency

This effect can be evaluated within a structural equation modeling framework using a regression approach, or a multiple groups approach. The data are in a data frame named d. Model syntax for the regression model is named model1, and that model is then run using the sem() function. In Lavaan syntax, the symbol “~” means ‘regressed on’, hence “ del ~ male” means that del (delinquency, the outcome) is regressed on male (the predictor). The intercept of del is requested by regressing del on a constant value of 1 – this is written as del ~ 1. Additional parameters can be created and tested in Lavaan using the “:=” operator.

The model is first set up, and labelled model1. The model runs, creating an output object fit1, and finally a summary of that object is created. Code and results (with some superfluous parts removed) are shown below:

> model1 <- “
+  del ~ male
+  del ~ 1
+  ”
> fit1 <- sem(model1, data=d)
> summary(fitModel1)

lavaan (0.5–16) converged normally after	1 iterations
Number of observations	2533
Estimator	ML
Minimum Function Test Statistic	0.000
Degrees of freedom	0
P-value (Chi-square)	1.000
Parameter estimates:
Information	Expected
Standard Errors	Standard

	Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
male	0.069	0.020	3.471	0.001
Intercepts:
del	1.431	0.013	106.730	0.000
Variances:
del	0.247	0.007

The results of the regression show that males have delinquency scores which are, on average, 0.069 points higher than females. The standard error for this coefficient is 0.020 and p = 0.001. The intercept, which is the mean score for females, is 1.431, with a standard error of 0.013. The regression equation could be written as: Delinquency = 1.431 + 0.0.069 * male.

The model results have provided the mean delinquency score for females as the intercept of the model (1.431), as well as the standard error (0.013), and the difference between the mean score for females and males (0.069) along with its standard error (0.021). We have not been provided with the mean score for males–this is calculated as 1.431 + 0.069 = 1.500, but the standard error is not easily calculated. However, Lavaan allows the creation of new parameters in the model as functions of other parameters. These new parameters are created by naming the regression and intercept parameters.

Lavaan names parameters implicitly, but parameters can be named explicitly in the model. To be consistent with the regression equation, b0 is used for the intercept, and b1 for the slope. A new parameter is defined as a function of other parameters using the := operator. This is model1a, code and results follow.

> model1a <- “
+  del ~ b1 * male
+  del ~ b0 * 1
+    maleMean:= b0 + b1
+  ”
>
>
> fit1a <- sem(model1a, data=d)
> summary(fit1a)

		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
male	(b1)	0.069	0.020	3.471	0.001
Intercepts:
del	(b0)	1.431	0.013	106.730	0.000
Variances:
del		0.247	0.007
Defined parameters:
maleMean		1.500	0.015	102.658	0.000

The intercept ( b0) and slope ( b1) have been labelled, and a new parameter ‘ maleMean’, which is their sum has been defined. This parameter has a value of 1.500 (as calculated based on the previous model) but a standard error is now also provided.

As an alternative to the regression approach, the same model can be fit via a multiple group approach. In the multiple group approach only the mean of each variable is estimated, and the effect of gender is calculated by finding the difference between the two means. When a multiple group model is estimated two parameter labels are needed (one for each group), and these are combined into a vector using the c() function (c being short for ‘combine’). When the sem() function is called, the group argument is used to tell sem() that the grouping variable is ‘ male’ and it will estimate separate models for each group. This is model 2, shown below.

> model2 <- “
+  del ~ c(maleMean, femaleMean) * 1
+  diff:= maleMean – femaleMean
+ ”
> fit2 <- sem(model2, data=d, group=“male”)
> summary(fit2)

Group 1 [1]:
		Estimate	Std.err	Z-value	P(>|z|)
Intercepts:
del	(mlMn)	1.500	0.018	85.195	0.000
Variances:
del		0.359	0.015
Group 2 [0]:
		Estimate	Std.err	Z-value	P(>|z|)
Intercepts:
del	(fmlM)	1.431	0.011	135.617	0.000
Variances:
del		0.153	0.006
Defined parameters:
diff		0.069	0.021	3.353	0.001

In these results, group 1 is the male group, and so the results the male mean in this section. Group 2 is the female group, where the female mean is calculated. In the regression approach (model 1) the female mean and the difference were presented, and a parameter was added to calculate the male mean. In this approach, two means appear in the results, and add a parameter, named diff, must be added to calculate the difference.

The same result for the means, and the difference between the means, was obtained using the using the regression approach (model 1) and the multiple group approach (model 2). However, there is a difference between the standard error using the regression approach and the standard error using the multiple groups approach. This difference occurs because the regression approach assumes homogeneity of variance, and the multiple group approach does not. The multiple group results (model2) show that the variance is considerably higher in the males (0.359) than the females (0.153). This discrepancy is resolved by either (a) using a technique that relaxes the assumption of homogeneity of variance in the regression approach, or (b) constraining the variances to equality in the multiple group approach.

For the regression approach the ‘mlr’ estimator is used. The mlr estimator is an implementation of the T2* chi-square statistic (Yuan and Bentler, 2000), itself a modification of the Satorra-Bentler scaled chi-square (Satorra and Bentler, 1994), which uses a sandwich estimator and does not assume homogeneity of variance. The argument estimator=“mlr” is addted to the call to the sem() function to use this estimator. The code and relevant part of the output is shown below:

> fit1b <- sem(model1a, data=d, estimator=“mlr”)
> summary(fit1b)

		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
male	(b1)	0.069	0.021	3.353	0.001

The standard errors of this regression approach now match the standard errors of the multiple group approach (which also does not assume homogeneity of variance). Alternatively the multiple group model can be fit constraining the variances of the males and females to be equal. This constrained is added by giving the the same name to the two parameters in the model (in this case, res, for residual variance) thereby forcing the homogeneity of variance assumption. Code and edited output:

model2a <- “
  del ~ c(maleMean, femaleMean) * 1
  del ~~ c(var, var) * del
  diff:= maleMean – femaleMean
  ”
fit2a <- sem(model2a, data=d, group=“male”)
summary(fit2a)

Defined parameters:
diff	0.069	0.020	3.461	0.001

The standard error of the multiple group approach now matches the standard error of the regression approach (which assumes homogeneity of variance). As an aside, the same result can be shown by carrying out a Student’s t-test (which assumes homogeneity of variance) and Welch’s t-test (which does not make the assumption).

Evaluating the gender-moderated relationship between parental respect and delinquency

Next, it is shown how a moderator model can be coded in Lavaan. In the first moderated model focused on the association between parental respect and delinquency, and considered whether the association is moderated by gender. The model can again be estimated using a regression based approach – by creating a multiplicative interaction term, or using multiple groups. A multiplicative interaction term is created first, by multiplying the two variables together, as in regression. The new variable representing the interaction is named maleXResp. This variable is generated in R with the following syntax:

> d$maleXResp <- d$male * d$respect

All three variables are then entered as predictors of MHI.

> model3 <- “
+ del ~ b1 * respect + b2 * male + b3 * maleXResp
+ ”
> fit3 <- sem(model3, data=d, estimator=“mlr”)
> summary(fit3)

		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respect	(b1)	−0.160	0.029	−5.473	0.000
male	(b2)	0.006	0.213	0.029	0.977
maleXRsp	(b3)	0.014	0.055	0.252	0.801
Intercepts:
del		2.036	0.115	17.772	0.000
Variances:
del		0.241	0.029

The labels for the parameters are in parentheses before each variable name are. Hence b1 is the regression of delinquency on respect, b2 is the effect of being male, and b3 is the regression of delinquency on the multiplicative interaction term. The regression parameter associated with respect is −0.160, with a standard error of 0.029. This is the regression effect for the females (because gender is dummy coded, and female is the reference). The difference between the males and females is given by the interaction term maleXresp (shortened to maleXRsp), which is 0.014, with a standard error of 0.055. The regression equation can be written as:

$$\text{delinquency}={\mathrm{b}}_0+{\mathrm{b}}_1\ast \text{respect}+{\mathrm{b}}_2\ast \text{male}+\mathrm{b}3\ast \text{male}\ast \text{respect}$$

Values for male and female can be substituted to determine the slope for each group. For females, male = 0. Substituting 0 into the equation:

$$\text{delinquency}={\mathrm{b}}_0+{\mathrm{b}}_1\ast \text{respect}+{\mathrm{b}}_2\ast 0+\mathrm{b}3\ast 0\ast \text{respect}$$

Any term that is multiplied by zero can obviously be ignored; therefore for the females, the parameter b₁ represents the effect of respect.

$$\text{delinquency}={\mathrm{b}}_0+{\mathrm{b}}_1\ast \text{respect}$$

To find the male slope, substitute the value 1 for males. Multiplying any value by 1 does not change the value, so:

$$\text{delinquency}={\mathrm{b}}_0+{\mathrm{b}}_1\ast \text{respect}+{\mathrm{b}}_2\ast 1+\mathrm{b}3\ast 1\ast \text{respect}$$

$$\text{delinquency}={\mathrm{b}}_0+{\mathrm{b}}_1\ast \text{respect}+{\mathrm{b}}_2+\mathrm{b}3\ast \text{respect}$$

Rearranging that equation:

$$\text{delinquency}={\mathrm{b}}_0+{\mathrm{b}}_2{(\mathrm{b}}_1+\mathrm{b}3)\ast \text{respect}$$

The slope for males is therefore equal to the sum of b₁ and b₃. This is not currently a parameter in the model, but can be added as shown in model 3a.

> model3a <- “
+  del ~ b1 * respect + b2 * male + b3 * maleXResp
+  maleReg:= b1 + b3
+  ”
fit3a <- sem(model3a, data=d)
> summary(fit3a)

		Estimate	Std.err	Z-value	P(>|z|)
del ~
respect	(b1)	−0.160	0.028	−5.748	0.000
male	(b2)	0.006	0.140	0.044	0.965
maleXRsp	(b3)	0.014	0.037	0.375	0.707
Variances:
del		0.241	0.007
Defined parameters:
maleReg		−0.146	0.025	−5.970	0.000

This moderator model can also be estimated using a multiple group approach. The regression approach gave the slope for females, and the difference between males and females, and a line was added to the model to calculate the slope for males. The multiple group approach estimates the slope for males (which is labelled b1m) and the slope for females ( b1f). A new parameter is defined to calculate the difference between these two values ( diffSlopes).

> model4 <- “
+  del ~ c(b1m, b1f) * respect
+  diffSlopes:= b1m – b1f
+ ”
> fit4 <- sem(model4, data=d, group=“male”)
> summary(fit4)

Group 1 [1]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respect	(b1m)	−0.146	0.030	−4.940	0.000
Intercepts:
del		2.042	0.111	18.367	0.000
Variances:
del		0.351	0.015
Group 2 [0]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respect	(b1f)	−0.160	0.022	−7.346	0.000
Intercepts:
del		2.036	0.083	24.525	0.000
Variances:
del		0.147	0.006
Defined parameters:
diffSlopes		0.014	0.037	0.379	0.705

Some evidence of moderation is found in this model. There is a negative effect from parental respect to delinquency, indicating that greater respect is associated with less delinquency, however the effect is slightly stronger for females (−0.160) than for males (−0.146). The difference is given in the diffSlopes parameter, and this is not statistically significant.

Evaluating whether parental respect mediates the association between gender and delinquency

The next mediation model attempts to disentangle the association between gender and delinquency, determining if it is, in part or in whole, explained by parental respect. When estimating Model 1 it was established that the total effect (c in Figure 1) is equal to 0.069 and therefore ab + c′ = 0.069. Again, the mediation model can be estimated using a multiple group approach, or a single group approach. The single group approach is shown in path diagram format in Figure 3. The values for ab and c are calculated using the define parameter option.

Figure 3.

Path diagram showing mediation model.

Because the path of interest is given as ab, and this is not normally distributed, the bootstrap option in the sem() function is used to estimate the standard errors. The total effect (c) is also estimated in this model.

> model5 <- “
+  del ~ b * respect + cprime * male
+  respect ~ a * male
+  ab:= a * b
+  c:= ab + cprime
+  ”
> fit5 <- sem(model5, data=d, se=“bootstrap”)
> summary(fit5)

		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respct	(b)	−0.153	0.029	−5.253	0.000
male	(cprm)	0.058	0.020	2.914	0.004
respect ~
male	(a)	−0.068	0.022	−3.102	0.002
Variances:
del		0.241	0.029
respect		0.280	0.017
Defined parameters:
ab		0.010	0.004	2.679	0.007
c		0.069	0.020	3.358	0.001

Again, the mediation model can be estimated using a multiple groups approach. For this approach, the model represented in the path diagram shown in Figure 4 is used. However, only path b is represented in the diagram directly. On Model 1 and Model 2 at the start of this section the regression of delinquency on gender could be represented as the difference between the two groups’ means of delinquency in a multiple group model. In the same way, path a in the mediation model is represented by the difference between the means of respect for males and females, these are labelled respMeanMale and respMeanFemale, respectively. Path c′ is calculated as the difference between the intercepts of delinquency for males and females. (Because delinquency is an endogenous variable, its mean is not estimated as a model parameter; instead, its intercept is modelled.) The total effect c is calculated using ab + cprime, and the indirect effect as a * b. Because of non-normality, bootstrapping is used to estimate standard errors.

Figure 4.

Multiple groups path diagram for mediation.

One additional complication is that it is necessary to refer to the intercept of respect, and hence the fixed.x=FALSE argument must be added to the call to sem(). In the following code, the values of b (that is, the effects from respect to delinquency) are constrained to be equal across groups. The intercepts of delinquency are labelled delIntMale and delIntFemale, and so c′ ( cprime in the model) is the difference between these two values, and this represents the indirect effect of male on delinquency.

> model6 <- “
+  del ~ c(b, b) * respect
+  del ~ c(delIntMale, delIntFemale) * 1
+  respect ~ c(respMeanMale, respMeanFemale) * 1
+
+  a:= respMeanMale – respMeanFemale
+  ab:= a * b
+  cprime:= delIntMale – delIntFemale
+  c:= a * b + cprime
+  ”
> fit6 <- sem(model6, data=d, group = “male”, fixed.x=FALSE,
+ se=“bootstrap”)
> summary(fit6)
lavaan (0.5–16) converged normally after 21 iterations

Group 1 [1]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respect	(b)	−0.156	0.025	−6.187	0.000
Intercepts:
del	(dlIM)	2.076	0.097	21.289	0.000
respct	(rsMM)	3.703	0.017	214.797	0.000
Variances:
del		0.351	0.058
respect		0.345	0.030
Group 2 [0]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respect	(b)	−0.156	0.025	−6.187	0.000
Intercepts:
del	(dlIF)	2.017	0.099	20.463	0.000
respct	(rsMF)	3.772	0.012	314.200	0.000
Variances:
del		0.147	0.017
respect		0.225	0.020
Defined parameters:
a		−0.068	0.021	−3.232	0.001
ab		0.011	0.004	2.769	0.006
cprime		0.058	0.020	2.919	0.004
c		0.069	0.020	3.413	0.001

The results from model 6 very closely match the results from model 5. Of particular interest is the ab parameter, which represents the indirect (mediated) effect. Although this effect is small, it is statistically significant, indicating that some of the difference in delinquency between males and females may be explained by differences in respect.

Evaluating moderated mediation

That respect moderates the association between gender and delinquency, and that gender mediates the association between respect and delinquency has been establish. The next stage is to determine if there is a moderated mediation relationship.

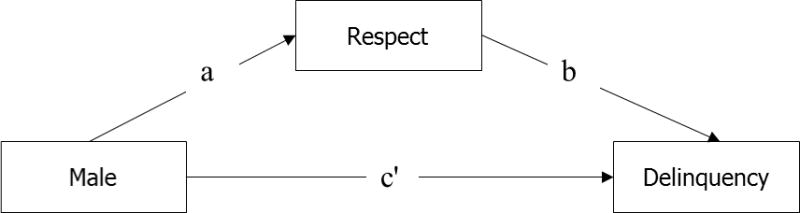
It is helpful to represent the moderated mediation model as a conceptual path diagram, as shown in Figure 5. This figure is based on Figure 2, although real labels are used, rather than X, M and Y. In addition, a path from male to path b has been added– this is the moderator effect. It is hypothesized that the path from Respect to Delinquency varies as a function of gender.

Figure 5.

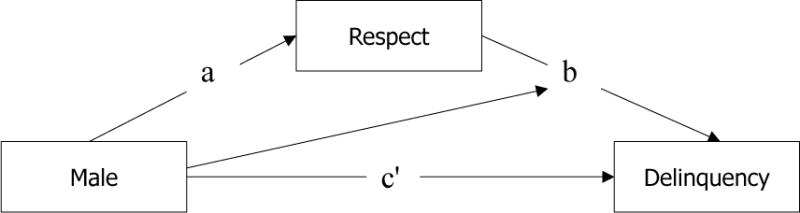
Conceptual path diagram showing moderated mediation.

The model cannot be estimated in this format. Instead, the model can be estimated using either the multiplicative regression approach, or the multiple groups approach. Using the multiplicative regression approach, as previously, multiplicative interaction term is created, and model represented in Figure 6 (Figure 6 is equivalent to Figure 5, but can be estimated directly) is fit. An additional parameter, b′ is added to the model, to represent the b parameter for the interaction term.

Figure 6.

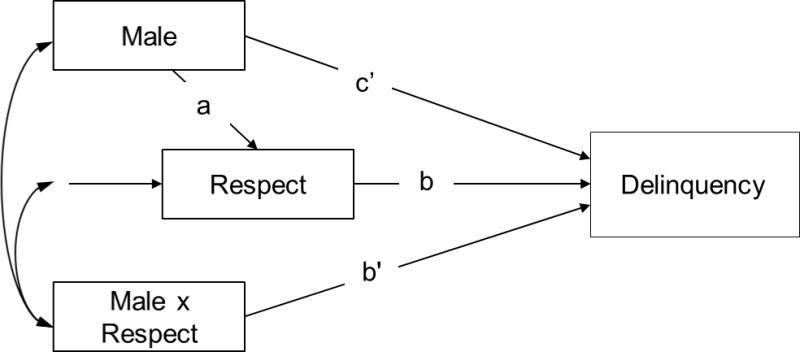
Path model for moderated mediation using multiplicative interaction term.

The path b now represents the path from respect to delinquency for the females. The b′ parameter is the difference between the male and female paths, and hence the regression of delinquency on respect for males is given by b + b′. The indirect effect of the predictor male is given by a * b. An indirect effect for each group can be calculated. For the females, the indirect effect is given by a * b, for the males, the effect is a * (b + b′). The code and output is shown below. The difference in the indirect effects – that is the moderated mediation effect – is given by the difference between the indirect effect for males and the indirect effect for females, labelled as indDiff in the model.

> model7 <- “
+  del ~ cprime * male
+  del ~ b * respect
+  del ~ bprime * maleXResp
+  respect ~ a * male
+  respect ~~ maleXResp
+  male ~~ maleXResp
+
+  bmale:= b + bprime
+  indMale:= bmale * a
+  indFemale:= b * a
+  indDiff:= indMale – indFemale
+  ”
>
> fit7 <- sem(model7, data=d, fixed.x=FALSE,
+      se=“bootstrap”)
> summary(fit7)

		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
male	(cprm)	0.006	0.222	0.028	0.978
respct	(b)	−0.160	0.029	−5.485	0.000
mlXRsp	(bprm)	0.014	0.058	0.242	0.809
respect ~
male	(a)	−0.068	0.021	−3.192	0.001
Covariances:
respect ~~
maleXResp		0.158	0.014	10.999	0.000
male ~~
maleXResp		0.919	0.005	178.383	0.000
Variances:
del		0.241	0.031
respect		0.280	0.018
male		0.248	0.001
maleXResp		3.561	0.025
Defined parameters:
bmale		−0.146	0.048	−3.059	0.002
indMale		0.010	0.005	2.190	0.029
indFemale		0.011	0.004	2.569	0.010
indDiff		−0.001	0.004	−0.230	0.818

The indirect for males is 0.010 (labelled indMale), and is statistically significant. Similarly, the indirect effect for females (labelled indFemale), 0.011, is also statistically significant. However, the difference between the two indirect effects: −0.001 (labelled indDiff) is not statistically significant, indicating that the mediation effect is not moderated by gender. In other words, there is no evidence of moderated mediation.

As with the prior models, the model can also be estimated using a multiple group approach. This approach is more intuitive, with somewhat clearer interpretation of parameters. Only small changes are required to modify the previous multiple group model (model 6). The parameter b is estimated for the males and the females separately, and the effects of gender are estimated by subtracting means (or intercepts) as in the previous models.

> model8 <- “
+  del ~ c(bMale, bFemale) * respect
+  del ~ c(delIntMale, delIntFemale) * 1
+  respect ~ c(respMeanMale, respMeanFemale) * 1
+
+  a:= respMeanMale – respMeanFemale
+  abMale:= a * bMale
+  abFemale:= a * bFemale
+  bPrime:= bMale – bFemale
+  intDiff:= abMale – abFemale
+  ”
> fit8 <- sem(model8, data=d, group = “male”, fixed.x=FALSE,
+      se=“bootstrap”)
> summary(fit8)

Group 1 [1]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respct	(bMal)	−0.146	0.047	−3.123	0.002
Intercepts:
del	(dlIM)	2.042	0.179	11.395	0.000
respct	(rsMM)	3.703	0.017	220.355	0.000
Variances:
del		0.351	0.059
respect		0.345	0.030
Group 2 [0]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respct	(bFml)	−0.160	0.029	−5.576	0.000
Intercepts:
del	(dlIF)	2.036	0.112	18.120	0.000
respct	(rsMF)	3.772	0.013	287.831	0.000
Variances:
del		0.147	0.017
respect		0.225	0.021
Defined parameters:
a		−0.068	0.022	−3.149	0.002
abMale		0.010	0.005	2.207	0.027
abFemale		0.011	0.004	2.556	0.011
bPrime		0.014	0.054	0.256	0.798
intDiff		−0.001	0.004	−0.248	0.804

Again, a very close match is found between the two approaches. The indirect effect for males is 0.010 in both models, with standard errors equal to 0.005 (single group model) and 0.004 (multiple group model). Similarly, the indirect effect for females is similar −0.011 for both models, with standard errors of 0.004 for both models. The moderator effect is no longer statistically significant when the moderated mediation model is estimated. In both of these models the moderator effect is equal to 0.014 with standard errors of 0.054 and 0.058. The moderated mediation effect also fails to achieve statistical significance.

Evaluating additional outcome: mental health

One advantage of a structural equation modeling approach is that it allows us to estimate multivariate models with multiple outcome variables simultaneously where these measures might be considered parts of a multivariate system. Such an approach can also increase statistical power (Cole et al., 1993, Cole et al., 1994). An additional outcome variable, mental health functioning (MHI), is added to the models to demonstrate how a multivariate test is carried out. For each parameter of the model which is represented by a regression path to delinquency (i.e. a, b and b′) a value for delinquency and a value for mental health functioning is estimated. To indicate these paths in the model, ‘D’ is added to the path for delinquency, and ‘M’ is added to the path for MHI. In addition, add a covariance in the residual correlation of delinquency and MHI is added using ‘ del ~~ mhi’.

> model9 <- “
+  del ~ cprimeD * male
+  del ~ bD * respect
+  del ~ bprimeD * maleXResp
+
+  mhi ~ cprimeM * male
+  mhi ~ bM * respect
+  mhi ~ bprimeM * maleXResp
+
+  mhi ~~ del
+
+  respect ~ a * male
+  respect ~~ maleXResp
+  male ~~ maleXResp
+  bmaleD:= bD + bprimeD
+  indMaleD:= bmaleD * a
+  indFemaleD:= bD * a
+  indDiffD:= indMaleD – indFemaleD
+
+  bmaleM:= bM + bprimeM
+  indMaleM:= bmaleM * a
+  indFemaleM:= bM * a
+  indDiffM:= indMaleM – indFemaleM
+  ”
>
> fit9 <- sem(model9, data=d, fixed.x=FALSE,
+ se=“bootstrap”)
>        summary(fit9)

		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
male	(cprD)	0.006	0.217	0.028	0.977
respct	(bD)	−0.160	0.029	−5.546	0.000
mlXRsp	(bprD)	0.014	0.057	0.246	0.805
mhi ~
male	(cprM)	1.796	0.589	3.047	0.002
respct	(bM)	0.996	0.126	7.934	0.000
mlXRsp	(bprM)	−0.350	0.156	−2.234	0.025
respect ~
male	(a)	−0.068	0.022	−3.139	0.002
Covariances:
del ~~
mhi		−0.088	0.021	−4.271	0.000
respect ~~
maleXResp		0.158	0.014	11.052	0.000
male ~~
maleXResp		0.919	0.005	171.927	0.000
Variances:
del		0.241	0.028
mhi		3.622	0.096
respect		0.280	0.017
male		0.248	0.001
maleXResp		3.561	0.026
Defined parameters:
bmaleD		−0.146	0.047	−3.106	0.002
indMaleD		0.010	0.005	2.207	0.027
indFemaleD		0.011	0.004	2.537	0.011
indDiffD		−0.001	0.004	−0.230	0.818
bmaleM		0.646	0.093	6.979	0.000
indMaleM		−0.044	0.015	−2.862	0.004
indFemaleM		−0.068	0.024	−2.803	0.005
indDiffM		0.024	0.014	1.695	0.090

A multivariate test of the mediation effects can be done using the LavTestWald() function, which uses a Wald test of parameters. It is not possible (we believe) to use the Wald test when the estimates have been bootstrapped, and therefore the MLM estimator (which gives the Satorra-Bentler scaled chi-square) is used. The model is refit using the MLM estimator, and l this is labelled model 9a. A series of constraints is set up, in this case, that the two moderated mediation effects are both equal to zero. The specification for this model is named con9a. The Wald test function with is then used with the estimated model and constraints. The result gives a chi-square statistic of 3.21, with 2 df and p=0.201. The multivariate test has therefore not reached statistical significance.

> fit9a <- sem(model9, data=d, fixed.x=FALSE,
+        estimator=“mlm”)
>
> con9a <- “
+  indDiffM == 0
+  indDiffD == 0
+  ”
>
> lavTestWald(fit9a, constraints=con9a)
$stat
[1] 3.210631
$df
[1] 2
$p.value
[1] 0.2008262

As would be expected, this model can also be estimated using a multiple group approach, shown as model 10.

> model10 <- “
+  del ~ c(bMaleD, bFemaleD) * respect
+  del ~ c(delIntMaleD, delIntFemaleD) * 1
+
+  mhi ~ c(bMaleM, bFemaleM) * respect
+  mhi ~ c(delIntMaleM, delIntFemaleM) * 1
+
+  del ~~ mhi
+
+  respect ~ c(respMeanMale, respMeanFemale) * 1
+
+  a:= respMeanMale – respMeanFemale
+
+  abMaleD:= a * bMaleD
+  abFemaleD:= a * bFemaleD
+  bPrimeD:= bMaleD – bFemaleD
+  intDiffD:= abMaleD – abFemaleD
+
+  abMaleM:= a * bMaleM
+  abFemaleM:= a * bFemaleM
+  bPrimeM:= bMaleM – bFemaleM
+  intDiffM:= abMaleM – abFemaleM
+  ”
> fit10 <- sem(model10, data=d, group = “male”, fixed.x=FALSE,
+        se=“bootstrap”)
> summary(fit10)

Group 1 [1]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respct (bMlD)		−0.146	0.046	−3.151	0.002
mhi ~
respct	(bMlM)	0.646	0.093	6.922	0.000
Covariances:
del ~~
mhi		−0.035	0.034	−1.031	0.302
Intercepts:
del	(dIMD)	2.042	0.178	11.469	0.000
mhi	(dIMM)	4.441	0.352	12.601	0.000
respct	(rsMM)	3.703	0.017	215.633	0.000
Variances:
del		0.351	0.057
mhi		3.404	0.146
respect		0.345	0.030
Group 2 [0]:
		Estimate	Std.err	Z-value	P(>|z|)
Regressions:
del ~
respct	(bFmD)	−0.160	0.030	−5.346	0.000
mhi ~
respct	(bFmM)	0.996	0.119	8.349	0.000
Covariances:
del ~~
mhi		−0.132	0.023	−5.736	0.000
Intercepts:
del	(dIFD)	2.036	0.117	17.347	0.000
mhi	(dIFM)	2.645	0.456	5.800	0.000
respct	(rsMF)	3.772	0.013	296.438	0.000
Variances:
del		0.147	0.017
mhi		3.806	0.138
respect		0.225	0.020
Defined parameters:
a		−0.068	0.021	−3.220	0.001
abMaleD		0.010	0.004	2.277	0.023
abFemaleD		0.011	0.004	2.569	0.010
bPrimeD		0.014	0.054	0.256	0.798
intDiffD		−0.001	0.004	−0.240	0.811
abMaleM		−0.044	0.015	−2.923	0.003
abFemaleM		−0.068	0.023	−2.921	0.003
bPrimeM		−0.350	0.155	−2.257	0.024
intDiffM		0.024	0.014	1.758	0.079

The parameters match across the two models, and the two parameters of particular interest – the moderated mediation effects for mental health functioning and delinquency ( indDiffM and intDiffD) have the same estimates, and very similar p-values, across the two models. A Wald test gives the multivariate significance of the two effects, in much the same way as the single group model. Using the Wald test to obtain the multivariate significance test gives the same results as the model 9.

> fit10a <- sem(model10, data=d, group = “male”, fixed.x=FALSE,
+  estimator=“mlm”)
>
> con10a <- “
+  intDiffM == 0
+  intDiffD == 0
+  ”
>
> lavTestWald(fit10a, constraints=con10a)
$stat
[1] 3.209363
$df
[1] 2
$p.value
[1] 0.2009535

Controlling for potentially confounding variables

Finally, consider control variables are considered. Omitting important control variables might mean that spurious mediation effects are found. The models are re-estimated with the following control variables: race (entered as three dummy coded variables: Hispanic, Asian and other, with white as the reference); mother’s education, coded as 1 = did not complete high school, 2 = completed high school, 3 = some post-high school education, and 4=college degree, and age (in years).

To add these variables as covariates, the three endogenous variables (delinquency, mental health functioning and parental respect) are regressed on each of the covariates, and the exogenous variables (male and the male * respect interaction term) are correlated with the covariates. In addition, correlations between the covariates are added. One advantage of modeling in a statistical environment such as R is that models can be expanded, without rewriting the whole model. In the example below, model11 is created by adding the additional parameters to model9, using the paste0() function. Note that for model11, only the derived parameters are reported.

> model11 <- paste0(model9, “
+ mhi ~ hisp + asian + other + momed + age
+ del ~ hisp + asian + other + momed + age
+ respect ~ hisp + asian + other + momed + age
+
+ maleXResp ~~ hisp + asian + other + momed + age
+
+ male ~~ hisp + asian + other + momed + age
+ hisp ~~ asian + other + momed + age
+ asian ~~ other + momed + age
+ other ~~ momed + age
+ momed ~~ age
+ ”)
> fit11 <- sem(model11, data=d, fixed.x=FALSE, se=“bootstrap”)
> summary(fit11)

	Estimate	Std.err	Z-value	P(>|z|)
Defined parameters:
bmaleD	−0.140	0.048	−2.906	0.004
indMaleD	0.009	0.004	2.008	0.045
indFemaleD	0.010	0.004	2.282	0.022
indDiffD	−0.001	0.004	−0.188	0.851
bmaleM	0.667	0.095	7.008	0.000
indMaleM	−0.043	0.017	−2.576	0.010
indFemaleM	−0.065	0.026	−2.518	0.012
indDiffM	0.022	0.014	1.559	0.119

Similarly, a multiple group approach can be used. Again, model10 is modified to create model12 using the paste0() function. This is slightly complicated by the fact that explicitly regression parameters must be explicitly constrained across groups (failing to do this means that results are very difficult to interpret; the single group model implicitly has this constraint), and the means of the covariates must be free to vary across groups (this is the equivalent of allowing them to correlate with male).

> model12 <- paste0(model10, “
+  mhi ~ c(mh, mh) * hisp + c(ma, ma) * asian + c(mo, mo) * other + c(mm, mm) * momed + c(my, my) *age
+  del ~ c(dh, dh) * hisp + c(da, da) * asian + c(do, do) * other + c(dm, dm) * momed + c(dy, dy) *age
+  respect ~ c(rh, rh) * hisp + c(ra, ra) * asian + c(ro, ro) * other + c(rm, rm) * momed + c(ry, ry) *age
+
+  hisp ~ c(hMale, hFemale) * 1
+  asian ~ c(aMale, aFemale) * 1
+  other ~ c(oMale, oFemale) * 1
+  momed ~ c(mMale, mFemale) * 1
+  age ~ c(yMale, yFemale) * 1
+
+  hisp ~~ asian + other + momed + age
+  asian ~~ other + momed + age
+  other ~~ momed + age
+  momed ~~ age
+  ”)
> fit12 <- sem(model12, data=d, group=“male”, fixed.x=FALSE, se= “bootstrap”)
> summary(fit12)

Defined parameters:
a	−0.065	0.023	−2.823	0.005
abMaleD	0.009	0.004	2.043	0.041
abFemaleD	0.010	0.004	2.234	0.025
bPrimeD	0.012	0.057	0.208	0.835
indDiffD	−0.001	0.004	−0.192	0.848
abMaleM	−0.043	0.016	−2.665	0.008
abFemaleM	−0.065	0.025	−2.576	0.010
bPrimeM	−0.341	0.153	−2.226	0.026
indDiffM	0.022	0.014	1.588	0.112

Again, only the derived parameters are presented. The parameters of interest are equal to the single group model, and standard errors and p-values are very close. In conclusion, a mediated effect of parental respect on the association between gender and delinquency is found, as well as on the association between gender and mental health. However, support for either moderation or moderated mediation is not found.

Discussion

The goal of this investigation was to gain further understanding about which constructs might be influential in explaining gender effects on delinquency and mental health functioning (SAMHSA, 2014; Nock et al., 2007; see Albano and Kain, 2005; Moffit et al., 2001 for reviews). In order to do so, we utilized and provide a detailed overview of how moderated mediation can be applied. Specifically, we demonstrated how structural equation modeling can be applied to evaluate multiple variables simultaneously while controlling for potential confounding variables at the same time. This rigorous method allows for a more accurate evaluation of associations between multiple variables thus resulting in more robust conclusions.

We replicated and extended previous reports of gender differences in delinquency and mental health functioning (Bakker et al., 2010; Van Loon et al., 2014; Jacobson and Crocket, 2000). Specifically, based on a large multiethnic sample of adolescents, the results show that parental respect mediated the association between gender and delinquency, such that parental respect was a protective factor against delinquency for both females and males.

Limitations

This study has several limitations. First, the cross-sectional nature of the study precludes causation. Second, although we made significant effort to assure participants of confidentiality, the addition of behavioral data corroborating our self-report measure of parent-child interaction would strengthen our methodology. Third, our measure of delinquency is limited in that the focus is on overt aggressive behavior, which is more common among boys, rather than more covert, relational aggression, which is more common among girls. To improve upon our investigation, future studies would benefit from considering more gender-appropriate assessment instruments of delinquency. Finally, because mediation is not defined statistically (Kenny, 2014), we must presume a mediation model and then test that with statistical methods. If the mediation model is incorrect, the parameters used to estimate that model will not be meaningful (Maxwell and Cole, 2007). Finally, our conceptual model has parental respect causally preceding delinquency, which we cannot fully test due to the cross-sectional nature of the data.

Conclusions

Our results suggest that prevention and intervention efforts targeting parent-child relationship factors such as parental respect might be helpful in decreasing delinquent behavior (Barnes et al., 2000; Hawkins et al., 1992; Kumpfer et al., 1996). Still, there is a need for additional research in this area to better understand other factors that might contribute to these associations and thus help develop more comprehensive prevention approaches.

In addition, we demonstrated the use of structural equation modeling approaches for testing complex hypotheses about the relationship between variables. We present alternative parameterizations of equivalent models, which provide flexible means of thinking about our models. Given that “A model is a formal representation of a theory” (Bollen, 1989), this also allows us to advance our theory.