Abstract
A fundamental goal of systems biology is to create models that describe relationships between biological components. Networks are an increasingly popular approach to this problem. However, a scientist interested in modeling biological (e.g., gene expression) data as a network is quickly confounded by the fundamental problem: how to construct the network? It is fairly easy to construct a network, but is it the network for the problem being considered? This is an important problem with three fundamental issues: How to weight edges in the network in order to capture actual biological interactions? What is the effect of the type of biological experiment used to collect the data from which the network is constructed? How to prune the weighted edges (or what cut-off to apply)? Differences in the construction of networks could lead to different biological interpretations.
Indeed, we find that there are statistically significant dissimilarities in the functional content and topology between gene co-expression networks constructed using different edge weighting methods, data types, and edge cut-offs. We show that different types of known interactions, such as those found through Affinity Capture-Luminescence or Synthetic Lethality experiments, appear in significantly varying amounts in networks constructed in different ways. Hence, we demonstrate that different biological questions may be answered by the different networks. Consequently, we posit that the approach taken to build a network can be matched to biological questions to get targeted answers. More study is required to understand the implications of different network inference approaches and to draw reliable conclusions from networks used in the field of systems biology.
Introduction
Motivation and background
High-throughput biological data such as protein-protein interactions (PPIs), gene expression profiles, and metabolic interactions contain information about how different components of a cell interact in concert and can be used, for example, to elucidate potential drug targets and to further our understanding of disease (van’t Veer et al., 2002; van de Vijver et al., 2002). Because biological data are generally noisy and expensive to obtain, modern “systems biology” has produced integrative analysis frameworks to help overcome the challenges and pitfalls of these important collections.
One particular analysis is network-driven, where genes can be nodes and specific—but different—approaches are often used to infer edges that predict relationships between them (Nayak et al., 2009; Ivliev et al., 2010; Feizi et al., 2013). For example, gene co-expression networks constructed with correlation-based measures have been used to identify transitive relationships (Zhou et al., 2002), gene regulatory patterns (van Noort et al., 2004), and biological modules (Mason et al., 2009). Further, they have been successfully combined with transcription factor, eQTL, and PPI data into integrative Bayesian networks (Zhu et al., 2008). Gene co-expression networks are therefore one commonly used example of a complex model built from the high-throughput biological data collections. For this reason, we focus on gene co-expression networks, but our study is applicable to any type of biological networks.
Despite their importance in systems-level analysis, however, there is currently is no consensus about how to construct biological networks and gene co-expression networks in particular. Moreover, the link between a chosen network inference method to network topology and functional content (i.e., how to generate edges that encapsulate some biological knowledge) is not well understood. If the choice of a specific network construction has significant effects on the subsequent interpretation, biological advances will be significantly challenged unless done with considerable care.
To demonstrate this point, we investigate how variables in network construction affect the content of the resulting networks. Of all biological network types, we focus on gene co-expression networks as a proof of concept. Gene co-expression networks are commonly constructed as follows. Given a gene expression data set, the strength (or weight) of the co-expression relationship between each pair of genes can be quantified in a number of ways, each of which may be revealing different biological insights (Rider et al., 2011; Mason et al., 2009). Then, an arbitrary cut-off is chosen in order to include only the strongest edges into the network (Butte & Kohane, 2000; De Smet & Marchal, 2010; Markowetz & Spang, 2007; Barabasi & Oltvai, 2004). If the edge strength is positively correlated with the underlying biological knowledge, then the choice of a cut-off can be a major factor in determining the network’s ability to accurately uncover this knowledge.
Here we report significant differences in the biological information captured using two different types of gene expression data sets and different choices of network inference variables. This work shows that substantial care must accompany network analysis and is driven by the principle of induction: to conclude that a network construction variable has an effect, it is enough to find an example of two different choices for the variable (e.g., two different edge weighting measures) that result in significant differences; this constitutes a proof that the choice for that variable matters. And given one such example, it stands to reason that there may be other choices for the variable (e.g., other edge weighting measures) that also result in network differences. Because many other network inference methods rely on choosing an edge weighting method and a cut-off, and because in addition to gene co-expression networks many other biological network types rely on network inference, this study also has broad implications.
Our approach and contributions
In brief, we studied the effects of different edge weighting methods, data types, and edge cut-offs on the functional content and topology of resulting gene co-expression networks.
Edge weighting methods
To maximize the significance of the observations derived from the experiments discussed in the next sections, we chose popular edge weighting methods: correlation-based measures (Pearson’s correlation in particular) and mutual information (MI) (see Methods). Pearson’s correlation is vulnerable to perturbation from outliers and is constrained in that it captures only linear relationships. Mutual information is the common alternative, and has been used extensively in relevant frameworks such as ARACNE (Margolin et al., 2006), MRNET (Meyer et al., 2008), and CLR (Faith et al., 2007).
Data types
Because not all genes are active at all times, under all conditions, or in all strains (Jansen, 2001; Hughes et al., 2000), we studied the effect of the type of biological experiment used to collect gene expression data. We constructed networks from expression data obtained from two types of biological experiments: line cross (Brem & Kruglyak, 2005) and treatment. In the line cross experiment, two strains of yeast (Saccharomyces cerevisiae) were crossed and microarray experiments were performed on the strains and their progeny. In the treatment experiment, the same species of yeast was subjected to different chemicals or mutations before having expression levels measured through microarray experiments (Hughes et al., 2000) (see Methods). These are two very different types of experiments, which could affect the functional content and topologies of gene co-expression networks created from the data.
Edge cut-offs
For each combination of edge weighting method and data type we first constructed a network containing the top k strongest edges by varying k from 0% to 100% of the strongest edges (in increments of 6,000 edges). For our more detailed analyses, we focused on stronger edges by varying k from 2,500 to 75,000 of the strongest edges (in increments of 2,500 edges).
Evaluation
To evaluate how accurately a given co-expression network captured existing biological knowledge, we tested in a systematic precision-recall setting whether edges in the network corresponded to known interactions (e.g., PPIs), as well as whether genes that were connected by an edge in the network shared Gene Ontology (GO) annotations. This is a common approach to evaluation of biological networks (De Smet & Marchal, 2010; Ucar et al., 2007; Nayak et al., 2009; Ashburner et al., 2000; Faith et al., 2007; Marbach et al., 2010; Grigoriev, 2001). We focused on yeast data types (see above) because yeast is among the most studied and best annotated species to date.
Summary
We show that different network inference strategies result in networks that may contain answers to distinct biological questions. These results and conclusions highlight challenges in network construction, along with their impact, which most urgently require the attention of the systems biology community.
Methods
Data
Gene expression data sets
We use gene expression data resulting from two types of experiments: line cross and treatment.
In the line cross experiment, expression levels were measured from 130 segregants of a cross of two strains of yeast (Brem & Kruglyak, 2005). Just as Smith & Kruglyak (2008), we used all probes for which more than 80% of the expression data was present, resulting in a total of 5,829 unique open reading frames. We measured the strength of relationships between genes by relying on the normalized log ratios provided. Expression values for repeated probes were averaged. Line cross experiments can reveal relationships between heritability and expression (Jansen, 2001).
In the treatment experiment, 300 expression profiles were generated from mutant or chemical-treated cultures for 6,314 open reading frames. We measured the strength of relationships between 6,207 unique ORFs by relying on p-values resulting from a gene-specific error model that accounts for variation in genes as well as variation across chips (Hughes et al., 2000). Repeated measurements were averaged. Treatment experiments cause perturbations (whether due to environment or mutation) that affect gene expression levels and thus enable one to elucidate relationships between genes that may not be evident when the cell is “at rest” (Pe’er et al., 2001).
Known interactions
By known interactions, we mean the set of interactions that are already available in public databases. Known interactions are a valuable collection of ground truth data, but the completeness of the data can vary greatly between organisms. For example, baker’s yeast (Saccharomyces cerevisiae) is relatively well characterized, whereas non-model organisms, such as the pathogen of malaria (Plasmodium falciparum), are not. Hence, in our study, we focus on the well-studied yeast. Known interactions of various types were obtained from SGD (Saccharomyces Genome Database) (Supporting Table 2). 17 of the 26 interaction types have more than 500 genes involved into the corresponding interactions, and 14 of the 26 interaction types have more than 1,000 genes involved into the corresponding interactions (Supporting Table 2). Hence, known interaction data provides a strong basis for network comparison. Different interaction types describe relationships between genes that were discovered in experiments with different biological meanings. For example, Affinity Capture-MS interactions are determined by using a “bait” protein that is “captured” by a polyclonal antibody or an epitope tag. The associated partners are then identified by mass spectrometry. Affinity Capture-MS interactions typically correspond to physical interactions between proteins. In contrast, Synthetic Lethality interactions are determined by observing when mutations or deletions in separate genes, each of which causes a minimal change in phenotype alone, result in lethality to a cell.
Gene Ontology (GO) data
GO assigns biological process, molecular function, and cellular component labels (i.e., terms) to genes. GO terms are arranged in a hierarchical fashion. Genes that share a GO term are typically functionally related and may thus be more likely to interact than genes that do not share a GO term. We use GO-slim biological process data (Christie et al., 2009). GO-slim terms are a reduced set of GO terms corresponding to higher levels of the GO hierarchy.
Edge weighting methods
We measure the strength of the relationship between two genes by using either a signed variation of Pearson’s correlation or mutual information.
Correlation
The signed variation of Pearson’s correlation is given in Equation 1 (Mason et al., 2009).
| (1) |
Estimation of mutual information
Mutual information is a measure of the mutual dependence of two random variables (Equation 2) (Mason et al., 2009).
| (2) |
Calculation of mutual information is complicated by two factors. First, there are a low number of instances from which to estimate probability distributions. Second, expression data is continuous. To overcome these issues, we utilized the Parzen window approach to density estimation (Parzen, 1962). Equation 3 estimates the density function over N samples of variable x:
| (3) |
where δ (…) is the Parzen window function described in Equation 4, x(i) is the ith sample, and h is the window size. When d = 1, this equation returns the estimated marginal density. When d = 2, it gives an estimate of the joint density, p(x, y), which can be used to calculate the mutual information in Equation 2.
| (4) |
In Equation 4, z = x − x(i), his the window size, d is the dimension of the sample, and σ is the covariance of z. For further details and the implementation used, see Peng et al. (2005).
Evaluation
Precision and recall are defined in terms of true positives (t p), false positives ( f p), and false negatives ( f n). In the case of the networks we consider, a true positive is an edge in the network that corresponds to a known interaction or whose end nodes share a GO term. A false positive is an edge in the network that is not among the known interactions or whose end nodes do not share a GO term. A false negative is a pair of genes that are linked by a known interaction or that share a GO term but that are not linked by an edge in the network. Equations 5 and 6 define precision and recall.
| (5) |
| (6) |
Precision-recall curves have been identified as useful alternatives to receiver operating characteristic (ROC) curves in situations in which there is a large imbalance in the data (Kok & Domingos, 2005; Landgrebe et al., 2006). Namely, with only 220,009 known interactions and 5,892,199 pairs of genes that share a GO term out of approximately 18 million possible edges, the problem of network inference qualifies as imbalanced.
Increase in precision typically results in decrease in recall, and vice versa. The F-score reconciles precision and recall by combining them into a single score, namely their harmonic mean (Equation 7).
| (7) |
Given a network constructed using a given edge weighting method, data type, and edge cut-off, for each known interaction type, we counted how many interactions of the given type are present in the network. Then, we computed p, the probability of observing the same or higher number of interactions of the same type purely by chance, by using the model of hypergeometric distribution. If we denote by N the number of possible edges, by m the total number of known interactions of a given type, by n the number of edges in the network, and by k the number of known interactions of a given type that are in the network, the probability of observing exactly k known interactions in the network purely by chance is computed as shown in Equation 8. Then, to compute probability p, we sum Equation 8 over all possible numbers of known interactions equal to or greater than k.
| (8) |
Given a set of networks corresponding to 30 different edge cut-offs in the [2,500, 75,000] range, where the same edge weighting method and the data type are used for all 30 networks, we form a vector of 30 probabilities p for the set, where the probabilities are computed for a given known interaction type as explained above. We then compare two vectors of 30 elements corresponding two network sets constructed using the same data type but different edge weighting methods (Supporting Table 1). We also compare vectors of 30 elements corresponding to two network sets constructed using the same edge weighting method but different data types (Supporting Table 1). We do this for each known interaction type. We compare any two vectors by using the Wilcoxon signed-rank test, a nonparametric analog of the t-test (Demsar, 2006).
Topological analysis of networks
We use three network topological measures: the clustering coefficient, the closeness centrality, and the betweenness centrality (Milenkovic et al., 2008; Milenković et al., 2011).
The clustering coefficient of node v describes the proportion of v’s neighbors that are connected to each other. It is computed as shown in Equation 9, where d is the number of neighbors of v and k is the number of connected pairs of the neighbors (Luce & Perry, 1949). The global clustering coefficient of the network is the average of the clustering coefficients of all nodes.
| (9) |
The closeness centrality of node v measures the distance from v to every other node t in the network. It is computed as shown in Equation 10, where SP(v,t) is the length of the shortest path between v and t, and V is the set of nodes of the network (Sabidussi, 1966).
| (10) |
The betweenness centrality of node v measures the proportion of shortest paths in the network that go through v. It is computed as shown in Equation 11, where SPst is the number of shortest paths between nodes s and t and SPst(v) is the number of shortest paths between s and t that pass through v (Freeman, 1977).
| (11) |
For each of the three measures, we compute the corresponding “spectrum” as the average over all nodes of degree k, for each value of k. For example, clustering spectrum of a network is the average clustering coefficient of all nodes of degree k in the network (Supporting Figure 3). Spectra are often displayed in log scale for ease of interpretation.
Results
We constructed networks using each combination of edge weighting method, data type, and edge cut-off. We then compared networks of a given size constructed from the same data type but using different edge weighting methods. We additionally compared networks of a given size constructed using the same edge weighting method but from different data types. This was done for each of the edge cut-offs.
Effects of network construction on functional content of networks
In this section, we aim to answer whether the choice of edge weighting method, data type, and edge cut-off affects the functional content of networks.
Different networks uncover different amounts of functional content
We measured the functional content of networks in terms of known interactions and shared GO terms (see Methods). These are commonly used approaches to evaluate the extent to which networks reflect existing biological knowledge (De Smet & Marchal, 2010; Ucar et al., 2007; Nayak et al., 2009; Ashburner et al., 2000; Faith et al., 2007; Marbach et al., 2010). For example, there is a relationship between the similarity of genes’ expression patterns and interaction of the proteins that the genes encode (Grigoriev, 2001).
Specifically, we computed precision, recall, and the F-score in a network as follows. Precision is the proportion of edges in the network that correspond to known interactions or whose end nodes share a GO term. Recall is the proportion of the known interactions or gene pairs sharing a GO term that are in the network. Because there is a trade-off between precision and recall, in the sense that higher precision means lower recall and vice versa, the two measures were combined into F-score, their harmonic mean (see Methods). We computed precision, recall, and F-score for each combination of edge weighting method and data type, varying edge cut-off from 0% to 100%.
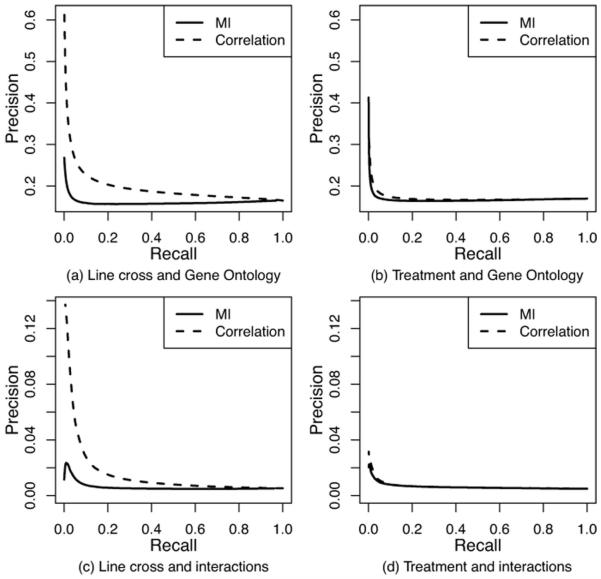
We found that the choice of edge weighting method affected the functional content in terms of both known interactions (when known interactions are combined independent of interaction type) and shared GO terms. Networks constructed with correlation nearly always had higher precision and recall (Figure 1), as well as F-score (Supporting Figure 1) than networks constructed with mutual information. This indicates that correlation-based networks more accurately uncover existing biological knowledge, where the level of their superiority varies depending on the edge cut-off (Figure 1 and Supporting Figure 1). This was much more pronounced for the line cross data than for the treatment data. The choice of data type also affects functional content: precision and recall were higher for networks constructed from the line cross data than for networks constructed from the treatment data. This was more pronounced for correlation than for mutual information.
Fig. 1. Precision-recall curves measuring how accurately networks constructed in different ways capture known biological knowledge.
Panel (a) shows curves for networks constructed from the line cross data with respect to shared GO terms. Panel (b) shows curves for networks constructed from the treatment data with respect to shared GO terms. Panel (c) shows curves for networks constructed from the line cross data with respect to known interactions. Panel (d) shows curves for networks constructed from the treatment data with respect to known interactions.
As expected, precision tended to decrease and recall tended to increase with an increase in edge cut-off, independent of edge weighting method or data type. This was true for both known interactions and shared GO terms. However, at smaller cut-offs, precision tended to drop significantly. Hence, the edge cut-off just before this drop in precision could be a good cut-off for constructing the network. Alternatively, one could choose the cut-off where precision and recall cross or where F-score starts to decrease (e.g., see “peaks” in Supporting Figure 1 c and d). Ultimately, which edge cut-off to choose depends on one’s preference for the trade-off between precision and recall or the desired network density. We conclude that the smaller the edge cut-off, the higher the precision, the lower the recall, and the sparser the network.
Note that, whereas uncovering existing knowledge is desirable for the purpose of testing the accuracy of network construction, there is no reason to assume that gene co-expression networks should fully uncover existing knowledge, as each piece of biological data could be capturing somewhat complementary functional slices of a cell.
Different networks uncover different types of known interactions
We also evaluated known interactions in greater detail by focusing on individual interaction types, instead of considering all known interactions combined as done above. For each network and interaction type, we counted how many interactions of the given type were present in the network. We then computed the probability of observing the same or higher number of interactions of the same type in the network purely by chance using the model of hypergeometric distribution (see Methods). Here, instead of varying the edge cut-off over the entire [0%, 100%] range, as above, we varied it from 2,500 to 75,000 edges in increments of 2,500 edges, hence focusing on stronger edges only. Such a more detailed, type-specific analysis of known interactions allowed us to make more biologically relevant observations about the potential differences in the functional content between networks constructed in different ways.
We found that the choice of edge weighting method affected the functional content in terms of individual interaction types (Figures 2, 3, and 4, and Supporting Figure 2). For example, if we focus on Affinity Capture-RNA interactions, we observe that the choice of edge weighting method made a noticeable difference for the line cross data: the presence of interactions of this type was statistically significant in networks constructed using correlation at each of the 30 cut-offs, while it was not significant in networks constructed using mutual information at any of the 30 cut-offs. On the other hand, the choice of edge weighting method made a small difference for the treatment data when it came to this interaction type: the presence of interactions of this type was statistically significant in networks constructed using both correlation and mutual information at most of cut-offs, and the two edge weighting methods differed in only six out of the 30 cut-offs (Figure 4). Hence, the choice of data type also affected the functional content in terms of individual interaction types.
Fig. 2.
Heat maps showing where the enrichment of a network of a given size (i.e., at a given edge cut-off; x-axis) in known interactions of a given type (y-axis) is statistically significant (denoted by black color) according to the hypergeometric test (see Methods). The cut-off for statistical significance was computed at a False Discovery Rate (FDR) of 0.05. Panel (a) shows enrichment results for networks constructed from the line cross data using mutual information. Panel (b) shows enrichment results for networks constructed from the line cross data using correlation. Panel (c) shows enrichment results for networks constructed from the treatment data using mutual information. Panel (d) shows enrichment results for networks constructed from the treatment data using correlation. For example, “Affinity Capture-RNA” interaction type is not significantly enriched at any edge cut-off in panel (a), it is enriched at all cut-offs in panel (b), and it is enriched at most cut-offs (particularly larger ones) in panels (c) and (d).
Fig. 3.
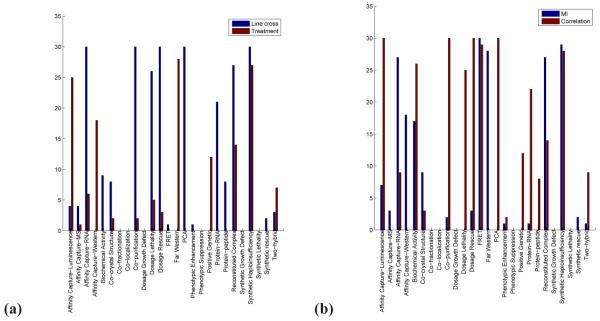
The absolute differences between networks constructed using different edge weighting methods (a) or data types (b) at different edge cut-offs (x-axis) with respect to the number of known interaction types that the networks are statistically significantly enriched in (y-axis). That is, based on Figure 2, for a given data type (line cross or treatment), for a given cut-off, we count for how many of the 26 known interaction types the significance of the enrichment of the network constructed using mutual information is different than the significance of the enrichment of the network constructed using correlation (panel (a)). By “different”, we mean that the enrichment with respect to one edge weighting method is significant (denoted by black color in Figure 2), while it is not significant with respect to the other edge weighting method (denoted by white color in Figure 2). Analogously, for a given edge weighting method (mutual information or correlation) and a given cut-off, we count for how many of the 26 known interaction types the significance of the enrichment of the network constructed from the line cross data is different than the significance of the enrichment of the network constructed from the treatment data (panel (b)). Now, by “different”, we mean that the enrichment with respect to one data type is significant (denoted by black color in Figure 2) while it is not significant with respect to the other data type (denoted by white color in Figure 2).
Fig. 4.
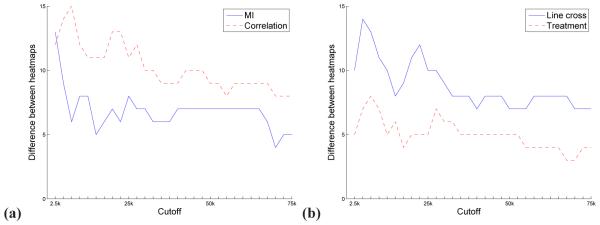
The differences between networks constructed using different edge weighting methods (a) or data types (b) for different known interaction types (x-axis) with respect to the number of edge cut-offs at which the enrichment in the known interactions is different (y-axis). That is, based on Figure 2, for a given data type (line cross or treatment), for a given known interaction type, we count for how many of the 30 edge cut-offs the significance of the enrichment of the network constructed using mutual information is different than the significance of the enrichment of the network constructed using correlation (panel (a)). Analogously, for a given edge weighting method (mutual information or correlation) for a known interaction type, we count for how many of the 30 edge cut-offs the enrichment of the network constructed from the line cross data is different than the significance of the enrichment of the network constructed from the treatment data (panel (b)).
In general, the significance of the enrichment of a network constructed when using one edge weighting method is often different than when using another edge weighting method. The same holds for using one data type compared to using another data type. This observation, specifically that significance may be unique to one edge weighting approach or one data type), allowed us to systematically quantify these differences further and determine that:
The difference between mutual information and correlation is more pronounced in the line cross data than in the treatment data, independent of the edge cut-off. Namely, the number of known interaction types (out of 26 of them) at which we observed a difference between the two edge weighting methods was higher for the line cross data than for the treatment data. Specifically, this number varied between 7 (27%) and 14 (54%) for line cross data and between 3 (12%) and 8 (31%) for treatment data, depending on the edge cut-off (Figure 3 a).
The difference between the line cross data and the treatment data is more pronounced for correlation than for mutual information, independent of the edge cut-off. Namely, the number of known interaction types (out of 26 of them) at which we observed a difference between the two data types was higher for correlation than for mutual information. Specifically, this number varied between 8 (31%) and 15 (58%) for correlation and between 4 (15%) and 13 (50%) for mutual information, depending on the edge cut-off (Figure 3 b).
Although there are some exceptions, for each of the two results above the differences tended to decrease with an increase of the edge cut-off used (Figures 3 a and b).
We reached the above conclusions by counting, for each cut-off, at how many of the 26 known interaction types the significance of the network constructed using one edge weighting method and one data type is different than the significance of the network constructed using either the different edge weighting method or the different data type. We reached the same conclusions when we counted, for each known interaction type, at how many of the 30 edge cut-offs we observe the difference in significance of the networks constructed in different ways, as follows:
The difference between mutual information and correlation is more pronounced in the line cross data than in the treatment data. Namely, mutual information and correlation were different at more cut-offs in the line cross data than in the treatment data (Figure 4 a).
The difference between the line cross data and the treatment data is more pronounced for correlation than for mutual information. Namely, the line cross data and the treatment data were different at more cut-offs for correlation than for mutual information (Figure 4 b).
The majority of the known interaction types show disagreement between the line cross data and the treatment data. Namely, only 11 out of the 26 known interaction types showed agreement between the line cross data and the treatment data in the sense that the number of cut-offs in which correlation and mutual information differ was similar for the two data types.
The majority of the known interaction types show disagreement between correlation and mutual information. Namely, only 11 out of the 26 known interaction types showed agreement between correlation and mutual information in the sense that the number of cut-offs in which the line cross data and the treatment data differ was similar for the two edge weighting methods.
Supporting Table 1 further supports the above conclusions: for the majority (18-21 out of 26) of known interaction types, there is a statistically significant difference (p-value ≤ 1.7 × 10−03) between the different edge weighting methods and data types with respect to the proportion of known interactions that they uncover across networks (corresponding to the 30 different cut-offs).
Different networks target different biological questions
In addition to quantifying the differences in the functional content between networks constructed using different edge weighting methods or data types, as above, we also qualitatively studied which combination of edge weighting method and data type can (or fails to) capture a given known interaction type. For each known interaction type, we checked whether its enrichment was significant in the majority of the 30 networks (corresponding to the 30 cut-offs) constructed using the given edge weighting method and data type. We then grouped known interaction types into those that were significantly enriched for both correlation and mutual information in both the line cross data and the treatment data, those that were significantly enriched for both correlation and mutual information in the line cross data but only for mutual information in the treatment data, those that were significantly enriched for both correlation and mutual information in the treatment data but only for correlation in the line cross data, … , and those that were significantly enriched for neither correlation nor mutual information in neither the line cross data nor the treatment data (Table 1).
Table 1.
Combinations of edge weighting methods/data types for which the given interaction type is significantly enriched at the majority of edge cut-offs.
| Combinations of edge weighting methods/data types | Interaction types |
|---|---|
| Found by both correlation and mutual information in both the line cross data and the treatment data. |
Affinity Capture-MS Co-crystal Structure Co-fractionation Positive Genetic Synthetic Rescue Two-hybrid |
|
| |
| Found by both correlation and mutual information in the line cross data but only by mutual information in the treatment data. |
Affinity Capture-Luminescence |
|
| |
| Found by both correlation and mutual information in treatment data but only by correlation in line cross data. |
Affinity Capture-RNA Reconstituted Complex |
|
| |
| Found by both correlation and mutual information in line cross data but none of correlation or mutual information in treatment data. |
Biochemical Activity FRET |
|
| |
| Found only by correlation in line cross data and only by mutual information in treatment data. |
Synthetic Haploinsufficiency |
|
| |
| Found by neither correlation nor mutual information in treatment data, but found only by correlation in line cross data. |
Co-purification Dosage Lethality Dosage Rescue PCA Protein-RNA |
|
| |
| Found by neither correlation nor mutual information in line cross data, but found only by mutual information in treatment data. |
Affinity Capture-Western Far Western |
|
| |
| Found by neither correlation nor mutual information in neither line cross data nor treatment data. |
Co-localization Dosage Growth Defect Phenotypic Enhancement Phenotypic Suppression Protein-peptide Synthetic Growth Defect Synthetic Lethality |
Only 6 out of the 26 known interaction types were found by both edge weighting methods in both data types. Specifically, if one’s goal was to construct networks that would enrich for Affinity Capture-MS, Co-crystal Structure, Co-fractionation, Positive Genetic, Synthetic Rescue, or Two-hybrid interactions, one could use either of the two edge weighting methods or data types (Table 1). Note however, that the actual interactions uncovered by the different networks could be different, because the overlap between the networks is small (Section ). Seven of the 26 known interaction types are missed by both edge weighting methods in both data types. In other words, neither the two edge weighting methods nor data types considered in this study enriched for Co-localization, Dosage Growth Defect, Phenotypic Enhancement, Phenotypic Suppression, Protein-peptide, Synthetic Growth Defect, or Synthetic Lethality interactions.
Clearly for 6 + 7 = 13 out of the 26 known interaction types, all four combinations of edge weighting methods and data types agree. For the same number of known interaction types, however, at least two of the four combinations disagree. For example, there exist interaction types that were captured by correlation in the line cross data but not in the treatment data. Also, there exist interaction types captured by mutual information in the treatment data but not in the line cross data. Interestingly, there are no interaction types captured by mutual information in the line cross data but not in the treatment data or by correlation in the treatment data but not in the line cross data (Table 1).
Bottom line
All of the above results demonstrate that networks constructed in this study with different combinations of edge weighting methods or data types were enriched with different functional content. Therefore, we have strong evidence that both the edge weighting method and the type of biological experiment underlying the data affect the functional content of networks, implying that they can optimized to answer certain—but different—biological questions.
Effects of network construction on topology of networks
In this section, we aim to answer whether the choice of edge weighting method, data type, and edge cut-off affects the topology of constructed networks.
Overlap of different networks is small
Considerable topological differences between networks constructed in different ways were immediately apparent based on the intersection of their edges (Table 2). Intersections were calculated between pairs of networks of a given size that shared either edge weighting method or data type. Because the size of the intersection between the networks appeared to have a linear relationship with the cut-off (networks with more strict cut-offs had nearly the same proportion of overlap as networks with less strict cut-offs), the intersections were averaged over different network sizes. Such averaged intersections were smaller between networks constructed by using the same edge weighting method but different data sets than between networks constructed by using the same data set but different edge weighting method (Table 2). This indicates that the choice of the data set may have a stronger effect on network construction than the choice of the edge weighting method. Nonetheless, the intersection was relatively small between all compared networks. This is an important result, since it is likely that different edges would lead to different biological interpretations, which is exactly what we demonstrated in the previous section.
Table 2.
Edge overlap between networks constructed using different data types and edge weighting methods, averaged over all edge cut-offs. Each column denotes the edge weighting method or data type used as the basis for comparison between networks. The column denoted by “Line cross” compares networks constructed from the line cross data using correlation to networks constructed from the line cross data using mutual information. The column denoted by “Treatment” compares networks constructed from the treatment data using correlation to networks constructed from the treatment data using mutual information. The column denoted by “Correlation” compares networks constructed from the line cross data using correlation to networks constructed from the treatment data using correlation. The column denoted by “MI” compares networks constructed from the line cross data using mutual information to networks constructed from the treatment data using mutual information.
| Line cross | Treatment | Correlation | MI | |
|---|---|---|---|---|
| mean | 30.85% | 40.23% | 11.98% | 14.06% |
| min | 29.41% | 32.08% | 9.23% | 11.70% |
| max | 33.12% | 45.82% | 13.37% | 18.82% |
| stdev | 0.51% | 4.30% | 1.35% | 2.13% |
Different networks have different topologies
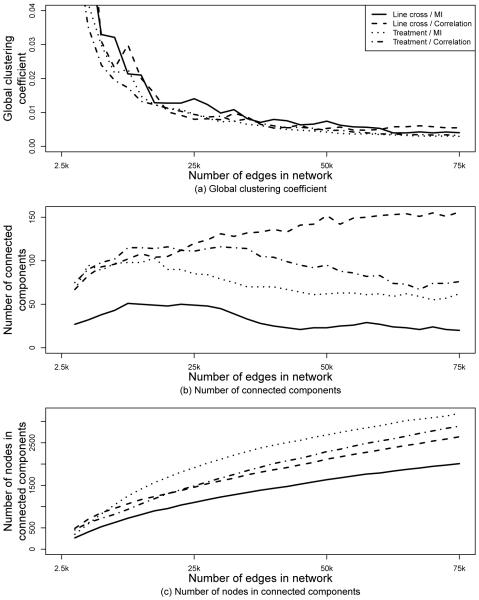
By comparing overall topological characteristics of networks constructed using different edge weighting methods or data types, we found that networks varied as follows. In general, average clustering coefficients (see Methods) were higher for networks constructed using mutual information than for networks constructed using correlation, independent of the data type, and they were higher for networks constructed from the line cross data than for networks constructed from the treatment data, independent of the edge weighting method (Figure 5 a). Figure 5 b and Figure 5 c further demonstrate topological differences between networks constructed with different edge weighting methods and data types. For example, networks for the line cross data and correlation had the most connected components (Figure 5 b) but they had the second fewest nodes involved in the components (Figure 5 c), indicating that these networks had many small components. On the other hand, networks for the treatment data and mutual information in general had the second fewest connected components (Figure 5 b) but they had the most nodes involved in the components (Figure 5c), indicating that these networks had few large components.
Fig. 5.
Global clustering coefficient (a), the number of connected components with at least two nodes (b), and the number of nodes that participate in the connected components (c) for networks constructed from a given data type (line cross or treatment) using a given edge weighting method (correlation or mutual information) at a given edge cut-off (x-axis).
To further understand the observed topological differences, we focused on one of the 30 analyzed edge cut-offs: 25,000. We chose the cut-off of 25,000 because it is a compromise between the the peak precision in Figures 1 a-d. We compared the different networks corresponding to this cut-off with respect to the clustering coefficient, closeness centrality, and betweenness centrality spectra (see Methods). Topological differences were immediately apparent. For example, in the line cross data-based networks, average clustering coefficients tended to decrease as node degrees increased for mutual information, whereas this was not necessarily the case for correlation (Supporting Figure 3 a). Clustering spectra were also different for the line cross data-based networks (Supporting Figure 3 a) and treatment-based networks (Supporting Figure 3 b): correlation-based networks in particular appear to have almost the opposite trends for the two data types. The observed differences were statistically significant for each pair of clustering spectra, both when the data type was shared but the edge weighting method was different (p-values < 2.2 × 10−16) and when the edge weighting method was the same but the data type was different (p-values of 0.008 and < 1.07 × 10−15) (Supporting Figure 3).
Similar observations were made with respect to closeness centrality spectra. For example, in the line cross data-based networks, while average closeness centralities were higher for correlation than for mutual information for low-degree nodes, they were lower for correlation than for mutual information for high-degree nodes (Supporting Figure 4 a). While the observed difference between the two edge weighting methods was not statistically significant for the line cross data (p-value of 0.3511), it was statistically significant for the treatment data (p-value of 0.0063; Supporting Figure 4 b). Further, the difference between closeness spectra was statistically significant when the edge weighting method is the same but the data type is different, with respect to both correlation (p-value of 2.81 × 10−6) and mutual information (p-value of 1.6 × 10−12) (Supporting Figure 4). Betweenness centrality spectra are statistically significantly different for all four combinations of edge weighting methods and data types as well (Supporting Figure 5).
We conclude that networks constructed using different edge weighting methods or data types have different topologies.
Discussion
The network construction problem is analogous to the problem of clustering genes based on similarity between their expression profiles (Hanisch et al., 2002; Datta & Datta, 2003; Eisen et al., 1998). Many clustering algorithms exist (each with its (dis)advantages (Fortunato, 2010; Solava et al., 2012; Ho et al., 2010)) that attempt to group together genes that have similar expression with respect to some distance metric. Hence, analogous to a network construction method, a clustering method first computes distances (or equivalently, similarities) between each pair of genes. Then, it partitions the resulting weighted fully connected network by employing a distance cut-off to determine cluster membership (Hartigan & Wong, 1979). Examples of popular clustering methods in this context include Walktrap (Pons & Latapy, 2005) and Markov Clustering (MCL) (Wittkop et al., 2007). The wide variety of available algorithms typically result in different clustering solutions, for reasons that are analogous to those studied in this paper.
One goal of this work was to study the effect of the choice of edge weighting method on the functional content and topology of the resulting network. We note that this is not the first study to analyze how different edge weighting methods affect biological content of the networks. For example, it has been found that modules in networks constructed with signed correlation show different functional enrichment than modules in networks constructed with the absolute correlation (Mason et al., 2009), and that correlation and mutual information are strongly related in the treatment data when their values are high (Steuer et al., 2002). This is the first study, however, to analyze how the choice of edge weighting method affects networks in terms of individual interaction types. This study is also more comprehensive than the previous ones because it examines multiple edge weighting methods and data types.
Our hypothesis is that the two edge weighting methods might be capturing different types of relationships. For example, Supporting Figure 6 represents a known Biochemical Activity interaction for which the gene pair ranking is discordant, i.e., high with respect to one edge weighting method but low with respect to the other edge weighting method. Supporting Figure 7 and Supporting Figure 8, on the other hand, represent known Synthetic Lethality interactions in the line cross data and the treatment data, respectively, for which the gene pair rankings are consistent across the two edge weighting methods—both rank each of these gene pairs high. Note that in our study we focus on answering whether different edge weighting methods captured different functional content to bring this important issue to the attention of the community, not on answering why different types of known interactions were captured differently by the different networks. The later is an important but complex question that is out of the scope of this study.
Another goal of this work was to study whether the type of biological experiment underlying the data affects the functional content of inferred networks because different types of biological experiments are expected to capture somewhat complementary aspects of the cell (Jansen, 2001; Hughes et al., 2000). To our knowledge this is the first study explicitly comparing networks constructed from line cross data with networks constructed from treatment data. We note that since we use one data set of each type, and since we do so for one species, our results should be used with caution: it is difficult to determine how much of the variation between the different networks is due to the data type versus noise in these particular data sets. Nonetheless, our analysis could be used as a strong suggestion that data types considered should also be carefully chosen to match the desired biological question(s).
Finally, we studied the effect of edge cut-off on resulting networks. There are a number of approaches to choosing a cut-off for network construction, including the precision-recall trade-off (Section ), the approximate topology of the resulting network, or the false discovery rate (FDR) (Carlson et al., 2006; Ucar et al., 2007). Under the assumption that gene co-expression networks should capture known biological knowledge, be it interactions, GO functional similarity, or anything else, the strongest relationships should hold the most reliable known biological information (which would be reflected in higher precision at lower edge cut-offs).
We demonstrated systematically and comprehensively that the four combinations of edge weighting methods and data types disagreed with respect to the functional content and topology of the corresponding networks. Because the overlap was small between networks constructed in different ways, and since their overall topologies were different, it is no surprise that the different networks led to different biological interpretations. We showed that: (1) of the two edge weighting methods, correlation seemed to more accurately uncover existing biological knowledge, especially for the line cross data; (2) of the two data types, the line cross data seemed to more accurately uncover existing biological knowledge, especially for correlation; (3) the strongest edges indeed hold the most reliable known biological information; (4) the difference between mutual information and correlation was more pronounced in the line cross data than in treatment data, independent of the edge cut-off; (5) the difference between the line cross data and the treatment data was more pronounced for correlation than for mutual information, independent of the edge cut-off; (6) the differences in points (4) and (5) above tended to decrease with an increase of the cut-off; (7) the type of experiment underlying the data can have at least as much of an effect on the functional content of networks as the choice of edge weighting method; and (8) different types of known interactions could be uncovered with different combinations of edge weighting methods and data types.
In summary, these results demonstrate that there is no single correct way to construct a network—and different approaches can produce different networks that are better suited to answer different biological questions. For example, using correlation and treatment data results in networks that contain the most significant amounts of Synthetic Lethality interactions among all considered networks. Thus, this combination of edge weighting method and data type may be the most appropriate for studying genes that are essential to an organism’s survival in combination with other genes. However, the same networks are the worst in terms of capturing Far Western interactions, which are a type of protein-protein interaction data set. As such they should probably not be used to study molecular processes that are carried out via physical interactions between proteins. We conclude that the three ubiquitous factors in network inference that were considered in this study each have significant effects on the functional content and topology of resulting biological networks and therefore do matter for future work in systems biology.
Supplementary Material
Acknowledgements
Research was supported in part by the National Science Foundation (NSF) Grants BCS-0826958 and EAGER CCF-1243295.
Bibliography
- Ashburner Michael, Ball Catherine A., Blake Judith A., Botstein David, Butler Heather, Cherry J. Michael, Davis Allan P., Dolinski Kara, Dwight Selina S., Eppig Janan T., Harris Midori A., Hill David P., Issel-Tarver Laurie, Kasarskis Andrew, Lewis Suzanna, Matese John C., Richardson Joel E., Ringwald Martin, Rubin Gerald M., Sherlock Gavin. Gene Ontology: tool for the unification of biology. Nature Genetics. 2000;25(1):25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabasi Albert-Laszlo, Oltvai Zoltan N. Network biology: understanding the cell’s functional organization. Nature Reviews Genetics. 2004;5(2):101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- Brem Rachel B., Kruglyak Leonid. The landscape of genetic complexity across 5,700 gene expression traits in yeast. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(5):1572–1577. doi: 10.1073/pnas.0408709102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butte AJ, Kohane IS. Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements. Pacific Symposium for Biocomputing. 2000;5:418–429. doi: 10.1142/9789814447331_0040. [DOI] [PubMed] [Google Scholar]
- Carlson M, Zhang B, Fang Z, Mischel P, Horvath S, Nelson S. Gene connectivity, function, and sequence conservation: predictions from modular yeast coexpression networks. BMC Genomics. 2006;7(1):40. doi: 10.1186/1471-2164-7-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christie Karen R., Hong Eurie L., Cherry J. Michael. Functional annotations for the Saccharomyces cerevisiae genome: the knowns and the known unknowns. Trends in Microbiology. 2009;17(7):286–294. doi: 10.1016/j.tim.2009.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta Susmita, Datta Somnath. Comparisons and validation of statistical clustering techniques for microarray gene expression data. Bioinformatics. 2003;19(4):459–466. doi: 10.1093/bioinformatics/btg025. [DOI] [PubMed] [Google Scholar]
- De Smet Riet, Marchal Kathleen. Advantages and limitations of current network inference methods. Nature Reviews Microbiology. 2010;8(10):717–729. doi: 10.1038/nrmicro2419. [DOI] [PubMed] [Google Scholar]
- Demsar J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research. 2006;7:1–30. [Google Scholar]
- Eisen Michael B., Spellman Paul T., Brown Patrick O., Botstein David. Cluster analysis and display of genome-wide expression patterns. Proceedings of the National Academy of Sciences of the United States of America. 1998;95(25):14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faith Jeremiah J., Hayete Boris, Thaden Joshua T., Mogno Ilaria, Wierzbowski Jamey, Cottarel Guillaume, Kasif Simon, Collins James J., Gardner Timothy S. Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles. PLoS Biology. 2007;5(1):e8. doi: 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feizi Soheil, Marbach Daniel, Medard Muriel, Kellis Manolis. Network deconvolution as a general method to distinguish direct dependencies in networks. Nature Biotechnology. 2013;31(8):726–733. doi: 10.1038/nbt.2635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortunato S. Community detection in graphs. Physics Reports. 2010;486:75–174. [Google Scholar]
- Freeman LC. A set of measures of centrality. Sociometry. 1977;40(1):35–41. [Google Scholar]
- Grigoriev Andrei. A relationship between gene expression and protein interactions on the proteome scale: analysis of the bacteriophage T7 and the yeast Saccharomyces cerevisiae. Nucleic Acids Research. 2001;29(17):3513–3519. doi: 10.1093/nar/29.17.3513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanisch Daniel, Zien Alexander, Zimmer Ralf, Lengauer Thomas. Co-clustering of biological networks and gene expression data. Bioinformatics. 2002;18(suppl 1):S145–S154. doi: 10.1093/bioinformatics/18.suppl_1.s145. [DOI] [PubMed] [Google Scholar]
- Hartigan JA, Wong MA. Algorithm AS 136: A K-Means Clustering Algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics) 1979;28(1):100–108. [Google Scholar]
- Ho H, Milenković T, Memišević V, Aruri J, Pržulj N, Ganesan A. Protein interaction network uncovers melanogenesis regulatory network components within functional genomics datasets. BMC Systems Biology. 2010;4(84) doi: 10.1186/1752-0509-4-84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, Kidd MJ, King AM, Meyer MR, Slade D, Lum PY, Stepaniants SB, Shoemaker DD, Gachotte D, Chakraburtty K, Simon J, Bard M, Friend SH. Functional discovery via a compendium of expression profiles. Cell. 2000;102(1):109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- Ivliev AE, AC’t Hoen P, Sergeeva MG. Coexpression network analysis identifies transcriptional modules related to proastrocytic differentiation and sprouty signaling in glioma. Cancer Research. 2010;70(24):10060–10070. doi: 10.1158/0008-5472.CAN-10-2465. [DOI] [PubMed] [Google Scholar]
- Jansen R. Genetical genomics: the added value from segregation. Trends in Genetics. 2001;17(7):388–391. doi: 10.1016/s0168-9525(01)02310-1. [DOI] [PubMed] [Google Scholar]
- Kok Stanley, Domingos Pedro. Learning the structure of Markov logic networks. Proceedings of the 22nd International Conference on Machine Learning; 2005. pp. 441–448. ACM. [Google Scholar]
- Landgrebe TCW, Paclik P, Duin RPW, Bradley AP. Precision-recall operating characteristic (P-ROC) curves in imprecise environments. Pattern Recognition; 2006. 2006. pp. 123–127. ICPR 2006. 18th International Conference on, vol. 4. IEEE. [Google Scholar]
- Luce RD, Perry AD. A method of matrix analysis of group structure. Psychometrika. 1949;14(2):95–116. doi: 10.1007/BF02289146. [DOI] [PubMed] [Google Scholar]
- Marbach Daniel, Prill Robert J., Schaffter Thomas, Mattiussi Claudio, Floreano Dario, Stolovitzky Gustavo. Revealing strengths and weaknesses of methods for gene network inference. Proceedings of the National Academy of Sciences of the United States of America. 2010;107(14):6286–6291. doi: 10.1073/pnas.0913357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margolin Adam, Nemenman Ilya, Basso Katia, Wiggins Chris, Stolovitzky Gustavo, Favera Riccardo, Califano Andrea. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinformatics. 2006;7(Suppl 1):S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowetz Florian, Spang Rainer. Inferring cellular networks - a review. BMC Bioinformatics. 2007;8(Suppl 6) doi: 10.1186/1471-2105-8-S6-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mason Mike, Fan Guoping, Plath Kathrin, Zhou Qing, Horvath Steve. Signed weighted gene co-expression network analysis of transcriptional regulation in murine embryonic stem cells. BMC Genomics. 2009;10(1):327. doi: 10.1186/1471-2164-10-327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer Patrick, Lafitte Frederic, Bontempi Gianluca. MINET: A R/Bioconductor Package for Inferring Large Transcriptional Networks Using Mutual Information. BMC Bioinformatics. 2008;9(1):461. doi: 10.1186/1471-2105-9-461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milenković T, Memišević V, Bonato A, Pržulj N. Dominating biological networks. PLOS ONE. 2011;6(8):e23016. doi: 10.1371/journal.pone.0023016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milenkovic Tijana, Lai Jason, Przulj Natasa. GraphCrunch: A tool for large network analyses. BMC Bioinformatics. 2008;9(1):70. doi: 10.1186/1471-2105-9-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nayak Renuka R., Kearns Michael, Spielman Richard S., Cheung Vivian G. Coexpression network based on natural variation in human gene expression reveals gene interactions and functions. Genome Research. 2009;19(11):1953–1962. doi: 10.1101/gr.097600.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parzen E. On estimation of a probability density function and mode. The Annals of Mathematical Statistics. 1962;33(3):1065–1076. [Google Scholar]
- Pe’er Dana, Regev Aviv, Elidan Gal, Friedman Nir. Inferring subnetworks from perturbed expression profiles. Bioinformatics. 2001;17(suppl 1):S215–S224. doi: 10.1093/bioinformatics/17.suppl_1.s215. [DOI] [PubMed] [Google Scholar]
- Peng Hanchuan, Long Fuhui, Ding Chris. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- Pons Pascal, Latapy Matthieu. Computing Communities in Large Networks Using Random Walks Computer and Information Sciences - ISCIS 2005. In: Yolum pInar, Güngör Tunga, Gürgen Fikret, Özturan Can., editors. Computer and Information Sciences - ISCIS 2005; Springer Berlin / Heidelberg. 2005. pp. 284–293. Chap. 31. Lecture Notes in Computer Science. [Google Scholar]
- Rider Andrew K., Siwo Geoffrey H., Chawla Nitesh V., Ferdig Michael T., Emrich Scott J. A Supervised Learning Approach to the Ensemble Clustering of Genes. International Journal of Data Mining and Bioinformatics. 2011 Jun; doi: 10.1504/ijdmb.2014.059062. [DOI] [PubMed] [Google Scholar]
- Sabidussi G. The centrality index of a graph. Psychometrika. 1966;31(4):581–603. doi: 10.1007/BF02289527. [DOI] [PubMed] [Google Scholar]
- Smith Erin N., Kruglyak Leonid. GeneEnvironment Interaction in Yeast Gene Expression. PLoS Biology. 2008;6(4):e83. doi: 10.1371/journal.pbio.0060083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solava RW, Michaels RP, Milenković T. Graphlet-based edge clustering reveals pathogen-interacting proteins. Bioinformatics; Also, in Proceedings of the 11th European Conference on Computational Biology (ECCB); Basel, Switzerland. Sep 9-12, 2012. 2012. pp. i480–i486. (acceptance rate: 14%) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steuer R, Kurths J, Daub CO, Weise J, Selbig J. The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics. 2002;18(suppl 2):S231–S240. doi: 10.1093/bioinformatics/18.suppl_2.s231. [DOI] [PubMed] [Google Scholar]
- Ucar D, Neuhaus I, Ross-MacDonald P, Tilford C, Parthasarathy S, Siemers N, Ji RR. Construction of a reference gene association network from multiple profiling data: application to data analysis. Bioinformatics. 2007;23(20):2716–2724. doi: 10.1093/bioinformatics/btm423. [DOI] [PubMed] [Google Scholar]
- van de Vijver Marc J., He Yudong D., van’t Veer Laura J., Dai Hongyue, Hart Augustinus A., Voskuil Dorien W., Schreiber George J., Peterse Johannes L., Roberts Chris, Marton Matthew J., Parrish Mark, Atsma Douwe, Witteveen Anke, Glas Annuska, Delahaye Leonie, van der Velde Tony, Bartelink Harry, Rodenhuis Sjoerd, Rutgers Emiel T., Friend Stephen H., Bernards René. A gene-expression signature as a predictor of survival in breast cancer. New England Journal of Medicine. 2002;347(25):1999–2009. doi: 10.1056/NEJMoa021967. [DOI] [PubMed] [Google Scholar]
- van Noort Vera, Snel Berend, Huynen Martijn A. The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model. EMBO Reports. 2004;5(3):280–284. doi: 10.1038/sj.embor.7400090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van’t Veer Laura J., Dai Hongyue, van de Vijver Marc J., He Yudong D., Hart Augustinus A., Mao Mao, Peterse Hans L., van der Kooy Karin, Marton Matthew J., Witteveen Anke T., Schreiber George J., Kerkhoven Ron M., Roberts Chris, Linsley Peter S., Bernards René, Friend Stephen H. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415(6871):530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- Wittkop T, Baumbach J, Lobo FP, Rahmann S. Large scale clustering of protein sequences with force-a layout based heuristic for weighted cluster editing. BMC Bioinformatics. 2007;8(1):396. doi: 10.1186/1471-2105-8-396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Xianghong, Kao Ming-Chih C., Hung Wing. Transitive functional annotation by shortest-path analysis of gene expression data. Proceedings of the National Academy of Sciences of the United States of America. 2002;99(20):12783–12788. doi: 10.1073/pnas.192159399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Jun, Zhang Bin, Smith Erin N., Drees Becky, Brem Rachel B., Kruglyak Leonid, Bumgarner Roger E., Schadt Eric E. Integrating large-scale functional genomic data to dissect the complexity of yeast regulatory networks. Nature Genetics. 2008;40(7):854–861. doi: 10.1038/ng.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.