Sub-Rayleigh Imaging via Speckle Illumination

Abstract

We demonstrate sub-Rayleigh limit imaging of an object via speckle illumination. Imaging beyond the conventional Rayleigh limit is achieved by illuminating the object with pseudo-thermal light which exhibits a random speckle pattern. An object image is reconstructed from the second-order correlation measurement and the resolution of the image, which exceeds the Rayleigh limit, is shown to be related to the size of the speckle pattern that is tied to the lateral coherence length of the pseudo-thermal light.

Improving resolution of optical imaging systems is among the most important goals of both classical and quantum optics. In a diffraction-limited system, the resolution limit, defined as the minimum resolvable distance between two points of an object, is given by the Rayleigh criterion, and expressed as δx = 0.61λ/NA where λ is the wavelength of the light and NA is the numerical aperture of the imaging system.

Over the course of the past decades, several microscopy techniques based on fluorescence have been introduced to improve resolution, for instance, by increasing the effective NA in 4PI-imaging systems [1], taking advantage of fluorescence saturation [2] or blinking [3,4], and by structured illumination [5]. A great effort is also being placed in exploiting quantum features of light to reach the Heisenberg limit [6], although practical quantum imaging systems are not yet within the reach of present-day technology.

Recently, it has been demonstrated that certain quantum-like features can be obtained from classical systems, as first exhibited in ghost imaging [7,8]. This then has generated widespread development of classical imaging systems that replicate quantum-like features for remote imaging [9, 10], communication [11, 12], and fluorescence imaging [13, 14]. In this context, it was proposed in Ref. [15] that sub-Rayleigh features could be obtained in both coherent and incoherent imaging systems by combining point-by-point illumination, as in a sketch of pointillism, combined with N-photon detection. Recently, this proposal has been demonstrated experimentally in a coherent system using a focused laser beam that sequentially illuminated sub-portions of an object mask via a sophisticated N-photon detection scheme [16] or electronic thresholding of a standard CCD [17].

In this paper, we demonstrate sub-Rayleigh imaging of an object in an incoherent imaging system via random speckle illumination generated from a pseudo-thermal light source. An object image is reconstructed from the second-order correlation measurement of the light field and it is shown that the resolution of the image exceeds the Rayleigh limit. Conceptually, our protocol is analogous to that of Ref. [15] in that, as the size of the ‘illumination point’ limits the resolution for the first-order intensity measurement, the size of the transverse coherence of pseudo-thermal light limits the resolution for the second-order correlation measurement [18]. In this respect, we show that the lateral resolution of the imaging system can be controlled by adjusting the transverse coherence of the illumination light.

The conceptual schematic of our protocol is shown in Fig. 1. A source of chaotic light, i.e., thermal light, located at r⃗ produces a random speckle pattern, causing speckle illumination of an an object mask placed at $\overrightarrow{r_o}$. The object is then imaged, by using a lens with an effective aperture of 2R, onto the CCD camera located at $\overrightarrow{r_i}$. For comparison, let us first assume a conventional imaging scheme in which light intensity at the image plane is measured. The intensity at the image plane is given as $I(\overrightarrow{r_i})\propto \text{tr}[\rho E_i^{(-)}(\overrightarrow{r_i},t)E_i^{(+)}(\overrightarrow{r_i},t)]$, where $E_i^{(-)}$ is the negative-frequency component of the electric field at the image plane, $E_i^{(+)}={[E_i^{(-)}]}^{†}$, and ρ is the state of the light field which may be coherent or incoherent. For a point object located at $\overrightarrow{r_o}$, the intensity distribution at the image plane $\overrightarrow{r_i}$ is calculated to be [15]

Fig. 1.

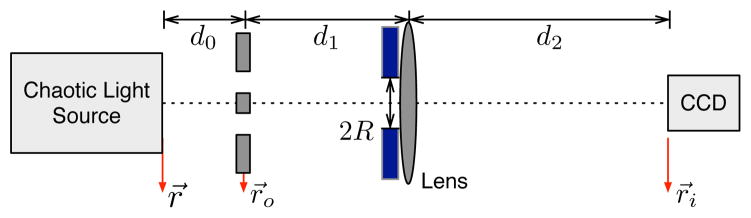
Conceptual scheme for sub-Rayleigh imaging via speckle illumination. See text for details.

$$I(\overrightarrow{r_i})\propto {\text{somb}}^2\left(\frac{Rk}{d_1}\left|\overrightarrow{r_o}+\frac{\overrightarrow{r_i}}{M}\right|\right),$$ (1)

where somb(x) = J₁(x)/x, J₁(x) is the spherical Bessel function of the first kind, k is the wavenumber, and the magnification factor M = d₂/d₁. It is clear from Eq. (1) that the resolution of the imaging system depends on the wavelength of the light and the size of the imaging aperture. Note that, in a conventional imaging system based on light intensity measurement, the Rayleigh limit holds regardless of the state of the light field.

Let us now consider our imaging protocol based on speckle illumination and second-order correlation measurement. The size of the speckle is assumed to be sufficiently smaller than the features of the object, analogous to the ‘point illumination’ scheme in Ref. [15–17]. The second-order correlation function is given as $G^{(2)}(\overrightarrow{r_i},\overrightarrow{r_j})=\text{tr}[\rho E_i^{(-)}(\overrightarrow{r_i},t)E_j^{(-)}(\overrightarrow{r_j},t)E_j^{(+)}(\overrightarrow{r_j},t)E_i^{(+)}(\overrightarrow{r_i},t)]$ and, in experiment, we consider only the AC-component ΔG⁽²⁾. For a point object located at $\overrightarrow{r_o}$, the autocorrelation function at the image plane $\overrightarrow{r_i}$ is calculated as

$$\mathrm{\Delta }{G}^{(2)}(\overrightarrow{r_i},\overrightarrow{r_i})\propto {\left|\int \mathrm{\Gamma }(\overrightarrow{r_o},{\overrightarrow{r_o}}^{\prime })\text{somb}\left(\frac{Rk}{d_1}\left|\overrightarrow{r_o}+\frac{\overrightarrow{r_i}}{M}\right|\right)\times \text{somb}\left(\frac{Rk}{d_1}\left|{\overrightarrow{r_o}}^{\prime }+\frac{\overrightarrow{r_i}}{M}\right|\right)\mathrm{d}{\overrightarrow{r_o}}^{\prime }\right|}^2,$$ (2)

where $\mathrm{\Gamma }(\overrightarrow{r_o},{\overrightarrow{r_o}}^{\prime })$ reflects the degree of second-order transverse coherence of the source. For a chaotic light with a non-zero transverse coherence length l_c, $\mathrm{\Gamma }(\overrightarrow{r_o},{\overrightarrow{r_o}}^{\prime })=exp[-{(\overrightarrow{r_o}-{\overrightarrow{r_o}}^{\prime })}^2/2l_c^2]$. It is clear from Eq. (2) that, as l_c is reduced, the resolution of the imaging system is improved. For infinitely small second-order transverse coherence l_c, we reach the ‘point speckle limit’ which is analogous to ‘point illumination’ in Ref. [15–17] and, in this case, $\mathrm{\Gamma }(\overrightarrow{r_o},{\overrightarrow{r_o}}^{\prime })=\delta (\overrightarrow{r_o}-{\overrightarrow{r_o}}^{\prime })$ so that

$$\mathrm{\Delta }{G}^{(2)}(\overrightarrow{r_i},\overrightarrow{r_i})\propto {\text{somb}}^4\left(\frac{Rk}{d_1}\left|\overrightarrow{r_o}+\frac{\overrightarrow{r_i}}{M}\right|\right).$$ (3)

The size of the ‘Airy disk’ is reduced by a factor of 0.6 in Eq. (3) compared to that of Eq. (1) and this shows the promise of image resolution surpassing that of a conventional imaging scheme based on light intensity measurement. Further increase in resolution can be obtained by using higher-order correlation measurements [19,20] or applying reconstructing algorithms and detection schemes for accurate localization of the transverse coherence peak [4, 15, 21].

The experimental setup to demonstrate sub-Rayleigh imaging via speckle illumination and second-order correlation measurement is schematically shown in Fig. 2. The source of speckle illumination, in which the speckle size can be easily varied, is pseudo-thermal light generated by focusing (with lens L1, f = 100 mm) a laser beam (783 nm) on a rotating ground disk (RD). The object mask (USAF resolution target) is placed right after RD for speckle illumination. The object is then imaged on the CCD by using lens L2 (f = 60 mm) whose aperture diameter, hence the Rayleigh limit, is controlled by an iris. The overall magnification factor M = 2.5 and the Rayleigh limit of the imaging system is δx · M [17].

Fig. 2.

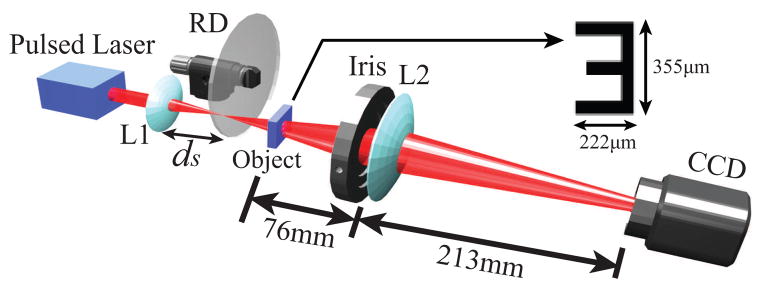
Experiment setup. Inset shows the object mask used in the experiment. See text for details.

The size of the speckle for speckle illumination can be varied by changing d_s, the distance between L1 and RD. Two such cases are shown in Fig. 3. The transverse coherence length l_c, measured with the second-order correlation measurement, is directly related to the size of the speckle and hence the resolution of the imaging system. As we shall show in Fig. 4, the smaller speckle (hence the smaller l_c) results in better image resolution as expected from Eq. (2) and Eq. (3).

Fig. 3.

Speckle illumination with different transverse coherence l_c observed at the image plane through the fully open iris. (a) l_c = 119 μm. (b) l_c = 63 μm.

Fig. 4.

(a) Conventional intensity imaging. Image cannot be resolved. (b) and (c) Second-order correlation measurement with, respectively, speckle illumination shown in Fig. 3(a) and in Fig. 3(b). Sub-Rayleigh imaging is clearly demonstrated.

To demonstrate the sub-Rayleigh imaging capability of our protocol, we chose the OCR-a numeric character ‘3’ of the USAF target for the object. We first fully open the iris (approximately 2.5 cm in diameter) so that the Rayleigh limit is δx · M = 6.0 μm. At this setting, we imaged the object using the conventional imaging scheme which fully illuminated the object with an unfocused coherent beam and found that the gap between two horizontal lines is about 126 μm. The iris is then closed down fully (approximately 0.9 mm in diameter) so that the new Rayleigh limit is δx · M = 168 μm. Since object is now smaller than the minimum resolvable length of the imaging system (the Rayleigh limit), the object image cannot be resolved with the conventional imaging scheme. The result of this experiment is shown in Fig. 4(a) and it is evident that the OCR-a numeric character ‘3’ cannot be resolved. Similar results were obtained with an incoherent light source and this is expected from Eq. (1) as we employ the conventional imaging system based on intensity measurement.

Let us now test our protocol involving speckle illumination and second-order correlation measurement. For the second-order correlation measurement, we take N = 500 frames of images with speckle illumination. The CCD has the minimum exposure time of 50 μs but we achieve an effective exposure time of 3.5 μs by using a pulsed laser for producing the pseudo-thermal light. To extract the second-order autocorrelation image, all N frames are averaged pixel by pixel. The average value is then subtracted from each frame, again, pixel by pixel, leaving only fluctuation terms. These results are then squared and summed over for all N frames, giving the autocorrelation result. The experimental data are shown in Fig. 4(b) and Fig. 4(c).

In Fig. 4(b), we used speckle illumination shown in Fig. 3(a). Although some horizontal structures begin to appear, it is difficult to see a clear image of the object. In Fig. 4(c), we used speckle illumination shown in Fig. 3(b). In this case, the object image is clearly identifiable even though the conventional imaging scheme failed to do so in Fig. 4(a). The experimental data shown in Fig. 4(b) and 4(c) clearly demonstrate sub-Rayleigh imaging via speckle illumination by a factor of 0.75 below the Rayleigh limit. The results also clearly demonstrate the smaller the speckle size, the better the image resolution for our imaging scheme using speckle illumination and second-order autocorrelation measurement, as expected from Eq. (2) and Eq. (3).

In conclusion, we have demonstrated that sub-Rayleigh imaging is possible by using speckle illumination and second-order correlation measurement. While the point-by-point illumination scheme requires sequential scanning of the point source over the object as well as repeated measurement at each location of the object for frame-averaging [16,17], our scheme requires no scanning as speckles are already distributed over the object, allowing rapid and sub-Rayleigh acquisition of the image. The demonstration in this work was done using pseudo-thermal light to easily control the transverse coherence length. Real chaotic light with small transverse coherence length should easily offer the resolution advantage of our scheme over the conventional scheme. Our scheme is also extremely simple to implement, without requiring precision scanning stages, well-collimated light sources, and special experimental configuration. Finally, we note that, using the principle demonstrated in this paper, it is straightforward to obtain higher resolution by incorporating n-th order autocorrelation measurement [19, 20]. However, increasing the order of correlation measurement would degrade the signal-to-noise ratio [22], hence requiring longer integration times (with the increasing order of correlation measurement) to acquire clear super-resolution images. Further resolution improvement is also possible by using reconstruction algorithms or detection schemes for the accurate localization of the peak of the transverse coherence [4, 15, 21].