Range of applicability of modified Fick-Jacobs equation in two dimensions

Abstract

Axial diffusion in a two-dimensional channel of smoothly varying geometry can be approximately described as one-dimensional diffusion in the entropy potential with position-dependent effective diffusivity by means of the modified Fick-Jacobs equation. In this paper, Brownian dynamics simulations are used to study the range of applicability of such a description, as well as the accuracy of the expressions for the effective diffusivity proposed by different researchers.

I. INTRODUCTION

The Fick-Jacobs (FJ) equation¹ provides an approximate one-dimensional description of axial diffusion in two-dimensional channels and three-dimensional tubes of varying geometry. Denoting the channel width by w(x) and the tube radius by r(x), where the x-coordinate is measured along the channel/tube axis (centerline), one can write the FJ equation in two and three dimensions, respectively, as

$${\displaystyle \frac{\partial c(x,t)}{\partial t}=\frac{\partial }{\partial x}\left[D_{0}w\left(x\right)\frac{\partial }{\partial x}\left(\frac{c(x,t)}{w\left(x\right)}\right)\right]}$$ (1.1)

and

$${\displaystyle \frac{\partial c(x,t)}{\partial t}=\frac{\partial }{\partial x}\left[D_0{r}^2\left(x\right)\frac{\partial }{\partial x}\left(\frac{c(x,t)}{r^2\left(x\right)}\right)\right].}$$ (1.2)

Here, c(x, t) is the effective one-dimensional concentration of diffusing particles at point x at time t, and D₀ is the intrinsic particle diffusivity in free space. The channel width in Eq. (1.1) and the square of the tube radius in Eq. (1.2) can be interpreted as Boltzmann factors with corresponding entropy potentials.

The first attempt to give a rigorous derivation of this equation was made by Zwanzig² more than two decades ago. Assuming that the channel width and the tube radius are slowly varying functions of x,

$${\displaystyle \left|w^{\prime }\left(x\right)\right|,\left|r^{\prime }\left(x\right)\right|<<1,}$$ (1.3)

where w′(x) = dw(x)/dx and r′(x) = dr(x)/dx, Zwanzig derived a modified FJ equation which has the form of Eqs. (1.1) and (1.2) with D₀ replaced by a position-dependent effective diffusivity D(x), which is smaller than D₀. According to Zwanzig (Zw), the effective diffusivity is given by

$${\displaystyle D_{Zw}\left(x\right)=\frac{D_0}{1+w^{\prime }{\left(x\right)}^2/12}}$$ (1.4)

and

$${\displaystyle D_{Zw}\left(x\right)=\frac{D_0}{1+r^{\prime }{\left(x\right)}^2/2}}$$ (1.5)

in two and three dimensions, respectively.

During the last two decades, the problem of the derivation of the modified FJ equation has attracted attention of many researchers.^3–14 The reason is that quasi-one-dimensional systems of varying geometry play an important role in different processes ranging from controlled drug delivery to entropic transport of different substances in soils and biological tissues. Along with the problem of deriving the modified FJ equation, there are also questions of the range of applicability of this approximate one-dimensional description and the accuracy of the expressions for the effective position-dependent diffusivity obtained by different researchers. These questions were studied numerically for three-dimensional tubes in Refs. ¹⁵ and ¹⁶ and recently discussed in Ref. 17. Here, we analyze the range of applicability of the modified FJ equation and accuracy of the available expressions in the case of two-dimensional channels.

We do this by applying the methodology proposed in Ref. 15. Specifically, we take advantage of the fact that the effective diffusivity is a function of the channel width variation rate w′(x). Therefore, when this rate is a constant, w′(x) = const = 2λ, the effective diffusivity is also a constant, which we denote by D_λ. In such a case, which is schematically shown in Fig. 1, the modified FJ equation, if applicable, reduces to Eq. (1.1) with D₀ replaced by D_λ. This equation is used to derive simple analytical formulas for the mean first-passage times of the particle between the narrow (n) and wide (w) ends of the channel, τ_n→w and τ_w→n. The obtained formulas give these times as the ratios of functions of the geometric parameters λ and L of the channel to the effective diffusivity, D_λ.

FIG. 1.

Schematic representation of a two-dimensional channel of length L and variable width w(x), w(x) = 2(1 + λx), 0 ≤ x ≤ L, where 2λ is the width variation rate. The half-width of the narrow end of the channel is used as a unit of length.

We use these formulas and the mean first-passage times obtained from Brownian dynamics simulations to find the effective diffusivity as a function of λ and L for the n → w and w → n particle transitions between the two channel ends. This diffusivity is used (1) to establish the range of applicability of the modified FJ equation and (2) to assess the accuracy of several expressions for D_λ obtained in deriving this equation by different methods.

II. RESULTS AND DISCUSSION

The mean first-passage times between the two ends of the channel of length L and the constant width variation rate w′(x) = 2λ, schematically shown in Fig. 1, are given by (see the derivations in the Appendix)

$${\displaystyle {\tau }_{n\to w}(\lambda ,L)=\frac{1}{4{\lambda }^2{D}_{\lambda }}\left[\lambda L\left(2+\lambda L\right)-2ln\left(1+\lambda L\right)\right]}$$ (2.1)

and

$${\displaystyle {\tau }_{w\to n}(\lambda ,L)=\frac{1}{4{\lambda }^2{D}_{\lambda }}\left[2{\left(1+\lambda L\right)}^{2}ln\left(1+\lambda L\right)-\lambda L\left(2+\lambda L\right)\right].}$$ (2.2)

These mean first-passage times were obtained from Brownian dynamics simulations for wide ranges of λ and L, 0 ≤ λ ≤ 2, and 0.5 ≤ L ≤ 50, where length is measured in units of the half-width of the narrow end of the channel. The numerically obtained τ_n→w(λ, L) and τ_w→n(λ, L) were used to find effective diffusivities $D_{\lambda }^{n\to w}\left(L\right)$ and $D_{\lambda }^{w\to n}\left(L\right)$ defined as

$${\displaystyle D_{\lambda }^{n\to w}\left(L\right)=\frac{1}{4{\lambda }^2{\tau }_{n\to w}(\lambda ,L)}\left[\lambda L\left(2+\lambda L\right)-2ln\left(1+\lambda L\right)\right]}$$ (2.3)

and

$${\displaystyle D_{\lambda }^{w\to n}\left(L\right)=\frac{1}{4{\lambda }^2{\tau }_{w\to n}(\lambda ,L)}\left[2{\left(1+\lambda L\right)}^{2}ln\left(1+\lambda L\right)-\lambda L\left(2+\lambda L\right)\right].}$$ (2.4)

The values of the effective diffusivities as functions of λ and L are given in Tables I and II.

TABLE I.

Effective diffusivity $D_{\lambda }^{n\to w}\left(L\right)$ as a function of λ and L, given by Eq. (2.3) with τ_n→w(λ, L) obtained from Brownian dynamics simulations.

		L
		0.5	1	2	4	6	8	10	20	50
λ	0	0.974	0.988	0.976	0.993	1.001	1.007	1.004	1.005	1.003
	0.2	0.968	0.976	0.972	0.978	0.992	0.999	0.987	0.991	0.994
	0.4	0.955	0.959	0.947	0.953	0.961	0.968	0.959	0.961	0.963
	0.6	0.937	0.933	0.921	0.916	0.925	0.928	0.922	0.924	0.921
	0.8	0.918	0.899	0.890	0.885	0.887	0.893	0.888	0.891	0.884
	1	0.900	0.877	0.856	0.850	0.851	0.857	0.853	0.856	0.847
	1.2	0.884	0.854	0.829	0.817	0.819	0.827	0.820	0.827	0.814
	1.4	0.865	0.831	0.803	0.793	0.793	0.796	0.790	0.801	0.785
	1.6	0.849	0.811	0.779	0.770	0.770	0.770	0.765	0.777	0.761
	1.8	0.836	0.790	0.763	0.748	0.747	0.751	0.744	0.754	0.743
	2	0.823	0.778	0.744	0.730	0.732	0.732	0.724	0.733	0.728

TABLE II.

Effective diffusivity $D_{\lambda }^{w\to n}\left(L\right)$ as a function of λ and L, given by Eq. (2.4) with τ_w→n(λ, L) obtained from Brownian dynamics simulations.

		L
		0.5	1	2	4	6	8	10	20	50
λ	0	0.966	0.976	0.995	1.000	0.990	1.000	1.004	1.010	1.013
	0.2	0.959	0.968	0.981	0.993	0.983	0.991	0.981	0.986	1.009
	0.4	0.939	0.946	0.953	0.960	0.957	0.952	0.952	0.951	0.960
	0.6	0.907	0.905	0.913	0.900	0.921	0.910	0.904	0.901	0.907
	0.8	0.869	0.853	0.868	0.864	0.866	0.847	0.852	0.861	0.849
	1	0.822	0.789	0.804	0.798	0.798	0.794	0.789	0.793	0.782
	1.2	0.764	0.741	0.747	0.744	0.741	0.739	0.739	0.748	0.733
	1.4	0.715	0.696	0.695	0.690	0.682	0.687	0.687	0.689	0.678
	1.6	0.667	0.646	0.641	0.641	0.633	0.637	0.638	0.645	0.608
	1.8	0.610	0.599	0.592	0.600	0.584	0.589	0.588	0.592	0.596
	2	0.568	0.550	0.543	0.560	0.546	0.550	0.552	0.561	0.551

The approximate one-dimensional description in terms of the modified FJ equation is applicable when the effective diffusivities $D_{\lambda }^{n\to w}\left(L\right)$ and $D_{\lambda }^{w\to n}\left(L\right)$ are (i) equal to one another and (ii) independent of the channel length, L. Table III gives the diffusivity ratio, $D_{\lambda }^{n\to w}\left(L\right)/D_{\lambda }^{w\to n}\left(L\right)$, for 0 ≤ λ ≤ 2 and 0.5 ≤ L ≤ 50. The results presented in Tables I–III show that for sufficiently large L the diffusivity is independent of the length (see also Ref. 16 for a three dimensional case) and the deviations of the diffusivity ratio from unity do not exceed 3% when λ and L satisfy the inequalities λ ≤ 0.6 and 2 ≤ L ≤ 50. The deviations from unity increase with λ. For λ = 0.8 and λ = 1, the deviations are within the range of 6% and 8%, respectively. Based on the results presented in Tables I–III, we conclude that the modified FJ equation provides a reasonably accurate one-dimensional description of axial diffusion in two-dimensional channels when λ and L satisfy

$${\displaystyle \lambda \le 1,L\ge 2.}$$ (2.5)

These inequalities establish the range of applicability of the modified FJ equation.

TABLE III.

The ratio of the effective diffusivities $D_{\lambda }^{n\to w}\left(L\right)/D_{\lambda }^{w\to n}\left(L\right)$, as a function of λ and L.

		L
		0.5	1	2	4	6	8	10	20	50
λ	0	1.008	1.012	0.981	0.993	1.011	1.007	1.000	0.995	0.989
	0.2	1.009	1.009	0.990	0.984	1.009	1.008	1.006	1.005	0.985
	0.4	1.017	1.014	0.994	0.993	1.004	1.017	1.007	1.010	1.003
	0.6	1.033	1.030	1.009	1.017	1.005	1.019	1.020	1.026	1.016
	0.8	1.057	1.054	1.025	1.025	1.024	1.054	1.043	1.035	1.042
	1	1.095	1.111	1.064	1.065	1.067	1.080	1.081	1.080	1.083
	1.2	1.157	1.152	1.109	1.099	1.106	1.119	1.110	1.105	1.111
	1.4	1.210	1.194	1.155	1.149	1.162	1.158	1.151	1.163	1.158
	1.6	1.274	1.256	1.215	1.200	1.216	1.210	1.199	1.204	1.253
	1.8	1.370	1.319	1.287	1.247	1.278	1.274	1.266	1.273	1.246
	2	1.449	1.413	1.370	1.302	1.341	1.331	1.312	1.308	1.320

Next we compare the effective diffusivities $D_{\lambda }^{n\to w}$ and $D_{\lambda }^{w\to n}$, obtained from our simulations with the λ-dependences of the effective diffusivity, which follow from the expressions for D(x) obtained by different researchers. In addition to the Zwanzig formula in Eq. (1.4), we also consider formulas for D(x) proposed by Reguera and Rubi (RR)³ and Kalinay and Percus (KP)⁶, which are, respectively, given by

$${\displaystyle D_{\mathit{RR}}\left(x\right)=\frac{D_0}{{\left[1+w^{\prime }{\left(x\right)}^2/4\right]}^{1/3}}}$$ (2.6)

and

$${\displaystyle D_{\mathit{KP}}\left(x\right)=\frac{arctan\left(w^{\prime }\left(x\right)/2\right)}{w^{\prime }\left(x\right)/2}{D}_0.}$$ (2.7)

An alternative derivation of the second formula is given by Martens et al.¹⁰

Recently, Dagdug and co-authors proposed a new approach to the reduction of axial diffusion of point particles in two-dimensional channels to the effective one-dimensional description, which allows them to treat channels of arbitrary shapes.¹³ The key idea of the approach is to perform the reduction in a curvilinear coordinate system chosen so that the channel boundaries are straight lines. The developed formalism provides an iteration procedure for finding the effective position-dependent diffusivity D(x). When the channel axis is a straight line, the first iteration recovers the Kalinay-Percus formula for the effective diffusivity.

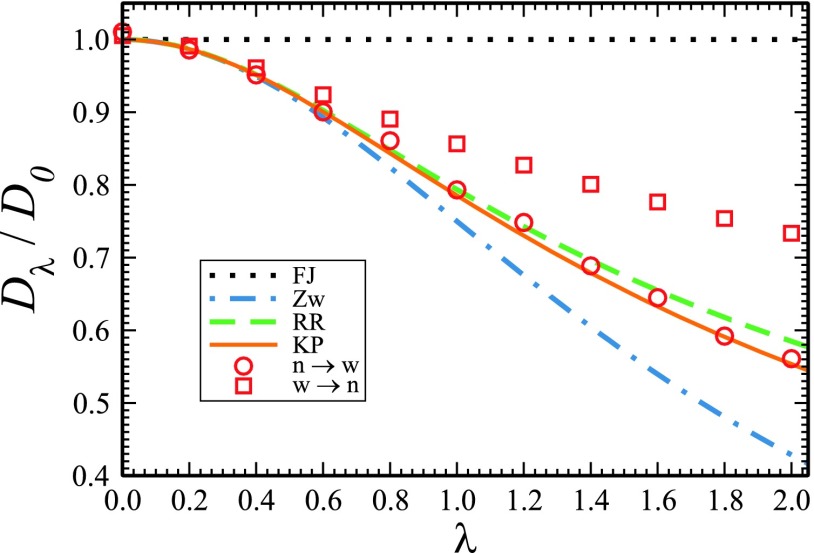
In Fig. 2, we compare the values of the effective diffusivity obtained using the simulation results with the λ-dependences which follow from the different expressions for D(x),

$${\displaystyle D_{\lambda }^{\mathit{FJ}}/D_0=1\text{(Fick-Jacobs)},}$$ (2.8)

$${\displaystyle D_{\lambda }^{\mathit{Zw}}/D_0=\frac{1}{1+{\lambda }^2/3}\text{(Zwanzig)},}$$ (2.9)

FIG. 2.

Comparison of different dependences D_λ drawn using Eqs. (2.8)-(2.11) (curves) with the values of D_λ,n→w and D_λ,w→n obtained from Brownian dynamics simulations (symbols). The symbols give the simulation results for the channel of length L = 20.

$${\displaystyle D_{\lambda }^{\mathit{RR}}/D_0=\frac{1}{{\left(1+{\lambda }^2\right)}^{1/3}}\text{(Reguera-Rubi)},}$$ (2.10)

$${\displaystyle D_{\lambda }^{KP}/D_0=\frac{1}{\lambda }arctan\left(\lambda \right)\text{(Kalinay-Percus)}.}$$ (2.11)

One can see that Zwanzig’s formula for the effective diffusivity, Eq. (1.4), leads to the lower boundary for D_λ given by Eq. (2.9). One can also see that the λ-dependences given by Eqs. (2.10) and (2.11) are very close to one another. In addition, both are in good agreement with the values of $D_{\lambda }^{w\to n}/D_0$ obtained from the simulations of the w → n transitions over the entire range of λ, 0 ≤ λ ≤ 2. This is not the case with the values of $D_{\lambda }^{n\to w}/D_0$ obtained from the simulations of the n → w transitions, which are markedly larger than the values of $D_{\lambda }^{w\to n}/D_0$ when λ > 1.

Figure 2 shows that for λ > 1 the modified FJ equation with D(x) given by RR or KP formulas, Eqs. (2.6) and (2.7), works well when the particle goes in the w → n direction and fails when it goes in the opposite, n → w direction. The physical reason for this direction dependence can be explained as follows. Moving in the w → n direction, the particle has to climb the entropy barrier. It reaches the barrier top and gets trapped by the absorbing narrow end of the channel after many unsuccessful attempts during which the particle suffers many collisions with the channel walls. Due to these collisions, the particle learns about the entropy potential. Reduction to the effective one-dimensional description of the particle motion in the entropy potential is accompanied by the λ-dependent decrease of the effective diffusivity.^2,12 The situation is qualitatively different when the particle goes in the n → w direction in the channel with λ > 1. Here, the reduction to the effective one-dimensional description is not justified because the particle does not experience enough collisions with the channel walls.

To summarize, our simulation results have shown that the reduction of axial diffusion in two-dimensional channels to the effective one-dimensional description in terms of the modified FJ equation is applicable when the channel width variation rate does not exceed unity, $\left|w^{\prime }\left(x\right)\right|\le 1$. This is a significantly weaker constraint than that in Eq. (1.3), imposed by Zwanzig² in deriving the modified FJ equation. When the one-dimensional description is applicable, the best approximations for the position-dependent effective diffusivity, entering into the modified FJ equation, are given by the Reguera-Rubi and Kalinay-Percus formulas, Eqs. (2.6) and (2.7), respectively, which give very close values for this quantity.

APPENDIX: MEAN FIRST PASSAGE TIMES τ_n→w AND τ_w→n

Consider a particle diffusing in a channel shown in Fig. 1, assuming that the reduction to the effective one-dimensional description is applicable. Let G(x, t|x₀) be the particle one-dimensional propagator (Green’s function) on the interval (0,   L), where x and x₀ are the particle positions at time t and at t = 0, respectively, 0 < x,   x₀ < L. This propagator satisfies Eq. (1.1) with D₀ replaced by D_λ, which has the form

$${\displaystyle \frac{\partial G}{\partial t}=D_{\lambda }\frac{\partial }{\partial x}\left[w\left(x\right)\frac{\partial }{\partial x}\left(\frac{G}{w\left(x\right)}\right)\right],}$$ (A1)

where channel width w(x) is given by

$${\displaystyle w\left(x\right)=2(1+\lambda x).}$$ (A2)

Let $\tau \left(x_0\to L\right)$ be the particle mean first-passage time from x₀ to the wide end of the channel located at x = L in the presence of a reflecting boundary at the narrow channel end located at x = 0. This time, considered as a function of x₀, satisfies^18,19

$${\displaystyle \frac{D_{\lambda }}{w\left(x_0\right)}\frac{d}{d{x}_0}\left[w\left(x_0\right)\frac{d\tau }{d{x}_0}\right]=-1,}$$ (A3)

subject to the boundary conditions

$${\displaystyle {\left.\tau \right|}_{x_0=L}={\left.\frac{d\tau }{d{x}_0}\right|}_{x_0=0}=0.}$$ (A4)

The solution for $\tau \left(x_0\to L\right)$ is given by

$${\displaystyle \tau \left(x_0\to L\right)=\frac{1}{D_{\lambda }}{\int }_{\hspace{0.17em}{x}_0}^{\hspace{0.17em}L}\frac{dx}{w\left(x\right)}{\int }_0^{x}w\left(y\right)dy.}$$ (A5)

The mean first-passage time τ_n→w is the mean first-passage time in Eq. (A5) with x₀ = 0, ${\tau }_{n\to w}=\tau \left(0\to L\right)$. Substituting w(x) in Eq. (A2) into Eq. (A5) with x₀ = 0, and performing the integrations, we arrive at the expression for τ_n→w given in Eq. (2.1).

The particle mean first-passage time from x₀ to the narrow end of the channel, $\tau \left(x_0\to 0\right)$, when the wide channel end at x = L is a reflecting boundary, considered as a function of x₀, satisfies the same Eq. (A3). The boundary conditions for $\tau \left(x_0\to 0\right)$ differ from those in Eq. (A4) and are given by

$${\displaystyle {\left.\tau \right|}_{x_0=0}={\left.\frac{d\tau }{d{x}_0}\right|}_{x_0=L}=0.}$$ (A6)

Integrating Eq. (A3) with the boundary conditions in Eq. (A6), we obtain

$${\displaystyle \tau \left(x_0\to 0\right)=\frac{1}{D_{\lambda }}{\int }_{\hspace{0.17em}0}^{\hspace{0.17em}{x}_0}\frac{dx}{w\left(x\right)}{\int }_x^{L}w\left(y\right)dy.}$$ (A7)

The mean first-passage time τ_w→n is the mean first-passage time in Eq. (A7) with x₀ = L, ${\tau }_{w\to n}=\tau \left(L\to 0\right)$. To obtain the expression for τ_w→n in Eq. (2.2), it remains to substitute w(x) in Eq. (A2) into Eq. (A7) with x₀ = L and to perform the integrations.