Mixed Brownian alignment and Néel rotations in superparamagnetic iron oxide nanoparticle suspensions driven by an ac field

Abstract

Superparamagnetic iron oxide nanoparticles with highly nonlinear magnetic behavior are attractive for biomedical applications like magnetic particle imaging and magnetic fluid hyperthermia. Such particles display interesting magnetic properties in alternating magnetic fields and here we document experiments that show differences between the magnetization dynamics of certain particles in frozen and melted states. This effect goes beyond the small temperature difference (ΔT ~ 20 °C) and we show the dynamics to be a mixture of Brownian alignment of the particles and Néel rotation of their moments occurring in liquid particle suspensions. These phenomena can be modeled in a stochastic differential equation approach by postulating log-normal distributions and partial Brownian alignment of an effective anisotropy axis. We emphasize that precise particle-specific characterization through experiments and nonlinear simulations is necessary to predict dynamics in solution and optimize their behavior for emerging biomedical applications including magnetic particle imaging.

I. INTRODUCTION

Superparamagnetic iron oxide nanoparticles (SPIOs) made of magnetite can possess magnetic moments that saturate in biologically relevant magnetic fields of the order of tens of milliteslas. This strong magnetization response allows noninvasive control and readout during biomedical applications. Because SPIOs are biocompatible, they have been extensively used to realize drug delivery, cell separation, magnetic resonance imaging (MRI), localized hyperthermia therapy [1], and, most recently, magnetic particle imaging (MPI) [2], which exploits the nonlinear response of magnetic nanoparticles to oscillating magnetic fields as a signal. In MPI and most biomedical applications (separation being a notable exception), the particles are activated with an alternating magnetic field, and thus magnetization reversal dynamics plays a critical role [3–8]. There are two possible rotation mechanisms: Néel rotation [9] governs the restructuring of electronic spin states to allow the magnetic moment to reorient irrespective of the orientation of the whole particle, and Brownian rotation [10] occurs when the particle itself rotates in the solution, carrying with it the magnetic moment fixed in a direction relative to the particle’s crystal lattice. As an illustrative instance of why both mechanisms are important, hyperthermia therapy usually relies on Néel rotations that locally heat when the response of the moment lags behind the driving field, yet several studies now show the influence of particle alignment or orientations on the heating capabilities, indicating Brownian rotations may be useful, if not inherently used, as a mechanism of heating [11–13].

In this paper, combining experiments and modeling, we have uncovered interesting solution-phase-dependent magnetic dynamics through rigorous testing of magnetization responses in various frozen and melted configurations. For example, we observed a change in magnetic response of a dilute suspension of particles to an alternating field upon freezing, which reversed upon melting. We attribute differences between the liquid and frozen responses to the additional (Brownian) rotational freedom of the particles. To be clear, we assume that in the liquid suspension the particles can reorient their easy axes to align with the applied field, and this Brownian rotation is not possible in the frozen state. When a static magnetic field was applied concurrently with the freezing process, possibly imparting a net alignment of the easy axes, further variation in magnetic behavior was observed. The basic idea of the title phrase “Brownian alignment and Néel rotation” is shown in Fig. 1: (1) the entire crystal rotates slightly to align one of its easy axes and (2) the subsequent magnetization rotation with the Néel mechanism is different than the unaligned case.

FIG. 1.

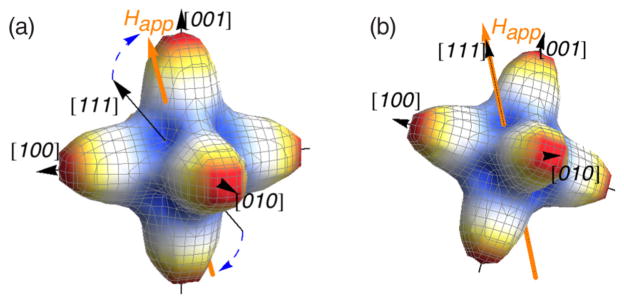
(Color online) The magnetocrystalline energy surface for cubic magnetite (negative K₁), which has easy directions in the [111] family. After (a) applying an arbitrary magnetic field vector H_app in a fixed direction, particles in solution undergo Brownian rotation through a small angle until (b) the nearest easy axis is aligned with the applied field.

We compare these results to nonlinear stochastic simulations and find the behaviors can be replicated when the direction of the effective easy axis is no longer random but is partially aligned in the field. From these observations, we conclude that the relative rotational freedom of nanoparticles, and the orientation of easy axes with respect to an applied field, can have a significant impact on the response to an oscillating field even when the Néel reversal process dominates. This can impact biomedical applications such as magnetic particle imaging or magnetic fluid hyperthermia.

II. EXPERIMENTAL MATERIALS AND METHODS

A. Materials characterization

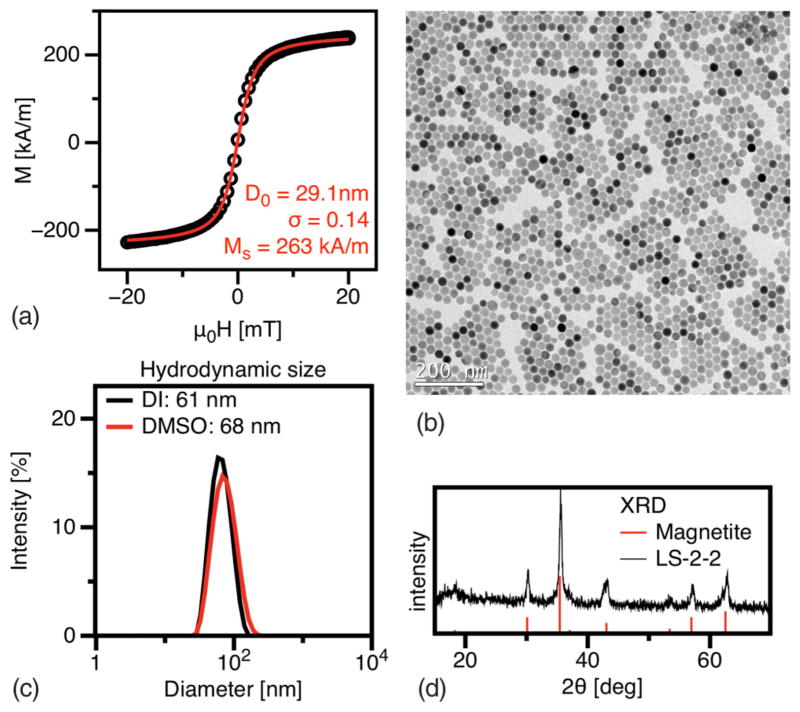
Magnetite nanoparticles (sample LS-002-2) were obtained from LodeSpin Labs, LLC. The nanoparticles contained crystalline magnetite cores that were coated with a poly(ethylene glycol) (PEG)-based amphiphilic polymer. Sample LS-002-2 was coated with poly(maleic anhydride-alt-1-octadecene) (PMAO, Mn 40 000 Da) PEG (Mn 20 000 Da). The PMAO was loaded with PEG such that 25% of the available carboxylates in the PMAO were bonded to a PEG molecule. For this study, sample LS-002-2 was dispersed in dimethyl sulfoxide (DMSO), which freezes at 19°C. The hydrodynamic diameter (Z average, i.e., the intensity-based harmonic mean) of nanoparticles in liquid DMSO was 68 ± 25 nm, measured by dynamic light scattering (DLS). The diameter of the same sample dispersed in water was 61 ± 20 nm.

Magnetic performance was the same in DMSO and water, which have similar viscosities (for reference, the viscosity of DMSO is 1.996 cP, while water is 0.894 cP). Transmission electron microscopy (TEM) images in Fig. 2 showed the nanoparticle samples to be monodisperse, with median diameter of 26 ± 1.5 nm. Multiple images (6000 particles) were analyzed to determine size distribution using IMAGEJ, an open-source image-processing software developed by the National Institutes of Health. Shape anisotropy of the particles was estimated from TEM images, also using IMAGEJ. Each particle measured for size determination was fit with an ellipse and the ratio of long axis to short axis determined. The resulting histogram was fit with a log-normal distribution to determine the median aspect ratio (1.04 ± 0.03). This equates to a typical elongation of approximately 1 nm. Figure 2 also shows the vibrating sample magnetometer (VSM) curve and the log-normal size distribution of nanoparticles obtained by fitting the magnetization curve to the Langevin function using Chantrell’s method [14]. We calculate that the median magnetic core diameter is 29.1 ± 1.5 nm, with σ_nw = 0.05 (number weighted), where exp(σ_nw) is the geometric standard deviation of the log-normal distribution. The measured saturation magnetization of 263 kA/m was used for fitting to determine the magnetic size from VSM measurements. Powder x-ray diffraction patterns matched a magnetite reference [Fig. 1(d)], although we note the saturation magnetization was about 57% of bulk magnetite, which may be due to some phase impurity. Magnetite is ferrimagnetic, having an inverse spinel crystalline structure, and displays a cubic magnetocrystalline anisotropy, with easy axes along the [111] directions, i.e., the body diagonals of a cube. The angles between the eight equivalent easy axes in a perfect cube are 70.53°.

FIG. 2.

(Color online) SPIOs were characterized by complementary methods to obtain magnetic, size, and structural information: (a) VSM curve, (b) TEM image of nanoparticles showing monodisperse size distribution, (c) DLS plot, and (d) x-ray diffraction plot.

B. Immobilization of SPIOs

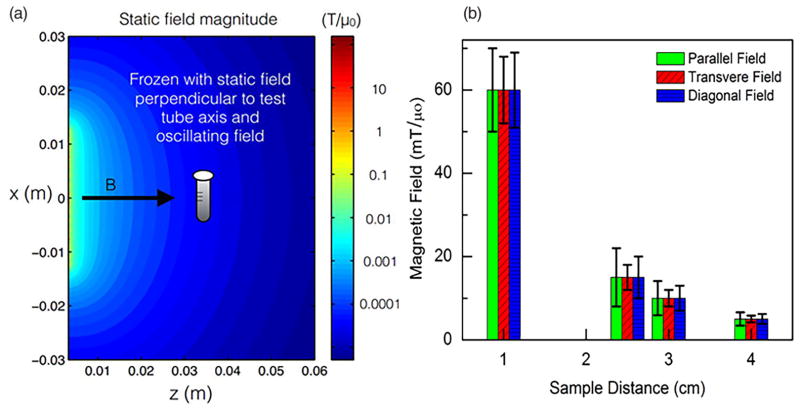
Sample SPIOs were suspended in DMSO and immobilized by freezing in the absence or presence of a static magnetic field. To prepare samples, a solution containing 200 μL of magnetic nanoparticles (MNPs) with concentration 1.22 g Fe/L was transferred to a 0.6-mL microcentrifuge tube and sonicated for 5 min at room temperature (23 °C). After sonication, the DMSO solution was visibly in the liquid phase. The sample was immobilized by freezing at −20°C inside a commercial freezer. During freezing, a magnetic field was applied to the sample to orient the nanoparticles by aligning their magnetic easy axes. The magnetic field was arranged with field lines parallel, transverse, or diagonal to the reference axis, defined to be along the axis of the sample tube (see Fig. 3). The magnetic field was generated by a NdFeB permanent magnet (K&J magnetics, grade N42; dimensions: 1.5 × 1 × 0.125 in.³). The liquid sample was frozen in three different magnetic fields (5, 10, and 15 mT) with a zero-field control sample, and for the three respective orientations. For each freezing condition, the sample was cooled to −20°C under the applied field and kept at that temperature for 30 min. After freezing, the sample tube was transferred to an ice bath (0 °C) to maintain the frozen state of the ferrofluid during magnetic particle spectroscopy (MPS) measurements. Repeated MPS measurements showed that the freezing process was fully reversible and the sample behavior upon melting was the same as before freezing. In another study, a dilution series (0.05, 0.1, 0.5, 1, and 1.22 g Fe/L) was prepared and analyzed with the same measurement procedure after freezing in different fields (0, 10, and 60 mT) to determine whether the freezing process introduced interparticle interactions into the magnetic behavior of the system.

FIG. 3.

(Color online) (a) The simulated magnetic field of the permanent magnet (lines of equal field strength are shown in the figure). The test tube containing the SPIOs was frozen in this orientation at various distances to achieve the varying magnetic field amplitudes. In the example illustrated in (a), the aligning field was applied perpendicular to the direction of the oscillating (drive) field, which was always applied parallel to the long axis of the sample tube. The surface field for these magnets is 0.12 T, so we see that at 5 cm the field is in the single millitesla range as shown in experiment. Notably at this distance we can see the variations in the field are minimal within the test tube. (b) Measured variation of field strength with distance from the magnet. Error bars represent the variation in field within the sample tube for the stated field orientation, and they differ because the tube geometry is anisotropic.

The magnetic field profile of the NdFeB magnet was measured using a handheld gauss meter (Lakeshore model 410). Distance was measured from the center of the magnet to the center of the sample volume. Uncertainties in the magnetic field profile, represented by error bars in Fig. 3(b), were estimated based on the range of field values measured over the sample volume along the magnetic field vector (maximum 1.4 cm, for the parallel orientation). The largest field corresponded to the volume of sample closest to the magnet, and the smallest field to the volume farthest from the magnet. The parallel orientation admitted the largest uncertainty, as the sample volume was longest in this direction.

C. Magnetic measurements

A custom-built magnetic particle spectrometer was used to determine the magnetization response of MNPs [3,15]. The system applies an oscillating magnetic field to the sample of MNPs and measures the voltage signal induced in a receiver coil from the response of the magnetic particles. The signal is thus the time derivative of the magnetization and must be integrated numerically to obtain the magnetization response.

D. Landau-Lifshitz-Gilbert simulations with effective anisotropy

Simulations of magnetization reversal were incorporated to support experiments. There have been many models introduced in the literature to model the rotational dynamics of magnetic particles [16–19]. Here, state-of-the-art simulations integrate the stochastic Landau-Lifshitz-Gilbert (LLG) equation, Eq. (1). The equation describes a classical magnetic dipole with a phenomenological damping term and can be used to discuss Néel rotations of magnetic particles [16,20]:

$$\frac{d\mathbf{m}}{dt}=-\frac{\gamma }{1+{\alpha }^2}\{\mathbf{m}\times [\mathbf{H}+\alpha \mathbf{m}\times \mathbf{H}]\}.$$ (1)

In the LLG dynamics, the magnetization m evolves over time depending on the gyromagnetic ratio γ and the unitless LLG damping parameter α. To model magnetic spectroscopy of SPIOs with core volume V_c and magnetic moment μ, we considered the total field H to contain contributions from an applied oscillating excitation field of magnitude H₀ and frequency f = ω/2π, an effective uniaxial anisotropy direction with magnitude K, and easy axis in direction n. Particles in liquid suspension are not fixed spatially and undergo Brownian motion; in all samples the concentration of nanoparticles was on the order of 1 g/L, making the volume fraction of particles 0.025%. For both of these reasons we modeled the particles as noninteracting dipoles. We could thus ignore translational movement in the model. However, it was essential to introduce thermal fluctuations of the direction of the magnetization using a random field h(t) so that the total field of the model was

$$\mathbf{H}=H_{0}cos(\omega t)\widehat{z}+\frac{2K{V}_c}{\mu }(\mathbf{m}·\mathbf{n})\mathbf{n}+\mathbf{h}(t),$$ (2)

with a zero-mean, δ-time correlated random field

$$\langle \mathbf{h}(t)\rangle =0\langle {\mathbf{h}}_i(t){\mathbf{h}}_j(t^{\prime })\rangle =\frac{2k_{\mathrm{B}}T}{\mu \gamma }\frac{(1+{\alpha }^2)}{\alpha }{\delta }_{ij}\delta (t-t^{\prime })$$ (3)

so that the field is Markovian in time and i,j ∈ x,y,z describes the lack of correlation between the random fields in different Cartesian directions. The thermal energy k_BT is written in terms of Boltzmann’s constant and temperature T.

The model assumes the particles are effectively single domain, which is a reasonable assumption given that the critical diameter for multiple domains in magnetite is approximately 85 nm [21]. A distribution for the magnetic moments was determined from the measured saturation magnetization and the measured core size distribution. The anisotropy is of particular interest and because the underlying mechanism is not fully understood, we used an effective anisotropy distribution that could incorporate crystalline anisotropy and shape anisotropies potentially caused by minor chaining (e.g., dimerization). This approach was taken by Jamet et al. to discuss multiple anisotropic contributions in clustered nanoparticles and by Tamion et al. to numerically account for the distribution of anisotropy constants [22,23]. We expect that in solutions, the particles were rotating with the Brownian mechanism to align one of their cubic axes along the applied field. The required angle of rotation is small on average because there are several equivalent axes in a cubic magnetite particle, and any one could align along the applied field. To simulate this behavior, we made nonrandom choices for the direction of an effective easy axis of each particle. We stress that the strength of the anisotropy was also considered a log-normal distribution and that the alignment with the field was modeled as a distribution of the angle of each particle’s easy axis dependent on the extent of the alignment. For example, in the freezing experiments, we imagine a single particle immersed in a static field potentially allowing one of its easy axes—geometrically, the closest—to rotate and align with the field. The ensemble of particles thus develops a distribution of alignments that are locked in place when the solution is subsequently frozen. The alignment then persisted during spectroscopy. Coupled differential equations describing the Brownian and Néel rotation can be found in the works of Shliomis and Stepanov [24] as well as Coffey, Cregg, and Kalmykov [25], though because of the foggy nature of the anisotropy in this work and the excellent fit of the experimental data with the current model, these approaches were not used.

E. Numerical implementation

We use the Heun scheme to integrate the stochastic differential equation. Excellent descriptions of numerical methods for stochastic problems can be found in Gardiner’s handbook [26]. Heun’s method converges in the sense of Stratonovich [27] and can be written in general for the change in magnetization as

$$d\mathbf{m}=f(\mathbf{m},t)dt+g(\mathbf{m},t)d\mathbf{W}.$$ (4)

Here the numerical integration scheme has predictor

$$\overline{\mathbf{m}}(t+\mathrm{\Delta }t)=\mathbf{m}(t)+f(\mathbf{m},t)\mathrm{\Delta }t+g(\mathbf{m},t)\mathrm{\Delta }\mathbf{W}$$ (5)

and then the true value is

$$\mathbf{m}(t+\mathrm{\Delta }t)=\mathbf{m}(t)+\frac{f(\mathbf{m},t)+f(\overline{\mathbf{m}},t+\mathrm{\Delta }t)}{2}\mathrm{\Delta }t+\frac{g(\mathbf{m},t)+g(\overline{\mathbf{m}},t+\mathrm{\Delta }t)}{2}\mathrm{\Delta }\mathbf{W},$$ (6)

where an increment of the Wiener process is defined by $\mathrm{\Delta }\mathbf{W}=\sqrt{\mathrm{\Delta }t}\mathbf{N}(0,1)$ where N(0,1) is a vector of normal or Gaussian-distributed random numbers each with mean zero and unit variance.

The predicted size distributions for particle diameters are log-normal (see Fig. 2) [14]. This means the probability of having a particle with a certain radius r can be modeled by

$$p(r)=\frac{1}{\sqrt{2\pi }}\frac{1}{r{\sigma }_r}exp\left[-\frac{{\left\{ln\left(\frac{r}{m_r}\sqrt{1+\frac{s_r^2}{m_r^2}}\right)\right\}}^2}{2{\sigma }_r^2}\right]$$ (7)

with

$${\int }_0^{\infty }p(r)dr=1.$$ (8)

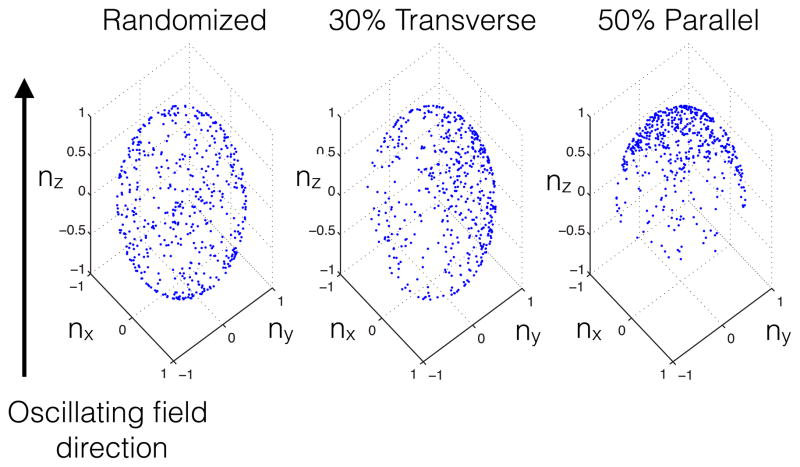
We have used that the mean and standard deviation of the distribution are m_r and s_r, respectively, and the scale parameter ${\sigma }_r=\sqrt{ln(1+\frac{s_r^2}{m_r^2})}$. An equivalent log-normal distribution for the anisotropy constants allows for a mixture of effects, including crystalline anisotropy and chaining. Simulations were always performed at the correct temperature [implemented in the thermal field, Eq. (3)] corresponding to the desired experimental procedure. The LLG damping parameter was held constant at α = 1. Changing this value did not change the dynamics but required more time steps. It is typical to choose the value between 0.01 and 1 [18,28,29], though new studies are shedding light on the variation of this parameter during ferromagnetic resonance [30]. The integration required 2¹² time steps and 10⁵ nanoparticles, or equivalently 10⁵ simultaneous integrations of the stochastic equation. We included a signal at the background frequency to mimic any feedthrough from the apparatus (at most 10% of the magnitude of the nanoparticle signals and usually below 5%). The magnetite density was 4.9 g/cm³ and the saturation magnetization was found from experiment to be 50 emu/g or equivalently 263 kA/m. The measurement techniques are discussed in Sec. II C. We used the bulk value for the gyromagnetic ratio of 1.3 GHz/T as opposed to the single electron value [31]. The best fit to experimental data was achieved using a mean anisotropy constant of 3.4 kJ/m³ with a 3 kJ/m³ standard deviation, which is consistent with recent measurements of similar samples [32]. In a suspension of particles, the easy axis, n, for each particle is typically assumed to be in a random direction. However, the experiments showed that, by freezing the particles in a static field, their subsequent magnetic dynamics were different. Two possible physical mechanisms were considered: the Brownian alignment of the closest magnetocrystalline easy axes, or formation of short chains in the direction of the applied field. Either way, this would replace the cubic anisotropy of the particles by an effective uniaxial anisotropy. To simulate this behavior, we allowed that an effective single easy axis for each particle was partially aligned with the direction of the static field. This was implemented by choosing a random orientation for each particle, adding a vector in the direction of alignment, and then normalizing again. Three realizations of this procedure are shown in Fig. 4: a fully randomized sample, a sample that has been aligned 30% to the transverse direction of the oscillating field, and a sample that has been aligned 50% parallel to the direction of the oscillating field.

FIG. 4.

(Color online) Distribution of the effective easy axes of 500 particles. This figure should aid the visualization of the asymmetry that was included in the simulations in order to mimic partial alignment of an effective easy axis with the static field.

III. RESULTS

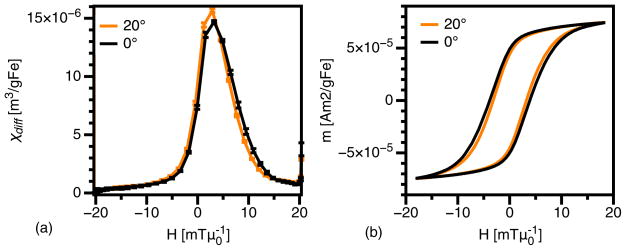
Freezing the sample altered its dynamic magnetization, as shown in Fig. 5, which compares the response of a single sample in liquid and frozen states. Measurements were taken for a drive field of f = 26 kHz and H₀ = 50 mT/μ₀. By convention, only half of the full period (forward scan) is shown in all plots of the differential susceptibility χ_diff = dm/dH vs field with respect to the field amplitude. The fluid sample had greater maximum differential susceptibility ${\chi }_{\text{diff}}^{\text{max}}$, and χ_diff decayed to its minimum at lower field magnitude.

FIG. 5.

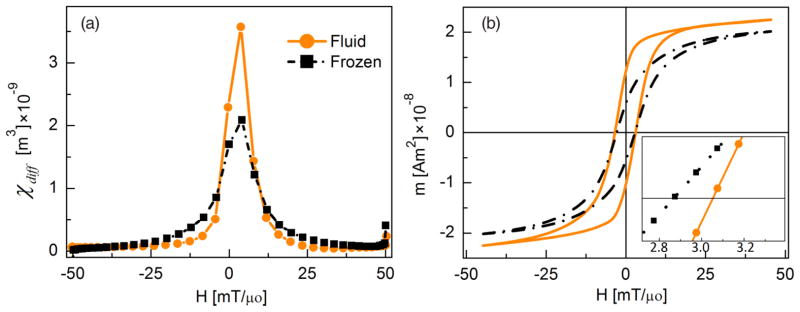
(Color online) MPS results of the same sample measured in fluid state (at 20°C) and frozen (in zero magnetic field, 0 mT/μ₀). The excitation field was 50 mT/μ₀ amplitude at 26 kHz: (a) χ_diff and (b) m(H) curves calculated by integrating data in (a).

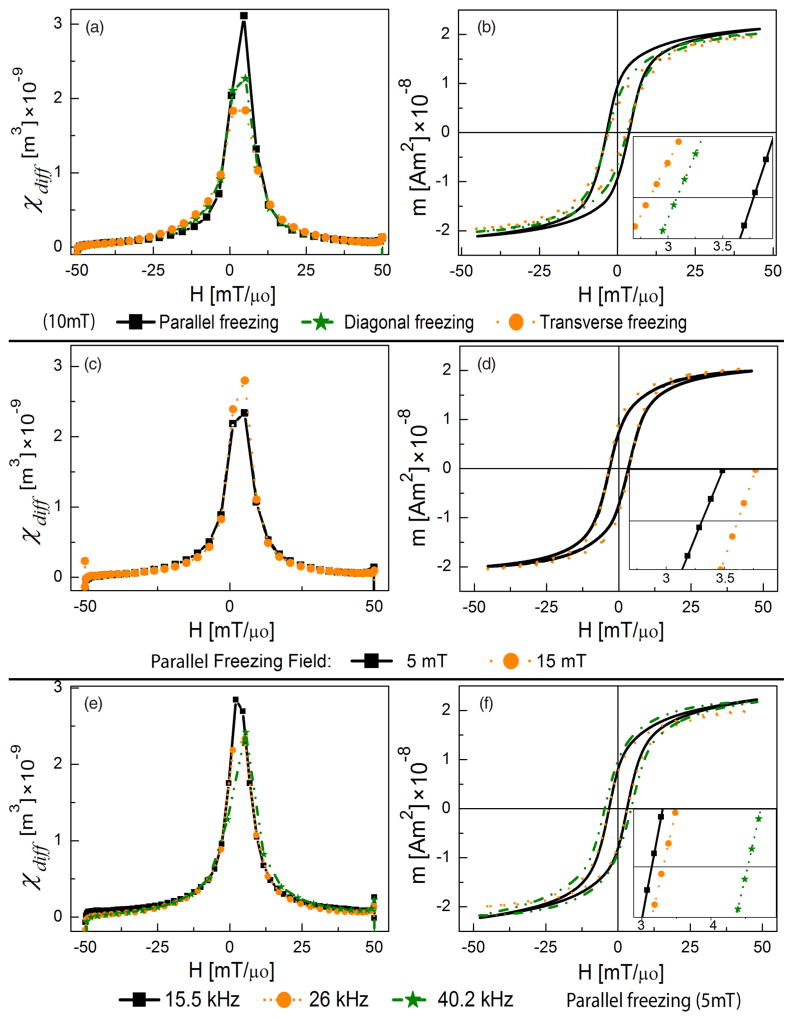
When the sample was frozen in the presence of an applied field, both χ_diff and its integrated value, the magnetization m(H), varied with the angle of the applied field with respect to the reference axis (Fig. 6). Among the field-freezing data, the parallel orientation had the highest value of ${\chi }_{\text{diff}}^{\text{max}}$ [i.e., the maximum value of dm/dH (m³), which is proportional to the maximum MPS signal intensity (V)] and highest coercivity, H_c. Freezing in the transverse orientation showed the minimum values of ${\chi }_{\text{diff}}^{\text{max}}$ and H_c and the diagonal orientation showed intermediate values.

FIG. 6.

(Color online) MPS (26 kHz, 50 mT/μ₀) signal parameters of MNPs, field frozen (10 mT/μ₀) along different directions with respect to the MPS applied field. (a) χ_diff and (b) integrated m(H) curves. MPS (26 kHz, 50 mT/μ₀) signal parameters of MNPs, frozen in different magnetic fields along parallel orientation: (c) χ_diff and (d) m(H) curves. MPS (50 mT/μ₀, different frequencies) signal parameters of MNPs, frozen in 5 mT/μ₀ along parallel orientation: (e) _diff and (f) m(H) curves.

The magnetic response also varied with the intensity of the freezing field for a given angular orientation. Figures 6(c) and 6(d) show the magnetization response of MNPs frozen in different magnetic fields along parallel orientation. Among the field-freezing data, the smallest freezing field led to the smallest values of ${\chi }_{\text{diff}}^{\text{max}}$ and H_c. All these values increased with increasing freezing fields (Fig. 6), although the variation was relatively small, most probably due to the small range of freezing fields (15 mT/μ₀ maximum) that were achievable with our experimental apparatus. ${\chi }_{\text{diff}}^{\text{max}}$ was the highest at 15 kHz and it decreased slightly as the frequency was increased. Coercivity H_c increased for increasing frequencies.

A summary of immobilized sample behavior is provided in Fig. 7, which plots variation of the peak value of the differential susceptibility ${\chi }_{\text{diff}}^{\text{max}}=dm/dH$ and coercive field, H_c, for various combinations of freezing fields, orientations, and drive frequencies. Parallel freezing gave the highest values for ${\chi }_{\text{diff}}^{\text{max}}$ as well as H_c, whereas transverse freezing showed the smallest values. Diagonal freezing gave intermediate response. For field-frozen samples, ${\chi }_{\text{diff}}^{\text{max}}$ H_c and increased with greater freezing field for parallel and diagonal orientations, but decreased for transverse orientation. However, increasing the freezing field from 10 to 15 mT/μ₀ did not produce a monotonic change in the response. The field-frozen sample response varied with the excitation field frequency [Figs. 6(e) and 6(f)], in agreement with previous investigations [3]. Here drive field frequencies were varied but amplitude was fixed at 50 mT/μ₀. ${\chi }_{\text{diff}}^{\text{max}}$ varied slightly with frequency but with no clear trend, while coercivity increased monotonically with frequency. We note some variation in ${\chi }_{\text{diff}}^{\text{max}}$ could have resulted from undersampling due to the finite sample acquisition rate of our system (2M samples/s), which is exacerbated at higher frequencies.

FIG. 7.

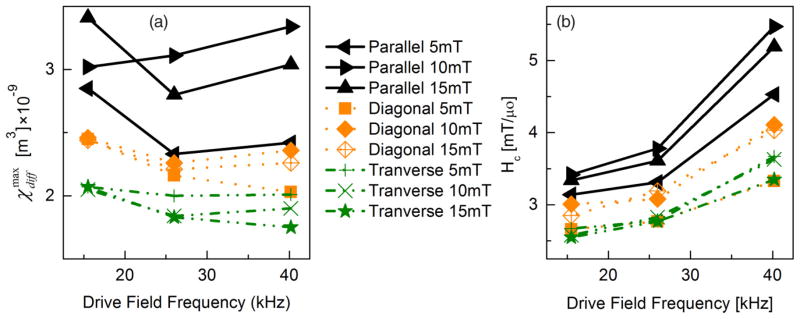
(Color online) Comparison plot of MNPs response for various combinations of freezing fields, orientations, and drive frequencies: (a) ${\chi }_{\text{diff}}^{\text{max}}$ and (b) coercive field.

The MPS response of the liquid sample (dispersed in water) was measured at room temperature and 0 °C. We note the slight variation in magnetic response due to temperature, particularly in the differential susceptibility [Fig. 8(a)]. While the variation is close to the experimental error, the slightly higher value of ${\chi }_{\text{diff}}^{\text{max}}$ and reduced coercive field observed in the warmer sample may be expected in terms of the relaxation dynamics of the particles. When colder, magnetic reversal requires slightly greater energy, and therefore greater applied field, since thermal energy is reduced. These phenomena can be seen in Fig. 8, particularly in the differential susceptibility curve. The MPS responses of water-dispersed and liquid DMSO-dispersed samples were identical (data not shown).

FIG. 8.

(Color online) MPS (26 kHz, 20 mT/μ₀) response of SPIOs in water at room temperature and 0°C (liquid state). Error bars in (a) represent the standard deviation of three measurements.

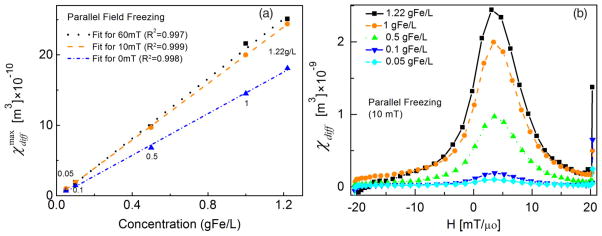
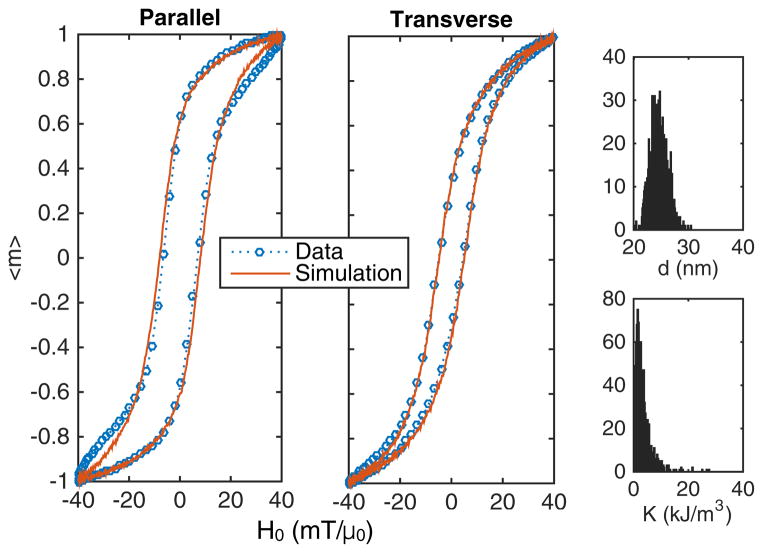
A dilution series was prepared and frozen to observe how the freezing process affected sample magnetization dynamics. MPS analysis showed linear variation of signal intensity with the concentration for all freezing fields, as shown in Fig. 9, but with greater intensity per unit concentration at higher freezing fields. We found good agreement between simulations and experimental results and in particular show that the frozen particles act as if they are partially aligned by the field-freezing procedure. The linear change with concentration indicates that a combination of Brownian alignment and Néel rotations is possible in these particles, and, to first order, the formation of chains can be ruled out. In Fig. 10, we show that the hysteresis loops change dramatically when frozen in the directions parallel to and perpendicular to the oscillating field that is applied. The simulations are identical except for an average reorientation of the easy axes. In each case, we simulate a 50% alignment in the direction of the static field in which the particles were frozen.

FIG. 9.

(Color online) ${\chi }_{\text{diff}}^{\text{max}}$ data (at 26 kHz and 20 mT/μ₀) of different concentrations: (a) at different freezing fields and (b) at 10 mT/μ₀ parallel freezing.

FIG. 10.

(Color online) Comparison between simulation and experiment for nanoparticles that were frozen while exposed to a 10 mT/μ₀ static field aligned parallel or perpendicular to the oscillating field. Then spectroscopy was performed using a 40-kHz, 20 mT/μ₀ field. The log-normal distributions of particle diameter and anisotropy constant are shown on the right by number in a representative 1000-particle subsample.

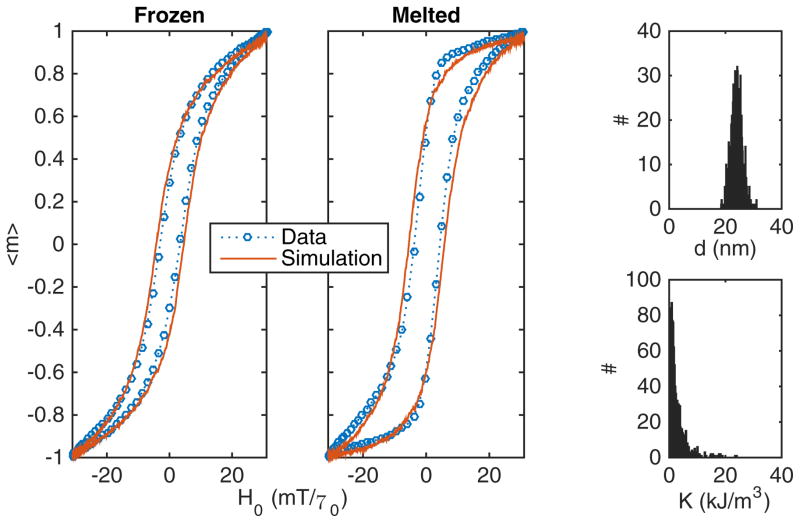
In Fig. 11 we show that the simulated hysteresis loops are quite different based on the phase of the suspending liquid, an effect much beyond simply changing the temperature, that has been previously studied in cobalt nanoparticle solutions [33]. In particular, the melted sample shows an increase in the amount of saturation. This indicates potentially that the easy axes become slightly polarized in the direction of the oscillating field due to Brownian rotation. In this simulation, we account for partial (30%) alignment to the field. In the frozen sample, however, the Brownian rotations should be restricted, and the fit is the most accurate without any alignment.

FIG. 11.

(Color online) Comparison between simulation and experiment for nanoparticles either in either a frozen or melted state. Spectroscopy was performed with a 26-kHz, 31 mT/μ₀ field. The log-normal distributions of particle diameter and anisotropy constant are shown on the right by number in a representative 1000-particle subsample.

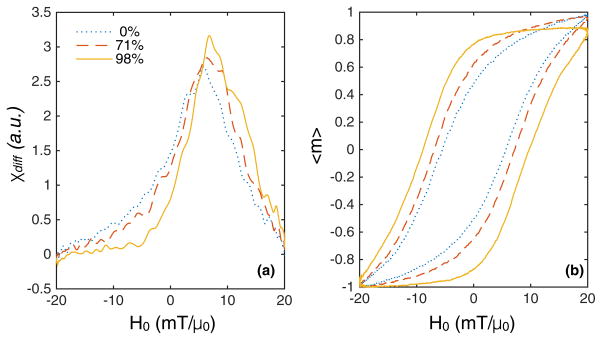
To show that increasing the strength of the applied static field affects the simulations in a similar way to the experiment, we simulated the hysteresis loops and the susceptibility of the magnetization at various applied field strengths, leading to various alignment percentages (Fig. 12). As the Brownian alignment increased, we saw the expected increase in the slope of the hysteresis as well as the delay in the peak of the slope caused by the anisotropy field parallel to the applied field. The susceptibility data were smoothed using a Gaussian window to avoid the artifacts that arise from taking a numerical derivative.

FIG. 12.

(Color online) Magnetizations were simulated using a 40-kHz, 20 mT/μ₀ field at room temperature to show how the (a) differential magnetic susceptibility in arbitrary units χ_diff (arb. units) and (b) hysteresis loops are affected by increasing the percentage of particles aligned in the direction of the applied field. The size and anisotropy distribution are identical to that in other simulations.

IV. DISCUSSION

The most significant result of this work was the observed difference in response between immobilized and liquid samples, indicating that both Néel relaxation and Brownian alignment mechanisms are possible in the liquid sample. In fact, for these particles, if the relaxation times are computed using the standard zero-field expressions for Néel and Brownian relaxation, they are of the same order of magnitude. Admittedly, these expressions are inappropriate to describe the dynamic response of particles forced to oscillate in a magnetic field, but if the relaxation times were many orders of magnitude different an adiabatic approximation would be reasonably made to ignore the slower mechanism [34]. Though both mechanisms seem to occur, the Néel mechanism appears to dominate, because a significant response can be measured from immobilized samples in which Brownian rotation should be quenched.

We hypothesized that variation between liquid and immobilized samples could result from significant magnetic anisotropy in the nanoparticles. To investigate our hypothesis, we immobilized the SPIOs in DMSO, since the DMSO-nanoparticle suspension could be reproducibly frozen and melted to orient and reorient the nanoparticles. Furthermore, DMSO stabilized the nanoparticles in solution and solid phases, with the nanoparticles displaying behaviors consistent with noninteracting particles (see Fig. 9 for the linear increase in magnetization with concentration).

To complement the experimental results, we simulated the dynamic particle magnetizations using a model based on the stochastic Landau-Lifshitz-Gilbert equation [20]. From the modeling, we saw almost identical magnetizations when the easy axes were partially aligned and a log-normal size distribution for the particle sizes, and effective uniaxial anisotropy constant was included. We interpret the agreement with the effective uniaxial simulations to mean that an initial Brownian alignment causes one of the easy cubic axes to align with an applied static field, at which point the particles are frozen and fixed spatially. Subsequent Néel rotations depend on the direction of the alignment. The distribution of the anisotropy constant allows for several possible contributions to the anisotropy, and the form of the anisotropy energy depends on the constant and simply how much the magnetization is aligned with the effective easy axis.

The parallel field-freezing alignment leads to higher slopes in the hysteresis curves (higher differential susceptibility χ_diff ) and wider hysteresis loops (larger coercive fields H_c) than the diagonally or perpendicularly aligned particles. This behavior can be conceptualized by imagining a two-state system where the energy barrier to magnetization reversal is the highest when the magnetic field is aligned with the easy axis as in the parallel case.

The result that the fluid samples displayed steeper hysteresis curves is potentially more surprising and can be interpreted with simultaneous combinations of the Néel and Brown dynamics. It is possible to imagine that because the rotational timescales are comparable, the oscillating field might induce alignment of one of the easy crystalline axes. This effect is not extreme—the simulations only needed 30% alignment in some cases—but it is absolutely noticeable in the data [see, for example, Figs. 6(a) and 7].

The origin of the anisotropy is not fully clear. Magne-tocrystalline anisotropy is expected for these particles and may be sufficient to explain the observed behavior, but only true simultaneous in situ experiments such as high-resolution electron microscopy of liquid samples under applied fields could rule out the possibility of chaining. Moreover, it is hard to quantify the shape anisotropy of the particles from TEM imaging, though in the data of Fig. 2 it is clear they are quite monodisperse and any elongation is minor. Notwithstanding the fact that a TEM image renders a two-dimensional projection of a three-dimensional nanoparticle, a rough estimate of shape anisotropy of the particles was measured from TEM images using IMAGEJ. Each particle measured for size determination was fit with an ellipse and the ratio of the long axis to the short axis determined. The resulting histogram was fit with a log-normal distribution to determine the median aspect ratio (1.04 ± 0.03). This equates to a typical elongation of approximately 1 nm for the 26-nm-diam particles. We can estimate the anisotropy energy due to this minor elongation by considering the particles to be prolate ellipsoids of revolution with axes a,b,c, where a > b = c. In this case, the critical field for switching due to shape anisotropy is H_k = M_s(N_b − N_a) [35], where M_s is the saturation magnetization (263 kA/m), and N_a and N_b are the demagnetization factors along the a and b directions, respectively. For the measured aspect ratio of 1.04 ± 0.03, H_k is about 5.2 mT/μ₀. For magnetocrystalline energy H_k would be expected of the order K/M_s, or 13 mT/μ₀, assuming K = 3.4 kJ/m³; specifically, H_k = 4K/3M_s for cubic systems, H_k = 2K/M_s for uniaxial systems when the field is aligned antiparallel to the moment, and H_k = K/M_s for uniaxial systems when the field is aligned perpendicular to the moment, with the moment always assumed initially to be directed along an easy axis [36]. Since the magnetocrystalline anisotropy energy is greater, it should dominate in this sample, but shape anisotropy may contribute a slight uniaxial character. The magnetocrystalline and shape anisotropies would be similar with approximately 1.1 average particle aspect ratio.

In addition to alignment of individual particles, chain formation can be thought of as contributing to the effective anisotropy. Saville et al. showed that magnetite particles coated with 20-kDa PEG (with M_s = 264 kA/m, core diameter of 24 nm, and hydrodynamic diameter of 170 nm) formed chains averaging 3 μm long were observed after applying a steady field of 270 mT/μ₀ for 30 s [37]. Chain formation may have occurred during the field-freezing experiments reported here, although it is less likely to have affected the MPS of liquid samples, since only weak oscillating fields were applied and our MPS has a 50% duty cycle (the field is switched off for 0.5 s every 1 s).

The magnetically optimized, monodisperse SPIOs used in this study showed highly nonlinear behavior, producing a sharp magnetization response useful for sensing and imaging applications that use magnetic induction, such as MPI. With uniformly sized magnetic cores and well-defined hydrodynamic size, the samples were also ideal for studies of how particle behavior responds to variations in the drive field, since variations in response can be assumed to come from uniform changes in the response of each particle, rather than from multiple fractions of varying size, as in clustered-core particles like Resovist.

V. CONCLUSIONS

This work arose from the observation that immobilized (frozen) SPIOs displayed distinctly different rotational dynamics than the same particles in a liquid state. This phenomenon was well beyond the respective change in the relaxation time purely due to the temperature. It was previously expected that the particles would reorient their magnetic moment internally, with the Néel mechanism, and thus the local environment (e.g., the phase of the solution) should have had no impact. The large change in the dynamics is equivalent to an effective uniaxial anisotropy that could be due to small chain formations or local reorientation of the particles themselves. For spherical nanoparticles with cubic symmetry, only a slight physical rotation, referred to here as Brownian alignment, is required to align one of the magnetocrystalline easy axes along the applied field direction. The dynamics of the particles in a randomly frozen state were still different from the liquid-state dynamics. This indicates that even while Néel oscillations occur, a general alignment through Brownian rotation is possible in the liquid sample. All of these dynamical behaviors could be replicated using Langevin equation simulations. The partial alignment of the easy axes could be incorporated into the model through the effective field of the Landau-Lifshitz-Gilbert equation. We also found that while the magnetic particles are predicted to have cubic anisotropy, a single effective axis with a large distribution over the anisotropy constant is adequate to account for the observable dynamical effects.

In the future, it appears wise to specifically characterize any magnetic particles used in dynamical applications, as typical equilibrium calculations of relaxation times alone are inadequate predictors of rotational mechanisms. We have demonstrated that an initial Brownian alignment, leading to an effective uniaxial anisotropy, plays an important role for magnetic nanoparticles conventionally thought to only rotate with the Néel mechanism. This result has far-reaching implications for emerging biomedical technologies such as MPI.