Abstract
Background
Hospital report cards, in which outcomes following the provision of medical or surgical care are compared across health care providers, are being published with increasing frequency. Essential to the production of these reports is risk-adjustment, which allows investigators to account for differences in the distribution of patient illness severity across different hospitals. Logistic regression models are frequently used for risk-adjustment in hospital report cards. Many applied researchers use the c-statistic (equivalent to the area under the receiver operating characteristic curve) of the logistic regression model as a measure of the credibility and accuracy of hospital report cards.
Objectives
To determine the relationship between the c-statistic of a risk-adjustment model and the accuracy of hospital report cards.
Research Design
Monte Carlo simulations were used to examine this issue. We examined the influence of three factors on the accuracy of hospital report cards: the c-statistic of the logistic regression model used for risk-adjustment, the number of hospitals, and the number of patients treated at each hospital. The parameters used to generate the simulated datasets came from analyses of patients hospitalized with a diagnosis of acute myocardial infarction in Ontario, Canada.
Results
The c-statistic of the risk-adjustment model had, at most, a very modest impact on the accuracy of hospital report cards, whereas the number of patients treated at each hospital had a much greater impact.
Conclusions
The c-statistic of a risk-adjustment model should not be used to assess the accuracy of a hospital report card.
Keywords: Hospital report cards, risk-adjustment, c-statistic, logistic regression, Monte Carlo simulations
1. Introduction
Cardiovascular report cards have been released comparing patient outcomes between different health care providers for medical conditions (e.g. acute myocardial infarction or AMI) and for cardiovascular procedures (e.g. coronary artery bypass graft or CABG surgery). California [1], Pennsylvania [2], Scotland [3], and Ontario, Canada [4] have released hospital-specific reports for mortality following admission for AMI. Massachusetts [5], New Jersey [6], New York [7], and Pennsylvania [8], have published hospital and surgeon-specific mortality rates following CABG surgery, while Ontario has published hospital-specific mortality rates [9].
A vital component of comparing outcomes across different providers of medical and surgical care is statistical risk-adjustment [10,11]. Risk-adjustment models allow researchers to account for differences in the distribution of patient characteristics and risk factors between different health care providers, so that providers that care for more acutely ill patients are not unfairly penalized. Since hospital report cards frequently focus on short-term mortality, the logistic regression model is the most commonly used method for risk-adjustment in cardiovascular report cards. The predictive accuracy of a logistic regression model is frequently assessed using the c-statistic (equivalent to the area under the receiver operating characteristic (ROC) curve, which can be abbreviated as the AUC), which is a measure of model discrimination [12–14]. If the outcome is short-term mortality, then the c-statistic can be interpreted as the probability that a randomly selected subject who died will have a higher predicted probability of dying compared to a randomly selected subject who did not die.
The development and implementation of risk-adjustment methods for the purposes of hospital profiling is highly complex [15–17]. A common criticism of hospital report cards is that inadequate risk-adjustment was conducted [18]. Critics argue that statistical methods were insufficient to fully account for differences in the distribution of patient characteristics and risk factors across health care providers. The statistical evaluation of a risk-adjustment model to determine its accuracy and appropriateness for hospital profiling is complex and can involve a number of different metrics including discrimination (i.e., c-statistic), goodness-of-fit or calibration, residual plots, R2 or AIC measures, and cross-validation [15].
Iezzoni has stated that “no consensus exists about the most appropriate performance measure for models predicting a dichotomous outcome. Nevertheless, most agree that the c-statistic, one measure of performance, should be reported” [10] (page 432). Our subjective assessment is that the credibility of individual hospital report cards is often condensed into a single measure - the c-statistic. Hospital report cards that employ logistic regression models with higher c-statistics may be perceived as being more accurate than are hospital report cards that use logistic regression models with lower c-statistics. For instance, one study concluded that regression models that incorporated stroke severity (i.e., National Institute of Health Stroke Scale [NIHSS]) were preferable for profiling hospital performance for acute ischemic stroke based on the increase in the c-statistic due to the inclusion of this variable [19]. A second study used changes in the c-statistic to make conclusions about the value of enhancing administrative claims data with information on which conditions were present on admission and with laboratory values to improve risk-adjustment of hospital mortality [20]. A third study, in the context of provider profiling, used the change in the c-statistic to examine the incremental utility of including clinical data to regression models based on administrative data [21]. However, the link between the c-statistic of the risk-adjustment model and the accuracy of hospital report cards has not been formally examined. Moreover, other characteristics of the data used in hospital profiling – such as the number of hospitals or the number of patients treated at each hospital may be of equal or greater importance [22,23].
The objective of the current paper is to examine the relationship between the c-statistic of the logistic regression model used for risk-adjustment and the accuracy of hospital report cards. We used an extensive series of Monte Carlo simulations to examine the issue. In order to increase the face-validity of our simulations, the parameters of the Monte Carlo simulations were based on analysis of hospitalized AMI patients in Ontario, Canada.
2. Methods
In this section we describe an extensive set of Monte Carlo simulations that were used to examine the effect of the c-statistic of the regression model used for risk-adjustment, the number of hospitals, and the number of patients treated at each hospital on the accuracy of hospital report cards. As in prior studies of the accuracy of different methods for provider profiling [24–27], Monte Carlo simulations were used because it is only in simulated data that the true performance of each hospital is truly known. These analyses cannot be conducted using real data since, in real data, the true performance of each hospital is not truly known. Parameters for the Monte Carlo simulations were obtained from analyses conducted in a dataset consisting of all patients hospitalized with a diagnosis of AMI in the Canadian province of Ontario.
2.1 Data sources
The Ontario Myocardial Infarction Database (OMID) is an electronic administrative health care database that contains information on all patients hospitalized in Ontario with a diagnosis of AMI between April 1, 1992 and March 31, 2011. Details on its creation are provided in greater detail elsewhere [28]. For the current study, we used data on 31,183 hospital separations (i.e. patients who were discharged alive or who died in hospital) that occurred between April 1, 2008 and March 31, 2010 from 159 acute care hospitals in the province. Of these patients, 3,469 (11.1%) died within 30 days of hospital admission (both in-hospital and out-of-hospital deaths were captured).
2.2 Parameters for the Monte Carlo simulations
We conducted a series of analyses of the data described in Section 2.1 to generate parameters for our Monte Carlo simulations. By using this approach, we would be able to simulate data similar to that observed in a recent population of AMI patients treated by Ontario hospitals. To do so, we needed to determine the following information: a risk-score determining a patient’s risk of death, the distribution of this risk-score across the population of AMI patients in Ontario (including both the between-hospital variation and the within-hospital variation of this risk-score; thereby allowing systematic differences in case-mix across hospitals), and the variation in patient outcomes across hospitals in Ontario.
The Ontario AMI mortality prediction model, which predicts both short- and long-term mortality following hospitalization with an AMI, was developed and validated using patients from OMID in an earlier period [29]. The prediction model consists of 11 variables that are captured in electronic health administrative data: age, sex, cardiac severity (congestive heart failure, cardiogenic shock, arrhythmia, and pulmonary edema), and comorbid status (diabetes mellitus with complications, stroke, acute and chronic renal disease, and malignancy). These variables are derived from the secondary diagnostic fields of the hospitalization database. The Ontario electronic discharge abstract databases permit one to distinguish between diagnoses present at the time of hospital presentation and those that arose subsequent to hospital admission (e.g. in-hospital complications). Only diagnoses coded as pre-admit diagnoses were used for defining the presence or absence of the above conditions. In its initial derivation and validation it had a c-statistic of 0.78 for predicting 30-day mortality in Ontario. It was subsequently validated in both Manitoba, Canada and in California, USA, with c-statistics of 0.77 in both of these jurisdictions [29].
In the AMI dataset, we used this logistic regression model to regress the occurrence of death within 30-days of hospital admission on the 11 variables. For each patient, we standardized the linear predictor (the log-odds of the predicted probability of 30-day mortality) for use as a risk-score, so that it would have mean zero and unit variance. Thus, the standardized linear predictor served as a risk-score in our empirical analyses.
We used a variance components model to decompose the total observed variability in the risk-score into between-hospital variation and within-hospital variation. In doing so, we explicitly modeled the systematic difference in case-mix between hospitals. The following variance components model was fit to the data: xij ~ μj +εij, where xij denotes the risk-score for the ith patient treated at the jth hospital, μj denotes the hospital-specific component of the risk-score for patients treated at the jth hospital, and εij denotes the patient-specific deviation from the hospital-specific component. The estimated variance component model was: μj ~ N(0, σ2 = 0.03695) and εij ~ N(0,σ2 = 0.96359). Thus, only 3.7% of the variation in the patient-specific risk score was due to systematic variation in the risk-score between hospitals (i.e. systematic differences in case-mix between hospitals), while the remaining 96.3% was due to variation between patients.
We then fit the following random effects (or hierarchical) logistic regression model to the Ontario AMI data:logit(pij) =α0j + βxij, where pij denotes the probability of 30-day mortality for the ith patient treated at the jth hospital, xij denotes the standardized risk-score for this patient, and α0j denotes the hospital-specific random effect for the jth hospital. The following estimates were obtained: α0 j ~ N(−2.5144, σ2 = 0.05276) and β = 1.1618. Since the risk-score was standardized to have mean zero, the hospital-specific random effect indicates the log-odds of 30-day mortality at a given hospital for a patient whose risk-score is equal to zero (i.e. a patient of average risk). From the estimated distribution of the random effects, the probability of 30-day mortality for an average patient treated at an average hospital was 0.075. Ninety-five percent of hospitals will have a probability of 30-day mortality for an average patient that lies between 0.049 and 0.113. A regression coefficient of 1.1618 for the risk-score indicates that a one standard deviation increase in the risk-score is associated with a 3.2 relative increase in the odds of 30-day mortality.
We used these parameters (the within- and between-hospital variation in the patient risk-score, β, and the mean and variance of the distribution of hospital-specific random effects) in the following Monte Carlo simulations. By doing so, we will simulate synthetic datasets in which the distribution of patient risk is similar to that observed in Ontario. In particular, systematic differences in case-mix between hospitals will be similar to those observed in Ontario. Furthermore, the variation in hospital performance will also be similar to that observed in Ontario. In doing so, we increase the face-validity of our simulations, since the simulated datasets will be similar to those of hospitalized AMI patients in a jurisdiction in which AMI report cards have been produced in the past. The design of these Monte Carlo simulations can be seen as a template for studying the accuracy of hospital report cards in other jurisdictions and for other medical conditions or for other surgical procedures.
2.3 Monte Carlo simulations
We simulated synthetic datasets, each consisting of Npatients patients admitted to each of Nhospital hospitals. Thus, each simulated dataset consisted of N = Npatients × Nhospitals patients. We first simulated a risk-score for each of the N patients. To do so, we simulated a hospital-specific component: μj ~ N(0,σ2 = 0.037) for each of the Nhospitals hospitals, and a patient-specific component for each of the N patients: εij ~ N(0,σ2 = 0.963). The patient risk-score for the ith patient at the jth hospital was set equal to xij = μj +εij. By using this approach, we randomly generated a continuous risk-score for each patient so that the distribution of patient risk was similar to that observed in AMI patients in Ontario. Furthermore, with an intraclass correlation coefficient of 0.037, the systematic difference in case-mix between hospitals in the simulated data will be similar to that observed in Ontario.
We then generated a hospital-specific random effect for 30-day mortality for each of the Nhospital hospitals: α0j ~ N(0, σ2 =0.05276). This random effect will be used to define each hospital’s true performance. Patients admitted to hospitals with higher random effects have an increased risk of 30-day mortality compared to comparable patients admitted to hospitals with lower random effects. The simulated hospital-specific random effect will serve as each hospital’s gold standard: the true performance of that hospital. By using Monte Carlo simulations, the true performance of each hospital is known, since we know the true α0j for each hospital, and the definition of quality of care is based on this known quantity. In contrast, when using actual data, the true performance of each hospital is not known.
Finally, we generated an outcome for each subject in the simulated dataset. For each of the synthetic subjects in the simulated dataset, the probability of death within 30-days of admission was equal to: logit(pij ) = −2.514+α0j +βxij, where α0j is the randomly generated hospital-specific random effect, xij is the randomly generated patient risk-score (the average intercept was set equal to -2.514 because that was the mean of the distribution of the hospital-specific random intercepts in Section 2.2). A dichotomous outcome was randomly generated for each subject in the synthetic dataset from a Bernoulli distribution with subject-specific parameter pij. Thus, we have simulated a risk-score and an outcome for each subject. The within- and between-hospital variation in this risk-score is similar to that observed in Ontario, and the between-hospital variation in outcomes is also similar to that observed in Ontario.
Under the assumption of binormality of a predictor variable (i.e. the variable is normally distributed in those with the condition and in those without the condition), the c-statistic is a function of the variance of the predictor variable in those with and without the condition and the odds ratio relating the predictor variable to the outcome [30]. However, the formula relating these quantities to the c-statistic has been shown to approximate the c-statistic when the predictor variable is normally distributed in the overall population [30]. In our simulations, the subject-specific risk-score has a variation that is fixed by the study design. By varying β (the regression coefficient relating the simulated risk-score to the outcome in the data-generating process), we can allow the c-statistic of the underlying risk-adjustment model to vary.
We allowed three factors to vary in our Monte Carlo simulations. We allowed β to vary in from 0.1 to 2.5 in increments of 0.1. In doing so, we allowed the empirical c-statistic to vary from approximately 0.53 to 0.96 [30]. We allowed each of Nhospitals and Npatients to take on the values of 50, 100, and 200. Our Monte Carlo simulations used a full factorial design. We thus considered 225 (25 values of β × 3 values of Nhospitals × 3 values of Npatients). In each of these 225 scenarios, we simulated 500 random datasets. It is important to note that none of the simulated datasets consisted of actual AMI patients. The original sample of AMI patients was only used to estimate parameters for use in the Monte Carlo simulations.
The above set of simulations created synthetic datasets in which the intraclass correlation coefficient for the patient risk-score was 0.037. In doing so, the systematic between-hospital variation in case-mix reflect that observed in Ontario. To examine the effect of this between-hospital variation in case-mix on our results, we repeated the above simulations with an intraclass correlation coefficient of 0.10. In doing so, we simulated datasets in which there was very strong between-hospital variation in patient case-mix.
2.3 Statistical methods for hospital profiling
Within each of the simulated datasets, we used two different statistical methods to assess hospital performance. First, we used model-based indirect standardization to compute ratios of observed-to-expected mortality. Second, we used hierarchical logistic regression models to compute ratios of predicted-to-expected mortality. These methods are described in greater detail in the subsequent two paragraphs.
Model-based indirect standardization is commonly used in cardiovascular hospital report cards [10,15]. A conventional logistic regression model was fit to each simulated dataset, in which the dichotomous outcome for each subject was regressed on each subject’s risk-score. The c-statistic of the fitted model was determined. We refer to this as the empirical c-statistic of the fitted risk-adjustment model. Using the estimated logistic regression model, the predicted probability of the outcome was determined for each subject in the synthetic dataset. These predicted probabilities were summed up within each hospital to determine the expected number of deaths within that hospital based on its case-mix. The observed number of deaths at each hospital was divided by the expected number of deaths at that hospital based on its case-mix. We refer to the resultant ratio as the O-E (observed-to-expected) ratio.
The predicted-expected (P-E) ratio is a modification of the above-approach [15,31]. A random intercept logistic regression model is used to model the relationship between the patient-specific risk-score and patient outcomes. The model includes a hospital-specific random effect. Using the fitted logistic regression model (including the hospital-specific random effects), the predicted probability of the occurrence of the outcome is estimated for each patient. These predicted probabilities are summed up within each hospital to obtain the predicted number of deaths at each hospital based on its case-mix. The hospital-specific random effects (or deviations from the average intercept) are then set to zero. Using this modified model predicted probabilities of the occurrence of the outcome are obtained for each subject. These predicted probabilities are summed up within each hospital to obtain the expected number of deaths at each hospital. This is the expected number of deaths at the given hospital, based on the case-mix of its patients, if the hospital had the same performance as an average hospital (note that this expected number of deaths could differ from that used when calculating the O-E ratio, since it is based on a modification of a different regression model). The ratio of these two quantities is the P-E ratio.
In each of the 500 simulated datasets for a specific scenario, we determined the correlation of each of the O-E and the P-E ratio with the hospital-specific random effects (α0j) that were used as the gold-standard of hospital performance using the Spearman rank correlation coefficient. The mean correlation coefficient was determined across the 500 simulated datasets. A higher correlation indicates greater concordance (or accuracy) between the estimated hospital performance (i.e. O-E or P-E ratio) and the true hospital performance (i.e. α0j).
As is also commonly done in hospital profiling reports, we also classified hospitals into performance categories. In each of the 500 simulated datasets, we used the true hospital-specific random effects (α0j), which were simulated during the data-generating process, to categorize hospitals into the top 20% of hospitals, the middle 60% of hospitals, and the bottom 20% of hospitals. In each simulated dataset, we also classified hospitals into categories according to their estimated performance using both the O-E ratio and the P-E ratio. As with the gold-standard (α0j), we divided hospitals into the top 20%, the middle 60%, and the bottom 20% of hospitals based on the hospitals’ O-E and P-E ratios. In each of the 500 simulated datasets, we determined the proportion of hospitals that were correctly classified (i.e. we determined the proportion of the Nhospital hospitals, that had been correctly classified: those that were truly in the top 20% and were classified as being in the top 20%, those that were truly in the middle 60% and were classified as being in the middle 60%, and those that were truly in the bottom 20% and were classified as being in the bottom 20%). The estimated proportions were averaged across the 500 simulated datasets for each of the 225 scenarios.
The statistical simulations were conducted using the R statistical programming language (version 2.11.1: R Foundation for Statistical Computing, Vienna, Austria). The conventional logistic regression model was fit using the glm function, while the random effects logistic regression model was fit using the glmer function in the lme4 package, as this has been shown to perform well for estimating random effects models [32]. The c-statistic was computed using the roc.area.test function in the clinfun package for R.
3. Results
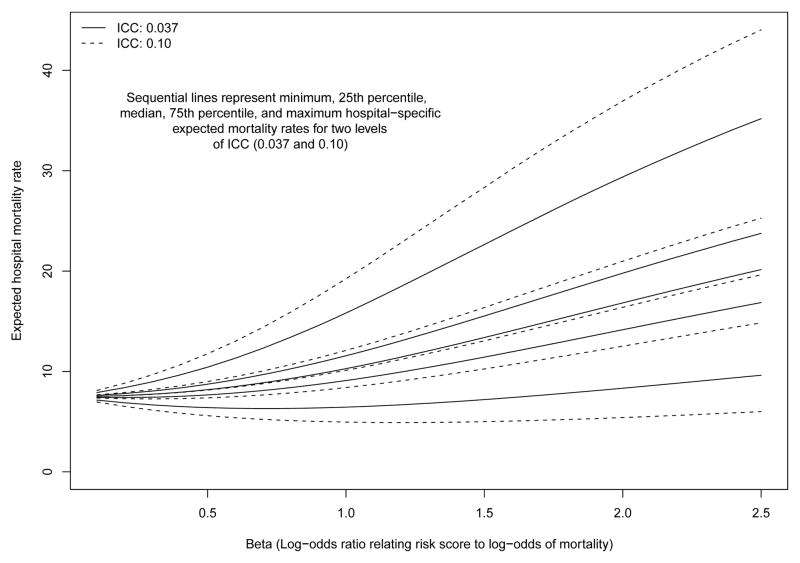
The relationship between β (the regression coefficient relating the risk-score to the log-odds of the outcome) and between-hospital variation in the expected probability of the outcome in a setting in which there was no between-hospital variation in performance (i.e. if the random effects were set to have zero variance) and with 100 hospitals and 100 patients per hospital is described in Figure 1. It is important to note this figure describes between-hospital variation in the crude or unadjusted outcome. For each of the two ICC settings (ICC = 0.037 and ICC = 0.10), we report the minimum, 25th percentile, median, 75th percentile, and maximum hospital-specific expected probability of the outcome. As β increased (i.e. the magnitude of the effect of the risk score on the outcome increased), the between-hospital variation in the expected probability of the outcome increased. Furthermore, when the ICC was higher (i.e. greater between-hospital variation in case-mix), then there was greater between-hospital variation in expected outcomes than when the ICC was lower (as demonstrated in Figure 1 by the more extreme minimum and maximum values for ICC = 0.10 compared to ICC = 0.037).
Figure 1.
Relationship between the magnitude of the effect of the risk score on mortality and between−hospital variation in expected 30−day mortality rates
For a given value of the ICC, the differences in the distribution of the expected hospital-specific mortality rate described by the lines of the graph reflect differences in case-mix across hospitals. These lines were generated in a setting in which there were no differences in hospital-performance: all differences in outcomes between hospital were solely due to differences in case-mix and random variation.
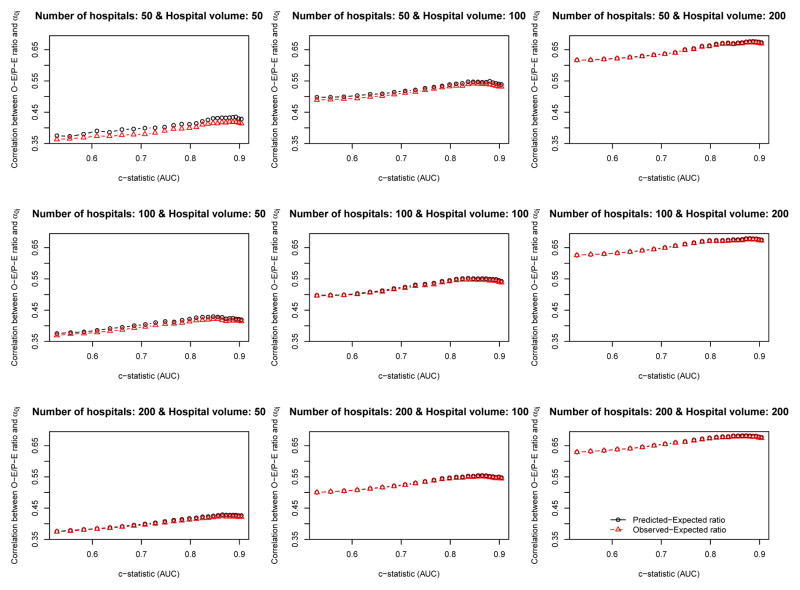
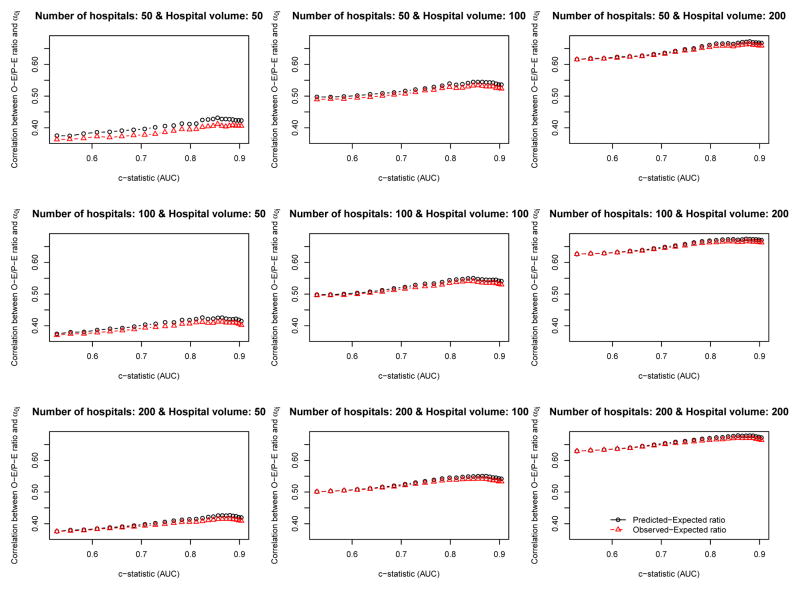
The relationship between the empirical c-statistic of the risk-adjustment model and the correlation of the O-E ratio and the P-E ratio with the hospital-specific random effect (the gold standard of hospital performance) is described in Figures 2 (ICC = 0.037) and 3 (ICC = 0.10). There are nine panels in each of these figures: one for each of the scenarios defined by different combinations of the number of hospitals (n= 50, 100, and 200) and the number of patients per hospital (n= 50, 100, and 200). Several observations bear comment. First, the empirical c-statistic of the risk-adjustment model had, at most, only a modest impact on the accuracy the O-E and PE ratios: the accuracy of the O-E and P-E ratios increased only very gradually with increasing c-statistic. It should be noted that the c-statistic varies from approximately 0.5 to approximately 0.95, which covers the full range of model performance that are plausibly encountered in real-world settings. Second, the number of subjects per hospital had a strong impact on the accuracy of the O-E and P-E ratios. The effect of hospital volume had a much greater effect on accuracy than did the empirical c-statistic of the risk-adjustment model. Third, the number of hospitals had no appreciable impact on the accuracy of the O-E and P-E ratios. Fourth, in most of the nine scenarios defined by the different combinations of hospital volume and number of hospitals, O-E ratios and P-E ratios had approximately similar accuracy. When both the number of hospitals and the hospital volume were low, then the P-E ratio was slightly more accurate than the O-E ratio. However, there were no qualitatively important differences between the two approaches. Fifth, the relationship between the c-statistic and the accuracy of hospital report cards was very similar between the setting with typical ICC (0.037) (Figure 2) and the setting with a high ICC (0.10) (Figure 3).
Figure 2.
Relationship between AUC and the correlation between the O−E/P−E ratio and the hospital−specific random effect (ICI = 0.037)
Figure 3.
Relationship between AUC and the correlation between the O−E/P−E ratio and the hospital−specific random effect (ICC = 0.10)
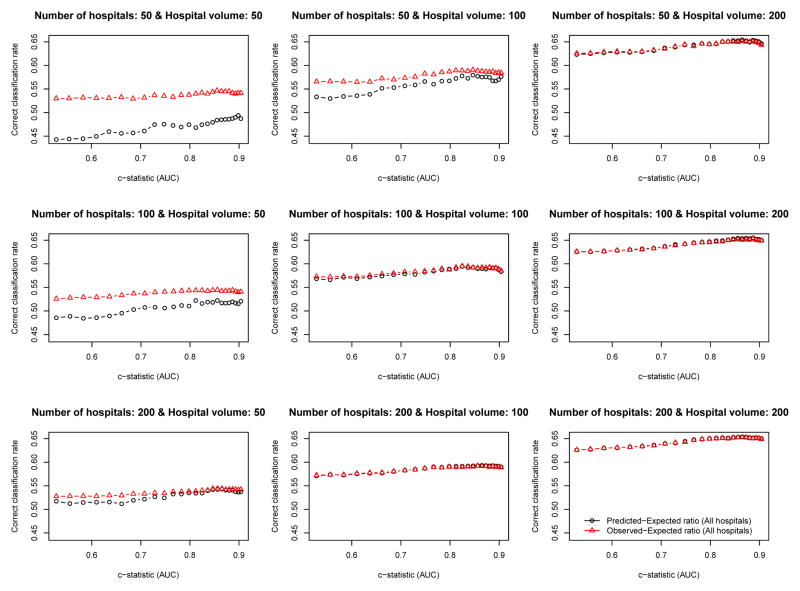
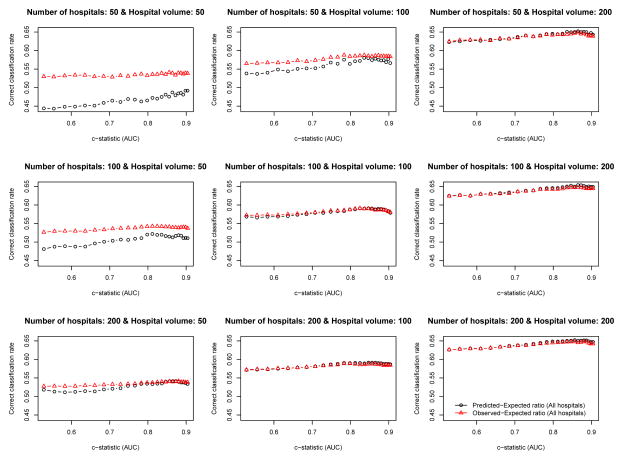
The relationship between the empirical c-statistic of the risk-adjustment model and the proportion of hospitals that were correctly classified is described in Figures 4 (ICC = 0.037) and 5 (ICC = 0.10). There are nine panels for each figure: one for each of the scenarios defined by different combinations of the number of hospitals and the number of patients per hospital. Several observations merit comment. First, the empirical c-statistic of the risk-adjustment model had at most a modest impact on the proportion of hospitals correctly classified. Second, the proportion of hospitals that were correctly classified increased as the number of patients per hospital increased. Third, as the total number of patients increased, the differences between the accuracy of the O-E and the P-E ratios diminished. Fourth, the results were very similar between setting with moderate ICC (0.037) (Figure 4) and the setting with high ICC (0.10) (Figure 5).
Figure 4.
Relationship between the c−statistic and percentage of hospitals correctly classified (ICC = 0.037)
Figure 5.
Relationship between the c−statistic and percentage of hospitals correctly classified (ICC = 0.10)
4. Discussion
We used an extensive series of Monte Carlo simulations to examine the relationship between the c-statistic of a logistic regression model used for risk-adjustment and the accuracy of hospital report cards. The parameters of our Monte Carlo simulations were based on an analysis of hospitalized AMI patients in Ontario, Canada so that the synthetic datasets created in the Monte Carlo simulations would be similar to those of a population-based sample of AMI patients in a jurisdiction in which AMI report cards have been publicly released. The design of our Monte Carlo simulations provides a template for studying the accuracy of hospital report cards in other jurisdictions and for other clinical conditions or surgical procedures. Our primary finding was that there was, at best, only a modest relationship between the c-statistic of the risk-adjustment model and the accuracy of hospital report cards. Instead, we found that the factor that most influenced the accuracy of hospital report cards was the number of subjects included per hospital: increasing patient-volume was associated with increased accuracy.
Prior studies have demonstrated that even if perfect risk-adjustment was possible, random error will result in some hospitals being misclassified [24,27]. Furthermore, the likelihood of misclassification increases as the number of patients treated at each hospital decreases. These studies have not examined the effect of varying the predictive accuracy of the risk-adjustment model. Instead, these studies have examined the ability of report cards to correctly classify hospital performance in specific settings. The current study builds on these earlier studies by allowing the predictive accuracy of the risk-adjustment model to vary. In doing so, we found that the predictive accuracy of the risk-adjustment model had, at best, a modest impact on the accuracy of hospital report cards.
The results of the current study may come as a surprise to many health services researchers and to those involved in the production and dissemination of hospital report cards. To many researchers and practitioners, it may be counterintuitive that the c-statistic of the risk-adjustment model would have a minimal impact on the accuracy of hospital profiling. However, this apparently counterintuitive finding is due to a fundamental misunderstanding as to the meaning and interpretation of the c-statistic. If a predictor variable has a normal distribution in those with the outcome and in those without the outcome, as well as the same standard deviation (σ) in each of those two groups, then the c-statistic is equal to , where β is the log-odds ratio relating the predictor variable to the outcome and Φ denotes the cumulative normal distribution function [30]. Thus, the c-statistic is a function only of the variance of the predictor variable and the strength of its association with the outcome. Greater discrimination (i.e. a higher c-statistic) is possible only when the predictor variable displays greater variation or when the predictor variable is more strongly associated with the outcome. The above formula was found to relatively accurately approximate the c-statistic in settings in which the predictor variable had a normal distribution in the combined sample of those with and without the outcome. A consequence of the above formula is that the c-statistic will be higher in a population in which there is greater heterogeneity in risk; conversely, the c-statistic will be lower in populations in which there is less heterogeneity in risk. It would appear that many applied researchers want to interpret the c-statistic as a measure of whether the risk-adjustment model has been correctly specified. However, that is not the case. It is solely a measure of discrimination or separation: the degree to which the model can discriminate between those with the outcome of interest and those without the outcome of interest. In all of our Monte Carlo simulations, the fitted risk-adjustment model was identical to the model used in the data-generating process. Thus, all our risk-adjustment models were correctly specified: they included all variables related to the outcome and the functional form of the model was correctly specified. The risk-adjustment models only differed in their discrimination (by virtue of allowing the log-odds ratio β to vary across scenarios).
The primary conclusion of the current study is that the credibility and accuracy of published hospital report cards cannot be assessed solely using the c-statistic of the logistic regression model used for risk-adjustment. Instead, careful attention must be paid to the specification of the risk-adjustment model. Clinical expertise must be used to develop sets of prognostically important variables for the clinical condition (e.g. AMI) or procedure (e.g. CABG surgery or percutaneous coronary intervention). The credibility of the published study should rest, in part, on the study authors having included the required variables in the risk-adjustment model. If prognostically variables have been omitted from the risk-adjustment (e.g. for reasons due to availability of data), readers need to assess the evidence that the distribution of the omitted risk-factor differs across the patients cared for by different health care providers.
Finally, once the important set of prognostically important covariates has been identified, care must be taken in specifying the functional form of the risk-adjustment model. In particular, investigators are encouraged to carefully consider how continuous covariates are used in the risk-adjustment model. Use of methods to allow for non-linear relationships between covariates and the outcome, such as restricted cubic splines, generalized additive models, or fractional polynomials are encouraged [13,14,33].
When considering whether to include an additional risk factor in an existing risk-adjustment model, investigators often examine the change in c-statistic when the risk factor is added to the model to assess whether risk-adjustment has been improved. However, when comparing outcomes across hospitals, it is possible that any meaningful increase in the c-statistic of the risk-adjustment model is a red-herring. The increase in the model c-statistic indicates that the discrimination of the enhanced model is better than that of the simplified model. However, if the distribution of the additional risk factor is the same across all hospitals, then it may be that the accuracy of the hospital report card will remain unchanged, since this additional risk factor does not introduce confounding at the hospital level. The c-statistic does not incorporate or account for differences in the distribution of risk factors across hospitals. Instead, it only accounts for between-patient variation in outcomes.
In conclusion, the c-statistic of the model used for risk-adjustment provides only limited information on the accuracy of hospital report cards.
Acknowledgments
The Institute for Clinical Evaluative Sciences (ICES) is supported in part by a grant from the Ontario Ministry of Health and Long Term Care. The opinions, results and conclusions are those of the authors and no endorsement by the Ministry of Health and Long-Term Care or by the Institute for Clinical Evaluative Sciences is intended or should be inferred. This research was supported by operating grant from the Canadian Institutes of Health Research (CIHR) (MOP 86508). Dr. Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation.
Reference List
- 1.Luft HS, Romano PS, Remy LL, Rainwater J. Annual Report of the California Hospital Outcomes Project. Sacramento, CA: California Office of Statewide Health Planning and Development; 1993. [Google Scholar]
- 2.Pennsylvania Health Care Cost Containment Council. Focus on heart attack in Pennsylvania: research methods and results. Harrisburg, PA: Pennsylvania Health Care Cost Containment Council; 1996. [Google Scholar]
- 3.Scottish Office. Clinical outcome indicators, 1994. Vol. 1995 Scottish Office; 1995. [Google Scholar]
- 4.Naylor CD, Rothwell DM, Tu JV, Austin PC . the Cardiac Care Network Steering Committee. Outcomes of Coronary Artery Bypass Surgery in Ontario. In: Naylor CD, Slaughter PM, editors. Cardiovascular Health and Services in Ontario: An ICES Atlas. Institute for Clinical Evaluative Sciences; Toronto: 1999. pp. 189–198. [Google Scholar]
- 5.Massachusetts Data Analysis Center. Adult Coronary Artery Bypass Graft Surgery in the Commonwealth of Massachusetts: Fiscal Year 2010 Report. Boston, MA: Department of Health Care Policy, Harvard Medical School; 2012. [Google Scholar]
- 6.Jacobs FM. Cardiac Surgery in New Jersey in 2002: A Consumer Report. Trenton, NJ: Department of Health and Senior Services; 2005. [Google Scholar]
- 7.Coronary artery bypass graft surgery in New York State 1989–1991. Albany, NY: New York State Department of Health; 1992. [Google Scholar]
- 8.Pennsylvania Health Care Cost Containment Council. Consumer Guide to Coronary Artery Bypass Graft Surgery. Vol. 4. Harrisburg, PA: Pennsylvania Health Care Cost Containment Council; 1995. [Google Scholar]
- 9.Naylor CD, Rothwell DM, Tu JV, Austin P the Cardiac Care Network Steering Committee. Outcomes of coronary artery bypass surgery in Ontario. Cardiovascular Health and Services in Ontario: An ICES Atlas. 1999:189–198. [Google Scholar]
- 10.Iezzoni LI. Risk Adjustment for Measuring Health Outcomes. Health Administration Press; Chicago: 1997. [Google Scholar]
- 11.Krumholz HM, Brindis RG, Brush JE, Cohen DJ, Epstein AJ, Furie K, Howard G, Peterson ED, Rathore SS, Smith SC, Jr, Spertus JA, Wang Y, Normand SL. Standards for statistical models used for public reporting of health outcomes: an American Heart Association Scientific Statement from the Quality of Care and Outcomes Research Interdisciplinary Writing Group: cosponsored by the Council on Epidemiology and Prevention and the Stroke Council. Endorsed by the American College of Cardiology Foundation. Circulation. 2006;113(3):456–462. doi: 10.1161/CIRCULATIONAHA.105.170769. [DOI] [PubMed] [Google Scholar]
- 12.Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, Pencina MJ, Kattan MW. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010;21(1):128–138. doi: 10.1097/EDE.0b013e3181c30fb2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Steyerberg EW. Clinical Prediction Models. Springer-Verlag; New York: 2009. [Google Scholar]
- 14.Harrell FE., Jr . Regression modeling strategies. Springer-Verlag; New York, NY: 2001. [Google Scholar]
- 15.Ash AS, Fienberg SE, Louis TA, Normand SLT, Stukel TA, Utts J. Statistical Issues in Assessing Hospital Performance. 2012. [Google Scholar]
- 16.Concato J, Feinstein AR, Holford TR. The risk of determining risk with multivariable models. Annals of Internal Medicine. 1993;118(3):201–210. doi: 10.7326/0003-4819-118-3-199302010-00009. [DOI] [PubMed] [Google Scholar]
- 17.Shahian D, Normand S-L. Comparison of “Risk-Adjusted” Hospital Outcomes. Circulation. 2008;117:1955–1963. doi: 10.1161/circulationaha.107.747873. [DOI] [PubMed] [Google Scholar]
- 18.Werner RM, Asch DA. The unintended consequences of publicly reporting quality information. Journal of the American Medical Association. 2005;293(10):1239–1244. doi: 10.1001/jama.293.10.1239. [DOI] [PubMed] [Google Scholar]
- 19.Fonarow GC, Pan W, Saver JL, Smith EE, Reeves MJ, Broderick JP, Kleindorfer DO, Sacco RL, Olson DM, Hernandez AF, Peterson ED, Schwamm LH. Comparison of 30-day mortality models for profiling hospital performance in acute ischemic stroke with vs without adjustment for stroke severity. Journal of the American Medical Association. 2012;308(3):257–264. doi: 10.1001/jama.2012.7870. [DOI] [PubMed] [Google Scholar]
- 20.Pine M, Jordan HS, Elixhauser A, Fry DE, Hoaglin DC, Jones B, Meimban R, Warner D, Gonzales J. Enhancement of claims data to improve risk adjustment of hospital mortality. Journal of the American Medical Association. 2007;297(1):71–76. doi: 10.1001/jama.297.1.71. [DOI] [PubMed] [Google Scholar]
- 21.Hammill BG, Curtis LH, Fonarow GC, Heidenreich PA, Yancy CW, Peterson ED, Hernancez AF. Incremental value of clinical data beyond claims data in predicting 30-day outcomes after heart failure hospitalization. Circulation: Cardiovascular Quality and Outcomes. 2011;4:60–67. doi: 10.1161/?CIRCOUTCOMES.110.954693. [DOI] [PubMed] [Google Scholar]
- 22.Dimick JB, Welch HG, Birkmeyer JD. Surgical mortality as an indicator of hospital quality: the problem with small sample size. Journal of the American Medical Association. 2004;292(7):847–851. doi: 10.1001/jama.292.7.847. [DOI] [PubMed] [Google Scholar]
- 23.O’Brien SM, Delong ER, Peterson ED. Impact of case volume on hospital performance assessment. Archives of Internal Medicine. 2008;168(12):1277–1284. doi: 10.1001/archinte.168.12.1277. [DOI] [PubMed] [Google Scholar]
- 24.Austin PC, Alter DA, Tu JV. The use of fixed- and random-effects models for classifying hospitals as mortality outliers: a Monte Carlo assessment. Medical Decision Making. 2003;23(6):526–539. doi: 10.1177/0272989X03258443. [DOI] [PubMed] [Google Scholar]
- 25.Austin PC, Tu JV, Alter DA, Naylor CD. The impact of under coding of cardiac severity and comorbid diseases on the accuracy of hospital report cards. Medical Care. 2005;43 (8):801–809. doi: 10.1097/01.mlr.0000170414.55821.27. [DOI] [PubMed] [Google Scholar]
- 26.Austin PC. The impact of unmeasured clinical variables on the accuracy of hospital report cards: a Monte Carlo study. Medical Decision Making. 2006;26(5):447–466. doi: 10.1177/0272989X06290498. [DOI] [PubMed] [Google Scholar]
- 27.Austin PC, Brunner LJ. Optimal Bayesian Probability Levels for Hospital Report Cards. Health Services & Outcomes Rese arch Methodology. 2008;8:80–97. doi: 10.1007/s10742-007-0025-4. [DOI] [Google Scholar]
- 28.Tu JV, Austin P, Naylor CD. Temporal changes in the outcomes of acute myocardial infarction in Ontario, 1992–96. Canadian Medical Association Journal. 1999;161(10):1257–1261. [PMC free article] [PubMed] [Google Scholar]
- 29.Tu JV, Austin PC, Walld R, Roos L, Agras J, McDonald KM. Development and validation of the Ontario acute myocardial infarction mortality prediction rules. Journal of the American College of Cardiology. 2001;37(4):992–997. doi: 10.1016/s0735-1097(01)01109-3. [DOI] [PubMed] [Google Scholar]
- 30.Austin PC, Steyerberg EW. Interpreting the concordance statistic of a logistic regression model: relation to the variance and odds ratio of a continuous explanatory variable. BMC: Medical Research Methodology. 2012;12:82. doi: 10.1186/1471-2288-12-82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Krumholz HM, Wang Y, Mattera JA, Wang Y, Han LF, Ingber MJ, Roman S, Normand SL. An administrative claims model suitable for profiling hospital performance based on 30-day mortality rates among patients with heart failure. Circulation. 2006;113(13):1693–1701. doi: 10.1161/CIRCULATIONAHA.105.611194. [DOI] [PubMed] [Google Scholar]
- 32.Austin PC. Estimating Multilevel Logistic Regression Models When the Number of Clusters is Low: A Comparison of Different Statistical Software Procedures. International Journal of Biostatistics. 2010;6(1) doi: 10.2202/1557-4679.1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Royston P, Sauerbrei W. Multivariable Model-Building. John Wiley & Sons, Ltd; West Sussex: 2008. [Google Scholar]