The Mortality Risk Score and the ADG Score: two points-based scoring systems for the Johns Hopkins Aggregated Diagnosis Groups (ADGs) to predict mortality in a general adult population cohort in Ontario, Canada

Abstract

Background

Logistic regression models that incorporated age, sex, and indicator variables for the Johns Hopkins’ Aggregated Diagnosis Groups (ADGs) categories have been shown to accurately predict all-cause mortality in adults.

Objectives

To develop two different point-scoring systems using the ADGs. The Mortality Risk Score (MRS) collapses age, sex, and the ADGs to a single summary score that predicts the annual risk of all-cause death in adults. The ADG Score derives weights for the individual ADG diagnosis groups.

Research Design

Retrospective cohort constructed using population-based administrative data.

Subjects

All 10,498,413 residents of Ontario, Canada between the ages of 20 and 100 years who were alive on their birthday in 2007. Subjects were randomly divided into derivation and validation samples.

Measures

Death within one year.

Results

In the derivation cohort, the MRS ranged −21 to 139 (median value 29, IQR 17–44). In the validation group, a logistic regression model with the MRS as the sole predictor significantly predicted the risk of 1-year mortality with a c-statistic of 0.917. A regression model with age, sex, and the ADG Score has similar performance. Both methods accurately predicted the risk of 1-year mortality across the twenty vigintiles of risk.

Conclusions

The MRS combined values for a person’s age, sex, and the John Hopkins ADGs to accurately predict one-year mortality in adults. The ADG Score is a weighted score representing the presence or absence of the 32 ADG diagnosis groups. These scores will facilitate health services researchers conducting risk-adjustment using administrative health care databases.

1. Introduction

The ability to characterize the comorbidity burden of a population is of great importance in many areas of health services and comparative effectiveness research. When using observational or non-randomized studies to compare outcomes between subjects receiving different treatments, exposures, or interventions, the ability to adjust for systematic differences in outcome risk between treatment groups can reduce bias when comparing outcomes between treatment groups.

The Johns Hopkins Adjusted Clinical Groups (ACGs)® are a person-focused, diagnosis-based method of categorizing subjects’ illnesses. The ACG system assigns each International Classification of Disease (ICD) code (−9 version, −9-CM version, or −10 version) to one of 32 diagnosis clusters known as Aggregated Diagnosis Groups (ADG). Individual diseases or conditions are placed into a single ADG based on five clinical dimensions: duration of the condition; severity of the condition; diagnostic certainty; etiology of the condition; and specialty care involvement [1–4]. ICD codes within the same ADG are similar in both clinical criteria and expected need for healthcare resource. Each individual may have diagnoses belonging to between zero and 32 ADGs. Finally, subjects are assigned to exactly one of 106 ACGs. Subjects within the same ACG are expected to have similar healthcare resource utilization. The ADG/ACG definitions do not rely solely on the use in-patient health administrative data, but also use data contained in ambulatory health care records. Therefore, ACG/ADG-based methods can use health record data from both in-patient and out-patient health administrative data.

In a recent study, we showed that regression models that used age, sex, and indicator variables for the ADG categories accurately predicted one-year all-cause mortality in population-based cohorts of subjects [5]. The objective of the current study was to develop two different point-based scoring systems based on the ADG groups, which will allow researchers to summarize this risk into a single summary score. A secondary objective was to compare the performance of these ADG-based point-scoring systems to the Charlson comorbidity index and to a score based on the Elixhauser comorbidities [6–8].

2. Methods

2.1 Data sources

We used four different population-based administrative healthcare databases that were linked by encrypted health number. First, the Registered Persons Database (RPDB) contains basic demographic information on all Ontarians who were ever eligible for Ontario’s universal health care insurance program. The RPDB contains information on each resident’s date of birth, sex, and date of death (if applicable). Information on mortality is enriched by including information on deaths from other Ontario administrative health care databases [9]. Second, the Canadian Institute for Health Information (CIHI) Discharge Abstract Database (DAD) contains information on all inpatient hospitalizations in the province of Ontario. For each hospitalization record, there are 25 fields recording acute and chronic diagnoses noted for the patient during their hospitalization. Since 2002, diagnoses have been coded using the International Classification of Disease, 10^th Revision (ICD-10) coding scheme. Third, the Ontario Health Insurance Plan (OHIP) physician billing database contains billing claims submitted by Ontario physicians to the provincial universal health insurance program. Each claim contains a fee code describing the type of service provided, and a single diagnosis code denoting a reason for the service. The diagnosis field is coded using a truncated version of the ICD-9 coding scheme [10]. Fourth, the Ontario Mental Health Reporting System (OMHRS) collects data on patients in adult-designated inpatient mental health beds. This includes beds in general, provincial psychiatric, and specialty psychiatric facilities. The OMHRS contains data on reasons for admission and for discharge and on psychiatric and non-psychiatric diagnoses.

2.2 Study subjects

The study sample consisted of all subjects in the RPDB who were alive and eligible for OHIP benefits on their birthday in 2007. Each subject’s birthday in 2007 served as the subject-specific index date. We excluded subjects who were aged less than 20 years or older than 100 years on the index date. For each subject we determined whether they died within the 365 days following their index date. Unless they died during the year following his or her index date, each subject was followed for one year following his or her birthday in 2007.

For each subject, we identified all diagnoses associated with all hospital admissions from the CIHI DAD and all physician billing claims in the OHIP database for physician services provided in the two years prior to the subject-specific index date. The same window of two years prior to the index date was used for all subjects. For each subject, we used the Johns Hopkins ACG® software program to collapse these diagnoses to the 32 ADGs. Thus, for each subject, we determined whether an ICD diagnosis code within each of the 32 ADGs had occurred in the two years prior to the index date.

Furthermore, for each subject we calculated the Charlson comorbidity index and the Elixhauser comorbidities [11–12] using data from hospitalizations occurring in the two years prior to the index date. Diagnoses for coding both the Charlson and Elixhauser comorbidity index were obtained from the CIHI DAD. The OMHRS database was also used to identify Elixhauser mental health and addiction comorbidities,. Subjects who had not been hospitalized in the previous two years had their Charlson score set to zero. Similarly, these subjects had their values of each of the 30 Elixhauser comorbidities set to absent.

2.3 Statistical Methods

To assess the performance of ADG-based point-based scoring systems to predict mortality, we randomly divided our sample into approximately equally-sized derivation and validation samples using a random number generator.

In the initial paper, a logistic regression model was developed to predict one-year mortality that used age, sex, and indicator variables for 28 of the 32 ADG categories [5]. In the current paper, we describe two different point-scoring systems for use with the ADGs. First, we used methods described by Sullivan et al. to develop a point-based scoring system based on our previous logistic regression model that incorporated age, sex, and 28 of the ADGs. These methods are similar to those used to develop clinical point scoring systems such as the Framingham risk score for cardiovascular disease [13]. To do this, logistic regression was used in the derivation sample to regress one-year mortality on age, sex, and the 28 indicator variables from our previously derived logistic regression model. We then divided each of the estimated regression coefficients by the estimated regression coefficient for age. Each of these ratios was then rounded to the nearest integer. An individual’s score was then determined by the adding together the following quantities: (subject age – 20), the component for the subject’s sex, and the components for each of the 28 ADGs in which the subject had diagnoses. We refer to this score as the Mortality Risk Score (MRS). Second, we developed a point-scoring system that assigned weights to the 32 individual ADGs, similar to the Charlson Score. This approach did not account for age or sex, but determined weights for each of the 32 ADG variables. To do so, we used logistic regression to regress mortality on the 32 indicator variables for the ADGs in the derivation sample. A weight was determined for each ADG variable by multiplying each regression coefficient by 10 and rounding the resultant value to the nearest integer [14–15]. A score was then determined for each individual by weighting each ADG variable (1 = present; 0 = absent) by the estimated weight. We refer to this second score as the ADG Score.

We assessed the discrimination and calibration of a univariate logistic regression model that used the Mortality Risk Score as the only predictor variable. We similarly assessed the performance of a multivariable regression model that used age, sex, and the ADG Score as predictor variables. The coefficients for each logistic regression model were estimated using subjects in the derivation sample. Predicted probabilities of mortality were then obtained for all subjects in the validation sample using the coefficients estimated in the derivation sample. Model discrimination was assessed using the c-statistic [15–16].

Model calibration was assessed in four different ways. First, the mean predicted probability of death in the validation sample was compared with the observed probability of death in the validation sample using calibration-in-the-large, as described by Steyerberg [15]. Second, we determined the calibration slope (deviation of the calibration slope from unity denotes miscalibration) [15]. The calibration slopes assess deviation between observed and expected probabilities of mortality across the range of predicted risk. To do so, we used logistic regression to regress the occurrence of death within one year of the index date in the validation sample on the linear predictor of mortality obtained using the regression coefficients from the final logistic regression model (estimated in the derivation sample) applied to the subjects in the validation sample. Third, we divided the validation sample into twenty approximately equal sized groups according to the predicted probability of death (the vigintiles of risk). We graphically examined the relationship between observed mortality and the mean predicted probability of death across the 20 strata of risk. Fourth, using the subjects from the validation sample, we used a loess scatter-plot smoother to graphically describe the relationship between observed and predicted mortality [14,16]. Deviation of this calibration plot from a diagonal line with unit slope indicates miscalibration.

We examined whether prediction of mortality could be improved by examining interactions between age and the ADG Score. To do so, we regressed mortality on age, sex, the ADG Score, and the interaction between age and the ADG score (we did not conduct this analysis with the Mortality Risk Score since age is a component of the score and thus is not included as a separate covariate in the regression model). Furthermore, to examine whether the nature of the relationship between mortality and the ADG Score was non-linear, we used restricted cubic smoothing splines with five knots to model the relationship between age and the ADG score and the log-odds of one-year mortality [16].

We also examined the performance of scores based on the Charlson and Elixhauser comorbidities. For the Charlson score, we regressed one-year mortality on age, sex, and the Charlson comorbidity score. For the Elixhauser comorbidities, we developed a point-scoring system by using logistic regression to regress one-year mortality on indicator variables for the 30 Elixhauser comorbidities. As above, we determined a weight for each of the Elixhauser comorbidities by multiplying each regression coefficient by ten and rounding to the nearest integer. We then regressed one-year mortality on age, sex, and the resultant Elixhauser score. The discrimination and calibration of these two scores were assessed in the validation sample.

The above analyses used data from the two years prior to each subject’s index date to identify diagnoses within each of the ADGs and within each of the Charlson and Elixhauser comorbidities. As a sensitivity analysis, we restricted this period for identifying comorbidities to the one year immediately prior to each subject’s index date.

The ADG system employs out-patient billing claims in addition to in-patient hospitalization records. We examined the sensitivity of the accuracy of predictions using the Mortality Risk Score in rural areas of Ontario. For each resident of Ontario, we determined the Rurality Index of Ontario (RIO2008: range 0 – 100) for the community in which they resided [17]. Communities with a RIO2008 of 40 or greater were classified as rural. This threshold was chosen since the Ontario Ministry of Health and Long-Term Care and the Ontario Medical Association uses this threshold to determine incentives and bonus payment levels for physicians to practice in underserviced areas of the province [18]. We applied the regression model estimated in the entire derivation sample that used the Mortality Risk Score to predict 1-year mortality for subjects in the validation sample who resided in rural communities.

3. Results

As in our original study, the study sample consisted of 10,498,413 subjects aged 20 to 100 years. The median age was 46 (25^th and 75^th percentiles: 34 and 59, respectively). Women comprised 51% of the study sample. A more extensive description of the study sample and of the prevalence of each of the 32 ADGs is provided in the initial publication [6]. Overall, 85,007 (0.81%) subjects died within 365 days of their index date.

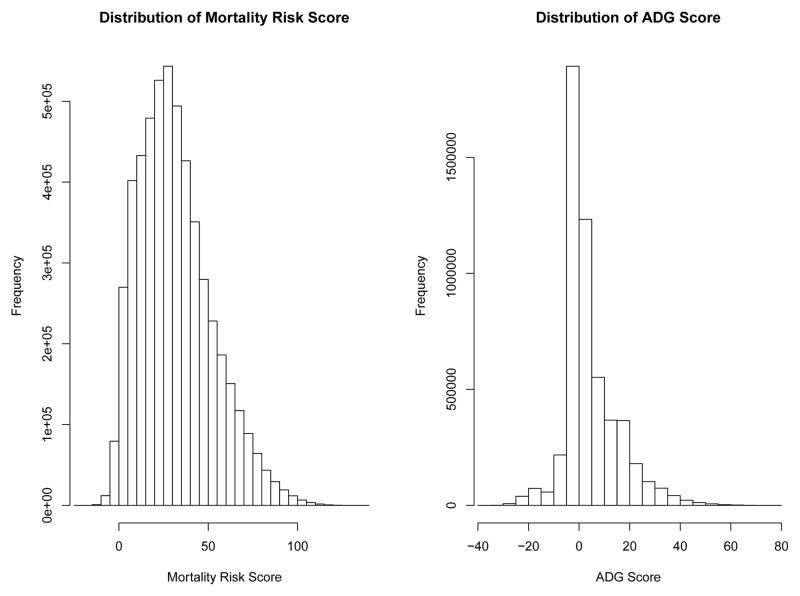
The scoring for the Mortality Risk Score is reported in Table 1. Males received an additional three points compared to females. The points for the different ADGs ranged from −5 (for diagnoses classified as allergies; unstable-ENT; dermatologic) to 13 (for psychological diagnoses classified as recurrent or persistent, unstable). In the derivation sample, the scores ranged from a low of −21 to a high of 139. The median score was 29, while the 25^th and 75^th percentiles were 17 and 44, respectively. The weights assigned to the individual ADG categories for calculating the ADG Score are reported in Table 2. Weights for the different ADGs ranged from a low of −19 to a high of 16. In the derivation sample, the ADG Score ranged from a low of −37 to a high of 76. The median ADG Score in the derivation sample was 2, while the 25^th and 75^th percentiles were zero and nine, respectively. The distributions of the Mortality Risk Score and the ADG Score in the derivation sample are described in Figure 1.

Table 1.

The Mortality Risk Score: an Age-based point scoring system.

Predictor variable	Score
Age (for each year over 20 years old)	1
Male subject	3
ADG GROUPS
-Time Limited: Minor	−1
-Time Limited: Minor-Primary Infections	1
-Time Limited: Major	6
-Time Limited: Major-Primary Infections	6
-Allergies	−5
-Asthma	2
-Likely to Recur: Progressive	6
-Chronic Medical: Stable	−2
-Chronic Medical: Unstable	8
-Chronic Specialty: Stable-Orthopedic	−3
-Chronic Specialty: Stable-Ear,Nose,Throat	−3
-Chronic Specialty: Stable-Eye	−3
-Chronic Specialty: Unstable-Orthopedic	−2
-Chronic Specialty: Unstable-Ear,Nose,Throat	−5
-Chronic Specialty: Unstable-Eye	−2
-Dermatologic	−5
-Injuries/Adverse Effects: Major	2
-Psychosocial: Time Limited, Minor	2
-Psychosocial:Recurrent or Persistent,Stable	1
-Psychosocial:Recurrent or Persistent,Unstable	13
-Signs/Symptoms: Minor	3
-Signs/Symptoms: Uncertain	1
-Signs/Symptoms: Major	3
-Discretionary	−2
-Prevention/Administrative	−2
-Malignancy	11
-Pregnancy	−4
-Dental	2

Table 2.

The ADG Score: weights for the presence of each of the 32 ADG categories.

ADG Category	Weight
Time Limited: Minor	0
Time Limited: Minor-Primary Infections	0
Time Limited: Major	6
Time Limited: Major-Primary Infections	4
Allergies	−6
Asthma	0
Likely to Recur: Discrete	0
Likely to Recur: Discrete-Infections	0
Likely to Recur: Progressive	8
Chronic Medical: Stable	4
Chronic Medical: Unstable	12
Chronic Specialty: Stable-Orthopedic	−3
Chronic Specialty: Stable-Ear,Nose,Throat	0
Chronic Specialty: Stable-Eye	3
Chronic Specialty: Unstable-Orthopedic	−2
Chronic Specialty: Unstable-Ear,Nose,Throat	−4
Chronic Specialty: Unstable-Eye	1
Dermatologic	−4
Injuries/Adverse Effects: Minor	−1
Injuries/Adverse Effects: Major	2
Psychosocial: Time Limited, Minor	−1
Psychosocial:Recurrent or Persistent,Stable	−3
Psychosocial:Recurrent or Persistent,Unstable	16
Signs/Symptoms: Minor	3
Signs/Symptoms: Uncertain	2
Signs/Symptoms: Major	2
Discretionary	−2
See and Reassure	1
Prevention/Administrative	−2
Malignancy	13
Pregnancy	−19
Dental	−1

Figure 1.

Distribution of risk scores in derivation sample

When one-year mortality was regressed on each subject’s Mortality Risk Score in the derivation sample, the estimated regression model was: logit(p) = −9.0096+0.0800X, where p denotes the probability of death within one year of the index date and X denotes the subject-specific Mortality Risk Score. An example of applying the ADG point score system to an individual subject is provided in Appendix A. When the logistic regression model estimated in the derivation sample was applied to subjects in the validation sample, the c-statistic was 0.917.

When one-year mortality was regressed on each subject’s age, sex, and ADG Score in the derivation sample, the estimated regression model was:

$$\text{logit}(p)=-10.4267+0.0740\times \text{Age}+0.2434\times \text{Male}+0.0625\times X,$$

where p denotes the probability of death within one year of the index date and X denotes the subject-specific ADG Score. When the logistic regression model estimated in the derivation sample was applied to subjects in the validation sample, the c-statistic was 0.913.

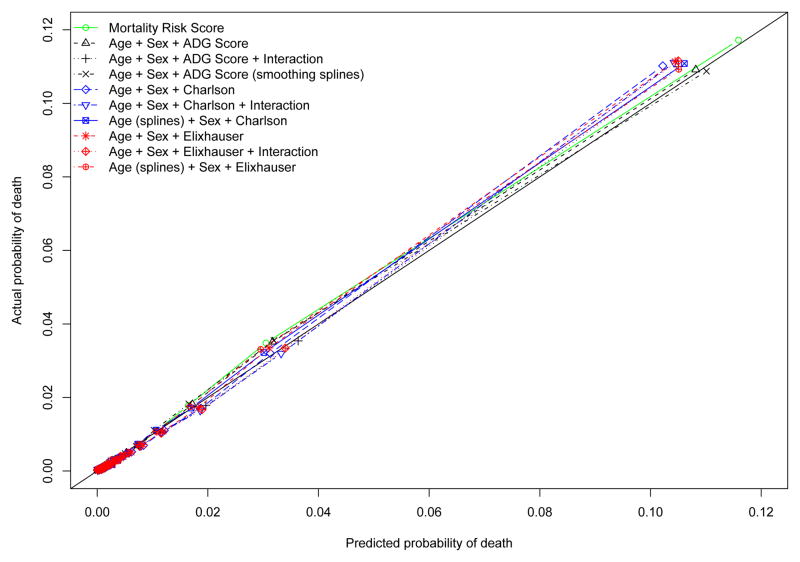
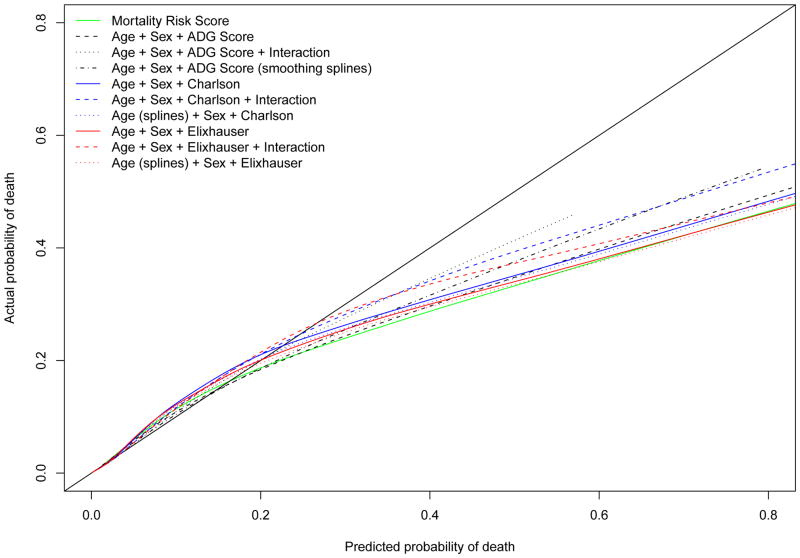
The estimated univariate logistic regression model with the Mortality Risk Score demonstrated excellent calibration-in-the-large, with an intercept of 0.0066 (calibration results are summarized in Table 4). The difference in log-odds between predictions and observed outcomes in the validation sample was not statistically significantly different from zero (P = 0.1998). The calibration slope was not significantly different from unity (0.996, 95% CI: 0.990 to 1.002). The concordance between the observed probability of mortality and the predicted probability of mortality across the twenty vigintiles of risk in the validation sample is described in Figure 2. There was some evidence of modest under-prediction of risk in upper vigintiles of risk. The smoothed calibration plots are displayed in Figure 3. There was evidence of substantial over-prediction of risk amongst subjects whose predicted probability of death exceeded 0.20. However, it should be noted that only 0.47% of subjects had a predicted probability of death that exceeded this threshold according to the MRS model. Thus, overall, the univariate logistic regression model that used the MRS displayed very good calibration in the validation sample. The calibration of the model that used age, sex, and the ADG Score was very similar to that of the MRS model, with better concordance between observed and predicted mortality in the upper vigintiles of risk. Adding interactions between age and the ADG Score or using cubic smoothing splines modestly improved model calibration or discrimination in the upper tail of the distribution of predicted risk.

Table 4.

Calibration of the different scoring systems in the validation sample

Scoring system	Calibration-in-the large: Calibration intercept (P-value)	Calibration slope (95% CI)
Mortality Risk Score	0.0066 (P = 0.1998)	0.996 (0.990, 1.002)
Age + sex + ADG Score	0.0063 (P = 0.2141)	0.996 (0.990, 1.002)
Age + sex + ADG Score + Age*ADG Score	0.0064 (P = 0.2082)	0.996 (0.990, 1.002)
Age + sex + ADG Score; Cubic smoothing splines for Age and ADG Score	0.0062 (P = 0.2221)	0.996 (0.990, 1.002)
Age + sex + Charlson score	0.0062 (P = 0.2243)	0.995 (0.989, 1.001)
Age + sex + Charlson score + Age*Charlson score	0.0064 (P = 0.2093)	0.994 (0.988, 1.000)
Age + sex + Charlson score; Cubic smoothing splines for Age	0.0063 (P = 0.2235)	0.995 (0.990, 1.001)
Age + sex + Elixhauser score	0.0062 (P = 0.2302)	0.995 (0.989, 1.001)
Age + sex + Elixhauser score + Age* Elixhauser score	0.0064 (P = 0.2102)	0.994 (0.988, 1.000)
Age + sex + Elixhauser score; Cubic smoothing splines for Age	0.0062 (P = 0.2303)	0.995 (0.990, 1.001)

Figure 2.

Calibration plot: observed vs. predicted mortality

Figure 3.

Calibration plot: observed vs. predicted mortality

The discrimination of the logistic regression model that used age, sex, and the Charlson score was 0.906 in the validation sample. Similarly, the discrimination of the model that used age, sex, and the Elixhauser score was 0.907 in the validation sample. Both of these methods displayed good calibration (Table 4). These methods displayed modestly poorer concordance between observed and predicted risk in the upper vigintiles of risk compared the ADG Score method. The discrimination of the Charlson and Elixhauser models that were modified to include interactions between age and the comorbidity scores are reported in Table 3, as are the discrimination of the models that used cubic smoothing splines to model the relationship between age and the outcome. We were unable to use smoothing splines to model the relationship between the Charlson and Elixhauser scores and mortality since over 95% of the subjects had scores of zero. This did not permit the estimation of the required components for the smoothing splines. In Figure 3, one observes that the Charlson and Elixhauser models modestly underpredict the risk of death in those with a predicted probability of less than about 0.20.

Table 3.

Discrimination (c-statistic or area under the ROC curve) of the different scoring systems in the derivation and validation samples.

Regression model	2-year look-back window for identifying comorbidities in administrative data		1-year look-back window for identifying comorbidities in administrative data
	Derivation sample	Validation sample	Derivation sample	Validation sample
Mortality Risk Score	0.918	0.917	0.916	0.916
Age + sex + ADG Score	0.914	0.913	0.913	0.913
Age + sex + ADG Score + Age*ADG Score	0.914	0.913	0.913	0.913
Age + sex + ADG Score; Cubic smoothing splines for Age and ADG Score	0.914	0.913	0.914	0.914
Age + sex + Charlson score	0.906	0.906	0.902	0.902
Age + sex + Charlson score + Age*Charlson score	0.907	0.906	0.903	0.902
Age + sex + Charlson score; Cubic smoothing splines for Age	0.908	0.907	0.904	0.903
Age + sex + Elixhauser score	0.908	0.907	0.903	0.903
Age + sex + Elixhauser score + Age* Elixhauser score	0.909	0.908	0.905	0.904
Age + sex + Elixhauser score; Cubic smoothing splines for Age	0.909	0.908	0.905	0.904

As a sensitivity analysis, we restricted our examination of health administrative data for the purpose of determining the presence of comorbidities to the one year prior to each subject’s index date. The c-statistics of the different prediction methods are summarized in the two rightmost columns of Table 3. Each method had approximately the same discrimination regardless of whether one or two years of data were used for ascertaining the presence of comorbidities. However, it should be noted that the change in the c-statistic in the validation sample when one year of data was used compared to when two years of data were used was smaller for the ADG-based methods compared to the Charlson and Elixhauser methods.

In the validation sample there were 395,009 subjects who resided in rural communities. When the univariate logistic regression model with the Mortality Risk Score as the sole predictor was estimated in the entire derivation sample and applied to the rural residents in the validation sample, the c-statistic was 0.901. For calibration-in-the large, the calibration intercept was 0.1421. The difference in log-odds between predictions and observed outcomes in the rural residents in the validation sample was statistically significantly different from zero (P < 0.0001). The calibration slope was 0.9603 (95% CI: 0.942 to 0.979). Thus, there was some evidence of mis-calibration of the model when applied to rural residents. The difference in log-odds between predictions and observed mortality was likely due to the fact that the observed probability of one-year mortality in the overall derivation sample was 0.0081, whereas it was 0.0113 amongst the rural residents in the validation sample. When the logistic regression model was recalibrated to the rural residents in the derivation sample and applied to the rural residents in the validation sample, it demonstrated good calibration-in-large and the calibration slope was not significantly different from one.

4. Discussion

We derived the Mortality Risk Score, a point-scoring system that used age, sex, and the Johns Hopkins Aggregated Diagnosis Groups (ADGs) to predict the probability of death within one year. We also developed the ADG Score, a system for weighting the 32 ADG categories to create a single summary score. A univariate logistic regression model that used the Mortality Risk Score to predict mortality had excellent discrimination and calibration. A logistic regression model that used age, sex, and the ADG Score had similar performance.

There are advantages to using these simple point-scoring systems that we derived. When adjusting for comorbidities in small samples or in settings in which outcomes are rare, the use of a single covariate may allow for more comprehensive risk-adjustment. In some settings, insufficient outcomes may be observed to include parameters for age, sex, and the 28 indicator variables for the ADG categories in the regression model. The use of our simple point-scoring systems allows researchers to use a single covariate to summarize an individual’s risk of subsequent mortality. In addition, examining for important interactions between other covariates and risk of death is greatly simplified when the latter is summarized into a single score.

Using our ADG Score in a regression model as an alternative to including indicator variables for each individual ADGs is similar to how the Charlson comorbidity score is used in practice. The original implementation of the Charlson comorbidity index used a weighted sum of different comorbidities [6–7]. This weighted sum can be used as a predictor variable in a regression model. However, in practice, many researchers include indicator variables for the individual Charlson comorbidities in regression models.

There are certain limitations to the current study. First, the scores that we developed were for predicting one-year mortality. The scores have not been validated for predicting mortality within different time frames. Similarly, we have not examined the ability of the scores to predict morbidity outcomes such as hospitalizations. Second, the scores were developed for predicting mortality in a general population-based cohort. We have not examined the performance of these risk scores in disease-specific cohorts. However, we speculate that performance would be modestly diminished in more homogeneous disease-specific cohorts.

In conclusion, point-score systems based on the Johns Hopkins Aggregated Diagnosis Groups accurately predicted one-year mortality in a general population cohort. This method may be useful for risk-adjustment or comorbidity adjustment in health services research when using observational studies to estimate the effects of exposures, treatments, and interventions on mortality.

Appendix A. Illustration of determining Mortality Risk Score for a specific subject

Consider a male subject of age 45 years with diagnoses in the following ADG categories: i) Time Limited: Minor; (ii) Asthma; (iii) Chronic Medical: Stable; (iv) Psychosocial: Time Limited, Minor.

The value of the score for this subject would be: (45 − 20) + 3 + (−1) + 2 + (−2) + (2) = 25 + 3 − 1 + 2 −2 + 2 = 29.

This subject’s probability of death within one year would be: $\frac{exp(-9.0096+0.0800\ast 29)}{1+exp(-9.0096+0.0800\ast 29)}=0.00124\text{or}0.124\%$.