Using G-computation to estimate the effect of regionalization of surgical services on the absolute reduction in the occurrence of adverse patient outcomes

Abstract

Background

Numerous studies have found that increased hospital or surgeon operative volumes, as measured by the number of procedures performed, are associated with improved patient outcomes following surgery. These findings have been used to support important health policy decisions about regionalization of surgical services, in which provision of specific surgical services is restricted to hospitals that maintain operative volumes above a specified threshold. The most common statistical approach in volume-outcome studies is to regress patient outcomes on a set of patient characteristics and a variable denoting provider volume. When outcomes are binary, such as operative mortality, logistic regression is used, resulting in the odds ratio being the reported measure of association. However, the odds ratio is a relative measure of effect and does not allow policy-makers to estimate the absolute benefit of regionalization.

Objectives

To describe how G-computation can be used to estimate the expected number of lives saved due to regionalization of surgical services.

Research Design

Retrospective cohort design of patients undergoing one of three different surgical procedures in Ontario, Canada.

Results

Regionalization of colorectal cancer surgery, esophagectomy, or pancreaticoduodenectomy in Ontario could reduce the average annual number of peri-operative deaths by 20.2, 2.0, and 3.6, for the three procedures respectively.

Conclusions

The absolute reduction in number of operative deaths due to regionalization of surgical procedures can be calculated. This can help inform health policy debate about benefits of regionalization.

1. Introduction

Numerous studies have found that increased hospital or surgeon operative volumes, as measured by the number of procedures performed, are associated with improved patient outcomes following surgery [1–4]. These findings have been consistent across a wide range of surgical procedures and across different health care systems. These findings have been used to support important health policy decisions. In particular, decisions about the regionalization of surgical services, in which provision of specific surgical services is restricted to hospitals that maintain operative volumes above a specified threshold, have been justified based on the volumes-outcome literature.

The most common statistical approach in volume-outcome studies is to use a parametric regression model to regress patient outcomes on a set of patient demographic and clinical characteristics and a variable denoting provider volume. One can then estimate the effect of provider volume on patient outcomes after adjusting for patient demographic and clinical characteristics. When outcomes are binary (e.g. peri-operative mortality), the relative change in the odds of the occurrence of the outcome due to increasing or decreasing surgical volume can be estimated. A limitation to this type of analysis is that the odds ratio is a relative measure of effect and can be difficult to interpret. When outcomes are rare, the odds ratio approximates the relative risk [5]. However, neither the odds ratio nor the relative risk allows one to directly estimate the absolute reduction in the occurrence of the outcome due to changes in provider volume.

Most studies in the volume-outcome literature have reported only relative effects of volume on patient outcomes. A few studies have used ad hoc methods to estimate the absolute effect of increases in hospital volume on patient outcomes [6–8]. The objective of the current paper is to describe G-computation and how it allows one to estimate directly the absolute effect of hospital volume on patient outcomes. We illustrate our paper by estimating the average annual number of lives saved due to the regionalization of three surgical procedures (resection of the colon or rectum for colorectal surgery, esophagectomy, and pancreaticoduodenectomy) in the Canadian province of Ontario.

2. Potential outcomes framework

The potential outcomes framework allows one to formalize the definition of the effects of treatments or exposures [9]. We initially describe this framework in a setting in which one active or experimental treatment is compared with one control or null treatment. We then extend this framework for use in studies examining the relationship between the volume of surgical procedures and patient outcomes.

The two potential outcomes, Y(1) and Y(0), are the outcomes under the active and control treatments, respectively. Y(1) denotes the subject’s outcome after receiving the active treatment, while Y(0) denotes the subject’s outcome when receiving the control treatment, under identical circumstances. Let Z be an indicator variable denoting the actual treatment received: Z = 1 denoting receipt of the active treatment and Z = 0 denoting receipt of the control treatment. For an individual subject, the effect of treatment is defined as Y(1) – Y(0). The effect of treatment on a subject is the difference between the subject’s outcomes under the two treatments, when the two treatments were received under identical circumstances. The average treatment effect is defined as E[Y(1) – Y(0)], the average effect of treatment in the population.

In many applications, there are only two treatments or exposures (an experimental exposure and a control exposure). However, the potential outcome framework can easily incorporate more than two exposures. In volume-outcome studies, one could conceive of each possible operative volume being a different exposure. Thus, there would be a potential outcome under each possible operative volume: the patient’s outcome had he or she undergone surgery at a hospital with the given operative volume. For patients who underwent surgery at low-volume hospitals, two exposures would be of particular interest: first, undergoing surgery at a hospital whose operative volume was equal to that of the hospital at which the patient underwent the procedure (the null or control exposure – the actual exposure received by the patient); second, undergoing surgery at a hospital whose operative volume was equal to that of a hospital with a large volume or whose volume was equal to that used to define large regionalized programs (the experimental exposure – that exposure that would have occurred had regionalization been present).

3. G-computation for estimating the effect of regionalization

Parametric G-computation is a regression-based approach to estimating the outcomes of subjects under different treatments or exposures. Using this approach, a multivariable parametric regression model is used to regress the outcome on treatment status and baseline covariates [10]. In conventional parametric G-computation, assuming outcomes are binary, the following regression model can be fit to the data:

$$\text{logit}(p)={\beta }_0+{\beta }_{1}X+{\beta }_2\mathrm{Z}$$

where p denotes the probability of the occurrence of the binary outcome, Z denotes exposure status (Z = 0 for unexposed; Z = 1 for exposed), and X denotes a vector of baseline covariates (note that the analyst may specify the regression model to include interactions between covariates and/or higher order terms for continuous covariates). Using the fitted logistic regression model, the predicted outcome is estimated for each subject as if that subject had been unexposed: $\widehat{Y}(0)=\frac{exp({\beta }_0+{\beta }_1{X}_i)}{1+exp({\beta }_0+{\beta }_1{X}_i)}$. Second, the predicted outcome is estimated for each subject as if that subject had been exposed: $\widehat{Y}(1)=\frac{exp({\beta }_0+{\beta }_1{X}_i+{\beta }_2)}{1+exp({\beta }_0+{\beta }_1{X}_i+{\beta }_2)}$. Thus, for each subject, the expected outcome, when unexposed and exposed can be estimated directly from the single multivariable regression model. For a given subject, the effect of treatment can be estimated as the difference between the two imputed potential outcomes: Ŷ(1) −Ŷ(0). Finally, the average treatment effect of interest can be estimated by averaging the subject-specific treatment effects over the entire sample.

G-computation can easily be adapted for use with volume-outcome studies. The binary exposure variable in the multivariable regression model can be replaced with a continuous variable denoting hospital (or surgeon) operative volume. Using the fitted regression model, one can estimate each patient’s outcome had he or she been treated at a hospital with a specific operative volume. In particular, one could determine the expected change in mortality if patients treated at low-volume hospitals had instead been treated at high-volume hospitals. If the outcome was binary, the following model could be fit to the data:

$$\text{logit}(\mathrm{p})={\beta }_0+{\beta }_{1}X+{\beta }_{2}f(\text{HV})$$

where p denotes the probability of the occurrence of the binary outcome, X denotes a vector of baseline covariates (e.g. age, sex, risk factors and comorbid conditions), while HV denotes the hospital’s operative volume (HV = hospital volume) for the surgical procedure in question, and f() denotes a function of hospital volume (to allow for possible non-linearity of the relationship between hospital volume and the log-odds of death). One could modify the above regression model to allow for smoothed, non-linear relationship between the baseline covariates and the log-odds of the outcome. From the estimated logistic regression model, for each subject, we could estimate the probability of the outcome if the patient underwent surgery at a hospital with a given volume (HV_L) and the probability of outcome if the patient underwent surgery at a hospital with a different volume (HV_H). These probabilities are $\frac{exp({\beta }_0+{\beta }_{1}X+{\beta }_2\mathrm{f}({\text{HV}}_{\mathrm{L}}))}{1+exp({\beta }_0+{\beta }_{1}X+{\beta }_2\mathrm{f}({\text{HV}}_{\mathrm{L}}))}$ and $\frac{exp({\beta }_0+{\beta }_{1}X+{\beta }_2\mathrm{f}({\text{HV}}_{\mathrm{H}}))}{1+exp({\beta }_0+{\beta }_{1}X+{\beta }_2\mathrm{f}({\text{HV}}_{\mathrm{H}}))}$, respectively. The difference between these two probabilities is the expected reduction in the probability of the occurrence of outcome due to having surgery at a hospital with operative volume HV_H, rather than at a hospital with operative volume HV_L. Averaging this quantity over the population of patients who underwent the procedure allows one to estimate the population absolute reduction in the probability of mortality due to increases in surgical volume. One can multiply this absolute reduction in the probability of mortality by the number of patients who underwent the procedure to determine the potential number of lives saved due to increases in surgical volume. Note that the value of HV_L would vary across patients, depending on the surgical volume at the hospital at which each underwent surgery. However, the value of HV_H could be fixed if one were examining the effect of moving all patients to hospitals with volumes equal to a given threshold of surgical volume.

4. Case Study – Methods

We present a case-study in which we examine the average annual number of lives saved due to regionalization of surgery for colorectal cancer, esophagectomy, and pancreaticoduodenectomy. We chose to study these procedures because they are high-risk operations that are not completely regionalized in Ontario, and have been studied extensively in the literature.

4.1 Data sources

In the Canadian province of Ontario, all medically necessary services are provided within a single-payer public health care system, with no parallel private system. Hospital services are funded by the Ministry of Health and Long-Term Care. These services are provided to all residents of Ontario, without deductibles or co-payments.

We used two different population-based administrative health care databases. The Canadian Institute for Health Information (CIHI) Discharge Abstract Database (DAD) contains information on all inpatient hospitalizations in the province of Ontario. For each hospitalization record, there are 25 fields for recording diagnoses made on the patient during the course of the hospitalization. Since 2002, diagnoses have been coded using the International Classification of Disease, 10^th Revision (ICD-10) coding scheme. Furthermore, for each hospitalization record, there are 20 fields for recording procedures and interventions which the patient underwent while in hospital. Since 2002, these interventions have been coded using the Canadian Classification of Interventions (CCI) coding scheme. The Registered Persons Database (RPDB) contains basic demographic information on all Ontarians who were ever eligible for Ontario’s universal health care insurance program. The RPDB contains information on each resident’s date of birth, sex, and date of death (if applicable). These two databases can be deterministically linked using an encrypted version of each patient’s health insurance number.

4.2 Study population

We created three different populations of patients undergoing high-risk non-cardiovascular surgical procedures in Ontario between April 1, 2002 and March 31, 2011. These populations consisted of patients undergoing: (i) esophagectomy; (ii) resection of the colon or rectum for colorectal cancer; and (iii) pancreaticoduodenectomy. The CCI intervention codes and the ICD-10 diagnosis codes for defining these three samples are described in the Appendix. All 20 fields for recording interventions and procedures were examined to determine whether the procedure of interest had been conducted. We restricted each sample to patients over the age of 18 years. For each patient in each of the three samples, we determined whether the patient died within 30 days of the surgical procedure. We also determined each subject’s value of the Charlson comorbidity score using diagnoses recorded in the 25 diagnoses fields in the CIHI DAD [11–13].

Appendix.

Procedure/intervention and diagnosis codes used to define study cohorts

Procedure	CCI procedure/intervention codes	ICD-10 diagnosis codes
Esophagectomy	1.NA.89.^^, 1.NA.90.^^, 1.NA.91.^^, 1.NA.92.^^
Resection of colon or rectum for colorectal cancer	1.NM.87. DF, RN, DE, RD, DN, RE, DX, TF, DY, TG 1.NM.89.^^ 1.NM.91.^^ 1.NQ.87. RD, DF, PB, TF, DX 1.NQ.89.^^ 1.NQ.90.^^	C18.^ C19 C20
Pancreaticoduodenectomy	1.OJ.89.^^ 1.OK.87.^^ 1.OK.89.^^ 1.OK.91.^^

4.3 Defining hospital volume

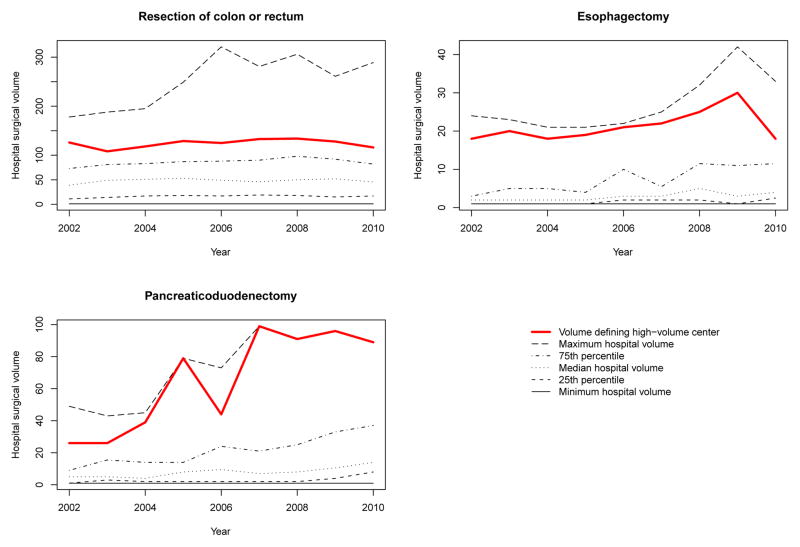
We determined the number of each of the three surgical procedures that were performed at each hospital in each of the fiscal years of the study. For each procedure and for each fiscal year, we ranked hospitals according to their operative volume for the given surgical procedure. For each year, we divided the hospitals into four strata based on operative volume, so that approximately 25% of the patients in a given year were treated within each of the four strata. Hospitals in the highest stratum were defined to be high-volume centers in that year for the given surgical procedure. We determined the minimum operative volume that qualified a hospital as a high-volume center in each of the study years. While this approach to defining “high-volume” hospitals lacks a substantive theoretical justification, distribution-based methods have been commonly used in the health services and policy literature to classify hospitals [14], and is useful for illustrative purposes.

When determining the effect of regionalization on the number of lives saved, we determined the reduction in the expected number of deaths that would occur if patients who underwent surgery at non-high-volume centers had instead had their surgery performed that year at a hospital whose operative volume was equal to the threshold of operative volume that was used for defining high-volume centers in that year.

It should be noted that there is no universally accepted manner for defining hospital volume. Some studies have used the approach that we have employed [15,16]. Other studies have determined a hospital’s average annual volume over the entire study period [1,17], while others have defined volume as the number of operative cases in the 12 months prior to a given patient’s surgical procedure [18,19]. A recent study found that the manner of defining hospital volume did not have an impact on the conclusions of volume-outcome studies [20]. In specific applications of the described methods, investigators may choose to use volume thresholds that are informed by expert opinion instead of the method that we have used.

4.4 Statistical methods

4.4.1 G-computation for estimating potential number of lives saved due to regionalization

For each of the three surgical procedures we regressed the binary outcome variable denoting death within 30 days of the surgical procedure on five variables: patient age, patient sex, the patient’s Charlson comorbidity score (as a continuous variable), the year in which the patient underwent surgery, and the hospital’s operative volume for that surgical procedure in the year in which the patient underwent surgery. Restricted cubic smoothing splines were used to model the relationship between age, year, and hospital operative volume and the log-odds of patient mortality [21] (alternative parametric and non-parametric regression methods for use with G-computation are examined in the online supplemental material section). Using the estimated regression model, we estimated each patient’s probability of death within 30-days of the procedure had they been operated on at a hospital whose operative volume was identical to that of the hospital at which they underwent surgery. This quantity denotes the potential outcome after undergoing surgery at a hospital with a volume equal to that of the hospital at which the patient underwent surgery. We then estimated an alternative potential outcome. For each patient who underwent surgery in a given year at a hospital that was not a high-volume hospital in that year, we used the estimated regression model to predict his or her probability of mortality had he or she undergone surgery at a hospital whose operative volume was equal to the threshold value for that year. We then estimated the mean difference in potential outcomes across all patients treated at non-high-volume hospitals. Multiplying the average reduction in the probability of mortality by the number of patients treated at non-high-volume hospitals allows one to estimate the number of lives saved by regionalization. We then divided this quantity by the number of years in the study to determine the average number of lives saved per year. Bootstrap methods were used to estimate 95% confidence intervals for the number of lives saved due to regionalization [22]. We drew 200 bootstrap samples from each of the three cohorts. Within each of the 200 bootstrap samples, we estimated the number of lives saved. We then determined the standard deviation of the number of lives saved across the 200 bootstrap samples and used this quantity to estimate 95% confidence intervals for the number of lives saved due to regionalization of each of the three procedures.

4.4.2 Conventional odds ratio-based approach to volume-outcome studies

For comparative purposes we conducted a conventional volume-outcome analysis. For each of the three surgical procedures, we used logistic regression to regress patient mortality on the following variables: patient age, sex, Charlson score, the year in which the patient underwent surgery, and a categorical variable denoting the quartile of hospital operative volume. Annual hospital volume was defined as described in Section 4.3. We then divided hospitals into four strata according to the quartiles of the distribution of annual hospital volume. The highest volume quartile was used as the reference level for hospital volume. The models were estimated using generalized estimating equation methods to account for the clustering of patients within hospitals. We report the odds ratios for the association between lower levels of hospital volume and the risk of 30-day mortality.

5. Case-study - Results

The annual number of patients undergoing each surgical procedure and the annual number of hospitals performing each procedure are reported in Table 1. Resection of the colon or rectum for colorectal cancer was the most frequently performed of the three procedures, with between 5,287 and 6,357 cases performed per year. It was also performed at the largest number of hospitals. Esophagectomy was the least frequently performed of the three procedures, with between 115 and 177 cases performed per year. Pancreaticoduodenectomy was the surgical procedure performed at the lowest number of hospitals. The number of hospitals performing this procedure ranged from 14 to 28.

Table 1.

Number of patients and hospitals per study year.

	2002	2003	2004	2005	2006	2007	2008	2009	2010
Resection of the colon or rectum
Number of patients	5287	5598	5850	6027	6026	6109	6357	6057	5669
Number of hospitals	110	105	104	102	103	102	103	103	102
30-day mortality rate (%)	3.4	3.8	3.3	3.6	3.4	3.2	3.4	3.2	3.4
Esophagectomy
Number of patients	115	131	145	134	137	149	165	177	152
Number of hospitals	30	27	31	31	23	24	20	23	20
30-day mortality rate (%)	5.2	6.9	4.1	5.2	2.2	2.0	3.6	5.6	3.9
Pancreaticoduodenectomy
Number of patients	227	227	255	277	316	333	285	328	317
Number of hospitals	28	24	26	22	20	22	19	16	14
30-day mortality rate (%)	6.2	3.5	1.6	4.7	2.8	2.1	2.5	2.7	3.5

The distribution of hospital surgical volumes for each of the years of the study is reported in Figure 1. We report the minimum hospital volume each year, the 25^th, 50^th, and 75^th percentiles, and the maximum hospital volume for each of nine years of the study. On each of the three panels we have added a line denoting the volume threshold required to be defined as a high-volume center (the minimum hospital volume such that 25% of patients were treated at a hospital whose volume was at least equal to this threshold).

Figure 1.

Distribution of annual hospital surgical volume

The average annual number of deaths was 199.3, 9.1, and 6.2 for resection of the colon or rectum for colorectal cancer, pancreaticoduodenectomy, and esophagectomy, respectively. The 30-day mortality rate for each procedure and for each year is reported in Table 1.

For each procedure, the 30-day mortality rate for each quartile of hospital volume is reported in Table 2. The results of the conventional volume-outcome relationship are also reported in Table 2. For each of the three lower quartiles of hospital volume, we report the adjusted odds ratio for mortality comparing patients in the given quartile to patients in the highest-volume quartile. For both the crude and adjusted analyses, there was a trend toward decreasing risk of death with increased hospital volume.

Table 2.

Volumes and outcomes in the four strata of hospital volume.

	Quartile 1	Quartile 2	Quartile 3	Quartile 4
Resection of the colon or rectum
Volume range (procedures/year)	1 – 61	62 – 88	89 – 126	128 – 321
Crude 30-day mortality rate (%)	4.0	3.4	3.4	2.8
Adjusted odds ratio (95% CI)	1.45 (1.18 – 1.79)	1.19 (0.98 – 1.45)	1.12 (0.92 – 1.35)	Reference category
Esophagectomy
Volume range (procedures/year)	1 – 4	5 – 13	14 – 21	22 – 42
Crude 30-day mortality rate (%)	7.0	4.2	2.5	3.7
Adjusted odds ratio	2.02 (1.00 – 4.09)	1.30 (0.67 – 2.53)	0.69 (0.31 – 1.53)	Reference category
Pancreaticoduodenectomy
Volume range (procedures/year)	1 – 14	15 – 27	28 – 48	49 – 99
Crude 30-day mortality rate (%)	4.2	4.2	3.2	1.1
Adjusted odds ratio	4.16 (2.91 – 5.94)	4.06 (2.28 – 7.23)	3.63 (2.29 – 5.74)	Reference category

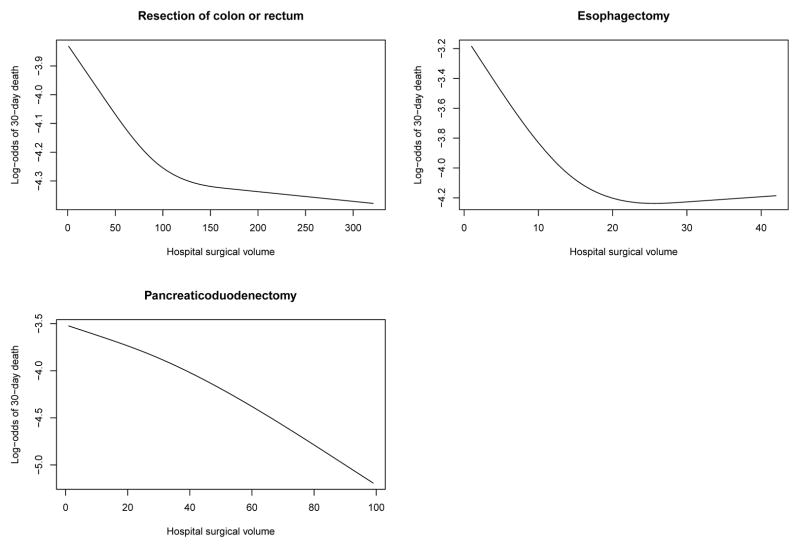
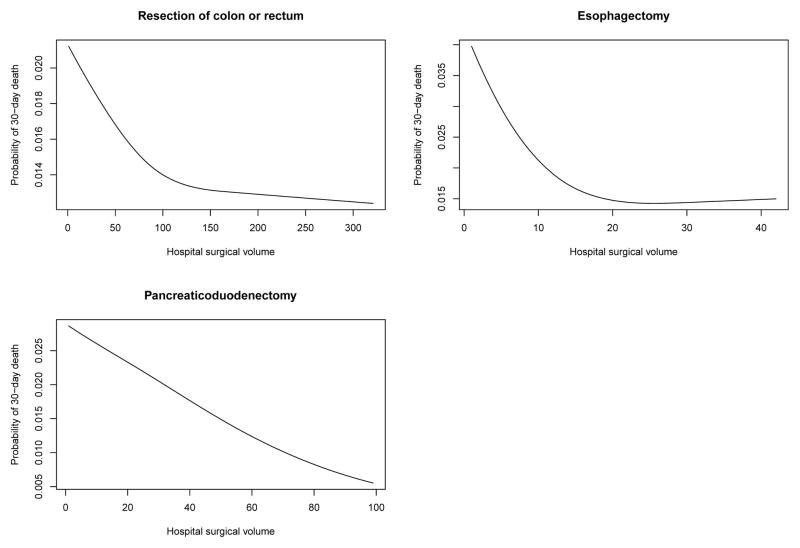
The relationship between hospital surgical volume and the log-odds of 30-day mortality and the probability of 30-day mortality are described in Figures 2 and 3, respectively. Each figure describes the relationship between hospital volume and the risk of 30-day mortality for a patient whose covariates (age, sex, Charlson score and year of operation) were set to the sample median. In each figure, there is one panel for each of the three procedures. Figure 2 uses the logit scale, allowing one to examine whether the relationship between hospital volume and the log-odds of mortality is approximately linear. For pancreaticoduodenectomy, we observed that the relationship was approximately linear across the range of volume. However, for colorectal cancer surgery and esophagectomy, we observed that mortality initially decreased rapidly with increasing volume. However, after this initial period of rapid decrease, improvements in patient outcomes were increasingly marginal with subsequent improvements with increasing volume. Figure 3 allows one to determine the range of predicted probability of 30-day death for a typical patient across the range of hospital volume.

Figure 2.

Relationship between surgical volume and 30-day mortality

Figure 3.

Relationship between surgical volume and 30-day mortality

Regionalization of colorectal cancer surgery would result in the greatest average annual number of lives saved (an average of 20.2 lives saved per year; 95% confidence interval: 12.3 to 28.2), while regionalization of either esophagectomy (2.0; 95% CI: 0.7 to 3.2) or pancreaticoduodenectomy (3.6; 95% CI: 1.8 to 5.4) would result in a more modest reduction in the average annual number of deaths. Regionalization of colorectal cancer surgery would reduce the average annual number of deaths by 10.1%. Similarly, regionalizing esophagectomy surgery would reduce the average annual number of deaths by 32.3%, while regionalizing pancreaticoduodenectomy would reduce the average annual number of deaths by 39.6%. While the relative reduction in the average annual number of deaths would be the greatest for the latter two procedures, the absolute reduction in the average annual number of deaths would be the greatest for colorectal cancer surgery.

6. Discussion

In randomized controlled trials, the effect of treatment on dichotomous outcomes can be reported using a variety of measures of treatment effect: absolute risk reduction, the relative risk reduction, the number needed to treat, and the odds ratio. Schechtman argues that both relative and absolute measures should be reported [23]. Cook and Sackett argue that for clinical decision making the number needed to treat is more meaningful that either the relative risk reduction or the odds ratio [24], while Jaeschke et al. suggest that the odds ratio and the relative risk provide limited information [25]. Finally, Sinclair and Bracken argue that clinically important questions are best addressed using relative risks, relative risk reductions, risk differences, and the number needed to treat [26]. In the face of these proposals, some medical journals require that absolute risk reductions and the associated number needed to treat (NNT) be reported for any randomized controlled trial with a dichotomous outcome (http://www.bmj.com/about-bmj/resources-authors/article-types/research. Site accessed December 7, 2011). Clinical consensus is that medical decision making requires knowledge of absolute measures of treatment effect.

In most volume-outcome studies, patient outcomes are regressed on a set of patient demographic and clinical characteristics and a variable denoting provider volume. When outcomes are binary, the logistic regression model is usually employed. From the resultant model, one can estimate the odds ratio associated with increased or decreased provider volume. However, odds ratios are relative measures of effect – they provide no information about the absolute benefit of increased provider volume. In order to quantify the absolute benefit of increasing provider volume one must incorporate the number of patients undergoing the procedure, the probability of peri-operative mortality, and the reduction in mortality due to increased volume. In light of the discussion above, one could argue that reporting relative reductions in patient mortality due to increasing provider volume is inadequate for making health policy decision on the regionalization of surgical services. Our use of G-computation in volume-outcome studies permits estimation of the absolute changes in mortality due to regionalization of surgical services.

Prior studies in the health services literature have examined the absolute reduction in mortality that could be observed if the performance of different hospitals or health services regions were equal to that of the hospital or region whose performance was at the 80^th percentile [27,28]. These prior studies emphasized that estimating lives saved permits health authorities to set priorities for improving the delivery of health care. Our study is similar to these two prior studies in its emphasis on the importance of estimating the absolute reduction in the number of deaths due to changes in the health care system. However, our study differs from these prior studies in one important aspect. The prior studies focused on raising the performance of all hospitals to be equal to that of the best performing hospitals. We focused on increasing hospital volume as a mechanism for improving patient outcomes. Since the demand for a specific surgical procedure is relatively fixed in a jurisdiction such as a province or state, our focus was on the effect of moving patients from small-volume hospitals to high-volume hospitals (all hospitals cannot become high-volume centers). We are thus, not trying to improve outcomes at all hospitals, but rather, to estimate outcomes if all patients were moved to a subset of the hospitals. Thus, while two prior studies used random effect or multilevel models, we focused on the use of marginal models.

We examined the effect of regionalization of surgical services on three different surgical procedures: resection of the colon or rectum for cancer, esophagectomy, and pancreaticoduodenectomy. The first is performed relatively frequently in Ontario, while the latter two are performed relatively less frequently. These procedures were selected for inclusion in our case study because they are commonly studied in volume-outcome analyses that seek to estimate mortality benefits from regionalization of surgical care [6–8]. In the conventional volume-outcome analyses, the odds ratios for the three lower volume quartiles were greatest for pancreaticoduodenectomy (4.16, 4.06, and 3.63 for the three lower quartiles of hospital volume). The odds ratios for colorectal surgery tended to be the most attenuated compared to the other two procedures. Thus, a conventional volume-outcome analysis would conclude that undergoing surgery at a low-volume hospital conferred a greater increase in the risk of death for pancreaticoduodenectomy or esophagectomy compared to colorectal cancer surgery. However, using G-computation, we found that the benefits of regionalization in terms of lives saved was substantially greater for colorectal surgery than it was for the other two procedures. Indeed, the average annual number of lives saved for the latter two procedures was relatively low. By including procedures that are performed relatively infrequently, a conventional volume-outcome analysis can mask the minimal benefits of regionalization, despite the relatively high mortality rate associated with the procedure. Thus, as advocated by others [27,28], the reporting of the absolute number of lives saved permits health planners to allocate resources and prioritize changes to the health care system in order to bring about the greatest benefit to patients.

A limitation of the current study is that unbiased estimation of the benefit of regionalization requires the assumption of no unmeasured confounders – that we have incorporated all variables that affect patient outcomes. In our case study, we used age, sex, and the Charlson comorbidity index as predictors of death within 30-days of the surgical procedure. While administrative data may not capture all information related to prognosis such as cancer stage or functional status, our analysis included information similar to the volume-outcome literature which relies largely on administrative health data. The primary purpose of this study was to describe a method for estimating the benefit of regionalization in terms of the reduction in the number of peri-operative deaths. To the extent that incomplete information on covariates created a bias in the results of our analyses, it would nevertheless not limit the generalizability of the application of the methods we describe. A second limitation pertains to a limitation of G-computation itself. G-computation requires the specification of either a model to predict patient outcomes conditional on exposure and patient covariates. Misspecification of this model will result in biased estimation of the potential outcomes. The data in the current study were of low-dimension, thus it is unlikely that the parametric regression models with smoothing terms were grossly misspecified. However, when using high-dimensional data with complex relationships, the concern over misspecification may be greater. A third limitation is that we have assumed that improvements in patient outcomes due to regionalization were due, on average, solely to increases in hospital volume, and were not due to other characteristics of hospitals (e.g. to the presence of specific surgeons). Finally, our use of marginal logistic regression models to estimate the probability of the outcome occurring for each patient did not take into account the clustering of patients within hospitals. However, the fitted models were used only to obtain estimated predicted probabilities, and we were not interested in the statistical significance of individual regression coefficients. However, it is important that marginal, rather than conditional (e.g. hierarchical) models be used, since one is trying to estimate the average effect of being treated at a high-volume hospital, and not the effect of being treated at a specific high-volume hospital.

In conclusion, traditional volume-outcome studies report the relative effects of provider volume on patient outcomes. The use of G-computation permits estimation of the absolute effects of the regionalization of surgical services. Widespread adoption of this method will provide health care policy makers with appropriate evidence on the benefits of the regionalization of health services.