Temporal Structure of Support Surface Translations Drive the Temporal Structure of Postural Control During Standing

Abstract

A healthy biological system is characterized by a temporal structure that exhibits fractal properties and is highly complex. Unhealthy systems demonstrate lowered complexity and either greater or less predictability in the temporal structure of a time series. The purpose of this research was to determine if support surface translations with different temporal structures would affect the temporal structure of the center of pressure (COP) signal. Eight healthy young participants stood on a force platform that was translated in the anteroposterior direction for input conditions of varying complexity: white noise, pink noise, brown noise, and sine wave. Detrended fluctuation analysis was used to characterize the long-range correlations of the COP time series in the AP direction. Repeated measures ANOVA revealed differences among conditions (P < .001). The less complex support surface translations resulted in a less complex COP compared to normal standing. A quadratic trend analysis demonstrated an inverted-u shape across an increasing order of predictability of the conditions (P < .001). The ability to influence the complexity of postural control through support surface translations can have important implications for rehabilitation.

Introduction

Maintaining upright stance is the result of a complex interaction of the sensory systems, the central nervous system (CNS), and the muscular system.²⁰ During normal standing the body has a natural postural sway in both the anteroposterior (AP) direction as well as the mediolateral (ML) direction. In order to stay upright the postural control system has to maintain the body's center of mass (COM) within the confines of the base of support. Allowing the body's COM to travel outside the base of support will lead to a loss of balance and possibly a fall if corrective strategies are not implemented in time. The body's position in space is determined from a combination of visual, somatosensory, and vestibular cues.²⁰ Visual cues help to determine postural sway by recognizing the movement of the body in relation to the environment. Somatosensory cues provide information about the position of the body through proprioceptive receptors in the joints and cutaneous pressure receptors. The vestibular system helps to determine the position of the head with respect to the body and environment. Within the vestibular system semicircular canals and otoliths provide information about angular and linear accelerations respectively. The CNS is responsible for integrating the sensory information and reweighting it according to the perceived reliability of the information.² For example if standing in a dark room, the visual information may be perceived as less reliable and more weight will be given to the somatosensory and vestibular information. The other main component for maintaining upright stance is the muscular system. In order to adjust postural sway and keep the COM within the base of support the muscular system produces forces against the support surface and changes the position of joints, most notably the ankles and hips.³⁴ These forces and changes in joint position alter the position of the COM within the base of support in order to maintain upright stance.

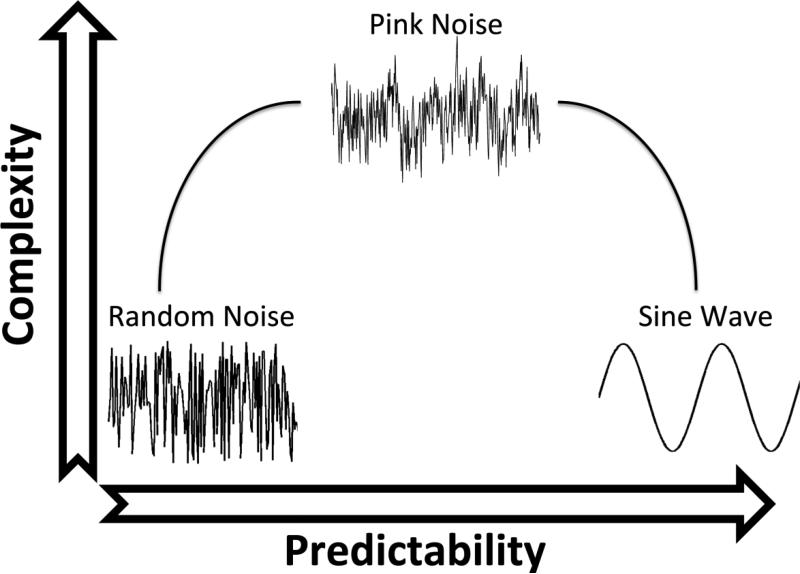
Center of pressure (COP) is a commonly used metric that can assess the neuromuscular control of standing posture,⁴⁰ and is considered to reflect the mechanisms utilized to maintain balance. Humans naturally sway during static stance resulting in an inherent variability present in the COP time series.¹⁷ A commonly held belief is that variability in a movement pattern, such as standing posture, represents error or random noise in the movement and that variability is a negative aspect of human movement.²⁷ Thus, it seems intuitive that the goal of postural control should be to reduce the variability in standing posture measures.²⁴ However, this approach does not consider how posture evolves over time, or how postural sway at one point in time may be related to postural sway at another point in time. Understanding how posture evolves over time reveals information about the control of posture that is not gained from looking at overall movement. This is important because it could reveal differences in neuromuscular control that would not be seen when looking at magnitude of variability. It is possible to have a reduced amount of sway accompanied with a loss of complexity in the temporal structure,³ which could mistakenly be considered a positive change if one is not considering how posture evolves over time. Recent research has demonstrated that the movement variability of a healthy biological system is not just stochastic noise but has a complex, ordered pattern.³² A complex system refers to a system that has components which are dependent on each other and cannot be decomposed into individual components.⁴ Nonlinear methods have been used to explore the temporal structure of variability and quantify the amount of determinism and complexity exhibited by such a system. A healthy biological system is characterized by a temporal structure that exhibits fractal properties and is highly complex.^{8, 32} One way to assess the complexity of a system is to analyze the power spectral density in relation to the frequencies.²¹ When doing so a range of colored noises can emerge. A completely random, or white noise, signal will contain equal power across all frequencies, a pink noise signal will have a power spectrum that is equal to the reciprocal of the frequency (1/f), and brown noise will have a power spectrum that is equal to the reciprocal of the frequency squared (1/f²).²¹ Healthy systems resemble a pink noise like structure.²⁸ Pink noise structures are found in biological systems that include, but are not limited to, cognitive processes,^{35, 36} heartbeat intervals,^{1, 8} gait,³⁸ and standing posture.⁶ Unhealthy systems demonstrate low complexity and have either low or high predictability.³⁰ Predictability simply refers to the ability to predict a future state based on the current and/or previous states. White noise, for example, is completely unpredictable whereas a sine wave is completely predictable. A system with low predictability and low complexity will be noisy and unpredictable.¹⁹ An unpredictable system will not be able to produce a consistent motor output, and not be able to maintain a movement pattern that is capable of achieving the desired goal. A system with high predictability and low complexity is too stiff and rigid.¹⁸ A rigid system will not be able to adapt to changes in the environment or respond to perturbations appropriately. A healthy system however is moderately predictable and contains a rich, complex structure that can be described using mathematical chaos. The theory of Optimal Movement Variability (Figure 1) describes this phenomenon seen in the temporal structure of variability of a movement time series.³² This model follows an inverted-u relationship between predictability and complexity. Because aging and disease are characterized by a lower complexity in several biological signals,^{21, 31} it is believed that restoring a healthy structure of variability in these signals will lead to a healthier functionality in such biological systems.

Figure 1.

Model of optimal variability shows the interaction between predictability and complexity of the temporal structure of a biological time series. A healthy variability is characterized by having a highly complex temporal structure that can be characterized using mathematical chaos. An unhealthy temporal structure can be characterized by a loss of complexity toward a more regular and ordered pattern, or toward a more noisy and unpredictable pattern.

One potential intervention to restore or improve variability towards a healthy structure is through somatosensory input. Previous research has investigated altering somatosensory input and its effect on standing posture.^{7, 10, 33} The application of vibration to the Achilles tendons caused individuals to exhibit an altered postural response. This vibration led to afferent muscle spindle activation, which during standing posture resulted in individuals swaying toward the direction where the vibratory stimulus was applied.⁷ Vibrations and pressure applied to the surface of the skin also activated cutaneous mechanoreceptors, which play a large role in standing posture.³⁷ Priplata et al. had participants stand on vibrating insoles that provided a stochastic subthreshold input to the plantar surface of the foot, resulting in a reduction in several sway parameters.²⁴ Another study found similar results by applying an electrical stimulus to the medial and lateral side of the support knee during single leg stance.⁹ These reductions in sway parameters demonstrate that it is possible to alter standing posture by utilizing somatosensory input. However, each of these studies used stochastic noise as input and primarily focused on variables that measure amount of variability, but not the evolution of the system over time.

Recently, several studies have investigated the effect of providing sensory input that has a temporal structure based on different complexities. This work has demonstrated promise in being able to drive a system towards a specific temporal structure based on the input. Kaipust et al. had individuals walk while listening to music that had inter-beat intervals that followed different variability patterns derived from fractal sound, white noise, and metronome.¹⁴ Gait characteristics such as step time were affected by applying an auditory stimulus with these varying temporal structures. The tempo was based on each individual's preferred walking cadence and the participants were not instructed to walk to the beat of the music. The resulting step times were analyzed using detrended fluctuation analysis (DFA) and results demonstrated that the temporal structure of their step times entrained to the temporal structure of the auditory stimulus. Rhea, et al. conducted a similar study in which the participants walked to a visual metronome that had either a random or a 1/f structure and also found similar results of subjects entraining to the stimulus.²⁶ Walking to a visual metronome that had a random temporal structure resulted in stride times that had weaker long-range correlations, and walking to the metronome with 1/f structure resulted in stride times that had stronger long-range correlations.²⁶ Another study was able to restore the 1/f fluctuations in the gait timing of patients with Parkinson’s disease by using a metronome that used interactive rhythmic cueing based on nonlinear oscillators.¹³ This research also compared a fixed-tempo rhythmic auditory stimulus and saw a weakening of the long-range correlations. It has also been demonstrated that when watching movements on a screen containing different temporal structures, gaze entrained to the temporal structure of the visual stimulus.¹² These studies demonstrate that it is possible to drive the complexity of biological signals by providing a complexity specific stimulus. In the current study we aim to achieve this goal by manipulating the complexity of support surface translations. This method of sensory input was chosen in order to extend the previous findings of altering somatosensory input. Utilizing signals with different temporal structures to drive the translations and analyzing the temporal structure of the COP signal will provide new information about the ability to alter temporal structure with sensory input.

Therefore, the purposes of this study were to 1) determine if healthy young individuals exhibited a pink noise type structure in their natural COP and when undergoing pink noise support surface translations, and 2) determine if support surface translations with different temporal structures affect the temporal structures of the resultant COP signal. We hypothesized first that healthy young subjects would exhibit a pink noise type structure in their COP whether they undergo a quiet standing condition or pink noise translations, and second that the temporal structure of COP variability can be affected by support surface translations of varying temporal structure. Aging and disease are characterized by a loss of complexity in biological signals, therefore, these findings would provide support for the ability to develop more effective rehabilitation procedures through the use of sensory input based on natural or pink noise type stimulus.

Methods

Subjects

Eight healthy participants (6M/2F; Age 29.8 ± 11.4 years; Height 178.1 ± 14.1 cm; Mass 75.0 ± 14.1 kg) participated in this study. Exclusion criteria included any lower limb dysfunction, peripheral neuropathy, or incidence of falling in the previous year. Approval was obtained from the Institutional Review Board at the University of Nebraska Medical Center, and all subjects provided informed consent.

Experimental Protocol

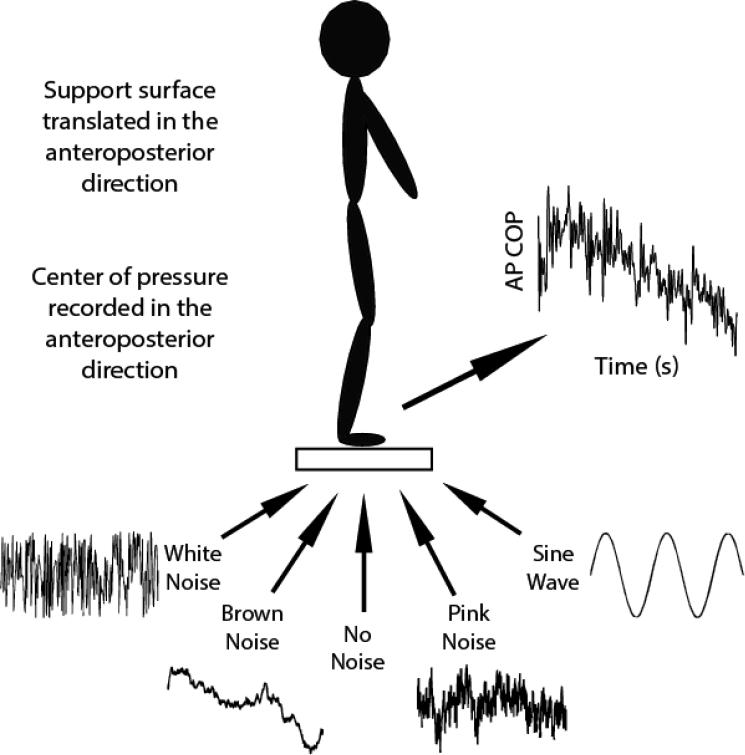
The Neurocom® Balance Master® was used to provide support surface translations and record COP data. The research module of the Neurocom has the ability to translate or rotate the force platform in the AP direction according to a user specified waveform. There were five separate conditions that were presented in randomized order, normal standing with no input waveform, i.e. no translations, and four conditions with waveforms of different temporal structures (white noise, pink noise, brown noise, sine wave; Figure 2). These conditions were chosen to represent a range of temporal structures that contain varying levels of complexity and predictability. White noise represents a complete lack of predictability and a state of low complexity. Pink noise is highly complex and moderately predictable. Brown noise is more predictable than pink noise and less complex. A sine wave represents complete predictability and no complexity. The no noise condition served as a control condition. The brown and pink noise waveforms were created using custom Matlab (Mathworks, Natick, MA) software, the white noise waveform was created using the “rand” function in Matlab, and the sine wave function was entered directly into the function field of the Neurocom. The noise waveforms that were generated in Matlab were then saved to a text file and imported into the researcher module of the Neurocom. Each waveform was created with 1800 data points and the frequency of platform translation was 10 Hz, which resulted in a three-minute trial. Each signal was created to maintain a global variance by normalizing to the range of the sine wave signal. All of the support surface movements were suprathreshold but well below the range that would induce a loss of balance. Participants were allowed breaks between trials if needed but everyone declined and completed the five trials without breaks. Participants stood on the force platform barefoot in a side-by-side stance. The feet were not adjusted during testing so participants maintained the same stance width for all conditions. The movement of the motor that was driving the platform was also recorded to ensure the input signals were producing the desired support surface translations. This was confirmed by calculating DFA for the signal producing each of the conditions (Table 1).

Figure 2.

Experimental protocol. Participants stood on a force platform on the Neurocom® balance manager while the platform was translated in the anteroposterior direction. The platform was translated according to waveforms of different complexities. White noise represented a completely random movement, sine wave represented a completely periodic movement, and pink and brown noise represented different strengths of long-range correlation. Center of pressure was analyzed in the AP direction to determine if the complexity of standing posture would change based on the complexity of the input signal.

Table 1.

Results from running the DFA algorithm on the position of the motor that was driving the support surface translations. All conditions were significantly different from each other after adjusting for multiple comparisons.

Condition	DFA α-value of motor
	Mean	SD
White Noise	0.472	0.005
Pink Noise	1.103	0.005
Brown Noise	1.556	0.004
Sine Wave	0.374	0.001

Data Analysis

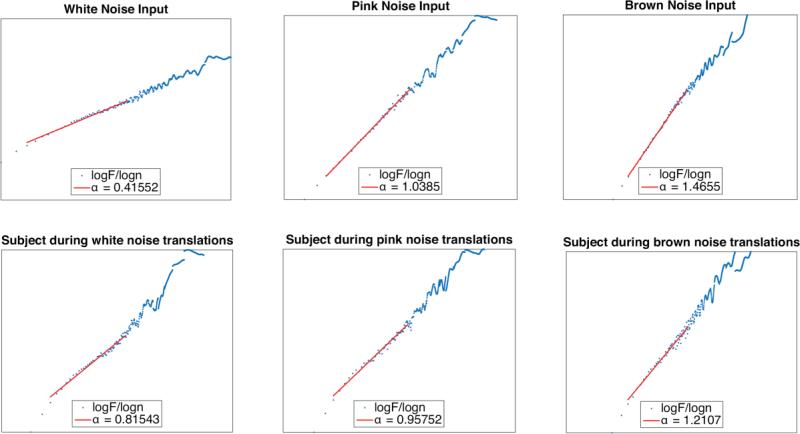
Each condition was recorded at 100 Hz for one three-minute trial and down sampled to 10 Hz for analysis. The Neurocom has a fixed sampling rate and spectral analysis was used to determine the down sampled frequency. The temporal structure of the COP signal was analyzed using DFA. All variables were calculated using custom Matlab software. DFA analysis was implemented according to the methods of Peng, et al.²³ DFA analysis results in a scaling exponent α that quantifies the long-range correlations in a time series. Briefly, the time series is integrated and divided into boxes of equal length n. Each box is then detrended by subtracting the least squares fit line from that box. The root mean square fluctuation is determined for each box. This process is repeated over all box sizes and a relationship is found between the box size, n, and the root mean square of the box, F(n). This relationship is plotted on a double log (log(n) by log(f(n)) graph and the slope of this line is the scaling exponent α (Figure 3). The scaling exponent, or α-value, has a distinct relationship with different types of noise. DFA α-values for different types of noise are as follows: 0.5 for completely uncorrelated white noise, 1.0 for pink noise, and 1.5 for brown noise signals.²⁹

Figure 3.

Example log/log plots from running the DFA algorithm. The top row contains the log/log plots of the input signals and the bottom row contains the log/log plots of the COP signal during conditions where the support surface was translated with the waveforms from the top row. The red lines indicate the scaling region that was chosen for analysis and the alpha value is the slope of these lines.

Before calculating DFA the range of box sizes needs to be determined, which is called the scaling region. This process involved generating a pink noise signal that contained 1800 data points, the same as the experimental data. This signal was processed through the DFA algorithm and the double log plot was visually inspected. A scaling region was selected and an α-value with standard deviation was returned. Once the scaling region was considered reasonable based on the visual inspection it was tested against computer generated pink noise signals. To test the scaling region pink noise was generated 100 times and processed through the DFA algorithm using the chosen scaling region. The scaling region was accepted as long as the 100 pink noise signals were not statistically different from an α-value of 1.0. For this experiment a scaling region of 3 to 56 was chosen. This process ensures that the DFA algorithm is correctly identifying colors of noise based on the number of data points used in the experiment.

Statistical Analysis

To determine if the healthy individuals exhibited a pink noise type of structure in their COP the DFA α-values from the COP in the “no noise” condition and pink noise condition were compared to the DFA α-values from eight computer generated pink noise signals. These eight signals were created independently to compare to the experimental data for these two conditions. Each of the pink noise signals was created with 1800 data points and DFA α-values were computed using the same scaling region of 3 to 56. A one-way ANOVA was used to compare the generated pink noise with the no noise and pink noise conditions. In order to determine if there were differences in the long-range correlations of the participants COP signal a 1×5 repeated measures ANOVA was used to compare the DFA α-values among the conditions. Tukey post-hoc analysis was used to determine which conditions were different. After determining if there was a difference in conditions a quadratic trend analysis was conducted to describe the results across conditions. A trend analysis is particularly useful when the study has a quantitative independent variable.¹⁵ In this study the long-range correlations of the input signal are the quantitative independent variable. Instead of comparing the means of the different groups the general shape of the data is compared. For this study a quadratic trend analysis was performed to try and identify an inverted-u shape when the data are organized in an increasing order of predictability. The trend analysis utilizes predictive values and then compares the experimental results to determine if there is a trend in the data. The coefficients for the quadratic trend were found in a stats table and used to find the predicted values for the quadratic trend. For this study the coefficients were (2, −1, −2, −1, 2). Statistical significance (α) was set to 0.05.

Results

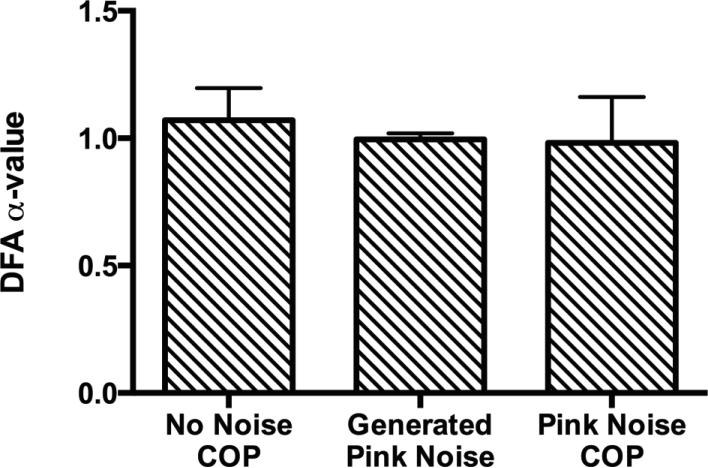
For the first hypothesis computer generated pink noise signals were used to determine if the COP signals of the individuals in this study had a structure that resembled pink noise (Figure 4). No significant differences were found when comparing the generated pink noise signals to the “no noise” standing trials and the pink noise input trials (F(2, 21) = 1.144, P = .338).

Figure 4.

Eight computer generated pink noise signals were created with 1800 data points to match the experimental data. The pink noise signals were run through the DFA algorithm with the same parameters as the experimental data. These generated pink noise signals were not different from natural standing or standing with the pink noise input. This indicates that the anteroposterior sway during normal standing and with a pink noise input contained a pink noise type structure.

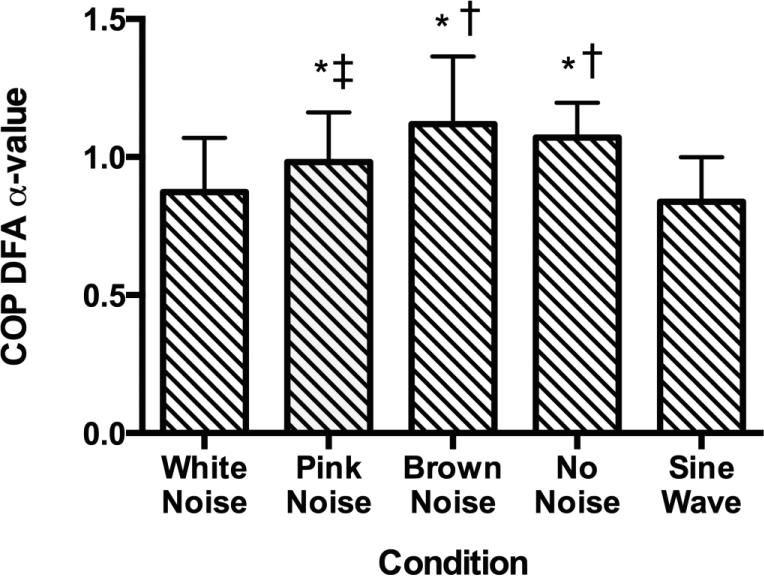
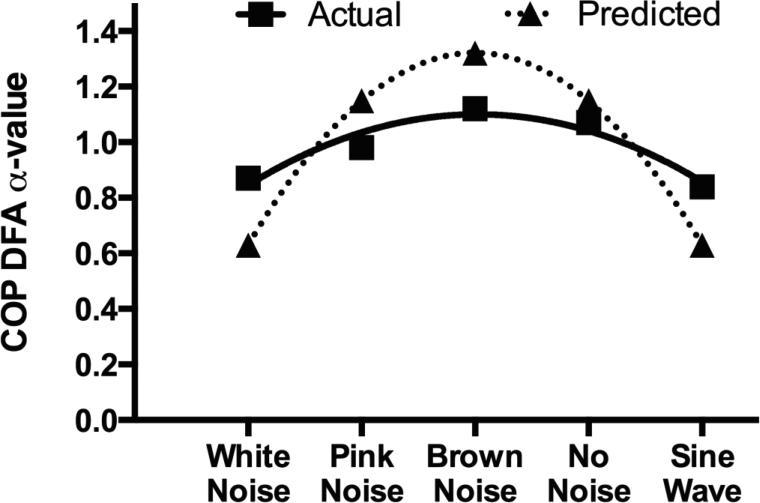
For the second hypothesis conditions were organized with low predictability (white noise) on the left and high predictability (sine wave) on the right and the results exhibited an inverted-u relationship similar to the theory of Optimal Movement Variability (Figure 5). The ANOVA revealed significant differences in the DFA α-values of the COP between conditions (F(4, 28) = 15.69, P < .001, η_p² = .692). Tukey post-hoc analysis revealed that the sine wave condition resulted in a lower α-value compared to the pink noise, brown noise, and no noise conditions. The white noise condition presented a lower α-value compared to the brown noise and no noise conditions, and the pink noise condition resulted in a lower α-value compared to the brown noise condition (Table 2). Low complexity signals (sine wave and white noise) had the most effect on the COP. The inverted-u shape of the experimental data was confirmed by quadratic trend analysis (Figure 6; P < .001, η_p²= .905).

Figure 5.

DFA α-values for the five conditions. The “no noise” condition was placed within the noise conditions based on the model of optimal variability and knowing that the “no noise” condition was not different from the pink noise condition. Significant differences were found in the α-values when comparing both the sine wave and white noise conditions with the no noise, brown noise and pink noise conditions as well as when comparing the pink noise and brown noise conditions. * = P < .05 compared to the sine wave condition, † = P < .05 compared to the white noise condition, ‡ = P < .05 compared to the brown noise condition.

Table 2.

Results from the Tukey post-hoc comparison. Comparison of DFA α-values and the P-values adjusted using a bonferroni correction are reported.

Tukey's multiple comparisons test of COP	DFA α-values	Adjusted P Value	Cohen's d
White Noise vs. Brown Noise	0.873 vs. 1.119	* < 0.001	1.11
White Noise vs. No Noise	0.873 vs. 1.071	* < 0.001	1.20
White Noise vs. Pink Noise	0.873 vs. 0.981	0.123	0.57
White Noise vs. Sine Wave	0.873 vs. 0.838	0.927	0.19
Brown Noise vs. No Noise	1.119 vs. 1.071	0.797	0.25
Brown Noise vs. Pink Noise	1.119 vs. 0.981	* 0.027	0.64
Brown Noise vs. Sine Wave	1.119 vs. 0.838	* < 0.001	1.36
No Noise vs. Pink Noise	1.071 vs. 0.981	0.26	0.58
No Noise vs. Sine Wave	1.071 vs. 0.838	* < 0.001	1.61
Pink Noise vs. Sine Wave	0.981 vs. 0.838	* 0.021	0.84

Figure 6.

Trend analysis revealed a significant quadratic trend exhibiting an inverted-u relationship similar to the model of optimal variability. The solid line with squares is the experimental data and the triangles along the dotted line are the predicted values from the quadratic trend.

Discussion

As a first step, we sought to examine if the DFA α-value of natural standing posture would resemble pink noise and if natural standing posture resembles postural sway during pink noise support surface translations. Our hypothesis was confirmed (Figure 4) and by using the same parameters on all sets of data it was determined that there was no difference between the no noise, pink noise translations, and generated pink noise conditions. This finding indicates that the subjects in this experiment exhibited a pink noise structure to their COP during normal standing, and a pink noise support surface translation did not significantly alter the temporal structure of their COP. This result demonstrates that a healthy system, which already exhibits a pink noise structure, can respond to perturbations of the same structure without altering the inherent structure of the COP. This information could be useful for designing training protocols based on support surface translations.

Secondly, we examined the effect of support surface translations of varying temporal structures on the temporal structure of the resulting COP signal. The temporal structure of the COP time series demonstrated reduced complexity when the support surface translations had a reduced complexity (e.g. sine wave and white noise). Conversely, the temporal structure of COP did not demonstrate a change in complexity with either of the higher complexity (e.g. pink noise and brown noise) support surface translations. Even though the higher complexity conditions were not different from the “no noise” condition, they were different from each other. This is due to the pink noise input resulting in a lower DFA α-value and the brown noise input resulting in a higher DFA α-value. Although neither of these inputs produced enough of a response to be significant, the small changes drove COP variability in opposite ways enough to make the two sway responses different from each other. This is interesting because it demonstrates the adaptability of the system to respond to environmental changes of very specific structures.

Long-range correlations were used to describe postural control in response to the environmental variations. Long-range correlations provide a unique look into the temporal qualities of a time series. Movement patterns can be influenced by the memory of previous movements, and the current movements can influence future movements. Analyzing long-range correlations allows exploration of how movements on different time scales are related to each other. Stronger long-range correlations indicate that future movements rely more heavily on previous movements. In this study, stronger long-range correlations for postural sway indicates that the system has reduced degrees of freedom for maintaining posture and therefore sways in a very constricted manner. In comparison, weaker long-range correlations indicate that movements rely less heavily on the memory of past events. This means that the system has more available degrees of freedom to maintain posture and a low reliance on past events. The time scales for long-range correlations when using DFA depend on the sampling frequency and scaling region. The current study resulted in a time scale between 0.6 and 11.2 seconds. The scaling region of 3 to 56 resulted in a range from 300 boxes with 6 data points (0.6 seconds) to 16 boxes with 112 data points (11.2 seconds), along with all box sizes in between. Therefore, in this study the long-range correlations indicate how the root mean square fluctuations are related along the continuum from 0.6 to 11.2 seconds. To put this in perspective of what was stated regarding the available degrees of freedom, a rehabilitation protocol for training/retraining optimal postural control may involve support surface oscillations that have an inherent temporal structure – specifically it may have a DFA value that reflects this scaling region of 3 to 56, such that the resultant postural sway demonstrates Optimal Movement Variability.

Based on the theory of Optimal Movement Variability there is an optimal strength of long-range correlations that allows for information from previous movements to be used, but still allows flexibility in the movements. It has been well demonstrated that humans naturally exhibit a 1/f, or pink noise, structure in many biological processes,^{8, 28, 35} which will result in a DFA α-value of 1. This pink noise like structure would represent that optimal variability. Deviation from pink noise in either direction would indicate a system that is becoming unhealthy. A lower DFA α-value indicates a weakening of the long-range correlations, which means a decrease in the predictability, and a higher DFA α-value indicates a strengthening of the long-range correlations, which means an increase in the predictability. Both of these situations result in lowered complexity. In the current study we demonstrated that the postural control system in young participants was driven towards a less complex pattern when the support surface was translated according to a random signal (white noise) or a predictable signal (sine wave). In a healthy postural control system these changes in the long-range correlations of COP could indicate an adaptability that is used to respond to environmental changes encountered in the different conditions. When looking at the conditions in an increasing order of predictability the trend analysis revealed an inverted-u relationship, which would be expected based on the model of optimal movement variability. When comparing the predicted trend values to the experimental data there is less concavity with the experimental data, most likely due to the biomechanical constraints of the system. It is unlikely for a healthy system to move from a pink noise structure all of the way to a white noise structure. In order to avoid a loss of balance the system will maintain long-range correlations even when faced with white noise perturbations.

It is also possible that 1/f fluctuations are present in multiple components of the system, and the alteration of long-range correlations in the COP signal do not necessarily represent moving away from 1/f fluctuations in the whole system. This type of response has been noted when analyzing stride times during walking to a metronome.⁵ Walking to a metronome weakened the long-range correlations of the stride times, but when analyzing the asynchronies of the strides to the metronome the 1/f fluctuations were still present. This could mean the individuals are able to adapt to a walking pattern that exhibits weakened long-range correlations in one component but are able to maintain the long-range correlations in other components of the system. In the current study the weakened long-range correlations exhibited by the COP signals may be one component of the postural control system while 1/f fluctuations may have been maintained by other components such as neuronal firing rate or center of mass movements. Future research in this direction may reveal the presence of such phenomenon.

This research may have important implications for rehabilitation. In the current study the participants already exhibited a healthy temporal structure to their COP movement, and it was demonstrated that this structure could be affected with support surface translations of different levels of complexity. Because aging and disease result in an alteration of the 1/f fluctuations in several biological processes it may be beneficial to train individuals with a sensory input that more accurately reflects a healthy 1/f fluctuation. The next step is to test this concept with individuals who have an altered temporal structure in their COP, in order to restore a healthy variability of COP patterns in both acute and chronic situations. This provides advantages over current rehabilitation protocols where the complexity of temporal structure of a movement is not considered. It has been shown that when walking to a metronome the long-term memory of the movement pattern is lost^{11, 38} and the DFA α-value for several gait parameters is reduced,^{13, 14, 26} It is also common to test the effectiveness of a balance-training program by quantifying the amount of sway,^{9, 39} assuming that a reduction in sway is a positive outcome. The increased sway that is seen in aging and disease may actually be a protective mechanism. As the somatosensory input becomes reduced through peripheral neuropathy or other mechanisms, an increased sway may allow the individual to gain more sensory information about their position within the base of support. It is important to investigate more than just the amount of sway to get a complete understanding of the neuromuscular control involved in standing. Apparently healthy older individuals who exercised regularly have demonstrated increased amount of sway, but no changes in their temporal structure of sway.^{22, 25} This could indicate that they are exploring the boundaries of stance more, yet maintaining a healthy and organized structure within their movement patterns.

This study has some limitations. This research only applied the support surface translations in the anteroposterior direction and the resulting COP was analyzed in the anteroposterior direction. Support surface translations were chosen to be supra-threshold yet subtle so as not to induce a fall response. Because the mediolateral control of COP has been shown to be a moderate predictor of falls¹⁶ it would be beneficial to determine if these findings also translate to the control of mediolateral sway. The small sample size (n = 8) could be considered a limitation. However, based on the statistical analysis it was deemed sufficient to detect a large effect with certainty.

In conclusion, support surface translations driven by different temporal structures demonstrated the ability to alter the temporal structure of the COP time series in healthy young adults in the AP direction. Further work needs to be done in order to explore this phenomenon in individuals who have an unhealthy temporal structure to determine if these same effects can be demonstrated by restoring a healthy temporal structure to their COP time series. This has important implications for rehabilitation by improving existing training programs through the restoration of healthy variability in postural control.