A neural mechanism for sensing and reproducing a time interval

SUMMARY

Timing plays a crucial role in sensorimotor function. The neural mechanisms that enable the brain to flexibly measure and reproduce time intervals are however not known. We recorded neural activity in parietal cortex of monkeys in a time reproduction task. Monkeys were trained to measure and immediately afterwards reproduce different sample intervals. While measuring an interval, neural responses had a nonlinear profile that increased with the duration of the sample interval. Activity was reset during the transition from measurement to production, and was followed by a ramping activity whose slope encoded the previously measured sample interval. We found that firing rates at the end of the measurement epoch were correlated with both the slope of the ramp and the monkey’s corresponding production interval on a trial-by-trial basis. Analysis of response dynamics further linked the rate of change of firing rates in the measurement epoch to the slope of the ramp in the production epoch. These observations suggest that, during time reproduction, an interval is measured prospectively in relation to the desired motor plan to reproduce that interval.

INTRODUCTION

Timing is essential for many different aspects of brain function, from classical and instrumental conditioning to complex cognitive faculties such as coordinating thoughts and actions in humans [1–3]. A basic understanding of the neural basis of interval timing could shed light on how the brain integrates information about the recent past with plans for the near future, a process that is at the core of central information processing.

To incorporate knowledge about elapsed time into behavior, neural circuits must be able to measure and produce time intervals. These capacities are typically discussed under the rubrics of sensory timing and motor timing [4]. Animal models of interval timing in the sub-second to seconds range have focused on relatively simple tasks. Sensory timing tasks are typically concerned with the ability to anticipate a sensory event [5] or to categorize time intervals [6,7]. Motor timing tasks, on the other hand, focus on the ability to produce fixed time intervals in ongoing movements [8] or in actions learned through trace [9,10] and operant conditioning [11–14]. However, in many natural settings, sensory and motor aspects of timing are heavily intertwined. For example, in sports, music and imitation, humans continuously measure time intervals and use those measurements to control the timing of their actions. To investigate the mechanisms that flexibly link sensory and motor timing capacities, we developed a time reproduction task for rhesus monkeys in which the animals measured an interval demarcated by two time markers and reproduced it by a proactive saccade.

Neural mechanisms of interval timing engage multiple brain areas and are thought to depend on time scale [3,4]. In the sub-second to seconds range, where temporal processing is crucial for anticipation, prediction and planning in sensorimotor function, correlates of interval timing have been reported in higher cortical areas, the basal ganglia and the cerebellum [4]. We focused our work on the lateral intraparietal cortex (LIP), which is thought to play a central role in sensorimotor function [15–20], and where neurons represent elapsed time during both sensory [5,6] and motor timing tasks [13,21].

We found that single neurons in LIP conveyed information about the animal’s internal estimate of elapsed time during both measurement and reproduction of time intervals. The response profile associated with the measurement and production of time intervals were remarkably different yet linked such that modulation of activity during the measurement predicted the response dynamics during the ensuing production.

RESULTS

Behavior

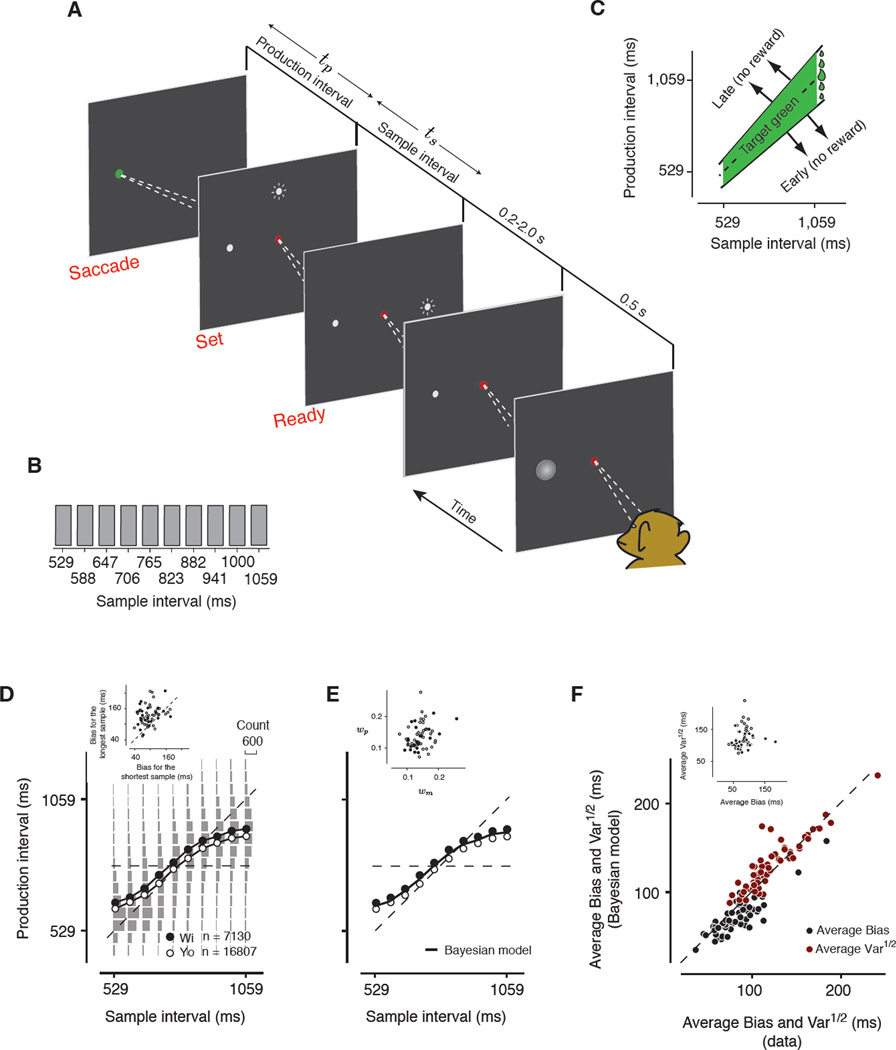
We trained monkeys on an interval reproduction task [22], which we refer to as the ‘Ready, Set, Go’ (RSG) task. The task (Figure 1A) consisted of two successive epochs. In the first ‘measurement epoch’, monkeys measured a sample interval, demarcated by two peripheral flashes, a Ready cue (‘Ready’ from here on) followed by a Set cue (‘Set’, from here on). In the immediately ensuing ‘production epoch’, monkeys had to reproduce the sample interval by making a self-initiated saccadic eye movement to a visual target (i.e., no explicit ‘Go’ cue was presented). On each trial, the sample interval was drawn randomly from a discrete uniform distribution ranging between 529 and 1059 ms (Figure 1B). We refer to this distribution as the prior. The production interval was measured as the interval between Set and when monkeys acquired the saccade target. In timing tasks, the variability of responses usually scales with the duration of the interval [1]. To compensate for this so-called “scalar variability”, the width of the window in which monkeys received reward scaled with the sample interval (Figure 1C). This manipulation made the task difficulty more or less the same for all the sample interval. To encourage animals to be as accurate as possible, the reward size was scaled as a function of accuracy (see Supplemental Experimental Procedures).

Figure 1. The Ready, Set, Go (RSG) task and behavior.

(A) Sequence of events during a trial. The monkey fixated a central spot. A saccade target was then presented in the response field (RF) of the neuron (gray zone) followed in succession by two transiently flashed peripheral cues (Ready followed by Set). The monkey then made an eye movement to the saccade target. To receive maximum reward, monkeys were required to time their saccade to the target so as to match the time interval between Set and saccade (production interval) to the interval between Ready and Set (sample interval). The target changed color to green on successful trials. (B) Sample intervals were drawn from a discrete uniform distribution with 10 values ranging between 529 and 1059 ms. (C) Reward schedule. The width of the window for which animals received liquid reward (green area) scaled with the sample interval (see Supplemental Experimental Procedures). The amount of reward within this window increased linearly with accuracy, as shown schematically by the size of liquid drops to the right. No feedback or reward was provided for production intervals outside the green region. (D) Production interval as a function of sample interval. Mean production intervals (open and filled circles) for the two monkeys (Yo and Wi) are plotted as a function of sample interval (SEM are smaller than the circles). Gray histograms show the distribution of production intervals for each sample interval for both monkeys. On average, production intervals deviated from the line of equality (diagonal dashed line) and towards the mean of the sample interval distribution (horizontal dashed line). The inset shows the magnitude of the bias for the longest sample interval (ordinate) versus the bias for the shortest sample interval (abscissa) across the 58 recording sessions for the two animals (open and filled circles). The magnitude of the bias was significantly larger for the longest sample interval (37.08+/−5.55 ms; t-test, p<1e–7). (E) The fit (solid line) of a Bayesian model to the behavior of the two monkeys. Data points are replicated from panel A. The inset shows the Weber fractions associated with measurement and production noise derived from the fit of the Bayesian model to each behavioral session (see Supplemental Experimental Procedures). (F) Comparison of the variability and bias of production intervals between the animals’ behavior and the Bayesian model across sessions. The bias (“average Bias”) was measured as the root-mean square of the production interval bias across all sample intervals. The variability (“average Var^1/2”) was similarly measured as the root-mean square of the standard deviation across sample intervals. The data shows that the average Bias (black) and the average Var^1/2 (red) predicted from the Bayesian model fits (ordinate) accurately captures the corresponding values derived from the animal’s behavior. The inset is a plot of average Var^1/2 versus average Bias for all behavioral sessions, showing that monkeys’ behavior was stable across sessions.

Production intervals increased monotonically with the sample interval (Figure 1D) and were more variable for longer sample intervals, which is consistent with the scalar variability of timing. However, production intervals exhibited systematic biases toward the mean of the prior distribution (horizontal line). The magnitude of the bias was larger for sample intervals at the long end of the prior distribution (Figure 1D, inset) where measurements are more variable (due to scalar variability). Following earlier work in humans [22], we found that this trade-off between bias and variance was accurately captured by a Bayesian model that optimizes performance by exploiting knowledge about the prior distribution to reduce the variability associated with uncertain measurements (Figure 1E,F).

Physiology

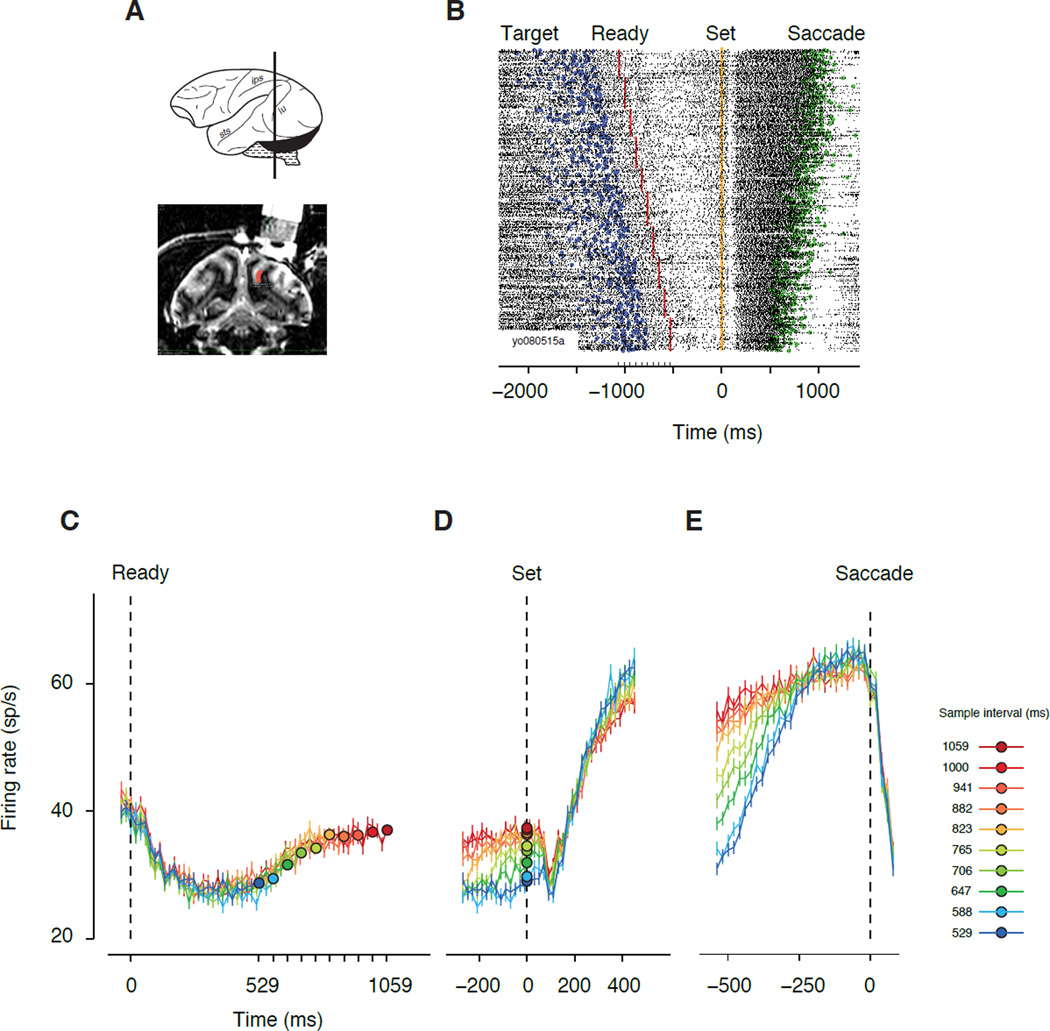
We placed the saccade target in the RF of individual LIP neurons and recorded their spiking activity as the animals performed the RSG task. Neural responses were modulated during the measurement epoch between Ready and Set, underwent a reset after Set, and increased before saccade initiation (Figure 2B). These observations were consistent across LIP and were readily evident in the population-average response profile (Figure 2C–E). After the appearance of Ready, which was well outside the RF, LIP responses initially declined and stayed low for approximately 500 ms, and then increased monotonically until Set was presented (Figure 2C). The appearance of Set, which was also flashed well outside the RF, triggered a dip in the activity followed by a monotonic rise (Figure 2D). Activity associated with the dip (100–250 ms after Set) did not vary significantly with the sample interval (regression; beta = 0.44, CI=[−9.33 10.21], p = 0.46). In the production epoch, LIP responses increased monotonically and reached a plateau shortly before saccade initiation (Figure 2E). At the plateau phase (100–250 ms before saccade initiation), responses did not vary significantly with the sample interval (regression; beta = −1.49, CI=[−12.82 9.83], p = 0.40).

Figure 2. LIP electrophysiology in the RSG task.

(A) Recording site. On top, a macaque brain is shown schematically along with a coronal plane through the intraparietal sulcus (ips). The bottom panel shows the structural magnetic resonance image of a coronal section of one of the monkeys (Yo) after the placement of the recording cylinder. All recorded neurons were within the ventral portion of area LIP along the lateral bank of the ips (red). (B) Raster plot of the spiking activity of a single neuron from before the onset of the saccade target through completion of the saccadic eye movement. Each trial is displayed as a row of spikes (black tics) aligned to the time of Set. Colored symbols mark the times of target onset (blue), Ready (red), Set (orange), and when the saccade reaches the target (green). Trials are sorted by duration of the sample interval; the order was random in the experiment. (C) Response averages (N=58) aligned to the onset of Ready. Sample intervals are indicated by colors (see legend at E). Each trace terminates at the time of the corresponding Set, indicated by a filled circle. After an initial decline, activity increased monotonically with elapsed time. (D) Response averages aligned to the time of Set. After Set, responses underwent a stereotyped dip and then diverged according to the sample interval. Filled colored circles are identical to those in A. (E) Response averages aligned to the time of saccade. Firing rate increased towards a common plateau approximately 200 ms before saccade initiation. The build-up of firing rate was shallower for longer sample intervals.

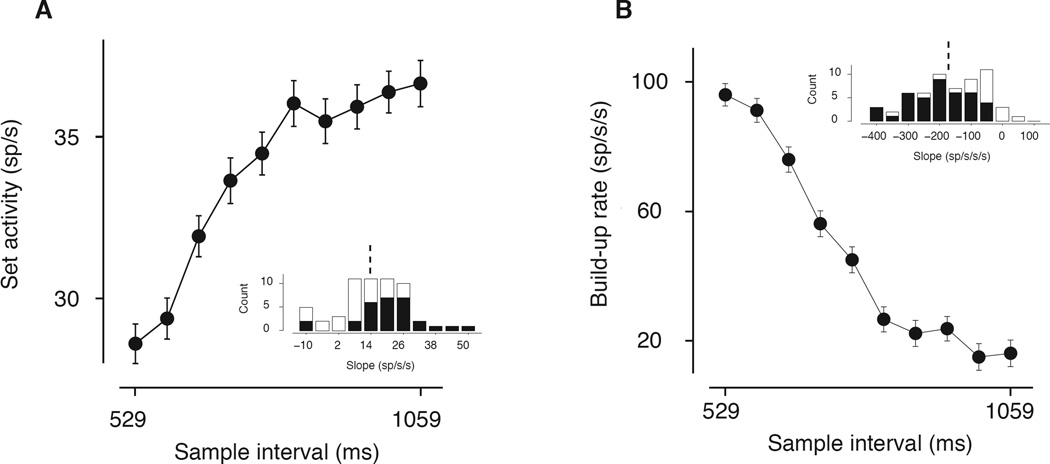
Our initial analysis focused on two time windows, (1) an interval near the time of Set, and (2) an interval between Set and saccade. The average firing rate near the time of Set (from 50 ms before to 50 ms after Set) increased monotonically with sample intervals (Figure 3A), both across the population (regression: beta =17.90 sp/s/s, CI=[10.92 24.87], p <1e–6) and for 22/58 individual neurons (t-test, p<0.05). In the interval between Set and saccade, the build up rate (estimated 200–500 ms before saccade time) was progressively shallower for longer sample intervals (Figure 3B) both across the population (regression: beta = −144.62 sp/s/s/s; CI=[−164.15 −125.09], p <1e–10), and for 40/58 of individual neurons (t-test, p<0.05). These analyses indicate that both the activity near the time of Set and the following ramping activity (i.e., linear increase of firing rates) during the production epoch provide a correlate of the sample interval.

Figure 3. Representation of the sample interval in the RSG task in LIP activity.

(A) Average firing rate from 100 ms before to 50 ms after Set (Set activity), as a function of sample interval. Firing rate near the time of Set increased monotonically with elapsed time. Error bars are SEM (N=58 neurons). For each neuron, we computed the slope of the regression line relating Set activity to sample interval. Inset histogram shows the distribution of slopes across 58 neurons. Dashed line indicates the mean regression slope; filled bars indicate slopes significantly different from zero (regression; t-test, p<0.05 for 22/58 cells). (B) Average build-up rate of the neural response from 500 to 200 ms before the saccade, as a function of sample interval. The build-up was more gradual with longer sample intervals. Error bars are SEM (N=58 neurons). Inset histogram shows the distribution of regression coefficient in a linear regression of the build-up rate against sample interval for 58 neurons. Dashed line indicates mean; filled bars indicate slopes significantly different from zero (regression; t-test, p<0.05 for 40/58 cells).

Linking neural activity to behavior

To assess the link between the neural activity and behavior, we first focused on the production epoch. Computing a reliable estimate of the build-up rate from spike times of individual neurons in single trials is challenging. To tackle this problem, we modeled the ramping activity by a non-homogeneous Poisson process with a linear rate function, and used the spike times 200–500 ms before saccade time to estimate the linear rate function, which corresponds to the slope of the build-up rate. Using this estimate, we found a significant negative correlation between the build-up rate and the production interval for every sample interval (correlation coefficient = −0.26 ± 0.04 [mean ± s.e.], p<0.005 for all 10 intervals). Importantly, the correlation analysis was performed for each sample interval independently so that the pairwise relationships could not be attributed to an indirect effect of the sample interval on the firing rates and the behavior (see Figure S1 for an alternative analysis combining values across all trials). This significant negative correlation indicates that, for every sample interval, trials with a steeper build-up rate were followed by shorter production intervals, consistent with previous electrophysiological recordings in motor timing tasks [12,21,23–26].

We then asked whether the activity in the measurement epoch predicts the build-up rate in the production epoch. We measured the trial-by-trial correlation between the build-up rate and the activity at the time of Set, and found that the quantities were negatively correlated for every sample interval (correlation coefficient = −0.23+/−0.02 (mean ± s.e.), p<1e–6 for all 10 intervals). Again, by performing the correlation analysis for each sample interval independently, we ensured that the pairwise correlation was not due to an indirect effect of the sample interval (see Figure S1 for an alternative analysis combining values across all trials). Moreover, this correlation was not explained by a autocorrelation in LIP firing rates within a trial because there was no significant correlation between build-up rate and LIP activity early in the measurement epoch or during the dip after the Set (p>0.05).

The results from the simple pairwise correlation analyses is consistent with a model in which the sample interval controls the activity at the time of Set (Figure 2D, 3A), which in turn sets the build-up rate (Figure 2E, 3B), which in turn forecasts the saccade initiation time. However, with four interrelated variables (sample interval, Set activity, build-up rate and production interval), it is important to ascertain that pairwise correlation between any two variables is not explained by their association with the other two variables. Thus, we performed a partial correlation analysis looking at the strength of association between each pair of variables while the variation in the other variables are accounted for – for example, the correlation between build-up rate and the production interval while accounting for the sample interval and Set activity. Table 1 shows the magnitude of the simple pairwise correlations (top right; black) and pairwise partial correlations (bottom left; red). The results of the partial correlation analysis upheld the original results about the linkage between (1) the sample interval and Set activity, (2) the Set activity and the build-up rate, and (3) the build-up rate and the production interval. This analysis also led to two additional findings. First, the association between sample interval and build-up rate was greatly diminished were accounted for. Second, the correlation between Set activity and production interval was no longer statistically significant after accounting for build-up rate and sample interval. Both of these observations strengthen the interpretation of the pairwise correlations in terms of an association between the build-up rate with the production interval, and an association between the Set activity with the sample interval.

Table 1.

Simple and partial pairwise correlations between the sample interval, the activity near the time of Set (Set activity), the build-up rate prior to saccade initiation and the production interval.

	Sample interval	Set Activity	Buildup rate	Production interval
Sample interval		0.13*	−0.27*	0.62*
Set Activity	0.07*		−0.26*	0.11*
Buildup rate	−0.04*	−0.23*		−0.37*
Production interval	0.58*	−0.03	−0.26*

The pairwise correlations are shown in the upper right triangle of the table, and the partial correlations in the bottom left triangle (bold). The partial correlation between each pair of variables is measured after accounting for the effect of the other two variables.

The asterisks (*) correspond to correlation values that are significantly different from zero (p<0.01). The diagonal values correspond to correlation of a variable with itself, and are left blank.

Response dynamics in LIP

LIP responses preceding saccade initiation increased approximately linearly (Figure 2E). This ramping activity is consistent with an increase in the salience of the saccade target [27,28] mediated by an evolving motor plan [21] or an expectation of reward [18]. In contrast, the response dynamics in the measurement epoch (Figure 2C) is unexpected. In this epoch, neither the motor plan nor the reward times were known before the appearance of Set. More specifically, it is unclear why the responses underwent a slow and prolonged suppression until approximately 500 ms after Ready and why they increased with a decelerating nonlinearity until the time of Set.

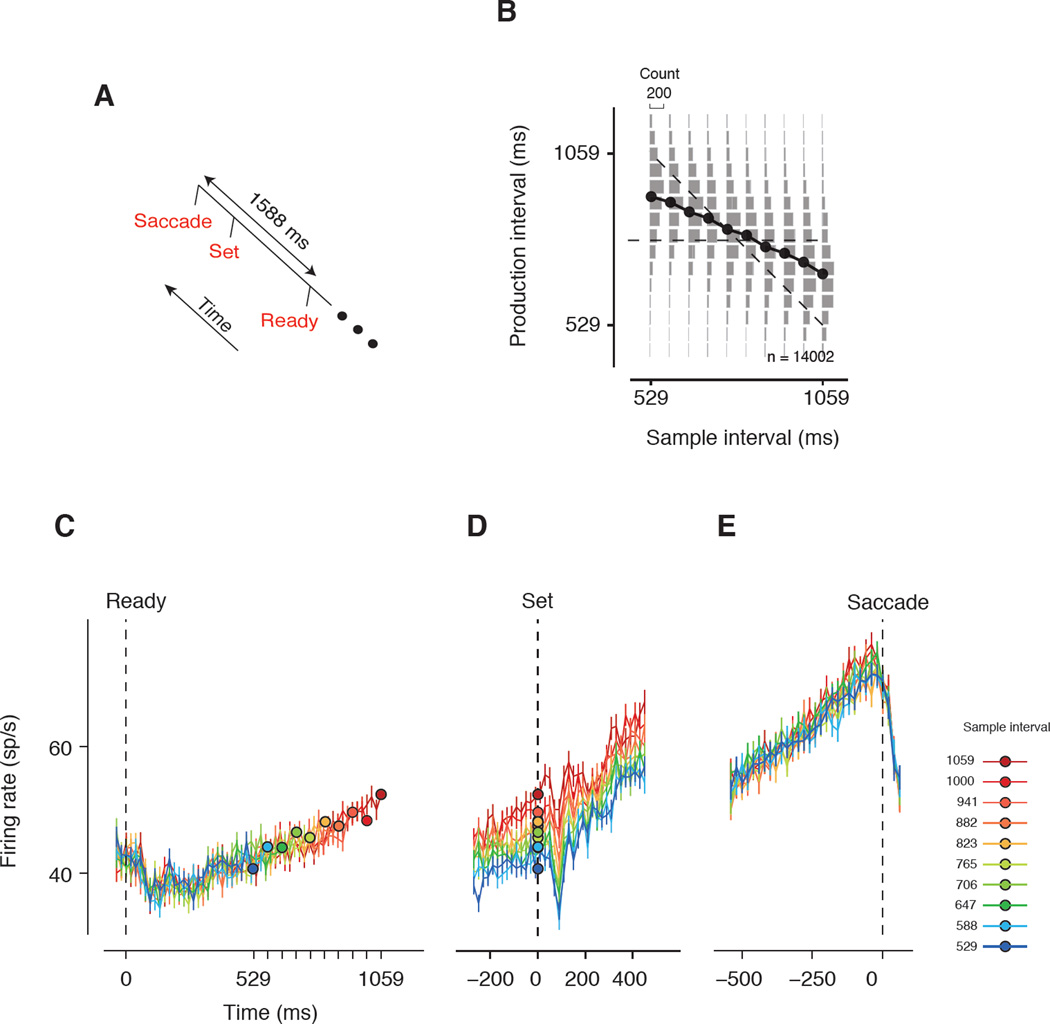
One possibility is that LIP response dynamics are explained by modulations of attention, induced by the sensory and motor events in the task, irrespective of computations needed for interval reproduction. For example, visual flashes could modulate exogenous attention. Similarly, the firing rate dynamics after Ready could be due to a slow shift of endogenous attention to the saccadic target. To examine these possibilities, we designed a control task, which we refer to as the Ready-Go (RG) task (Figure 4). The sequence of events in the RG task were identical to the RSG task: fixation followed by the presentation of Ready and Set (demarcating an interval sampled from the prior), followed by a proactive saccade to a visual target, followed by reward for accurately timed saccades. However, in the RG task, monkeys had to produce a fixed 1588 ms interval from the time of Ready, irrespective of when Set was presented (Figure 4A). Importantly, the RG task maintained the spatial and temporal structure of sensory and motor events but inverted the relationship between the duration of two epochs: the longer the interval between Ready and Set, the shorter is the remaining interval to the fixed 1588 ms. Accordingly, if LIP responses were explained by modulations of attention due to sensory and motor events, we would expect to see the same response dynamics in the two tasks.

Figure 4. The Ready, Go (RG) control experiment.

(A) Task design. The animal had to make a saccade to visual target 1588 ms after Ready. To make the sensory events of the RG and RSG tasks identical, a Set cue was also presented in the RG task. The interval between Ready and Set was drawn randomly from the same distribution used in the RSG task (Fig, 1B). (B) Animals’ behavior in the RG task. The behavior is plotted in the same format as in the RSG task (Figure 1D); i.e., the Set-saccade intervals as a function of the Ready-Set interval. In this task, maximum reward was given when the Ready-saccade interval (i.e., the sum of the Ready-Set and Set-saccade intervals) was 1588 ms (anti-diagonal). As expected, the Set-saccade intervals were on average shorter for longer Ready-Set intervals. However, saccade times exhibited systematic biases away form the anti-diagonal. (C–E) The time course of average population activity (N=39) plotted in the same format as in Fig. 2C–E.

Both monkeys learned the RG task, as evidenced by the inverted relationship between the duration of the two epochs: the interval between Set and saccade was progressively shorter for longer Ready-Set intervals (Figure 4B). There were, however, systematic biases away from the target 1588 ms. In particular, saccades were initiated earlier when Set occurred shortly after Ready, and later when Set occurred at a longer interval. This counterintuitive observation is predicted by a Bayesian model similar to the RSG task in which knowledge about the prior distribution of the time of Set helps to reduce variability and improve performance (Supplemental Experimental Procedures).

In the RG task, LIP activity began to rise shortly after Ready (Figure 4C), underwent a transient dip after Set (Figure 4D), and continued its climb to a maximum firing rate shortly before saccade initiation (Figure 4E). Notably, responses increased with an approximately constant build-up rate in both Ready-Set and Set-saccade epochs. The response dynamics in the RSG and RG tasks differed in two important ways (Figure 5). First, the responses immediately after Ready were remarkably different. Unlike the RSG task where responses were suppressed for nearly 500 ms, in the RG task, responses underwent a rapid dip and recovery, which was similar to how LIP responses changed after Set in the RSG task. Second, unlike in the RSG task, where responses increased nonlinearly 500 ms after Ready, in the RG task, responses exhibited a ramp-like activity with firing rates increasing linearly until the time of Set. The linear rise of activity before Set in the RG task was similar to the ramping activity of the RSG task before saccade initiation.

Figure 5. Comparison of LIP responses in the RSG and RG tasks.

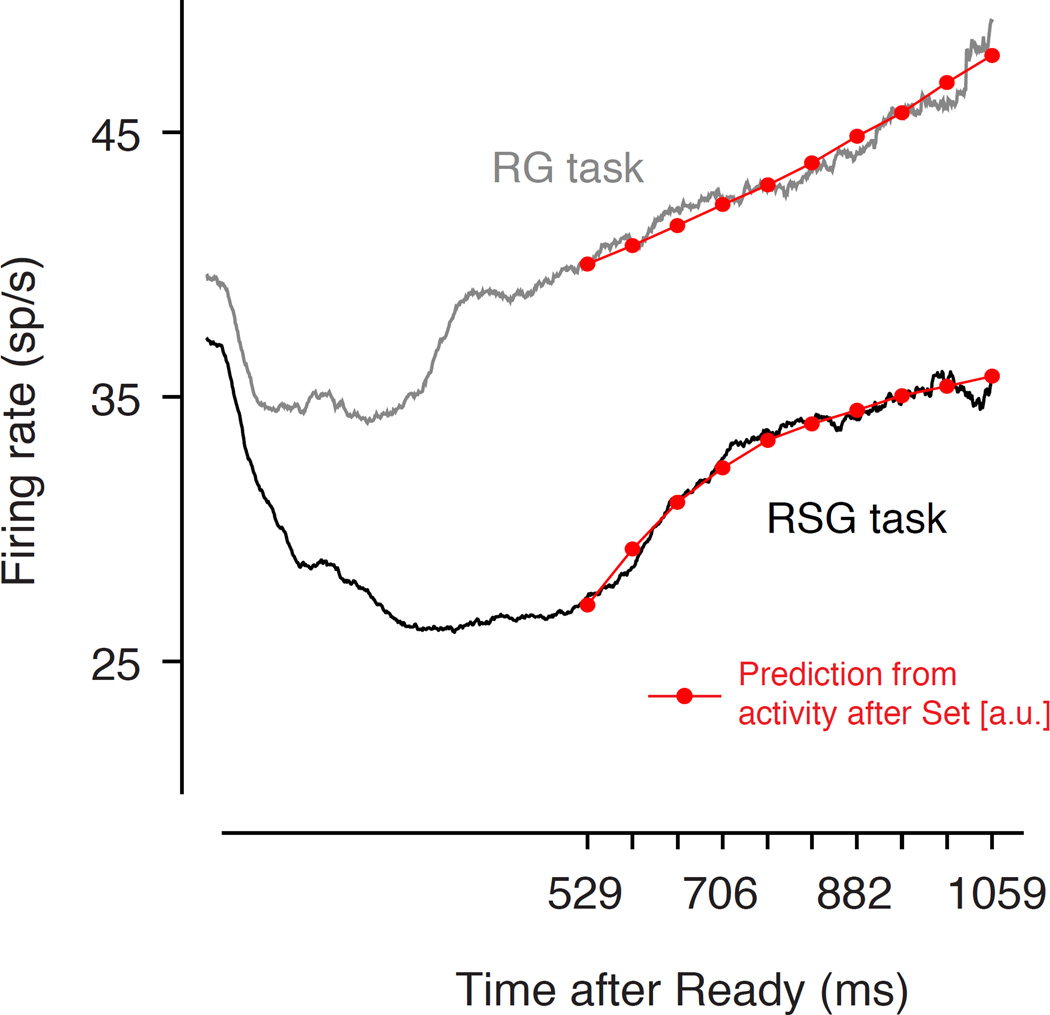
The black and gray traces show the average LIP activity between Ready and Set in the RSG and RG tasks, respectively. The spike train from each trial was convolved with a 50 ms boxcar filter, and the smoothed firing rates were used to compute a running mean across neurons and trials that combined all spikes elicited after Ready and before 50 ms after Set. The superimposed red curves are fits based on the preplanning model. Each red trace is a piecewise linear function with 10 line segments (for 10 sample intervals). The slope of each line segment was derived directly from the corresponding ramping activity in the production epoch. Specifically, the slope of the line segment between each pair of consecutive sample intervals, t_i and t_i+1, was equal to the slope of the ramping activity associated with reproducing t_i. We then used linear regression (i.e., two parameters: offset and scaling) to fit this piecewise linear function to LIP firing rates.

Importantly, the differences between the response dynamics in the two tasks are not explained by a difference in the baseline activity or response gain of the recorded neurons, as evidenced by the similar average firing rate in both tasks early in the measurement epoch (Figure 5). Since the RG and RSG tasks had identical sensory and motor components, the striking differences in firing rate modulations associated with the two tasks rule out an interpretation of the prolonged suppression in the RSG task in terms of low-level sensory interactions or a gradual shifts of attention from Ready to the RF in anticipation of the saccade. Instead, the differences in firing rate dynamics must be related to the differences in temporal demands of the two tasks: in the RG task, the desired production interval (1588 ms) was known through the trial, whereas in the RSG task, the desired interval changed depending on the time between Ready and Set.

Computational models of response dynamics in the measurement epoch

We considered several computational models to explain the response profile in the measurement epoch of the RSG task. Each model sought to predict the observed dynamics based on the dynamics of a candidate variable such as the anticipation of Set or the anticipation of reward. In all models, we allowed ourselves the freedom to scale and offset the predicted dynamics to fit the neural data. This procedure ensures that the nonlinearities in the neural data could only be explained by the variable of interest and not the model parameters (see Supplemental Experimental Procedures).

1. Anticipation of Set

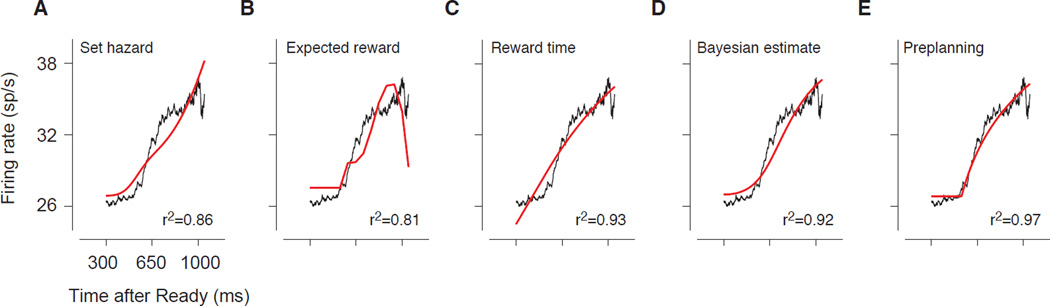
The earliest time when Set was presented was 529 ms, which matches the observed 500 ms delay in the rise of LIP responses after Ready. Based on this observation and motivated by previous work [5,29], we asked whether LIP responses represent a hazard function of the time of Set (the probability that Set will occur now, given that it has not yet occurred). As evident from Figure 6A, the best fit of this model is inadequate since the hazard function associated with a uniform prior distribution increases expansively, whereas LIP firing rates exhibited a compressive nonlinearity.

Figure 6. Model comparison.

Comparison of the activity profile in the RSG task (black traces, same in all panels) from 300 ms after Ready to the time of the latest possible Set with predictions of different models (red). The models are constructed as a linear function of (A) the subjective hazard of the Set, (B) the expected reward, (C) the expected time of reward, (D) the Bayesian estimate of the sample interval, and (E) the preplanning model in which the instantaneous slope predicts the slope of the corresponding ramping activity in the production epoch.

2. Anticipation of Reward

Since reward expectation modulates LIP activity [18], we asked whether the observed response dynamics represent the probability of expected reward. Since the animal never received reward before the time of Set, we can reject the strongest form of this hypothesis–that firing rates represent the instantaneous probability of reward. However, we considered a more nuanced version of this hypothesis in which the firing rate before Set represents the probability that the animal will receive reward at the end of that trial (see Supplemental Experimental Procedures), which we estimated directly from the average reward the animal received. The response dynamics predicted by this model also do not match the observed LIP dynamics (Figure 6B).

3. Anticipation of the expected time of reward

This is a timing model, but one in which firing rates adopt a slope that is predictive of the expected time (as opposed to the probability) of reward. This scheme was motivated by the observation of response dynamics in the production epoch of the RSG task where the buildup rate was adjusted such that the ramping activity reached a terminal firing rate shortly before the expected time of reward. We formulated this model by a first order linear differential equation that adjusts the instantaneous slope of firing rate according to the expected time of reward (see Supplemental Experimental Procedures). As shown in Figure 6C, this model predicts a decelerating response dynamics after 529 ms, which is consistent with our data. However, it additionally predicts a linearly rising activity in the early part of the measurement epoch, which is similar to what we observed in the RG task (Figure 4C), but not in the RSG task.

4. Bayesian estimate of the sample interval

Our analysis of behavior showed that the production interval was based on a Bayesian estimate of the sample interval (Figure 1E,F). This finding motivates a model in which the activity during the measurement epoch reflects the the Bayesian estimate of the sample interval. This idea is appealing because the Bayesian estimate is bounded by the range of the prior distribution, which could explain the ~500 ms delay in the rise of responses after Ready. Moreover, the Bayesian regression toward the mean of the prior might explain the nonlinear response dynamics beginning ~500 ms after Ready. As evident in Figure 6D, this scheme is broadly consistent with a rise of firing rates after approximately 500 ms and the decelerating nonlinearity, albeit somewhat different from the LIP response profile. This difference, however, might be due to our particular implementation of the Bayesian model (see Discussion).

5. Preplanning the production dynamics

A simple observation from LIP response dynamics is that both the instantaneous slope of the activity as a function of sample interval before Set, and the slope of the ramping activity after Set decrease progressively with longer sample intervals. We therefore considered a “preplanning” hypothesis in which the slope of activity in the measurement interval is predictive of the slope of activity in the production epoch. This is an attractive computational strategy as it obviates the need to rapidly compute the build-up rate during the transition between the measurement and production epochs. Based on this scheme, the instantaneous slope of activity at the time of Set should provide an estimate of the build-up rate after Set. To test the hypothesis, we constructed a model in which the instantaneous slope of activity at the time of Set was linearly related to the build-up rate after Set (Experimental Procedures). This model captures the response dynamics in the measurement epoch better than the other models we considered (Figure 6E).

The preplanning model has the additional virtue that it provides a common framework to explain responses in both the RSG and RG tasks. To demonstrate this point, we developed a data-driven analogue of the preplanning model is which we aimed to fit the firing rate dynamics prior to Set based on the observed slope of the ramping activity after Set. To do so, we constructed a piecewise linear function in which the slope of each line segment was derived directly from the corresponding slope after Set. As shown by the red traces in Figure 4, the piecewise linear functions constructed in this way matched the observed response dynamics for both tasks remarkably well (R²=0.98, and 0.95 for RSG and RG tasks, respectively). This result indicates that the response profiles before Set in both tasks are consistent with the preplanning hypothesis.

DISCUSSION

Previous animal studies of interval timing have mainly focused on either sensory or motor aspects of timing [4]. To understand the mechanisms by which sensory and motor aspects of timing are coordinated, we recorded neural activity in area LIP of monkeys performing a time interval reproduction task. Monkeys reproduced time intervals by making saccades toward a visual target inside the RF of individual neurons in area LIP. As many previous studies have shown, this experimental design exploits the spatial tuning of LIP neurons to investigate the computational mechanisms of various cognitive functions such as anticipation, planning and decision making [13,18,28,30–33]. Here, we adapted this scheme to study the neural computations associated with time interval reproduction.

LIP firing rates in both measurement and production epochs were modulated by the sample interval, and the trial-by-trial fluctuations of neural activity in both epochs were predictive of the fluctuations of animals’ production intervals. Our partial correlation analyses (Table 1) supports the presence of associations between (1) the sample intervals and firing rates in the measurement epoch, (2) the firing rates in the measurement epoch and the ramping activity in the production epoch, and (3) the ramping activity in the production epoch and the production intervals.

Response dynamics

In the production epoch, firing rates leading up to the saccade increased linearly and reached a fixed plateau regardless of the duration of the sample interval. This observation was reinforced by the RG control experiment. There, the ramping activity began shortly after Ready, which is consistent with the fact the animal knew the desired interval irrespective of when Set was presented. These observation are not surprising as ramping activity in anticipation of a potentially rewarding motor response has been observed in many previous reaction-time and self-timed tasks [12,21,23–26,34–36]. This pattern of activity might either be related to the anticipation of an imminent reward or might reflect an ongoing saccadic motor plan.

The second, more surprising observation was the discovery of an evolving signal during the measurement epoch of the RSG task. In this epoch, responses began to rise approximately 500 ms after Ready and increased monotonically until the time of Set. Our first concern was that these features might be explained by low-level sensory responses, or by attentional modulations during the trial. To evaluate those possibilities, we designed a control (RG) task that comprised the same exact sensory and motor elements, and compared responses in the Ready–Set interval. We found striking differences between the response in the RSG and RG tasks that were not explained by differences in baseline activity or gain differences (Figure 5). More generally, no linear transformation of average firing rates could explain the the difference between the profile of the firing rate dynamics in the two tasks. This observation suggest that the activity during the Ready-Set interval of the RSG task is unrelated to low-level stimulus-driven interactions, and cannot be explained by a gradual shift of attention to the location of Set or the saccade target.

We then formulated a series of models that sought to explain the response dynamics in the measurement epoch in terms of anticipation of Set or reward. Anticipation of Set is captured by a hazard-like function of Set time [5] predicts an accelerating nonlinearity—opposite to the decelerating nonlinearity observed in the data (Figure 6A). A model based on experienced reward [17,18] also failed because the probability of reward as a function of time did not match the LIP response profile (Figure 6B). A third model that tested the response dynamics against an anticipation of the time of reward (or the time of saccade, which occurred at the same time in our study) could predict the decelerating nonlinearity in the measurement epoch of the RSG task (Figure 6C). However, it additionally predicts that LIP responses should exhibit identical ramping activity in the first 500 ms of the RG and RSG tasks, which is not supported by data. In sum, although LIP responses are likely to be influenced by sensory, motor or reward anticipations, our modeling results render it highly unlikely that these functions explain LIP response dynamics during the measurement epoch of the RSG task.

Two novel hypotheses: Bayesian estimation and preplanning

LIP responses in the measurement epoch of the RSG task cannot be interpreted as a direct measure of elapsed time because firing rates do not increase monotonically with time until approximately 500 ms after Ready. According to our analysis of behavior, production intervals were based on the Bayesian estimate of the sample interval. We therefore developed a model that tested whether LIP responses in the measurement epoch were consistent with a Bayesian estimate of the sample interval. This model, like the model associated with the hazard rate of Set, explains the ~500 ms delay in the rise of response after Ready, and it additionally predicts a decelerating nonlinearity thereafter (Figure 6D). Although the exact predicted profile was somewhat different from LIP activity, we think that this model deserves further investigation. In our implementation of the Bayesian estimator, we assumed that the animal has accurate knowledge about the prior distribution of sample intervals and uses a least square cost function. It may be that an alternative implementation with more realistic assumptions about the prior and cost function could capture the observed dynamics more accurately. Future experiments involving multiple prior distributions will provide a critical test for this possibility.

The last model we considered was motivated by the observation that both the instantaneous slope of responses before Set and the slope of the ramping activity after Set decreased with longer sample intervals. We therefore developed a preplanning model in which the instantaneous slope of the response during the measurement epoch anticipates—or pre-plans—the buildup rate of the ensuing ramp after the Set and dip in activity. In this model, it is expected that LIP activity begins to rise with an initial slope when the earliest Set is anticipated (529 ms), and the slope is reduced dynamically to adjust for the attenuated buildup rate needed for producing longer production intervals. For this scheme to work, the brain must possess implicit knowledge of (i) the fixed delay between Set and the beginning of the ramping activity, (ii) the difference in firing rate at the beginning of the ramping phase and some threshold level, and (ii) the fixed delay between when responses reach a terminal point and saccade initiation. When we estimated these values from the average LIP activity, we found that the preplanning model was able to capture the observed LIP response profile quite well (Figure 6E). Moreover, this model readily explains the response dynamics in both RSG and RG tasks, as evidenced by the quality of fits derived directly from slopes of ramping activity after the Set (Figure 5, red). To test this model more definitively, we must record from multiple neurons simultaneously to have a more accurate estimate of the instantaneous slope on single trials.

Unresolved questions

One of the notable features of firing rate dynamics is the presence of a strong and transient suppression after Set in the RSG task. The function of this so-called dip, which has been observed in different oculomotor areas [24,37–39], is unclear. In our work, the dip transiently masks the information about the interval, and it is not clear how this information reappears after the dip. The suppression during the dip may be due to a temporary shift of exogenous attention to Set [40]. However, regardless of the source of this suppressive effect, the recovery of signal after the dip implies that either the recurrent networks in LIP can maintain an estimate of the build-up rate through the externally triggered suppression, or the signals associated with the build-up rate are available in other brain areas that do not undergo such strong suppression, or the maintenance of the information in mediated by an intrinsic cellular mechanism [41].

An important issue is whether LIP plays a causal role in interval timing or whether it is modulated indirectly through anatomical connections that support functions other than timing [5,6,13,15,18–21,28,42–48]. Without a careful causal manipulation, we cannot distinguish between these two possibilities, nor can we rule out a third possibility that LIP neurons multiplex behaviorally relevant variables [49] including time [5,6]. Regardless however, our analysis of how LIP signals in the measurement epoch seem to pre-plan the build-up rate in the production epoch raises the speculative but intriguing hypothesis that the sense of time could be established through an embodied scheme that models the parameters of a motor plan.

EXPERIMENTAL PROCEDURES

General procedures

Behavioral protocols, animal care and surgical procedures were all in accordance with the US National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the University of Washington Animal Care Committee. We recorded from 97 well-isolated LIP neurons in the ventral portion of area LIP (LIPv) in the right hemisphere of two monkeys (Yo and Wi), 58 in the RSG task (35 in Yo, and 23 in Wi), and 39 in the RG task (26 in Yo, and 13 in Wi). We analyzed the behavior using a Bayesian model following earlier work [22]. Population, single-cell, and single-trial analyses were based on either the average firing rates (e.g., at the time of Set), or the change of firing rate per unit time (e.g., buildup rate before saccade initiation). General experimental procedures, behavioral tasks, electrophysiological recording technique, data analysis, and mathematical models are described in detail in the Supplemental Experimental Procedures.